引 言
超材料是一种具有人工周期性设计的复合材料, 它具有天然材料所不具备超常物理特性[1-4]. 例如, 由亚波长结构组成的声学超材料具有可以抑制声波或弹性波传播的带隙[5]. 超材料的应用主要包括机械波衰减[6-8]、低频隔振[9-11]和能量采集[12-13]等. 实际的工程中, 如一些特殊工况下(飞行器帆板、飞机机翼的支撑板等)不仅需要对特定频率范围内的振动进行隔离, 而且需要将有害振动产生的能量转换为电能, 以达到检测传感器供能的目的. 因此, 本文研究的重点是设计振动隔离和能量采集相结合的双功能超材料, 在隔振的同时, 把有害的振动能量转换为可用于电力设备的更有用的电能[14-16]. 然而到目前为止, 关于振动隔离和能量采集相结合的双功能超材料[17-19]的研究很少.
由于低频处的振动对工程构件的损耗最大, 所以低频振动隔离问题一直是许多****研究的热点. 最近, Yu等[20]报道了Timoshenko梁与局部谐振器的横向振动试验, 并实现了其横向振动的隔离. EI-Borgi等[21]对具有多个共振频率的超材料进行了试验, 扩大了隔振频率范围. Hao等[22]设计了弯曲波激励下的多跨超材料梁, 这拓宽了带隙的频率范围, 表明隔振性能有所改善. Park和Jeon[23]提出了一种用于横波的具有宽低频带隙的锥形超材料梁, 它改善了宽带和低频特性. Li和Wang[24]将多个谐振器放置在一个双周期排列的系统中, 以在低频范围内构建具有指数纵波隔离带隙的超材料. Sharma和Sun[25]研究了低频波在具有周期性嵌入谐振器的夹层梁中的传播行为, 发现了带隙之间的相互作用, 从而进一步拓宽了带宽. Wang等[26]在Euler-Bernoulli梁中放置横向局部谐振器, 以产生多个横向带隙, 从而抑制横波的传播. Hu等[27]交替地将固有频率不同但质量相同的周期谐振器连接到梁上, 并通过调整频率间隔来减少振动的传播, 从而获得宽带隔离范围. 然而, 将低频振动从超材料主体上转移到谐振器之后, 振动的能量并未对其进行回收利用.
目前, 对于超材料的研究, 考虑到实际工程应用中的环境, 许多****设计了具有多个功能相结合的超材料. Li等[28]通过将非球形纳米颗粒植入圆柱形结构中, 设计了一种用于热隐身和电隐身的双功能超材料. Shen等[29]通过将形状记忆合金和各向同性材料组装在一起, 设计了一种用于热斗篷和聚光器的双功能超材料. Maldovan[30]设计的热声超材料成功地实现了波隔离和热流导向功能. Sugino和Erturk[31]在超材料悬臂梁振子上黏贴压电片实现了对振动的能量采集.
受上述研究的启发, 为了在低频隔振的同时, 对隔离的振动能量进行采集, 本文设计一种低频振动隔离和能量采集的双功能超材料, 将有害振动产生的能量转化为电能为无线传感器等低功耗电器供电. 将固接了感应线圈的滑动球摆周期性阵列在基体梁上的球形磁腔内, 以实现振动隔离和能量采集的统一. 首先建立了双功能超材料梁在横向激励下的动力学方程, 应用Bloch’s定理得到了超材料的能带关系, 对其进行有限元分析, 并设计了横向激励超材料的试验, 验证了超材料的带隙内振动隔离特性; 最后, 对二维双功能超材料的低频振动隔离和能量采集性能进行了研究.
1.
双功能超材料梁的设计
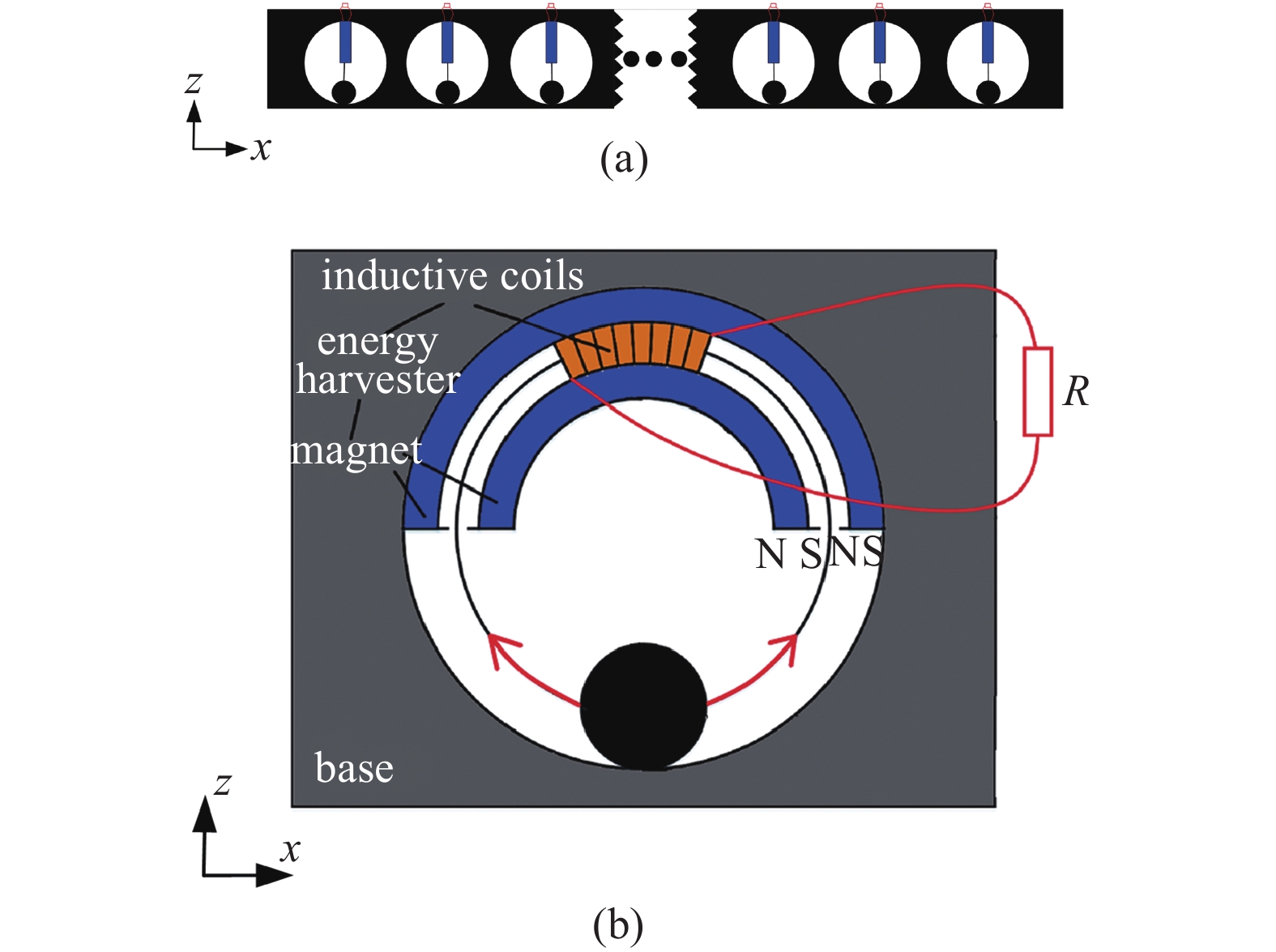
本节对双功能超材料梁进行建模和分析, 通过将带有球型空腔的梁基体与带能量采集功能的球摆型谐振器相耦合, 以实现低频隔振和能量采集的功能性统一. 双功能超材料梁的示意图如图1(a)所示, 附加的带有能量采集功能谐振器如图1(b)所示. 将带有能量采集功能的球摆型谐振器被放置在具有周期性排列球形腔的超材料梁上, 当弹性波在双功能超材料中传播时, 会在谐振器处产生局域共振现象, 从而阻止弹性波的传播, 实现振动的隔离. 当超材料梁受到激励时, 滑动小球在球腔内表面来回滑动, 同时驱动感应线圈切割磁场, 产生电能.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
(a) 双功能超材料模型图; (b)带能量采集功能谐振器模型图
Figure
1.
(a) View of the dual-functional metamaterial; (b) a spherical pendulum energy harvester
下载: 全尺寸图片
幻灯片
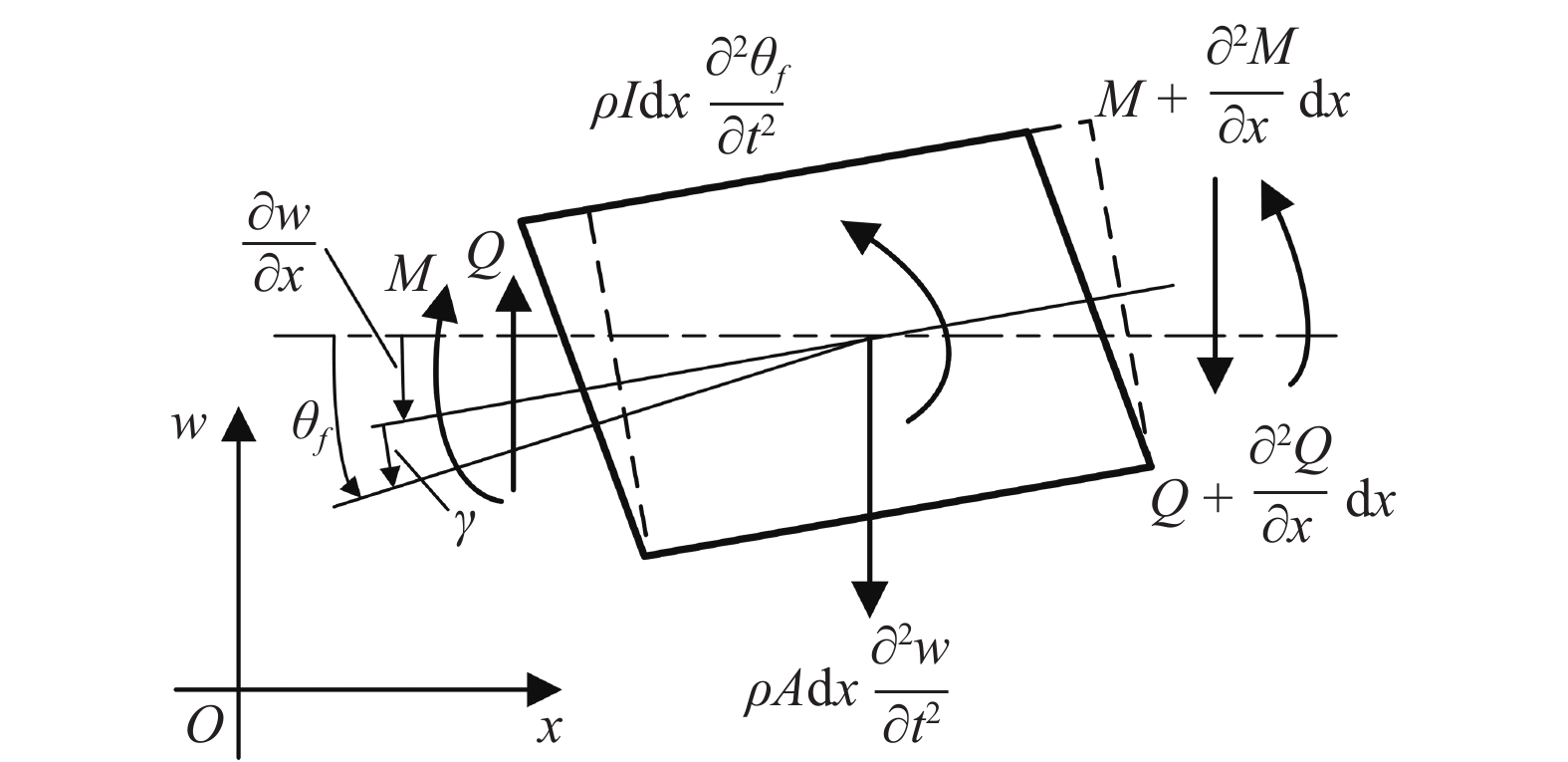
本文所研究超材料的主要部分是一个无限长梁, 当高长比小于1∶5的梁受到横向激励时, 需要考虑横截面中性轴转动惯量的影响. 如图2所示, 超材料梁的典型晶胞单元在本研究中可以等效为Timoshenko梁.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
超材料典型单胞的微元分析图
Figure
2.
The infinitesimal analysis of Timoshenko beams
下载: 全尺寸图片
幻灯片
将超材料梁等效Timoshenko梁, l为梁单元长度, A为梁截面面积, I为梁截面转动惯量,
ho $
$$ {theta _f}(x,t) = frac{{partial w(x,t)}}{{partial x}} + gamma (x,t) tag{1a}$$  |
$$ M(x,t) = EIfrac{{{partial ^2}w(x,t)}}{{partial {x^2}}} tag{1b}$$  |
$$ Q(x,t) = beta GAgamma (x,t)tag{1c} $$  |
式中,
根据质心运动定理和动量定理, 可得梁单元的动力学方程为
$$ left. begin{array}{l} ho Adfrac{{{partial ^2}w(x,t)}}{{partial {t^2}}} + beta GAleft[dfrac{{partial theta (x,t)}}{{partial x}} - dfrac{{{partial ^2}w(x,t)}}{{partial {x^2}}} ight] = 0 ho Idfrac{{{partial ^2}theta (x,t)}}{{partial {t^2}}} - EIdfrac{{{partial ^2}theta (x,t)}}{{partial {x^2}}} + qquad GAleft({theta _f}(x,t) - dfrac{{partial w(x,t)}}{{partial x}} ight) = 0 end{array} ight} $$  | (2) |
式(2)为关于梁横向位移
$$ begin{split}& ho Afrac{{{partial ^2}w(x,t)}}{{partial {t^2}}} + EIfrac{{{partial ^4}w(x,t)}}{{partial {x^4}}} - ho Ifrac{{{partial ^4}w(x,t)}}{{partial {x^2}partial {t^2}}} - &qquad frac{{ ho IE}}{{beta G}}frac{{{partial ^4}w(x,t)}}{{partial {x^2}partial {t^2}}} + frac{{{ ho ^2}I}}{{beta G}}frac{{{partial ^4}w(x,t)}}{{partial {t^4}}} = 0 end{split} $$  | (3) |
将球摆型谐振器附加进基体梁形心位置(
ight|_{x = l/2}} $
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
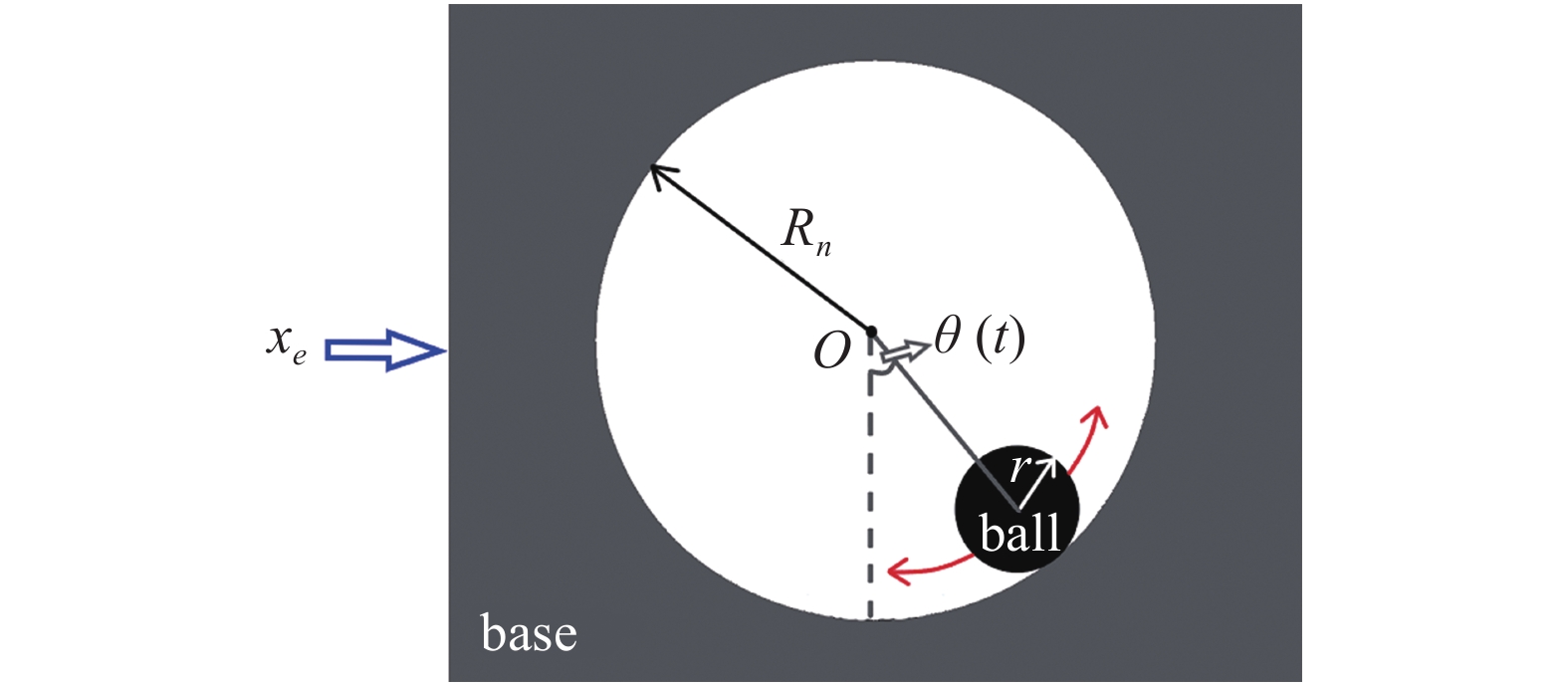
球摆型谐振器模型
Figure
3.
A spherical pendulum resonator
下载: 全尺寸图片
幻灯片
$$ frac{partial }{{partial t}}left[frac{{partial L}}{{partial dot theta (t)}} ight] - frac{{partial L}}{{partial theta (t)}} = 0 $$  | (4) |
式中,
将图3中球腔质心O所在的水平面为零势能面, 则滑动小球的动能T、势能U分别为
$$;;;;;;; begin{split} T =& frac{{text{1}}}{{text{2}}}{m_1}Biggr[{R_{text{b}}^2}{frac{{{text{d}}theta (t)}}{{{text{d}}t}}^2} + {frac{{partial {{left. {w(x,t)} ight|}_{x = l/2}^2}}}{{partial t}}} + & 2{R_{text{b}}}frac{{{text{d}}theta (t)}}{{{text{d}}t}}frac{{partial {w_{l/2}}(x,t)}}{{partial t}}Biggr] end{split} tag{5a}$$  |
$$ U = - {m_1}g{R_{text{b}}}cos theta (t) tag{5b}$$  |
式中,
ho _1}}}{3}$
ho _1} $
将式(5)代入拉格朗日方程, 得到球摆谐振器的动力学方程为
$$ frac{{{{text{d}}^2}theta (t)}}{{{text{d}}{t^2}}} + frac{1}{{{R_{text{b}}}}}left[g - frac{{{partial ^2}{{left. {w(x,t)} ight|}_{x = l/2}}}}{{partial {t^2}}} ight]sin theta (t) = 0 $$  | (6) |
将能量采集装置附加到球摆型谐振器中, 可以得到球摆型能量采集器. 根据基尔霍夫定律, 得到具有能量采集功能的球摆型谐振器的动力学方程为
$$ left. begin{array}{l} dfrac{{{{text{d}}^2}theta (t)}}{{{text{d}}{t^2}}} + dfrac{1}{{{R_{text{b}}}}}left[g - dfrac{{{partial ^2}{{left. {w(x,t)} ight|}_{x = l/2}}}}{{partial {t^2}}} ight]sin theta (t) -qquad dfrac{{B{L_{{text{coil}}}}}}{{{m_1}}}i(t) = 0 dfrac{{{text{d}}i(t)}}{{{text{d}}t}} + dfrac{R}{{{L_{{text{ind}}}}}}i(t) + dfrac{{B{L_{{text{coil}}}}{R_{text{b}}}}}{{{L_{{text{ind}}}}}}dfrac{{{text{d}}theta (t)}}{{{text{d}}t}} = 0 end{array} ight} $$  | (7) |
式中, B为磁感应强度;
m{ind}}} }} $
基于牛顿第二定律, 将基体梁中空腔质量等效为负质量, 则附加球摆谐振器的超材料梁单元的动力学方程为
$$ begin{split}& ho Afrac{{{partial ^2}w(x,t)}}{{partial {t^2}}} + EIfrac{{{partial ^4}w(x,t)}}{{partial {x^4}}} - ho Ifrac{{{partial ^4}w(x,t)}}{{partial {x^2}partial {t^2}}} - frac{{ ho IE}}{{beta G}}frac{{{partial ^4}w(x,t)}}{{partial {x^2}partial {t^2}}} + & qquad frac{{{ ho ^2}I}}{{beta G}}frac{{{partial ^4}w(x,t)}}{{partial {t^4}}} = [{R_1}(t) + {R_2}(t)]delta (x - l) [-15pt]end{split} $$  | (8) |
式中,
$$ left. begin{array}{l} {R_1}(t) = dfrac{{{m_1}g}}{{{R_{text{b}}}}}sin {theta _i}(t) {R_2}(t) = - dfrac{{4{text{π}}{R_{text{n}}^3} ho }}{3}dfrac{{{partial ^2}{{left. {w(x,t)} ight|}_{x = l/2}}}}{{partial {t^2}}} end{array} ight} $$  | (9) |
式中,
联立球摆型谐振器的动力学方程可得到典型超材料单元的控制方程
$$ left. begin{array}{l} ho Adfrac{{{partial ^2}w(x,t)}}{{partial {t^2}}} + EIdfrac{{{partial ^4}w(x,t)}}{{partial {x^4}}} - quad ho Idfrac{{{partial ^4}w(x,t)}}{{partial {x^2}partial {t^2}}} - dfrac{{ ho IE}}{{beta G}}dfrac{{{partial ^4}w(x,t)}}{{partial {x^2}partial {t^2}}} + quad dfrac{{{ ho ^2}I}}{{beta G}}dfrac{{{partial ^4}w(x,t)}}{{partial {t^4}}} - Biggr[dfrac{{{m_1}g}}{{{R_{text{b}}}}}sin {theta _i}(t) - quad dfrac{{4{text{π}}{R_{text{n}}}^3 ho }}{3}dfrac{{{partial ^2}{{left. {w(x,t)} ight|}_{x = l/2}}}}{{partial {t^2}}}Biggr]delta left(dfrac{l}{2} ight) = {text{0}} dfrac{{{{text{d}}^2}{theta _i}(t)}}{{{text{d}}{t^2}}} + dfrac{1}{{{R_{text{b}}}}}Biggr[g - dfrac{{{partial ^2}{{left. {w(x,t)} ight|}_{x = l/2}}}}{{partial {t^2}}}Biggr]sin {theta _i}(t) = 0 end{array} ight}$$  | (10) |
根据基尔霍夫定律, 具有能量采集功能的双功能超材料梁的动力学方程为
$$ left. begin{array}{l} ho Adfrac{{{partial ^2}w(x,t)}}{{partial {t^2}}} + EIdfrac{{{partial ^4}w(x,t)}}{{partial {x^4}}} - ho Idfrac{{{partial ^4}w(x,t)}}{{partial {x^2}partial {t^2}}} - quad dfrac{{ ho IE}}{{beta G}}dfrac{{{partial ^4}w(x,t)}}{{partial {x^2}partial {t^2}}} quad + dfrac{{{ ho ^2}I}}{{beta G}}dfrac{{{partial ^4}w(x,t)}}{{partial {t^4}}} - Biggr[dfrac{{{m_1}g}}{{{R_{text{b}}}}}sin {theta _i}(t) - quad dfrac{{4{text{π}}{R_{text{n}}}^3 ho }}{3}dfrac{{{partial ^2}{{left. {w(x,t)} ight|}_{x = l/2}}}}{{partial {t^2}}}Biggr]delta left(dfrac{l}{2} ight) = {text{0}} dfrac{{{{text{d}}^2}{theta _i}(t)}}{{{text{d}}{t^2}}} + dfrac{1}{{{R_{text{b}}}}}left[g - dfrac{{{partial ^2}{{left. {w(x,t)} ight|}_{x = l/2}}}}{{partial {t^2}}} ight]sin {theta _i}(t) - dfrac{{B{L_{{text{coil}}}}}}{{{m_1}}}i(t) = 0 dfrac{{{text{d}}i(t)}}{{{text{d}}t}} + dfrac{R}{{{L_{{text{ind}}}}}}i(t) + dfrac{{B{L_{{text{coil}}}}{R_{text{b}}}}}{{{L_{{text{ind}}}}}}dfrac{{{text{d}}{theta _i}(t)}}{{{text{d}}t}} = 0 end{array} ight} $$  | (11) |
对未知量进行Fourier展开, 并利用Bloch's定理将其设为
$$ w(x,t) = {W_0}{{ m{e}}^{{ m{j}}(omega t - qx)}} tag{12a}$$  |
$$ w(t) = {W_0}{{ m{e}}^{{ m{j}}omega t}} tag{12b}$$  |
$$ {theta _i}(t) = {varTheta _{i0}}{{ m{e}}^{{ m{j}}omega t}} tag{12c}$$  |
$$ i(t) = {I_0}{{ m{e}}^{{ m{j}}omega t}} tag{12d}$$  |
式中, ω为振动频率, q为x方向的波矢量, 本文将一维向量q写成标量形式.
上述应用于简谐弯曲弹性波通过双功能超材料梁单元的控制方程可写为
$$ left. begin{array}{l} displaystyleint_{ - frac{l}{2}}^{frac{l}{2}} {Biggr{ ho Adfrac{{{partial ^2}[{W_0}{{ m{e}}^{{ m{j}}(omega t - qx)}}]}}{{partial {t^2}}} + dfrac{{{ ho ^2}I}}{{beta G}}dfrac{{{partial ^4}[{W_0}{{ m{e}}^{{ m{j}}(omega t - qx)}}]}}{{partial {t^4}}}} + quadquad dfrac{{4{text{π}}{R_{text{n}}}^3 ho }}{3}dfrac{{{partial ^2}[{W_0}{{ m{e}}^{{ m{j}}(omega t - qx)}}]}}{{partial {t^2}}}Biggr}{ m{d}}x + displaystyleint_{ - frac{l}{2}}^{frac{l}{2}} {Biggr{EIdfrac{{{partial ^4}[{W_0}{{ m{e}}^{{ m{j}}(omega t - qx)}}]}}{{partial {x^4}}} - ho Idfrac{{{partial ^4}[{W_0}{{ m{e}}^{{ m{j}}(omega t - qx)}}]}}{{partial {x^2}partial {t^2}}}} Biggr}{ m{d}}x - quadquad displaystyleint_{ - frac{l}{2}}^{frac{l}{2}} {dfrac{{ ho IE}}{{beta G}}dfrac{{{partial ^4}[{W_0}{{ m{e}}^{{ m{j}}(omega t - qx)}}]}}{{partial {x^2}partial {t^2}}}} { m{d}}x - dfrac{{{m_1}g}}{{{R_{text{b}}}}}{varTheta _{i0}}{{ m{e}}^{{ m{j}}omega t}} = 0 dfrac{{{{ m{d}}^2}{varTheta _{i0}}{{ m{e}}^{{ m{j}}omega t}}}}{{{ m{d}}{t^2}}} + dfrac{1}{{{R_{text{b}}}}}Biggr[g - dfrac{{{partial ^2}{{left. {w(x,t)} ight|}_{x = l/2}}}}{{partial {t^2}}}Biggr]{varTheta _{i0}}{{ m{e}}^{{ m{j}}omega t}} - quad quad dfrac{{B{L_{{text{coil}}}}}}{{{m_1}}}{I_0}{{ m{e}}^{{ m{j}}omega t}} = 0 dfrac{{{ m{d}}{I_0}{{ m{e}}^{{ m{j}}omega t}}}}{{{ m{d}}t}} + dfrac{R}{{{L_{{text{ind}}}}}}{I_0}{{ m{e}}^{{ m{j}}omega t}} + dfrac{{B{L_{{text{coil}}}}{R_{text{b}}}}}{{{L_{{text{ind}}}}}}dfrac{{{ m{d}}{varTheta _{i0}}{{ m{e}}^{{ m{j}}omega t}}}}{{{ m{d}}t}} = 0 end{array} ight} $$  | (13) |
对方程(13)积分后, 可以用欧拉公式化简可以得到
$$ left.begin{array}{l} dfrac{{ ho A{W_0}{omega ^2}}}{q}{k_{text{T}}} + dfrac{{2I{ ho ^2}{W_0}{omega ^4}}}{{qbeta G}}{k_{text{T}}}+ quad dfrac{{8{text{π}} R_{text{n}}^3 ho {W_0}{omega ^2}}}{{3q}}{k_{text{T}}} + 2EI{W_0}{q^3}{k_{text{T}}} - quad 2 ho I{W_0}{omega ^2}q{k_{text{T}}} - dfrac{{2EI ho {W_0}{omega ^2}q}}{{beta G}}{k_{text{T}}} - quad dfrac{{{m_1}g}}{{{R_{text{b}}}}}{varTheta _{i{text{0}}}} = 0 {varTheta _{i0}}{omega ^2} + dfrac{1}{{{R_{text{b}}}}}(g + {left. {{omega ^2}W} ight|_{x = l/2}}){varTheta _{i0}} - dfrac{{B{L_{{text{coil}}}}}}{{{m_1}}}{I_0} = 0 {I_0}omega + dfrac{R}{{{L_{{text{ind}}}}}}{I_0} + {varTheta _{i0}}omega dfrac{{B{L_{{text{coil}}}}{R_{text{b}}}}}{{{L_{{text{ind}}}}}} = 0 end{array} ight} $$  | (14) |
式中,
ight)$
控制方程的系数矩阵可以写成
$$ left[ {begin{array}{*{20}{c}} {Re {k_{text{T}}}}&{ - dfrac{{{m_1}g}}{{{R_{text{b}}}}}}&0 0&varPsi &{ - dfrac{{B{L_{{text{coil}}}}}}{{{m_1}}}} 0&{dfrac{{B{L_{{text{coil}}}}{R_{text{b}}}omega }}{{{L_{{text{ind}}}}}}}&{dfrac{R}{{{L_{{text{ind}}}}}}} end{array}} ight] left[ {begin{array}{*{20}{c}} {{W_0}} begin{gathered} {varTheta _{i0}} {I_0} end{gathered} end{array}} ight] = 0 $$  | (15) |
式中
$$ begin{gathered} Re {text{ = }}frac{{ ho A{omega ^2}}}{q} + frac{{2I{ ho ^2}{omega ^4}}}{{qbeta G}} + frac{{8{text{π}} R_{text{n}}^3 ho {omega ^2}}}{{3q}} + quad 2EI{q^3} - 2 ho I{omega ^2}q - frac{{2EI ho {omega ^2}q}}{{ ho G}} end{gathered} $$  |
$$ varPsi = {omega ^2} + frac{1}{{{R_{text{b}}}}}(g + {left. {{omega ^2}W} ight|_{x = l/2}}{text{)}} $$  |
通过求解上式的系数项, 使系数行列式为零, 可得到频率ω与波矢量q的关系, 即本文所研究的双功能超材料梁的能带结构关系.
2.
有限元分析
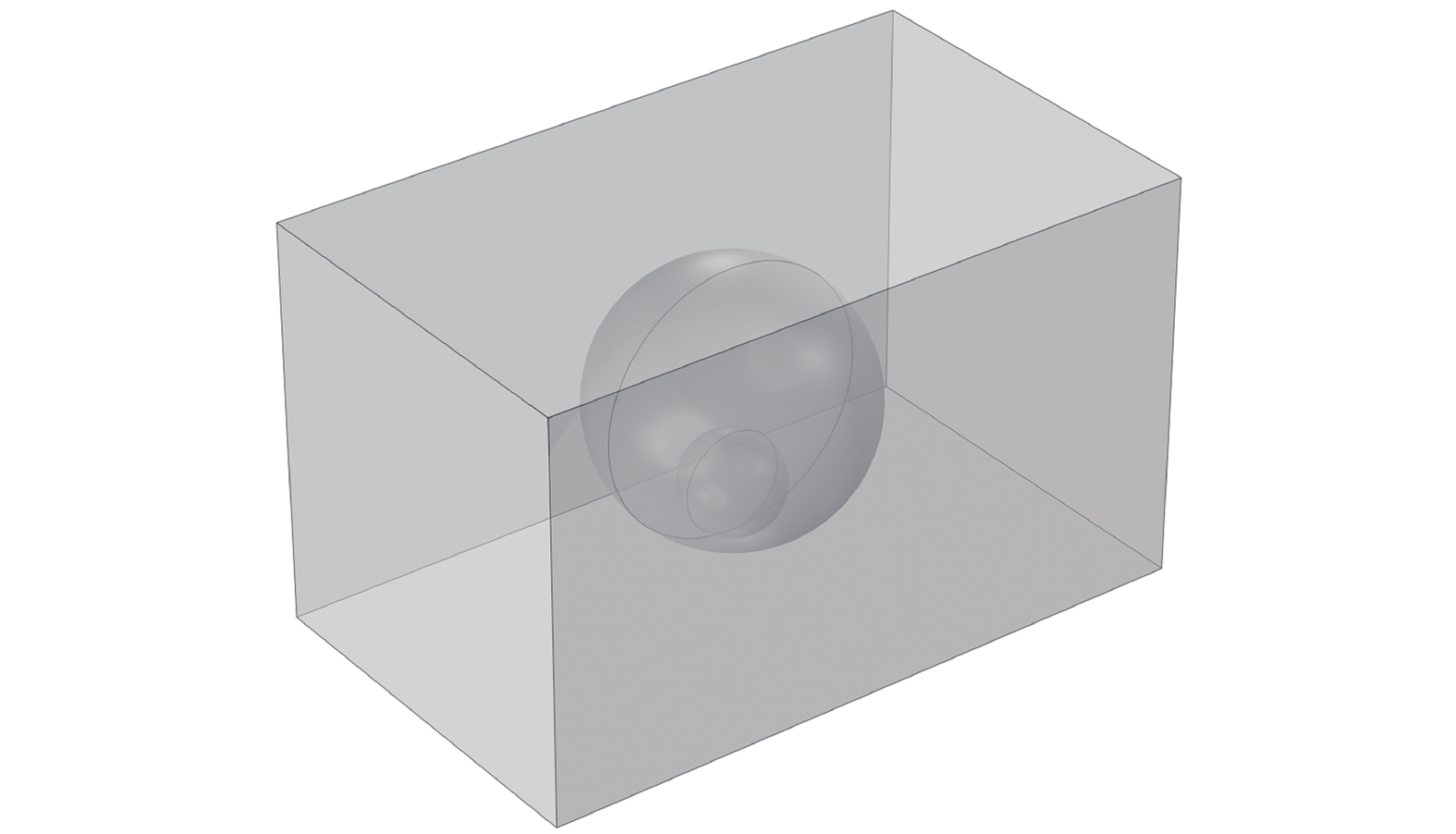
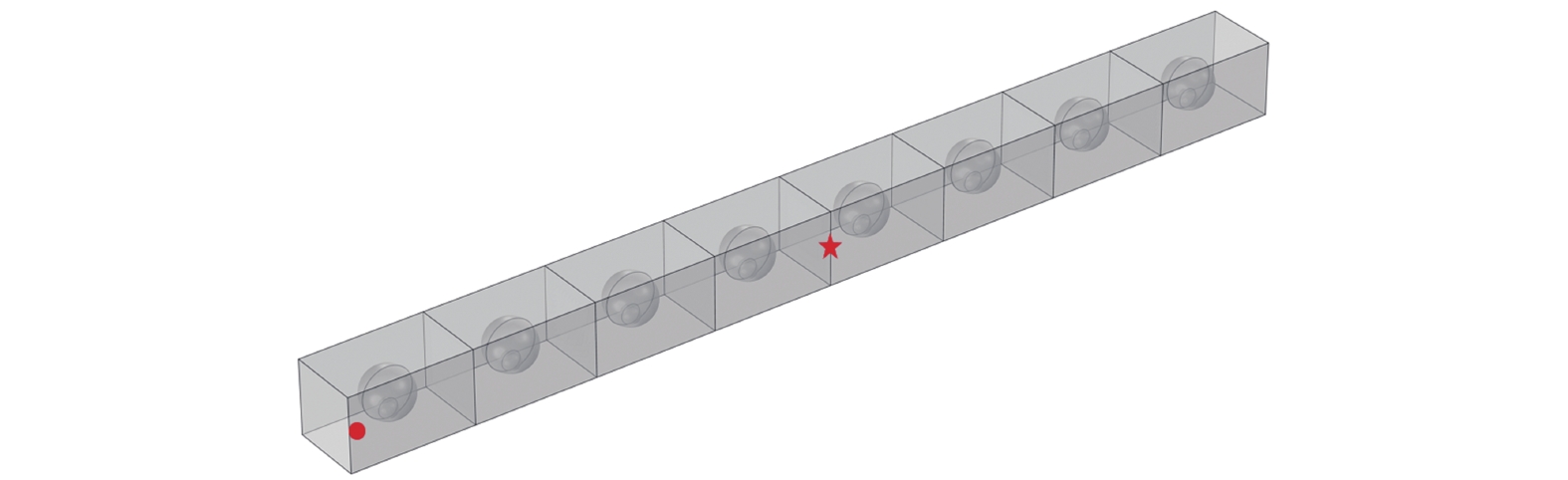
本文利用有限元方法分析了附加局部谐振器的双功能超材料梁的动力学特性. 图4表示了附加谐振器单元有限元模型. 本研究计算得到了由8个局部谐振腔单元组成的双功能超材料梁的能带结构和频率响应函数曲线, 有限元模型如图5所示. 在有限元的环境下, 对双功能超材料梁的中间位置施加恒定加速度的谐波激励, 在梁的另一端设置探针对端部的响应进检测.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
附加谐振器单元有限元模型
Figure
4.
Finite element model of unit cell
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
附加谐振器超材料梁有限元模型
Figure
5.
Finite element model of metamaterial beam
下载: 全尺寸图片
幻灯片
图5中五角星标记位置为激励位置, 圆点标记位置为监测点位置.
在有限元环境下, 超材料的频率响应函数矩阵表示为
$$ {boldsymbol{M}} {ddot {boldsymbol{p}}} + {boldsymbol{C}}left( {{boldsymbol{p}},dot {boldsymbol{p}}} ight) {dot {boldsymbol{p}}} + {boldsymbol{K}}left( {boldsymbol{p}} ight) {boldsymbol{p}} = {boldsymbol{F}} tag{16a}$$  |
$$ begin{split}& {boldsymbol{F}} = left{ {il ho A{omega ^2}{X_{text{e}}}cos (omega t),0,0,} ight. & quad quad quad {left. {il ho A{omega ^2}{X_{text{e}}}cos (omega t),0,0, cdots } ight}^{text{T}}} end{split}tag{16b} $$  |
$$ {boldsymbol{p}} = {[ - {omega ^2}{boldsymbol{M}} + { m{j}}omega {boldsymbol{C}} + {boldsymbol{K}}]^{ - 1}} {boldsymbol{F}} tag{16c} $$  |
式中, M, C, K为离散有限双功能超材料梁的质量矩阵、阻尼矩阵和刚度矩阵. i为无限周期超材料梁中的单元数. p和F分别表示位移矢量和力矢量. 采用有限元分析方法对模型进行求解, 计算超材料梁另一端的动态响应数据, 得到梁的频率响应.
3.
结果和讨论
本节比较了有无附加带能量收集装置球摆型谐振器时双功能超材料梁的低频隔振性能. 为了更好的控制超材料带隙的频率范围, 还讨论了双功能超材料单胞参数对带隙的影响, 对双功能超材料的输出电压进行了研究. 表1为双功能超材料的物理参数.
表
1
双功能超材料物理参数
Table
1.
Parameters of a dual-functional metamaterial
table_type1 ">
| Item | Notation | Value |
| length | $ l/{ m{m}} $ | $ 0.1 $ |
| cross-sectional area | $ A/{ m{m}}^2$ | $ 0.003;6 $ |
| density of material | $ ho /left( {{ m{kg}} cdot {{ m{m}}^{ - { m{3}}}}} ight) $ | $ 1810 $ |
| Young's modulus | $E/{ m{Pa}}$ | $ 761;761 $ |
| radius of spherical cavity | $ R/{ m{m}} $ | $ 0.0{text{2}} $ |
| radius of sliding-ball | $r/{ m{m}}$ | $ 0.009 $ |
| density of sliding-ball | $ { ho _{ m{b}}}/left( {{ m{kg}} cdot {{ m{m}}^{ - { m{3}}}}} ight) $ | $ {text{7780}} $ |
| magnetic flux | $B/{ m{T}} $ | $ {text{0}}{text{.5}} $ |
| inductance | $ {L_{{ m{ind}}}}/{ m{H}}$ | $ {text{0}}{text{.5}} $ |
| coil length | $ {L_{{ m{coil}}}}/{ m{m}} $ | $ {text{0}}{text{.1}} $ |
下载: 导出CSV
|显示表格
3.1
有无附加谐振器对超材料带隙特性的影响
为了研究在超材料梁中附加谐振器对其带隙和振动特性的影响, 本节对比有无球摆型谐振器超材料梁的能带结构和幅频响应曲线. 对于有限周期数的超材料, 当周期数很大时, 带隙的起始频率和结梁频率趋向于带隙的理论值, 这为用有限周期超材料替代无限周期超材料的研究提供了基础.
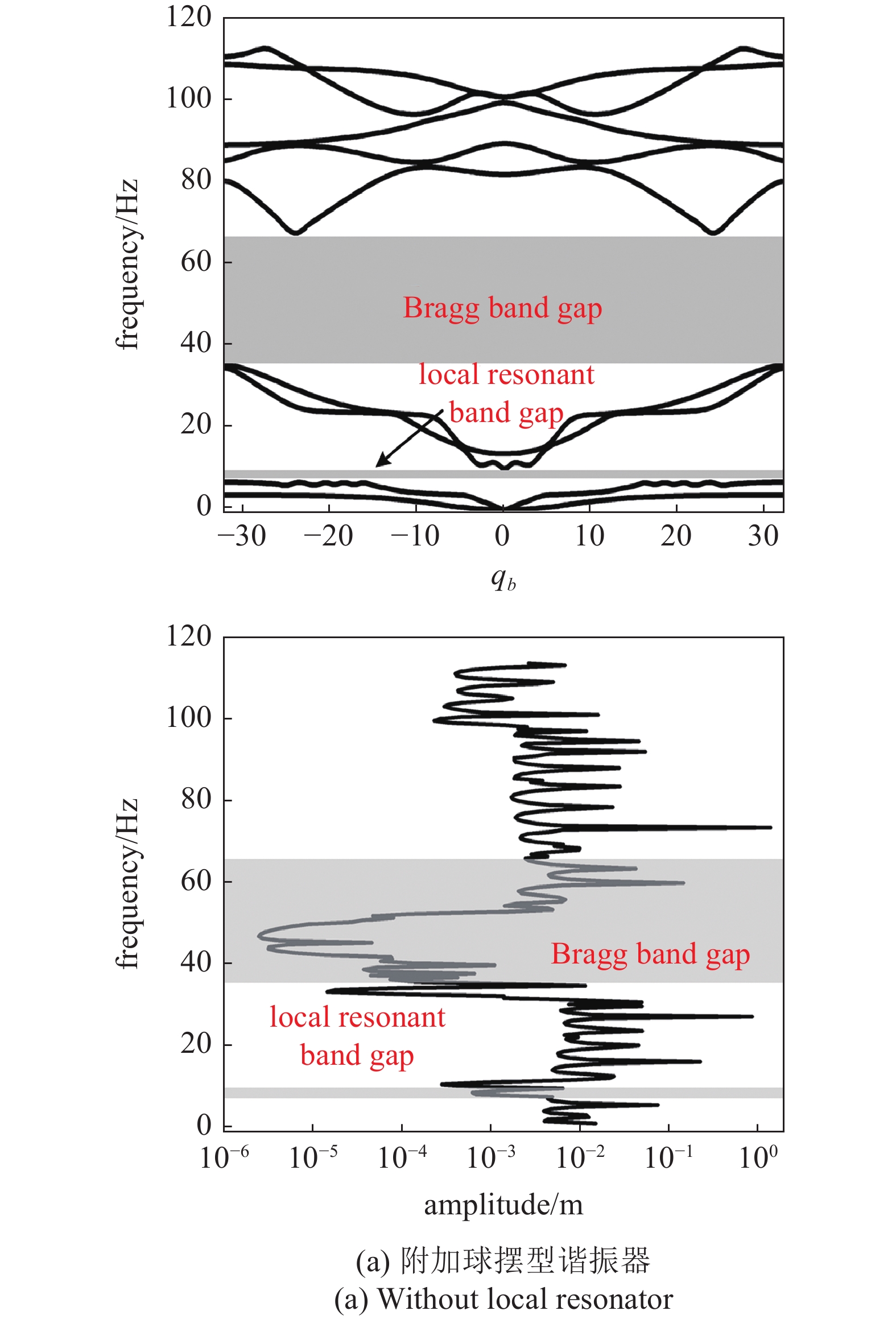
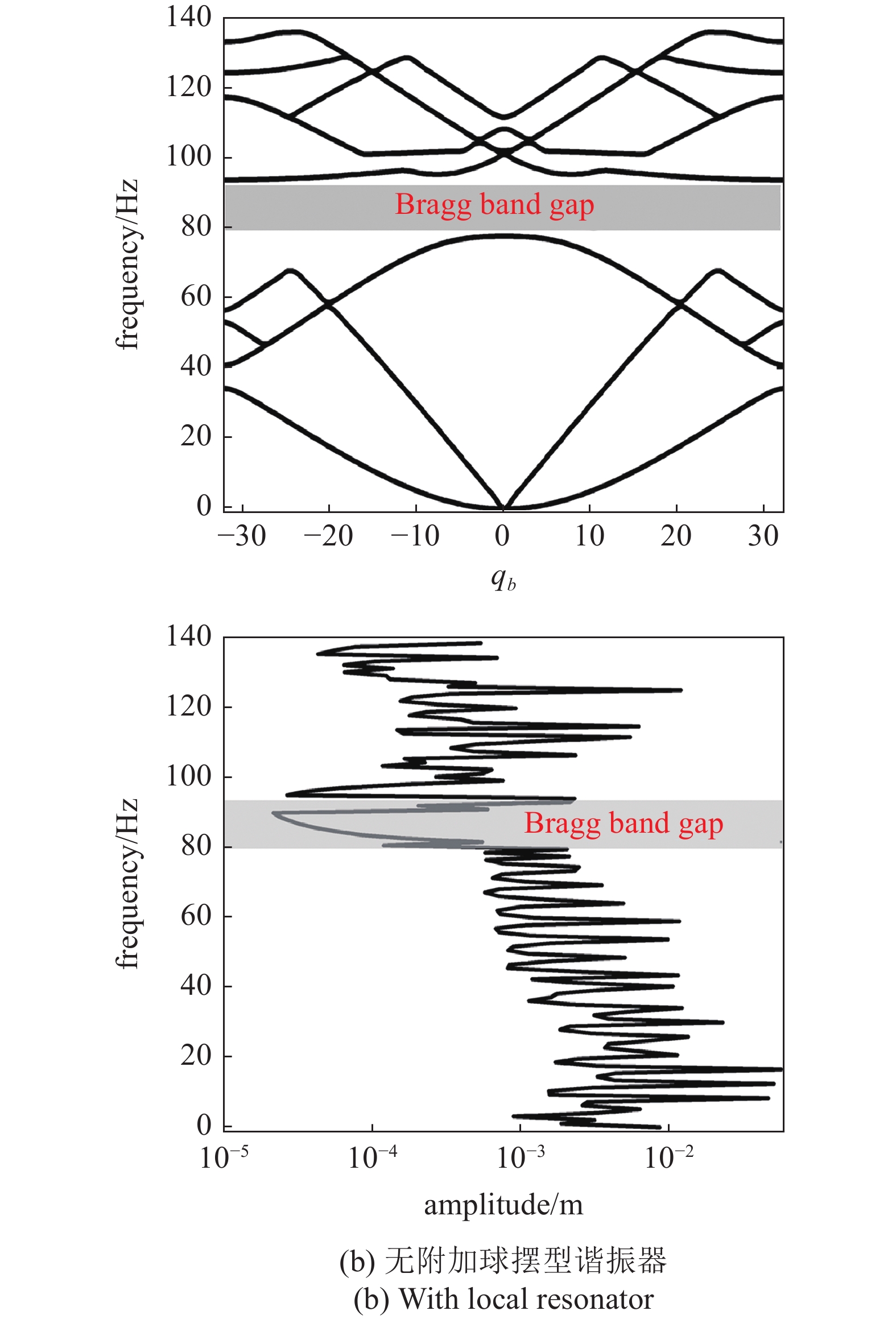
图6(a)显示了附加谐振器超材料梁的能带结构和幅频响应曲线. 在0 ~ 120 Hz范围内, 存在Bragg带隙(37 ~ 66 Hz)和低频处的局域共振带隙(7 ~ 9 Hz), 在幅频响应图中, 带隙相应频率范围的振动响应被明显抑制. 图6(b)表示了在相同物理参数下, 没有附加谐振器超材料梁的能带结构和幅频响应曲线. 可以明显的看出在0 ~ 140 Hz 的频率范围内存在一个Bragg带隙(79 ~ 92 Hz), 在带隙频率范围内的响应明显小于带隙频率外的响应, 因此只含有阵列球型空腔的超材料也可以有效地对振动进行抑制.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-6-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure6-1" />
6
超材料梁的能带结构与幅频响应对比
6.
Band-gaps and amplitude-frequency response of metamaterial
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
超材料梁的能带结构与幅频响应对比(续)
Figure
6.
Band-gaps and amplitude-frequency response of metamaterial (continued)
下载: 全尺寸图片
幻灯片
通过对比图6(a)和图6(b)可以看出, 无限周期数超材料的带隙频率与有限周期数超材料振动抑制频率范围基本一致, 说明振动的衰减现象是由于带隙行为引起的. 理论上, 振动可以在带隙的频率范围内被完全隔离. 然而, 幅频响应的结果表明, 振动仍然是传播的. 这是因为理论上超材料的周期结构是无限的, 这里通过8个单元模拟得到频率响应, 所以在实际的工程应用中, 带隙内的有害振动可以显著降低, 但不会完全被隔离. 一般情况下, 在超材料中附加球摆型谐振器可以明显的降低Bragg带隙的频率范围, 中心频率从85.5 Hz降为51.5 Hz, 拓宽隔振带宽. 在较低的频率范围内, 由于球摆型谐振器的共振, 会产生一个较窄的局域共振带隙(7 ~ 9 Hz). 综上所述, 附加球摆型谐振器可以增大隔振带隙频率范围. 同时, 附加了谐振器超材料梁的响应显著减小. 通过对附加谐振器和没有附加谐振器的能带结构和幅频响应的对比, 发现球摆型谐振器的加入可以在低频范围内形成了一个局域共振带隙, 提高了超材料梁在低频处的隔振性能.
3.2
超材料几何参数研究
本文还讨论了超材料单胞的几何参数, 如图7所示, 分别为单胞的尺寸(m)、谐振小球的尺寸(本质上是质量/kg)和球型空腔的尺寸(m)对超材料梁隔振带隙频率范围的影响.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
几何参数对带隙的影响
Figure
7.
Effects of geometric parameters on band gap
下载: 全尺寸图片
幻灯片
图7(a)显示了单胞尺寸对超材料带隙频率范围的影响. 当弯曲波在超材料梁中传播时, 对低频处局域共振带隙的影响不大, 其中心频率保持在8 Hz左右, 带隙宽度为3 Hz; 对于高频处的Bragg带隙, 其中心频率从90 Hz降低到21.5 Hz, 带宽从4 Hz拓宽到23 Hz. 图7(b)显示了谐振质量对带隙频率范围的影响. 谐振质量对低频处局域共振带隙调节能力更强, 带隙中心频率从37 Hz降低到5.5 Hz, 使其具有更好的低频隔振性能, 带宽始终保持在4 Hz左右; 对于高频处的Bragg带隙, 带宽从25 Hz拓宽到30 Hz, 带隙的中心频率从67.5 Hz降低到49 Hz. 因此, 附加谐振器可以降低Bragg带隙的中心频率并拓宽带隙宽度, 提高超材料梁的低频隔振性能. 图7(c)表示了空腔尺寸对超材料带隙频率范围的影响. 超材料的空腔尺寸对低频处的局域共振带隙影响不大, 中心频率始终为8.3 Hz, 带隙宽度为2.5 Hz; 对于高频处的Bragg带隙, 通过增大空腔尺寸, 带宽从34 Hz降低为24 Hz, 带隙的中心频率从62 Hz降低到48 Hz, 削弱了Bragg带隙的隔振性能.
3.3
能量输出特性
本节讨论附加谐振器的双功能超材料的能量采集特性. 通过有限元计算得到了谐振器中滑动小球的位移, 根据电磁感应定律, 在第i个谐振器中产生的输出电压为
$$ {V_{{text{b}}i}}left( t ight) = MSleft[ {{E_i}left( t ight)} ight]{{ = MS}}left[ {B{L_{{text{coil}}}}{{dot x}_i}left( t ight)} ight] $$  | (17) |
式中,
将有限元计算得到不同位置处谐振器中滑动小球位移代入式(17), 可以得到如图8所示的输出电压曲线.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
不同位置谐振器的输出电压曲线
Figure
8.
Output voltage curve of resonator at different positions
下载: 全尺寸图片
幻灯片
图8为不同位置处谐振器的输出电压曲线, 黑色实线为在激振点附近(图5中五角星)处谐振器的输出电压曲线, 蓝色点划线为远离激振点(图5中圆点)处的谐振器的输出电压曲线. 从图8中可以看出, 电压输出响应在7 ~ 10 Hz的频率范围内产生一个峰值, 电压值达到了0.2806 V, 这与球摆型谐振器的共振频率范围接近. 因此, 附加球摆型谐振器的超材料梁由于谐振器共振产生局域共振带隙, 在局域共振带隙的频率范围内, 超材料基体梁的振动被转移到谐振器中球摆上, 带动线圈做切割磁感线运动, 将机械能转化为电能, 同时减弱基体梁的振动强度. 在局域共振带隙的频率范围内, 靠近激振点处谐振器的输出电压曲线出现了峰值, 远离激振点处谐振器的电压曲线并没有出现峰值验证了激振点附近处的能量集中结论. 因为超材料带隙频率内的振动隔离效果和梁基体的阻尼耗散作用, 在远离激励点处的谐振器的能量输出要比激振点附近谐振器的能量输出低两个量级乃至更多. 在Bragg带隙的频率范围内, 振动主要局限在基体梁中, 所以在谐振器中球摆的振动被抑制, 采集到的电压输出响应稳定.
4.
试验验证
为了验证附加谐振器超材料梁的低频局部共振带隙和Bragg带隙, 本文采用橡胶作为超材料梁的基体, 并将滑动球摆置于球形腔内形成球摆型谐振器. 对超材料梁进行谐波激励, 以研究其在带隙频率范围内的振动隔离特性. 试验所用仪器如表2所示, 附加球摆型谐振器超材料梁的物理参数与表1一致.
表
2
试验仪器
Table
2.
Experiment instruments
table_type1 ">
| Instruments | Version | Manufacturer |
| shaker | TV-51140 | TIRA |
| accelerometer | 352C03 | PCB |
| vibration controller | SCM2E02V | SIEMENS |
下载: 导出CSV
|显示表格
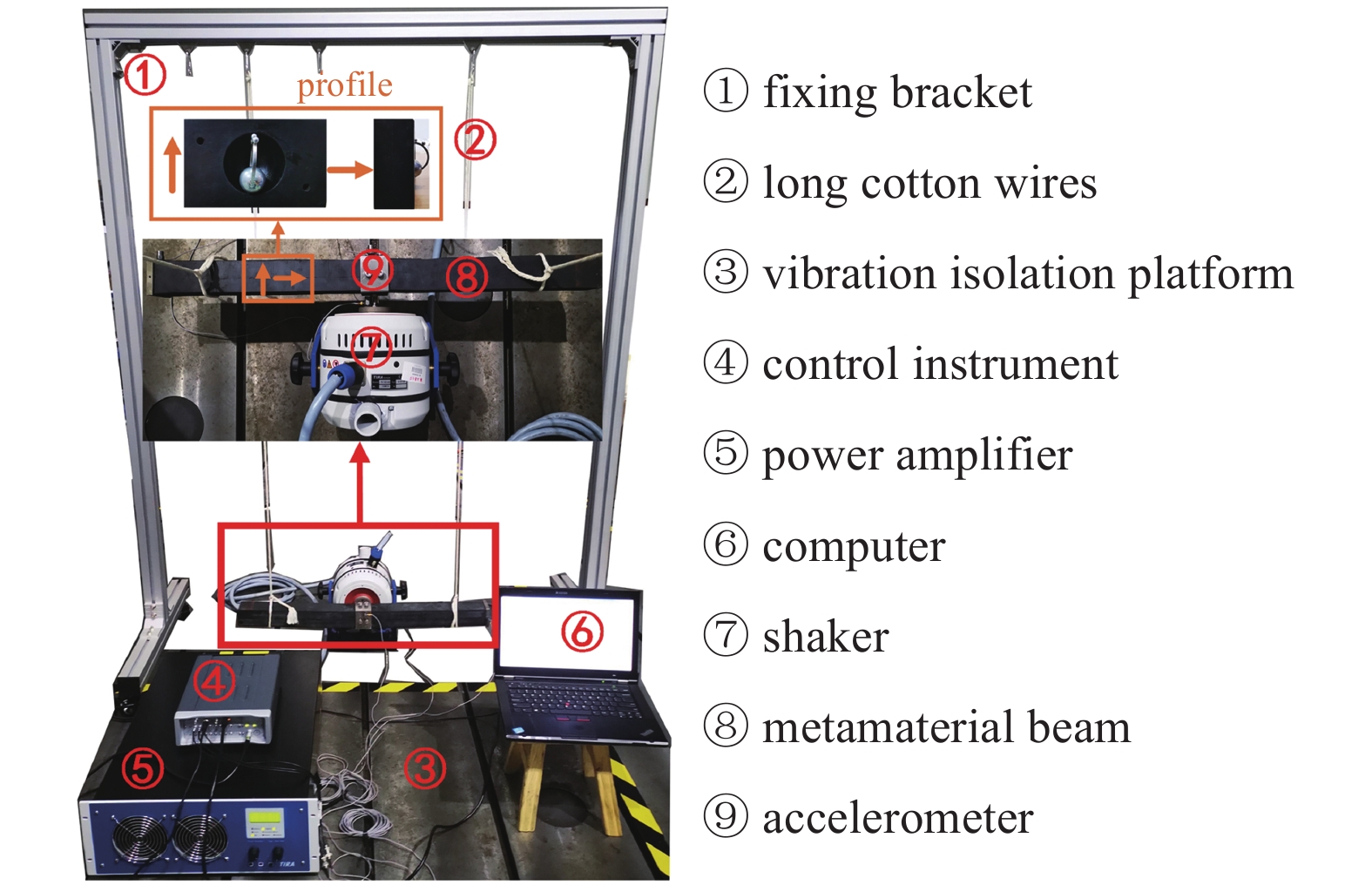
图9为横向激励下附加球摆型谐振器超材料梁的试验照片. 在试验中, 利用两根多节的长棉线将超材料梁吊起, 以模拟自由边界条件. 为了避免超材料梁在振动时产生的弯矩, 本文将激励点设置在超材料梁的中间位置, 以抵消弯矩的影响. 超材料梁与能产生谐波激励的激振器固接. 激振器对激振位置施加一个a = 0.1g的恒定加速度激励, 在激振器上放置一个反馈加速度传感器形成闭环, 使谐波激励更为稳定, 激励位置和响应位置的加速度响应由两个加速度传感器记录.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
横向激励下超材料梁试验照片
Figure
9.
photograph of the transverse excited metamaterial beam
下载: 全尺寸图片
幻灯片
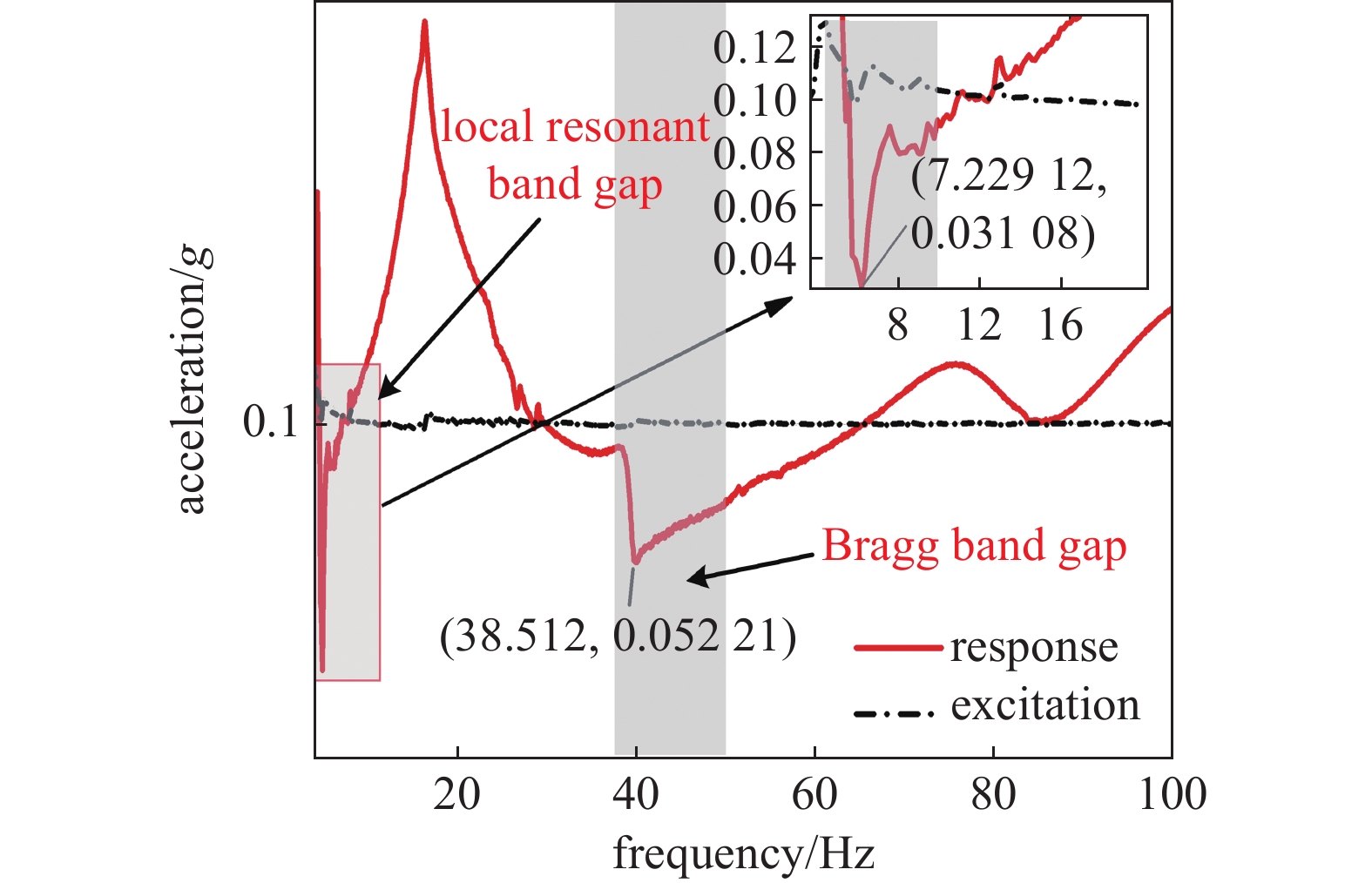
图10为横向激励下超材料梁的扫频曲线. 从图中可以看出, 在6 ~ 10 Hz的低频范围内产生了由于谐振器共振引起的局域共振带隙, 在该带隙的频率范围内, 抑制了加速度响应, 抑制效果达到了0.0311g; 在38 ~ 47 Hz的频率范围存在隔振带隙, 该范围内的加速度响应也明显被抑制, 抑制效果达到0.052 2g. 与超材料的能带结构对比可以发现, 扫频试验中产生的隔振带隙与有限元计算得到的带隙频率范围相一致.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-10.jpg'" class="figure_img
figure_type1 bbb " id="Figure10" />
图
10
横向激励下超材料梁的扫频曲线
Figure
10.
Sweep curve of metamaterial beam under transverse excitation
下载: 全尺寸图片
幻灯片
为了可以定量的反映超材料梁的隔振效率, 引入带隙内振动隔离效率
$$ mu = left(1 - frac{{{A_{text{R}}}}}{{{A_{text{E}}}}} ight) times 100% $$  | (18) |
式中,
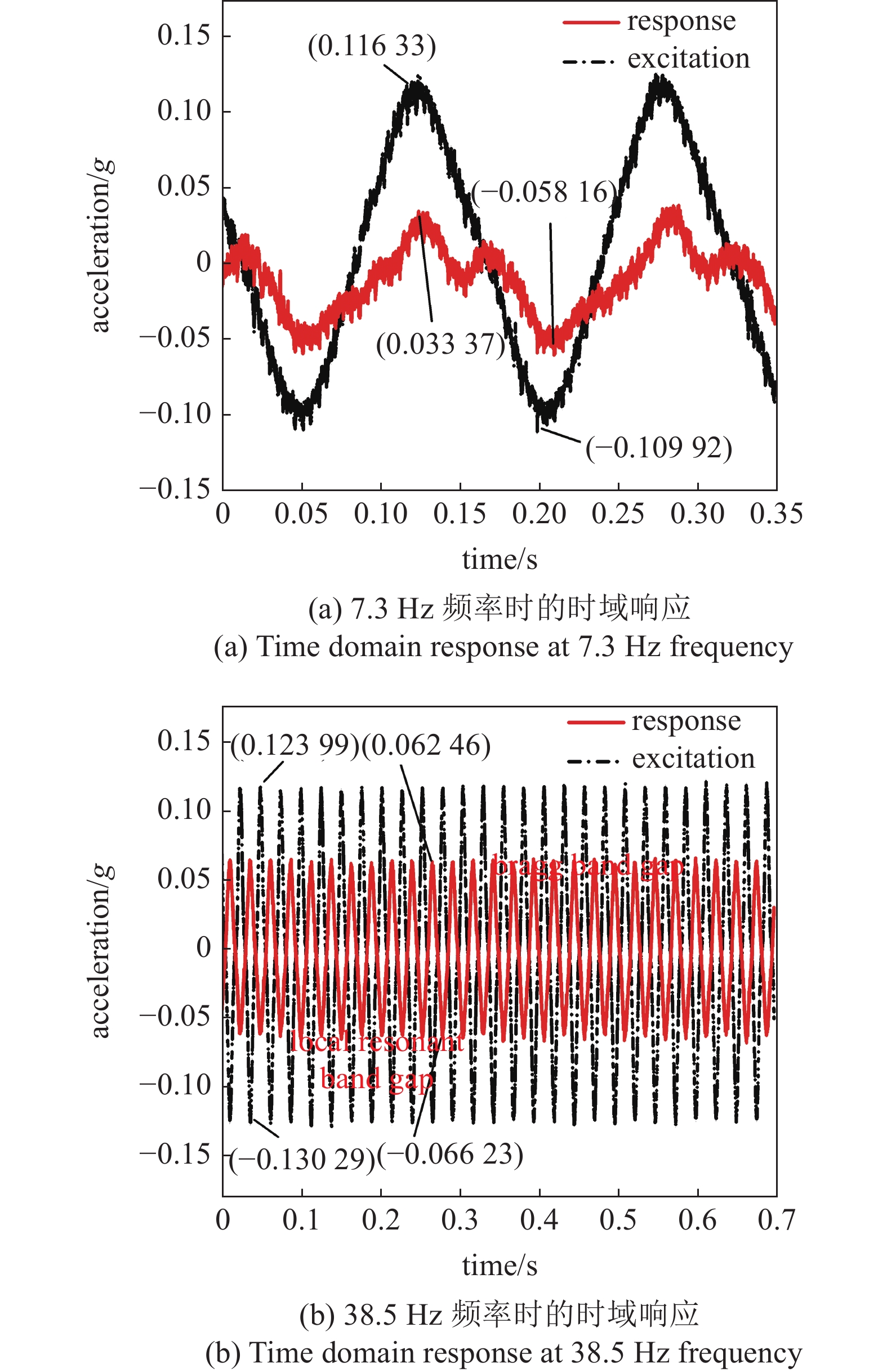
图11(a)为横向激励下超材料梁在7.3 Hz时的时域响应, 试验时选取局域共振带隙频率范围内隔振效果最好的频率(7.3 Hz)进行驻留, 通过该频率下时域响应可以看出, 振动响应明显被抑制, 且处于一个稳定的振动隔离状态. 图11(b)为横向激励下超材料梁在38.5 Hz频率下的时域响应, 在Bragg隔振带隙的频率范围内选取隔振效果最好的频率(38.5 Hz)进行驻留, 通过该频率下的时域响应可以看出端部响应被明显抑制. 表3为超材料隔振带隙内的振动隔离效率, 从表中可以看出横向激励下该超材料梁在局域共振频率范围内的振动隔离效率达到了59.54%, 在Bragg带隙内的振动隔离效率达到了49.39%. 因此, 对该附加球摆型谐振器的超材料梁的试验显示其具有良好的振动隔离特性.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-11.jpg'" class="figure_img
figure_type1 bbb " id="Figure11" />
图
11
不同频率的时域响应
Figure
11.
Time domain response at different frequency
下载: 全尺寸图片
幻灯片
表
3
带隙内隔振效率
Table
3.
Vibration isolation efficiency of band gap
table_type1 ">
| Band-gaps | $ {mu _{{text{BGIE}}}} $/% |
| local resonant band-gap | 59.54 |
| Bragg band-gap | 49.39 |
下载: 导出CSV
|显示表格
5.
二维双功能超材料板
本节对超材料梁拓展的超材料板进行研究. 将带能量采集功能的球摆型谐振器周期性的阵列在橡胶板基体中, 探索该超材料板纵向的振动隔离特性与能量采集性能.
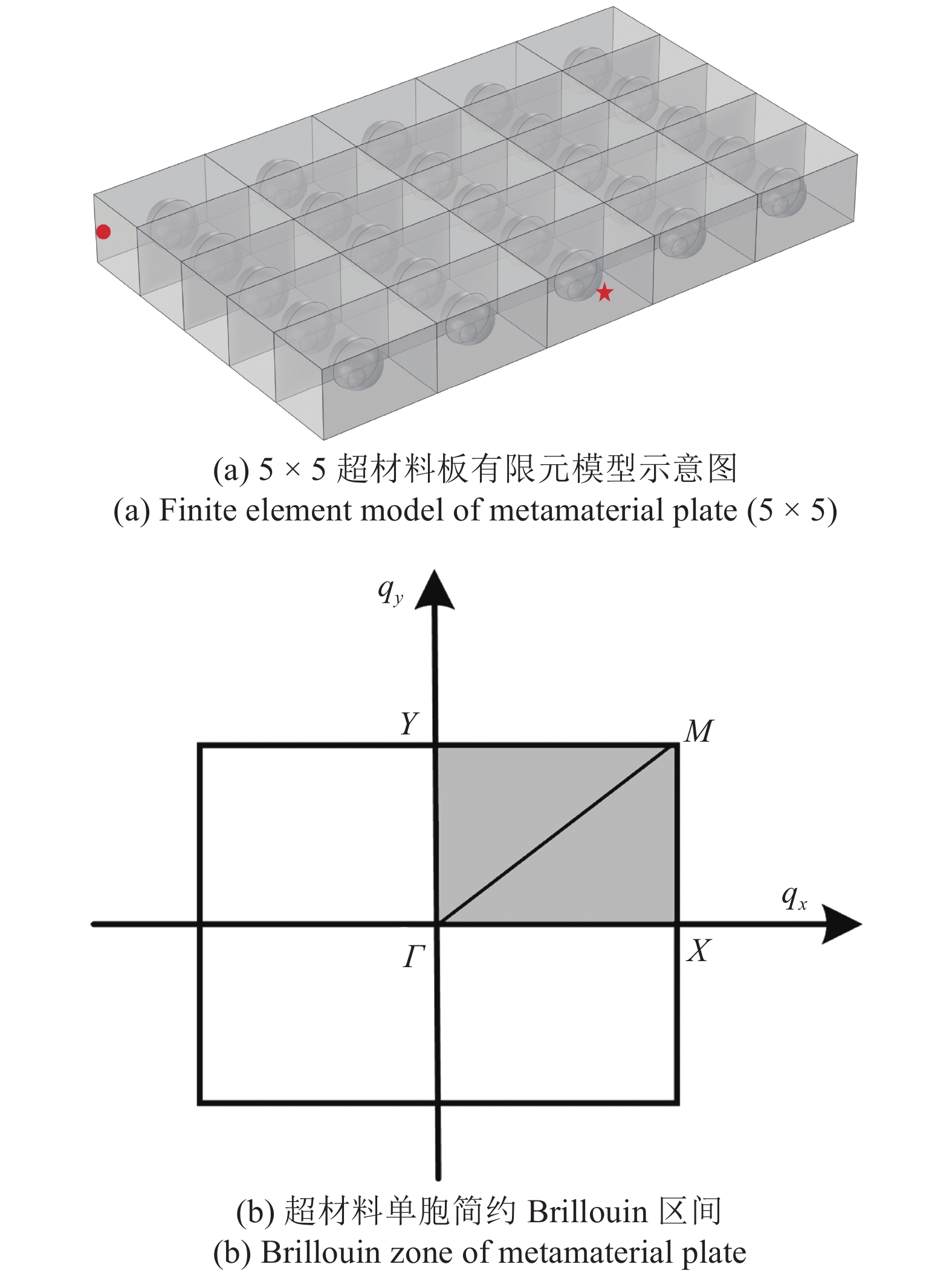
5×5双功能超材料板的有限元模型示意图如图12(a)所示, 图中五角星标记位置为激励位置, 圆点标记位置为监测点位置. 二维单胞的几何参数与前文一维单胞的几何参数一致; 图12(b)表示了二维超材料单胞所对应的简约Brillouin区间(
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-12.jpg'" class="figure_img
figure_type1 bbb " id="Figure12" />
图
12
5 × 5超材料板有限元模型示意图和超材料单胞简约Brillouin区间
Figure
12.
Finite element model of metamaterial plate and Brillouin zone of metamaterial plate (5 × 5)
下载: 全尺寸图片
幻灯片
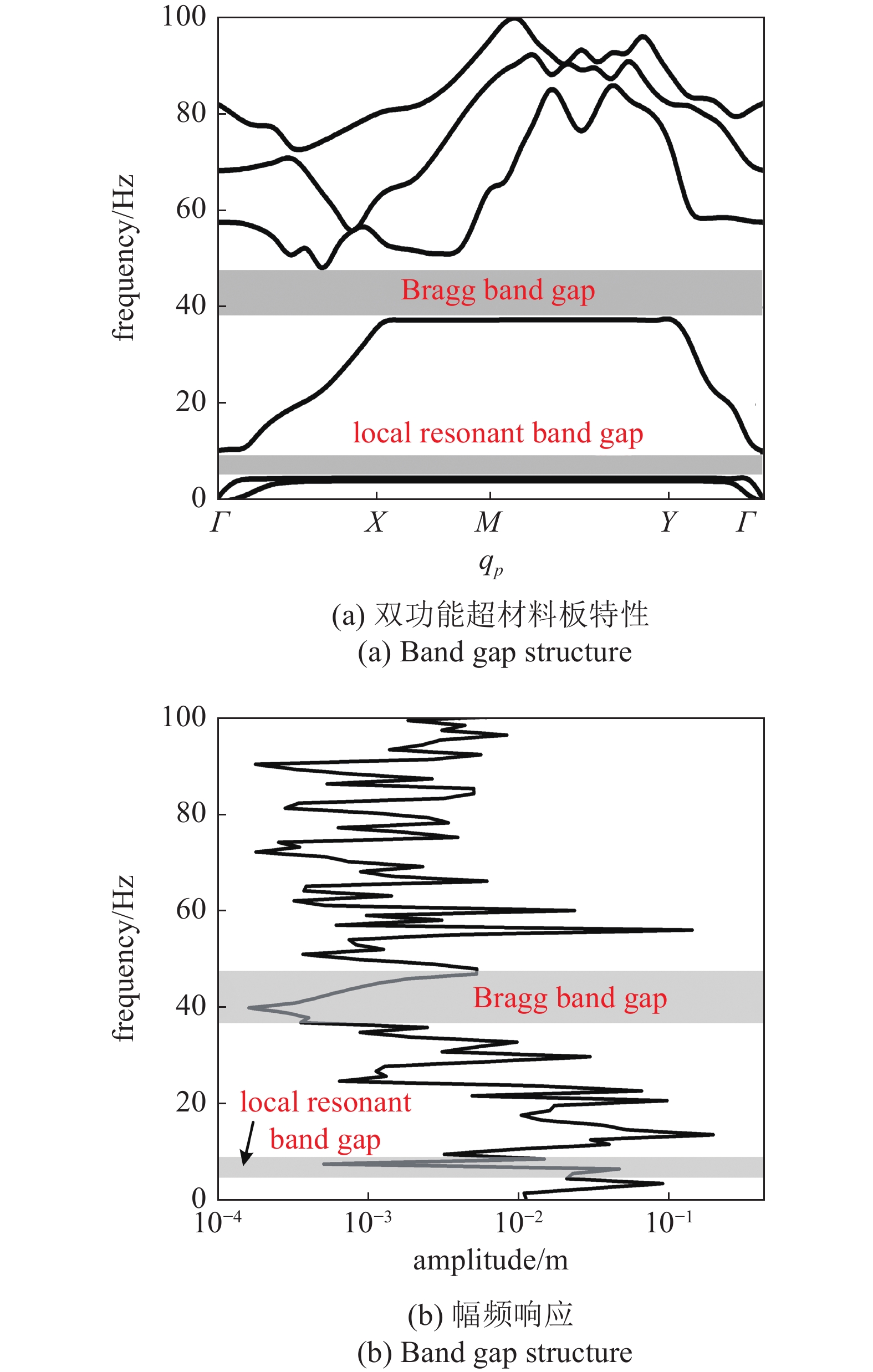
图13(a)为双功能超材料板的带能结构, 从带能结构中可以看出该双功能超材料板存在两个明显的带隙(6 ~ 10 Hz的局域共振带隙、38.5 ~ 47 Hz的Bragg带隙). 图13(b)为相同条件下超材料板的幅频响应曲线, 通过与有限周期数的超材料板的幅频响应对比发现, 在局域共振带隙与Bragg带隙的频率范围内, 响应点的振动明显被抑制, 在带隙频率内具有明显的振动隔离效果.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-13.jpg'" class="figure_img
figure_type1 bbb " id="Figure13" />
图
13
双功能超材料板特性和幅频响应
Figure
13.
Band gap structure and amplitude frequency response
下载: 全尺寸图片
幻灯片
为了验证具有能量采集功能超材料板的能量采集性能. 通过有限元计算得到了激励点附近谐振器中滑动小球的位移. 根据电磁感应定律, 在第(i, j)个谐振器的输出电压为
$$ {V_{pleft( {i,j} ight)}}(t) = MS{text{[}}B{L_{{text{coil}}}}{dot x_{left( {i,j} ight)}}(t)] $$  | (19) |
式中,
ight)}}(t) $
ight)}}(t) $
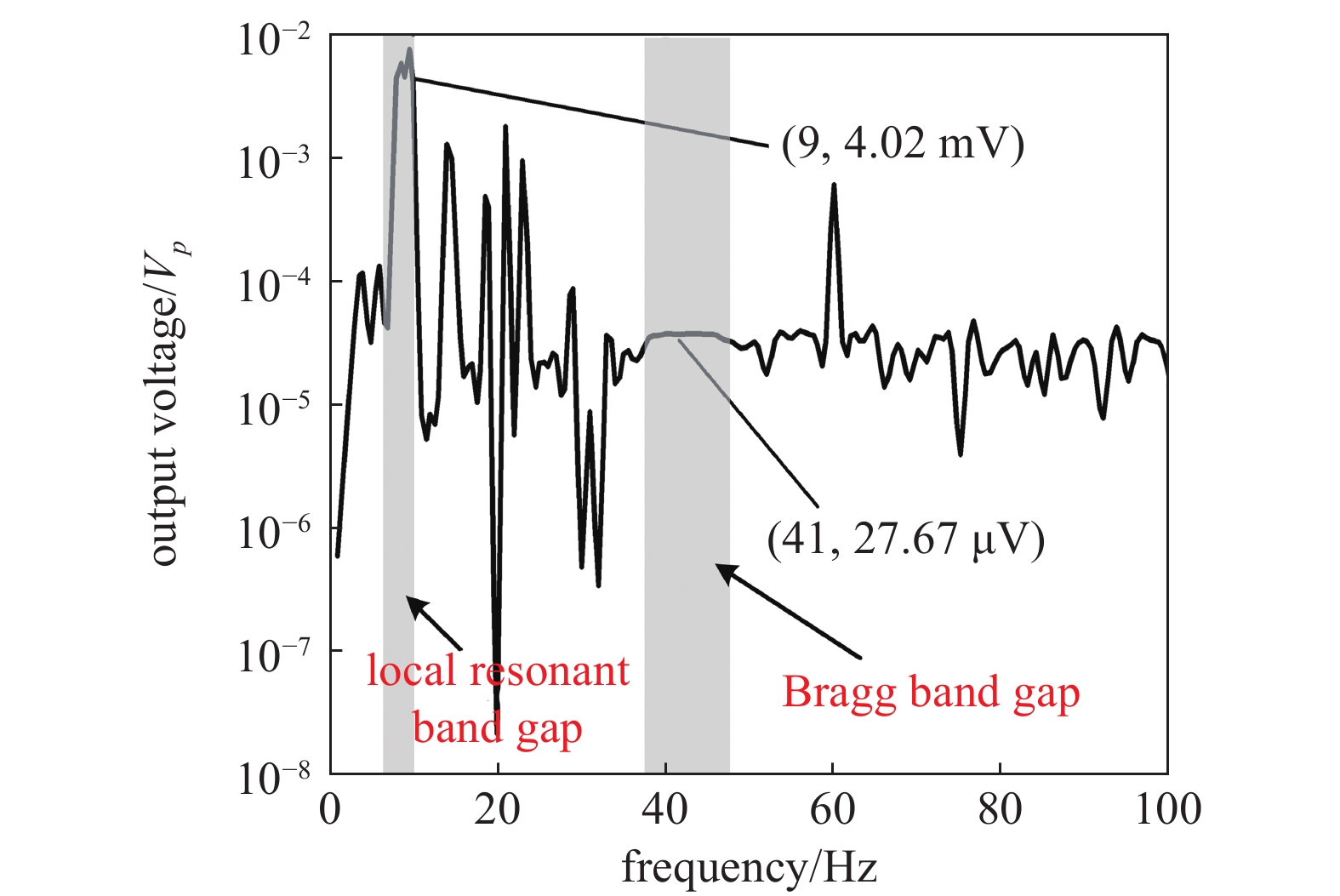
将有限元计算得到的激振点附近谐振器内滑动小球位移代入式(19)可以得到其输出电压响应曲线. 图14为超材料板激振点附近谐振器输出电压响应曲线. 通过分析输出电压响应曲线可知, 响应曲线在6 ~ 10 Hz的频率范围内产生峰值, 最大输出电压为4.02 mV, 这与谐振单元中球摆的共振频率相近. 因此, 在低频处局域共振带隙的频率范围内, 超材料板的振动被局限在谐振器处, 通过能量采集装置将机械能转化为电能, 使得超材料板振动衰减, 起到减振作用. 在38.5 ~ 47 Hz的Bragg带隙的频率范围内, 板的振动没有传递到谐振器中, 此时谐振器中感应线圈处于一个稳定的状态, 采集到的电压较少.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-471-14.jpg'" class="figure_img
figure_type1 bbb " id="Figure14" />
图
14
激励点附近谐振器的输出电压曲线
Figure
14.
Output voltage curve of resonator near excitation point
下载: 全尺寸图片
幻灯片
6.
结论
本文设计了一种低频振动隔离和能量采集的双功能超材料, 在实现低频振动隔离的同时, 对振动进行能量采集, 以实现隔振和能量采集的统一. 这种双功能超材料梁是将一个固接了感应线圈的球摆周期的放置在球型磁腔之中构成超材料, 从而利用带隙特性进行振动隔离, 并在带隙内采集到更多的能量. 首先建立了双功能超材料梁在横向激励下的动力学方程, 应用布鲁赫定理得到了超材料的能带关系, 并进行有限元计算, 设计了横向激励超材料的试验, 验证了超材料的带隙内振动隔离特性; 最后, 对二维双功能超材料的振动隔离和能量采集性能进行了研究. 主要结论如下:
(1) 在带隙的频率范围内, 振动响应能得到有效抑制. 控制超材料的参数可以对带隙的频率范围进行调控;
(2) 在谐振器中球摆滑动时所产生的能量可以转化为电能被利用, 在局域共振带隙的频率范围内采集到输出电压相比与带隙外的输出电压更大;
(3) 增加单胞尺寸和空腔尺寸对局域共振带隙的频率范围影响较小, 但它会显著降低Bragg带隙的频率范围, 拓宽频带, 提高超材料的隔振性能;
(4) 增加谐振质量可以显著降低由于谐振器共振引起的局域共振带隙的频率范围, 试验结果与理论结果基本一致. 对于二维的双功能超材料, 同样拥有较好的低频隔振性能和带隙内的振动能量采集性能. 综上所述, 本文所提出的双功能超材料梁在实现低频隔振的同时, 可以实现对振动能量更好的采集.
