删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

多个椭圆柱波浪力的一种解析解

本站小编 Free考研考试/2022-01-01


引 言


近年来, 中国的近海工程迅猛增加, 如人工岛, 跨海桥梁等, 对近海结构的研究日益受到人们的重视. 由于上述工程常年遭受波浪的威胁, 其支撑结构可能承受着强度相当大的波浪力, 而支撑结构广泛使用了多柱体, 柱体截面形式不再局限于圆形, 因此对非圆多柱体体系中波浪力的研究可为实际工程提供一定的理论指导.

近海工程中对波浪力的研究根据结构尺寸, 可以划分为对小尺度结构所受波浪力的研究和对大尺度结构所受波浪力的研究. 其中小尺度结构上的波浪力可以通过莫里森方程求解[1]; 当结构截面尺寸与波长之比大于0.2时, 大尺寸结构阻碍了波浪运动, 波浪在结构表面生成不可忽略的散射波, 因此波浪力的计算需要考虑波浪散射现象[2-3]. MacCamy和Fuchs[4]提出了绕射波浪理论来计算有限水域中大尺寸圆柱线性波浪力. 当波陡大时, 波浪中的非线性成分增多, 用线性波浪理论计算的结果误差增大, 国内外****就此提出了解决波浪二阶作用的方法[5-6]. Tao等[7]和Song等[8]利用比例边界元法(SBFEM)分析短峰波在圆柱上绕射以及多个任意截面形状柱体和线性波浪相互作用, 比例边界元对于解决波浪在柱面绕射问题较高的求解效率. Wang等[9]利用有限元方法, 解决了倾斜圆柱的波浪绕射问题. 流场中只存在单个结构的情形很少, 大多数情况下近海结构的承重构件由多柱体构成. Linton和Evans[10]提出了计算多个圆柱附近波浪速度势的简化公式. Kagemoto 和Yue[11]提出了一种精确代数方法来分析水波中多个三维物体之间的相互作用问题. Chen等[12]利用Null-Field积分方程来解决波浪在多直立圆柱体中散射问题, 以免带来用格林函数分析产生的不规则频率问题. 缪国平等[13]假设柱体表面有若干波动源, 就100根以上的单排圆桩体系在波浪中的响应进行了研究, 得到了多柱体对流体干扰的特点. Wang等[14]将流场分为结构附近的有限域和无限域, 用椭圆吸收边界模拟无限域, 最后利用有限元方法求出波浪对群桩的影响, 该方法可应用到任意光滑截面的多柱体上.

实际工程中同样存在非圆形截面柱体, 如椭圆形和类椭圆等. Chen和Mei[15]基于椭圆柱坐标系引入Mathieu函数, 将椭圆形固定平台表面的波浪力分解为角向分量和径向分量, 分析了结构表面绕射问题, 并得到相应解. William[16]简化了文献[15]中复杂级数展开, 并得到两种近似方法, 第一种适用于小曲率椭圆截面柱体, 另一种利用格林函数获得了柱体表面的流体速度势. Liu等[17-18]利用线性绕射理论和傅里叶展开, 推导了任意光滑截面的铅直柱体和截断柱体表面波浪力. Zhang和Williams[19]研究了水平刚性椭圆形薄板对入射波浪的绕射效应. Bhatta[20]推导了椭圆截面桩和圆形截面桩的波浪力计算公式, 并实现了前者到后者的变换. Wang等[21-22]首先提出针对单根椭圆柱上地震引起的动水力的解析解, 再利用有限元方法改进该发法为适用于工程的附加质量矩阵方法, 并且针对短峰波浪下的椭圆柱, 推导得到波浪力的解析表达式, 比较短峰波和一般线性波下椭圆柱周围的波爬.

对于多个非圆形截面柱体阵列结构, Chatjigeorgiou等[23-25]利用Bessel函数和Mathieu函数的加法定理, 依次研究了流体中椭圆截面群桩波浪散射问题, 椭圆柱和圆柱间的波浪散射问题和截断椭圆群桩上的波浪散射问题. Lee[26]则应用Collocation Multipole方法来解决椭圆截面多柱体间散射问题, 免除了Mathieu函数加法定理的繁复. Liu等[27]利用傅里叶级数将径向函数展开, 以求解任意光滑截面群桩(如余弦形截面、类椭圆截面等)上的波浪力.

上述多个柱体波浪力解析分析方法中, 多数考虑了入射波及入射波引起的单柱体散射波, 但没有考虑该散射波入射其他柱体后产生的第二次散射波以及高次散射波[25]. 本文基于椭圆坐标系和绕射波理论等, 推导得到考虑高次散射波的椭圆多柱体波浪力公式, 研究波数等参数变化时高次波对总波浪力的贡献, 以期为实际工程中估算波浪力提供参考数据.


1.
问题描述



1.1
控制方法和边界条件


流场中椭圆形截面柱体的阵列如图1所示. 假设所有柱体刚性, a为椭圆的半长轴, b为椭圆的半短轴, 底端固定在深度为h的流体中, 流体无旋、无黏性并且不可压缩. 该多柱体体系受到与x轴成α, 频率为$ omega $, 幅值为H/2的简谐波浪作用.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
柱体布置和坐标系统



Figure
1.
Arrangement of bodies and coordinates systems



下载:
全尺寸图片
幻灯片


本文使用的椭圆柱坐标系(ξ, μ, z)中, ξ和μ分别为椭圆柱坐标系的径向坐标和角向坐标, 两坐标互相正交; 坐标原点位于椭圆柱底部, z轴沿柱体轴线向上. 椭圆坐标系和笛卡尔直角坐标系转换关系如下







$$left. begin{array}{l}{x = mu cosh xi cos eta } {y = mu sinh xi sin eta } {z = z} end{array}
ight} $$
(1)

式中, $ {mu ^2} = {a^2} - {b^2} $；ξ，μ和z 取值范围分别为$ 0 leqslant xi < infty $, $ 0 leqslant mu < 2{text{π}} $和$ 0 leqslant z leqslant h $.

简谐波浪下流场中波浪压力为







$$ {p^e} = p{{
m{e}}^{ - {text{i}}omega t}} $$
(2)

椭圆柱坐标系中, 频域下的波浪压力$ p $满足如下流体控制方程







$$ frac{2}{{{mu ^2}left[ {cosh (2xi) - cos (2eta) }
ight]}}left( {frac{{{partial ^2}p}}{{partial {xi ^2}}} + frac{{{partial ^2}p}}{{partial {eta ^2}}}}
ight) + frac{{{partial ^2}p}}{{partial {z^2}}} = 0 $$
(3)

水体自由表面、刚性地面、水体与结构交界面和无穷远处的边界条件分别为







$$ {left. { - frac{{{omega ^2}}}{g}p + frac{{partial p}}{{partial z}} = 0}
ight|_{z = h}} $$
(4)







$$ {left. {frac{{partial p}}{{partial z}} = 0}
ight|_{z = 0}} $$
(5)







$$ {left. {frac{{partial p}}{{partial xi }} = 0}
ight|_{xi = {xi _0}}} $$
(6)







$$ mathop {lim }limits_{xi to infty } sqrt {mu cosh xi } left( {frac{1}{{mu sinh xi }}frac{{partial p}}{{partial xi }} - {text{i}}kp}
ight) = 0 $$
(7)

式中, 波数k满足$ {omega ^2} = gktanh (kh) $; $ {xi _0} $为柱体表面在柱体局部坐标系中的径向坐标.


1.2
波场分解


根据绕射波浪理论[4]: 当波浪入射后, 波浪会在大尺寸结构物表面产生散射波, 入射波场和散射波场叠加后, 形成的新的波场. 波浪入射后, 多柱体阵列中柱体周围的波场不同于单柱体周围的波场, 多柱体阵列中柱体上的波浪作用需要考虑入射波和散射波, 其中散射波还需考虑其在柱间多次绕射, 柱体上总的波浪力可以写为







$$ p{text{ = }}p_{text{ }}^{In} + p^{Sc} $$
(8)

式中, $ p^{Sc} $不仅考虑了入射波浪在该柱体上引起的散射波, 而且考虑了阵列中其他柱产生散射波、该散射波引起的高次散射波, 因此$ p^{Sc} $可以写为







$$ p^{Sc} = p^{S,left( 1
ight)}{text{ + }}sumlimits_{q = 2}^infty {left( {p_{text{ }}^{I,left( {q - 1}
ight)} + p^{S,left( q
ight)}}
ight)} $$
(9)

对式(3)应用分离变量法, $ pleft( {xi,eta,z}
ight) $可以写为







$$ pleft( {xi,eta,z}
ight){text{ = }}Zleft( z
ight)Pleft( {xi,eta }
ight) $$
(10)







$$ Zleft( z
ight){text{ = }}frac{{
ho gHcosh left( {kz}
ight)}}{{2cosh left( {kh}
ight)}} $$
(11)

因此柱体总的波浪力可以写为







$$ p{text{ = }}Zleft( z
ight)left( {P_{text{ }}^{In} + P^{Sc}}
ight) $$
(12)







$$ P^{Sc} = P^{S,left( 1
ight)}{text{ + }}sumlimits_{q = 2}^infty {left( {P_{text{ }}^{I,left( {q - 1}
ight)} + P^{S,left( q
ight)}}
ight)} $$
(13)


1.3
入射波浪压力


如图1所示, 流场中任意一点Q的入射波浪压力可以表达为







$$ P_i^{In}{text{ = }}{{
m{e}}^{{text{i}}kleft[ {left( {{X_i} + {x_i}}
ight)cos alpha + left( {{Y_i} + {y_i}}
ight)sin alpha }
ight]}} $$
(14)

式中$ {X_i} $和$ {Y_i} $是i号局部坐标系原点在整体坐标系中的坐标, xi和yi是Q点在i号局部坐标系中的坐标.

本文采用Abramowitz和Stegun[28]提出的符号记法, 因此在椭圆柱坐标系下, 入射波浪压力可以表示为[25]







$$ begin{split} &P_i^{In}left( {{xi _i},{eta _i},}
ight) = &;;;;;;2{varLambda _i};left[ {sumlimits_{m = 0}^infty {{{text{i}}^m}{{Mc}}_m^{left( 1
ight)}left( {{xi _i},{q_i}}
ight){{{{{ce}}} }_m}left( {{eta _i},{q_i}}
ight){{{{{ce}}} }_m}left( {alpha,{q_i}}
ight)} } +
ight. &left. {;;;;;;; sumlimits_{m = 1}^infty {{{text{i}}^m}{{Ms}}_m^{left( 1
ight)}left( {{xi _i},{q_i}}
ight){{s}}{{{e}}_m}left( {{eta _k},{q_i}}
ight){{{{{se}}} }_m}left( {alpha,{q_i}}
ight)} }
ight] end{split} $$
(15)

式中, ${varLambda _i}{text{ = }}{{
m{e}}^{{text{i}}kleft( {{X_i}cos alpha + {Y_i}sin alpha }
ight)}}$, $ {q_i}{text{ = }}left( {a_i^2 - b_i^2}
ight){k^2}/4 $. ${{Mc}}_m^{left( 1
ight)}$和${{Ms}}_m^{left( 1
ight)}$是第一类变形径向马蒂厄函数, ${{{{ce}}} _m}$和${{{{se}}} _m}$是角向马蒂厄函数.


2.
散射波浪压力求解



2.1
散射波浪压力


波浪入射到i号柱体后, 产生的第一次散射波满足式(3) ~式 (5)和式(7), 其一般表达式可以写为







$$ begin{split} &P_i^{S,left( 1
ight)}left( {{xi _i},{eta _i}}
ight) = & qquadsumlimits_{m = 0}^infty {C_{i,m}^{S,left( 1
ight)}{{Mc}}_m^{left( 3
ight)}left( {{xi _i},{q_i}}
ight){{{{{ce}}} }_m}left( {{eta _i},{q_i}}
ight)} + &qquadsumlimits_{m = 1}^infty {D_{i,m}^{S,left( 1
ight)}{{Ms}}_m^{left( 3
ight)}left( {{xi _i},{q_i}}
ight){{s}}{{{e}}_m}left( {{eta _i},{q_i}}
ight)} end{split} $$
(16)

式中$ C_{i,m}^{S,left( 1
ight)} $和$ D_{i,m}^{S,left( 1
ight)} $是待定系数, ${{Mc}}_m^{left( 3
ight)}$和${{Ms}}_m^{left( 3
ight)}$是第三类变形径向马蒂厄函数.

将式(15)和式(16)代入式(6), 求得







$$ left. begin{array}{l}C_{i,m}^{S,left( 1
ight)} = - {varLambda _i}dfrac{{2{{text{i}}^m}dot {{Mc}}_m^{left( 1
ight)}left( {{xi _{i0}},{q_i}}
ight){{{{{ce}}} }_m}left( {alpha,{q_i}}
ight)}}{{dot {{Mc}}_m^{left( 3
ight)}left( {{xi _{i0}},{q_i}}
ight)}} D_{i,m}^{S,left( 1
ight)} = - {varLambda _i}dfrac{{2{{text{i}}^m}dot {{Ms}}_m^{left( 1
ight)}left( {{xi _{i0}},{q_k}}
ight){{{{{se}}} }_m}left( {alpha,{q_i}}
ight)}}{{dot {{Ms}}_m^{left( 3
ight)}left( {{xi _{i0}},{q_i}}
ight)}} end{array}
ight} $$
(17)

式中$dot {{Mc}}_m^{left( 1
ight)}$和$dot {{Ms}}_m^{left( 1
ight)}$，$dot {{Mc}}_m^{left( 3
ight)}$和$dot {{Ms}}_m^{left( 3
ight)}$分别为相应径向马蒂厄函数对径向坐标的一阶导函数.

同一个流场中的其他柱产生的第一次散射波也会入射到i号柱体上, 表示为$ P_{i{text{ due to }}P_j^{S,left( 1
ight)}{text{ }}}^{I,left( 1
ight)} $. 所有柱产生的散射波再入射到i柱后, 波浪压力可以写为







$$begin{split} &P_{i{text{ }}}^{I,left( 1
ight)}{text{ = }}sumlimits_{scriptstyle j = 1hfillatopscriptstyle j ne ihfill}^N {P_{i{text{ due to }}P_j^{S,left( 1
ight)}{text{ }}}^{I,left( 1
ight)}} = &qquadsumlimits_{scriptstyle j = 1hfillatopscriptstyle j ne ihfill}^N {left[ {sumlimits_{m = 0}^infty {C_{j,m}^{S,left( 1
ight)}{{Mc}}_m^{left( 3
ight)}left( {{xi _j},{q_j}}
ight){{{{{ce}}} }_m}left( {{eta _j},{q_j}}
ight)} }
ight.} + &qquadleft. {sumlimits_{m = 1}^infty {D_{j,m}^{S,left( 1
ight)}{{Ms}}_m^{left( 3
ight)}left( {{xi _j},{q_j}}
ight){{s}}{{{e}}_m}left( {{eta _j},{q_j}}
ight)} }
ight]end{split} $$
(18)

根据马蒂厄函数的加法定理[29-30], 将式(18)中j号局部坐标(ξj, μj)变换到i号局部坐标系(ξi, μi)下, 如下所示. 马蒂厄函数的加法定理详见附录1







$$ begin{split} &P_i^{I,left( 1
ight)} = sumlimits_{scriptstyle j = 1hfillatopscriptstyle j ne ihfill}^N {sumlimits_{m = 0}^infty {C_{j,m}^{S,left( 1
ight)}} } cdot &qquadleft[ {sumlimits_{n = 0}^infty {Q_{n,m}^{left( 3
ight),ji}{{Mc}}_n^{left( 1
ight)}left( {{xi _i},{q_i}}
ight){{{{{ce}}} }_n}left( {{eta _i},{q_i}}
ight)} }
ight. - &qquad left. {{text{i}}sumlimits_{n = 1}^infty {{{left( { - 1}
ight)}^{ - n}}Q_{ - n,m}^{left( 3
ight),ji}{{Ms}}_n^{left( 1
ight)}left( {{xi _i},{q_i}}
ight){{s}}{{{e}}_n}left( {{eta _i},{q_i}}
ight)} }
ight] + &qquadsumlimits_{scriptstyle j = 1hfillatopscriptstyle j ne ihfill}^N {sumlimits_{m = 1}^infty {D_{j,m}^{S,left( 1
ight)}} } cdot &qquadleft[ {sumlimits_{n = 1}^infty {{{left( { - 1}
ight)}^{m - n}}Q_{ - n, - m}^{left( 3
ight),ji}{{Ms}}_n^{left( 1
ight)}left( {{xi _i},{q_i}}
ight){{s}}{{{e}}_n}left( {{eta _i},{q_i}}
ight)} }
ight. + &qquad left. {{text{i}}sumlimits_{n = 0}^infty {{{left( { - 1}
ight)}^m}Q_{n, - m}^{left( 3
ight),ji}{{Mc}}_n^{left( 1
ight)}left( {{u_i},{q_i}}
ight){{c}}{{{e}}_n}left( {{eta _i},{q_i}}
ight)} }
ight] end{split} $$
(19)


2.2
高次散射波浪压力


多柱体阵列中低次散射波在柱间传播, 并在柱体表面产生高次散射波. 其他柱产生的q?1次散射波使i号柱体产生第q次散射波, i号柱体q次散射波浪力可以表示为







$$begin{split} &P_i^{S,left( q
ight)}left( {{xi _i},{eta _i}}
ight) = &qquadsumlimits_{m = 0}^infty {C_{i,m}^{S,left( q
ight)}{{Mc}}_m^{left( 3
ight)}left( {{xi _i},{q_i}}
ight){{{{{ce}}} }_m}left( {{eta _i},{q_i}}
ight)} + &qquadsumlimits_{m = 1}^infty {D_{i,m}^{S,left( q
ight)}{{Ms}}_m^{left( 3
ight)}left( {{xi _i},{q_i}}
ight){{s}}{{{e}}_m}left( {{eta _i},{q_i}}
ight)} end{split} $$
(20)

如式(18), 流场中其他柱产生的q?1次散射波传播到i号柱体上产生的波浪压力可以写为







$$ begin{split} &P_{i{text{ }}}^{I,left( q
ight)}{text{ = }}sumlimits_{scriptstyle j = 1hfillatopscriptstyle j ne ihfill}^N {P_{i{text{ due to }}P_j^{S,left( {q - 1}
ight)}{text{ }}}^{I,left( q
ight)}} = &qquad sumlimits_{scriptstyle j = 1hfillatopscriptstyle j ne ihfill}^N {left[ {sumlimits_{m = 0}^infty {C_{j,m}^{S,left( {q - 1}
ight)}{{Mc}}_m^{left( 3
ight)}left( {{xi _j},{q_j}}
ight){{{{{ce}}} }_m}left( {{eta _j},{q_j}}
ight)} }
ight.} + &qquad left. {sumlimits_{m = 1}^infty {D_{j,m}^{S,left( {q - 1}
ight)}{{Ms}}_m^{left( 3
ight)}left( {{xi _j},{q_j}}
ight){{s}}{{{e}}_m}left( {{eta _j},{q_j}}
ight)} }
ight] end{split}$$
(21)

将式(21)转换坐标到i柱局部坐标系下为







$$ begin{split} &P_i^{I,left( q
ight)} = sumlimits_{scriptstyle j = 1hfillatopscriptstyle j ne ihfill}^N {sumlimits_{m = 0}^infty {C_{j,m}^{S,left( {q - 1}
ight)}} } cdot &qquadleft[ {sumlimits_{n = 0}^infty {Q_{n,m}^{left( 3
ight),ji}{{Mc}}_n^{left( 1
ight)}left( {{xi _i},{q_i}}
ight){{{{{ce}}} }_n}left( {{eta _i},{q_i}}
ight)} }
ight. - &qquad left. { {text{i}}sumlimits_{n = 1}^infty {{{left( { - 1}
ight)}^{ - n}}Q_{ - n,m}^{left( 3
ight),ji}{{Ms}}_n^{left( 1
ight)}left( {{xi _i},{q_i}}
ight){{s}}{{{e}}_n}left( {{eta _i},{q_i}}
ight)} }
ight] + &qquadsumlimits_{scriptstyle j = 1hfillatopscriptstyle j ne ihfill}^N {sumlimits_{m = 1}^infty {D_{j,m}^{S,left( {q - 1}
ight)}} } cdot&qquad left[ {sumlimits_{n = 1}^infty {{{left( { - 1}
ight)}^{m - n}}Q_{ - n, - m}^{left( 3
ight),ji}{{Ms}}_n^{left( 1
ight)}left( {{xi _i},{q_i}}
ight){{s}}{{{e}}_n}left( {{eta _i},{q_i}}
ight)} }
ight. + &qquad left. {{text{ i}}sumlimits_{n = 0}^infty {{{left( { - 1}
ight)}^m}Q_{n, - m}^{left( 3
ight),ji}{{Mc}}_n^{left( 1
ight)}left( {{u_i},{q_i}}
ight){{c}}{{{e}}_n}left( {{eta _i},{q_i}}
ight)} }
ight] end{split} $$
(22)

为求式(20)中的待定系数, 将式(20)和式(22)代入式(6), 得到待定系数$ C_{i,m}^{S,left( q
ight)} $和$ D_{k,m}^{S,left( q
ight)} $如下







$$ left. begin{aligned} &C_{i,m}^{S,left( q
ight)} = - frac{{dot {{Mc}}_m^{left( 1
ight)}left( {{xi _{i0}},{q_i}}
ight)}}{{dot {{Mc}}_m^{left( 3
ight)}left( {{xi _{i0}},{q_i}}
ight)}} cdot &qquadsumlimits_{scriptstyle j = 1hfillatopscriptstyle j ne ihfill}^N {left[ {sumlimits_{n = 0}^infty {C_{j,n}^{S,left( {q - 1}
ight)}Q_{m,n}^{left( 3
ight),ji}} }
ight.} + &qquadleft. { {text{i}}sumlimits_{n = 1}^infty {D_{j,n}^{S,left( {q - 1}
ight)}{{left( { - 1}
ight)}^n}Q_{m, - n}^{left( 3
ight),ji}} }
ight] &D_{i,m}^{S,left( q
ight)} = - frac{{dot {{Ms}}_m^{left( 1
ight)}left( {{xi _{i0}},{q_i}}
ight)}}{{dot {{Ms}}_m^{left( 3
ight)}left( {{xi _{i0}},{q_i}}
ight)}} cdot &qquadsumlimits_{scriptstyle j = 1hfillatopscriptstyle j ne ihfill}^N {left[ {sumlimits_{n = 1}^infty {D_{j,n}^{S,left( {q - 1}
ight)}{{left( { - 1}
ight)}^{n - m}}Q_{ - m, - n}^{left( 3
ight),ji}} }
ight.} - &qquadleft. { {text{i}}sumlimits_{n = 0}^infty {C_{j,n}^{S,left( {q - 1}
ight)}{{left( { - 1}
ight)}^{ - m}}Q_{ - m,n}^{left( 3
ight),ji}} }
ight] end{aligned}
ight} $$
(23)


2.3
总波浪力


多柱体体系中, i号柱体上总的波浪压力可以写为







$$ {p_i}{text{ = }}Zleft( z
ight){P_i} $$
(24)







$$ {P_i} = P_{i{text{ }}}^{In} + P_i^{S,left( 1
ight)}{text{ + }}sumlimits_{q = 2}^infty {left( {P_{i{text{ }}}^{I,left( {q - 1}
ight)} + P_i^{S,left( q
ight)}}
ight)} $$
(25)

i号柱体所受的总波浪力可以表示为







$$ F_i^{} = sqrt {{{left( {F_i^y}
ight)}^2} + {{left( {F_i^x}
ight)}^2}} $$
(26)







$$ F_i^x = - int_0^h {int_0^{2{text{π}} } {{p_i}{b_i}cos {eta _i}{text{d}}{eta _i}} } {text{d}}z $$
(27a)







$$ F_i^y = - int_0^h {int_0^{2{text{π}} } {{p_i}{a_i}sin {eta _i}{text{d}}{eta _i}} } {text{d}}z $$
(27b)


3.
数值算例



3.1
方法验证


首先, 由于本方法在计算求解时会对式(25)中高次散射波的累加进行截断, 而截断会引入一定的截断误差, 所以先讨论该截断误差对计算结果的影响; 其次, 通过Wang等[14]提出的波浪压力数值解验证本文提出的椭圆形截面柱体波浪压力的解析解. 四柱体阵列如图2所示, 图2中D为柱体间净距, 定义其与椭圆长轴的比值$ {D_r} = 1.0 $, 4个椭圆柱柱体具有相同的尺寸, 长轴和短轴比值$ a/b{text{ = }}1.5 $. 图3给出了图2布置下不同截断数q时, $ F_i^x $随波数ka变化的曲线, 可以看出当q > 12时本方法获得波浪力计算结果基本稳定, 因此为使解析解求解高效且准确, 后续计算采用q = 15为高次散射波的截断数. 图4为$ ka = 1 $时, 本文解析方法和数值方法得到的柱体上波浪压力, 图5为$ {D_r} = 1 $时, 本文解析方法和数值方法得到的柱体上波浪力, 假设波浪以两个入射角α入射; 图6为$ ka = 1 $时, 本文解析方法和数值方法得到的流场波浪压力云图, 图7为解析方法与数值方法计算得到的C1和C2柱上波浪压力的相对误差; 可以看出本文解和椭圆数值解相对误差较小, 各图中本文解结果和数值解结果吻合良好.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
四柱体阵列图



Figure
2.
Sketch of four bodies arranged in a square form.



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
截断误差对本文解计算结果的影响



Figure
3.
Impacts of truncation error on the present method



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
不同入射角($ alpha {text{ = }}{{text{0}}^{ circ }} $和$ alpha {text{ = 9}}{{text{0}}^{ circ }} $)下数值解[14]与本文解的对比



Figure
4.
The wave pressures on bodies $ {P_i} $ versus $ theta $ with N = 4 and ka = 1 obtained present method by and the FEM[14]



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
不同入射角($ alpha {text{ = }}{{text{0}}^{ circ }} $和$ alpha {text{ = 9}}{{text{0}}^{ circ }} $)下数值解[14]与本文解的对比



Figure
5.
The wave forces on bodies $ {F_i} $ versus ka with N = 4 obtained by the present method and FEM[14]



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
入射角$ alpha {text{ = }}{{text{0}}^{ circ }} $时数值解[14]与本文解云图



Figure
6.
The wave fields with N = 4, $ alpha {text{ = }}{{text{0}}^{ circ }} $ and ka = 1 obtained by the FEM[14] and present method



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
入射角$ alpha {text{ = }}{{text{0}}^{ circ }} $时数值解与本文解的相对误差



Figure
7.
The relative error of the wave pressure between the present method and the FEM with N = 4, $ alpha {text{ = }}{{text{0}}^{ circ }} $ and ka = 1



下载:
全尺寸图片
幻灯片



3.2
方法应用


本节将讨论高次波的影响, 根据柱体排列设置了两种柱体阵列: ①双柱(图8)、②四柱(图2). 所示各工况中柱体截面尺寸相同, 长轴和短轴之比a/b = 1.5. q = 2代表的曲线是不考虑高次散射波的解析解, q = 15代表的曲线是考虑高次散射波的解析解. 从图9可以观察到, 单柱情况下的波浪力和多柱情况下的波浪力是不同的, 该现象随着柱数的增加而显著, 且和椭圆长轴与水流方向的夹角有关.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
双柱体阵列图



Figure
8.
Sketch of arrangement of twin bodies standing side by side



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
不同入射角($ alpha {text{ = }}{{text{0}}^{ circ }} $和$ alpha {text{ = 9}}{{text{0}}^{ circ }} $)下两种阵列的本文解与单柱解的对比



Figure
9.
The wave forces on bodies $ {F_i} $ versus ka with N = 2 and 4 compared with that of an isolated body



下载:
全尺寸图片
幻灯片


图10给出了双柱阵列中, 高次散射波对柱体上波浪作用影响的结果. 图中纵坐标为波浪力比值$ F_i^{q = 15}/F_i^{q = 2} $, $ F_i^{q = 15} $表示各柱体上考虑高次散射波的总波浪力, $ F_i^{q = 2} $表示各柱体上不考虑高次散射波的总波浪力. 图中给出了3种波浪入射角度下(0°，45°和90°), ka取值在0.2~2.0之间的结果. 图9(a)中, 因为阵列沿x轴对称所以C1和C2上的波浪力比值相等, 高次波的影响不明显; 从图10 (a)和图10(b)中可以看出, 当ka小于0.5时, 高次波对两柱体的影响可以忽略, 当ka大于0.5后, 高次波的影响增大到不可忽略. 图11给出了ka = 1时Dr取值在0.5~5.0之间的结果. 图11(b)和图11(c)表明Dr大于2后, 二柱阵列的柱体受高次波的影响才会趋于减少, 但即使净距为柱体长轴两倍以上, 高次波的影响仍然明显; 图11(c)中, C1受到上游柱体C2的保护, C1受到高次波的影响比C2小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
双柱阵列中各柱体总受力比值



Figure
10.
Scaling values of total wave force $ F_i^{q = 15}/F_i^{q = 2} $ on bodies versus ka as twin bodies standing side by side



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
双柱阵列中各柱体总受力比值



Figure
11.
Scaling values of total wave force $ F_i^{q = 15}/F_i^{q = 2} $ on bodies versus Dr as twin bodies standing side by side



下载:
全尺寸图片
幻灯片


图12给出了四柱阵列中, 高次散射波对柱体上波浪作用影响的结果. 由于对称性, 波浪沿x轴入射时($ alpha {text{ = }}{{text{0}}^{ circ }} $), C1和C3计算结果相同, C2和C4计算结果相同; 同理, 波浪沿y轴入射时($ alpha {text{ = 9}}{{text{0}}^{ circ }} $), C1和C2计算结果相同, C3和C4计算结果相同. 比较两个入射波浪方向不同的结果, 可以发现因为柱体在x轴上的投影面积大于柱体在y轴上的投影面积, 所以波浪沿y轴入射时高次波对柱体所受波浪力的影响更大. 图13给出了ka = 1时Dr取值在0.5~5.0之间的结果. 四柱阵列的下游柱体波浪力比值在0.5 < Dr < 1.0间大于上游柱体的比值, 在Dr > 2.0之后才小于上游柱体的比值并趋于减小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
四柱阵列中各柱体总受力比值



Figure
12.
Scaling values of total wave force $ F_i^{q = 15}/F_i^{q = 2} $ on bodies versus ka as four bodies arranged in a square form



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
四柱阵列中各柱体总受力比值



Figure
13.
Scaling values of total wave force $ F_i^{q = 15}/F_i^{q = 2} $ on bodies versus Dr as four bodies arranged in a square form



下载:
全尺寸图片
幻灯片


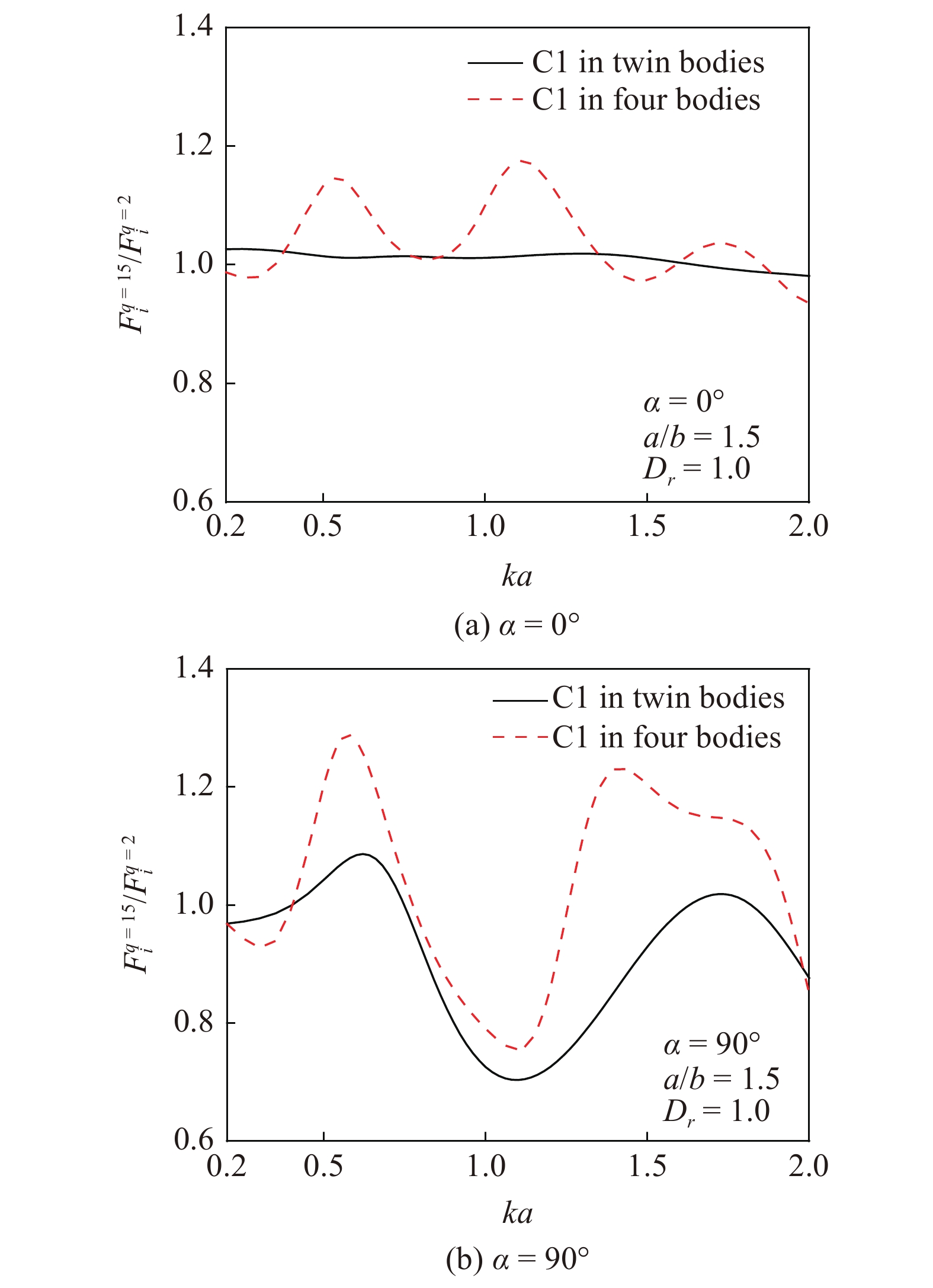
图14和图15给出了柱体数量不同的情况下, C1上波浪力比值随参数(ka，Dr)的变化. 综合来看, 随ka和Dr增加, 四柱阵列中C1波浪力比值变化, 比双柱阵列情况下的比值变化要剧烈; 随着柱体数量的增多, 由于叠加效应, 高次波影响也随之增加.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
两种阵列中C1柱体总受力比值



Figure
14.
Scaling values $ F_1^{q = 15}/F_1^{q = 2} $ of C1 versus ka in two arrangements



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-15-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15-1" />



15
两种阵列中C1柱体总受力比值



15.
Scaling values $ F_1^{q = 15}/F_1^{q = 2} $ of C1 versus Dr in two arrangements



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-318-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />



图
15
两种阵列中C1柱体总受力比值(续)



Figure
15.
Scaling values $ F_1^{q = 15}/F_1^{q = 2} $ of C1 versus Dr in two arrangements (continued)



下载:
全尺寸图片
幻灯片


表1对比了本文解和参考解[14]在ka = 1时, 不同柱数, 不同柱间距时波浪力计算效率. 因为有限元方法计算耗时和网格单元划分大小以及网格数目成正相关, 所以当柱数增加或者柱间距增加后, 用来模拟水域的单元也随之增多, 所以本文解比参考解效率高.




表
1
计算波浪力的用时 (s)



Table
1.
The numerical costs for calculating the total wave forces (s)



table_type1 ">
NMethodDr = 0.5Dr = 1.0
2analytical9.518.87
FEM2.9410.54
4analytical52.9548.61
FEM9.6994.18





下载:
导出CSV
|显示表格



4.
结论


根据绕射波理论等, 基于椭圆柱坐标系, 首先通过求解马蒂厄方程, 得到椭圆单柱体结构波浪压力公式, 再考虑多柱体体系中高次散射波问题, 推导得到多柱体体系中椭圆柱体结构波浪力计算公式. 本文方法与已有数值方法对比结果表明, 本文解和数值解吻合的较好, 而当柱数目增加或柱间距增大时, 本文解的计算效率比有限元方法的高.

将本文方法应用于计算双柱阵列和四柱阵列的波浪力, 分析了高次散射波对结构所受波浪作用的影响. 结果表明: 波数ka<0.5时, 高次散射波影响较小, 大波数的情况下, 不能忽略高次波的影响; 随着柱体间距离的增加, 高次波的影响有减小的趋势, 但仍存在波动; 高次波对上游柱体波浪力的影响比下游柱体大; 多柱体体系中, 柱体数量增加后, 柱体产生的高次散射波会叠加, 高次波影响也随之增加, 而结构所受的高次波作用因参数发生的波动会变剧烈.

附录1$ ;$

Chatjigeorgiou等[17]在S?rmark等[21]的基础上化简了将马蒂厄函数的加法定理, 具体可以表示为






$$ begin{split} &{{Mc}}_n^{left( l
ight)}left( {{xi _j},{q_j}}
ight){{{{ce}}} _n}left( {{eta _j},{q_j}}
ight){text{ = }} &qquad sumlimits_{m = 0}^infty {Q_{m,n}^{left( l
ight),ji}{{Mc}}_m^{left( 1
ight)}left( {{xi _i},{q_i}}
ight){{{{{ce}}} }_m}left( {{eta _i},{q_i}}
ight)} - &qquad {text{i}}sumlimits_{m = 1}^infty {{{left( { - 1}
ight)}^{ - m}}Q_{ - m,n}^{left( l
ight),ji}{{Ms}}_m^{left( 1
ight)}left( {{xi _i},{q_i}}
ight){{s}}{{{e}}_m}left( {{eta _i},{q_i}}
ight)} end{split} tag{A1}$$






$$ begin{split} &{{Ms}}_n^{left( l
ight)}left( {{xi _j},{q_j}}
ight){{s}}{{{e}}_n}left( {{eta _j},{q_j}}
ight){text{ = }} &qquad sumlimits_{m = 1}^infty {{{left( { - 1}
ight)}^{n - m}}Q_{ - m, - n}^{left( l
ight),ji}{{Ms}}_m^{left( 1
ight)}left( {{xi _i},{q_i}}
ight){{s}}{{{e}}_m}left( {{eta _i},{q_i}}
ight)} + &qquad {text{ i}}sumlimits_{m = 0}^infty {{{left( { - 1}
ight)}^m}Q_{m, - n}^{left( l
ight),ji}{{Mc}}_m^{left( 1
ight)}left( {{xi _i},{q_i}}
ight){{c}}{{{e}}_m}left( {{eta _i},{q_i}}
ight)} end{split} tag{A2}$$

其中$Q_{m,n}^{left( l
ight),ji}$可以表示为






$$ begin{split} &Q_{m,n}^{left( l
ight),ji} = sumlimits_{s = - infty }^infty {sumlimits_{p = - infty }^infty {d_{m - p,p}^prime left( {{q_i}}
ight)} } times &qquadZ_{p - s}^lleft( {{k_0}{R_{ji}}}
ight){d_{s - n,n}}left( {{q_j}}
ight){{
m{e}}^{{text{i}}left( {s - p}
ight){theta _{ji}}}} end{split}tag{A3}$$






$$ Z_m^lleft( {{k_0}{R_{ji}}}
ight) = left{ begin{aligned} &{{text{J}}_m}left( {{k_0}{R_{ji}}}
ight) , ;; l = 1 &{{text{Y}}_m}left( {{k_0}{R_{ji}}}
ight) , ;; l = 2 &{text{H}}_m^{left( 1
ight)}left( {{k_0}{R_{ji}}}
ight) , ;; l = 3 &{text{H}}_m^{left( 2
ight)}left( {{k_0}{R_{ji}}}
ight) , ;; l = 4 end{aligned}
ight. tag{A4}$$






$$ left. begin{aligned} &d_{m - p,p}^prime left( {{q_i}}
ight) = &qquad {2^{ - 1/2}}{left( { - 1}
ight)^{left( {m - p}
ight)/2}}A_p^mleft( {{q_i}}
ight) ;; left( {m = 0,1,2,...}
ight) &d_{ - m - p,p}^prime left( {{q_i}}
ight) = &qquad - {2^{ - 1/2}}{left( { - 1}
ight)^{left( { - m - p}
ight)/2}}B_p^mleft( {{q_i}}
ight) ;; left( {m = 1,2,3,...}
ight) &d_{2m,0}^prime left( {{q_i}}
ight) = &qquad {2^{1/2}}{left( { - 1}
ight)^n}A_0^{2m}left( {{q_i}}
ight) ;; (p = 0) &{d_{s - n,n}}left( {{q_j}}
ight) = &qquad {2^{ - 1/2}}{left( { - 1}
ight)^{left( {s - n}
ight)/2}}A_s^nleft( {{q_j}}
ight) ;; left( {n = 0,1,2,...}
ight) &{d_{s + n, - n}}left( {{q_j}}
ight) = &qquad - {2^{ - 1/2}}{left( { - 1}
ight)^{left( {s + n}
ight)/2}}B_s^nleft( {{q_j}}
ight) ;; left( {n = 1,2,3,...}
ight) &{d_{ - 2n,2n}}left( {{q_j}}
ight) = &qquad {2^{1/2}}{left( { - 1}
ight)^{ - n}}A_0^{2n}left( {{q_j}}
ight) ;; (s = 0) end{aligned}
ight} tag{A5}$$

式中, $ {text{J}}_{m}(·) $为第一类m阶贝塞尔函数, $ {text{Y}}_{m}(·) $为第二类m阶贝塞尔函数,$ {text{H}}_{m}^{left(1
ight)}(·) $为第一类m阶汉克尔函数, $ {text{H}}_{m}^{left(2
ight)}(·) $为第二类m阶汉克尔函数. 当n?p和s?m为奇数时, $ {d^prime } $和$ d $为0.

相关话题/结构 计算 图片 柱体 工程
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于人工神经网络的非结构网格尺度控制方法
    引言网格生成是计算流体力学(computationalfluiddynamics,CFD)数值计算的第一步,也是未来CFD六大重要研究领域之一[1-2].在现代CFD应用过程中,自动生成复杂构型的高质量网格(包括网格自适应)依然是一个重大挑战性问题.自动化程度和网格质量是网格生成过程中最重要的两个问 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 考虑混凝土塑性耗散的CDM-XFEM裂缝计算方法
    引言混凝土结构是建筑、交通、水利等领域的重要基础材料,其可塑性高、耐久性好是受广泛应用的主要原因.但混凝土抗拉强度远低于抗压强度[1],结构在服役期间受外界载荷的影响容易产生裂缝[2],裂缝的出现不仅会降低结构刚度,还为外部侵蚀介质的侵入提供了快捷通道,从而加速内部钢筋锈蚀[3-4]、降低结构承载力 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • K<sub>0</sub>超固结结构性黏土的本构模型
    引言自然界存在的天然黏土通常是K0固结与结构性并存的状态[1-2],而K0固结又按照当前竖向应力是否大于先期固结压力而分为K0正常固结与K0超固结黏土.大量的室内试验以及现场测试表明,K0正常固结黏土由于初始固结为偏压固结,与等方向正常固结黏土相比,其在大主应力与先期固结压力一致的情况下,K0固结黏 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 一种新的玻尔兹曼方程可计算模型构造与分析
    引言近年来,随着对临近空间战略意义认识的加深,各航空航天大国发展了众多临近空间飞行器.为满足长航时、大载荷、高超声速巡航等需求,这类临近空间飞行器通常整体尺寸较大,各部件间差异显著,飞行过程会出现多物理多场耦合、多流区共存的多尺度复杂流动现象,传统的数值模拟方法如基于宏观连续介质假设的纳维?斯托克斯 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 页岩凝析气藏相平衡的快速准确计算方法
    引言随着以煤炭、石油和木柴为代表的传统能源消耗带来的巨量的空气污染日益引起全社会的关注,天然气作为一种相对较为清洁的能源得到了广泛的重视[1].近年来在非常规油气藏勘探和开发技术上的迅猛发展,使得具有巨大潜在储量但一直得不到有效开发的以页岩气为代表的非常规油气资源成为了投资热点和研究焦点[2].中国 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 软材料粘接结构界面破坏研究综述
    引言因其特有的低模量和能量耗散等“软”的特性以及优异的“小激励大响应”等特征,多种多样的软材料,如水凝胶、介电弹性体以及聚甲基氧硅烷等被广泛应用在软机器人、生物医学和柔性电子等各个领域[1-4].近些年,软材料的力学行为已经成为学术界和工业界广泛关注的热点之一.在实际应用中,软材料一般需要粘附于某种 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于喷流拟序结构预测的SGS模型比较研究
    引言拟序结构普遍存在于湍流中[1–3],并影响湍流的发生、输运与耗散等过程,对湍流拟序结构的研究、对于理解湍流机理、分析流动相互作用有重要的意义.从大涡模拟来看,正确预测湍流拟序结构的关键就在于算法和亚网格尺度(sub-grid-scale,SGS)模型的准确性.在算法方面,传统的大涡模拟方法求解网 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于Darcy-Stokes耦合模型的多孔介质颗粒悬浮液等效黏性系数计算
    引言颗粒悬浮液广泛存在于自然界及工程应用领域,其黏性特征对悬浮液的流动行为有着重要的影响[1-4].早在1905年,Einstein[5]就研究了低浓度条件下球形固体颗粒对流体黏性的影响,给出了悬浮液等效黏度系数计算的一个强有力的理论框架,并得到了低浓度球形颗粒悬浮液的著名的Einstein黏性公式 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 新型负刚度吸能结构力学特性分析
    引言在冲击载荷作用下,吸能材料的应用具有重要的工程意义.传统的减振吸能方法主要有两种:其一,利用材料的塑性变形实现能量吸收耗散[1],如汽车保险杠和轻型自行车头盔均是基于这一原理进行结构以及超材料设计,然而破坏性的塑性变形使得材料无法重复利用;其二,利用材料的黏弹特性[2-3],实现重复性的能量吸收 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.