引言

流体运动广泛存在于工程应用中, 例如航空航天工程、海洋工程、土木工程等领域. 理论上, 流体运动可用纳维?斯托克斯(Navier?Stokes, N-S)方程描述. 但对流项的存在使得该方程具有高度非线性、多尺度特性, 给方程求解带来巨大困难, 方程仅在少数情况可求得解析解或近似解. 复杂流动问题的研究通常借助计算流体力学与实验流体力学. 当采用数值方法模拟流场时, 由于多尺度特性带来的巨大计算量使得高精度的直接数值模拟(direct numerical simulation, DNS)技术难以实现; 雷诺平均(Reynolds averaged N-S simulation, RANS)方法与大涡模拟(large eddy simulation, LES)方法仍是求解工程流动问题的主要手段. 但是由于依赖经验, 传统雷诺应力或亚格子应力闭合模型无法精准模拟复杂流动. 由于实验环境、实验设备限制, 实验流体力学获得流场丰富时空细节依然存在困难.

近年来, 机器学习和深度学习技术飞速发展. 依赖于灵活的网络架构、强大的非线性逼近能力与高效的优化算法, 深度学习在以数据为基础解决图像识别^[1], 自然语言处理^[2], 无人驾驶^[3]等问题时获得了巨大成功. 在过去的几十年里, 高性能计算机和先进流体实验设备的应用使得湍流等流动研究领域积累了大量数据. 深度学习可高效挖掘这些大规模高维数据中蕴含的丰富流动物理特征, 为研究流体力学建模方法与高效模拟方法带来新机遇^[4-5], 并且已经在湍流闭合模型领域取得重要进展. 例如, Edeling等^[6-7]基于实验数据采用高斯过程回归对k?ε两方程的多个系数进行校准, 提升了雷诺应力预测精度; Ling等^[8]采用全连接神经网络建立了Pope^[9]提出的不变量到雷诺应力非线性基函数系数的预测模型, 模型自动满足伽利略不变性, 在二次流、周期丘陵等流动问题模拟中显著提升了雷诺应力预测精度; Zhu等^[10]采用径向基神经网络建立了流场平均量到涡黏系数的代数模型, 在机翼绕流场求解中与Spallart?Allmaras模型涡黏系数偏微分方程求解方法相比, 求解精度保持不变的条件下求解效率得到了显著提升; Jiang等^[11]基于残差神经网络建立了雷诺应力各向异性张量预测模型, 并通过引入新的混合时间尺度作为输入成功解决了多值映射问题; Xie等^[12]采用神经网络成功建立了非线性亚格子应力代数模型, 有效提升了LES模拟精度. Duraisamy等^[13]和谢晨月等^[14]对人工智能在湍流闭合模型领域(包括雷诺应力模型和亚格子应力模型)的成功应用进行了系统综述.

不同于图像识别、自然语言处理、无人驾驶等典型人工智能任务, 深度学习模型预测的流场需满足流体物理规律, 如N-S方程、典型能谱等. 当仅基于流场数值模拟或实验测量数据建立流场深度学习模型时, 流体物理规律并未直接嵌入模型. 但在网络训练过程中, 待学习参数的调整使得网络逐渐逼近所模化流场的流体物理规律; 训练完成的网络若在测试集上具有良好的泛化能力, 则认为网络成功捕捉了流场预测所需流体物理规律. 另一方面, 流体物理规律可嵌入深度学习模型, 在网络输入特征选取、架构设计、损失函数设计时对其充分考虑, 提升深度学习模型预测精度、泛化能力, 此类方法称为物理增强的深度学习方法^[15]. 具体地, 根据流体物理规律选取网络输入特征或设计网络架构的方法称为物理启发的深度学习方法; 直接将流体物理规律显式融入网络损失函数或网络架构的方法称为物理融合的深度学习方法. 本文首先介绍深度学习灵活的网络架构、强大的非线性逼近能力与高效的优化算法, 进一步阐述基于深度学习上述优良特性发展的物理增强深度学习方法在流场降阶模型与流动控制方程求解领域的研究进展.

1.
深度神经网络

作为深度学习发展的开端, Hinton等^[16]利用贪婪逐层训练算法完成了深度置信网络与全连接神经网络^[17]的训练. 自此, 深度学习等数据驱动技术利用灵活网络结构, 借助高效优化算法, 获得了对高维、非线性问题的强大逼近能力, 在图像识别、自然语言处理等数据建模领域飞速发展.

1.1
神经网络模型

多层感知机(multi-layer perceptron, MLP)或深度神经网络(deep neural networks, DNN)为深度学习最基本模型. 以$ x in {{mathbb{R}}^d} $为输入, 隐藏层层数为L的DNN可表示为

$$ {f_theta }left( x ight) = left( {{f_{L + 1}} circ {f_L} circ cdots circ {f_1}} ight)left( x ight) $$

(1)

式中${f_theta }:{{mathbb{R}}^d} to {{mathbb{R}}^c}$为DNN含可训练参数$ theta $对应映射. $ {f_l} $为各隐藏层对应映射为

$$ left. {begin{array}{*{20}{l}} {{f_l}left( {{x_{l - 1}}} ight) = sigma left( {{W_l}{x_{l - 1}} + {b_l}} ight),{text{ }}l = 1:L} {f_{L + 1}left( x ight) = {W_{L + 1}}x + {b_{L + 1}}} end{array}} ight}$$

(2)

式中, $ {x_{l - 1}} $为第l个隐藏层的输入($ {x_0} = x $), $ {W_l} $和$ {b_l} $分别为可训练权重矩阵与偏置向量(并共同构成可训练参数$ theta $), $ sigma left( cdot
ight) $为非线性激活函数.

卷积神经网络(convolutional neural networks, CNN)^[18]是针对二维图像等具有网格状拓扑结构数据开发的神经网络架构, 被广泛用于图像识别^[1,19]、图像去噪^[20]、图像修复^[21]等领域. CNN主要包含卷积层、池化层和全连接层等隐藏层, 典型的CNN模块为: 特征图通过卷积层提取特征, 非线性激活函数作用于卷积层后提升网络非线性逼近能力, 进一步通过池化层完成降采样. Goodfellow等^[22]指出, 由于卷积层在输出特征图的同一通道引入了卷积核参数共享, 可以提取输入特征图中对平移保持等变的特征; 池化层(尤其是用于降采样的最大池化层)可有效提取输入特征图中对少量平移保持不变的特征. 卷积层中的卷积运算为

$$ left( {h circledast q} ight)left[ {{r_1},{r_2}} ight]: = sumlimits_{{k_1},{k_2} = - frac{{N - 1}}{2}}^{frac{{N - 1}}{2}} {qleft[ {{k_1},{k_2}} ight]h} left[ {{r_1} + {k_1},{r_2} + {k_2}} ight] $$

(3)

式中, h为卷积层输入特征图($L times L$维度矩阵), $q$为$N times N$维卷积核(设$N$为奇数), $ circledast $为卷积算子, 式(3)右端即为卷积层输出特征图在$ left( {{r_1},{r_2}}
ight) $位置取值; 进一步可以引入卷积核的矩函数$Mleft( q
ight) = $$ {left( {{m_{i,j}}}
ight)_{N times N}}$, 其中

$$ begin{split} &{m_{i,j}} = frac{1}{{i!j!}}sumlimits_{{k_1},{k_2} = - frac{{N - 1}}{2}}^{frac{{N - 1}}{2}} {k_1^ik_2^jqleft[ {{k_1},{k_2}} ight]}&qquad i,j = 0,1,cdots,N - 1 end{split}$$

(4)

对卷积运算在(x, y)位置泰勒级数展开, 可得^[23]

$$ begin{split}&sumlimits_{{k_1},{k_2} = - frac{{N - 1}}{2}}^{frac{{N - 1}}{2}} {qleft[ {{k_1},{k_2}} ight]hleft( {x + {k_1}delta x,y + {k_2}delta y} ight)} &qquad = {sumlimits_{i,j = 0}^{N - 1} {left. {{m_{ij}}delta {x^i}delta {y^j}frac{{{partial ^{i + j}}h}}{{{partial ^i}x{partial ^j}y}}} ight|} _{left( {x,y} ight)}} + oleft( {{{left| {delta x} ight|}^{N - 1}} + {{left| {delta y} ight|}^{N - 1}}} ight) end{split} $$

(5)

显然, 当${m_{i,j}}$取一定值时含可训练参数的卷积运算可等价于各阶偏微分项的高精度差分格式^[24-25]. 另一方面, 有限差分方法是传统数值模拟方法计算流场时空数据时的重要技术, 因此含可训练参数的卷积运算在提取流场时空数据时具有巨大潜力.

循环神经网络(recurrent neural networks, RNN)^[26]是针对时程和自然语言等具有序列结构的数据开发的神经网络架构. RNN相比传统DNN(式(1))在序列演化方向加入了递归连接

$$ {h^{left( t ight)}} = {f_theta }left( {{h^{left( {t - 1} ight)}},{x^{left( t ight)}}} ight) $$

(6)

式中, $ {x^{left( t
ight)}} $为序列在t时刻输入特征, $ {h^{left( t
ight)}} $为序列在t时刻输出特征. RNN在自然语言处理^[2]等任务中得到了重要应用. 双向RNN^[27]可以使模型既能纳入过去时段序列模型对当前时刻影响, 又能考虑未来时刻影响. 但传统RNN训练过程中在序列方向极易出现梯度消失与爆炸, 长短期记忆网络(long short-term memory networks, LSTM)^[28]和门控循环单元网络(gated recurrent unit, GRU)^[2]等门控RNN通过引入门控单元成功解决了梯度消失与爆炸问题.

生成对抗网络(generative adversarial networks, GAN)^[29-30]是一种有效的概率生成模型, GAN可有效捕捉高维观测数据内部统计规律(即联合概率分布)生成概率分布模型; 基于所得概率模型, 在GAN的输入中进行抽样可获得与观测数据不同、甚至在现实世界中不存在、但与高维观测数据服从同一联合概率分布的数据. 当深度学习与强化学习结合时, 拓展了强化学习寻找最优行动选择策略能力, 甚至在围棋等任务上达到或超越了人类水平^[31-32].

1.2
神经网络逼近能力

Cybenko^[33]等提出的通用近似定理(universal approximation theory, UAT)指出: 非线性激活函数为Sigmoid形且网络神经元数(网络宽度)足够大时, 单隐藏层神经网络即具有对任意连续函数达到任意精度的逼近能力. 对于浅层神经网络, 逼近任意连续函数时的误差界为^[34]

$$ mathbb{E}left(Vert f-{widehat{f}}_{n,N}{Vert }^{2} ight) leqslant mathcal{O}left(frac{{C}_{f}^{2}}{n} ight)+mathcal{O}left(frac{nd}{N}mathrm{lg}N ight) $$

(7)

式中, f为待逼近函数, ${hat f_{n,N}}$为浅层神经网络的最优函数估计(需满足一定正则化条件), n为神经网络宽度, N为训练样本数, d为神经网络输入维度, 系数${C_f} = int | omega {|_1}|tilde fleft( omega
ight)|{text{d}}omega $($tilde f$为函数f的傅里叶变换).

Hornik^[35]指出, 激活函数只需取非常数函数且网络足够宽时, 浅层神经网络即具有对任意连续函数达到任意精度的逼近能力. 当神经网络的层数加深时, Delalleau和Bengio^[36]指出浅层和积网络(和积网络的隐藏层单元通过前一层单元的乘积的加权之和获得)逼近特定函数时, 精度提升过程神经元数需以指数增长; 而提升相同精度时, 深层网络神经元数仅需以线性增长, 表明在逼近函数时深层网络比浅层网络能节省可训练参数. Eldan和Shamir^[37]指出在相同逼近精度下, 浅层神经网络需要$ mathcal{O}left( {{e^d}}
ight) $数量级神经元数逼近$ {{mathbb{R}}^d} $空间的简单径向函数, 而深层网络仅需要d的多项式数量级宽度, 同样表明逼近函数时若精度相同, 深层网络比浅层网络能节省可训练参数. 当全连接神经网络的激活函数为ReLU且网络宽度为大于输入数据维度的有限值时, 增大深度可以使其具有对任意连续函数达到任意精度的逼近能力.

综上所述, 深度学习为近似任意函数提供了一个特定的函数空间, 且该函数空间复杂非线性逼近能力强. 而在特定任务中采用深度学习算法时, 需利用优化算法在特定函数空间中优化可训练参数, 例如优化式(6)中的参数$theta $.

1.3
基于梯度下降的优化算法

深度学习通常由梯度下降算法更新网络可训练参数

$$ {theta ^{left( {k + 1} ight)}} = {theta ^{left( k ight)}} - eta {nabla _theta }{mathcal{L}} $$

(8)

式中, $ theta $的上角标为训练步数, $eta $为学习率, ${nabla _theta }{mathcal{L}}$为损失函数${mathcal{L}}$对可训练参数的梯度(通常由反向传播算法计算^[26]). 常用的梯度下降法包括随机梯度下降法^[38], 基于动量的随机梯度下降法, 自适应学习率算法(如文献[39]等). 深度神经网络可训练参数优化问题非凸, 但梯度下降算法用于深层网络的非凸优化问题时仍可搜索到全局最优点: 对于过参数化的全连接深度神经网络, Du等^[40]的研究指出当训练集大小为n, 深层网络隐藏层层数为H, 每层神经元数为m时, 若

$$ m = varOmega left[ {{text{poly}}left( n ight){2^{Oleft( H ight)}}} ight] $$

则梯度下降算法能以线性速率搜索到训练误差全局最优点. 式中, poly(n)为关于n的多项式, O和Ω分别为Big-O和Big-Ω.

由于深度学习具有上述优良性能, 近年来, 研究者开始利用其挖掘大规模高维数据中蕴含的丰富流动物理特征, 流体力学建模方法与高效模拟方法迎来新机遇.

2.
物理启发的流场深度学习降阶模型

深度学习可借助灵活的神经网络架构、强非线性逼近能力和优良优化算法高效挖掘大规模高维流场数据中蕴含的丰富流动物理特征. 然而, 当深度学习用于流体力学建模时仍需基于流体物理设计3部分核心内容: 深度神经网络的输入特征、网络架构、损失函数. 根据流体物理规律选取网络输入特征或设计网络架构的方法称为物理启发的深度学习方法, 以下介绍物理启发的流场深度学习降阶模型.

2.1
本征正交分解辅助的深度学习降阶模型

本征正交分解(proper orthogonal decomposition, POD)常用于提取流场紧凑空间表征降低自由度^[41]

$$qquad int {Cleft( {t,t'} ight)} {hbar _i}left( {t'} ight){text{d}}t' = {lambda _i}{hbar _i}left( {t'} ight) $$

(9)

$$ qquad{{{boldsymbol{varPsi}} }_i}left( {x} ight) = int {{hbar _i}left( t ight)} {{boldsymbol{u}}}'left( {{x},t} ight){text{d}}t $$

(10)

式中, t为时间, x为位置坐标, ${{boldsymbol{u}}}'$为速度${{boldsymbol{u}}}$的脉动值, $Cleft( {t,t'}
ight) = displaystyleint_varOmega {{{boldsymbol{u}}}'left( {{{boldsymbol{x}}},t}
ight){{boldsymbol{u}}}'left( {{{boldsymbol{x}}},t'}
ight)} {text{d}}{{boldsymbol{x}}}$为脉动速度在流场区域$varOmega$内的时间相关函数, ${hbar _i}$为特征向量, ${lambda _i}$为对应于第i阶POD模态${{{boldsymbol{varPsi}} }_i}$的特征值(${lambda _i} > {lambda _{i + 1}}$). 任意时刻速度脉动投影到第i阶POD模态的系数为

$$ {alpha _i}left( t ight) = int_varOmega {{{boldsymbol{u}}}'left( {{{boldsymbol{x}}},t} ight) cdot {{{boldsymbol{varPsi}} }_i}left( {{boldsymbol{x}}} ight)} {text{d}}{{boldsymbol{x}}} $$

(11)

结合平均流场$ {bar {boldsymbol{u}}}left( {{x},t}
ight) $可得POD重构流场为

$$ {{boldsymbol{u}}}left( {{{boldsymbol{x}}},t} ight) = {bar {boldsymbol{u}}}left( {{{boldsymbol{x}}},t} ight) + sumlimits_i {{alpha _i}left( t ight)} {{{boldsymbol{varPsi}} }_i}left( {{boldsymbol{x}}} ight) $$

(12)

当POD用于辅助深度学习建立流场降阶模型时, 首先用POD提取流场紧凑空间表征, 然后利用深度学习序列建模方法建立POD模态系数时程预测模型.

2.1.1
基于POD与深度学习的流动降阶模型

风洞实验是传统测量流场的常用方法. 风洞实验一般采用粒子图像测速技术(particle image velocimetry, PIV)测量流场, 然而由于相机分辨率和存储空间的限制, PIV测量流场的时间和空间分辨率是矛盾的. 基于POD的超时空分辨率方法在解决这一问题时具有广泛应用^[42-44]. 当已知流场中部分测点高时间分辨率速度测量值与给定的POD伽辽金模型时, Gerhard等^[45]用动态估计器估计了整个高时间分辨率流场. Druault等^[46]基于样条插值获取了POD模态的高时间分辨率系数, 从而重构了高时间分辨率流场. Borée^[47]在分析湍流相关性时引入了扩展POD (extended POD)方法. Hosseini等^[48]将速度信号在时间维度的延迟看成一组虚拟速度探针测量, 基于此并利用扩展POD方法估计了角锥的尾流. Discetti等^[49]随后提出了扩展POD方法中的时间相关系数截断准则, 从而移除了点测量与整场测量不相关成分, 并用于高时间分辨率槽道流和管道流重构^[50].

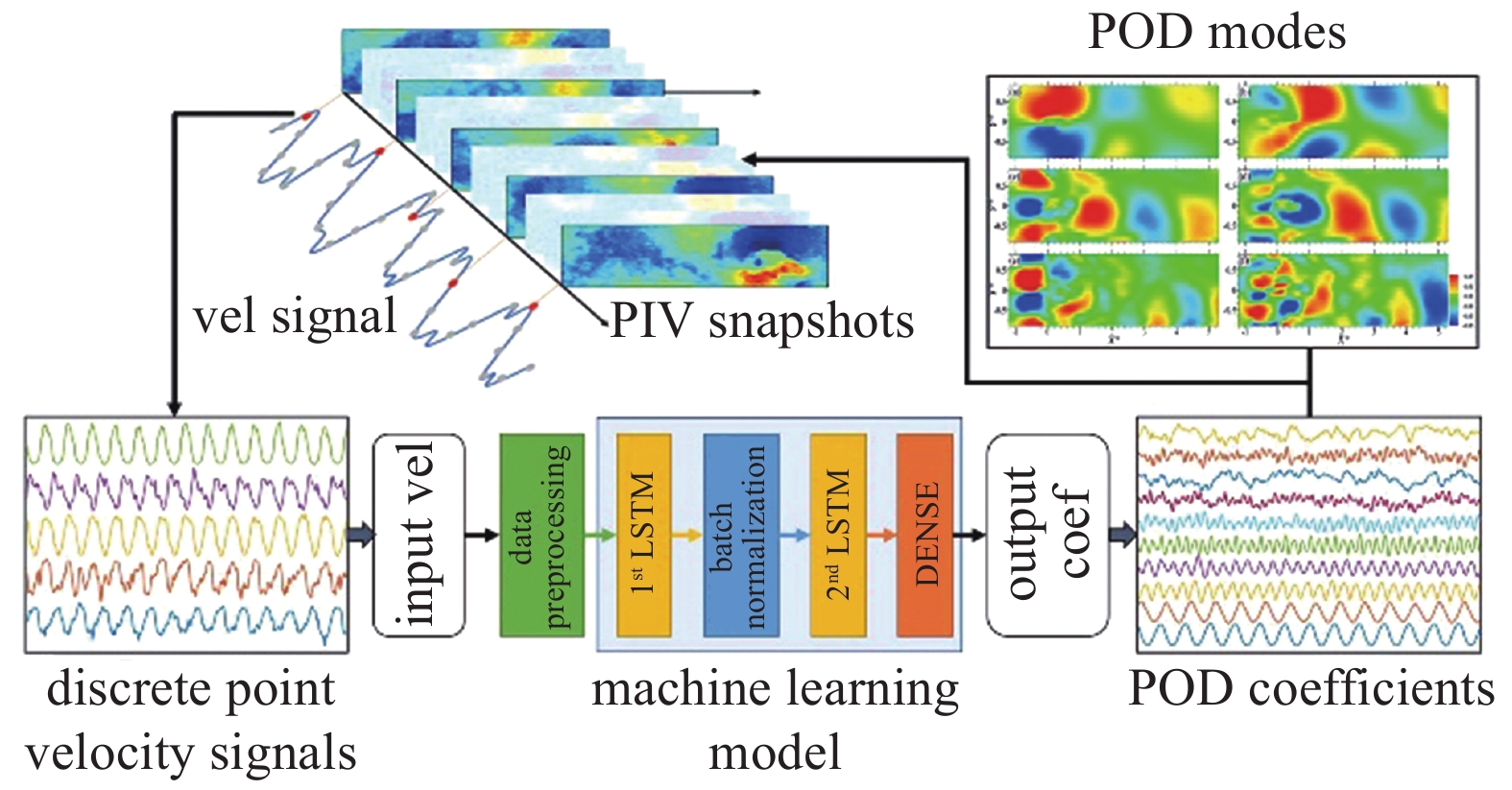
近年来, 充分利用深度神经网络的灵活网络架构、强非线性逼近能力与POD的流场紧凑空间提取能力, 发展出了POD辅助的深度学习流场降阶模型. Deng等^[51]在风洞试验中用PIV系统以采样频率2000 Hz测量了旗帜尾流, 并采用如图1所示基于LSTM的POD模型建立了流场离散测点速度时程(5个离散测点时程取自PIV测量结果)到流场POD模态系数时程间的映射: 首先将PIV及相应离散点测量结果降采样为5 Hz, 然后以离散点5 Hz速度时程为输入、以相应时刻流场POD模态系数为输出训练LSTM模型, 最后以离散点5 Hz速度时程为输入在2000 Hz测量结果上做预测即可获得流场2000 Hz的POD模态系数, 从而可利用式(12)重构高时间分辨率流场; Cai等^[52]进一步利用此方法成功重构了采样频率为千赫兹级的二维表面温度场. Wu等^[53]基于时间卷积神经网络(temporal con-volutional neural networks, TCN)建立了圆柱绕流场过去时刻POD模态系数时程与未来时刻POD模态系数时程间的映射关系, 从而得到了圆柱绕流场降阶模型; 训练完成的TCN模型相比传统数值模拟方法计算效率提升了数百至数千倍.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-373-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
基于LSTM的POD模型^[51]



Figure
1.
Architecture of LSTM-based POD model^[51]



下载:
全尺寸图片
幻灯片


然而, 需要指出的是, 上述基于POD与深度学习的流动降阶模型所依赖的POD模态来自对相同模型、相同流动参数(如马赫数、雷诺数、攻角等)流场的POD分析. 当模型或流动参数改变时, 流场POD模态亦发生变化, 此时上述基于POD与深度学习的流动降阶模型并无泛化能力. 近来, Zhao等^[54]基于POD与压缩感知精确重构了相同机翼模型不同流动参数或相同流动参数不同机翼模型的表面压力分布, 其提取的POD模态来自相同模型不同流动参数或相同流动参数不同模型的表面压力分布, 使得POD模态适用于不同流动状态, 有效提升了POD降阶模型在不同流态的泛化能力. 另一方面, 上述模型采用“端到端”方式建立流场输入特征与输出特征关系, 模型是否能精确建立并无物理解释. Jin等^[55]基于泰勒冻结假设启发引入了绕流场流速时空关联非线性函数, 理论推导了流场POD系数与绕流场离散测点速度时间历程的关系, 并利用双向RNN将其定量化, 对POD辅助的深度学习流场降阶模型进行了物理启发的深度网络设计.

2.1.2
物理启发的深度网络设计

将N-S方程中的动量方程投影到第i阶POD模态, 并结合边界条件可得t时刻的第i阶POD模态系数为^[55]

$$ begin{split} {alpha _i}left( t ight) =& int_{{t_0}}^t {int_varOmega {{{{boldsymbol{psi}} }_i}left( {{boldsymbol{x}}} ight) cdot left[ {{mathcal{G}}left( {{boldsymbol{u}}} ight) - {mathcal{H}}left( {{boldsymbol{u}}} ight)} ight]} {text{d}}tau {text{d}}{{boldsymbol{x}}}} + & int_varOmega {{{boldsymbol{u}}'}left( {{boldsymbol{x}},{t_0}} ight) cdot {{{boldsymbol{psi}} }_i}left( {{boldsymbol{x}}} ight){text{d}}{{boldsymbol{x}}}} end{split} $$

(13)

式中, t₀为积分起始时刻, $ {mathcal{G}}left( cdot
ight) $和$ {mathcal{H}}left( cdot
ight) $为关于速度的未知函数紧凑表示. 在流场下游布置n_vp个高时间分辨率速度探针, 受泰勒冻结假设启发可将式(13)进一步写为^[55]

$$ begin{split} {alpha _i}left( t ight) = & int_{{t_0}}^t {int_varOmega {{{{boldsymbol{psi}} }_i}left( {{boldsymbol{x}}} ight) cdot {mathcal{M}left( {{boldsymbol{u}}} ight)} } { m{d}}tau { m{d}}{{boldsymbol{x}}}} + & int_varOmega {mathcal{K}left[ {left( {{{boldsymbol{u}}}'} ight)_s^{{tau } + {{{{d}_s}} mathord{left/ {vphantom {{{{d}_s}} U}} ight. } U}}} ight] cdot {{{boldsymbol{psi}} }_i}left( {{boldsymbol{x}}} ight){ m{d}}{{boldsymbol{x}}}} end{split} $$

(14)

式中, $mathcal{M}left( {{boldsymbol{u}}}
ight) = mathcal{G}left[ {mathcal{K}left( {{{boldsymbol{u}}}_s^{{tau } + {{{{d}_s}} mathord{left/ {vphantom {{{{d}_s}} U}}
ight. } U}}}
ight)}
ight] - mathcal{H}left[ {mathcal{K}left( {{{boldsymbol{u}}}_s^{{tau } + {{{{d}_s}} mathord{left/ {vphantom {{{{d}_s}} U}}
ight. } U}}}
ight)}
ight]$, $ {{boldsymbol{u}}}_s^t $为t时刻所有探针速度测量值矢量, ${{boldsymbol{d}}_{s,j}}left( {boldsymbol{x}}
ight) = $$ left[ {{d_{x,j}}left( {boldsymbol{x}}
ight),};;{{d_{y,j}}left( {boldsymbol{x}}
ight)}
ight]$为第j个速度探针到x位置的距离矢量, $ mathcal{K}left( cdot
ight) $为将$ {{boldsymbol{u}}}_s^t $映射到 $ {{boldsymbol{u}}} $的未知函数, ${{boldsymbol{u}}}_s^{{{{t}}} + {{{{{{d}}}_s}} mathord{left/ {vphantom {{{{d}_s}} U}}
ight. } U}} = $$ Bigg[{{boldsymbol{u}}}left( {{{boldsymbol{x}}} + {{{boldsymbol{d}}}_{s,1}},t + {{{d_{x,1}}} mathord{left/ {vphantom {{{d_{x,1}}} U}}
ight. } U}}
ight),...,$${{boldsymbol{u}}}left( {{{boldsymbol{x}}} + {{{boldsymbol{d}}}_{s,{n_{vp}}}},t + {{{d_{x,{n_{vp}}}}} mathord{left/ {vphantom {{{d_{x,{n_{vp}}}}} U}}
ight. } U}}
ight)Bigg]$.

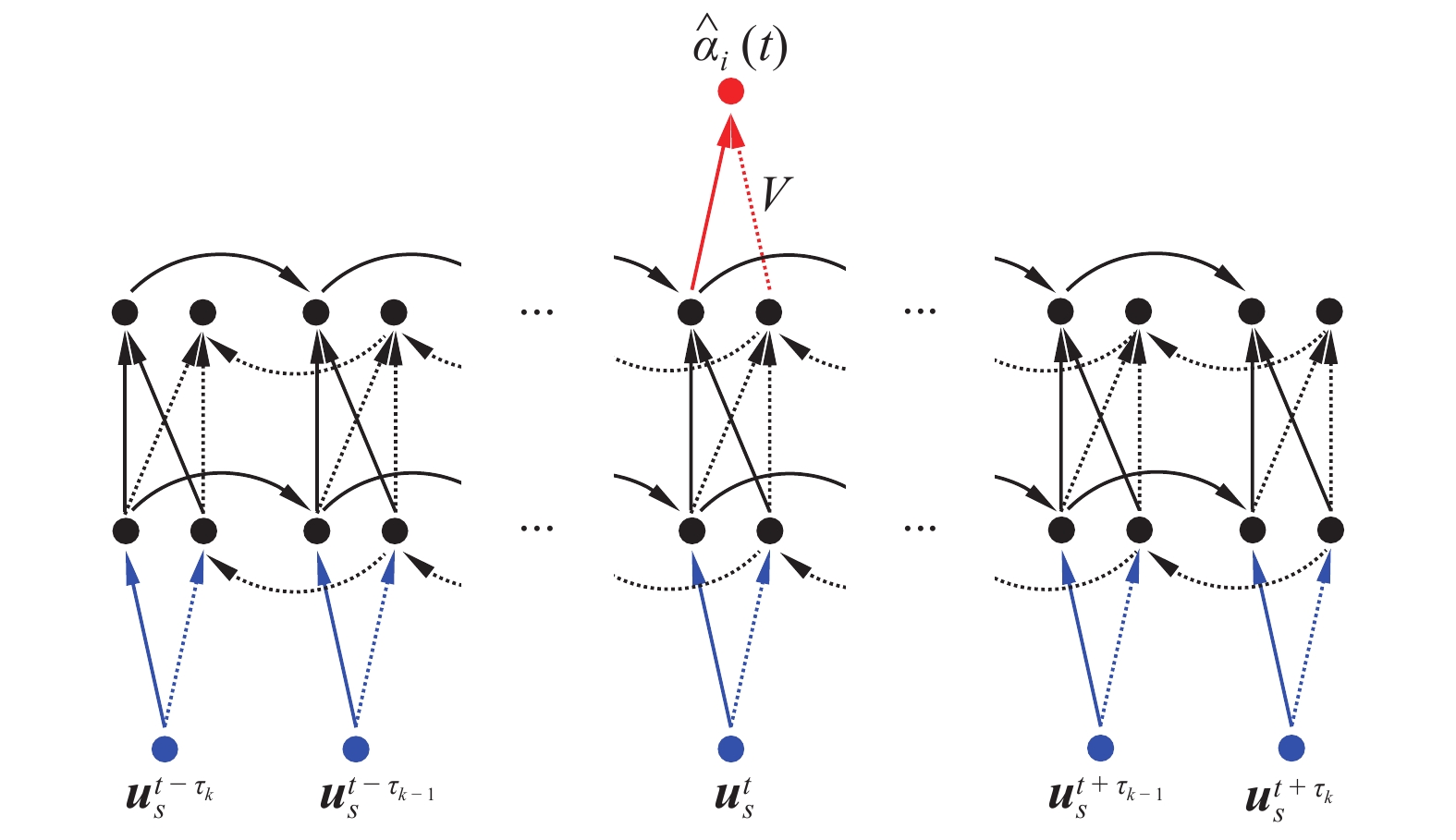
由式(14)可知, t时刻的第i阶POD模态系数与t时刻之前与之后的离散点速度时程均相关; 因此, 设计了如图2所示“多对一”的双向GRU RNN将包含未知函数的式(14)定量化. 上述研究理论推导得到流场POD模态系数与绕流场离散测点速度时间历程之间的定性关系, 图2中的神经网络输入特征和架构基于上述分析设计并将定性关系定量化, 因此称为物理启发的深度学习方法.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-373-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
流场重构神经网络架构: 多对一双向循环神经网络^[55]



Figure
2.
Architecture of many-to-one bidirectional RNN to reconstruct the flow field^[55]



下载:
全尺寸图片
幻灯片


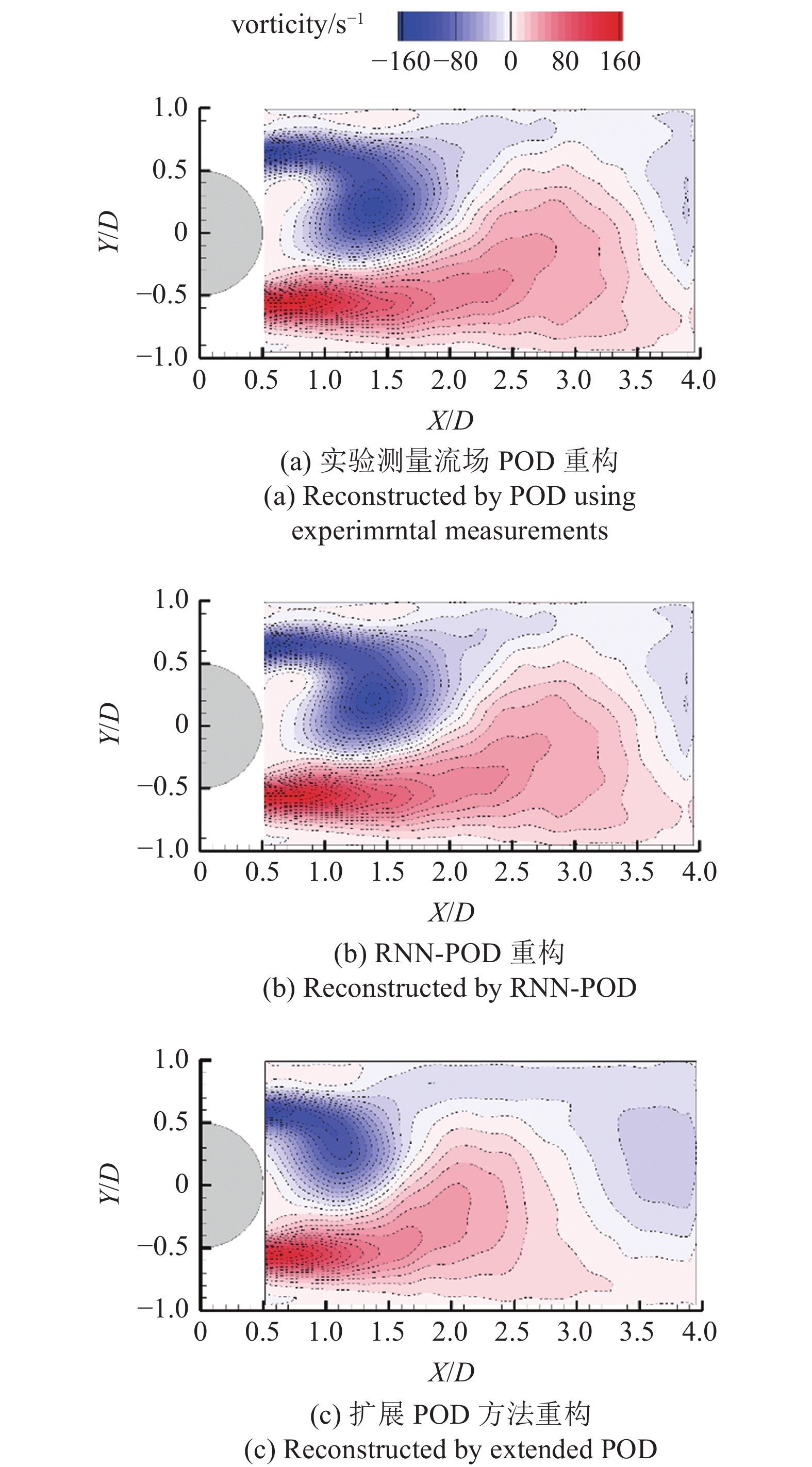
在风洞实验中对雷诺数为Re = 2.4 × 10⁴的圆柱绕流场进行了高时间分辨率重构测试: PIV采样频率为5 Hz, 在圆柱中心线下游4.5倍直径处布置1个采样频率为5000 Hz的Cobra传感器, 采用双向GRU RNN对流场前3阶POD模态进行建模, 与扩展POD方法的瞬态流场重构对比如图3所示. 由图可知, 双向GRU RNN与POD结合的方法重构的流场与真实流场相吻合, 但扩展POD方法的重构结果与真实流场存在明显差异. 由此可见POD辅助的流场深度学习建模方法比传统扩展POD方法具有明显优势. 然而, 以上模型仍依赖于确定雷诺数下的POD模态, 当雷诺数发生变化时POD模态发生变化, 以上流场建模方法将不再适用.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-373-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
Re = 2.4 × 10⁴时的瞬时尾流场^[55]



Figure
3.
Instantaneous wake-flow field^[55] for Re = 2:4 × 10⁴



下载:
全尺寸图片
幻灯片

2.2
基于深度学习的流场直接预测模型

当基于深度学习直接建立端到端预测模型时, 可有效避免POD模态对雷诺数的依赖. 例如, 惠心雨等^[56]基于GAN建立了非定常二维圆柱绕流场的预测模型, 与传统CFD方法相比, 计算效率得到明显提升. Sekar等^[57]基于深度学习建立了不同气动外形下的二维机翼绕流场快速预测模型: 该模型以CNN提取的机翼形状压缩表征、攻角、雷诺数以及流场位置坐标为DNN的输入, 压力场和速度场为DNN的输出. Fukami等^[58]借鉴U-Net^[59]中的多尺度特征融合思想设计了混合降采样和跳跃连接的多尺度深度神经网络模型, 以低分辨流场为输入、高分辨流场为输出成功完成了二维圆柱绕流、二维各向同性湍流等流场超分辨; Deng等^[60]则引入对抗损失函数, 采用超分辨率GAN^[61]和增强的超分辨率GAN^[30]完成了流场的超分辨率重构, 相比Fukami等^[58]的结果, 精度得到明显提升.

Jin等^[62]受钝体尾流中的雷诺应力、旋涡形成长度、基底压力强相关的流体流体物理基本理论^[63]启发, 采用深度卷积神经网络建立了钝体绕流问题表面压力$ {{{boldsymbol{C}}}_p} $与流场流速$ {{boldsymbol{u}}} $间的关系模型, 可在仅测量钝体表面压力的情况下快速预测尾流场

$$ {{boldsymbol{u}}} = {f_theta }left( {{{{boldsymbol{C}}}_p}} ight) $$

(15)

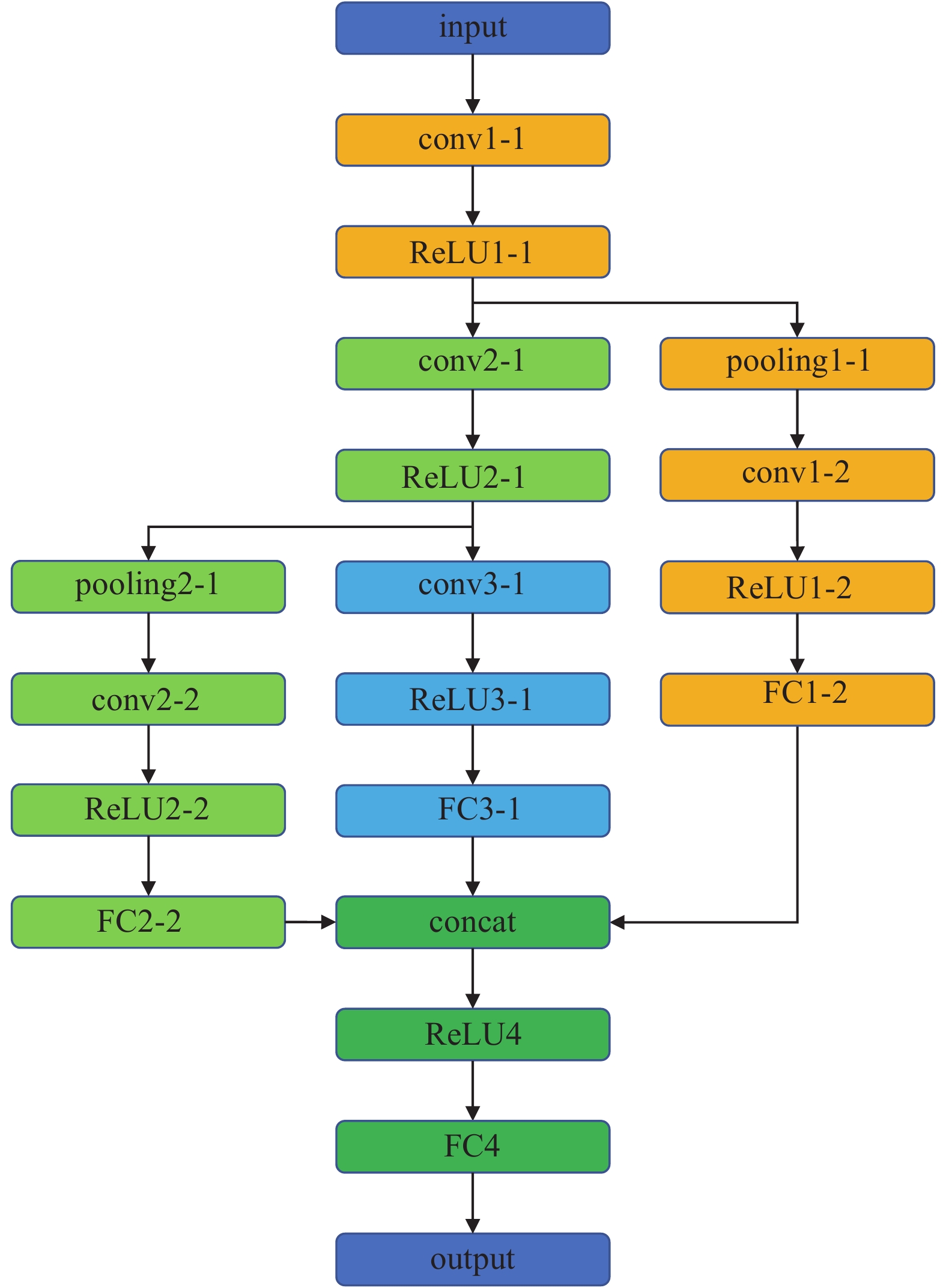
Jin等^[62]建立了如图4所示以圆柱表面压力为输入, 由含有池化层路径和不含池化层路径共同构成的融合卷积神经网络建立了压力?速度场模型, 卷积层可提取输入特征图中对平移保持等变的特征, 池化层可有效提取输入特征图中对少量平移保持不变的特征.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-373-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
用于建立压力?速度场模型的卷积神经网络架构. “conv”表示卷积层, “ReLU”是非线性激活函数, “pooling”表示最大池化层, “FC”表示全连接层, “concat”表示不同路径融合^[62]



Figure
4.
The architecture of the fusion CNN to establish the pressure?velocity model. “conv”denotes convolutional layer; “ReLU” denotes nonlinear rectified linear unit; “pooling” denotes max pooling layer; “FC” denotes fully-connected layer; “concat” denotes the concatenating of different paths^[62]



下载:
全尺寸图片
幻灯片


Jin等^[62]建立的训练集雷诺数范围为70 ~ 900, 测试数据集雷诺数范围为60 ~ 1100. 图5给出了4个具有代表性雷诺数上的流场预测结果. 由图可知, 在研究所考虑的亚临界雷诺数范围内精确预测了圆柱绕流速度场; 该压力?速度场模型不仅可以精确预测包含在训练集雷诺数范围内的圆柱绕流速度场, 而且能预测训练集雷诺数范围外的部分工况. 同时, 该压力?速度场模型对旋涡形成长度、速度幅值等的雷诺数效应以及流场时空演化特性做出了精确预测; 以上结果表明, Jin等^[62]建立的压力?速度场模型成功捕捉了圆柱绕流的内在流动本质, 并具有一定的雷诺数外延预测能力. 为改善此类数据模型在不同流动参数条件下的泛化能力, Zhu等^[64]在建立湍流黏性系数深度学习模型时, 利用验证集进行输入特征选取, 从备选输入特征中剔除在流动状态上外插过大的特征, 大幅提升了模型在机翼绕流场雷诺数、马赫数、攻角等流动参数上的外延预测能力.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-373-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
不同雷诺数下模型预测流场与CFD计算结果对比^[62]. CFD计算结果: (a) Re = 65, (c) Re = 170, (e) Re = 500, (g) Re = 1000; 模型预测结果: (b) Re = 65, (d) Re = 170, (f) Re = 500, (h) Re = 1000



Figure
5.
Comparisons of instantaneous flow fields between the model predictions and CFD results for various Reynolds numbers^[62]. CFD results for (a) Re = 65, (c) Re = 170, (e) Re = 500, and (g) Re = 1000; model predictions for (b) Re = 65, (d) Re = 170, (f) Re = 500, and (h) Re = 1000



下载:
全尺寸图片
幻灯片

3.
物理融合的流动控制方程深度学习求解

以上物理启发的流场深度学习降阶模型虽在网络架构设计、网络输入特征与输出量选取时充分考虑了流体物理机理, 但一方面以上模型仍依赖于完整流场数据, 然而在PIV获取流场时由于壁面反光和遮挡等, 近壁面流场无法解析, 难以获得完整流场数据; 另一方面, 流体物理机理并未显式嵌入深度学习模型.

3.1
基于通用近似定理的神经网络直接求解方法

不同与传统人工智能任务, 深度学习模型输出或预测的流场需满足流动控制方程. 因此, 可将网络输出流场需满足的流动控制方程以残差项的均方误差形式嵌入网络损失函数. 特别地, 基于UAT可用以时空坐标为输入以流场为输出的DNN逼近流场时空演化函数, 此DNN称为物理融合的神经网络(physics-informed neural networks, PINNs)^[65].

3.1.1
物理融合的神经网络架构

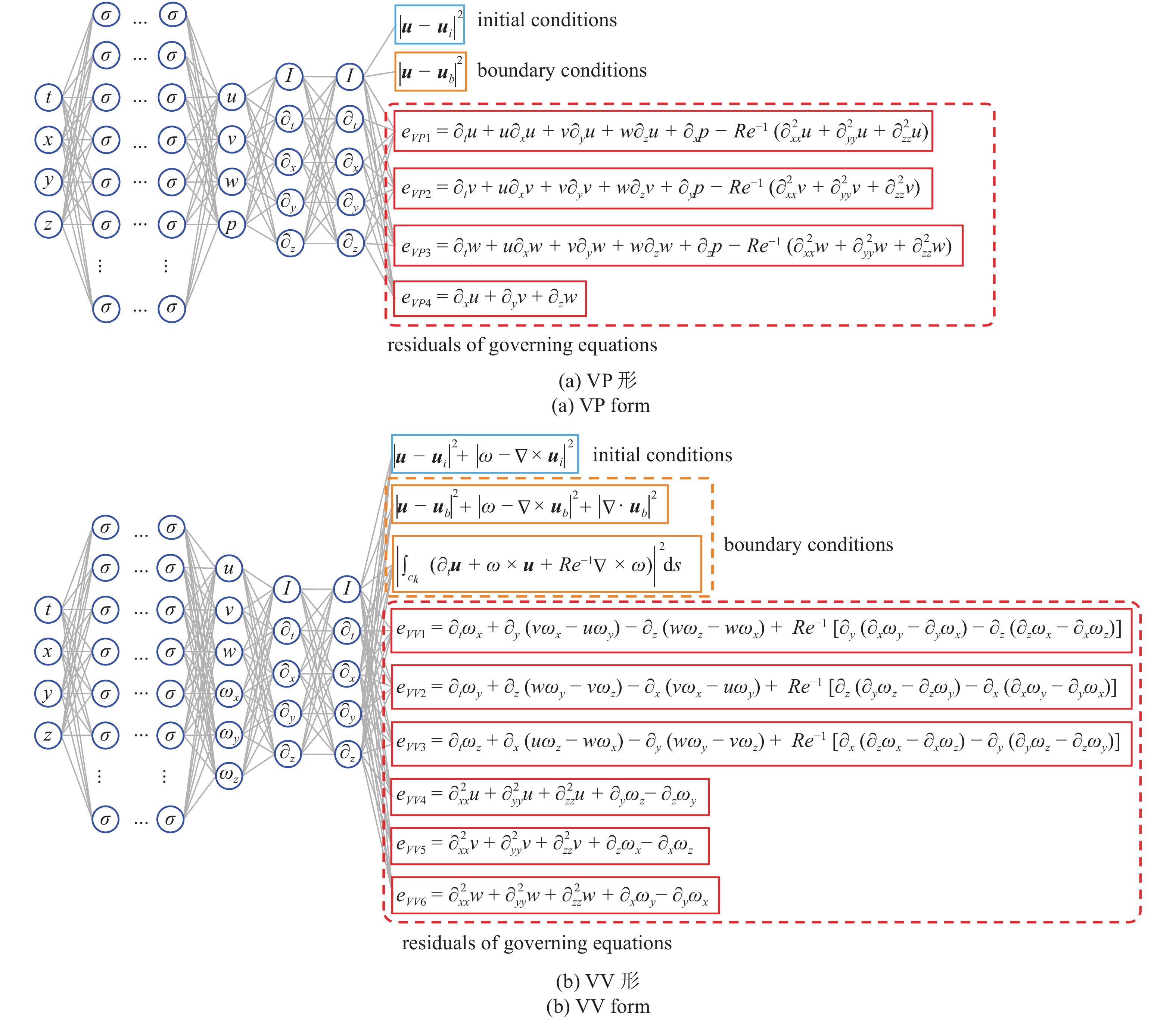
Jin等^[66]基于PINNs引入了求解不可压缩N-S方程的NSFnets (N-S flow nets)求解速度?压力(velocity?pressure, VP)形和涡量?速度(vorticity?velocity, VV)形控制方程, 如图6所示. NSFnets的损失函数包含在初始条件对应时空域采N_i个点计算的均方损失函数$ {{mathcal{L}}_i} $、在边界条件对应时空域采N_b个点计算的均方损失函数$ {{mathcal{L}}_b} $和在计算域采N_e个点计算的方程残差对应的均方损失函数$ {{mathcal{L}}_e} $(图6中e_VPi和e_VVi), 总损失函数${mathcal{L}}$为



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-373-6.jpg'"
class="figure_img
figure_type2 ccc " id="Figure6" />



图
6
NSFnets网络架构^[66]



Figure
6.
A schematic of NSFnets^[66]



下载:
全尺寸图片
幻灯片

$$ {mathcal{L}} = {{mathcal{L}}_e} + alpha {{mathcal{L}}_b} + beta {{mathcal{L}}_i} $$

(16)

式中, α和β为平衡损失函数下降过程中不同项梯度以加速收敛的权重系数. 方程残差中的偏导借助自动微分技术^[67]计算. 当损失函数收敛到较小值时即获得$ {{mathcal{L}}_e} $中所包含控制方程的解.

采用梯度下降算法训练NSFnets时, 参数更新过程可表示为

$$ {theta ^{(k + 1)}} = {theta ^{(k)}} - eta {nabla _theta }{{mathcal{L}}_e} - eta alpha {nabla _theta }{{mathcal{L}}_b} - eta beta {nabla _theta }{{mathcal{L}}_i} $$

(17)

式中, $ theta $为可训练参数, 上角标k为训练步数, $ eta $为学习率. α和β可看作超参数人工调整或用动态权重(dynamic weights, DW)策略调整^[66,68]. 在计算域采点时可采用随机策略或与自适应网格方法类似的自适应残差点细化(residual-based adaptive refinement, RAR)方法^[69]. 对NSFnets模拟结果定义如下L₂相对误差

$$ epsilon_{V}=parallel hat{V}-V{parallel }_{2}/parallel V{parallel }_{2} $$

(18)

式中, V表示参考速度分量u, v, w或压力p, $ hat V $表示由NSFnets计算的速度或压力值.

采用PINNs中的方程残差均方损失函数求解流动控制方程时获得的解为方程的经典解. E等^[70]利用残差网络, Zang等^[71]利用生成对抗网络搜索了变分形式下控制方程残差最小值点, 获得了方程的弱解.

3.1.2
正问题求解

Jin等^[66]在采用NSFnets求解Kovasznay流动时发现, RAR方法能增加较少的残差点获得较大的精度提升, 如表1所示. 表中VP-NSFnet在采用随机采样测量时采用了635个残差点, 采用RAR时增加了10个残差点; VV-NSFnet在采用随机采样测量时采用了629个残差点, 采用RAR时仅增加了4个残差点. 采用RAR后, 两种形式NSFnets求解精度均有约50%提升.




表
1
采用RAR增加残差点时NSFnets求解的速度和压力L₂相对误差^[66]



Table
1.
Relative L₂ errors of velocity and pressure solutions for NSFnets with residual points added via RAR^[66]



table_type2 ">

Sampling	VP-NSFnet				VV-NSFnet
	$ epsilon_{u} $/%	$ epsilon_{v} $/%	$ epsilon_{p} $/%		$ epsilon_{u} $/%	$ epsilon_{v} $/%
Random	0.0095 ± 0.0026	0.0823 ± 0.0167	0.0401 ± 0.0061		0.0254 ± 0.0058	0.0704 ± 0.0160
RAR	0.0056	0.0369	0.0315		0.0083	0.0280

下载:
导出CSV
|显示表格



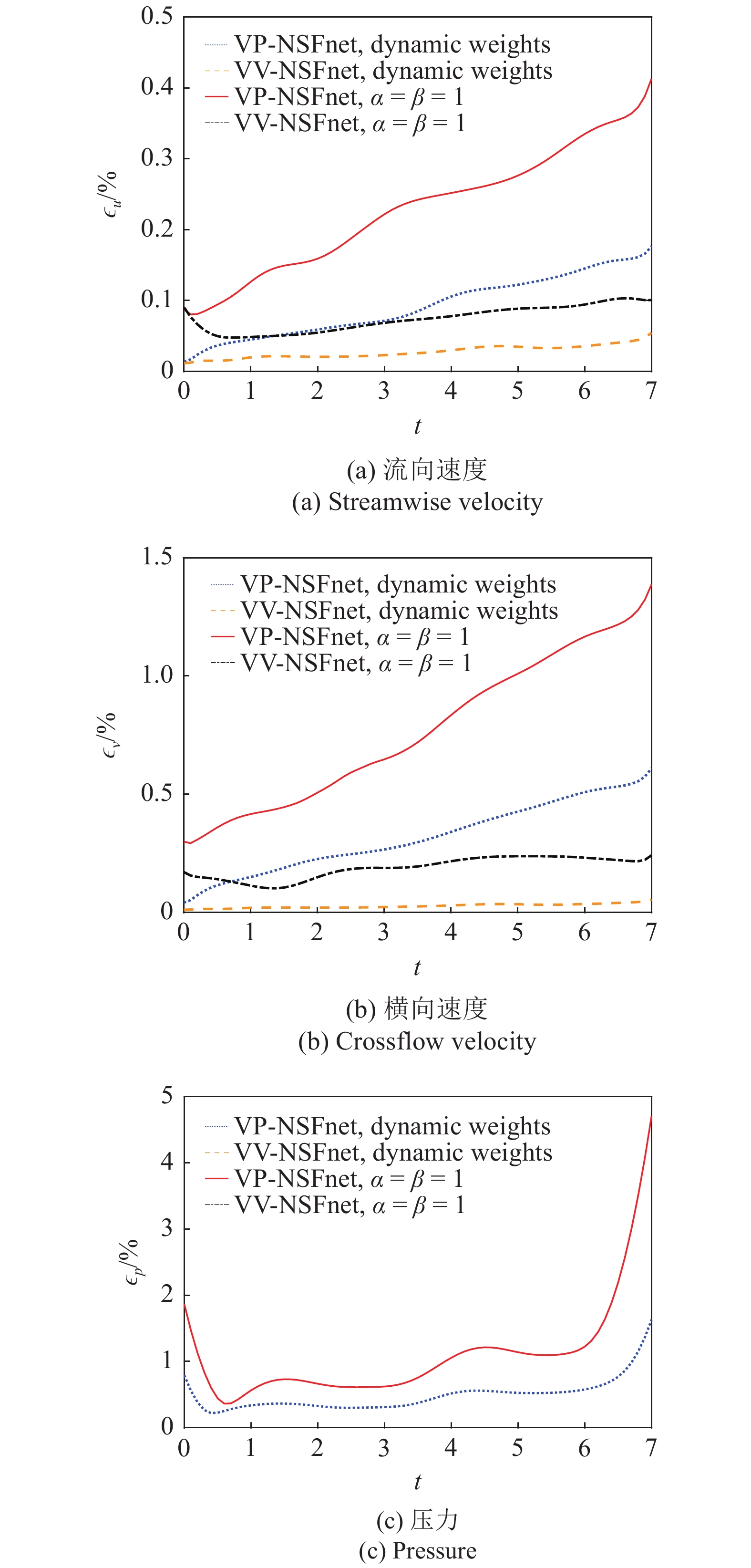
图7给出了NSFnets求解雷诺数为100的圆柱绕流时速度u, v和压力p误差随时间演化曲线, 此时VV-NSFnet和VV-NSFnet的隐藏层层数均为10, 每层节点数均为100. 由图可知, 两种形式的神经网络都达到了较高的求解精度, VV-NSFnet比VP-NSFnet具有更高的求解精度; 而且动态权重系数策略有效提升了NSFnets的求解精度. 此外, Jin等^[66]首次采用物理融合的神经网络模拟了槽道湍流, 并发现随着求解区域和求解时间间隔的增大, 结果并未发散.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-373-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
圆柱绕流求解误差^[66]: (a) 流向速度, (b) 横向速度和 (c) 压力的L₂相对误差



Figure
7.
Flow past a circular cylinder^[66]: relative L₂ errors of NSFnets simulations for (a) the streamwise velocity, (b) the crossflow velocity and (c) pressure



下载:
全尺寸图片
幻灯片


Mao等^[72]通过在高速流动解空间梯度剧烈变化区域增加残差点采用PINNs有效求解了高速可压流动. Mao等^[72]进一步将存在激波等梯度剧烈变化的解空间中分割为若干子区域, 各子区域采用不同深度网络求解, 流场求解精度得到地显著提升. 基于此, Jagtap等^[73]发展了将求解域划分为不同子区域求解的守恒PINNs: 每个子区域采用不同深度网络, PINNs的总损失函数加入表征子区域界面通量连续的损失函数和区域界面解的平均值一致的损失函数, 求解了可压缩欧拉方程、方腔流等.

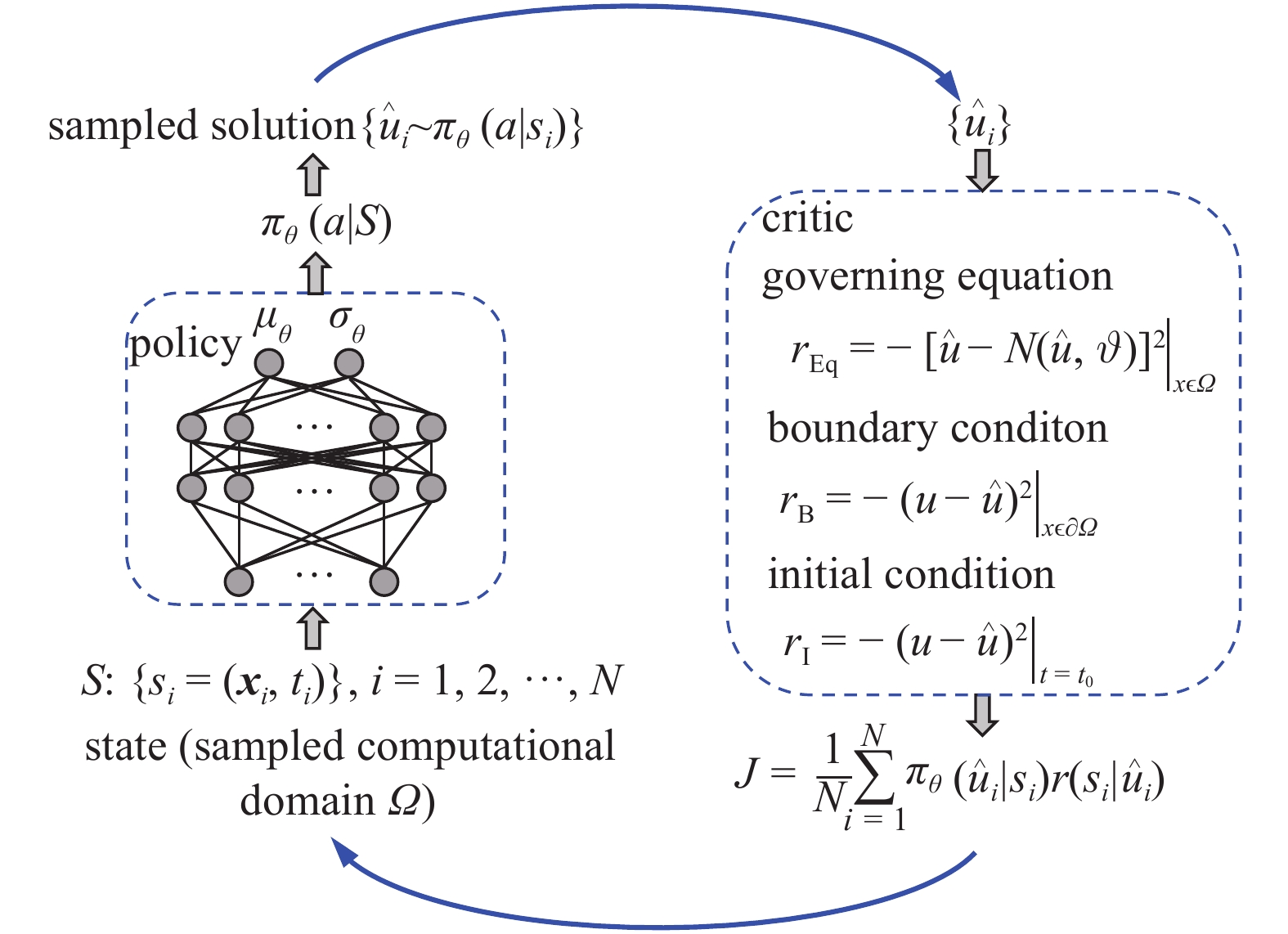
为了加快N-S方程求解过程, Wei等^[74]提出了基于深度强化学习(deep reinforcement learning, DRL)的流体力学微分方程统一求解框架(见图8), 求解了流体力学中的Burgers方程, 稳态N-S方程等. 在求解Burgers方程时, 发现该方法比传统的有限元方法更能有效地捕捉激波; 在方程求解过程中发现, 随着求解步数的增大, 求解速度提升, 具有迁移学习的特性; 研究了从求解低雷诺数迁移到高雷诺数时网络参数的训练策略^[15], 提高了计算效率. 此外, Meng等^[75]提出了时域上并行的PINNs: 首先将较长的时域分成N段子时域, 用一个粗尺度网络对应完整时域和N个细尺度网络对应N段子时域; 交替训练两类网络最终获得方程的解; 该方法提升了PINNs求解时域较长问题的计算效率.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-373-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
基于深度强化学习的微分方程求解框架^[74]



Figure
8.
DRL framework for equation solution^[74]



下载:
全尺寸图片
幻灯片

3.1.3
反问题求解

Jin等^[66]采用NSFnets求解了边界条件(狄利克雷边界条件)不完备或边界条件含噪声的Kovasznay流动, 发现NSFnets在此时仍可获得较高精度的解, 且其计算代价与求解正问题相当, 表明NSFnets处理含噪声数据同化问题时具有广阔前景. Raissi等^[76]采用PINNs求解了雷诺数为100的圆柱涡激振动数据同化问题: 首先当已测得含噪声的圆柱位移和部分测点速度时, 反演了求解域内完整的流场, 计算了气动力; 其次当在流场中布置了被动输运颗粒并已知颗粒扩散方程时, 同样反演了求解域内完整的流场, 计算了气动力时程. Raissi等^[77]进一步仅基于被动输运颗粒流动显示数据, 采用PINNs成功求解了圆柱绕流、动脉瘤等问题, 获得了高精度的流场和压力场数据. 根据圆柱流场先验信息, 求解此类反问题时需在圆柱附近的上游流场和近尾流场中随机布置观测点^[76-77]. Cai等^[78]基于多平面温度梯度测量视频, 利用物理融合的神经网络求解了咖啡杯上方流场细节, 并与独立PIV测量结果相吻合. 但在求解此类反问题时, 尚无法预先估计已测数据量、数据空间分布对求解精度的影响. Mao等^[72]在已知高速可压缩流动密度场梯度和部分离散测点压力值时, 采用PINNs反演了流场信息. Yang等^[79]进一步发展了使用贝叶斯神经网络代替PINNs中深度网络的贝叶斯PINNs, 有效缓解了求解反问题时含噪声数据带来的过拟合问题.

3.2
深度学习辅助的数值模拟方法

上述基于通用近似定理的神经网络直接求解方法在处理流动控制方程相关问题时并未依赖传统数值模拟方法. 但除利用神经网络直接求解方程, 还可利用深度学习辅助构建更快速、更精确的数值算法. 此时, 流体物理直接以离散控制方程形式反映在数值算法中.

3.2.1
深度学习辅助的求解效率提升

Raissi等^[65]利用网络经典解方法, 将用龙格-库塔方法构造的求解变量用神经网络近似, 结合控制方程、边界条件等形成损失函数, 成功实现了由于计算量过大传统数值格式难以完成的100阶隐式龙格?库塔方法.

Bar-Sinai等^[80]基于有限差分法, 首先利用细尺度网格解或解析解训练粗尺度网格解到细尺度网格有限差分算子系数的深度网络, 然后在粗尺度上利用此深度网络预测高精度有限差分算子系数, 在保持较高求解精度的前提下大幅提升了有限差分方法的求解效率. 随后, Kochkov等^[81]和Zhuang等^[82]利用此方法求解了二维湍流, 在相同求解精度下求解效率相比传统数值方法提升了40 ~ 80倍.

3.2.2
深度学习辅助的求解精度提升

Wang等^[83]将WENO格式中的数值通量计算格式用强化学习选择, 以长期计算精度构造强化学习的奖励函数训练网络, 获得了精度更高的RL-WENO格式(基于强化学习的WENO格式). Greenfeld等^[84]利用深度神经网络构造了多重网格法中的误差传递矩阵, 并以误差传递矩阵谱半径期望为损失函数, 训练网络将损失函数最小化可获得最优误差传递矩阵, 有效提高了多重网格法的计算精度. Li等^[85]通过在经典LSTM神经网络中引入Newmark-β数值方法, 利用网络中上一时间步输出气动力计算得到动力系统位移和速度响应并作为下一时间步网络输入, 构成闭环序列结构, 抑制了由于测量和模型参数识别误差导致的长期预测中出现的误差放大现象, 显著提高了模型长时间预测精度与鲁棒性.

4.
结论与展望

有别于传统图像识别、自然语言处理等典型人工智能任务, 深度学习模型预测的流场需满足流体物理规律, 如N-S方程、典型能谱等. 本文阐述了物理增强的深度学习方法(包括物理启发与物理融合的深度学习方法)在流体力学降阶模型、流动控制方程求解领域的研究进展, 结论和展望如下.

(1)在系统研究流体物理的基础上, 可通过设计深度网络输入特征和深度网络架构建立物理启发流场深度学习降阶模型, 完成流场高效、高精度预测或重构. 本征值正交分解辅助的深度学习降阶模型相比传统降阶模型, 精度得到有效提升.

(2)物理融合的神经网络求解可方便地用于流场反演问题, 且其计算代价与求解正问题相当.

(3)物理启发的流场深度学习降阶模型虽在输入特征选取与网络架构设计时充分考虑了流体物理规律, 物理融合的流动控制方程深度学习求解方法虽在损失函数中显式嵌入了表征物理规律的方程残差项, 但以上约束均为“软约束”, 即由于损失函数不能严格下降至零等原因无法保证深度网络所逼近的流场严格满足物理规律. 近来, Chen等^[86]结合离散的控制方程通过对网络输出的流场做进一步投影, 使网络输出流场严格满足离散的控制方程, 对网络施加了“硬约束”. 如何进一步设计深度网络组件, 如连接方式、激活函数等, 使其逼近的流场自然满足流体物理规律尚需得到关注.

(4)物理融合的神经网络求解正问题时效率依然较低. 一方面可以通过设计并行计算框架加速模拟, 如NVIDIA开发的并行计算程序SimNet^[87]极大提升了计算效率. 另一方面, Dong和Li^[88]结合极限学习机、区域分解和局部神经网络思想, 引入更多先验函数, 提出了局部极限学习机, 有效提升了网络求解效率.

(5)物理融合的神经网络求解正问题时无法解析地给出类似有限元或有限差分法的收敛性分析. 近期, Shin等^[89]首次在利用网络求解线性椭圆型和抛物型偏微分方程时分析了其收敛性, 但对高度非线性方程尚待进一步研究.