引言
湍流广泛存在于自然界和工程应用中, 准确认识和预测湍流现象十分重要. 湍流的研究有近百年的历史, 人们由理论、实验、和数值模拟方向出发取得了一系列的研究成果[1]. 然而, 在以航空航天为代表的工程应用中, 流动几何边界往往较为复杂, 且流动雷诺数较高, 研究的难度很大, 相应流动的基本规律和预测模型仍有待进一步深入研究. 因此, 湍流的机理、建模及控制仍然是航空航天等领域的重要瓶颈之一, 针对湍流的研究有着重要的基础和应用价值.
计算流体动力学(computational fluid dynamics, CFD)是湍流的重要研究手段, 常见的数值模拟方法可大致分为直接数值模拟(direct numerical simulation, DNS)、大涡模拟(large eddy simulation, LES)和雷诺平均模拟(Reynolds-averaged Navier?Stokes, RANS)等. 其中, 直接数值模拟和大涡模拟均需要较高的网格分辨精度. 对于航空航天等工程应用中的高雷诺数流动, 直接数值模拟和大涡模拟所需要的网格量巨大, 远超当前超级计算机的算力极限[2]. 相对而言, RANS虽然精度不及前两种方法, 但计算效率很高, 是各种工程应用中的主要研究手段.
雷诺平均模拟的结果往往受限于湍流模型的预测精度. 以雷诺应力输运模型[3]为代表的高阶矩封闭模型虽然精度较高, 但计算量较大且收敛性较差, 其应用范围较为有限. 实际工程中的常用湍流模型包括 SA模型[4]、k?ε模型[5]、k?ω模型[6]、SST模型[7]等. 这些模型均基于Boussinesq涡黏假设, 即假设雷诺应力的各向异性部分与应变率张量存在线性关系. 然而, 当流动较为复杂, 特别是出现如边界层分离、强烈混合等现象时, 雷诺应力与应变之间往往不再满足简单的线性关系, 因此基于涡黏假设的模型将会出现较大误差[8-9].
近年来, 随着相关算法的快速发展和可用数据的迅速增长, 机器学习方法开始在流体力学领域得到广泛关注[10], 其中一个重要的研究方向是利用机器学习方法开发湍流模型[11-12]. 如图1 所示, 可以将数据驱动的湍流建模大致分为3个步骤, 即数据预处理、模型训练以及模型验证和预测. 在数值模拟或者实验获得的高可信度(high-fidelity, Hi-Fi)流场基础上, 首先通过数据预处理提取输入特征变量(X表示)及输出变量(Y表示); 再由输入及输出变量出发, 采用不同的机器学习算法及策略训练模型; 最后一般要对训练得到的模型(Y = f (X))进行一定的测试, 验证其预测能力. 需要注意的是, 最终模型的预测能力依赖于训练数据、特征变量的选择、算法及策略等多种因素.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
机器学习湍流建模示意图
Figure
1.
Schematic for turbulence modelling with machine learning methods
下载: 全尺寸图片
幻灯片
根据输出变量的不同, 现有的数据驱动湍流建模研究大致可分为两个类型. 其中一部分研究关注于发展修正模型, 即采用不同的机器学习方法修正现有的模型及其参数, 以改善原有模型的预测精度. Edeling等[13]基于贝叶斯方法估计压力梯度边界层中模型误差并尝试修正模型参数. Parish和Duraisamy[14]提出了流场反演与机器学习(field inversion and machine learning, FIML)方法. 此框架首先通过统计方法反演得到修正参数场作为训练目标, 例如湍动能方程中湍流生成项的修正系数的空间分布; 进一步地, 采用机器学习方法重构这一修正场, 建立输入特征量与修正场之间的映射关系. FIML 框架的优势在于较为灵活, 其中流场反演部分可以使用贝叶斯方法[15], 也可基于伴随方法求解[16]; 另外, 机器学习部分也可以由高斯过程、神经网络等不同方法实现[17-18]. 值得注意的是, 这种框架中反演得到的修正场并不总是“可训练的”[19], 而训练过程的缺陷会导致反演场的误差, 进而导致最终预测精度和泛化能力的不足. 一种可能的改进方向是将反演和学习两个过程耦合, 但是相关的研究还较为初步[19].
另外一个大类的工作可归类为替代模型[12]的开发. 研究者们不满足于单纯修正现有的模型参数, 而是探索构建满足一定物理约束的RANS模型以替代原有模型. 针对RANS 和高精度流场的雷诺应力偏差, Wang等[20]采用随机森林方法构建模型, 在周期山测试算例中可以明显改善雷诺应力场的预测精度, 但是模型在后验测试中对于平均流场的预测精度还需要进一步验证. Ling等[21]采用深度神经网络方法训练满足伽利略不变性的雷诺应力模型. 训练基于速度梯度基张量和不变量[22], 得到的模型在后验测试中可以改善对于方腔流的预测精度. Yin 等[23]同样基于神经网络方法, 深入研究输入特征的选择标准以优化模型训练框架. 优化后的方法应用于周期山算例, 显著改善了流场的预测精度. 张伟伟等[12, 24-25]在机器学习湍流建模领域也开展了一系列工作, 例如利用神经网络方法直接构建基于平均流场的涡黏场预测模型[26], 针对近壁区、尾流区以及远场分别建模, 成功地预测了机翼的升阻力系数、阻力分布等. Xie等[27-29] 在一系列工作中采用不同方法针对大涡模拟的亚格子应力进行建模, 在后验测试中可以更为准确地预测湍流能谱等.
在众多数据驱动湍流建模研究中, 澳大利亚墨尔本大学Weatheritt和Sandberg[30]采用基因表达式编程方法(gene-expression programming, GEP)[30], 在最近的一些研究取得了一系列进展. GEP方法[31]是遗传算法的一种, 可以较为方便地实现符号回归, 近年来已在非稳态RANS[32]、湍流传热[33]、大涡模拟亚格子应力[34]以及燃烧[35]等多个领域的建模中得到了初步应用. 相较于神经网络等方法的“黑箱”模型, GEP 方法可以显式给出模型方程, 因此可以很方便地应用于工程软件中[36-37].
本文旨在对基于GEP方法的湍流显式模型相关工作进行简要总结. 文章的结构安排如下: 第1部分介绍基于GEP的模型训练方法及其框架; 第2部分, 介绍方法的几种典型应用; 最后第3部分是结论与展望.
1.
基因表达式编程
1.1
基本方法
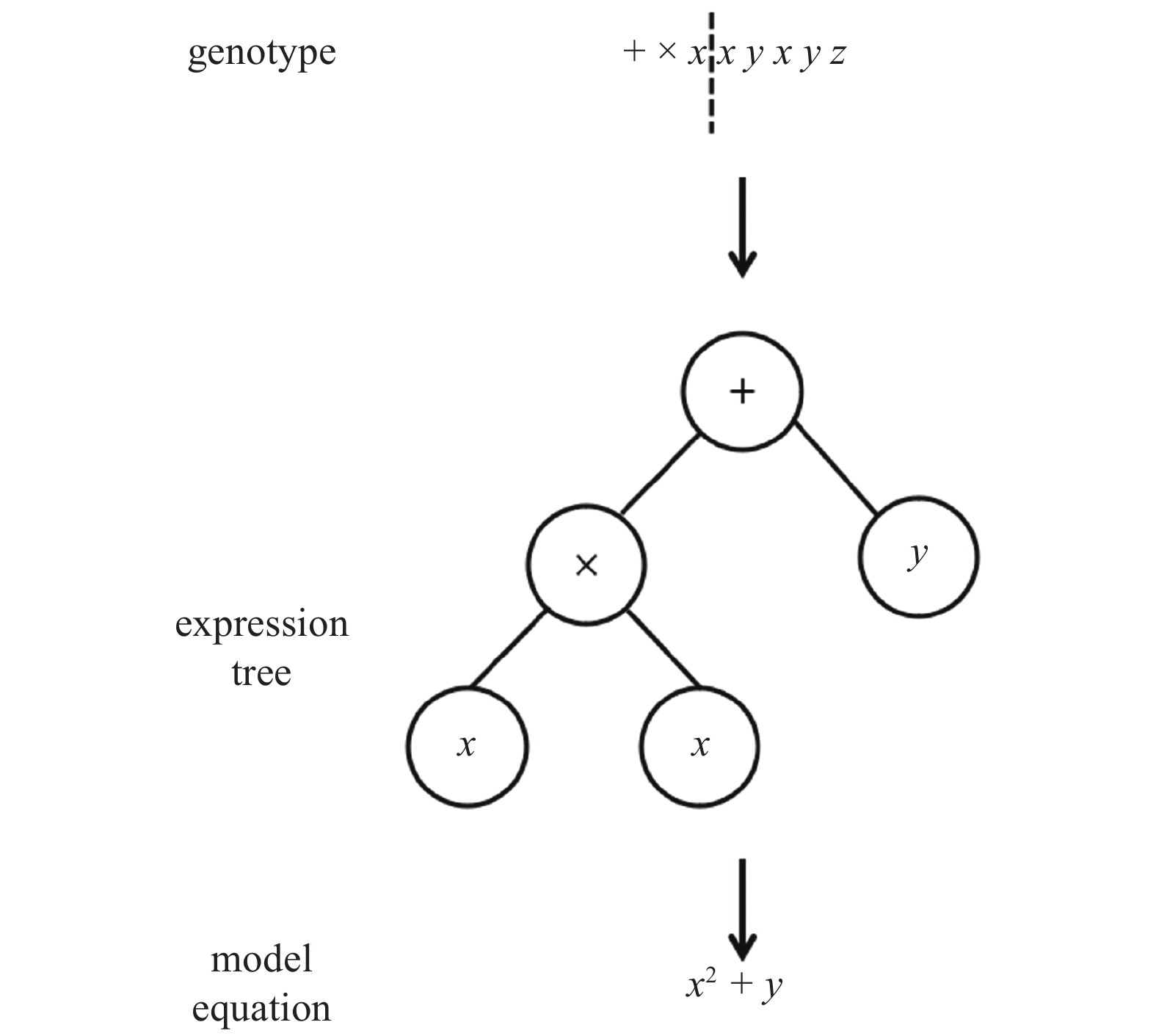
GEP方法[28]是遗传算法的一种, 基于达尔文自然选择理论, 通过种群的演化实现优化过程. 这里仅对GEP方法进行简要介绍, 方法的具体细节可参考文献[30]. GEP方法中的种群往往包含大量个体, 而每个个体均代表一个候选模型. 如图2所示, 模型的基因型(genotype)是一个字符串, 又被称作染色体. 该字符串由不同符号组成, 包括运算符(如 +, × 等)、常数项及变量符号(x, y). 在将字符串表达为方程形式的过程中, 首先将不同符号按照树结构(即表达树, expression tree)编码, 将运算符放置在非终端节点, 而常数项和变量符号放置在终端节点. 进一步地, 基于此树结构将其解码为表现型(phenotype), 该表达型就是一个候选模型方程. 这一基于树结构的表达过程保证公式符合语法规则, 可以被应用于实际运算.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
GEP方法的基因型及其表达过程
Figure
2.
Genotype and expression process in GEP
下载: 全尺寸图片
幻灯片
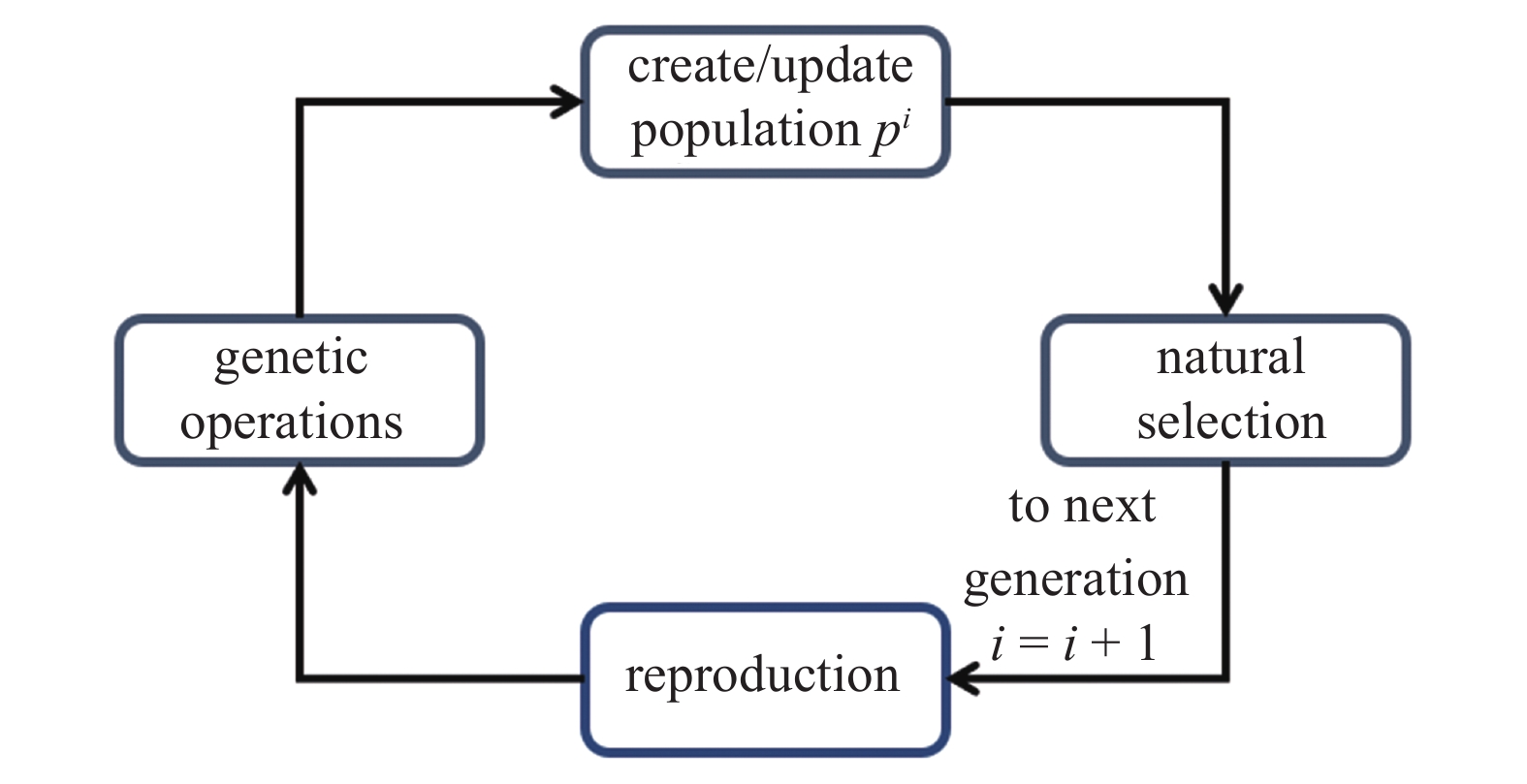
如图3所示, 在训练的开始, 首先随机生成一个包含大量个体的种群, 种群中个体的优劣可以由使用者定义的损失函数得到. 类似于自然界中的自然选择过程, 种群中损失函数较低的个体的“健壮度”较好, 因而有更大的概率进入下一代. 进一步地, 通过种群繁殖和基因变异等操作, 可以得到更新一代的种群. 正是通过这样的迭代过程, 整个种群向着更适应自然选择标准的方向演化, 演化最终得到的最优个体即为训练得到的模型.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
GEP方法流程图
Figure
3.
Schematic for GEP method
下载: 全尺寸图片
幻灯片
相较于其他机器学习方法, GEP方法的一个显著特点是可以通过符号回归得到显式的模型方程, 因而具有模型可解释、易应用的特点. 另外, 训练过程的寻优过程主要由基因的遗传和变异实现. 相较于梯度下降等方法, 这种训练过程更接近全局搜索, 不易收敛于局部最优解; 但同时收敛过程具有一定的随机性, 收敛速度无法得到保证, 特别是可能很难得到模型中常系数的最优解[31].
1.2
GEP与湍流建模
GEP方法近年来被应用于不同领域的湍流建模问题. 其中, 既包括RANS计算中的雷诺应力封闭模型, 也包括对湍流传热问题的建模. 本节分别介绍这两种典型的建模过程.
1.2.1
显式代数应力模型
在雷诺平均模拟中, 对Navier?Stokes方程进行雷诺平均, 动量方程中将产生一个非封闭项, 即雷诺应力
ho overline {{u_i}{u_j}} $
$$ {a_{ij}} = ho overline {{u_i}{u_j}} - frac{2}{3} ho k{delta _{ij}} = - 2{mu _t}{S_{ij}} $$  | (1) |
其中,
ho $
Boussinesq涡黏假设在大多数情况下并不适用. Pope[22] 基于量纲分析和坐标变换不变量, 进一步添加了非线性项, 将其扩展为
$$ {a_{ij}} = 2 ho ksumlimits_{k = 1}^{10} {{zeta _k}} left( {{I_1},{I_2}, cdots ,{I_5}} ight)V_{ij}^k $$  | (2) |
式中
$$ left. begin{split} {s_{ij}} =;& tau {S_{ij}} = tau left( {{U_{i,j}} + {U_{j,i}}} ight)/2 hfill {omega _{ij}} = ;&tau {varOmega _{ij}} = tau left( {{U_{i,j}} - {U_{j,i}}} ight)/2 hfillend{split} ight}$$  | (3) |
式中,
$$ left.begin{split} & V_{ij}^1 = {s_{ij}} & V_{ij}^2 = {s_{ik}}{omega _{kj}} - {s_{jk}}{omega _{ki}} & V_{ij}^3 = {s_{ik}}{s_{kj}} - frac{1}{3}{delta _{ij}}{s_{ik}}{s_{ki}} & V_{ij}^4 = {omega _{ik}}{omega _{kj}} - frac{1}{3}{delta _{ij}}{omega _{ik}}{omega _{ki}} & V_{ij}^5 = {omega _{ik}}{s_{km}}{s_{mj}} - {s_{im}}{s_{mk}}{omega _{kj}} & V_{ij}^6 = {omega _{im}}{omega _{mk}}{s_{kj}} + {s_{ik}}{omega _{km}}{omega _{mj}} - frac{2}{3}{delta _{ij}}{omega _{pm}}{omega _{mk}}{s_{kp}} & V_{ij}^7 = {omega _{im}}{s_{mk}}{omega _{kn}}{omega _{nj}} - {omega _{im}}{omega _{mk}}{s_{kn}}{omega _{nj}} & V_{ij}^8 = {s_{im}}{omega _{mk}}{s_{kn}}{s_{nj}} - {s_{im}}{s_{mk}}{omega _{kn}}{s_{nj}} & V_{ij}^9 = {omega _{im}}{omega _{mk}}{s_{kn}}{s_{nj}} - {s_{im}}{s_{mk}}{omega _{kn}}{omega _{nj}} - frac{2}{3}{delta _{ij}}{omega _{pm}}{omega _{mk}}{s_{kn}}{s_{np}} & V_{ij}^{10} = {omega _{im}}{s_{mk}}{s_{kn}}{omega _{np}}{omega _{pj}} - {omega _{im}}{omega _{mk}}{s_{kn}}{s_{np}}{omega _{pj}} hfill & {I_1} = {s_{ij}}{s_{ji}},;{I_2} = {omega _{ij}}{omega _{ji}},;{I_3} = {s_{ij}}{s_{jk}}{s_{ki}} & {I_4} = {omega _{ij}}{omega _{jk}}{s_{ki}},;{I_5} = {omega _{ij}}{omega _{jk}}{s_{km}}{s_{mi}} end{split} ight}$$  | (4) |
式(2)中给出的显式代数应力模型是Boussinesq线性涡黏假设的一种修正, 也是许多数据驱动湍流建模框架的基础[21, 27-28]. 在GEP湍流建模中, 以标量不变量
1.2.2
湍流传热模型
与雷诺应力相似, 对能量方程进行雷诺平均模拟时也将产生另一个非封闭项, 即湍流热通量
$$ - overline {{u_j}theta } = {alpha _t}{varTheta _{,j}}$$  | (5) |
式中
另外, SGDH中的扩散系数为各向同性, 且假设湍流热通量与平均温度梯度线性相关, 这也是模型误差的另外一个可能来源. 针对这一问题, 一种更为通用的模型可以将
$$ - overline {{u_i}theta } = tau {D_{ij}}{varTheta _{,j}} $$  | (6) |
如当
为进一步提高湍流传热模型的计算精度, 在机器学习建模中往往采用更为泛化的湍流扩散系数张量模型. 本文采用 Weatheritt等[33]对Younis 等[40]提出的显式湍流扩散系数张量模型的简洁表述
$$ - overline {{u_i}theta } = tau sumlimits_{n = 1}^{10} {{g_m}} left( {{I_1}, {I_2}, cdots ,{I_5};{J_0},{J_1}, cdots ,{J_{10}}} ight)D_{ij}^m{varTheta _{,j}} $$  | (7) |
式中
$$ left.begin{split} ;&k{delta _{ij}},{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {tau _{ij}},{kern 1pt} {kern 1pt} {kern 1pt} k {s_{ij}},{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {tau _{ik}}{tau _{kj}}/k,{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} k{s_{ik}}{s_{kj}} ;& {kern 1pt} {kern 1pt} {kern 1pt} k {kern 1pt} {kern 1pt} {omega _{ij}},{kern 1pt} {kern 1pt} {kern 1pt} k {kern 1pt} {omega _{ik}}{omega _{kj}},;kleft( {{s_{ik}}{omega _{kj}} + {omega _{ik}}{s_{kj}}} ight) ;&{kern 1pt} {kern 1pt} {tau _{ik}}{s_{kj}} + {s_{ik}}{tau _{kj}},{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {tau _{ik}}{omega _{kj}} + {omega _{ik}}{tau _{kj}} hfill end{split} ight}$$  | (8) |
$$ left. begin{split} ;&{omega _{ik}}{omega _{kj}},;{s_{ij}},;;{s_{ik}}{s_{kj}},;{omega _{ik}}{s_{kj}},;{omega _{ik}}{s_{km}}{s_{mj}} ;& {s_{ik}}{omega _{kp}}{s_{pm}}{s_{mj}},;;{omega _{ik}}{omega _{km}}{s_{mj}},;;{omega _{ik}}{omega _{kp}}{s_{pm}}{s_{mj}} ;&{omega _{ik}}{omega _{kp}}{s_{pm}}{omega _{mj}},;;{omega _{ik}}{s_{kp}}{s_{pm}}{omega _{mn}}{omega _{nj}}end{split} ight}$$  | (9) |
与雷诺应力相似, 在湍流传热建模中, 机器学习的目标是建立模型方程(7)中
1.3
模型的先验和后验测试
机器学习方法训练得到的模型在应用前必须进行充分的测试. 在湍流建模领域, 一般将测试分为先验(a priori)和后验(a posteriori). 所谓先验测试, 即将训练或者测试的高精度流场数据作为输入特征变量代入模型方程, 进而将模型预测的输出变量与高精度数据作对比, 以检测模型对于雷诺应力(或是湍流传热)的预测精度. 与之相对应, 后验测试则需要将训练得到的模型应用于实际RANS计算, 因此模型的输入特征变量由RANS计算的流场提供, 而模型的预测精度则根据RANS计算的结果进行判定. 需要指出的是, 一些数据驱动的湍流模型尽管可以给出令人满意的先验测试结果, 但是在实际计算中可能导致较大误差[41].
在机器学习建模中, 先验测试评价模型本身对于高精度训练数据的拟合和预测能力, 而后验测试则关注模型能否在实际计算中更好地预测流场信息. 对于湍流建模而言, 尽管先验测试十分重要, 但是后验测试的CFD计算中的预测效果往往才是最终的目标.
1.4
湍流建模中的损失函数
机器学习算法中损失函数的定义往往对于训练结果有决定性作用. 对于湍流建模问题而言, 也同样需要强调损失函数的重要性. 湍流建模问题中一个显著的特点是训练数据与最终模型的应用环境可能有很大区别. 一方面, 研究者一般认为直接数值模拟或者大涡模拟的结果为“真实值”, 作为训练和测试数据; 另一方面, 模型的最终需要应用于雷诺平均模拟, 而雷诺平均模拟中的湍动能、湍流耗散时间尺度等往往与训练数据存在较大区别. 这会给损失函数的定义带来一定的困难. 本节介绍两种不同的损失函数定义方法.
1.4.1
冻结训练
Akolekar等[37]基于GEP方法提出了冻结训练方法. 图4以二方程雷诺平均模型为例介绍冻结训练的流程. 由直接数值模拟等高可信度流场, 可以得到平均速度、平均速度梯度张量、雷诺应力、湍动能等数据, 并以此作为“真实值”. 在此基础上, 将“冻结”的平均速度和湍动能代入模型输运方程, 如k?ω模型中的ω方程, 得到适用于雷诺平均模拟的湍流耗散时间尺度. 采用这种湍流特征时间尺度对速度梯度张量进行无量纲化, 可以得到1.2.1小节中的张量基函数和标量不变量作为模型的输入变量. 进一步地, 使用GEP方法训练基于无量纲速度梯度张量基函数和标量不变量的显式代数应力模型.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-4.jpg'" class="figure_img
figure_type2 ccc " id="Figure4" />
图
4
冻结训练流程示意图
Figure
4.
Schematic for ‘frozen’ training method
下载: 全尺寸图片
幻灯片
在这一训练过程中, 通过求解k?ω模型中的ω方程得到湍流耗散时间尺度, 用于进一步的速度梯度张量无量纲化. 在求解过程中, 平均速度场和湍动能来自于“冻结的”高精度训练数据, 在迭代过程中不发生变化. 这里仅对ω进行迭代更新, 直至收敛. 因此该方法被称为冻结训练.
冻结训练方法中采用求解模型方程得到的湍流耗散时间尺度进行无量纲化, 而不是直接使用高精度训练数据中的特征时间尺度. 这是因为直接数值模拟等方法得到的湍流耗散时间尺度与实际雷诺平均模拟运算中的结果往往存在较大差异. 这种差异可以认为是高精度训练数据与雷诺平均模拟之间存在一定的相容性问题. 换而言之, 完全依据直接数值模拟等高精度流场训练得到的雷诺应力模型可能并不适用于雷诺平均模拟, 这种情况下尽管模型可能在先验测试中准确度较高, 但在后验测试中仍然存在较大误差. 因此, 必须在模型训练过程中考虑这种差异, 通过冻结方法增强模型在实际雷诺平均模拟中的适用性, 提升其后验精度.
冻结训练以修正模型预测的雷诺应力为目标, 对应的损失函数是通过对比高精度训练数据中的雷诺应力和模型给出的雷诺应力来得到. 通过求解模型输运方程, 冻结训练引入适用于雷诺平均模拟的特征时间尺度进行无量纲化, 从而可以在一定程度上缓解高精度训练数据与RANS模拟的相容性问题. 然而, 最近一些****研究发现[42-43], 即便将直接数值模拟得到的雷诺应力代入RANS计算中, 得到的平均流场也可能会产生较大的误差. Wu等[41]还发现, 这种预测误差在雷诺数增高时会进一步增大. 这种现象导致数据驱动的RANS模型很难在后验验证中准确预测平均流动.
1.4.2
双向耦合方法
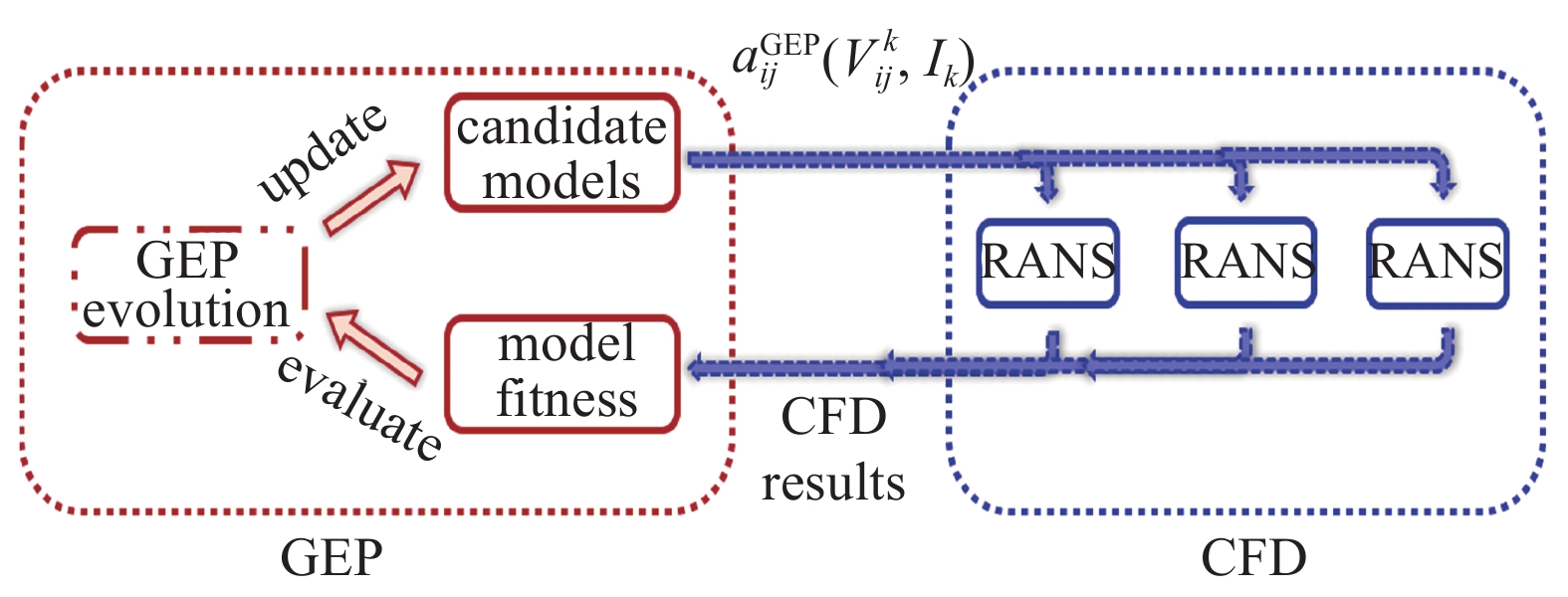
针对湍流建模中常见的高精度训练数据和RANS计算的相容性问题, Zhao等[44]首次提出了机器学习和CFD双向耦合的模型训练方法. 双向耦合方法的最大特点是训练过程中模型的优劣通过实际RANS计算的结果来评估, 而不是仅仅基于高精度训练数据判定对于雷诺应力的预测效果. 如图5所示, 对于每一代的候选模型, 将一系列模型方程读入到RANS求解器中, 并基于该模型实现RANS计算; 进一步将计算的结果返回GEP训练过程, 以评估模型方程的损失函数. 由于在训练过程中, 每一代模型的评估均需要GEP算法和RANS计算共同作用, 因此称之为机器学习和CFD双向耦合的训练方法. 双向耦合训练方法的步骤可以总结为以下几个步骤:
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
双向耦合方法训练流程示意图
Figure
5.
Schematic for CFD-driven machine learning method
下载: 全尺寸图片
幻灯片
(1)初始化种群, 得到一系列模型方程;
(2)种群中的一系列候选模型均由CFD运算进行评估, 这一过程可以并行操作, 具体步骤如下:
①模型方程写入文件, 再由RANS求解器读入此文件;
② RANS求解器基于GEP算法提供的候选模型运行CFD模拟;
③ RANS计算的结果分两类. 如果RANS收敛, 模型的损失函数可由收敛后流场计算得到; 如果RANS不收敛, 模型损失函数设为无穷大;
④ 将CFD计算得到的模型损失函数返回GEP算法, 以评估候选模型;
⑤ GEP算法迭代, 模型种群繁殖、变异, 进入下一代, 直到得到期望的模型.
相比于冻结方法, 双向耦合方法具有以下特点. 首先, 双向耦合方法的训练目标灵活, 可以根据RANS计算的结果设定不同的损失函数作为优化目标; 相对而言, 冻结方法只能对比模型预测的雷诺应力与高精度训练数据. 其次, 双向耦合方法对于训练数据的需求量较少, 实验测量得到的少许平均流场数据即可作为训练数据; 相对而言, 冻结训练往往需要高精度数值模拟得到的全场雷诺应力等高阶湍流统计量. 最后, 由于双向耦合方法得到的模型在训练过程中就已经经过RANS计算的检验, 因此模型的收敛性和后验预测精度均有一定保证; 相对而言, 冻结方法得到的模型在应用于真实RANS计算时, 对于平均流场的预测精度可能存在较大误差. 双向耦合方法面临的主要挑战在于计算效率方面. 与冻结训练相比, 尽管双向耦合方法在GEP训练中所需的种群代数相差不大(一般约为数百代), 但是由于其迭代过程中每一代候选模型的评估均需运行RANS计算, 因此训练所需的计算量往往远大于冻结方法.
2.
应用算例
第1部分介绍了基因表达式编程方法以及如何基于此方法训练湍流和传热模型. 接下来, 介绍GEP方法在几种湍流建模问题中的具体应用.
2.1
尾流混合问题的代数应力模型
2.1.1
统计稳态流动的RANS模型
在航空发动机内流中的叶片尾沿下游, 叶片压力侧和吸力侧的来流在强剪切层的主导下产生强烈混合, 这是典型的尾流混合问题. 尾流混合往往导致显著的流动损失, 因此准确模拟尾流混合问题对于内流预测和叶片设计十分重要, 然而基于Boussinesq假设的常用工程湍流模型对于尾流损失的预测精度往往不甚理想[45]. 最近几年来, GEP方法在一系列的工作中[37, 44, 46-47]被应用于尾流混合问题, 针对如图6所示的高压涡轮和低压涡轮平面叶栅算例, 目标为发展具有较高预测精度和较强泛化能力的尾流混合模型.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
航空发动机内流叶栅尾流混合算例示意图
Figure
6.
Simulation setup for cases
下载: 全尺寸图片
幻灯片
表1给出了一系列涡轮叶栅算例的参数. 基于直接数值模拟或是大涡模拟提供的高精度流场数据, 这些算例被用于模型的训练和测试. 以典型航空发动机工况下的高压涡轮(表1算例A)为研究目标, Weatheritt等[47]采用1.2.1小节中介绍的冻结方法训练显式代数应力模型. 训练中损失函数设置为
表
1
涡轮叶栅尾流混合算例
Table
1.
Parameters of turbine wake mixing cases
table_type1 ">
| Cases | Re | Ma | Flow features |
| HPT A | 570 000 | 0.9 | transition & shocks |
| HPT B | 1 100 000 | 0.9 | transition & shocks |
| LPT C | 60 000 | 0.4 | transition & open separation |
| LPT D | 100 000 | 0.4 | transition & closed separation |
下载: 导出CSV
|显示表格
$$ {J^{{ m{fro}}}} = frac{1}{N}sumlimits_{n = 1}^N {sumlimits_{i,j} {frac{{left| {a_{ij}^{{ m{HiFi}}} - a_{ij}^{{ m{GEP}}}} ight|}}{{left| {a_{ij}^{{ m{HiFi}}}} ight|}}} } , $$  | (10) |
即在N个网格点上, GEP模型得到的雷诺应力各向异性部分
m{GEP}}} $
m{HiFi}}} $
$$ begin{split} tau _{ij}^{{ m{fro}}} =;& frac{2}{3} ho k{delta _{ij}} - 2{mu _t}S_{ij}^prime + 2 ho k[ hfill ( -1.334 + ;& 0.438{I_1} + 2.653{I_2} hfill +0.010;2I_1^2 - ;& 1.021I_2^2 + 12.280{I_1}{I_2})V_{ij}^1 hfill + ;& (0.573 - 1.096{I_1} + 8.985{I_2} - hfill ;&0.110;2I_1^2 + 2.876I_2^2 + 90.633{I_1}{I_2})V_{ij}^2 hfill + ;& (12.861 - 25.094{I_1} + 6.449{I_2} + hfill ;& 1.020I_1^2 - 304.979{I_1}{I_2} - 184.519I_2^2)V_{ij}^3] end{split} $$  | (11) |
对这一模型进行先验测试, Weatheritt等[47]发现相较于传统Boussinesq假设, 该模型可以明显改善对于尾流区域雷诺应力的预测. 但是, 由于存在大量高阶非线性项, 该模型在后验测试中很难得到收敛的流场.
为进一步发展鲁棒性更强的尾流混合模型, Zhao等[44]提出了1.2.2小节中介绍的双向耦合训练方法, 并将其应用于高压涡轮算例A. 不同于式(10)中给出的冻结训练损失函数, 双向耦合方法训练过程中损失函数的设置较为灵活, 不仅可以对比雷诺应力等高阶统计量, 更可以选择实验、直接数值模拟等高可信度数据中可提供的任意感兴趣的平均流场信息. 以涡轮尾流混合问题为例, 这里选择根据RANS模拟结果中的平均尾流损失设置损失函数. 具体形式如下
$$ left. begin{aligned} &varOmega (y) = frac{{p_t^i - {p_t}(y)}}{{p_t^i - {p^o}}}hfill & {varDelta _x} = frac{1}{{{L_y}}}int_0^{{L_y}} {{{left[frac{{{varOmega ^{{ m{HiFi}}}}(y) - {varOmega ^{{ m{RANS}}}}(y)}}{{{{max }_y}({varOmega ^{{ m{HiFi}}}})}} ight]}^2}{ m{d}}y} hfill & {J^{{ m{CFD}}}} = {varDelta _{x1}} + {varDelta _{x2}} end{aligned} ight}$$  | (12) |
这里
m{CFD}}}} $
采用双向耦合方法训练并设置式(12)中的损失函数, Zhao等[44]得到的尾流混合模型如下
$$ begin{split} tau _{ij}^{{ m{CFD}}} = ;&frac{2}{3} ho k{delta _{ij}} - 2{mu _t}S_{ij}^prime + 2 ho k cdothfill ;& left[left( { - 2.57 + {I_1}} ight)V_{ij}^1 + 4.0V_{ij}^2 hfill ight.+ ;&left. left( { - 0.11 + 0.09{I_1}{I_2} + {I_1}I_2^2} ight)V_{ij}^3 ight] hfillend{split} $$  | (13) |
将此模型与冻结方法获得的模型式(10)作对比, 发现双向耦合方法得到的模型方程中高阶非线性项大大减少. 其原因在于这些高阶项往往导致实际RANS计算难以收敛, 因此在双向耦合训练过程中被自然选择所淘汰. 由此可见, 双向耦合方法获得的模型一般具有更强的收敛性和鲁棒性.
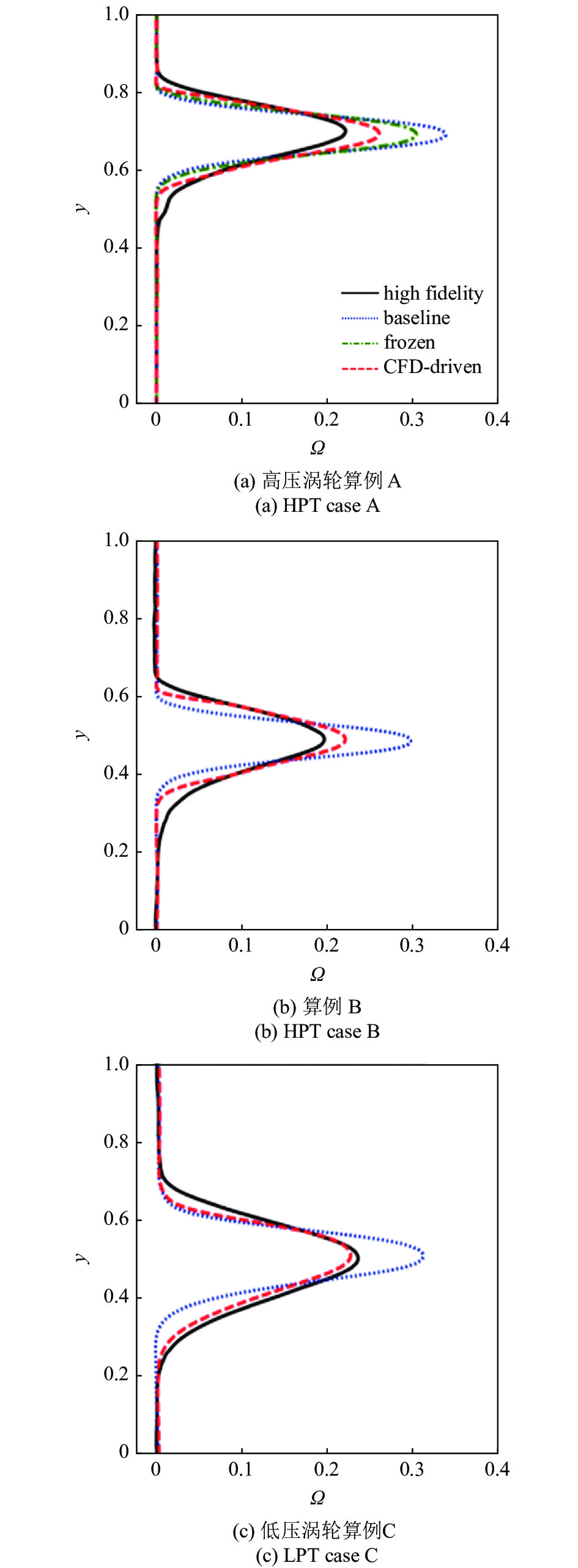
将式(11)中的双向耦合模型应用于后验测试, 并将其与去除高阶项后的简化冻结模型的预测结果作对比. 如图7(a) 所示, 相较于作为基准模型的k?ω SST模型和冻结模型, 双向耦合方法在后验测试中可以显著提高对于式(12)中尾流损失 的预测精度. 进一步对模型进行分析, Zhao等[44]指出双向耦合模型对于尾流损失预测的提升, 其主要原因在于方程中占主导的
ho kV_{ij}^1$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-7-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure7-1" />
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
不同涡轮叶栅算例(见表1)中的尾流损失剖面
Figure
7.
Kinetic wake loss profiles from test cases in Table 1
下载: 全尺寸图片
幻灯片
为进一步验证双向耦合模型的泛化能力, 还将其应用于表1所示的算例B, C和D中. 这些算例与训练算例A相比, 其雷诺数、出流马赫数、攻角以及几何外形均有很大差别. 如图7(b) ~图7(d)所示, 在这一系列后验测试中, 这种双向耦合方法训练得到的显式代数应力模型可以较为准确地预测尾流混合导致的流动损失. 因此该模型具有较强的泛化能力.
2.1.2
非稳态流动的unsteady RANS建模策略
上一节讨论了针对统计稳态流动的建模过程, 可以看到GEP方法能有效提升RANS对于尾流混合的预测精度. 但是当流动处于非稳态时, 往往应采用非定常雷诺平均(unsteady RANS)模拟, 而建模策略可能也需要相应调整.
航空发动机内流领域一种常见的非稳态现象是两排叶片之间存在的相对运动导致的流动周期性变化. Akolekar等[48]针对来流为周期性尾流扰动的低压涡轮叶栅展开研究, 探讨机器学习湍流建模的策略. 图8给出了锁相平均的叶栅湍动能云图. 将一个来流扰动周期分为20个不同的相, 由图8可发现周期性来流尾流对涡轮叶栅流场造成显著影响, 不同相的流动之间呈现显著差别.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
来流尾流扰动下低压涡轮叶栅的锁相平均湍动能云图[48]
Figure
8.
Phase-lock averaged TKE contours for LPT flow disturbed by incoming wakes[48]
下载: 全尺寸图片
幻灯片
针对这种非稳态流动, 湍流建模策略可有几种: (1)针对不同相的流场单独建模; (2)根据时间平均后的流场建模; (3)根据一定的流动物理分组建模. 显然, 针对不同相分别建模会给出适用于各相的一系列湍流模型, 但是模型间的切换会给使用者的实际模拟带来不便. Akolekar等[46]进一步发现, 针对时间平均的流场建模, 虽然可以一定程度改善预测精度, 但是由于忽略了各相间的差异导致其精度仍然有限. 相对而言, 最优的策略是根据流动物理将不同相分组, 进而针对各组具有相似物理的流动分别建模.
在这种根据流动物理对不同相进行分组的过程中, GEP方法可以起到关键作用. 针对低频来流尾流扰动下的低压涡轮叶栅流动, Akolekar等[48]首先对20相分别建模. 得到这些单相模型后, 一方面可以分别测试各模型的预测精度, 发现单相训练得到的模型在不同相的测试中表现并不理想. 另一方面, 也可以根据GEP方法显式给出的方程形式, 对不同相的模型进行分析. 在分析过程中, Akolekar等[48]发现不同相的模型方程大致可分为两组. 对于其中一组(包含大约10相), 其模型方程中
2.2
湍流传热模型
近年来, GEP方法也被应用于温度或标量场的建模之中. 本文首先针对竖直平板间自然对流这一较为简单的算例, 介绍基于GEP的标量系数湍流传热模型; 然后针对更为复杂的三维横向流中的射流算例, 介绍张量系数湍流传热建模.
2.2.1
自然对流的湍流标量系数建模
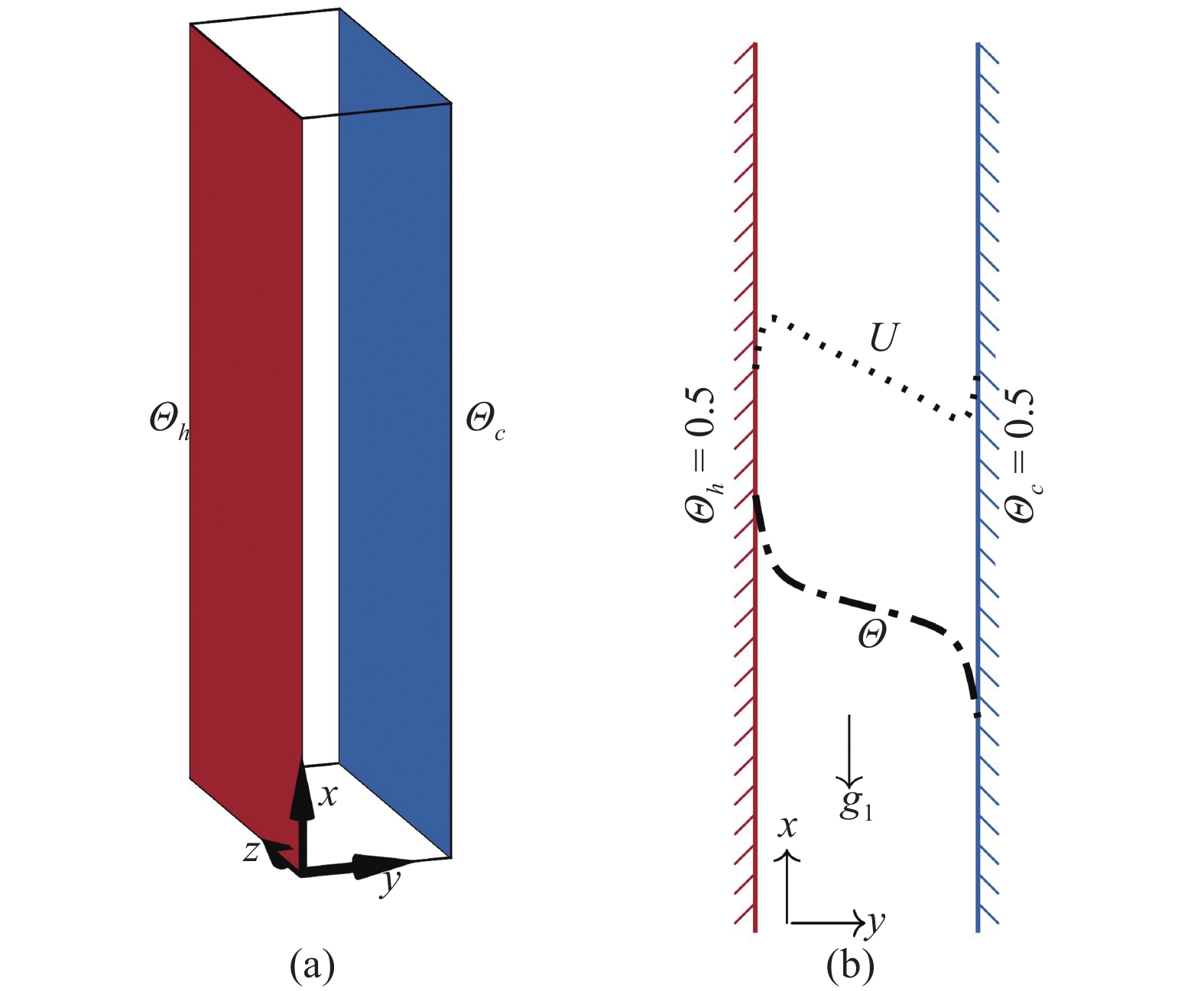
自然对流在室内通风环境(如双层玻璃窗)、电子设备冷却等场景中十分常见. 图9给出了以浮力驱动竖直充分发展槽道流中的自然对流计算域示意图, 其中两个竖直板沿
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
以竖直槽道流中的自然对流算例的计算域
Figure
9.
Computational domain of natural convection case in a differentially heated vertical channel
下载: 全尺寸图片
幻灯片
Ng等[49]通过直接数值模拟(DNS)中得到了该算例 的平均流场、雷诺应力和湍流热通量. Xu等[50]以此数据集中的算例为训练数据, 提取湍流涡黏系数, 并以垂直壁面方向的热通量为学习目标. 基于GEP方法, 通过最小化损失函数
$$J_{overline{vtheta}}^{{ m{fro}}} = frac{1}{N}sumlimits_{n = 1}^N {{{left( {{{overline {vtheta } }^{{ m{DNS}}}} - {{overline {vtheta } }^{{ m{GEP}}}}} ight)}^2}} $$  | (14) |
得到模型方程
$$ - {overline {vtheta } ^{{ m{GEP}}}} = left( {0.969 + 2{J_0}} ight)v_t^{{ m{DNS}}}{varTheta _{,j}}$$  | (15) |
根据
ight)}}$
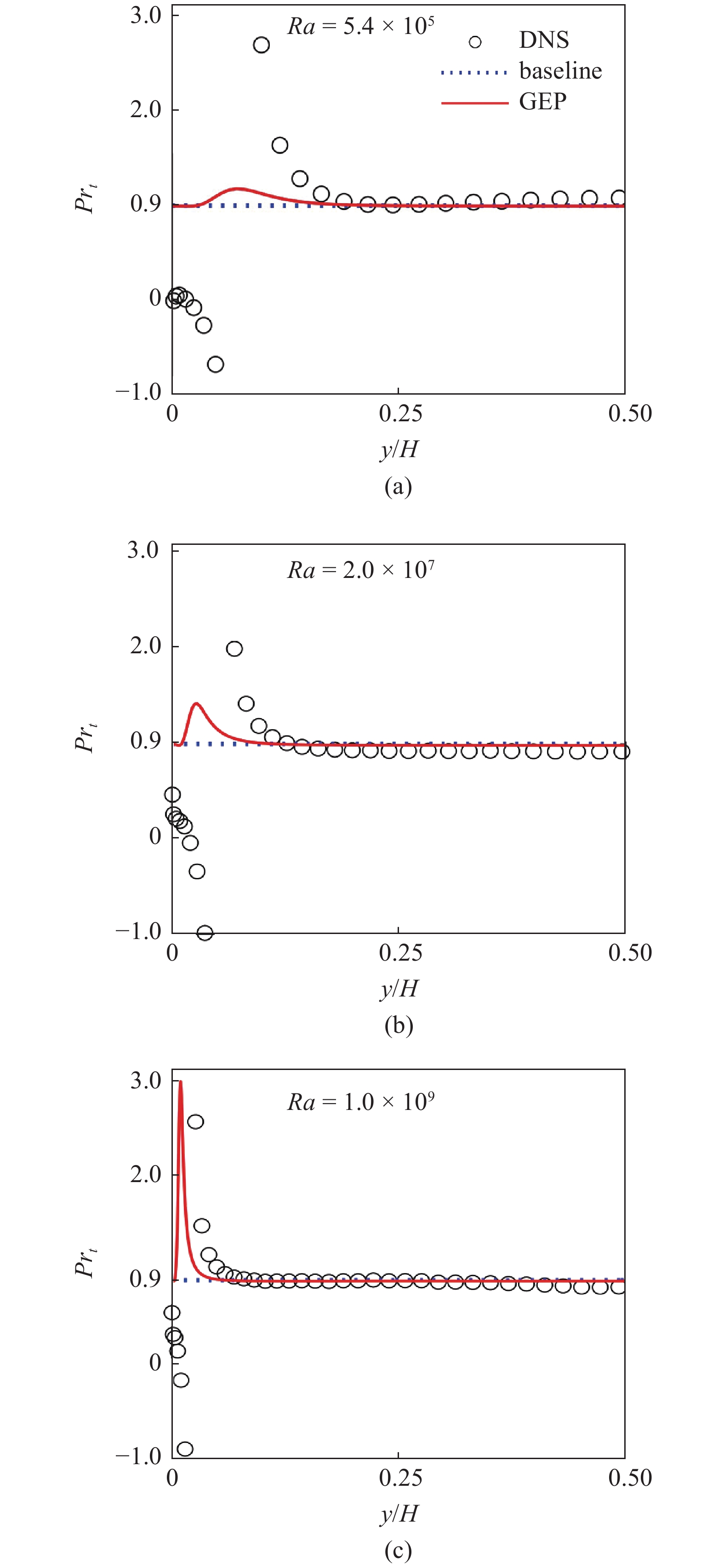
在先验测试中, 图10比较了基于DNS计算的
m{DNS}}} = overline {uv} {varTheta _{,y}}/left( {overline {vtheta } {U_{,y}}}
ight)$
m{DNS}}}$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-10.jpg'" class="figure_img
figure_type1 bbb " id="Figure10" />
图
10
湍流普朗特数的先验预测
Figure
10.
Prediction of turbulent Prandtl number
下载: 全尺寸图片
幻灯片
在后验测试中, Xu等[50]在给定DNS的速度场相关数据的基础上, 求解温度的对流?扩散输运方程, 来测试湍流传热模型的预测效果. 该模型被应用于3个不同
ight)$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-11.jpg'" class="figure_img
figure_type2 ccc " id="Figure11" />
图
11
平均温度剖面和垂直壁面方向的热通量的后验预测
Figure
11.
Prediction of mean temperature profiles and wall-normal heat flux
下载: 全尺寸图片
幻灯片
2.2.2
横向射流的湍流张量扩散系数建模
三维横向流中的射流 (jet in cross-flow, JICF)在航空发动机等涡轮叶片中有广泛应用, 准确预测其流场和温度场是工业界亟待解决的难题. 图12给出了典型JICF的算例设置示意图. 其中,
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-12.jpg'" class="figure_img
figure_type1 bbb " id="Figure12" />
图
12
横流中的射流示意图
Figure
12.
The schematic description of jet in crossflow case
下载: 全尺寸图片
幻灯片
Weatheritt等[33]基于Bodart等[51]的JICF大涡模拟数据进行GEP湍流传热建模, 其中展向宽度为
在三维算例中, 式(7)包含10个张量扩散系数基函数
$$ ho left( {overline {{u_i}theta } ,D_{ij}^m{varTheta _{,j}}} ight) = frac{{left| {overline {{u_i}theta } cdot D_{ij}^m{varTheta _{,j}}} ight|}}{{left| {overline {{u_i}theta } theta } ight|D_{ij}^m{varTheta _{,j}} }}$$  | (16) |
可以发现张量系数相关度的排序为
$$D_{ij}^4{varTheta _{,j}} > D_{ij}^9{varTheta _{,j}} > D_{ij}^2{varTheta _{,j}} > cdots > D_{ij}^8{varTheta _{,j}}$$  | (17) |
由此可见,
在此基础上, GEP模型训练中符号回归的方程设置为
$$ - {overline {{u_i}theta } ^{{ m{GEP}}}} = {g_2}tau D_{ij}^2{varTheta _{,j}} + {g_4}tau D_{ij}^4{varTheta _{,j}} + {g_9}tau D_{ij}^9{varTheta _{,j}}$$  | (18) |
其中,
此外, 损失函数为
$${J_{overline{{{u_i}theta }}}^{ m{fro}}} = dfrac{1}{{|V|}}sumlimits_{k in V} {{{left( {{{overline {{u_i}theta } }^{(k),{{ { m{DNS}} }}}} - {{overline {{u_i}theta } }^{(k),{ m{GEP}}}}} ight)}^2}} $$  | (19) |
其中,
$$left.begin{split} {g_2} = ;& - 2{I_1} - 2{I_2} - {I_3} + {J_1} + 3{J_2} - {J_4} + 5.02{g_4} = ;& - {I_2} + left( {{J_2} - 4} ight)left( {{I_2} - 3{J_2} + {J_4}} ight){g_9} =;& left( { - {I_1} + {J_2} + 2} ight)left( {2{I_2} + 2{J_1} + {J_3} + {J_4} - 4.01} ight)end{split} ight}$$  | (20) |
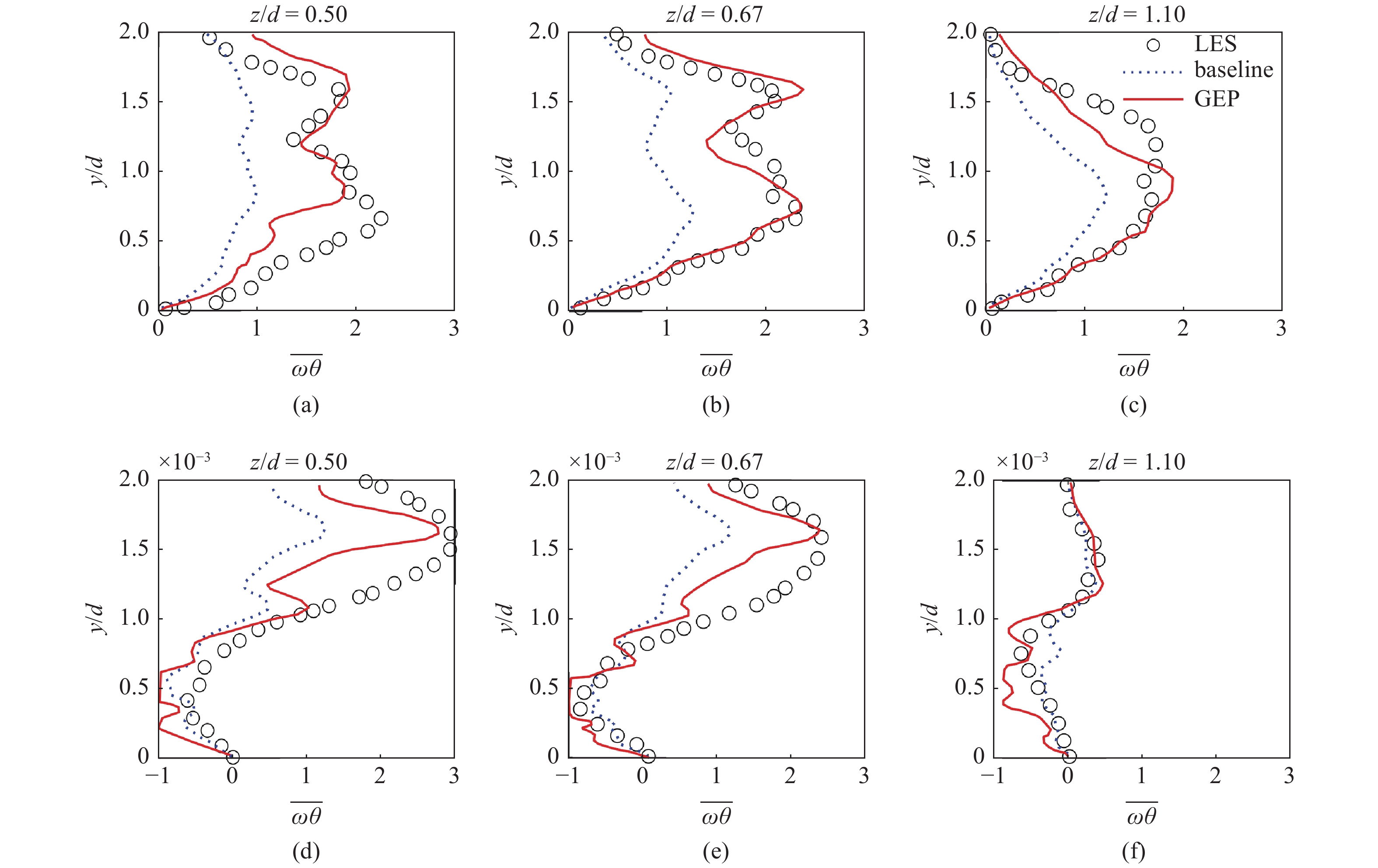
该模型被应用于Bodart算例. 图13给出了流向
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-13.jpg'" class="figure_img
figure_type2 ccc " id="Figure13" />
图
13
流向位置x/d=20的热通量预测
Figure
13.
The prediction of heat flux vector at x/d=20
下载: 全尺寸图片
幻灯片
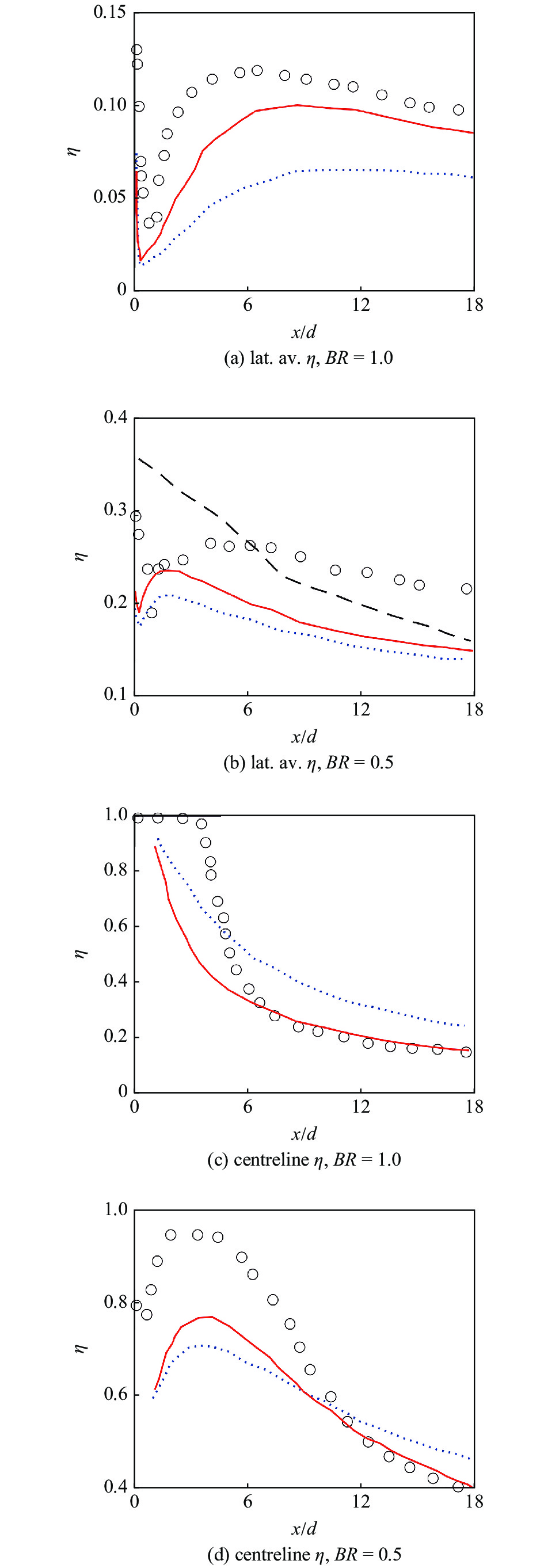
此外, 该模型还被应用于Sakai等[52]的JICF大涡模拟算例(Sakai算例), 以测试基于Bodart 算例的湍流张量扩散系数模型的泛化能力. 与Bodart算例相比, Sakai算例的几何尺寸和主要特征参数均不同, 其中, 展向宽度为
ight)/ $
ight) $
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-391-14.jpg'" class="figure_img
figure_type1 bbb " id="Figure14" />
图
14
壁面绝热效率的流向分布
Figure
14.
Wall adiabatic effectiveness streamwise distribution
下载: 全尺寸图片
幻灯片
综上所述, 无论是针对湍流标量系数(如湍流普朗特数)还是对湍流张量扩散系数进行建模, GEP方法均能提升对湍流传热的预测精度, 且具有一定程度的泛化能力.
2.3
GEP方法在湍流建模中的其他应用
自Weatheritt和Sandberg[30]首次将GEP应用于湍流建模以来, 此方法已在多个相关领域得到了成功应用. 2.1节和2.2节重点介绍了针对代数应力模型和湍流传热问题的典型建模过程. 在此基础上, 在本节简要介绍GEP方法在湍流建模领域的一些拓展和其他应用.
与1.2.1小节中的RANS建模过程非常类似, GEP方法还可应用于大涡模拟亚格子应力建模. Schoepplein等[35]首次将GEP方法应用于湍流预混火焰的亚格子应力建模. 与RANS建模中以平均流场为训练数据不同, 亚格子应力的建模基于滤波后的直接数值模拟瞬时流场. 该训练采用冻结方法, 所得到的亚格子应力代数表达式在先验测试中具有较高的准确度. 但是, 该模型并未经过后验测试, 且模型的泛化能力也需要进一步验证. 最近, Reissmann等[34]尝试将双向耦合方法[44]应用于泰勒?格林涡的亚格子应力建模中. 在后验测试中, 所得模型可较为准确预测湍动能等统计量演化过程. 当然, 这一模型对充分发展湍流的适用性还有待一步验证.
在最近的工作中, GEP方法还被尝试应用于边界层转捩问题的建模[53]. 基于层流动能(laminar kinetic energy, LKE)方法[54], Akolekar等[53]针对LKE方程中的层流涡黏系数等关键参数提出修正的代数模型. 在后验测试中, 该模型实现了对于低压涡轮叶栅中分离引起的边界层转捩的准确预测. 虽然该模型的鲁棒性等问题还有待进一步研究, 但该结果显示了GEP方法在边界层转捩等复杂流动的建模中具有良好的应用前景.
3.
结论与展望
近年来, 机器学习辅助的湍流建模研究发展迅速, 然而在训练数据和训练方法、模型可解释性和泛化能力等方面仍然存在较大挑战. 本文讨论的一系列工作基于GEP方法在这一领域取得了一定进展, 实现了多种类型的湍流建模. 在训练数据方面, 这些工作关注具有较强实际应用背景的复杂流动, 以发展实用工程湍流模型为目标. 在训练方法方面, 通过引入双向耦合方法等模型训练框架, 考虑RANS计算与高精度训练数据的差别, 强调模型的实际预测能力. 另外, 由于GEP方法可以提供显式模型方程, 因此模型可解释性较强.
值得注意的是, 目前大多数机器学习方法得到的湍流模型距离真实工程应用还存在明显的差距. 接下来的工作重点之一是提高模型的泛化能力. 一种具有较强应用前景的数据驱动模型应该可以较好地预测多种类型流动(如远离壁面的自由剪切流动和近壁面湍流)及多种流动物理(如强混合、转捩、流动分离等). 此外, 针对双向耦合方法, 还可以通过优化GEP算法的收敛速度或种群大小、改善CFD求解器等方式来提升训练的计算效率. 以上述工作重点为目标, 需要进一步完善现有的训练数据和训练方法.
