引言

近年来, 主动颗粒(active particle)的概念逐渐进入人们的视野. 流体中的主动颗粒通常指具有自推进能力的微型颗粒物, 例如游动的细菌^[1]和浮游生物^[2]等微生物, 或医用微纳机器人^[3]. 研究主动颗粒的行为特性有两个方面的意义: 从微观角度上, 单个颗粒的运动决定了其自身的状态. 例如, 浮游生物是否能躲避捕食者, 微纳机器人是否能完成给定的任务, 都取决于其自身的运动情况; 从宏观角度上, 群体中每个颗粒的运动模式决定了整个群体的运动性质. 例如, Reynolds^[4]提出的鸟群模型中就通过控制个体的运动来实现群体层面的运动特性, Li等^[5]也运用类似的原理, 利用功能简单的主动颗粒个体组成群体, 从而完成复杂的任务.

主动颗粒通常在流体介质中运动, 例如浮游生物在海洋或其他水域活动, 微纳机器人进入人体后在血液中运动. 因此, 大量研究聚焦于主动颗粒在各种流动环境下的运动特性, 包括游动速度、游动方向和聚集程度等. Durham等^[6]研究了基于微生物模型的主动颗粒在二维Taylor-Green涡中的分布和聚集情况, 并发现重力引起的恢复力矩(gyrotactic力矩)^[7]会使颗粒聚集在特定的驻点区域. Durham等^[8]发现在重力恢复力矩作用下, 湍流中的主动颗粒倾向于聚集在流速朝下的区域. 此后, 相关研究进一步揭示了不同形状的主动颗粒的聚集特性和原理^[9-10]. 另一方面, 由于主动颗粒获得的推力通常只沿特定方向, 它们的朝向特性也受到广泛的关注. 细长游动颗粒的游动方向会自发地沿着当地流体速度的方向^[11]; 受到重力恢复力矩作用的颗粒倾向于沿着重力的反方向游动^[12]; 在流体惯性作用下, 因重力而沉降的游动颗粒也会倾向于沿着重力反方向游动, 与受到重力恢复力矩的情况有相似的表现^[13].

上述研究中的主动颗粒都只能以简单且固定的模式运动. 然而, 实际问题中的主动颗粒往往可以主动改变自身的运动形式. 例如, 浮游生物能够感知周围流场的扰动, 做出相应的逃避行为^[14-15], 或是在湍流的影响下改变游动速率^[16]. 把这类能够以某种策略, 根据变化的环境来智能地调整自身的运动颗粒称为智能颗粒(smart particle). 如何定义一个具体的智能颗粒模型呢? 首先, 需要建立描述颗粒在环境中运动的模型. 第二, 需要明确智能颗粒能够感知何种环境信息. 例如, 浮游生物可以感知周围流场的扰动速度. 第三, 需要明确智能颗粒能够以何种行为方式对环境做出响应, 并在模型中准确描述颗粒的行为方式. 例如, 流体扰动会触发浮游生物改变游动方向、躲避捕食者的行为^[14], 而模型中需要描述这种行为. 第四, 需要明确智能颗粒的运动目标, 例如最大化浮游生物的生存率. 最后, 还需要确定智能颗粒的运动策略, 即在何种环境状态下采取何种响应. 实际上, 寻找运动策略是智能颗粒研究中最关键也最困难的一步. 当可能的状态和响应数量较大时, 遍历所有策略将花费很大的代价. 另一方面, 智能颗粒问题往往会考虑流体的影响, 进而引入非线性因素, 使理论求解最优策略变得更加困难.

幸运的是, 强化学习算法能够有效地解决智能颗粒的运动策略问题. Colabrese等^[17]首次利用强化学习算法寻找智能游动颗粒在二维Taylor-Green流动中的高效垂直迁移策略. 受到这一工作的启发, 近年来涌现出一系列结合强化学习的智能颗粒研究. Gustavsson等^[18]研究了三维解析流动中的智能颗粒的定向运动问题, 验证了强化学习方法的有效性. Biferale等^[19]和Buzzicoti等^[20]的相关工作则研究了二维湍流流动中智能颗粒的点对点运动问题, 并指出对于高度非线性的问题, 强化学习方法比传统的最优路径理论^[21]更具有实用价值.

智能颗粒的研究框架能够被应用于多种问题. 对于不同的问题, 需要建立相应的颗粒模型. 例如, 浮游动物通常可用无惯性点颗粒模型描述, 一些研究在此基础上探究了浮游生物的高效运动策略^{[17-18, 22-24]}. 此外, 某些浮游生物能够利用离子交换或伪空胞主动调节自身的密度^[25-26], 因此有研究者利用惯性点颗粒模型研究了浮游生物如何主动调节密度以控制沉降^[27], 或停留在特定涡量大小的区域^[28]. 智能颗粒同样能用于研究群体运动. 相关研究将鱼或浮游生物视为颗粒, 并考虑它们与流体的相互作用, 探究了具有低能耗或高隐蔽性的群体游动智能策略^[29-30]. 此外, 有研究者利用椭球体在流体中下落的模型, 研究了蚁类等昆虫利用足部控制下落姿态和轨迹的智能策略^[31].

最近, 浮游生物的运动策略研究取得了一定的进展. 虽然浮游生物的体型很小, 直径通常在几十到几百微米之间, 但是它们拥有对环境的感知能力, 能够响应环境的变化从而提高自身的生存几率. 过去的生物学研究^[14-15]已经证实桡足类浮游动物能够利用触须感受流体扰动, 以识别捕食者或猎物. 这种感知能力自然也有可能被浮游动物利用在其他重要的行为上. 例如, 浮游动物的昼夜间的垂直迁移与它们获取营养、逃离捕食者以及繁衍^[32-33]都有着密切的关系. 高效地完成垂直迁移有助于它们取得生存优势, 因此有人猜测浮游生物能利用对流体信号的感知能力加速垂直迁移. 然而, 受到浮游生物尺寸和实验观测难度的限制, 关于浮游生物是否能够利用流体信号加速垂直迁移, 目前还缺乏实验上的验证. 因此, 相关研究^{[17, 22-24]}借助智能颗粒模型和数值方法研究浮游生物加速垂直迁移的游动策略, 为日后的实验研究提供理论基础. 基于这一背景, 本文旨在介绍智能颗粒和强化学习方法在浮游生物运动策略研究中的应用与进展.

1.
研究方法

1.1
无惯性点颗粒模型

将浮游生物近似为球形或椭球形颗粒, 并考虑流体对浮游生物平动和转动的影响, 是一种常见的研究方法^{[6, 8, 12, 17]}. 浮游生物游动所引起的流动通常具有较低的雷诺数. 浮游生物的典型直径为0.1 mm量级, 游动速度为1 mm/s量级^[34], 而水的运动黏度约为1 mm²/s, 估算得雷诺数约为0.1. 在雷诺数远小于1的情况下, 可以近似忽略颗粒的有限体积效应, 将颗粒视为质点, 利用蠕流假设下的解析解计算颗粒所受的力和力矩, 以牛顿第二定律描述颗粒的运动^[35]. 这类模型被称为点颗粒模型. 当反映颗粒惯性的Stokes数St远小于1时, 颗粒自身的惯性可以忽略, 进而得到直接描述颗粒速度和角速度的无惯性颗粒模型. 其中, St = τ_p / τ_f, τ_p和τ_f分别为颗粒的弛豫时间^[36]与流体的特征时间尺度.

一般而言, 浮游生物的运动可以由以下的无惯性点椭球颗粒模型来描述

$$ dot {boldsymbol{x}} = {boldsymbol{v}} $$

(1)

$$ {boldsymbol{v}} = {boldsymbol{u}} + {v_s}{boldsymbol{n}} + {{boldsymbol{v}}_g} $$

(2)

$$ dot {boldsymbol{n}} = {boldsymbol{omega }} times {boldsymbol{n}} $$

(3)

$$ {boldsymbol{omega }} = {boldsymbol{varOmega }} + varLambda {boldsymbol{n}} times ({boldsymbol{S}} cdot {boldsymbol{n}}) + {{boldsymbol{omega }}_s} - frac{1}{{2B}}{boldsymbol{n}} times {{boldsymbol{e}}_g} $$

(4)

其中, x和n表示颗粒的位置和朝向, v和$ {boldsymbol{omega }} $表示颗粒的速度和角速度. 式(2)中等号右边的前3项分别代表颗粒当地的流体速度u, 颗粒沿着n方向、速率为v_s的游动速度, 以及颗粒的Stokes沉降速度v_g^{[23, 37]}. 式(4)中等号右边的前两项代表当地流体涡量$ {boldsymbol{varOmega }} $与应变率张量S的影响^[38]. 形状因子Λ = (λ² ? 1)/(λ² + 1), 其中λ是椭球颗粒的长轴与短轴之比, 也称长细比. 随着颗粒形状由球形变得越来越细长, $ {varLambda } $将从0增大至1. 式(4)的第3项ω_s表示颗粒的游动角速度. 第四项代表重力恢复力矩, 使颗粒的朝向n自发地趋于重力的反方向－e_g. 这种力矩通常源自于颗粒质量的非均匀分布^[7], 当质心与形心存在偏移时, 重力对于颗粒形心就会产生恢复力矩, 而B表征恢复力矩引起的颗粒转动的时间尺度. 图1(a)展示了主动颗粒的示意图.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-402-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
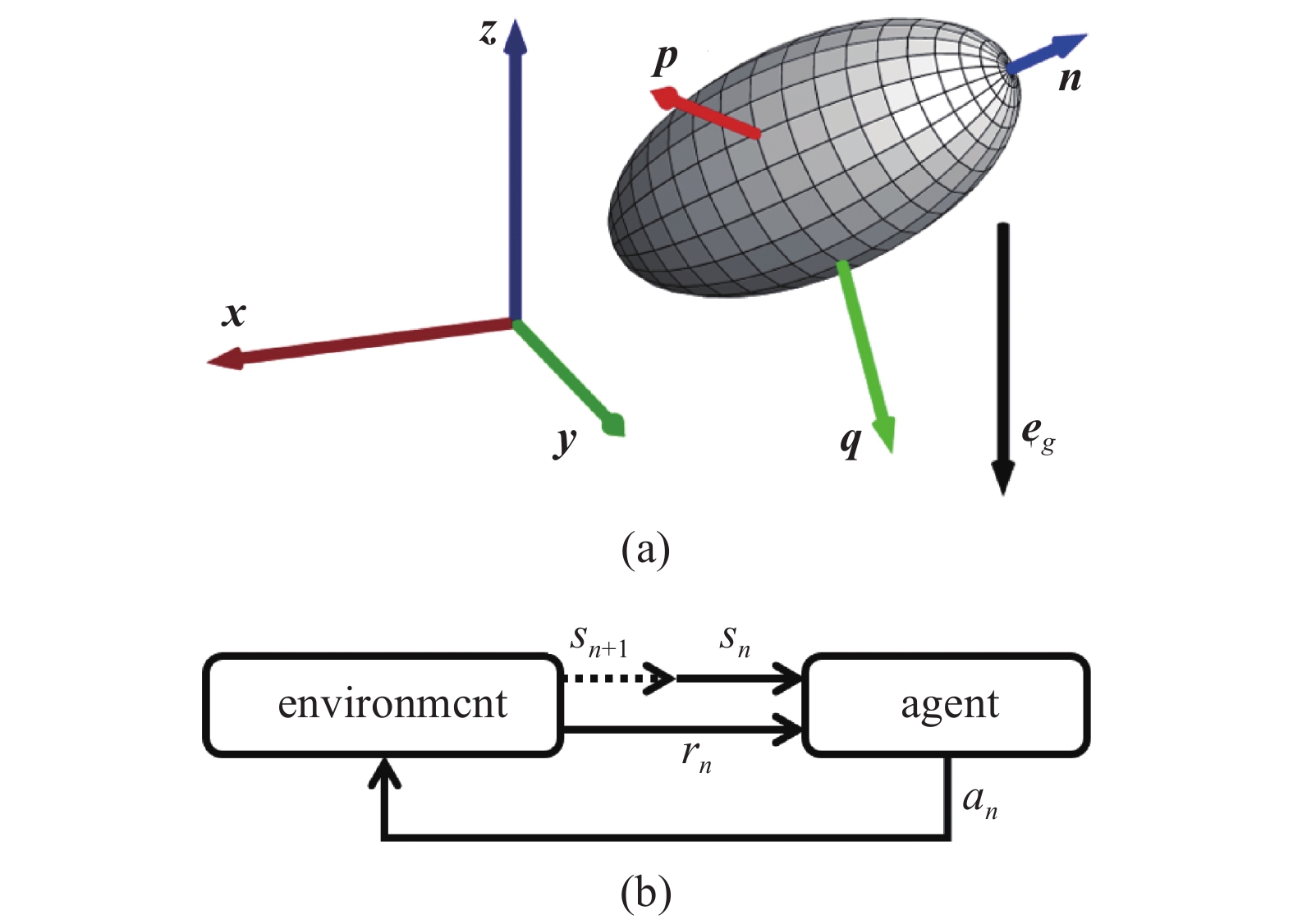
(a)智能颗粒示意图. x-y-z为全局坐标系, n-p-q为颗粒局部坐标系. (b)强化学习原理示意图^[39]



Figure
1.
(a) Sketch of smart particle. x-y-z defines the global frame of reference, and n-p-q defines the particle local frame of reference. (b) A diagram of reinforcement learning^[39]



下载:
全尺寸图片
幻灯片


这组模型在无惯性点颗粒模型的基础上, 考虑了颗粒的形状和游动效应, 同时也考虑了重力对颗粒平动与转动的影响. 由于游动速度和游动角速度的存在, 颗粒不再被动地被流体输运, 因此称之为主动颗粒. 而智能颗粒则能够根据自身所处的环境, 主动调节游动速度和角速度以完成特定任务.

1.2
强化学习算法

强化学习是一种典型的无监督机器学习方法^[39], 通常用于寻找智能体在特定环境下的最优行为策略. 通过让智能体反复探索环境, 尝试不同的行为, 强化学习利用智能体运动的“经验”对策略进行优化. 简而言之, 强化学习的本质是构建一个从环境状态到行为的映射, 使得目标函数(或回报)最大化. 此处以单步Q学习算法(one-step Q-learning)^[40]为例介绍强化学习的原理.

在强化学习中, 智能体会在环境中按照某个策略运动. 例如, 智能颗粒在环境中开始运动时, 首先确定初始状态s₀, 并根据当前价值函数选择行为$ {a}_{0} $. 颗粒在环境中运动直到进入下一个状态s₁, 根据目标函数的定义产生回报r₀, 接着确定下一个行为a₁, 并以此类推. 最终, 颗粒的运动将产生一段经验{s₀, a₀, r₀, s₁, a₁, r₁, ···, s_i, a_i, r_i, ···}, 描述了状态之间的转移和相应的回报. 在Q学习中, 价值函数$ Q({s}_{i},a) $是状态$ {s}_i $下执行动作$ a $所产生的所有未来回报之和的期望值. 显然, 如果已知一个问题的真实价值函数, 则状态$ {s}_i $下的最优行为就是$a' = arg {max _a}Qleft( {{s_i},a}
ight)$. 然而, 真实的价值函数往往很难求解, 而强化学习则通过对价值函数的逼近来求解近似最优策略. 在训练阶段, 智能体需要与环境反复交互并产生上述的经验, 并利用经验更新价值函数^[39]

$$ begin{split} Qleft( {{s_i},{a_i}} ight) leftarrow Qleft( {{s_i},{a_i}} ight) hfill + alpha left[ {{r_i} + gamma {{max }_a}Qleft( {{s_i},a} ight) - Qleft( {{s_i},{a_i}} ight)} ight] hfill end{split} $$

(5)

其中, 学习率$ alpha $控制了Q的更新步长. 折扣率$ gamma $衡量了远期回报对当前决策的影响, 通常取0 ≤ γ ≤ 1, 其值越小, 得到的策略就越短视, 反之亦然. 在实际运用中, 颗粒并不总是选择使Q最大的行为, 而是以很小的概率随机选择行为, 称之为ε-贪婪策略. 这种技巧有助于颗粒主动探索更多可能性, 避免策略被困于局部最优.

由上面的介绍可以总结强化学习方法所需的几个要素. 首先, 需要明确智能颗粒和其所处的流体环境. 第二, 根据具体问题的需要, 确定智能颗粒的任务目标, 并据此定义合适的目标函数或回报. 第三, 还需要定义颗粒的状态和其能执行的行为. 颗粒状态可以由自身的运动情况确定, 如颗粒位置^[19], 也可以由对环境的观测确定, 如流体信号^[23]. 颗粒的行为则根据具体问题有不同的定义方式. 以上要素确定后, 便能利用强化学习研究智能颗粒的运动策略.

2.
研究进展介绍

2.1
游动颗粒的定向运动

基于浮游生物垂直迁移的背景, Colabrese等^[17]在2017年首次利用强化学习研究了智能颗粒在在二维Taylor-Green涡中的定向运动能力. Taylor-Green涡是一种特殊的解析流动, 其流场由正反相间、等距排列的旋涡组成. Durham等^[41]发现游动颗粒在Taylor-Green流动中容易被困在高涡量区域, 使得颗粒无法进行垂直迁移. 因此, Colabrese等^[17]希望利用强化学习寻找颗粒的优化运动策略, 以克服旋涡的捕捉甚至利用流场本身的上升区域进行高效的垂直向上迁移.

Colabrese等^[17]假设颗粒能够感知当地的涡量大小和自身当前的游动方向作为状态, 并假设颗粒能够主动改变自身质心的位置, 通过重力恢复力矩的机制来调节颗粒游动方向, 即

$$ {{boldsymbol{omega }}_s} = frac{1}{{2B}}left( {{boldsymbol{n}} times {boldsymbol{k}}} ight) $$

(6)

其中k是颗粒主动选择的朝向. 此时他们不再考虑式(4)中等号右边的最后一项. 这种行为模式源于一些浮游生物能在外部流动状态变化时改变自身的外形或内部质量分布, 从而改变质心的位置^[42]. 微型机器人也能通过调节内部的质量块的位置来实现类似的行为模式. 为了最大化颗粒的垂直上升速度, 定义回报为

$$ {r_i} propto {z_{i + 1}} - {z_i} $$

(7)

其中z_i是状态s_i发生时颗粒的垂直高度位置. 利用强化学习, 他们得到了不同颗粒的游动速度v_s和重力恢复力矩的时间尺度B下的优化运动策略, 并与传统生物学模型对比(即k永远朝向上方, 也称之为简单策略). 对于大部分的参数范围, 智能运动策略下颗粒的垂直上升速度都远高于简单策略.

Colabrese等^[17]的工作证明了在二维Taylor-Green涡中, 存在比简单策略更优秀的智能游动策略. 智能颗粒能够基于有限的信息主动调整自身运动, 实现更高效的运动, 而强化学习则能够高效地找出这些智能策略. 虽然使用了高度简化的颗粒和流场模型, 得到的策略也难以应用于实际场景, 但其首次提出了一个完整的强化学习研究框架. 基于这一框架, 后续的研究从颗粒和流场模型、颗粒状态和行为方式、优化目标等多个方面进行改进, 并研究多种智能颗粒的游动问题.

2.2
重力作用和颗粒形状对游动策略的影响

Colabrese等^[17]的研究中使用了高度简化的模型与假设, 例如他们只考虑了球形颗粒的运动策略, 并忽略了重力引起的沉降作用. 然而, 真实的浮游生物往往具有不规则的形状. 此外, 由于浮游生物的密度通常略大于水, 它们在垂直迁移过程中势必要克服重力沉降作用. 若想通过强化学习研究真实浮游生物的运动策略, 就需要尽可能准确地描述浮游生物的运动. 基于此, 本文作者Qiu等^[22]在智能颗粒模型中引入了颗粒形状和重力沉降的影响, 考察了二者对智能游动策略的影响. 他们将浮游生物模型化为细长椭球, 并用长细比$ lambda $描述颗粒的形状. 重力沉降的影响则通过引入沉降速度来体现

$$ {{boldsymbol{v}}_g} = v_g^ bot {{boldsymbol{e}}_g} + left( {v_g^parallel - v_g^ bot } ight)left( {{{boldsymbol{e}}_g} cdot {boldsymbol{n}}} ight){boldsymbol{n}} $$

(8)

其中$ {v}_{g}^{parallel } $和$ {v}_{g}^{perp } $分别为椭球颗粒对称轴沿着重力方向和垂直于重力方向时的Stokes沉降速度^[37]. 颗粒形状主要通过式(4)中的流体应变率项影响颗粒的转动, 而沉降速度则通过式(2)影响颗粒的平动.

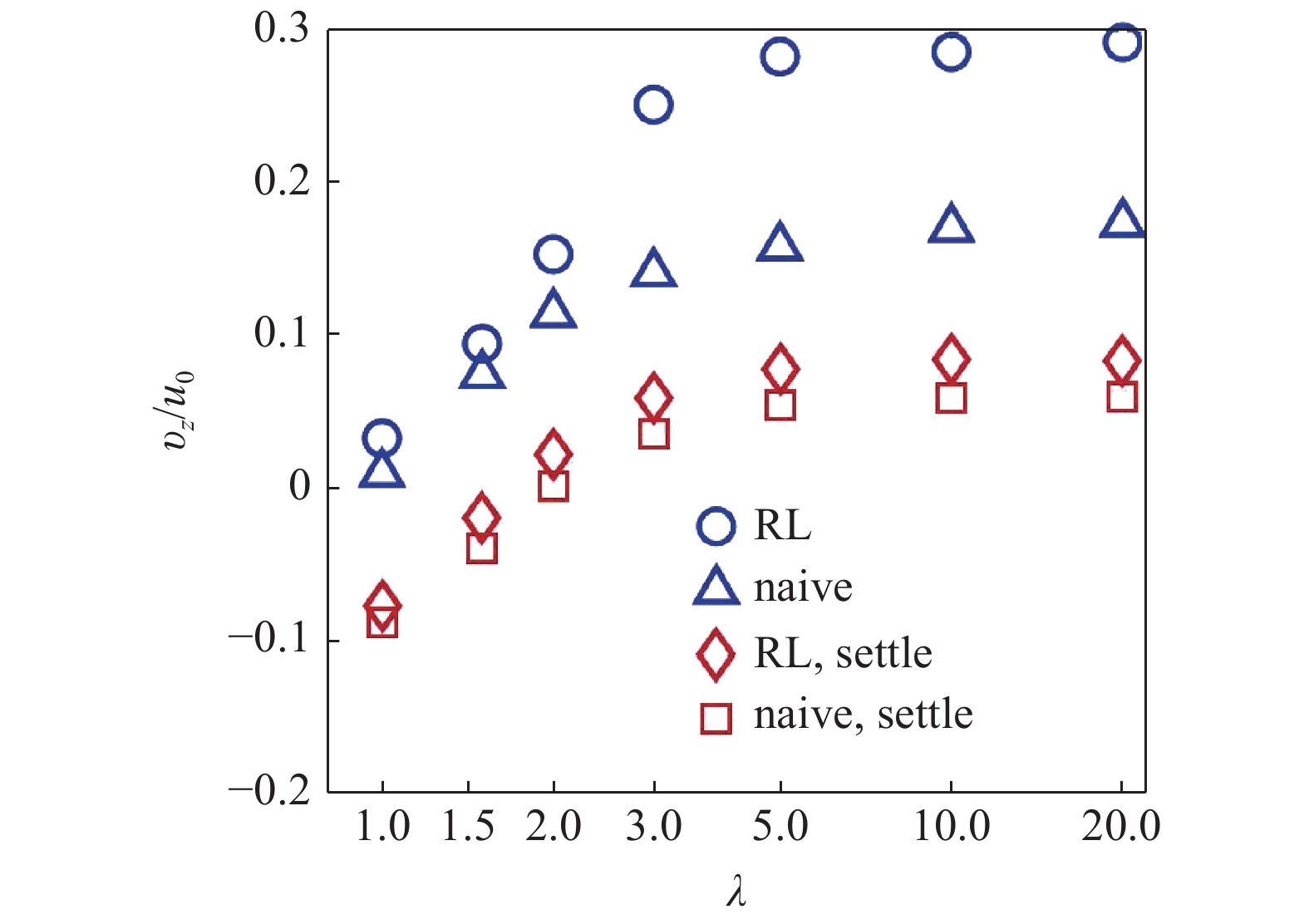
Qiu等^[22]发现, 在浮游生物的典型参数下, 随着椭球颗粒长细比$ mathrm{lambda } $的增加, 简单的非智能策略和强化学习得到的智能策略都有了更好的表现, 如图2所示. 当不考虑重力沉降时, 细长颗粒使用智能策略时垂直上升的速度要远高于简单策略. 然而, 在重力沉降的作用下, 智能策略虽然仍优于简单策略, 但二者的表现非常接近, 所导致的颗粒分布特征也非常相似. 前文提到, 简单策略来自于生物学模型——质量非均匀分布的浮游生物在重力恢复力矩作用下自发获得垂直向上的朝向. 由于强化学习没有找到远胜于简单策略的智能游动策略, 作者认为在有重力沉降的情况下, 简单策略或许已经是一种足够高效的垂直运动策略. 这一工作首次将智能颗粒研究的模型范围从理想情况下的球形颗粒拓展到更加真实和复杂的非球形沉降颗粒, 也进一步验证了强化学习和智能颗粒的研究框架.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-402-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
智能颗粒垂直运动速度v_z随形状和重力沉降作用的变化^[22]. 颗粒速度以流动的特征速度u₀无量纲化. RL: 强化学习得到的智能策略, naive: 简单策略, settle: 考虑沉降作用



Figure
2.
Vertical velocity of smart particles v_z as functions of the effects of gravitational settling and particle shape ^[22]. Particle velocity is normalized by velocity scale of the background flow u₀. RL: smart strategy found by reinforcement learning. Naive: naive strategy. Settle: the cases considering settling effect



下载:
全尺寸图片
幻灯片

2.3
局部流体信号和对称性

Colabrese等^[17]和Qiu等^[22]的研究中都假设游动颗粒能够直接感知当地的涡量大小和当前的游动方向, 并且颗粒能够调节自身的质心位置, 利用重力恢复力矩调整自身的游动方向. 然而, 实际问题中的颗粒难以获得这种感知和行为能力. 比如浮游生物难以直接测量周边流体的涡量, 更无法直接获取自身在全局坐标系下的游动方向. 对于浮游生物或者微型机器人之类的微型游动智能体, 更容易测量的是基于局部坐标系的变量. 例如, 浮游生物能够感知局部流体信号, 包括流体的变形率以及浮游生物相对于流体的转动和平动^[14]. 研究浮游生物如何利用有限的、局部坐标系下的信息, 在全局坐标系下高效地定向或定点运动, 将加深人们对浮游生物生态的认识, 也能为智能微型机器人的设计制造提供灵感.

基于这一背景, Qiu 等^[23]的工作集中讨论了局部坐标系下测量的信号如何为定向运动提供信息, 并基于式(1) ~ 式(4)的点颗粒模型, 构建了一个桡足类浮游动物的运动与感知模型. 颗粒能够感知流体变形率张量在自身坐标系下的两个分量

$$ left. begin{array}{l} begin{split}& {S_{nn}} = {boldsymbol{n}} cdot {boldsymbol{S}} cdot {boldsymbol{n}} hfill & {S_{np}} = {boldsymbol{n}} cdot {boldsymbol{S}} cdot {boldsymbol{p}} hfill end{split}end{array} ight} $$

(9)

以及颗粒相对流体的角速度和速度^{[14, 23]}在局部坐标系下的分量, 例如

$$left. begin{array}{l} begin{split}& Delta {{varOmega }} = left( {{boldsymbol{varOmega }} - {boldsymbol{omega}} } ight) cdot {boldsymbol{q}} hfill & Delta {u_n} = left( {{boldsymbol{u}} - {boldsymbol{v}}} ight) cdot {boldsymbol{n}} hfill & Delta {u_q} = left( {{boldsymbol{u}} - {boldsymbol{v}}} ight) cdot {boldsymbol{q}} hfill end{split} end{array} ight}$$

(10)

颗粒以定常的速度v_s游动, 并主动通过基于局部坐标系的游动角速度$ {boldsymbol{omega }}_{s}={omega }_{s}{boldsymbol{q}} $调节游动的方向, 其中ω_s = ?1, 0, 1 rad/s. Qiu等^[23]研究了这种游动颗粒在二维Taylor-Green涡与二维随机流场中的垂直运动策略, 并意识到了局部流体信号的局限性. Taylor-Green涡具有C4旋转对称性, 即流场沿任意轴旋转90°后所得的流场仍与原流场等价, 而二维随机流动则具有统计意义上的各向同性. 颗粒必须能够分辨目标方向才能够完成垂直迁移运动, 否则强化学习不能得到任何有效的策略. 为了分辨目标方向, 必须要破坏流场带来的对称性. Qiu等^[23]认为, 可以在强化学习的各环节中提供破坏对称性的信息, 包括状态和行为的定义、颗粒动力学系统特性等. 例如, Colabrese等^[17]和Qiu等^[22]的研究中颗粒能够感知自身在全局坐标系中的朝向, 而颗粒利用朝向信息即可分辨运动目标方向, 从而破坏了对称性. Biferale等^[19]的研究中, 颗粒能够感知自身的位置坐标, 也同样破坏了对称性. 颗粒的行为同样能够提供破坏对称性的信息. Colabrese等^[17]和Qiu等^[22]认为颗粒根据式(6)改变游动方向, 而式(6)中的k是根据全局坐标系定义的, 因而破坏了对称性. 然而, 上文中定义的基于的局部坐标系的流体信号和游动角速度无法提供任何全局坐标系的信息. 此时, 重力破坏了颗粒动力学的对称性, 使得定向运动成为可能. 沉降效应使颗粒相对于流体产生了重力方向的相对速度, 而重力恢复力矩则使颗粒获得了n沿着重力反方向的朝向倾向性.

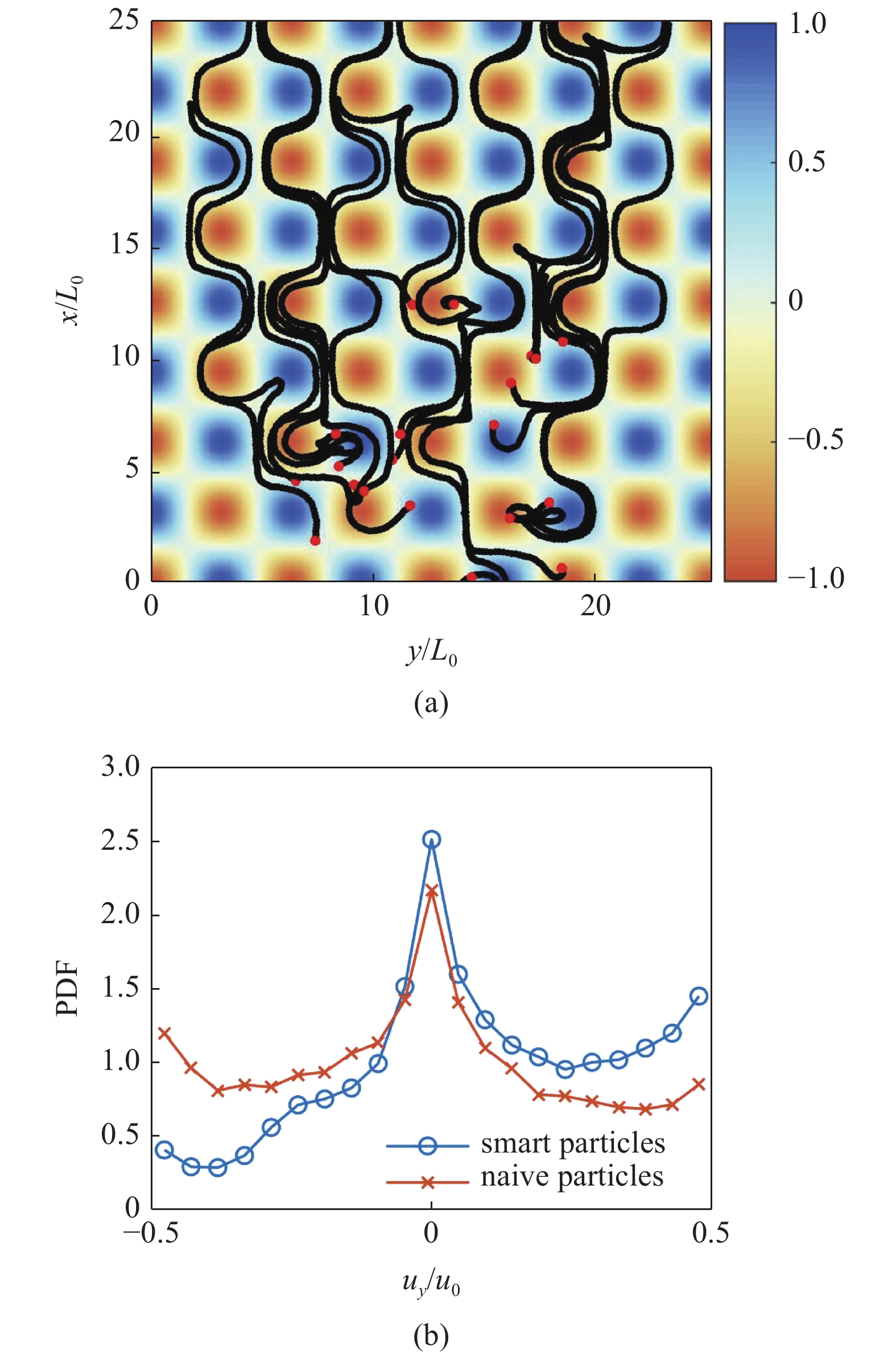
另一方面, 局部流体信号提供了有用信息, 使得智能颗粒在重力作用下能够得到高效的垂直上升策略. 变形率的分量S_np反映了流体的变形率对颗粒角速度的影响, 而侧向的相对速度分量Δu_p则反映了颗粒当前朝向与重力方向之间的关系^[23]. 利用这些信号, 颗粒能够主动转动以扩大流体变形率对颗粒角速度的影响, 等效地提高了颗粒的长细比, 躲避高涡量区域, 并利用上升的流动加速垂直向上迁移, 如图3所示. 图3中所有变量均以流动的特征速度和长度u₀和L₀无量纲化



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-402-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
(a)智能颗粒在二维Taylor-Green旋涡流动中的运动轨迹. 红点表示颗粒的初始位置, 背景为涡量云图. (b)智能颗粒与非智能颗粒当地流体垂直方向速度u_y的概率密度分布(PDF)^[23]



Figure
3.
(a) Trajectories of smart particles in two-dimensional Taylor-Green vortex flow. Red dots represent the initial position of particles. Background contour shows the vorticity of fluid. (b) The probability distribution function (PDF) of the vertical velocity of local fluid u_y^[23]



下载:
全尺寸图片
幻灯片

2.4
流场的三维和非定常效应

Qiu等^[23]在二维定常流动中证实了局部流体信号的有效性以及相关的物理机制, 然而实际中的浮游微生物生活在三维非定常湍流环境中. 对称性相关的结论在三维非定常流动中仍然适用. 在重力破坏了对称性的情况下, 游动颗粒理论上可以利用局部流体信号在各向同性均匀湍流里实现定向运动, 然而具体的游动策略和其背后的机制或许会有所不同.

所以, Qiu等^[24]探索了智能颗粒在三维湍流中利用局部信号的运动策略. 三维情况下, 游动颗粒感知的有效流体信号分量会更多, 如表1所示. 变形率分量从二维情况下的两个独立分量增加到三维情况下的5个分量, 相对角速度从1个分量增加到3个分量, 相对速度从2个分量拓展到3个分量. 以流体变形率为例, 假设每个流体信号值都被划分为3个区间, 由两个不同的信号组成的状态空间将有3² = 9个不同的状态, 三维情况下由5个信号组成的状态空间则有3⁵ = 243个状态. 若每个状态中颗粒都有3个可以选择的行为, 那么总策略数分别为3⁹ ~ 10⁴和3²⁴³ ~ 10¹¹⁶. 对于后者, 庞大的策略空间中存在大量的局部最优解, 使强化学习难以收敛到最优策略. 同时, 运动策略的可视化和解读也会变得很困难, 导致得到的策略成为一个“黑箱”, 难以挖掘其背后的机制. 因此, Qiu等^[24]基于此前在二维流动中发现的机制, 以及各种流体信号之间的关系, 最终确定了4个对垂直运动最重要的流体信号: S_np, S_nq, Δu_p和Δu_q.




表
1
二维与三维流场中独立流体信号分量



Table
1.
Independent fluid signals in two-dimensional (2D) and three-dimensional (3D) flows



table_type1 ">

Flow signals	2D	3D
deformation rate	${S_{nn}},;;{S_{np}}$	${S_{nn}},;{S_{np}},;{S_{nq}},;{S_{pp}},;{S_{pq}}$
relative angular velocity	$Delta {varOmega _q}$	$Delta {varOmega _n},;Delta {varOmega _p},;Delta {varOmega _q}$
relative velocity	$Delta {u_n},;Delta {u_p}$	$Delta {u_n},;Delta {u_p},;Delta {u_q}$

下载:
导出CSV
|显示表格



在湍流中研究智能颗粒运动策略的另一个困难来自于流体的非定常性. 在2.1节中曾提到, 强化学习的训练阶段需要反复模拟颗粒在流场中的运动以获取用于训练的经验. 为了求解颗粒运动轨迹, 非定常的湍流也需要同步求解. 与一般的数值模拟不同的是, 训练过程中颗粒的运动策略一直在更新, 从而无法事先模拟大量的颗粒轨迹用于训练. 换言之, 需要对流场进行反复的模拟, 使得训练的计算量急剧增加.

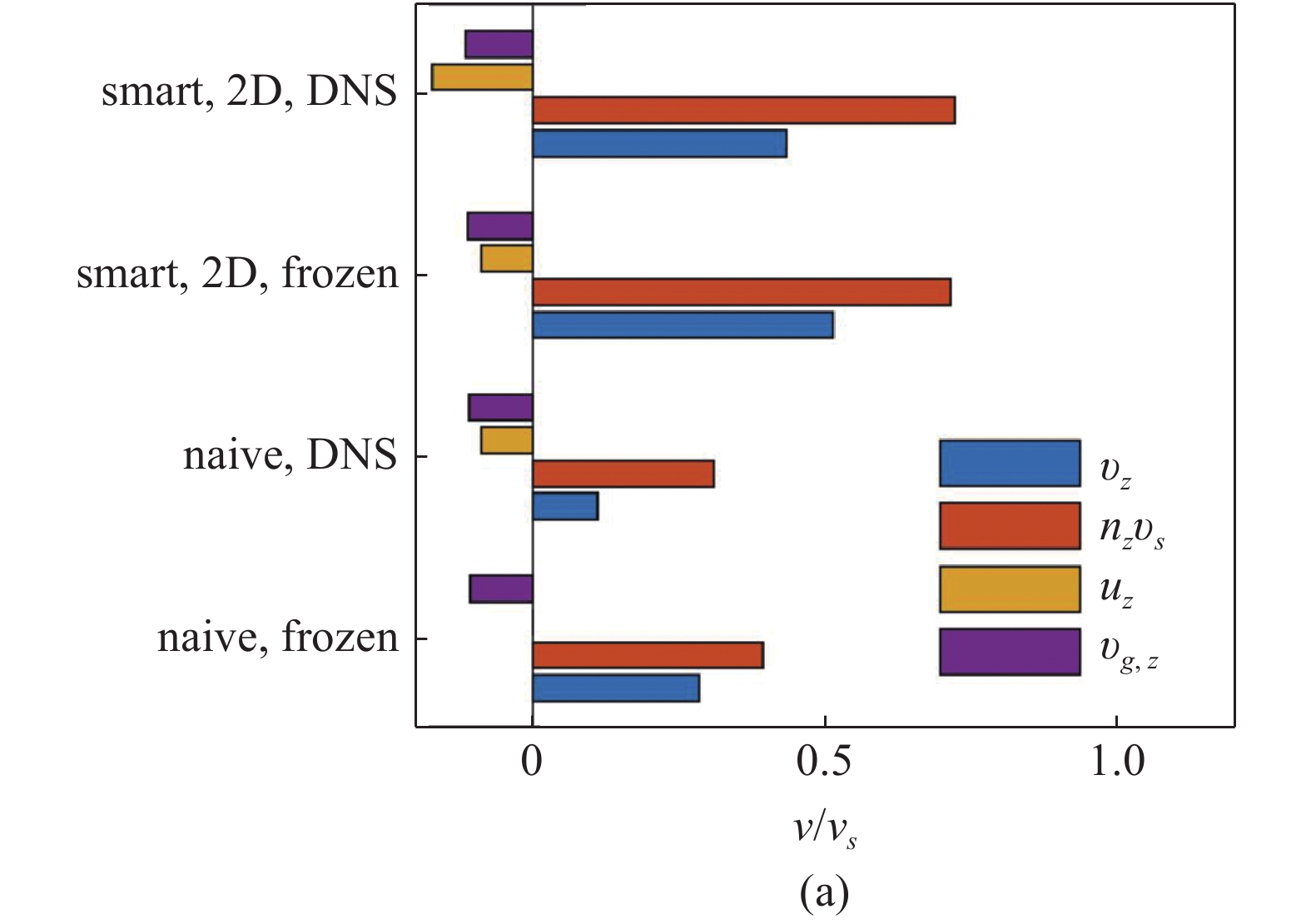
目前, 这一问题有3种应对方法. 一是直接同步模拟流场. 尽管流场的计算量巨大, 但在二维情况或网格数较少的情况下计算量可以接受. 二是预先模拟并储存流场, 在反复的训练中读取并使用. 这一方法的优点在于将计算效率的瓶颈由流场求解转为流场的读取. 然而, 在面对网格量较大的三维流动时, 流场的读取速度仍然较慢. 三是使用非定常流场的时间快照进行训练. Qiu等^[24]将流场时间快照称为冻结流场, 并假设颗粒在冻结流场中的拉格朗日轨迹和在真实流场中的轨迹相似, 则冻结流场中学到的策略也适用于真实流场. 如图4(a)所示, 颗粒的智能游动策略在冻结流场和随时间变化的湍流场中都有较好的效果, 并优于简单策略. 这一方法无需同步计算流场, 也几乎不用读取流场, 因此计算量与在非定常流场中训练相差无几. 然而, 冻结和真实流场的始终存在差异, 因此强化学习得到的策略必须在真实流动中进行检验.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-402-4-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4-1" />



4
(a)颗粒在冻结流场(frozen)与随时间变化的流场(DNS)中的垂直方向速度v_z, 以及游动速度n_zv_s, 当地流体速度u_z和沉降速度v_g,z的贡献. smart 2D: $ mathrm{Delta }{u}_{p} $流体信号下的智能策略; naive: 简单策略智能颗粒. (b)不同策略下颗粒在三维各向同性均匀湍流中的运动速度及各部分贡献. naive: 简单策略; 2D: Δu_p信号下的二维策略; 3D2S: Δu_p, Δu_q信号下的三维策略; 3D4S: S_np, S_nq, Δu_p, Δu_q信号下的三维策略. (c)3D4S策略下的颗粒瞬时分布^[24]



4.
(a) Vertical velocity of particles v_z in frozen flow (frozen) and time-dependent flow (DNS), with the contributions of swimming velocity n_zv_s, local fluid velocity u_z, and settling velocity v_g,z. Smart 2D: smart strategy with signal $ mathrm{Delta }{u}_{p} $. Naive: naive strategy. (b) Vertical velocity of particles under different swimming strategies in homogeneous isotropic turbulence. Naive: naive strategy. 2D: two-dimensional strategy with Δu_p signal. 3D2S: two-dimensional strategy with Δu_p, Δu_q signals. 3D4S: two-dimensional strategy with S_np, S_nq, Δu_p, Δu_q signals. (c) Instanueous distribution of particles with 3D4S strategy^[24]



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-402-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
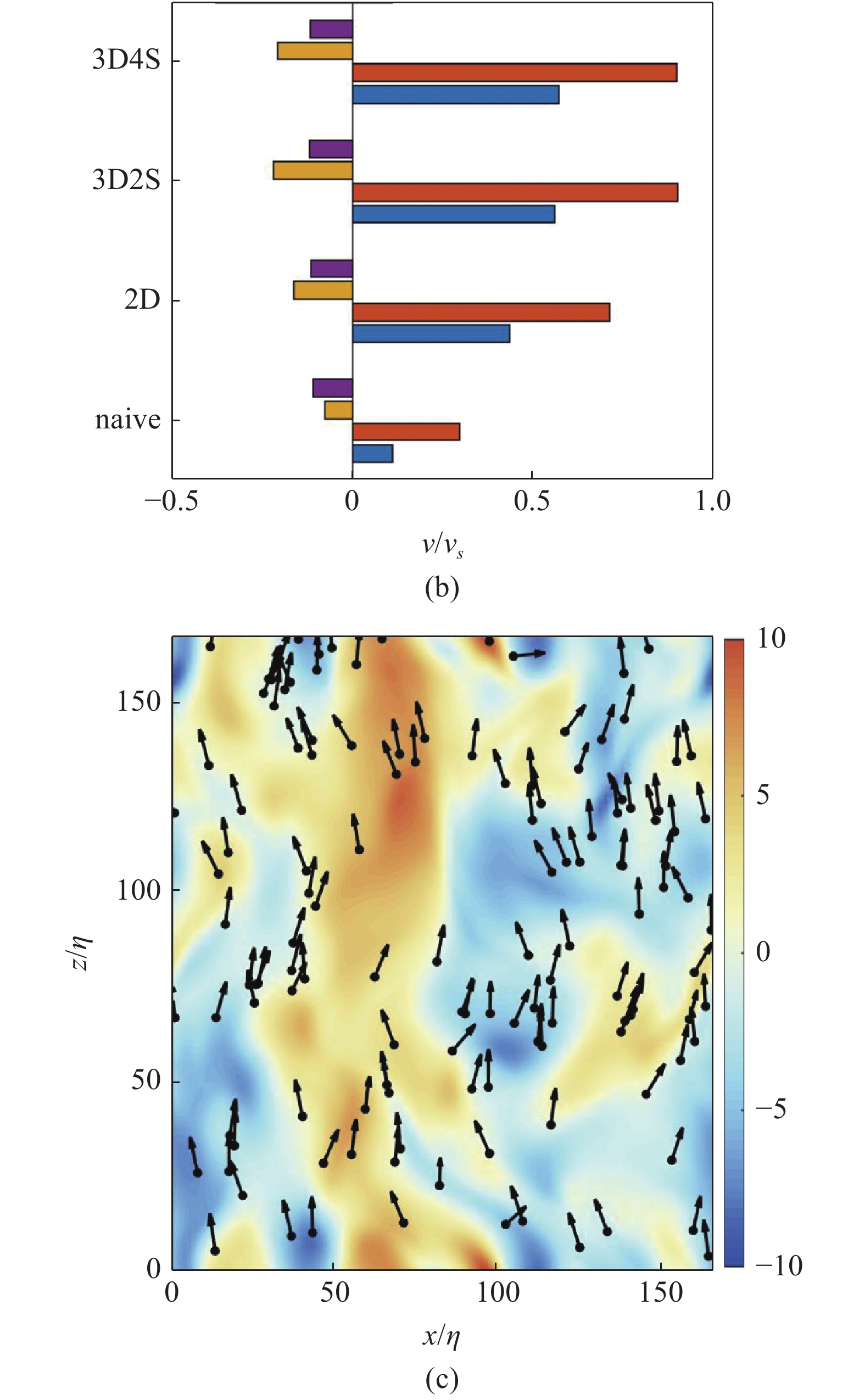
(a)颗粒在冻结流场(frozen)与随时间变化的流场(DNS)中的垂直方向速度v_z, 以及游动速度n_zv_s, 当地流体速度u_z和沉降速度v_g,z的贡献. smart 2D: $ mathrm{Delta }{u}_{p} $流体信号下的智能策略; naive: 简单策略智能颗粒. (b)不同策略下颗粒在三维各向同性均匀湍流中的运动速度及各部分贡献. naive: 简单策略; 2D: Δu_p信号下的二维策略; 3D2S: Δu_p, Δu_q信号下的三维策略; 3D4S: S_np, S_nq, Δu_p, Δu_q信号下的三维策略. (c)3D4S策略下的颗粒瞬时分布^[24] (续)



Figure
4.
(a) Vertical velocity of particles v_z in frozen flow (frozen) and time-dependent flow (DNS), with the contributions of swimming velocity n_zv_s, local fluid velocity u_z, and settling velocity v_g,z. Smart 2D: smart strategy with signal $ mathrm{Delta }{u}_{p} $. Naive: naive strategy. (b) Vertical velocity of particles under different swimming strategies in homogeneous isotropic turbulence. Naive: naive strategy. 2D: two-dimensional strategy with Δu_p signal. 3D2S: two-dimensional strategy with Δu_p, Δu_q signals. 3D4S: two-dimensional strategy with S_np, S_nq, Δu_p, Δu_q signals. (c) Instanueous distribution of particles with 3D4S strategy^[24] (continued)



下载:
全尺寸图片
幻灯片


对于各向同性均匀湍流, 冻结流场和真实流场具有定性上一致的拉格朗日统计量, 因此Qiu等^[24]在冻结湍流中进行强化学习训练, 得到了在4个流体信号的输入下的一系列局部最优解. 结合二维流动中发现的机制, 作者提出了全三维的运动策略. 在各向同性均匀湍流中, 这些策略能够让颗粒保持垂直向上的游动方向, 从而获得较高的垂直运动速度^[24], 如图4(b)和 图4(c)所示. 图4中箭头表示颗粒当前游动方向. 背景云图为流体垂直方向速度. 横纵坐标与流体速度分别以Kolmogorov长度尺度η与速度尺度u_η无量纲化. 因此认为浮游微生物具有利用流体信号实现高效垂直迁移的可能性. 这些流体信号能够帮助它们主动感知并调节自身的游动方向, 提升在湍流中垂直迁移的效率.

3.
总结与展望

本文介绍了近些年利用强化学习探究浮游生物运动策略的相关进展. 从最简单的智能颗粒模型^[17]出发, 逐步考虑重力和颗粒形状^[22]、局部流体信号^[23]以及复杂流动^[24]的影响, 最终得到了鲁棒的、有实际意义的智能颗粒游动策略. 这一系列工作检验并完善了基于强化学习的智能颗粒研究框架, 包括对颗粒和流体动力学的建模, 对颗粒状态和行为的定义, 以及目标函数的设计. 此外, 针对局部信号与对称性的讨论, 也对状态、行为和目标函数的选择提供了指导意义. 在这些工作中, 强化学习作为一个工具, 能够为一个具体目标提供一系列局部最优解. 尽管局部最优解有时可以足以满足解决问题的需要, 进一步探究其背后的机制有助于加深对物理问题的理解. 对于具体问题, 可以结合这些物理机制和先验知识, 人为提出优于强化学习局部最优解的策略或者实际中更具可行性的策略.

此外, 随着强化学习框架的日渐成熟, 研究者已经不满足于在简单流动中研究颗粒的智能运动策略. 尽管目前还存在2.4节中提及的问题, 研究者正在尝试将强化学习应用于更加复杂的流动^{[20, 24, 43-44]}. 对于不同的问题, 颗粒的状态有不同的定义. 除了本文着重介绍的流体信号之外, 颗粒也可以根据自身的位置^[19], 当地流体速度和涡量^[44], 或附近障碍物的信息^[45]进行运动. 目前, 大部分智能颗粒研究中并没有考虑颗粒获取推力的具体方式, 因而利用强化学习研究颗粒的高效运动方式也是研究热点之一^[46-47].

智能颗粒相关研究的快速发展为许多问题带来了新的思路. 强化学习作为机器学习的一个重要分支, 近年来也广泛应用于力学研究中. 如何发掘新的分析问题的角度, 以及如何发挥新兴数学工具的优势, 将会是人们在未来面临的重要挑战.