删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于SBFEM和深度学习的裂纹状缺陷反演模型

本站小编 Free考研考试/2022-01-01


引 言


无损检测技术于20世纪50 ~ 60年代开始得到广泛应用, 在无损检测的初级阶段, 其技术和任务都较为简单, 在技术手段上可选择的并不丰富, 主要采用超声、射线等技术; 在任务上主要是检测结构或试件是否存在缺陷或者异常, 其基本任务是在不破坏结构或试件本身的情况下发现其中的缺陷, 以满足工程需要. 随着各方面技术的发展, 人们越来越关注缺陷的位置、尺寸和形状, 结构的无损检测技术需由定性阶段向定量阶段发展和提高[1].

智能优化算法与计算力学方法相结合已广泛应用于缺陷检测的定量反演问题中[2-12]. 文献[2-4]将扩展有限元法与遗传算法相结合进行缺陷反演, 但传统的遗传算法在目标函数最小化迭代过程中效率低下并且容易陷入局部最优解; Nanthakumar等[5]将扩展有限元法与多层坐标搜索方法相结合, 用于检测压电材料中的缺陷; 江守燕和杜成斌[6]将扩展有限元法与人工蜂群算法相结合进行结构内部孔洞状和裂纹状缺陷的反演; 这些研究主要用于检测单个缺陷. Sun等[7]提出了一种基于扩展有限元法和改进的人工蜂群算法的结构多缺陷检测与量化新算法, 后来, Sun等[8]进一步提出了一种新的多尺度算法来检测结构中的多个缺陷, 该方法在收敛速度上有了显著地提高; 为了研究建模误差和测量噪声对检测结果的影响, Yan等[9]提出了一种贝叶斯方法, 可以有效地识别缺陷的数量, 并量化每个缺陷的参数不确定性; 王佳萍等[10-11]将扩展有限元法与遗传算法和改进人工蜂群算法相结合进行结构内部多缺陷反演. 最近, Zhao等[12]和Ma等[13]将扩展有限元法与蜂群和鱼群算法相结合, 通过引入聚类算法, 显著提高了反演分析的收敛性. 然而, 在这些研究中测量的响应被认为是静态响应, 即位移和应变. 在实际无损检测中, 安装在结构上的一组传感器很难记录静态响应数据, 实际操作性也困难.

相比之下, 在实际问题中, 传感器较易测得结构的动态响应. 文献[14-17]为了检测结构的内部缺陷, 基于结构的动态响应构造了目标函数; 在时域中使用计算力学方法来解决正问题的方法已用于非均匀介质中的缺陷检测[14]以及压电结构[15], 动态载荷已被证明对裂纹检测问题更有效[16]. Du等[18]最近的一项研究提出了一种基于时域动力扩展有限元法和改进的人工蜂群算法的多缺陷检测新策略; Ma等[19]开发了动态可变节点扩展有限元法, 采用三步算法检测多个复杂缺陷簇. 虽然动态变节点扩展有限元法[19-20]大大减轻了正分析的计算工作量, 但动力分析的时间需求仍然大大超过静力分析, 特别是在目标函数极小化迭代过程中计算工作量巨大, 甚至难以迭代收敛.

为了降低计算成本, 将计算力学方法和机器(深度)学习相结合是一种行之有效的途径, 机器(深度)学习是人工智能和模式识别的一个快速发展的分支学科, 其理论和方法已广泛应用于解决工程和应用科学中的复杂问题[21-22]. 此外, 超声波检测技术是结构无损检测最重要的手段之一, 已广泛应用于各种工程领域[23-25], 传统的超声波检测技术主要通过对回波信号的分析定性地反映缺陷的存在[26], 难以准确定量缺陷, 且强信号中的反映结构微缺陷的信号成分较难提取[27]. 基于神经网络模型的缺陷识别算法可有效提取结构中反映缺陷的信号成分[28], 进而识别缺陷, 但由于基于试验的数据样本有限, 限制了缺陷识别正确率和精度的进一步提高.

本文提出一种将深度学习与比例边界有限元法(scaled boundary finite element methods, SBFEM)相结合的裂纹状多缺陷无损检测方法, SBFEM仅需对结构边界离散可最小化网格重划分过程[29], 大大提高了计算效率, 用于解决与深度学习所需的大量输入数据相关的问题. 首先, 在结构内部随机地生成大量的模拟缺陷数据; 其次, 针对每个有效缺陷数据, 采用SBFEM模拟Lamb波在结构内的传播过程, SBFEM分析结果生成的数据用于深度学习的训练; 最后, 利用训练后的深度学习模型, 根据实测的结构动响应定量识别缺陷的位置和大小. 建议的方法避免了传统反分析问题的目标函数极小化迭代过程, 为结构的无损检测提供了一条新的有效途径.


1.
动力问题的比例边界有限元法



1.1
比例边界有限元法基本方程


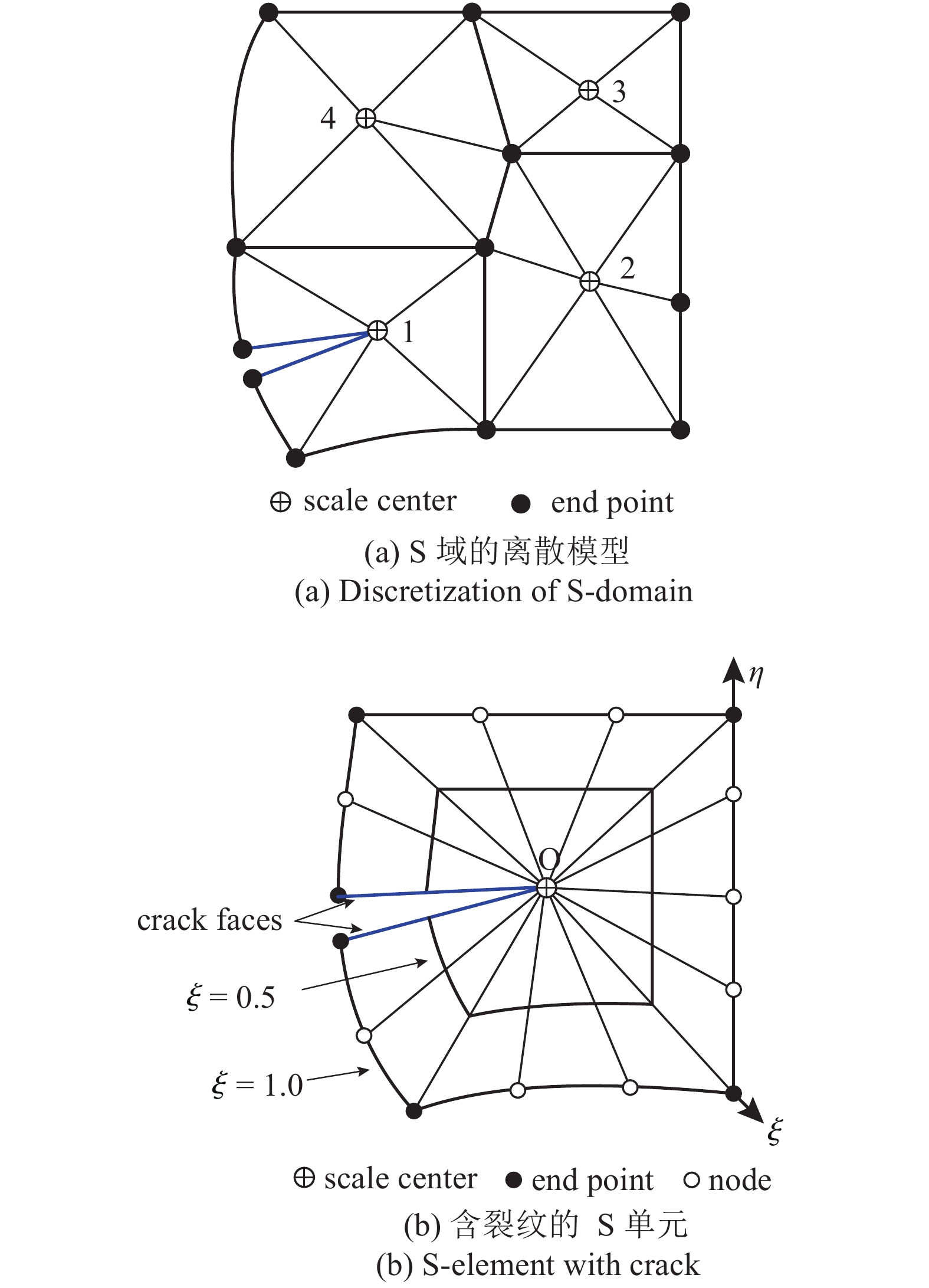
SBFEM是一种半解析的数值方法, 它的半解析性为断裂问题的分析提供了很大的优势, 裂尖局部无需网格细化, 也无需引入解析的改进函数, 裂尖的应力奇异性在求解过程中能被解析地表征[29]. 对于有限域问题, SBFEM和有限元法类似, 先将S域离散成一个或者多个S单元, 然后按照顺序将各个S单元组装起来, 进而求解方程的基本未知量. 如图1所示为SBFE的S域以及S单元的示意图, 图1(a)为含有裂纹的任意多边形S域, 模型将S域划分为4个多边形S单元, 其中S单元1包含裂纹信息(即裂纹S单元), 裂纹S单元的构造如图1(b)所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-360-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
比例边界有限元S域和S单元示意图



Figure
1.
Schematic diagram of S-domain and S-element in SBFEM



下载:
全尺寸图片
幻灯片


在比例边界坐标系$ left(xi ,eta
ight) $中, $ xi $为径向坐标, $ eta $为环向坐标. 在比例中心$ O $点处, 径向坐标$ xi =0 $, 环向坐标$ eta $沿着边界, 且在边界上$ eta =1 $. S单元中的任意一点在笛卡尔坐标系下的坐标$ left(x,y
ight) $可由$ xi $和$ eta $表示为







$$ left.begin{array}{c}x=xi {boldsymbol{N}}left(eta
ight){{boldsymbol{x}}}_{mathrm{s}} y=xi {boldsymbol{N}}left(eta
ight){{boldsymbol{y}}}_{mathrm{s}}end{array}
ight} $$
(1)

式中, $ {boldsymbol{N}}left(eta
ight) $为形函数矩阵, 与有限元中的形函数类似, 但只与环向坐标$ eta $有关; $ {{boldsymbol{x}}}_{mathrm{s}} $和$ {{boldsymbol{y}}}_{mathrm{s}} $分别为S单元结点$ x $方向和$ y $方向坐标向量. SBFEM位移模式可以表示为







$$ {boldsymbol{u}}left(xi ,eta
ight)={boldsymbol{N}}left(eta
ight){boldsymbol{u}}left(xi
ight) $$
(2)

式中, $ {boldsymbol{u}}left(xi
ight) $是沿径向的位移, 由$ N $个解析函数组成.

由SBFEM的位移模式式(2)并假定计算域为线弹性各向同性材料, 根据虚功原理, 不计阻尼, 可推导出动力问题的SBFEM控制方程为







$$ {boldsymbol{M}}{ddot{boldsymbol{u}}}+{boldsymbol{K}}{boldsymbol{u}}={boldsymbol{F}}left(t
ight) $$
(3)

式中, $ {boldsymbol{M}} $为整体质量矩阵, K为整体劲度矩阵, $ {boldsymbol{F}}left(t
ight) $为整体荷载向量. 上述方程形式上与有限元法完全一致, 但$ {boldsymbol{M}} $, K和$ {boldsymbol{F}}left(t
ight)$的组装方式与SBFEM动力刚度矩阵有关, 与有限元法不同. 采用动力刚度矩阵$ {boldsymbol{S}}left(omega ,xi
ight) $表示的SBFE方程为[30]







$$ begin{split}&Big[{boldsymbol{S}}left(omega ,xi
ight)-xi {{boldsymbol{E}}}_{1}Big]{left(xi {{boldsymbol{E}}}_{0}
ight)}^{-1}Big[{boldsymbol{S}}left(omega ,xi
ight)-xi {{boldsymbol{E}}}_{1}^{mathrm{T}}Big]-xi {{boldsymbol{E}}}_{2}+&qquadomega {{boldsymbol{S}}left(omega ,xi
ight)}_{,omega }+{omega }^{2}{xi }^{3}{{boldsymbol{M}}}_{0}={bf{0}} end{split}$$
(4)

式(4)是关于$ xi $的解析方程, 系数矩阵$ {{boldsymbol{E}}}_{0} $, $ {{boldsymbol{E}}}_{1} $和$ {{boldsymbol{E}}}_{2} $与$ xi $无关, 仅与子域几何形状和材料参数有关, $ {{boldsymbol{M}}}_{0} $类似有限元法中的质量矩阵, 它们的表达式参见文献[31], 可采用连分式法[31]求解SBFEM的动力刚度矩阵.


1.2
Lamb波


Lamb波又称板波, 其物理实质是薄板对声波波长的选择特性和多频率纵横波的合成特性, 通常是指在自由边界固体板中的弹性波, 当板的厚度与波长处于同一数量级时板中的纵波和横波发生耦合, 在固体介质中形成一种特殊形式的弹性应力波. 这种弹性应力波必须要满足板的两个表面边界条件, 在板的两表面和中部都有质点的振动, 声场遍及整个板的厚度. 薄板两表面的质点振动是纵波和横波成分之和, 运动轨迹为椭圆形, 长轴与短轴的比例取决于材料的性质. Lamb波在板中传播时, 即有振动方向与板面垂直的横波, 又有振动方向与板面平行的纵波, 纵横波的合成波质点的振动与板共振, 并以特定的频率振动并获得最大能量的传输.

Lamb波在传播中会出现多个模态, 这些模态可以根据板中质点振动的相位关系分为对称模态$ {S}_{i} $和反对称模态$ {A}_{i} $两类. 在各向同性的板中, 纵波和横波的速度可根据拉梅常量计算. 自由边界条件时, 对称模态下波的频率特征方程为







$$left. {begin{array}{*{20}{l}}{dfrac{{{
m{tan}}(qh)}}{{{
m{tan}}(ph)}} = - dfrac{{4{k^2}pq}}{{{{left( {{q^2} - {k^2}}
ight)}^2}}}}{p^2} = dfrac{{{omega ^2}}}{{c_{
m{L}}^2}} - {k^2}{q^2} = dfrac{{{omega ^2}}}{{c_{
m{T}}^2}} - {k^2}end{array}}
ight}$$
(5)

反对称模态下为







$$begin{array}{l}dfrac{{{
m{tan}}(qh)}}{{{
m{tan}}(ph)}} = - dfrac{{{{left( {{q^2} - {k^2}}
ight)}^2}}}{{4{k^2}pq}}end{array}$$
(6)

式中, $ k $为波数, $ h $为板厚, $ {c}_{mathrm{L}} $为纵波波速, $ {c}_{mathrm{T}} $为横波波速, $ omega $为圆频率.


2.
基于深度学习的缺陷识别模型


深度学习是一种表示学习[32-33], 能够学到数据更高层次的抽象表示, 自动地从数据中提取特征[34].


2.1
卷积神经网络


卷积神经网络(convolutional neural network, CNN)是一种具有局部连接、权重共享等特性的深层前馈神经网络. CNN被广泛应用于分类和回归问题的研究, 其中一维CNN在时间序列、电信号以及音频信号等领域的分析有着出色的表现, 故深度学习反演模型将采用一维CNN. CNN的基本结构由输入层、卷积层、池化层、全连接层及输出层构成[35].

卷积层中卷积核对前一层输出的特征矢量进行卷积操作, 利用非线性激活函数构建输出特征矢量, 每一层的输出均为对多输入特征的卷积结果, 第$ j $个神经元第$ l $层的输出$ {{boldsymbol{x}}}_{j}^{l} $可表示为







$$ {{boldsymbol{x}}}_{j}^{l}=fleft(sum _{iin {{boldsymbol{M}}}_{j}}{{boldsymbol{x}}}_{i}^{l-1}{{boldsymbol{k}}}_{ij}^{l}+{{boldsymbol{b}}}_{j}^{l}
ight) $$
(7)

式中, $ {{boldsymbol{M}}}_{j} $为输入特征矢量集合; $ {{boldsymbol{k}}}_{ij}^{l} $为卷积核; $ {{boldsymbol{b}}}_{j}^{l} $为网络偏置; $ {{boldsymbol{x}}}_{i}^{l-1} $为第$ l $层输入. 在CNN中, 非线性激活函数通常选择修正线性单元(rectified linear unit, ReLU), ReLU的优势在于使一部分神经元的输出为0, 提高网络的稀疏性, 缓解了过拟合问题的发生. 同时将原本线性不可分割的多维特征映射到另一个空间中, 从而增强特征的线性可分离性. ReLU的输出值$ {{boldsymbol{a}}}_{i}^{l+1}left(j
ight) $可表示为







$$ {{boldsymbol{a}}}_{i}^{l+1}left(j
ight)=fleft[{{boldsymbol{y}}}_{i}^{l+1}left(j
ight)
ight]=mathrm{m}mathrm{a}mathrm{x}left{0text{, }{{boldsymbol{y}}}_{i}^{l+1}left(j
ight)
ight} $$
(8)

式中, $ {{boldsymbol{y}}}_{i}^{l+1}left(j
ight) $表示卷积层的输出值; $ fleft({*}
ight) $表示激活函数ReLU.

池化层主要作用是进行特征选择, 降低特征数量, 从而减少参数数量, 同时提高所提取特征的鲁棒性. 卷积层虽然可以显著减少网络中连接的数量, 但特征映射组中的神经元个数并没有显著减少, 很容易出现过拟合. 为了解决这个问题, 可以在卷积层之后加上一个池化层, 从而降低特征维数, 避免过拟合. 常用的池化函数有两种, 最大池化和平均池化, 最大池化变换函数如下所示







$$ {{boldsymbol{P}}}_{i}^{l+1}left(j
ight)=mathop {{
m{max}}}nolimits_{left( {j - 1}
ight)W + 1 leqslant t leqslant jW} left{{{boldsymbol{q}}}_{i}^{l}left(t
ight)
ight} $$
(9)

式中, $ {{boldsymbol{q}}}_{i}^{l}left(t
ight) $表示第$ l $层第$ i $个特征矢量中第$ t $个神经元的值, $ tin left[left(j-1
ight)W+1,jW
ight] $; $ W $为池化核的大小; $ {{boldsymbol{P}}}_{i}^{l+1}left(j
ight) $表示第$ l+1 $层神经元对应的值. 平均池化变换函数如下所示







$$ {{boldsymbol{P}}}_{i}^{l+1}left(j
ight)=mathop {{
m{avg}}}nolimits_{left( {j - 1}
ight)W + 1 leqslant t leqslant jW} left{{{boldsymbol{q}}}_{i}^{l}left(t
ight)
ight} $$
(10)

全连接层的每一个结点都与上一层的所有结点相连, 用来把前边提取到的特征综合起来. 全连接层一般负责分类或者回归.

输出层通常使用Sigmoid函数, Sigmoid函数的梯度平滑, 且输出值在0 ~ 1之间, 其函数表达式如下所示







$$begin{array}{l}{
m{Sigmoid}}left( x
ight) = dfrac{1}{{1 + {{
m{e}}^{ - x}}}}end{array}$$
(11)


2.2
缺陷识别模型


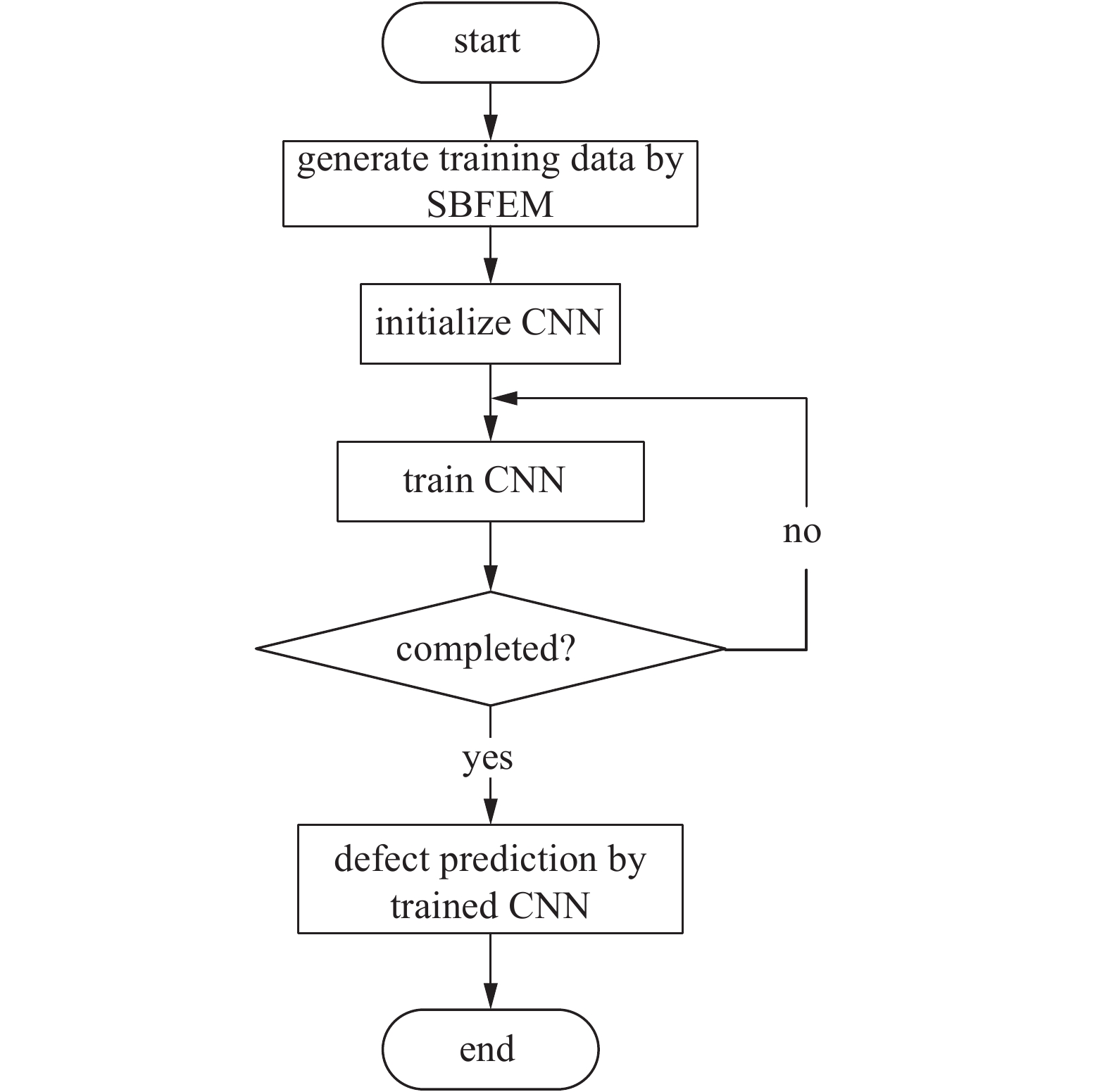
缺陷反演的流程图如图2所示, 首先通过SBFEM模拟Lamb波在含有缺陷薄板中的传播过程, 将观测点的动力响应作为深度学习神经网络模型的输入, 缺陷信息作为模型的输出, 训练神经网络, 最后使用训练好的网络识别薄板内部未知缺陷.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-360-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
缺陷识别流程图



Figure
2.
Flow chart of defect identification



下载:
全尺寸图片
幻灯片


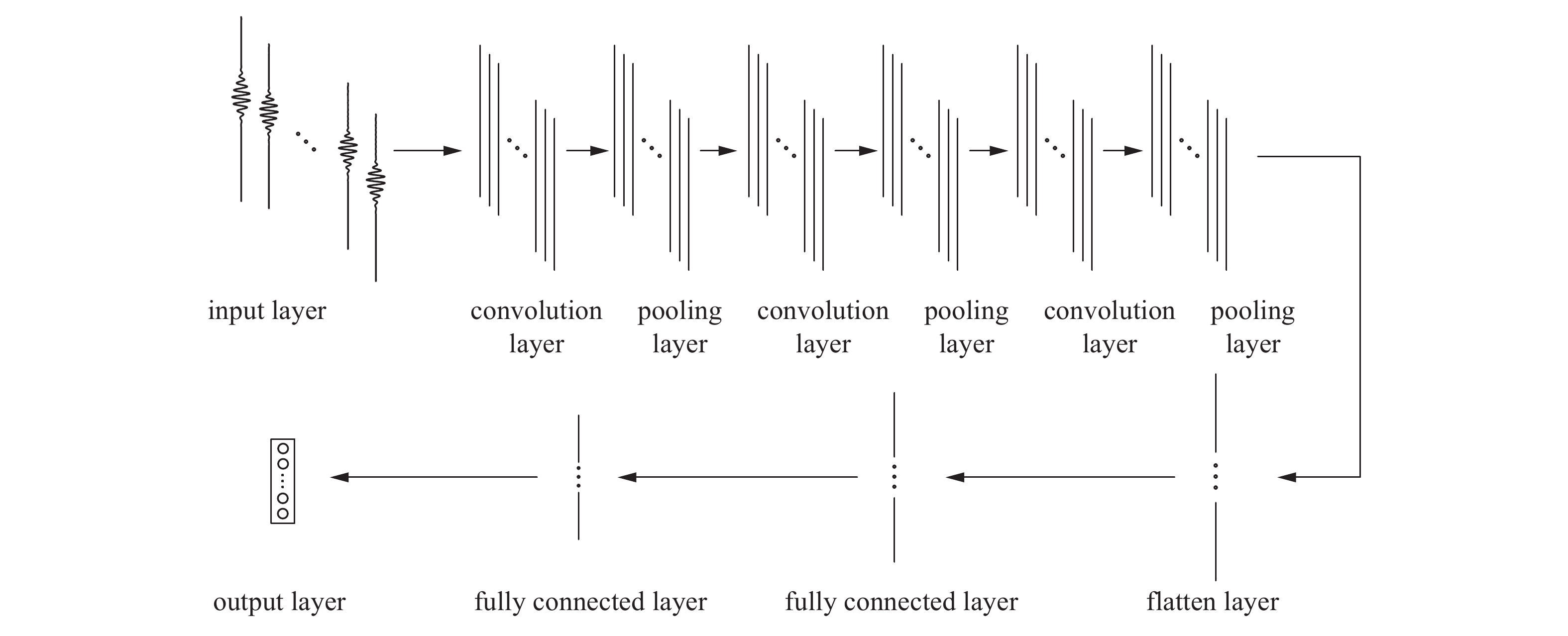
论文结合SBFEM数值模拟和深度学习算法, 提出一种基于一维卷积神经网络的缺陷识别模型, 相对于结合普通的机器学习模型, 该模型有以下的优点: (1)采用多个卷积层, 能够更好地学习到训练数据的深层特征, 有利于提高模型的泛化能力. (2)采用最大池化, 降低训练的计算量, 提高收敛速度. (3)采用dropout, 以一定的概率, 随机将某些神经元进行失效处理, 降低网络过拟合的风险, 能够提高整个网络的鲁棒性. (4)模型采用的一维卷积神经网络可以直接接受原始信号的输入, 不需要对原始数据进行过多的前处理. 基于Python语言自主研制了相应的程序, 具体的深度学习网络结构如图3所示. 先通过3对卷积层和池化层学习输入数据的深层特征, 然后通过一个拉直层, 将数据转化为一维矩阵, 最后通过两个全连接层得到输出.

搭建的卷积神经网络模型结构参数如表1所示, 网络的结构对计算结果具有一定影响, 同时神经网络的一些相关超参数也会影响到计算结果, 这里的结构参数是通过对模型的相关参数进行研究并考察验证集和测试集的准确率得出的优化组合.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-360-3.jpg'"
class="figure_img
figure_type2 ccc " id="Figure3" />



图
3
深度学习网络结构图



Figure
3.
Deep learning network structure chart



下载:
全尺寸图片
幻灯片





表
1
搭建的卷积神经网络模型参数



Table
1.
Parameters of convolution neural network model



table_type1 ">
ParameterValue
input layer size 2000 × 3000 × 1
convolution layer number 3
convolution kernel size 5 × 1
number of pooling layers 3
pooled core size 3 × 1
number of fully connected layers 2
optimizer RMSprop
optimizer learning rate 0.0001
number of batches 18
maximum number of iterations 24





下载:
导出CSV
|显示表格



虽然设定最大迭代次数为24, 但模型引入了early-stopping机制, 当模型的损失函数在一定步数内不再显著变化时即停止模型训练, 用于防止深度学习的过拟合现象.


3.
数值算例



3.1
单裂纹的反演


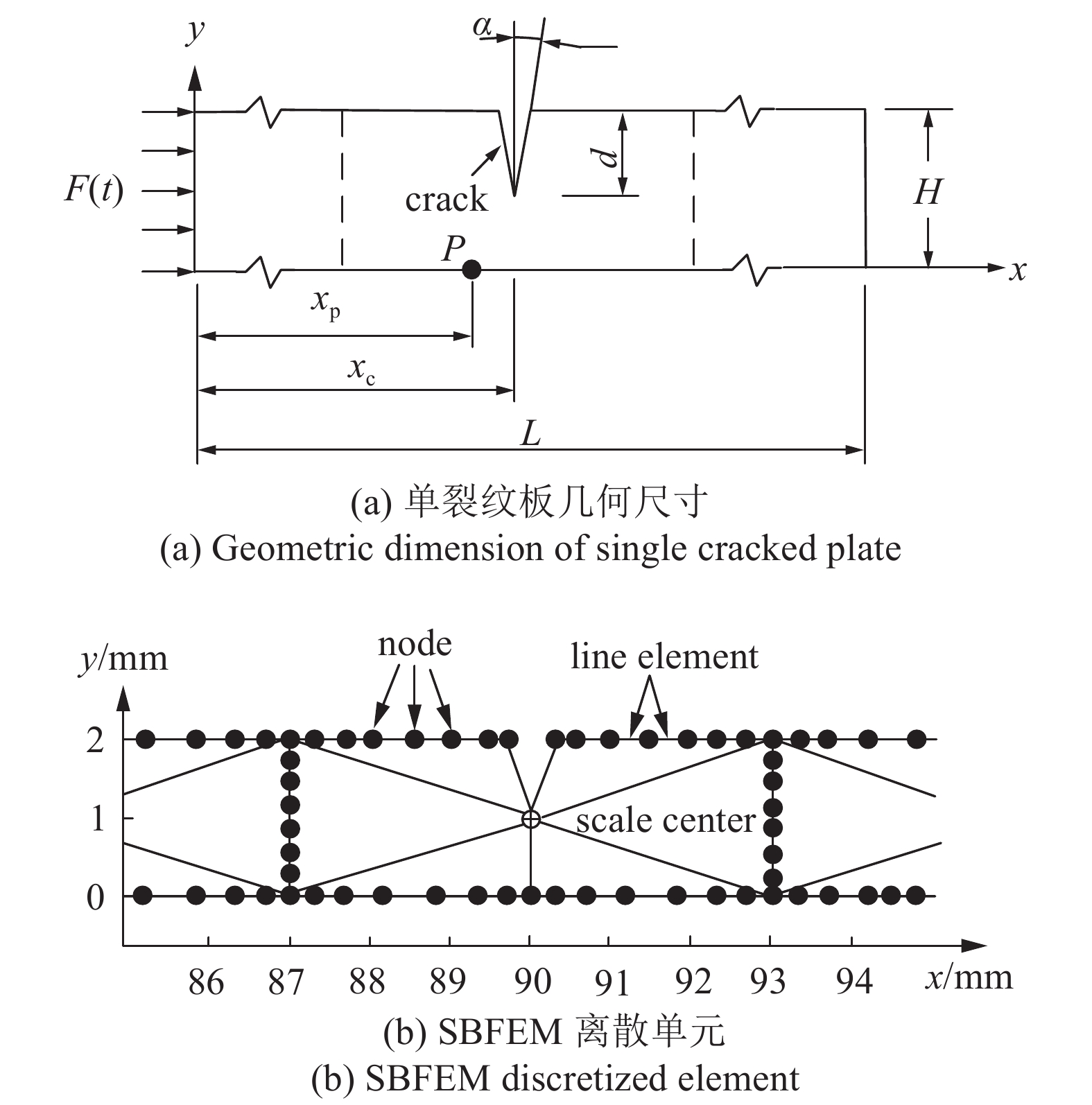
在本算例中, 待研究的对象为二维均质薄板, 板长$ L=180;mathrm{m}mathrm{m} $, 板厚$ H=2;mathrm{m}mathrm{m} $, 其几何尺寸如图4(a)所示. 板的边界为自由边界, 板的材料参数: 弹性模量$ E=200;mathrm{G}mathrm{P}mathrm{a} $, 泊松比$ nu =0.3 $, 质量密度 $;
ho =7850 $$ ;mathrm{k}mathrm{g}/{mathrm{m}}^{3}$. 板的上表面处存在一单向开口裂纹, 裂纹的位置和大小通过3个参数确定, 即: 裂纹尖端坐标$ {x}_{mathrm{c}} $、裂纹的半开裂角$ alpha $、裂纹垂直向深度d. 在板的最左端施加均匀分布的对称荷载$ Fleft(t
ight) $激发Lamb波, $ Fleft(t
ight) $的表达式为



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-360-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
单缺陷板几何尺寸及SBFEM边界离散



Figure
4.
Geometric dimension of single cracked plate and boundary discretization of SBFEM



下载:
全尺寸图片
幻灯片








$$begin{array}{l}Fleft( t
ight) = {
m{sin}}left( {2{text{π}} ft}
ight){{
m{e}}^{ - tfrac{{{{left( {t - mu }
ight)}^2}}}{{2{sigma ^2}}}}}left( {{
m{GPa}}}
ight)end{array}$$
(12)

式中, $mu =6$μs, $ sigma =2 $μs, $ f=0.6;mathrm{M}mathrm{H}mathrm{z} $. 固定的信号观测点P设置在板的下表面距离左边界$ {x}_{mathrm{P}}=90;mathrm{m}mathrm{m} $处, 观测点的位置对反演结果影响较小, 因此, 对于实际问题可根据现场实际情况、传感器布置的方便性等影响因素选取合适的观测点.

数值计算时, 采用Gauss?Lobatto?Legendre积分的高阶单元, 板边界被离散成889个结点, 25个子域, 8984个自由度, 部分离散单元如图4(b)所示. 连分式展开阶数取5, 数值计算的总时间$ t $为90 μs, 每个时间步$ {Delta }t $为0.03 μs.

建立缺陷预测模型时, 将观测点P的动位移作为神经网络的输入, 对应的缺陷参数$left({x}_{mathrm{c}}{
m{,}}; alpha {
m{,}}; d
ight)$作为输出. 训练过程中, 暂用2000组数据作为深度学习模型的训练集, 从训练集中随机划分10%的数据对作为神经网络的验证集, 根据验证集准确率确定网络模型参数后使用10组待反演数据作为测试集. 2000组训练数据的生成过程包括: (1)在待检测薄板域内随机生成2000组缺陷信息, 即参数$ left({x}_{mathrm{c}}{
m{,}}; alpha {
m{,}}; d
ight) $, 本算例中$ {x}_{mathrm{c}}in left(0;mathrm{m}mathrm{m}, 180;mathrm{m}mathrm{m}
ight) $, $ din left(0;mathrm{m}mathrm{m}, 1;mathrm{m}mathrm{m}
ight) $, $ alpha in left(0^ circ , 5^ circ
ight) $ ; (2)对于每组缺陷参数, 在板的最左端施加式(12)给出的均匀分布的对称荷载$ Fleft(t
ight) $激发Lamb波, 采用SBFEM计算观测点$ {x}_{mathrm{P}} $的竖向动位移响应$ yleft(t
ight) $. 每组缺陷参数与观测点的动位移响应$ yleft(t
ight) $构成一组训练数据.

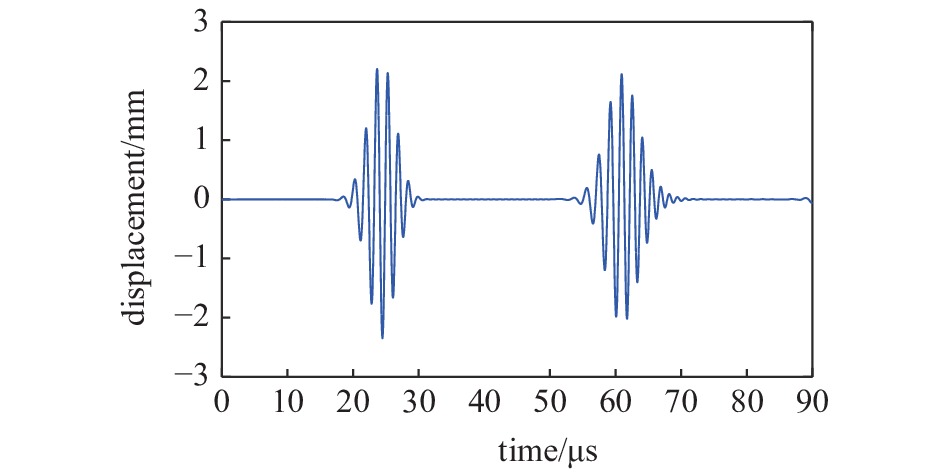
训练结束后, 将实测的观测点处的动位移响应$ yleft(t
ight) $作为网络模型的输入, 本算例中的实测响应通过SBFEM数值计算获取(图5), 在深度学习模型中进行一次正向传播, 得出相应的缺陷参数的预测值, 该预测值就是薄板内未知缺陷的反演值. 值得指出的是文中用于预测的缺陷信息都没有用于训练过程. 图6给出了网络的精度和损失函数随训练过程的变化曲线, 从图中可以看出, 训练集和验证集经过约10代训练后, 网络模型的精度基本趋于稳定, 且经过若干代训练以后, 训练集和验证集的损失函数亦迅速下降.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-360-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
实测的观测点动位移响应



Figure
5.
Measured dynamic displacement responses of observation point



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-360-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
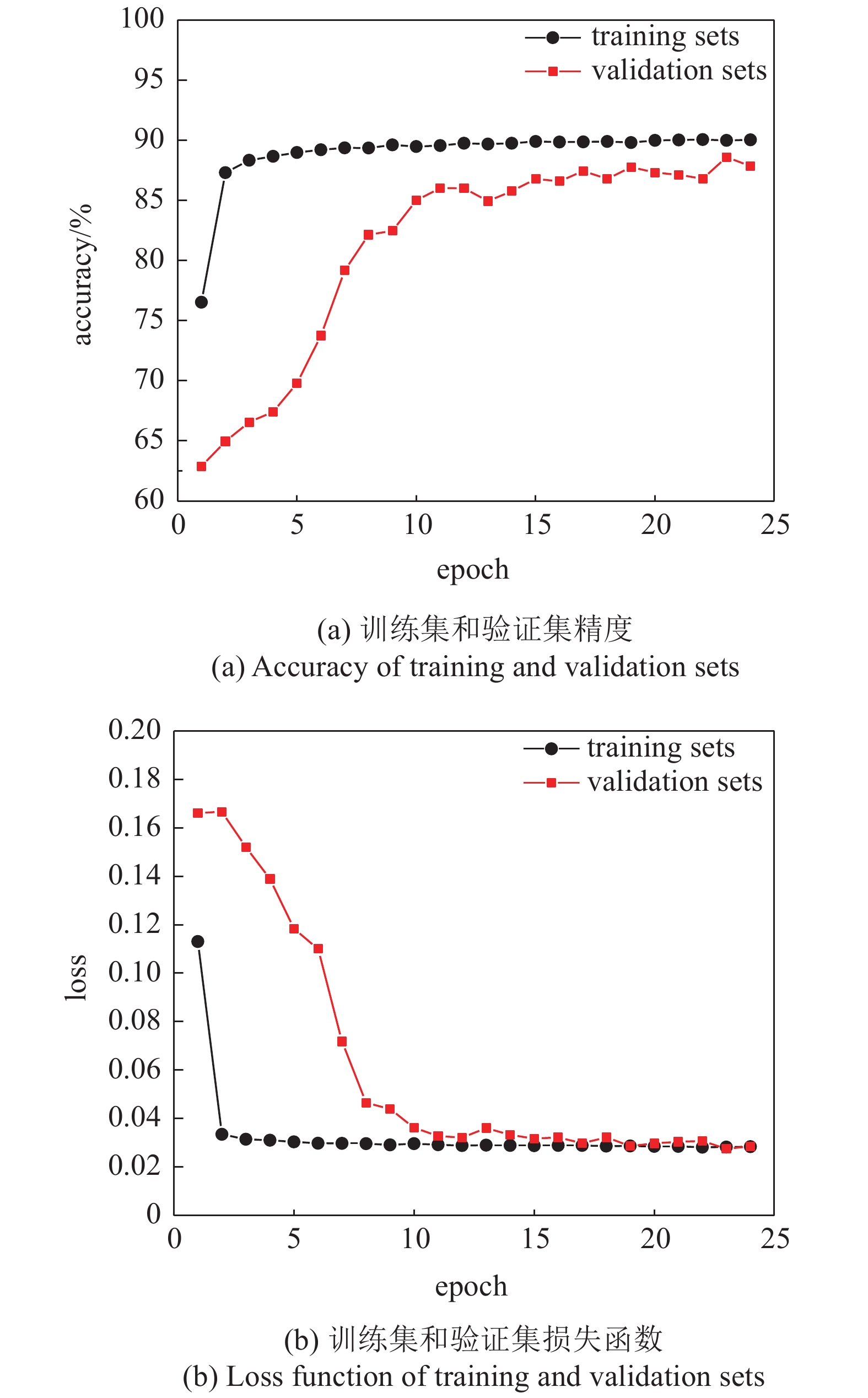
6
网络的精度和损失函数随训练过程变化曲线



Figure
6.
Accuracy and loss function varies as epoch increases



下载:
全尺寸图片
幻灯片


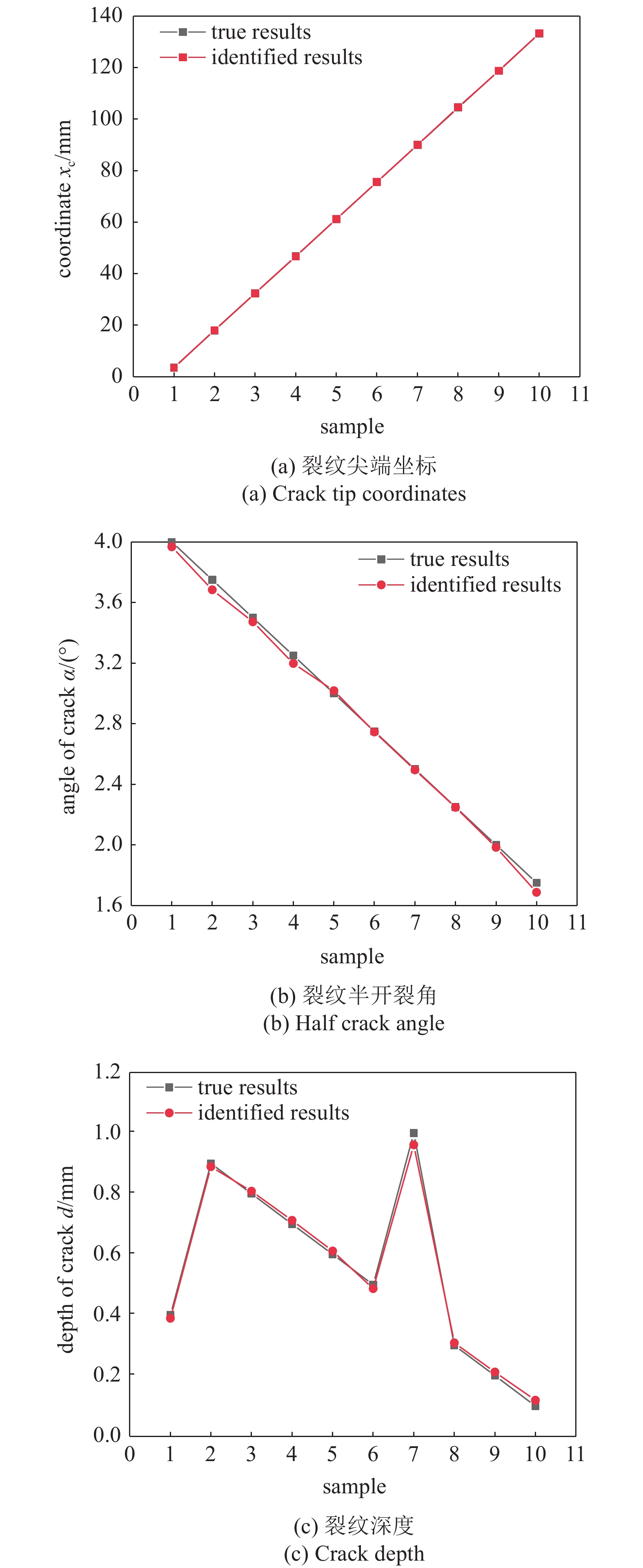
在实际的反演过程中, 由于神经网络初始化的随机性, 比如dropout层的随机性等, 以及GPU计算产生的随机性, 会导致每次反演的结果不同, 为了解决随机性对反演结果的影响, 反演过程将独立运行1000次, 然后运用统计学方法来获得缺陷的反演值, 测试集中10组数据的反演结果如图7所示, 其中某一次反演结果直方图及正态分布拟合曲线如图8所示, 横坐标表示的是参数的反演值, 纵坐标表示1000次反演结果在一定范围内的次数, 同时对这1000次反演的结果进行正态分布拟合, 并绘制正态分布拟合曲线, 图8中的实线就是正态分布拟合曲线, 以正态分布拟合曲线的期望值$ mu $作为反演的结果, 该次缺陷参数的最终反演结果如表2所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-360-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
测试集反演结果图



Figure
7.
Inversion results of test sets



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-360-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
单裂纹1000次反演结果正态分布拟合图



Figure
8.
Fitting diagram of normal distribution of 1000 inversion results of single crack



下载:
全尺寸图片
幻灯片





表
2
单开口裂纹的反演结果和误差



Table
2.
Inversion results and errors of single crack



table_type1 ">
Identified parametersTrue resultsIdentified resultsError /%
${x}_{mathrm{c} }/mathrm{m}mathrm{m}$9090.0210.023
$alpha/ (^ circ )$2.52.4950.200
$d/mathrm{m}mathrm{m}$10.9613.900





下载:
导出CSV
|显示表格



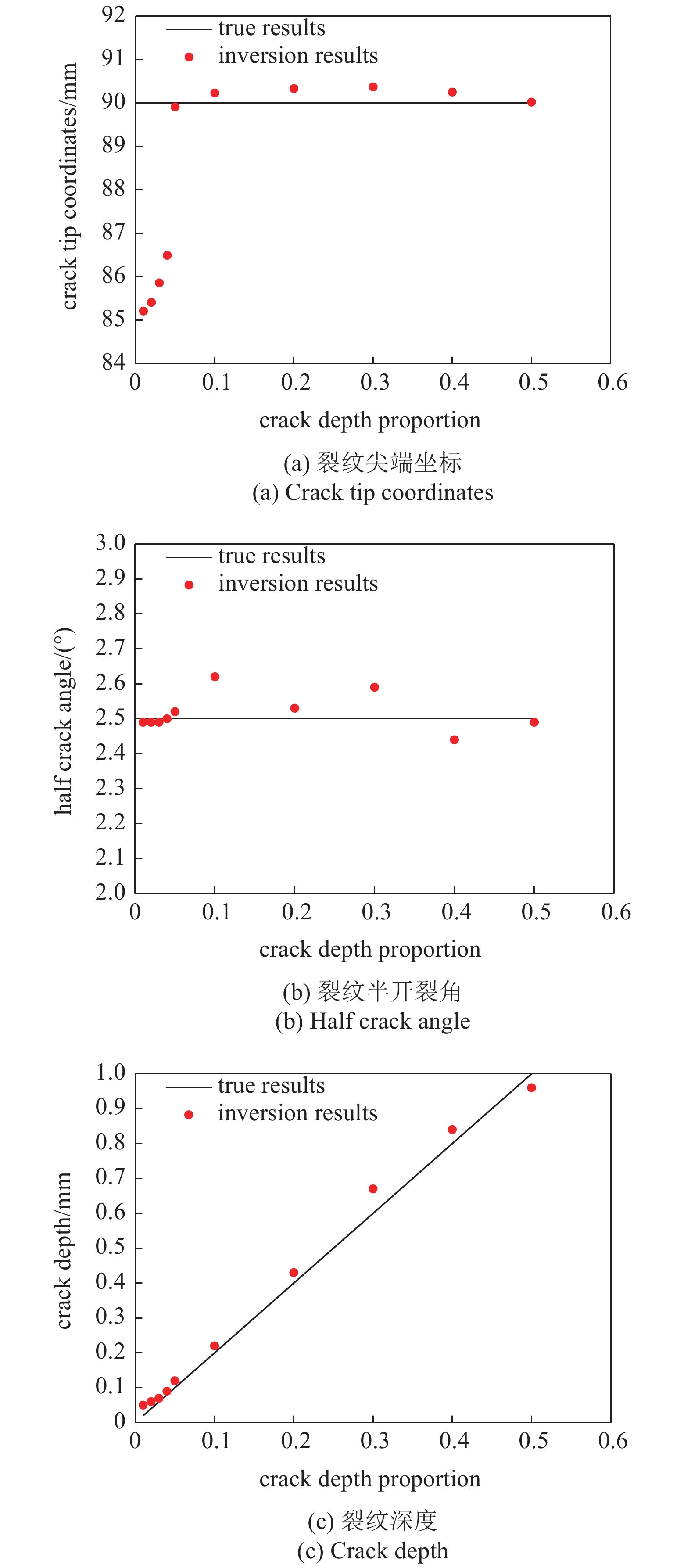
为探究模型对裂纹尺度的反演能力, 尤其是对浅表裂纹的反演能力, 将待反演的裂纹深度比$ delta =d/H $设置为: 0.01, 0.02, 0.03, 0.04, 0.05, 0.1, 0.2, 0.3, 0.4和0.5共10个不同水平. 待反演裂纹位置仍为距离板左端90 mm处, 裂纹半开裂角为2.5°. 不同深度反演裂纹的结果如图9所示, 从图中可看出, 反演深度比$ delta < 0.05 $时, 裂纹位置的反演精度会降低, 而裂纹的半开裂角和裂纹的深度反演精度仍较好. 由此可见, 裂纹的位置信息对模型反演精度的影响较大, 建议的模型对反演深度比$ delta > 0.05 $的裂纹具有较好的反演精度. 深度比$ delta < 0.05 $时, Lamb波透过裂纹时发生的变化较小, 导致观测点测得的响应与健康板的响应相差不大, 因而会影响模型的反演结果.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-360-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
不同深度裂纹的反演结果



Figure
9.
Inversion results of cracks with different depths



下载:
全尺寸图片
幻灯片


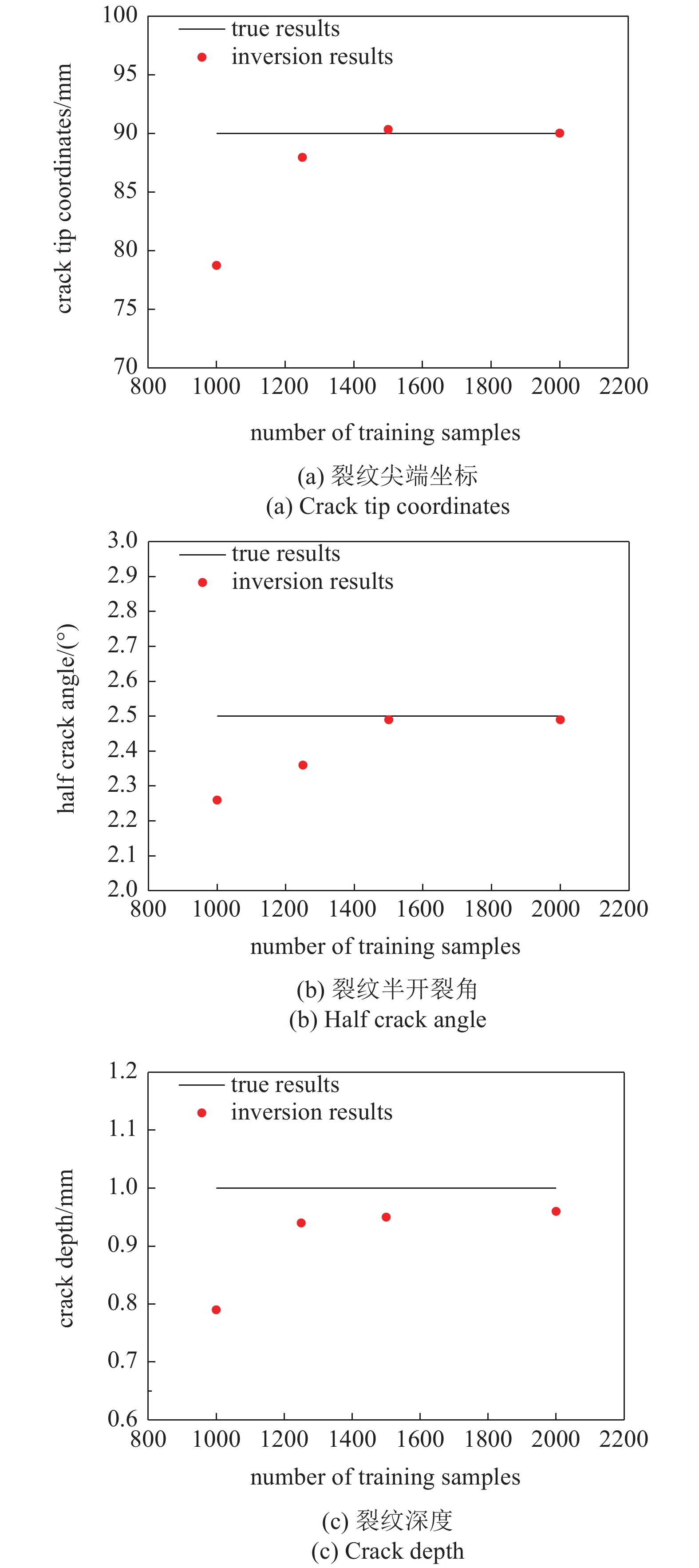
在深度学习反演模型中, 虽然对样本的要求是尽可能大, 但是过大的样本数量会提高计算成本, 同时会降低反演的效率. 为了探究不同数量的样本对反演能力的影响, 将反演样本数量设置为1000, 1250, 1500和2000共4个不同水平. 不同样本数量下的缺陷反演结果如图10所示, 从图10中可以看出, 样本的数量对反演精度有较大影响, 样本数量过少时, 网络出现过拟合的情况, 反演结果与真实值相差较大, 而当样本数量达到1500时模型能够很好地反演出缺陷.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-360-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
不同样本数量的缺陷反演结果



Figure
10.
Inversion results with different training samples



下载:
全尺寸图片
幻灯片



3.2
多裂纹的反演


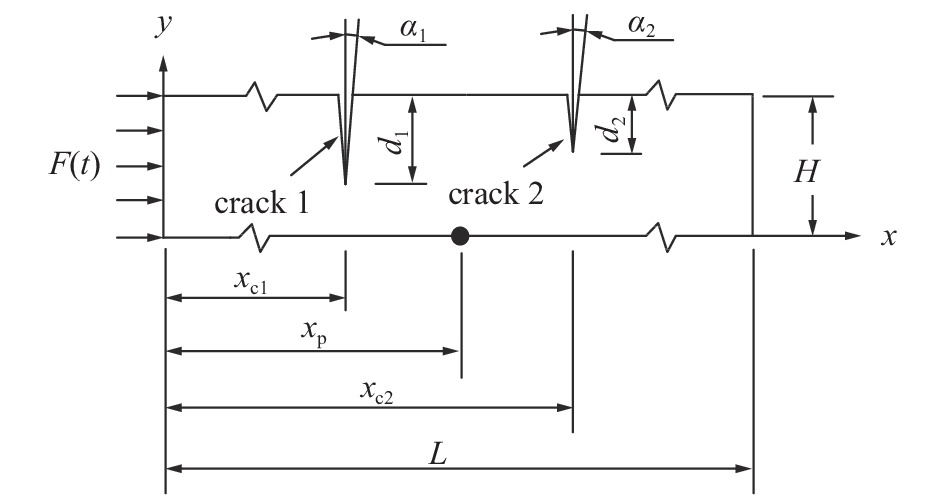
为了研究模型反演多裂纹时的适用性, 研究板中存在两个开口裂纹情况下的反演效果. 本算例中, 板的尺寸、裂纹的参数范围、边界条件、材料参数以及荷载条件均与3.1节相同, 为了使Lamb波充分地在裂纹边界上反射, 观测点P处能够捕获反射信号, 数值计算的总时间$ t $为90 μs, 每个时间步$ {Delta }t $为0.03 μs. 含两个裂纹板的示意图如图11所示, 两裂纹的反演参数为: 第一个裂纹尖端坐标$ {x}_{mathrm{c}1} $、裂纹的半开裂角$ {alpha }_{1} $、裂纹垂向深度$ {d}_{1} $; 第二个裂纹尖端坐标$ {x}_{mathrm{c}2} $、裂纹的半开裂角$ {alpha }_{2} $、裂纹垂向深度$ {d}_{2} $. 观测点P设置在板的下表面$ {x}_{mathrm{P}}=90;mathrm{m}mathrm{m} $处.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-360-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
多裂纹板示意图



Figure
11.
Schematic diagram of multi crack plate



下载:
全尺寸图片
幻灯片


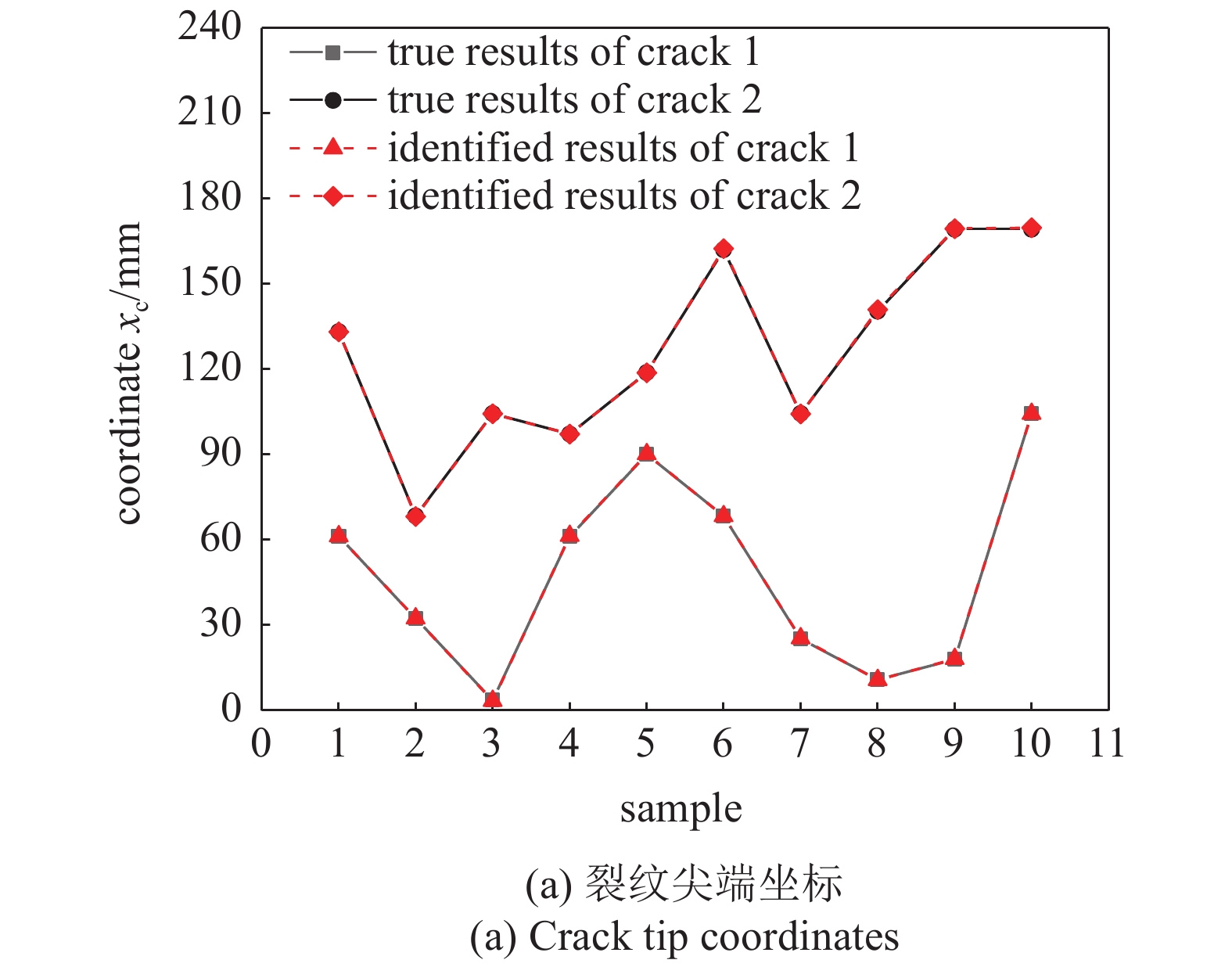
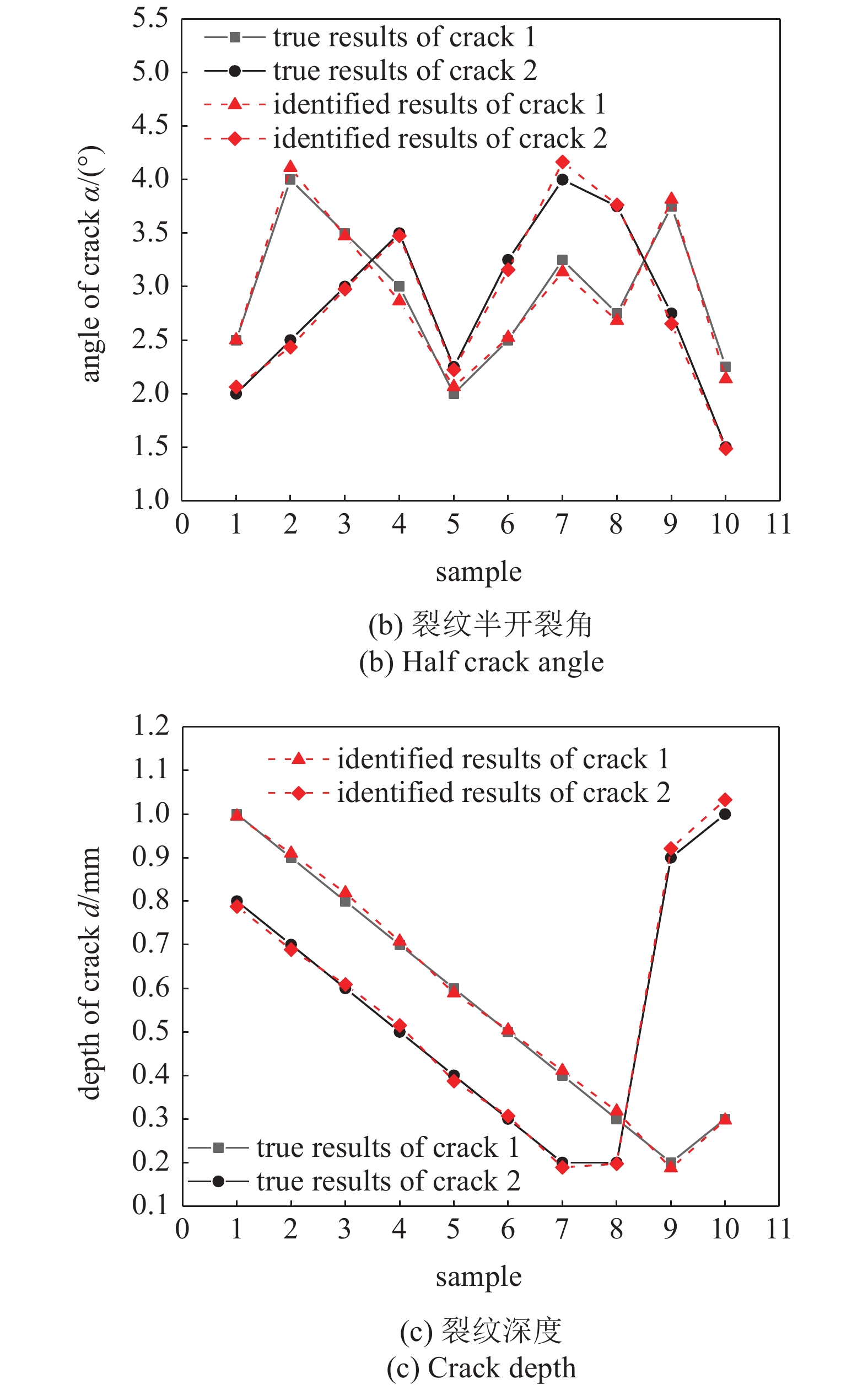
在本算例中, 暂使用2000组训练数据, 这些数据是由SBFEM计算2000个缺陷板得到的动力响应, 2000个缺陷板的缺陷信息及其对应的观测点动力响应作为深度学习神经网络模型的训练集数据, 验证集从训练集中随机分配10%, 根据验证集准确率确定网络模型参数后使用10组待反演数据作为测试集. 训练结束后, 用待反演板的动力响应作为输入, 在深度学习模型中进行一次正向传播, 得出相应的预测值, 该预测值就是未知缺陷薄板的反演值. 同样地, 使用统计学方法来获得缺陷的反演值, 测试集反演结果如图12所示, 最终反演结果如表3所示.

此外, 为探究不同的样本数对多裂纹反演结果的影响, 研究了样本数分别为1000, 1250, 1500和2000共4个不同水平时反演的结果, 如表4所示. 从表中可以看出, 与单缺陷相同, 样本的数量对反演精度有较大影响, 本节建立的多裂纹反演的模型, 在样本数量大于1500时, 能够保证一定的反演精度, 将多裂纹的相关参数准确地反演出来.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-360-12-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12-1" />



12
多裂纹测试集反演结果图



12.
Inversion results of multi crack on test sets



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-360-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
多裂纹测试集反演结果图(续)



Figure
12.
Inversion results of multi crack on test sets (continued)



下载:
全尺寸图片
幻灯片





表
3
多裂纹的反演结果和误差



Table
3.
Inversion results and errors of multi cracks



table_type1 ">
Identified parametersTrue resultsIdentified resultsError /%
crack 1${x}_{mathrm{c}1}/mathrm{m}mathrm{m}$61.20061.2770.126
${alpha }_{1}/(^ circ )$2.5002.5010.040
${d}_{1}/mathrm{m}mathrm{m}$1.0000.9950.500
crack 2${x}_{mathrm{c}2}/mathrm{m}mathrm{m}$133.200133.1370.047
${alpha }_{2}/(^ circ )$2.0002.0633.150
${d}_{2}/mathrm{m}mathrm{m}$0.8000.7882.500





下载:
导出CSV
|显示表格






表
4
不同样本数量时多裂纹反演结果



Table
4.
Inversion results and errors of multi cracks with different training samples



table_type2 ">
Identified parametersTrue resultsNumber of training samples
1000Error /%1250Error /%1500Error /%2000Error /%
crack 1 ${x}_{mathrm{c}1}/mathrm{m}mathrm{m}$ 61.200 59.899 2.126 61.479 0.456 61.287 0.142 61.277 0.126
${alpha }_{1}/(^ circ )$ 2.500 2.529 1.160 2.504 0.160 2.504 0.160 2.501 0.040
${d}_{1}/mathrm{m}mathrm{m}$ 1.000 0.917 8.300 0.920 8.000 0.984 1.600 0.995 0.500
crack 2 ${x}_{mathrm{c}2}/mathrm{m}mathrm{m}$ 133.200 132.243 0.718 131.777 1.068 133.358 0.119 133.137 0.047
${alpha }_{2}/(^ circ )$ 2.000 2.533 26.650 2.518 25.900 2.055 2.750 2.063 3.150
${d}_{2}/mathrm{m}mathrm{m}$ 0.800 0.733 8.375 0.724 9.500 0.824 3.000 0.780 2.500





下载:
导出CSV
|显示表格



4.
模型鲁棒性分析


在实际的问题中, 由于传感器的精度、实验环境等问题, 可能会导致测量的结果混入噪声. 为了分析噪声的干扰对缺陷反演结果的影响, 在待反演信号中混入不同程度的噪声, 来验证文中提出的反演模型的鲁棒性. 本算例与3.2相同, 不同的是在观测点P测得的动力响应真实值的基础上, 加入一定水平的高斯白噪声, 来模拟含有噪声的数据. 含有噪声的动力响应计算公式如下所示







$$ {boldsymbol{X}}^{mathrm{m}}={boldsymbol{X}}^{mathrm{c}mathrm{l}mathrm{e}mathrm{a}mathrm{n}}+omega cdot {{boldsymbol{RM}}{boldsymbol{S}}}_{mathrm{X}} cdot p $$
(13)

式中, $ {boldsymbol{X}}^{mathrm{c}mathrm{l}mathrm{e}mathrm{a}mathrm{n}} $表示通过SBFEM计算的含有缺陷板的真实位移, $ omega $为高斯白噪声变量, $ {{boldsymbol{R}}{boldsymbol{M}}{boldsymbol{S}}}_{mathrm{X}} $为真实位移的均方根, $ p $为噪声水平.

考虑到在实际工程中, 如果测得的动响应中存在较大的噪声干扰, 会进行去噪处理, 所以在本节的鲁棒性分析中, 最大的噪声水平为10%. 其他参数与3.2节中相同, 同样运行1000次, 反演结果如表5和表6. 在待反演信号中添加不同程度的噪声, 模型能够反演出缺陷. 但随着噪声水平的增长, 缺陷识别的精度会有所下降.




表
5
引入5%噪声的反演结果



Table
5.
Inversion results with 5% noise



table_type1 ">
Identified parametersTrue resultsIdentified resultsError/%
crack 1 ${x}_{mathrm{c}1}/mathrm{m}mathrm{m}$ 61.200 61.813 1.002
${alpha }_{1}/(^ circ )$ 2.500 2.453 1.880
${d}_{1}/mathrm{m}mathrm{m}$ 1.000 0.972 2.800
crack 2 ${x}_{mathrm{c}2}/mathrm{m}mathrm{m}$ 133.200 132.881 0.239
${alpha }_{2}/(^ circ )$ 2.000 2.160 8.000
${d}_{2}/mathrm{m}mathrm{m}$ 0.800 0.780 2.500





下载:
导出CSV
|显示表格






表
6
引入10%噪声的反演结果



Table
6.
Inversion results with 10% noise



table_type1 ">
Identified parametersTrue resultsIdentified resultsError/%
crack 1 ${x}_{mathrm{c}1}/mathrm{m}mathrm{m}$ 61.200 61.992 1.294
${alpha }_{1}/(^ circ )$ 2.500 2.597 3.880
${d}_{1}/mathrm{m}mathrm{m}$ 1.000 0.925 7.500
crack 2 ${x}_{mathrm{c}2}/mathrm{m}mathrm{m}$ 133.200 132.424 0.583
${alpha }_{2}/(^ circ )$ 2.000 2.407 20.350
${d}_{2}/mathrm{m}mathrm{m}$ 0.800 0.718 10.250





下载:
导出CSV
|显示表格



5.
结论


结合SBFEM和深度学习建立了结构内裂纹状缺陷的反演模型, 可以定量识别结构内多裂纹的位置和尺度. SBFEM仅需对结构边界进行离散, 通过设置比例中心的位置位于裂纹尖端可最小化网格重剖分, 模拟波动问题时计算效率极高, 可以快速地为深度学习模型提供足够多的训练数据. 深度学习模型能够学习到样本的深层特征, 大大提高了反演精度. Lamb波在含缺陷薄板中传播时, 缺陷的存在对波传播信号有明显影响, 仅采用一个观测点的动位移响应便能得到较好的反演结果, 相比于传统的无损检测方法为加快目标函数的最小化迭代过程需要布置较多的传感器, 文中建议的基于SBFEM和深度学习的反演模型避免了传统反分析问题的目标函数最小化迭代过程, 同一结构模型的训练数据可存储为数据库供多次反复使用. 对含单裂纹和多裂纹板的数值算例进行分析, 结果表明, 建立的缺陷识别模型能够准确地量化结构内部的缺陷, 对浅表裂纹亦有很好的识别效果, 且对于含噪信号模型仍具有较好的鲁棒性.

当前的研究在进行多裂纹反演时是在预先已知裂纹数量的情况下, 在后续的研究中将进一步拓展建议的模型用于未知裂纹数量情况下的缺陷反演. 此外, 后续的研究也将设计相关试验, 进一步验证反演模型.

相关话题/结构 数据 计算 网络 图片
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 考虑混凝土塑性耗散的CDM-XFEM裂缝计算方法
    引言混凝土结构是建筑、交通、水利等领域的重要基础材料,其可塑性高、耐久性好是受广泛应用的主要原因.但混凝土抗拉强度远低于抗压强度[1],结构在服役期间受外界载荷的影响容易产生裂缝[2],裂缝的出现不仅会降低结构刚度,还为外部侵蚀介质的侵入提供了快捷通道,从而加速内部钢筋锈蚀[3-4]、降低结构承载力 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • K<sub>0</sub>超固结结构性黏土的本构模型
    引言自然界存在的天然黏土通常是K0固结与结构性并存的状态[1-2],而K0固结又按照当前竖向应力是否大于先期固结压力而分为K0正常固结与K0超固结黏土.大量的室内试验以及现场测试表明,K0正常固结黏土由于初始固结为偏压固结,与等方向正常固结黏土相比,其在大主应力与先期固结压力一致的情况下,K0固结黏 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 面内变刚度薄板弯曲问题的挠度?弯矩耦合神经网络方法
    引言面内功能梯度材料薄板结构在土木工程、海洋工程等领域应用广泛,该结构由功能梯度材料所组成(functionallygradedmaterial,FGM),其材料特性随着空间位置的变化而表现为梯度性的变化[1].在现有研究中,于天崇等[2]研究了面内变刚度薄板在特定边界下弯曲问题的Levy解.朱竑祯 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 一种新的玻尔兹曼方程可计算模型构造与分析
    引言近年来,随着对临近空间战略意义认识的加深,各航空航天大国发展了众多临近空间飞行器.为满足长航时、大载荷、高超声速巡航等需求,这类临近空间飞行器通常整体尺寸较大,各部件间差异显著,飞行过程会出现多物理多场耦合、多流区共存的多尺度复杂流动现象,传统的数值模拟方法如基于宏观连续介质假设的纳维?斯托克斯 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 数据驱动印度洋海域全局动力学研究
    引言海洋系统天然受到多种环境因素(风速、温度、海水含盐量等)、人类活动和天体运动等不确定扰动的影响,导致其洋流运动复杂而多样[1-2].然而,一些观测和研究发现,其内部蕴含着能够对洋流的运动方向和趋势起限制和导向作用的复杂动力结构和特征,影响甚至主导了表面漂浮物的流动形式和演化路径.例如,经志友等[ ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 页岩凝析气藏相平衡的快速准确计算方法
    引言随着以煤炭、石油和木柴为代表的传统能源消耗带来的巨量的空气污染日益引起全社会的关注,天然气作为一种相对较为清洁的能源得到了广泛的重视[1].近年来在非常规油气藏勘探和开发技术上的迅猛发展,使得具有巨大潜在储量但一直得不到有效开发的以页岩气为代表的非常规油气资源成为了投资热点和研究焦点[2].中国 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 软材料粘接结构界面破坏研究综述
    引言因其特有的低模量和能量耗散等“软”的特性以及优异的“小激励大响应”等特征,多种多样的软材料,如水凝胶、介电弹性体以及聚甲基氧硅烷等被广泛应用在软机器人、生物医学和柔性电子等各个领域[1-4].近些年,软材料的力学行为已经成为学术界和工业界广泛关注的热点之一.在实际应用中,软材料一般需要粘附于某种 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 循环神经网络在智能天平研究中的应用
    引言随着航空航天技术的不断发展,高超声速技术受到各个航空航天大国的广泛关注和深入研究,其科学问题具有重要的战略意义[1].对于高超声速飞行器气动外形布局设计和优化问题,高精度气动力测量试验起到决定性作用.激波风洞测力试验可以为高温真实气体效应的研究提供可靠的数据,同时为我国高超声速飞行器研究提供关键 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于喷流拟序结构预测的SGS模型比较研究
    引言拟序结构普遍存在于湍流中[1–3],并影响湍流的发生、输运与耗散等过程,对湍流拟序结构的研究、对于理解湍流机理、分析流动相互作用有重要的意义.从大涡模拟来看,正确预测湍流拟序结构的关键就在于算法和亚网格尺度(sub-grid-scale,SGS)模型的准确性.在算法方面,传统的大涡模拟方法求解网 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.