引 言

在很多工业领域都会发生液滴的不稳定过程, 如喷墨打印^[1-2]、声悬浮技术^[3-6]、非接触式测量液体性质^[7-11]等. Rayleigh^[12]和Kelvin^[13]最先研究了无黏液滴受小扰动时界面衰减振荡的自然频率. 在形状振荡的过程中, 表面张力的作用为使液滴表面恢复为平衡位置的恢复力, 使液滴的振荡不断减小, 最终恢复为球形. 随后Reid^[14], Chandrasekhar^[15], Miller和Scriven^[16]考虑了自然振荡中液滴黏性的作用, 发现振荡衰减的主要原因是在界面附近边界层内的黏性耗散. Bauer等^[17-18]则关注了流变特性对液滴小振幅振荡时频率的影响, 发现流体的黏弹性可能会显著影响液滴的振荡行为. Khismatullin和Nadim^[19]对黏弹性液滴形状振荡的特征方程进行了线性理论分析, 发现对于黏弹性液滴, 即使在很小的弹性下也会使高黏度的液滴发生形状振荡. Apfel等^[20-24]对含表面活性剂液滴的形状振荡开展了一系列的研究, 发现由于表面活性剂的不均匀分布所导致的Gibbs弹性是改变自由振荡频率最重要的参数.

相比于液滴受小扰动的自由振荡, Li等^[25]研究了受任意方向加速度的黏性液滴在高速气流下的R-T不稳定过程, 并在忽略液滴黏度的情况下, 通过求解特征值问题确定了在中性稳定状态的一系列临界Bond数. 通过对递推关系的化简, 发现在大模式数l条件下增长率与经向模数m无关. 吴清等^[26]则在Li等^[25]的基础上考虑了环境流体的可压缩性, 并将液滴所受的动态惯性力视为是随时间变化的. 计算结果显示虽然气体的压缩性具有促进液滴破碎的作用, 但其影响却非常微小. Ebo Adou和Tuckerman^[27]首先研究了受时间周期径向加速度的黏性液滴稳定性问题, 并进行了相关数值模拟^[28]. 他们使用了与Kumar和Tuckerman^[29]类似的方法, 将Floquet理论应用于球坐标, 与处理水平液面问题所不同的是引入了球谐函数. 发现黏性的存在使中性曲线的不稳定舌尖变得光滑, 但其分析中却并未考虑周围环境介质密度的影响. Li等^[30]则在Ebo Adou和Tuckerman^[27]的基础上探究了环境流体密度对稳定性的影响, 发现增加环境流体的密度会使可能激发的球模态变窄. Liu等^[31]开展了液滴处于振动隔板上的试验, 近似计算了液滴上表面驻波的波长, 并与Lang’s方程求得的结果进行对比, 验证了在低频下Lang’s方程对球面Faraday不稳定的适用性.

本工作采用Floquet理论, 将Liu等^[31]所研究的牛顿黏性液滴拓展为黏弹性液滴, 考虑其受径向振荡的加速度情况下的稳定性问题, 推导得到了表面波增长率随各参数变化的系数矩阵, 讨论了黏弹性参数及振荡条件对液滴不稳定性的影响, 丰富了液滴Faraday不稳定的理论研究.

1.
控制方程

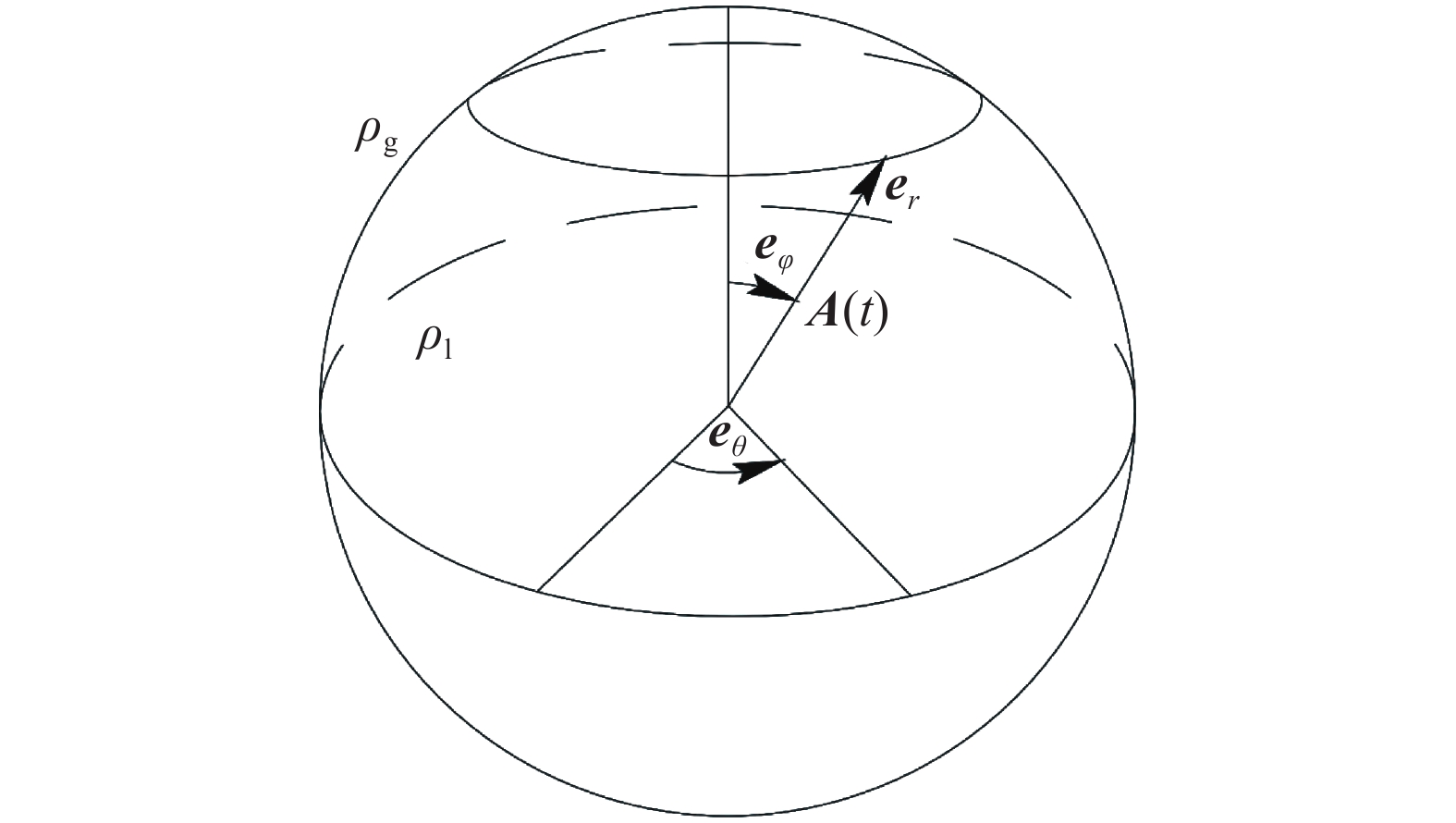
考虑一个黏弹性的不可压缩球形液滴在静止气流中受径向振荡的加速度, 物理模型如图1所示. 其加速度只沿着径向方向, 且可以表示成余弦函数的形式

$$ {boldsymbol{A}}left( t ight) = {A_0}cos left( {omega t} ight){{boldsymbol{e}}_r} $$

(1)

其中ω表示振荡频率, A₀表示振荡幅值.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2020-416-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
液滴受径向振荡示意图



Figure
1.
Schematic diagram of a droplet subjected to radial oscillation



下载:
全尺寸图片
幻灯片


液滴的线性化控制方程为

$$ nabla cdot {{boldsymbol{u}}_{ m{l}}} = 0 qquadqquadqquadquad;;$$

(2)

$$ { ho _{ m{l}}}frac{{partial {{boldsymbol{u}}_{ m{l}}}}}{{partial t}} = - nabla {p_{ m{l}}} + nabla cdot {{boldsymbol{tau}} _{ m{l}}} + { ho _{ m{l}}}{boldsymbol{A}} $$

(3)

式中, u_l = (u_lr, u_lθ, u_lφ)表示液滴的扰动速度, $ {p_{
m{l}}} $表示液滴的扰动压强, $ {{boldsymbol{tau}} _{
m{l}}} $表示液滴的偏应力张量. 变形的液滴表面为

$$ r = R + eta $$

(4)

其中, η表示扰动的液滴表面与平衡位置的偏离量, R为液滴平衡位置的半径.

类似地, 气相的控制方程为

$$ nabla cdot {{boldsymbol{u}}_{ m{g}}} = 0 qquadqquad$$

(5)

$$ { ho _{ m{g}}}frac{{partial {{boldsymbol{u}}_{ m{g}}}}}{{partial t}} = - nabla {p_{ m{g}}} + { ho _{ m{g}}}{boldsymbol{A}} $$

(6)

因为本文研究的是非牛顿黏弹性的液滴, 采用Jefferys模型来描述流体的本构方程

$$ {{boldsymbol{tau}} _{ m{l}}} + {lambda _{ m{1}}}frac{{partial {{boldsymbol{tau}} _l}}}{{partial t}} = 2{mu _0}left( {{boldsymbol{D}} + {lambda _2}frac{{partial {boldsymbol{D}}}}{{partial t}}} ight) $$

(7)

其中, ${{boldsymbol{D}} = {{left[ {nabla {{boldsymbol{u}}_{
m{l}}} + {{left( {nabla {{boldsymbol{u}}_{
m{l}}}}
ight)}^{
m{T}}}}
ight]} / 2}$为液体的应变率张量, $ {mu _0} $为零剪切黏度, $ {lambda _1} $为应力松弛时间, $ {lambda _2} $为应变驰豫时间.

将扰动量设为Floquet解的Fourier形式

$$ begin{split}& left( {eta,{{boldsymbol{u}}_{ m{l}}},{{boldsymbol{u}}_{ m{g}}},{p_{ m{l}}},{p_{ m{g}}},{{boldsymbol{tau}} _{ m{l}}}} ight) = &qquad sumlimits_{l = 2}^{ + infty } {sumlimits_{m = 0}^l {sumlimits_{n = 0}^{ + infty } {{{ m{e}}^{{zeta _n}t}}{ m{Y}}_l^mleft( {theta,varphi } ight)} } } left( {{eta _n},{{boldsymbol{u}}_{{ m{l}}n}},{{boldsymbol{u}}_{{ m{g}}n}},{p_{{ m{l}}n}},{p_{{ m{g}}n}},{{boldsymbol{tau}} _{{ m{l}}n}}} ight) end{split} $$

(8)

式中

$$ {zeta _n} = beta + { m{i}}left( {gamma + nomega } ight) $$

(9)

其中, $; beta +{
m{ i}}gamma $表示Floquet指数, $; beta $为扰动增长率, n表示展开的Fourier模态的阶数. 将扰动量的形式(8)代入本构方程(7)中, 可以将黏弹性流体的黏度写成一个和流变模型参数相关的有效动力黏度, 即

$$ {mu _{{ m{eff}}}} = {mu _0}frac{{1 + {lambda _2}{zeta _n}}}{{1 + {lambda _1}{zeta _n}}} $$

(10)

故此时液体的动量方程可写为

$$ { ho _{ m{l}}}frac{{partial {{boldsymbol{u}}_{ m{l}}}}}{{partial t}} = - nabla {p_{ m{l}}} + {mu _{{ m{eff}}}}{nabla ^2}{{boldsymbol{u}}_{ m{l}}} + { ho _{ m{l}}}{boldsymbol{A}} $$

(11)

为确定液滴的运动, 还需要满足一些边界条件. 首先, 速度的径向分量必须与液滴表面的变形相容, 即运动边界条件

$$ frac{{partial eta }}{{partial t}} = {u_{{ m{l}}r}},;;r = R + eta $$

(12)

$$ frac{{partial eta }}{{partial t}} = {u_{{ m{g}}r}},;;r = R + eta $$

(13)

在液滴表面, 需满足切应力平衡条件

$$ {tau _{{ m{l}}rtheta }} = {mu _{{ m{eff}}}}left( {frac{1}{r}frac{{partial {u_{{ m{l}}r}}}}{{partial theta }} - frac{{{u_{{ m{l}}theta }}}}{r} + frac{{partial {u_{{ m{l}}theta }}}}{{partial r}}} ight) = 0,;;r = R + eta qquad$$

(14)

$$ {tau _{{ m{l}}rvarphi }} = {mu _{{ m{eff}}}}left( {frac{1}{{rsin theta }}frac{{partial {u_{{ m{l}}r}}}}{{partial varphi }} - frac{{{u_{{ m{l}}varphi }}}}{r} + frac{{partial {u_{{ m{l}}varphi }}}}{{partial r}}} ight) = 0,;;r = R + eta $$

(15)

法应力平衡条件

$$ {p_{ m{l}}} - {p_{ m{g}}} = frac{{2sigma }}{R} - frac{sigma }{{{R^2}}}left( {2eta + nabla _{ m{H}}^2eta } ight) + 2{mu _{{ m{eff}}}}frac{{partial {u_{{ m{l}}r}}}}{{partial r}},;;r = R + eta $$

(16)

其中, $ nabla _{
m{H}}^2 equiv dfrac{1}{{sin theta }}dfrac{partial }{{partial theta }}left( {sin theta dfrac{partial }{{partial theta }}}
ight) + dfrac{1}{{{{sin }^2}theta }}dfrac{{{partial ^2}}}{{partial {varphi ^2}}} $表示水平方向的Laplace算子, 其特征值为?l(l + 1). 使用公式$ nabla times nabla times {{boldsymbol{u}}_{
m{l}}} = nabla left( {nabla cdot {{boldsymbol{u}}_{
m{l}}}}
ight) - {nabla ^2}{{boldsymbol{u}}_{
m{l}}} $, 而我们知道不可压流体的速度场是无散度场, 将该表达式代入式(11)中, 得

$$ { ho _{ m{l}}}frac{{partial {{boldsymbol{u}}_{ m{l}}}}}{{partial t}} = - nabla {p_{ m{l}}} - {mu _{{ m{eff}}}}nabla times nabla times {{boldsymbol{u}}_{ m{l}}} + { ho _{ m{l}}}{boldsymbol{A}} $$

(17)

将速度场$ {{boldsymbol{u}}_{
m{l}}} $分解为无旋部分和有旋部分之和, 即

$$ {{boldsymbol{u}}_{ m{l}}} = nabla {phi _{ m{l}}} + {{boldsymbol{psi}} _{ m{l}}} $$

(18)

将式(18)代入方程(2)和(17)中, 分别得到无旋部分$ nabla {phi _{
m{l}}} $和有旋部分$ {{boldsymbol{psi}} _{
m{l}}} $所满足的方程

$$ {nabla ^2}{phi _{ m{l}}} = {0} $$

(19)

$$ {p_{ m{l}}} = - { ho _{ m{l}}}frac{{partial {phi _{ m{l}}}}}{{partial t}} + { ho _{ m{l}}}{A_0}cos left( {omega t} ight)r + {X_1} $$

(20)

$$ nabla cdot {{boldsymbol{psi}} _{ m{l}}} = 0 $$

(21)

$$ frac{{partial {{boldsymbol{psi}} _{ m{l}}}}}{{partial t}} + {nu _{{ m{eff}}}}{nabla ^2} times {{boldsymbol{psi}} _{ m{l}}} = {boldsymbol{0}} $$

(22)

其中$ {X_1} $是积分常数, ν_eff = μ_eff/ρ_l为液滴的有效运动黏度. 在球坐标系下的Laplace方程的通解形式为

$$ {phi _l} = sumlimits_{l = 2}^{ + infty } {sumlimits_{m = 0}^l {left( {B{r^l} + frac{C}{{{r^{l + 1}}}}} ight){ m{Y}}_l^mleft( {theta,varphi } ight)} } $$

(23)

考虑到在$ r to 0 $时, $ {phi _{
m{l}}} $应为一有限值, 并将$ {phi _{
m{l}}} $写成Floquet解的Fourier展开

$$ {phi _{ m{l}}} = sumlimits_{l = 2}^{ + infty } {sumlimits_{m = 0}^l {sumlimits_{n = 0}^{ + infty } {{B_n}{{ m{e}}^{{zeta _n}t}}{r^l}{ m{Y}}_l^mleft( {theta,varphi } ight)} } } $$

(24)

而$ {{boldsymbol{psi}} _{
m{l}}} $是无散度的矢量场, 可以用单变量的标量函数$ {psi _{
m{l}}}left( r
ight) $表示成以下形式^[15]

$$ {psi _{{ m{l}}r}} = sumlimits_{l = 2}^{ + infty } {sumlimits_{m = 0}^l {sumlimits_{n = 0}^{ + infty } {{{ m{e}}^{{zeta _n}t}}frac{{lleft( {l + 1} ight)}}{{{r^2}}}{psi _{ m{l}}}left( r ight){ m{Y}}_l^mleft( {theta,varphi } ight)} } } $$

(25)

$$ {psi _{{ m{l}}theta }} = sumlimits_{l = 2}^{ + infty } {sumlimits_{m = 0}^l {sumlimits_{n = 0}^{ + infty } {{{ m{e}}^{{zeta _n}t}}frac{1}{r}frac{{{ m{d}}{psi _{ m{l}}}left( r ight)}}{{{ m{d}}r}}frac{{partial { m{Y}}_l^mleft( {theta,varphi } ight)}}{{partial theta }}} } } $$

(26)

$$ {psi _{{ m{l}}varphi }} = sumlimits_{l = 2}^{ + infty } {sumlimits_{m = 0}^l {sumlimits_{n = 0}^{ + infty } {{{ m{e}}^{{zeta _n}t}}frac{1}{{rsin theta }}frac{{{ m{d}}{psi _{ m{l}}}left( r ight)}}{{{ m{d}}r}}frac{{partial { m{Y}}_l^mleft( {theta,varphi } ight)}}{{partial varphi }}} } } $$

(27)

将方程(22)用$ {{boldsymbol{psi}} _{
m{l}}} $的标量函数$ {psi _{
m{l}}}left( r
ight) $表示, 得到

$$ frac{{{{ m{d}}^2}{psi _{ m{l}}}left( r ight)}}{{{ m{d}}{r^2}}} + left[ {q_n^2 - frac{{lleft( {l + 1} ight)}}{{{r^2}}}} ight]{psi _{ m{l}}}left( r ight) = 0 $$

(28)

式(28)是一个Raccati?Bessel函数, 其通解满足

$$ {psi _{ m{l}}}left( r ight) = sumlimits_{l = 2}^{ + infty } {sumlimits_{m = 0}^l {sumlimits_{n = 0}^{ + infty } {{C_n}{r^{{1 / 2}}}{{ m{J}}_{l + tfrac{1}{2}}}left( {{ m{i}}{q_n}r} ight)} } } $$

(29)

式中, $ {{
m{J}}_{l + tfrac{1}{2}}} $为$ l + dfrac{1}{2} $阶Bessel函数, $ {q_n} = sqrt {{{{zeta _n}} / {{nu _{{
m{eff}}}}}}} $, $ {B}_{n}, ;{C}_{n} $为积分常数. 将式(24) ~ 式(27)代入式(14)和式(15)中, 得到

$$ frac{{{{ m{d}}^2}{psi _{ m{l}}}left( r ight)}}{{{ m{d}}{r^2}}} - frac{2}{r}frac{{{ m{d}}{psi _{ m{l}}}left( r ight)}}{{{ m{d}}r}} + frac{{lleft( {l + 1} ight)}}{{{r^2}}}{psi _{ m{l}}}left( r ight) + 2left( {l - 1} ight){B_n}{r^{l - 1}} = 0 $$

(30)

将式(29)代入式(30)中, 得到两个常数之间的关系

$$ {C_n} = - frac{{2left( {l - 1} ight){R^{l - 1}}}}{{left[ {2left( {{l^2} - 1} ight) - {x^2}} ight]{R^{ - 3/2}}{{ m{J}}_{l + tfrac{1}{2}}}left( x ight) + 2x{R^{ - 3/2}}{{ m{J}}_{l + tfrac{3}{2}}}left( x ight)}}{B_n} $$

(31)

上式利用了Bessel函数的递推关系$ x{{
m{J}}_{l - tfrac{1}{2}}}left( x
ight) + $$ x{{
m{J}}_{l + tfrac{3}{2}}}left( x
ight) = left( {2l + 1}
ight){{
m{J}}_{l + tfrac{1}{2}}}left( x
ight) $, 且$ x = {
m{i}}{q_n}R $. 将式(24)?~?式(27)及式(29)代入运动学边界条件式(12)中, 得到

$$ {zeta _n}{eta _n} = {B_n}l{R^{l - 1}} + lleft( {l + 1} ight){C_n}{R^{ - 3/2}}{{ m{J}}_{l + tfrac{1}{2}}}left( x ight) $$

(32)

联立式(31)和式(32), 得到

$$ {B_n} = frac{{{eta _n}{zeta _n}}}{{l{R^{l - 1}}}}left[ {1 + frac{{2left( {{l^2} - 1} ight)}}{{2x{Q_{l + tfrac{1}{2}}}left( x ight) - {x^2}}}} ight] $$

(33)

$$ {C_n} = - frac{{2left( {l - 1} ight){eta _n}{zeta _n}{R^{3/2}}}}{{lleft[ {2x{{ m{J}}_{l + tfrac{3}{2}}}left( x ight) - {x^2}{{ m{J}}_{l + tfrac{1}{2}}}left( x ight)} ight]}} $$

(34)

其中, ${Q_{l + tfrac{1}{2}}}left( x
ight)={{
m{J}}_{l + tfrac{3}{2}}}left( x
ight) Bigr/ {{
m{J}}_{l + tfrac{1}{2}}}left( x
ight)$. 将式(33)代入式(24)后并将整体代入式(20)中, 得到p_l的表达式

$$ begin{split} &{p_{ m{l}}} = sumlimits_{l = 2}^{ + infty } {sumlimits_{m = 0}^l {sumlimits_{n = 0}^{ + infty } { - frac{{{ ho _{ m{l}}}{eta _n}zeta _n^2}}{{l{R^{l - 1}}}}left[ {1 + frac{{2left( {{l^2} - 1} ight)}}{{2x{Q_{l + tfrac{1}{2}}}left( x ight) - {x^2}}}} ight]} } } {{ m{e}}^{{zeta _n}t}}{r^l}{ m{Y}}_l^m + & qquad { ho _{ m{l}}}{A_0}rcos left( {omega t} ight) + {X_1} [-10pt] end{split} $$

(35)

因为假设气体是无黏的, 因此其速度场满足势函数

$$ {{boldsymbol{u}}_{ m{g}}} = nabla {phi _{ m{g}}} $$

(36)

将式(36)代入气相的控制方程(5)和(6)中, 得到

$$ {nabla ^2}{phi _{ m{g}}} = 0 $$

(37)

$$ {p_{ m{g}}} = - { ho _{ m{g}}}frac{{partial {phi _{ m{g}}}}}{{partial t}} + { ho _{ m{g}}}{A_0}rcos left( {omega t} ight) + {X_2} $$

(38)

其中X₂是积分常数. 考虑到r→∞时${phi _{
m{g}}} to {
m{const}}.$ 则${phi _{
m{g}}}$的通解满足

$$ {phi _{ m{g}}} = sumlimits_{l = 2}^{ + infty } {sumlimits_{m = 0}^l {sumlimits_{n = 0}^{ + infty } {{D_n}{{ m{e}}^{{zeta _n}t}}{r^{ - left( {l + 1} ight)}}{ m{Y}}_l^mleft( {theta,varphi } ight)} } } $$

(39)

其中$ {D_n} $是积分常数, 可通过运动边界条件确定. 将式(39)代入式(13)中, 得到$ {D_n} $的表达式为

$$ {D_n} = - frac{{{zeta _n}{eta _n}{R^{l + 2}}}}{{l + 1}} $$

(40)

将式(40)代入式(38)和式(39)中, 得到p_g的表达式

$$ begin{split}& {p_{ m{g}}} = sumlimits_{l = 2}^{ + infty } {sumlimits_{m = 0}^l {sumlimits_{n = 0}^{ + infty } {frac{{{ ho_{ m{g}}}zeta _n^2{eta _n}{R^{l + 2}}}}{{l + 1}}} } } {{ m{e}}^{{zeta _n}t}}{r^{ - left( {l + 1} ight)}}{ m{Y}}_l^m + &qquad { ho _{ m{g}}}{A_0}rcos left( {omega t} ight) + {X_2} end{split} $$

(41)

将式(35)和式(41)代入式(16), 得到

$$ begin{split}&sumlimits_{l = 2}^{ + infty } {sumlimits_{m = 0}^l {mathop sum limits_{n = 0}^{ + infty } } } left{ {left[ { - left( {frac{{{ ho _{ m{l}}}}}{l} + frac{{{ ho _{ m{g}}}}}{{l + 1}}} ight)Rzeta _n^2 + 2{mu _{{ m{eff}}}}{zeta _n}frac{{l - 1}}{{lR}}} ight.} ight.&qquadleft. {frac{{left( {2l + 1} ight)x - 2lleft( {l + 2} ight){Q_{l + frac{1}{2}}}left( x ight)}}{{2{Q_{l + frac{1}{2}}}left( x ight) - x}} - frac{{sigma left( {l - 1} ight)left( {l + 2} ight)}}{{{R^2}}}} ight]{eta _n} + &qquadleft. {frac{1}{2}left( {{ ho _{ m{l}}} - { ho _{ m{g}}}} ight){A_0}left( {{eta _{n - 1}} + {eta _{n + 1}}} ight)} ight}{{ m{e}}^{{zeta _n}t}}{ m{Y}}_l^m + & qquadleft( {{ ho _{ m{l}}} - { ho _{ m{g}}}} ight){A_0}cos left( {omega t} ight)R + {X_1} - {X_2} - frac{{2sigma }}{R} = 0end{split}$$

(42)

注意到在式(42)中, 除了第一项外, 其余项与球谐函数的参数l, m和Fourier模态的阶数n无关. 因此, 若要式(42)对于任何l, m及n等于零恒成立, 需要满足

$$ begin{split}& left[ { - left( {frac{{{ ho _{ m{l}}}}}{l} + frac{{{ ho _{ m{g}}}}}{{l + 1}}} ight)Rzeta _n^2 + 2{mu _{{ m{eff}}}}{zeta _n}frac{{l - 1}}{{lR}}frac{{left( {2l + 1} ight)x - 2lleft( {l + 2} ight){Q_{l + {textstyle{1 over 2}}}}left( x ight)}}{{2{Q_{l + {textstyle{1 over 2}}}}left( x ight) - x}} - } ight.& qquadleft. {frac{{sigma left( {l - 1} ight)left( {l + 2} ight)}}{{{R^2}}}} ight]{eta _n} + frac{1}{2}left( {{ ho _{ m{l}}} - { ho _{ m{g}}}} ight){A_0}left( {{eta _{n - 1}} + {eta _{n + 1}}} ight) = 0end{split} $$

(43)

$$ left( {{ ho _{ m{l}}} - { ho _{ m{g}}}} ight){A_0}cos left( {omega t} ight)R + {X_1} - {X_2} - frac{{2sigma }}{R} = 0 $$

(44)

而式(43)就是所需要的色散方程.

2.
线性稳定性分析

将色散方程(43)中的系数化为无量纲的形式

$$ frac{{ {4hat zeta _n^2 + c{{hat zeta }_n} + lambda } }}{q}{eta _n} - {eta _{n - 1}} - {eta _{n + 1}} = 0 $$

(45)

其中

$$ lambda = frac{{4sigma left( {l - 1} ight)lleft( {l + 1} ight)left( {l + 2} ight)}}{{left[ {{ ho _{ m{l}}}left( {l + 1} ight) + { ho _{ m{g}}}l} ight]{R^3}{omega ^2}}} $$

(46)

$$ q = frac{{2left( {{ ho _{ m{l}}} - { ho _{ m{g}}}} ight)lleft( {l + 1} ight){A_0}}}{{left[ {{ ho _{ m{l}}}left( {l + 1} ight) + { ho _{ m{g}}}l} ight]R{omega ^2}}} $$

(47)

$$ c = frac{{8{mu _{{ m{eff}}}}}}{omega }frac{{{l^2} - 1}}{{left[ {{ ho _{ m{l}}}left( {l + 1} ight) + { ho _{ m{g}}}l} ight]{R^2}}}frac{{left( {2l + 1} ight)x - 2lleft( {l + 2} ight){Q_{l + frac{1}{2}}}left( x ight)}}{{x - 2{Q_{l + frac{1}{2}}}left( x ight)}} $$

(48)

$$ {hat zeta _n} = frac{{{zeta _n}}}{omega } $$

(49)

式中λ和q可分别视为是无量纲的激励频率的倒数和无量纲的受迫加速度, c可以用来表征黏度的影响^[30].

当时, l $gg $ 1有如下Bessel函数的渐进展开式

$$ {{ m{J}}_l}left( x ight) = frac{{{{ m{e}}^l}{{left( {tfrac{1}{2}x} ight)}^l}}}{{{{left( {2{text{π}} l} ight)}^{{1 / 2}}}{l^l}}}left[ {1 + Oleft( {{l^{ - 1}}} ight)} ight] $$

(50)

此时$ {Q_l}left( x
ight) $可化简为

$$ begin{split}& {Q_l}left( x ight) = {{{{ m{J}}_{l + 1}}left( x ight)} / {{{ m{J}}_l}left( x ight)}} simeq {{frac{{{{ m{e}}^{l + 1}}{{left( {tfrac{1}{2}x} ight)}^{l + 1}}}}{{{{left[ {2{text{π}} left( {l + 1} ight)} ight]}^{{1 / 2}}}{{left( {l + 1} ight)}^{l + 1}}}}} Biggr/ {frac{{{{ m{e}}^l}{{left( {tfrac{1}{2}x} ight)}^l}}}{{{{left( {2{text{π}} l} ight)}^{{1 / 2}}}{l^l}}}}} = & qquad frac{{{ m{e}}x}}{{2l}} {left( {frac{l}{{l + 1}}} ight)^{l + 1+ frac{1}{2}}} approx frac{x}{{2l}} [-15pt]end{split} $$

(51)

此时c可近似为

$$ c simeq frac{{8{mu _{{ m{eff}}}}}}{{left( {{ ho _{ m{l}}} + { ho _{ m{g}}}} ight)omega }}{left( {frac{l}{R}} ight)^2} $$

(52)

随着时间的发展, 如果在液滴表面的扰动幅值一直保持相同的大小, 就称基本流是中性稳定的. 此时, 增长率$; beta = 0 $, 式(45)退化为

$$ frac{{left[ { - 4{{left( {hat gamma + n} ight)}^2} + { m{i}}cleft( {hat gamma + n} ight) + lambda } ight]}}{q}{eta _n} - {eta _{n - 1}} - {eta _{n + 1}} = 0 $$

(53)

根据方程(53), 取多个q的值, 得到一系列对应的λ, 根据这些(q, λ)的点集做出的曲线即为中性稳定曲线.

2.1
中性稳定曲线

因为本文的研究对象为非牛顿液滴, 因此这里我们主要考虑流变参数对稳定性的影响, 即: 零剪切黏度μ₀、应力松弛时间λ₁和应变驰豫时间λ₂. 为尽量贴近黏弹性液滴的实验工况和物性参数, 在这里取一组典型的实验工况. 取液滴的半径为R = 5 × 10^?4 m, 所施加的振荡频率为ω = 5 × 10⁵ rad/s, 参照Brenn和Teichtmeister^[32]所用的实验工质, 取质量分数为0.8%的普立清2500溶液, 其密度ρ_l = 1000.9 kg/m³, 表面张力系数σ = 0.07555 N/m,零剪切黏度μ₀ = 0.7588 Pa·s, 应力松弛时间λ₁ = 0.163 s. 在文献中并没有给出λ₂的取值, 参考Li等^[33]的做法, 取$lambda _2 $ = $lambda _1 $/10, 并令$mu _0 $ = $mu _0^* $ = 0.7588 Pa·s, $lambda _1 $ = $lambda _1^* $ = 0.163 s, $lambda _2 $ = $lambda _2^* $ = 0.0163 s为基本工况. 因为明确了要将μ₀ = 0.7588 Pa·s代入计算, 在这里c的取值就不同于参考文献[30]中直接给定的方式. 在这里取球波数l为20, 代入式(53)中, 再结合零剪切黏度、密度等参数即可确定c的值.

根据基本工况的参数中性稳定曲线的计算结果如图2所示. 在图2中, 实线表示谐波不稳定区域, 虚线表示亚谐波不稳定区域. 在基本工况下, 第一亚谐波不稳定区域位于$ lambda - q $平面的第4象限. 根据$ lambda $和q的定义不可能为负值, 所以认为在这种条件下第一亚谐波区域是稳定的. 不同于无阻尼项的Mathieu方程, 在这里不稳定区域左侧靠近$ lambda $轴的部分变得光滑, 且随着特征指标$ gamma $的增加, 距离$ lambda $轴越来越远. 图中红色实心圆点代表中性稳定曲线上q的值最小的点, 即其横坐标表示整条曲线上的q_min. 根据q的定义, 在波数l确定的情况下, q可以表征振荡幅值的大小, 因此曲线上q最小的点代表使不稳定发生的最小的受迫加速度幅值. 在图2所示的3个不稳定区域中, 随着$ gamma $的增加, q_min逐渐增大, 意味着若要在液滴表面激发出更高阶的不稳定需要更大的受迫加速度. 因此在下面的讨论中, 仅研究第一谐波不稳定区域的特征.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2020-416-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
基本工况条件下的中性稳定曲线(ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, μ₀ = 0.758 8 Pa·s, λ₁ = 0.163 s, λ₂ = 0.016 3 s)



Figure
2.
Neutral stability curve under base case condition (ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, μ₀ = 0.758 8 Pa·s, λ₁ = 0.163 s, λ₂ = 0.016 3 s)



下载:
全尺寸图片
幻灯片


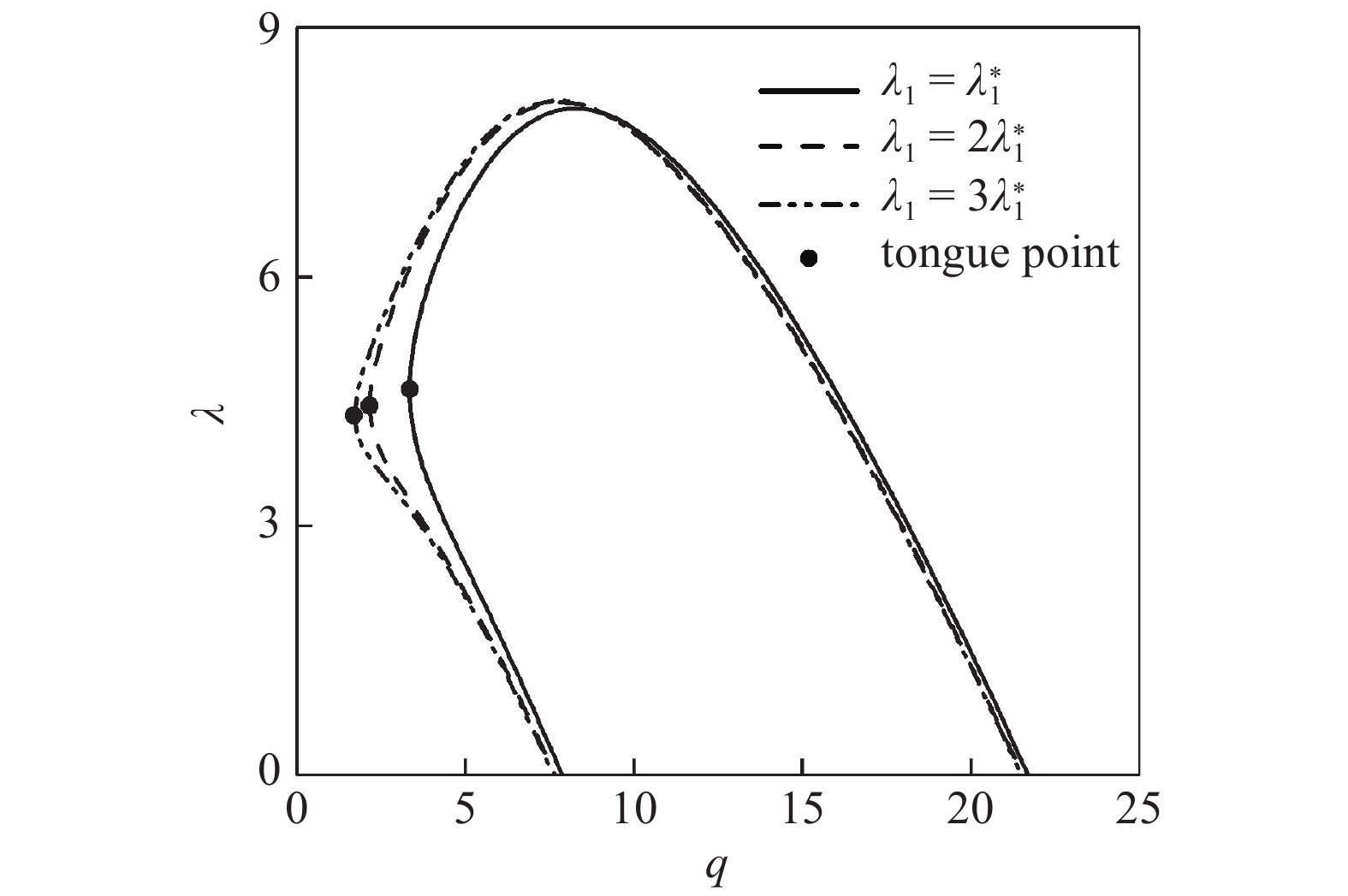
图3给出了不同零剪切黏度条件下第一谐波区域的中性稳定曲线. 随着零剪切黏度逐渐增大, 对应的不稳定区域在缩小, 不稳定舌尖变得越来越光滑, 且q_min值在逐渐增大, 这意味着随着液滴零剪切黏度的逐渐增加, 整体的稳定性增强, 激励幅值要响应提高才能使液滴发生谐波模式的振荡. 图4显示了不同应力松弛时间条件下液滴的中性稳定曲线. 当应力松弛时间逐渐增大时, 第一谐波区域的q_min值逐渐减小, 表现为液滴的不稳定性增加.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2020-416-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
不同零剪切黏度下的中性稳定曲线(ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, $mu_0^* $ = 0.7588 Pa·s, λ₁ = 0.163 s, λ₂ = 0.0163 s)



Figure
3.
Neutral stability curve under different zero-shear viscosity conditions (ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, $mu_0^* $ = 0.7588 Pa·s, λ₁ = 0.163 s, λ₂ = 0.0163 s)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2020-416-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
不同应力松弛时间下的中性稳定曲线(ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, μ₀ = 0.758 8 Pa·s, $lambda_1^* $ = 0.163 s, λ₂ = 0.0163 s)



Figure
4.
Neutral stability curve under different stress relaxation time conditions (ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, μ₀ = 0.7588 Pa·s, $lambda_1^* $ = 0.163 s, λ₂ = 0.0163 s)



下载:
全尺寸图片
幻灯片


图5计算了当应变驰豫时间改变时的中性稳定曲线. 当λ₂逐渐增加时, 中性稳定曲线向右收缩, 且q_min值逐渐增大, 其变化与零剪切黏度的变化趋势相同. 虽然在前人的研究中^[34], 与应力松弛时间相比, 应变驰豫时间对流动稳定性的影响不大, 但在这里却显示改变应变驰豫时间获得了更为明显的变化, 推测是因为在本文中, 基本情况的λ₂取得较小, 因此成倍地改变λ₂影响较为显著.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2020-416-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
不同应变驰豫时间下的中性稳定曲线(ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, μ₀ = 0.758 8 Pa·s, λ₁ = 0.163 s, $lambda_2^* $ = 0.016 3 s)



Figure
5.
Neutral stability curve under different deformation retardation time conditions (ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³,σ = 0.07555 N/m, μ₀ = 0.758 8 Pa·s, λ₁ = 0.163 s, $lambda_2^* $ = 0.016 3 s)



下载:
全尺寸图片
幻灯片

2.2
增长率曲线

在式(46)和式(47)中, q和λ里均含有球波数l, 如果给定一个l的值, 在一种确定的试验条件下, q和λ的值是确定的. 因此, 将球波数l固定为一个常数, 受迫振荡频率ω改变, 这导致λ随之变化, 在这里, 固定A₀的值, 使得q随着ω的变化而变化. 首先作出在不同加速度振荡幅值A₀条件下的增长率如图6所示. 对于一个确定的A₀, 在一特定的频率段内, 增长率呈阶梯状, 随着激励频率的增加, 增长率的值逐渐减小. 这相当于激励频率有一个阈值ω_cr, 当ω > ω_cr时, 液滴才会不稳定, 且增长率会迅速增加到最大值; 而超过这个阈值再进一步增加振荡频率, 液滴虽然还是不稳定的, 但其表面波的增长却在逐渐衰减.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2020-416-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
不同加速度振荡幅值条件下增长率随振荡频率的变化(ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, μ₀ = 0.7588 Pa·s, λ₁ = 0.163 s, λ₂ = 0.0163 s, l =20)



Figure
6.
The variation of growth rate versers oscillation frequency under different acceleration conditions (ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, μ₀ = 0.7588 Pa·s, λ₁ = 0.163 s, λ₂ = 0.0163 s, l =20)



下载:
全尺寸图片
幻灯片


为更好地理解图6, 这里要引入一个“三次方曲线”的概念: 在ρ_g→0的假设下, λ与q可通过消去l联系起来, 得到

$$ lambda = frac{{sigma {omega ^4}}}{{4{ ho _{ m{l}}}A_0^3}}qleft( {q - frac{{2{A_0}}}{{R{omega ^2}}}} ight)left( {q + frac{{4{A_0}}}{{R{omega ^2}}}} ight) $$

(54)

对于一种特定的实验工况, 可通过式(54)在λ?q平面上得到对应的曲线, 因λ是与q成三次方关系的, 所以这类曲线就叫三次方曲线^[30].

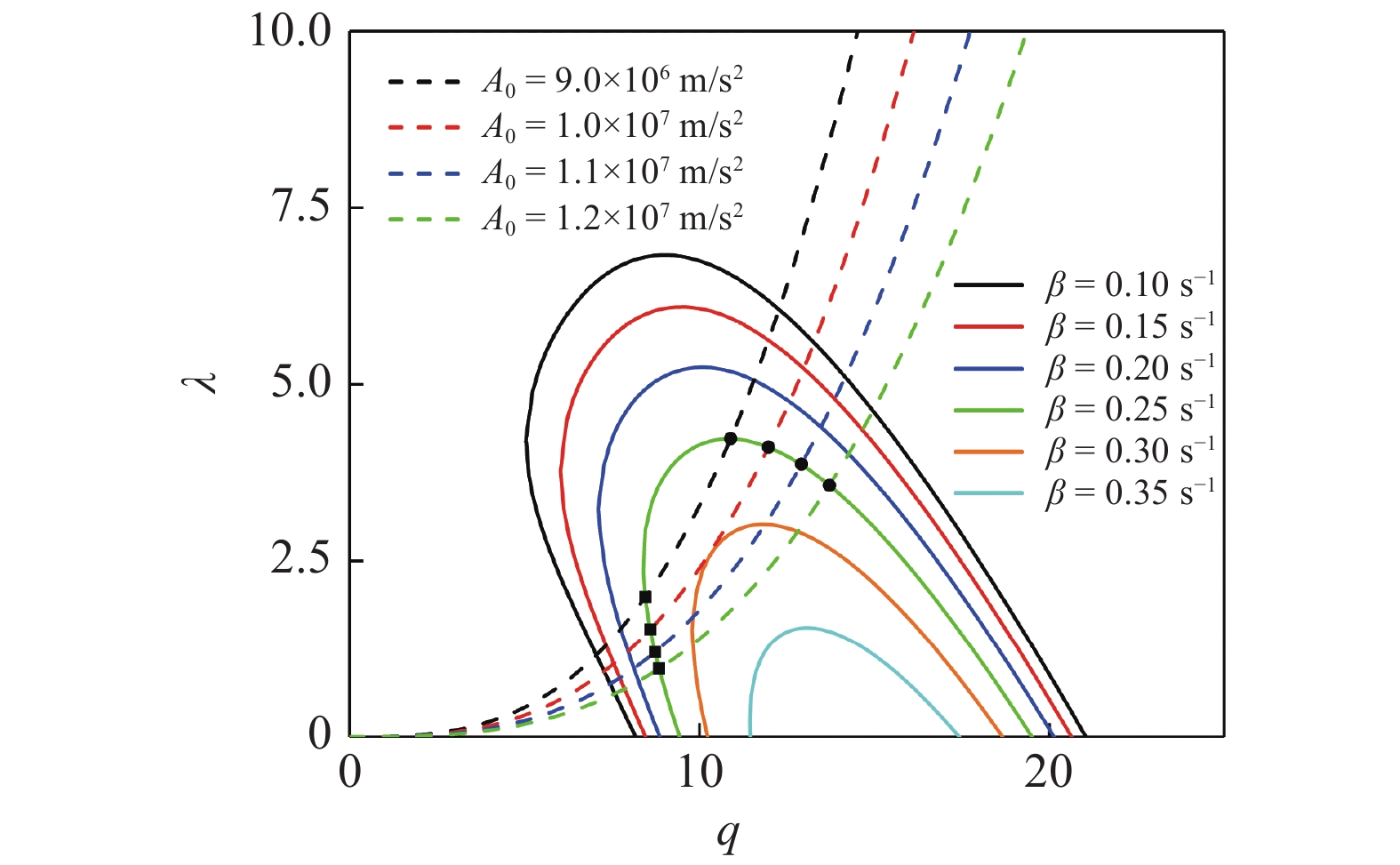
在图7中, 4条曲线是根据式(54)做出的不同振荡幅值的三次方曲线. 实线表示给定增长率的轮廓线, 这类似于图2中第一谐波区域中性稳定曲线的作图过程, 只不过是β不再视为零而取一些特定的值, 这表示特定增长率的轮廓线. 随着振荡幅值的增加, 虚线与不稳定区域相交的部分也越来越宽, 这表示不稳定也更容易发生. 以增长率为0.25的绿色轮廓线为例, 4条三次方曲线与该轮廓线的交点分别用黑色实心圆点和黑色实心方点标出, 方点表示三次方曲线进入轮廓线时的交点, 而圆点表示穿出轮廓线时的交点. 可发现无论是圆点还是方点, 随着加速度振荡幅值的增大, 黑色点的纵坐标都是逐渐减小的. 联系公式(46), 纵坐标λ可表征无量纲激励频率平方的倒数, 纵坐标的逐渐减小代表激励频率逐渐增大, 这也就解释了图6中所呈现的振荡幅值增大, 使液滴发生不稳定的振荡频率也相应增大.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2020-416-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
不同振荡幅值的三次方曲线与第一谐波不稳定区域轮廓线相交(ρ_l = 1000.9 kg/m³, ρ_g = 0 kg/m³, σ = 0.07555 N/m, μ₀ = 0.7588 Pa·s, λ₁ = 0.163 s, λ₂ = 0.0163 s, l = 20)



Figure
7.
The intersection of different oscillation amplitude cubic curves with the contours of the first harmonic instability region (ρ_l = 1000.9 kg/m³, ρ_g = 0 kg/m³, σ = 0.07555 N/m, μ₀ = 0.7588 Pa·s, λ₁ = 0.163 s, λ₂ = 0.0163 s, l = 20)



下载:
全尺寸图片
幻灯片


图8显示了球波数l对液滴增长率的影响, 在这里及以下的计算中, 设置A₀ = 30 m/s². 随着球波数l的增加, 液滴的最大增长率减小, 且使液滴不稳定的振荡频率升高. 在图9中, 定义$; mu _0^* = 0.758;8; {
m{Pa}} cdot {
m{s}} $, 分别减小和增大零剪切黏度的值, 观察其随着受迫频率的变化. 零剪切黏度增加时, 激励液滴不稳定的频率值ω_cr减小, 且最大增长率减小, 抑制了扰动的增长, 这与前面对于中性稳定曲线的分析是一致的.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2020-416-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
不同球波数l条件下增长率随振荡频率的变化(ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, μ₀ = 0.7588 Pa·s, λ₁ = 0.163 s, λ₂ = 0.0163 s, A₀ = 30 m/s²)



Figure
8.
The variation of growth rate versers oscillation frequency under different spherical wavenumber conditions (ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, μ₀ = 0.7588 Pa·s, λ₁ = 0.163 s, λ₂ = 0.0163 s, A₀ = 30 m/s²)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2020-416-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
不同零剪切黏度条件下增长率随振荡频率的变化(ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, λ₁ = 0.163 s, λ₂ = 0.0163 s, A₀ = 30 m/s², l = 20)



Figure
9.
The variation of growth rate versers oscillation frequency under different zero-shear viscosity conditions (ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, λ₁ = 0.163 s, λ₂ = 0.0163 s, A₀ = 30 m/s², l = 20)



下载:
全尺寸图片
幻灯片


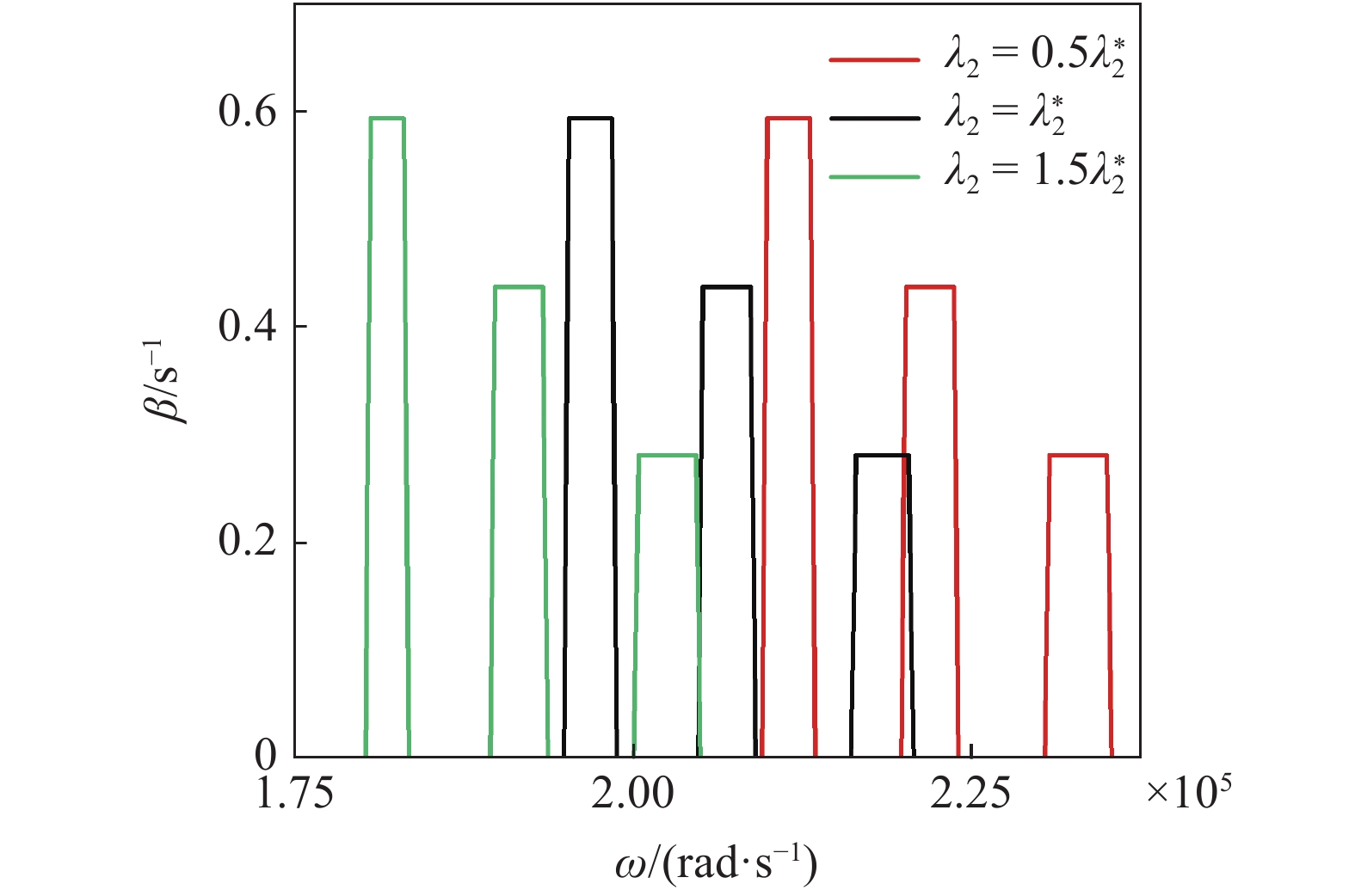
图10体现了应力松弛时间增加时, ω_cr逐渐增大. λ₁表征流体弹性的大小, 应力松弛时间越大, 液滴更容易发生失稳, 因此体现在图10中为λ₁大的情况, 最大增长率也较大. 图11显示了应变驰豫时间增加时, ω_cr逐渐减小. 在这里λ₂的变化趋势与零剪切黏度改变时对增长率的影响类似, 这与在分析中性稳定曲线时是相似的. 这是因为在式(10)中, μ₀和λ₂都是位于分子位置的, 改变μ₀或λ₂时对μ_eff的影响是同方向的, 这也就呈现在增长率或中性稳定曲线的结果中.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2020-416-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
不同应力松弛条件下增长率随振荡频率的变化(ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, μ₀ = 0.7588 Pa·s, λ₂ = 0.0163 s, A₀ = 30 m/s², l = 20)



Figure
10.
The variation of growth rate versers oscillation frequency under different stress relaxation time conditions (ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, μ₀ = 0.7588 Pa·s, λ₂ = 0.0163 s, A₀ = 30 m/s², l = 20)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2020-416-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
不同应变驰豫时间条件下增长率随振荡频率的变化(ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, μ₀ = 0.7588 Pa·s, λ₁ = 0.163 s, A₀ = 30 m/s², l = 20)



Figure
11.
The variation of growth rate versers oscillation frequency under different deformation retardation time conditions (ρ_l = 1000.9 kg/m³, ρ_g = 1.225 kg/m³, σ = 0.07555 N/m, μ₀ = 0.7588 Pa·s, λ₁ = 0.163 s, A₀ = 30 m/s², l = 20)



下载:
全尺寸图片
幻灯片

3.
结 论

本文通过分析在不同黏弹性参数下液滴中性稳定曲线和增长率的变化趋势, 可以得到以下几点结论:

(1) 若要在液滴表面激发出更高阶的不稳定, 需要更大的受迫加速度;

(2) 零剪切黏度和应变驰豫时间的增加, 使整体稳定性增强, 若要使液滴发生谐波模式的不稳定需要提高振荡幅值; 应力松弛时间的增加则会促进液滴的不稳定性;

(3) 在一定振荡幅值情况下, 不同振荡频率具有不同的扰动增长率, 且随着振荡频率的增加, 增长率的值逐渐减小;

(4) 与中性稳定曲线分析的结果类似, 增加液滴的零剪切黏度和应变驰豫时间使液滴的最大增长率减小, 同时, 增加液滴的球波数也具有相同的效果; 应力松弛时间增加, 最大增长率增加.