删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

可压缩两相流固耦合模型的间断Galerkin有限元方法

本站小编 Free考研考试/2022-01-01


引言


深入探索多孔介质中多相流动和固体变形特征对精准认识地下资源开发利用, 例如石油勘探开发、煤层气和页岩气开采、二氧化碳地质封存等领域, 具有重要的工程意义[1-4]. 在流体输送过程中局部压力和饱和度梯度下的渗流作用改变了孔隙结构特征, 打破了储层内部的水力平衡; 固体空间结构的变化影响了储层内部流体的运移路径和流通能力, 具体表现为多孔介质孔隙度和渗透率等物性参数的动态响应. 发展和建立两相渗流与固体变形耦合模型及其相应的数值方法是准确描述和阐明储层内水力行为的有效手段[5-7].

针对两相渗流和固体变形耦合模型的数值方法主要包括有限元法[8-10]、有限体积法[11-12]以及混合计算方法[13-14]等. 对于两相流问题的离散和数值求解, 传统有限元能够确保流体域内整体的质量平衡, 但是无法实现流体在跨越单元间的局部质量平衡, 因此不适用于求解对流占主导的非线性不混溶问题; 有限体积法在确保局部流量平衡的同时, 具有较高的计算效率, 因此在工业界和工程尺度模拟中得到了广泛应用. 在通常情况下, 有限体积方法的计算结果仅能满足低阶有效精度; 混合计算方法是指对流体和力学控制方程分别利用不同的数值方法进行求解, 该方法集成了各种数值方法的优势. Rutqivst[15]在耦联流体软件TOUGH2和固体变形软件FLAC3D的基础上, 开发了在油气、地热、可燃冰开采以及二氧化碳地质封存等领域广泛使用的TOUGH-FLAC耦合模拟器. 在此模拟器中, 负责流体计算的TOUGH2软件采用的是有限体积法, FLAC3D采用有限差分法计算固体变形, 此方法在网格划分和数据传递效率等方面具有一定的局限性.

间断伽辽金有限元(discontinuous Galerkin finite element method, DG-FEM)结合了有限体积与有限元两种方法的优点, 具有高阶精度和局部单元物理守恒性的特点, 容易实现局部网格加密和各单元多项式的单独选取[16-19]. 近些年来, DG-FEM在流体和弹性力学领域得到了广泛的关注和持续的发展[20-22]. Klieber和Riviere[23]在解耦两相渗流微分方程组的基础上, 提出了不可压缩两相流自适应间断有限元方法. Epshteyn和Rivière[24]提出了多孔介质不可压缩两相流完全隐式方程的不连续伽辽金方法, 该方法在结构化和非结构化网格计算中都具有较好的鲁棒性. 李子然和吴长春[25]、陈韵骋等[26]建立了基于线弹性力学问题的局部间断有限元方法. 在流固耦合方面, Liu等[27-28]提出了连续和间断伽辽金耦合框架, 利用自适应加罚方法提高间断伽辽金有限元方法在模拟大型多孔弹性问题时的适用性和计算效率, 并将此方法推广至多孔介质水力压裂模拟中. 目前关于间断伽辽金有限元方法在计算可压缩两相流固模型方面的研究鲜有报道, 还有待进一步深入研究.

基于上述认识, 本文首先建立可压缩两相流固耦合控制方程, 其中包括考虑毛细压力和重力作用的可压缩两相渗流方程以及线性多孔弹性方程. 在此基础上, 推导出流固耦合方程的间断伽辽金弱形式; 然后, 通过一维Terzaghi流固问题验证模型的准确性; 最后, 分别开展二维平面应变条件下和考虑重力效应的三维流固数值算例, 分析流体压力、饱和度以及固体应力、位移的分布特征, 探讨加罚因子对模拟结果的影响.


1.
两相流固耦合控制方程



1.1
两相渗流方程


假设模型中湿润相和非湿润相为不混溶流体, 两者在多孔介质中的流速满足达西定律. 在考虑毛细压力、重力效应和固体变形的基础上, 等温可压缩两相渗流控制方程可表示为[2, 29]







$$begin{split}&phi {S_{{
m{nw}}}}{
ho _{{
m{nw}}}}{C_{{
m{nw}}}}frac{{partial {p_{{
m{nw}}}}}}{{partial t}} - phi {
ho _{{
m{nw}}}}frac{{partial {S_{
m{w}}}}}{{partial t}} + {S_{{
m{nw}}}}{
ho _{{
m{nw}}}}frac{{partial {varepsilon _{
m{v}}}}}{{partial t}} + &qquadnabla cdot left[ { - {
ho _{{
m{nw}}}}frac{{{boldsymbol{k}}{k_{{
m{rnw}}}}}}{{{mu _{{
m{nw}}}}}}left( {nabla {p_{{
m{nw}}}} + {
ho _{{
m{nw}}}}{boldsymbol{g}}}
ight)}
ight] = {Q_{{
m{nw}}}}end{split}$$
(1)







$$begin{split}&phi {S_{
m{w}}}{
ho _{
m{w}}}{C_{
m{w}}}frac{{partial {p_{{
m{nw}}}}}}{{partial t}} + left( {phi {
ho _{
m{w}}} - phi {S_{
m{w}}}{
ho _{
m{w}}}{C_{
m{w}}}left| {{p_{
m{c}}}}
ight|}
ight)frac{{partial {S_{
m{w}}}}}{{partial t}}+&qquad {S_{
m{w}}}{
ho _{
m{w}}}frac{{partial {varepsilon _{
m{v}}}}}{{partial t}} + nabla cdot [ - {
ho _{
m{w}}}frac{{{boldsymbol{k}}{k_{{
m{rw}}}}}}{{{mu _{
m{w}}}}}(nabla {p_{{
m{nw}}}} - left| {{p_{
m{c}}}}
ight|nabla {S_{
m{w}}}+ &qquad {
ho _{
m{w}}}{boldsymbol{g}})] = {Q_{
m{w}}}end{split}$$
(2)

式中, 下标$;beta; 为;{
m{w}}$和$ {
m{n}}{
m{w}} $分别表示湿润相和非湿润相, $ {S}_{beta } $为饱和度, $; {
ho }_{beta } $和$ ;{mu }_{beta } $分别为流体密度和黏度, $ {C}_{beta } $为流体压缩系数, $ {p}_{beta } $为流体压力, $ {boldsymbol{k}} $为多孔介质绝对渗透率张量, ${k}_{{
m{r}}beta }$为相对渗透率, $ {Q}_{beta } $为源汇项, $ {varepsilon }_{
m{v}} $为体应变, $ {p}_{
m{c}} $和$ left|{p}_{
m{c}}
ight| $分别为毛细压力和毛细压力对湿相饱和度的导数.

为了求解方程, 需要补充如下辅助公式







$$ {S}_{{
m{w}}}+{S}_{{
m{n}}{
m{w}}}=1$$
(3)







$${p}_{
m{c}}={p}_{{
m{n}}{
m{w}}}-{p}_{{
m{w}}}={p}_{
m{e}}{left({S}_{
m{e}}
ight)}^{-frac{1}{lambda }}$$
(4)







$${S}_{
m{e}}=frac{{S}_{{
m{w}}}-{S}_{{
m{r}}{
m{n}}{
m{w}}}}{1-{S}_{{
m{r}}{
m{w}}}-{S}_{{
m{r}}{
m{n}}{
m{w}}}}$$
(5)

式中, $ {p}_{
m{e}} $为毛细管吸入压力, $ {S}_{
m{e}} $为有效饱和度, $ lambda $为孔径分布指数, $ {S}_{{
m{r}}{
m{w}}} $和$ {S}_{{
m{r}}{
m{n}}{
m{w}}} $分别为湿润相和非湿润相的残余饱和度.

此外, 选取Genuchten?Mualem相对渗透率模型描述湿润相和非湿润相的流通能力, 表达式如下所示[30]







$${k_{{
m{rw}}}} = left{ {begin{array}{*{20}{l}}{sqrt {{S_{
m{e}}}} {{left[ {1 - {{left( {1 - {S_{
m{e}}}^{1/omega }}
ight)}^omega }}
ight]}^2},}&{{
m{if}};{S_{
m{w}}} < 1}{1,}&{{
m{if}};{S_{
m{w}}} geqslant 1}end{array}}
ight.$$
(6)







$${k_{{
m{rnw}}}} = left{ {begin{array}{*{20}{l}}{1 - {k_{{
m{rw}}}},}&{{
m{if}};{S_{{
m{rnw}}}} = 0}{{{left( {1 - {S_{
m{e}}}}
ight)}^2}left( {1 - {S_{
m{e}}}^2}
ight),}&{{
m{if}};{S_{{
m{rnw}}}} > 0}end{array}}
ight.$$
(7)

模型的初始条件为







$$ {p}_{{
m{n}}{
m{w}}}left(x,t=0
ight)={p}_{{
m{n}}{
m{w}}0}$$
(8)







$${S}_{{
m{w}}}left(x,t=0
ight)={S}_{{
m{w}}0};;$$
(9)

模型中Dirichlet和Neumann边界条件如下所示







$${p}_{{
m{n}}{
m{w}}}left(x,t
ight)={p}_{{
m{n}}{
m{w}}}^{
m{b}}$$
(10)







$${S}_{{
m{w}}}left(x,t
ight)={S}_{{
m{w}}}^{
m{b}}$$
(11)







$${boldsymbol{lambda }}_{{
m{n}}{
m{w}}}left(nabla {p}_{{
m{n}}{
m{w}}}+{
ho }_{{
m{n}}{
m{w}}}{boldsymbol{g}}
ight)cdot {boldsymbol{n}}={g}_{{
m{n}}{
m{w}}}$$
(12)







$$ {boldsymbol{lambda }}_{{
m{w}}}left(nabla {p}_{{
m{n}}{
m{w}}}-left|{p}_{
m{c}}
ight|nabla {S}_{{
m{w}}}+{
ho }_{{
m{w}}}{boldsymbol{g}}
ight)cdot {boldsymbol{n}}={g}_{{
m{w}}} $$
(13)

式中, ${boldsymbol{lambda }}_{{
m{n}}{
m{w}}}=-{
ho }_{{
m{n}}{
m{w}}}dfrac{{boldsymbol{k}}{k}_{{
m{r}}{
m{n}}{
m{w}}}}{{mu }_{{
m{n}}{
m{w}}}}$, ${boldsymbol{lambda }}_{{
m{w}}}=-{
ho }_{{
m{w}}}dfrac{{boldsymbol{k}}{k}_{{
m{r}}{
m{w}}}}{{mu }_{{
m{w}}}}$, $ {boldsymbol{n}} $为单位法向量, $ {p}_{{
m{n}}{
m{w}}0} $和$ {p}_{{
m{n}}{
m{w}}}^{
m{b}} $分别为初始和边界上非湿润相孔隙压力, $ {S}_{{
m{w}}0} $和$ {S}_{{
m{w}}}^{
m{b}} $分别为初始和边界上湿润相饱和度, $ {g}_{{
m{w}}} $和$ {g}_{{
m{n}}{
m{w}}} $分别为边界上湿润相和非湿润相的流量.


1.2
两相渗流方程的间断伽辽金弱形式


图1为模拟几何区域、边界条件和网格示意图. 在计算域$ varOmega $中, 边界$ partial varOmega $由不与内部单元接触的外边界$ partial {varOmega }_{
m{o}} $和内部相邻单元共享的内边界$ partial {varOmega }_{
m{i}} $两部分组成. 由图1可知, 内边界$ partial {varOmega }_{
m{i}} $为相邻单元$ {E}^{+} $和$ {E}^{-} $共同拥有; 外边界$ partial {varOmega }_{
m{o}} $由Dirichlet边界$ partial {varOmega }_{{
m{o}}{
m{D}}} $和Neumann边界$ partial {varOmega }_{{
m{o}}{
m{N}}} $两者构成, 即$ partial {varOmega }_{
m{o}}=partial {varOmega }_{{
m{o}}{
m{D}}}cup partial {varOmega }_{{
m{o}}{
m{N}}} $. 设$ {cal{T}}_{
m{h}} $为$ bigcup left{E
ight} $, 是区域 $ varOmega $的正则剖分, $ partial E=partial {varOmega }_{
m{o}}cup partial {varOmega }_{
m{i}} $表示为所有边界的集合, 则间断有限元空间定义为



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-177-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
几何区域、边界条件和网格示意图



Figure
1.
Domain with boundary conditions and mesh skeleton



下载:
全尺寸图片
幻灯片








$$Qleft({cal{T}}_{
m{h}}
ight)=left{Vin {L}_{2}left(varOmega
ight):V{|}_{E}in {p}_{{
m{r}}}left(E
ight),forall Ein {cal{T}}_{
m{h}}
ight} $$
(14)

式中, 离散空间${p}_{{
m{r}}}left(E
ight)$为单元E上不超过r次的多项式的集合.

为了推导两相渗流方程的间断伽辽金弱形式, 首先在式(1)等号的两侧乘以试函数$ widetilde {{p}_{{
m{n}}{
m{w}}}} $, 并在单元计算域E内进行积分, 可得到







$$begin{split}& {int }_{E}left(phi {S}_{{
m{n}}{
m{w}}}{
ho }_{{
m{n}}{
m{w}}}{C}_{{
m{n}}{
m{w}}}dfrac{partial {p}_{{
m{n}}{
m{w}}}}{partial t}-phi {
ho }_{{
m{n}}{
m{w}}}dfrac{partial {S}_{{
m{w}}}}{partial t}
ight)widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}V+ &qquad {int }_{E}nabla cdot left[{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}left(nabla {p}_{{
m{n}}{
m{w}}}+{
ho }_{{
m{n}}{
m{w}}}{boldsymbol{g}}
ight)
ight]widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}V= &qquad {int }_{E}{Q}_{{
m{n}}{
m{w}}}widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}V end{split}$$
(15)

利用分部积分和散度定理, 式(15)中等号左侧第二项可表示为







$$begin{split}& {int }_{E}nabla cdot Big[{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}left(nabla {p}_{{
m{n}}{
m{w}}}+{
ho }_{{
m{n}}{
m{w}}}{boldsymbol{g}}
ight)Big]widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}V= &qquad {int }_{partial E}{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}left(nabla {p}_{{
m{n}}{
m{w}}}+{
ho }_{{
m{n}}{
m{w}}}{boldsymbol{g}}
ight)cdot {boldsymbol{n}}widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}S- &qquad {int }_{E}{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}left(nabla {p}_{{
m{n}}{
m{w}}}+{
ho }_{{
m{n}}{
m{w}}}{boldsymbol{g}}
ight)cdot nabla widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}V end{split}$$
(16)

将式(16)代入式(15), 累加所有单元区域, 可得







$$begin{split}& sumlimits_{Ein {cal{T}}_{
m{h}}}{int }_{E}left(phi {S}_{{
m{n}}{
m{w}}}{
ho }_{{
m{n}}{
m{w}}}{C}_{{
m{n}}{
m{w}}}frac{partial {p}_{{
m{n}}{
m{w}}}}{partial t}-phi {
ho }_{{
m{n}}{
m{w}}}frac{partial {S}_{{
m{w}}}}{partial t}
ight)widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}V - &qquadsumlimits_{Ein {cal{T}}_{
m{h}}}{int }_{E}{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}left({p}_{{
m{n}}{
m{w}}}+{
ho }_{{
m{n}}{
m{w}}}{boldsymbol{g}}
ight)cdot nabla widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}V+ &qquad sumlimits_{partial Ein partial {{Omega }}_{
m{i}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}left(nabla {p}_{{
m{n}}{
m{w}}}+{
ho }_{{
m{n}}{
m{w}}}{boldsymbol{g}}
ight)cdot {boldsymbol{n}}widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}S= &qquad sumlimits_{Ein {cal{T}}_{
m{h}}}{int }_{E}{Q}_{{
m{n}}{
m{w}}}widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}V end{split}$$
(17)

在间断伽辽金方法中, 变量在单元内边界$ partial {varOmega }_{
m{i}} $处满足不连续设定, 因此式(17)中等号左侧第三项可以改写为







$$begin{split}& sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}nabla {p}_{{
m{n}}{
m{w}}}cdot {boldsymbol{n}}widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}S= &qquad sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}^+left(nabla {p}_{{
m{n}}{
m{w}}}^++{
ho }_{{
m{n}}{
m{w}}}^+{boldsymbol{g}}
ight)cdot {{boldsymbol{n}}}^+widetilde {{p}_{{
m{n}}{
m{w}}}^+}+& qquad {boldsymbol{lambda }}_{{
m{n}}{
m{w}}}^-left(nabla {p}_{{
m{n}}{
m{w}}}^-+{
ho }_{{
m{n}}{
m{w}}}^-{boldsymbol{g}}
ight)cdot {{boldsymbol{n}}}^-widetilde {{p}_{{
m{n}}{
m{w}}}^-}{
m{d}}S= &qquad sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}[![{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}left(nabla {p}_{{
m{n}}{
m{w}}}+{
ho }_{nw}{boldsymbol{g}}
ight)widetilde {{p}_{{
m{n}}{
m{w}}}}]!]{
m{d}}S end{split}$$
(18)

将式(18)代入式(17)中, 结合稳定项、加罚函数项以及相应边界条件, 可得






$$begin{split}& sumlimits_{Ein {cal{T}}_{
m{h}}}{int }_{E}left(phi {S}_{{
m{n}}{
m{w}}}{
ho }_{{
m{n}}{
m{w}}}{C}_{{
m{n}}{
m{w}}}frac{partial {p}_{{
m{n}}{
m{w}}}}{partial t}-phi {
ho }_{{
m{n}}{
m{w}}}frac{partial {S}_{{
m{w}}}}{partial t}
ight)widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}V- &qquad sumlimits_{Ein {cal{T}}_{
m{h}}}{int }_{E}{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}left(nabla {p}_{{
m{n}}{
m{w}}}+{
ho }_{{
m{n}}{
m{w}}}{boldsymbol{g}}
ight)cdot nabla widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}V + &qquadsumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}leftlangle {}
ight.left(nabla {p}_{{
m{n}}{
m{w}}}+{
ho }_{{
m{n}}{
m{w}}}{boldsymbol{g}}
ight)left. {}
ight
angle [![widetilde {{p}_{{
m{n}}{
m{w}}}}]!]{
m{d}}S+ &qquad {omega }_{
m{f}}sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}leftlangle {}
ight.nabla widetilde {{p}_{{
m{n}}{
m{w}}}}left. {}
ight
angle [![{p}_{{
m{n}}{
m{w}}}]!]{
m{d}}S+end{split} $$







$$begin{split} &qquad sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}frac{{delta }_{
m{f}}}{h}[![{p}_{{
m{n}}{
m{w}}}]!]cdot [![widetilde {{p}_{{
m{n}}{
m{w}}}}]!]{
m{d}}S+ &qquad sumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{D}}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}left(nabla {p}_{{
m{n}}{
m{w}}}+{
ho }_{{
m{n}}{
m{w}}}{boldsymbol{g}}
ight)cdot {boldsymbol{n}}widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}S+ &qquad {omega }_{
m{f}}sumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{D}}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{n}}{
m{w}}}nabla widetilde {{p}_{{
m{n}}{
m{w}}}}cdot {boldsymbol{n}}left({p}_{{
m{n}}{
m{w}}}-{p}_{{
m{n}}{
m{w}}}^{
m{b}}
ight){
m{d}}S + &qquadsumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{D}}}}{int }_{partial E}frac{{delta }_{
m{f}}}{h}left({p}_{{
m{n}}{
m{w}}}-{p}_{{
m{n}}{
m{w}}}^{
m{b}}
ight)widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}S= &qquad sumlimits_{Ein {cal{T}}_{
m{h}}}{int }_{E}{Q}_{{
m{n}}{
m{w}}}widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}V -sumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{N}}}}{int }_{partial E}{g}_{{
m{n}}{
m{w}}}widetilde {{p}_{{
m{n}}{
m{w}}}}{
m{d}}S end{split}$$
(19)

式中, $ leftlangle {}
ight.{boldsymbol{X}}left. {}
ight
angle =dfrac{1}{2}left({boldsymbol{X}}cdot {{boldsymbol{n}}}^{+}-{boldsymbol{X}}cdot {{boldsymbol{n}}}^{-}
ight) $和$ [![{boldsymbol{X}}]!]={boldsymbol{X}}cdot {{boldsymbol{n}}}^{+}+{boldsymbol{X}}cdot {{boldsymbol{n}}}^{-} $分别为$ {boldsymbol{X}} $在相邻单元共同边界上的平均和跳跃, $ h $为单元尺寸, $ {delta }_{
m{f}} $为加罚因子, $ {omega }_{
m{f}} $的选取决定了间断有限元方法的类型. $ {omega }_{
m{f}}=1 $, 表示为非对称内罚伽辽金法(non-symmetric interior penalty Galerkin method, 简称NIPG); $ {omega }_{
m{f}}=0 $, 表示为非完全内罚伽辽金法(incomplete interior penalty?Galerkin method, 简称IIPG); $ {omega }_{
m{f}}=-1 $, 表示为对称内罚伽辽金法(symmetric interior penalty Galerkin method, SIPG). 在本文中, 选取$ {omega }_{
m{f}}=1 $[23], 则式(19)为流体方程的非对称内罚伽辽金弱形式.

利用上述类似的推导过程和方式, 可以得到式(2)的间断伽辽金弱形式, 如下所示






$$ begin{split}& sumlimits_{Ein {cal{T}}_{
m{h}}}{int }_{E}Biggr[phi {S}_{{
m{w}}}{
ho }_{{
m{w}}}{C}_{{
m{w}}}frac{partial {p}_{{
m{n}}{
m{w}}}}{partial t}+ &qquad left(phi {
ho }_{{
m{w}}}-phi {S}_{{
m{w}}}{
ho }_{{
m{w}}}{C}_{{
m{w}}}left|{p}_{
m{c}}
ight|
ight)frac{partial {S}_{{
m{w}}}}{partial t}Biggr]widetilde {{S}_{{
m{w}}}}{
m{d}}V+ &qquad sumlimits_{Ein {cal{T}}_{
m{h}}}{int }_{E}{boldsymbol{lambda }}_{{
m{w}}}left(left|{p}_{
m{c}}
ight|nabla {S}_{{
m{w}}}-nabla {p}_{{
m{n}}{
m{w}}}-{
ho }_{{
m{w}}}{boldsymbol{g}}
ight)cdot nabla widetilde {{S}_{{
m{w}}}}{
m{d}}V- &qquad sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{w}}}left|{p}_{
m{c}}
ight|leftlangle {}
ight.nabla {S}_{{
m{w}}}left. {}
ight
angle [![widetilde {{S}_{{
m{w}}}}]!]{
m{d}}S+ &qquad {omega }_{
m{f}}sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{w}}}left|{p}_{
m{c}}
ight|leftlangle {}
ight.nabla widetilde {{S}_{{
m{w}}}}left. {}
ight
angle [![{S}_{{
m{w}}}]!]{
m{d}}S+ &qquad sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}frac{{delta }_{
m{f}}}{h}[![{S}_{{
m{w}}}]!]cdot [![widetilde {{S}_{{
m{w}}}}]!]{
m{d}}S+ &qquad sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{w}}}leftlangle {}
ight.left(nabla {p}_{{
m{n}}{
m{w}}}+{
ho }_{{
m{w}}}{boldsymbol{g}}
ight)left. {}
ight
angle [![widetilde {{S}_{{
m{w}}}}]!]{
m{d}}S+ &qquad {omega }_{
m{f}}sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{w}}}leftlangle {}
ight.nabla widetilde {{S}_{{
m{w}}}}left. {}
ight
angle [![{p}_{{
m{n}}{
m{w}}}]!]{
m{d}}S+ &qquad sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}frac{{delta }_{
m{f}}}{h}[![{p}_{{
m{n}}{
m{w}}}]!]cdot [![widetilde {{S}_{{
m{w}}}}]!]{
m{d}}S- &qquad sumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{D}}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{w}}}left|{p}_{
m{c}}
ight|nabla {S}_{{
m{w}}}cdot {boldsymbol{n}}widetilde {{S}_{{
m{w}}}}{
m{d}}S+end{split}$$







$$begin{split} &qquad {omega }_{
m{f}}sumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{D}}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{w}}}left|{p}_{
m{c}}
ight|nabla widetilde {{S}_{{
m{w}}}}cdot {boldsymbol{n}}left({S}_{{
m{w}}}-{S}_{{
m{w}}}^{
m{b}}
ight){
m{d}}S +&qquadsumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{D}}}}{int }_{partial E}frac{{delta }_{
m{f}}}{h}left({S}_{{
m{w}}}-{S}_{{
m{w}}}^{
m{b}}
ight)widetilde {{S}_{{
m{w}}}}{
m{d}}S+ &qquad sumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{D}}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{w}}}left(nabla {p}_{{
m{n}}{
m{w}}}+{
ho }_{{
m{w}}}{boldsymbol{g}}
ight)cdot {boldsymbol{n}}widetilde {{S}_{{
m{w}}}}{
m{d}}S+ &qquad {omega }_{
m{f}}sumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{D}}}}{int }_{partial E}{boldsymbol{lambda }}_{{
m{w}}}nabla widetilde {{S}_{{
m{w}}}}cdot {boldsymbol{n}}left({p}_{{
m{n}}{
m{w}}}-{p}_{{
m{n}}{
m{w}}}^{
m{b}}
ight){
m{d}}S+ &qquad sumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{D}}}}{int }_{partial E}frac{{delta }_{
m{f}}}{h}left({p}_{{
m{n}}{
m{w}}}-{p}_{{
m{n}}{
m{w}}}^{
m{b}}
ight)widetilde {{S}_{w}}{
m{d}}S= &qquad sumlimits_{Ein {cal{T}}_{
m{h}}}{int }_{E}{Q}_{{
m{w}}}widetilde {{S}_{{
m{w}}}}{
m{d}}V -sumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{N}}}}{int }_{partial E}{g}_{{
m{w}}}widetilde {{S}_{{
m{w}}}}{
m{d}}Send{split}$$
(20)

式(19)和式(20)为考虑固体变形作用下可压缩两相渗流方程的间断伽辽金有限元方法的弱表达形式.


1.3
固体变形方程及其弱形式


假设多孔介质固体变形满足弹性小变形条件, 那么固体变形的平衡方程、几何方程、本构方程以及边界条件如下所示







$$nabla cdot {boldsymbol{sigma }}+{boldsymbol{f}}=0,;{
m{o}}{
m{n}};varOmega$$
(21)







$${boldsymbol{varepsilon }}=frac{1}{2}left(nabla {boldsymbol{u}}+nabla {{boldsymbol{u}}}^{
m{T}}
ight),;{
m{o}}{
m{n}};varOmega $$
(22)







$${boldsymbol{sigma }}={boldsymbol{D}}:{boldsymbol{varepsilon }},;{
m{o}}{
m{n}};varOmega$$
(23)







$${boldsymbol{u}}={{boldsymbol{u}}}^{bf{b}},;;{
m{o}}{
m{n}};partial {varOmega }_{{
m{o}}{
m{D}}} $$
(24)







$${boldsymbol{sigma }}cdot {boldsymbol{n}}=overline{boldsymbol{t}},;;{
m{o}}{
m{n}};partial {varOmega }_{{
m{o}}{
m{N}}}$$
(25)

式中, 总应力$ {boldsymbol{sigma }}={boldsymbol{sigma }}{{'}}-alpha {boldsymbol{I}}p $, 则式(21)可改写







$$nabla cdot left({boldsymbol{sigma }}{'}-alpha {boldsymbol{I}}p
ight)+{boldsymbol{f}}={bf{0}}$$
(26)

式中, $ {boldsymbol{sigma }}{{'}} $为有效应力张量, $ {boldsymbol{varepsilon }} $为应变张量, $ {boldsymbol{u}} $为位移张量, $ {boldsymbol{f}} $为体积力张量, $ alpha $为Biot常数, $ {boldsymbol{D}} $为4阶弹性张量, $ {boldsymbol{I}} $为单位张量, 平均孔隙压力$ p={S}_{{
m{n}}{
m{w}}}{p}_{{
m{n}}{
m{w}}}+{S}_{{
m{w}}}{p}_{{
m{w}}} $.

利用类似式(19)和式(20)的推导过程, 结合相应的边界条件, 可以得到固体变形方程的弱形式, 如下所示






$$ begin{split}& sumlimits_{Ein {cal{T}}_{
m{h}}}{int }_{E}{{boldsymbol{sigma }}}^{{{'}}}:{boldsymbol{varepsilon }}left(widetilde {{boldsymbol{u}}}
ight){
m{d}}V -sumlimits_{Ein {cal{T}}_{
m{h}}}{int }_{E}alpha {boldsymbol{I}}p:{boldsymbol{varepsilon }}left(widetilde {{boldsymbol{u}}}
ight){
m{d}}V- &qquad sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}leftlangle {}
ight.{{boldsymbol{sigma }}}^{{{'}}}-alpha {boldsymbol{I}}pleft. {}
ight
angle cdot {boldsymbol{n}}[![widetilde {{boldsymbol{u}}}]!]{
m{d}}S+ &qquad {omega }_{
m{s}}sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}leftlangle {}
ight.{{boldsymbol{sigma }}}^{{{'}}}left(widetilde {{boldsymbol{u}}}
ight)-alpha {boldsymbol{I}}pleft. {}
ight
angle cdot {boldsymbol{n}}[![{boldsymbol{u}}]!]{
m{d}}S+end{split}$$







$$begin{split} &qquad sumlimits_{partial Ein partial {varOmega }_{
m{i}}}{int }_{partial E}frac{G{delta }_{
m{s}}}{h}[![{boldsymbol{u}}]!]cdot [![widetilde {{boldsymbol{u}}}]!]{
m{d}}S- &qquad sumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{D}}}}{int }_{partial E}left[{{boldsymbol{sigma }}}^{{{'}}}left(widetilde {{boldsymbol{u}}}
ight)-alpha {boldsymbol{I}}p
ight]cdot {boldsymbol{n}}widetilde {{boldsymbol{u}}}{
m{d}}S+ &qquad {omega }_{s}sumlimits_{partial Ein partial {varOmega }_{oD}}{int }_{partial E}left[{{boldsymbol{sigma }}}^{{{'}}}left(widetilde {{boldsymbol{u}}}
ight)-alpha {boldsymbol{I}}p
ight]cdot {boldsymbol{n}}left({boldsymbol{u}}-{{boldsymbol{u}}}^{
m{b}}
ight){
m{d}}S+ &qquad sumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{D}}}}{int }_{partial E}frac{G{delta }_{
m{s}}}{h}widetilde {{boldsymbol{u}}}cdot left({boldsymbol{u}}-{{boldsymbol{u}}}^{
m{b}}
ight){
m{d}}S= &qquad sumlimits_{Ein {cal{T}}_{
m{h}}}{int }_{E}{boldsymbol{f}} cdot widetilde {{boldsymbol{u}}}{
m{d}}V-sumlimits_{partial Ein partial {varOmega }_{{
m{o}}{
m{N}}}}{int }_{partial E}overline{boldsymbol{t}}cdot widetilde {{boldsymbol{u}}}{
m{d}}S end{split}$$
(27)

式中, $ widetilde {{boldsymbol{u}}} $为试函数, $ G $为剪切模量, $ {delta }_{
m{s}} $为加罚因子. 本文选取$ {omega }_{
m{s}}=0 $[26], 则式(27)为固体变形方程的非完全内罚伽辽金弱形式.


1.4
数值方法的实现


方程式(19), 式(20)和式(27)是多孔介质中可压缩两相渗流和固体变形的弱形式. 本文利用通用有限元软件COMSOL Multiphysics内置的Weak Form PDE模块求解可压缩两相流固耦合模型. 基于二次不连续拉格朗日形函数构建对解域的间断伽辽金有限元逼近, 选取向后差分公式(backward differentiation formula, BDF)隐式求解器. 其中, BDF求解器采用自适应时间步长算法和可变离散化阶数, 离散化的BDF精度从1 ~ 5不等. 基于LU分解, 采用MUMPS (multifrontal massively parallel sparse)直接求解器对线性系统进行求解, 并选取完全耦合的求解器(fully coupled solver)将线性求解器应用于牛顿单步法的非线性问题. 默认情况下, 初始时间步长设置为结束时间的0.1%, 相对容差为0.01.


2.
模型验证


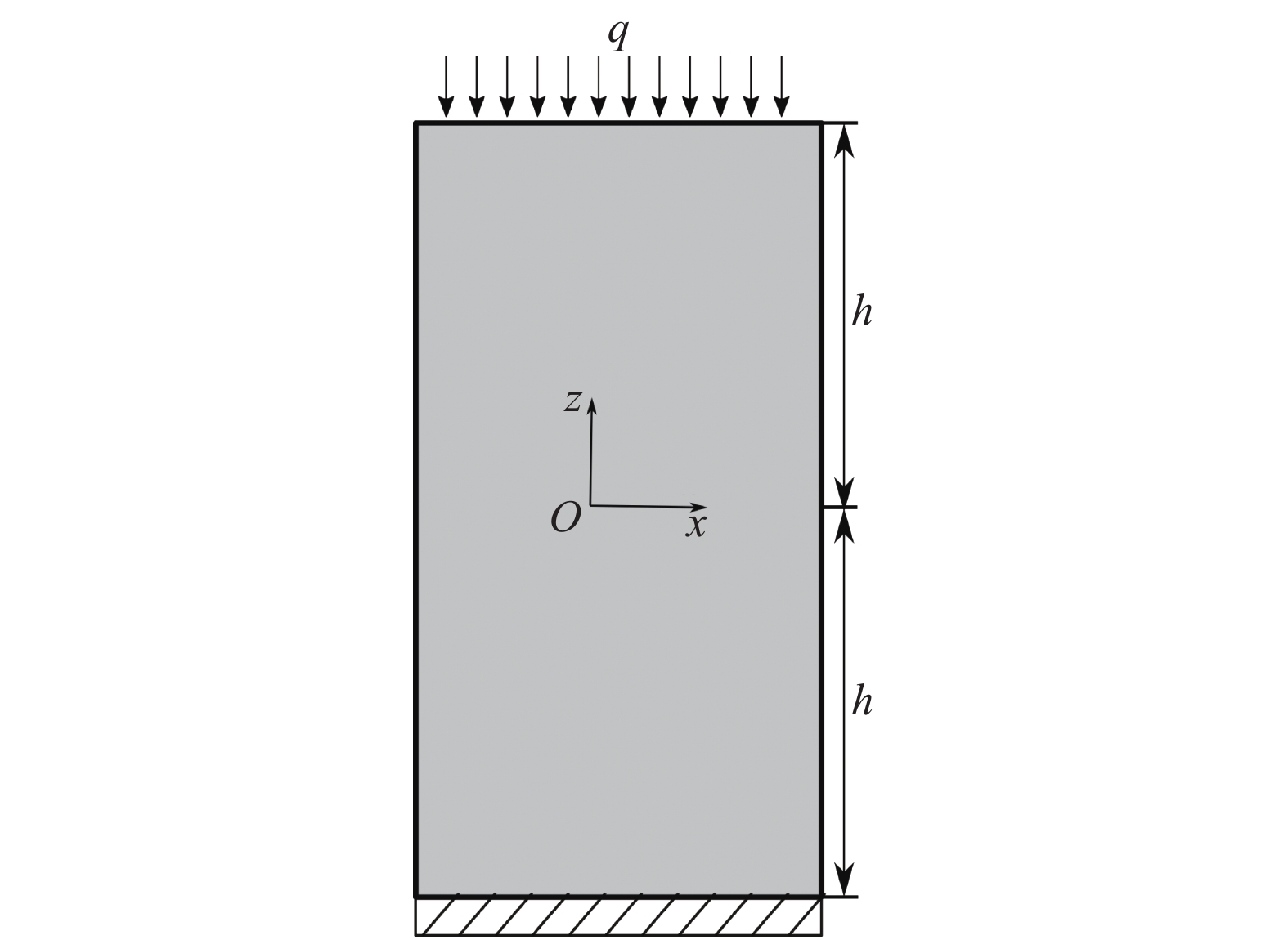
图2描述了一维Terzaghi固结问题的几何示意图以及相应的边界条件. 为了确保孔隙压力沿上下两端保持为零, 设置模型上下两端为排水边界. 在模型上边界瞬间施加均布载荷$ q=-5.00 $ MPa. 本模型长度$ 2 h=10.00 $ m, 其他参数的具体取值如下[2]: 剪切模量为30.00 GPa, 压缩模量为50.00 GPa, 多孔介质渗透率为$ {1.00times 10}^{-12};{
m{m}}^{2} $, 孔隙度为0.25, 流体压缩系数为$ {1.00times 10}^{-12};{{
m{Pa}}}^{-1} $, 流体黏度为 $ {1.00times 10}^{-3};{
m{Pa}}cdot {
m{s}} $, 加罚因子$ {delta }_{
m{f}} $和$ {delta }_{
m{s}} $分别设置为1.00和10.00[31].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-177-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
Terzaghi固结问题几何示意图



Figure
2.
Sketch of Terzaghi’s consolidation problem



下载:
全尺寸图片
幻灯片


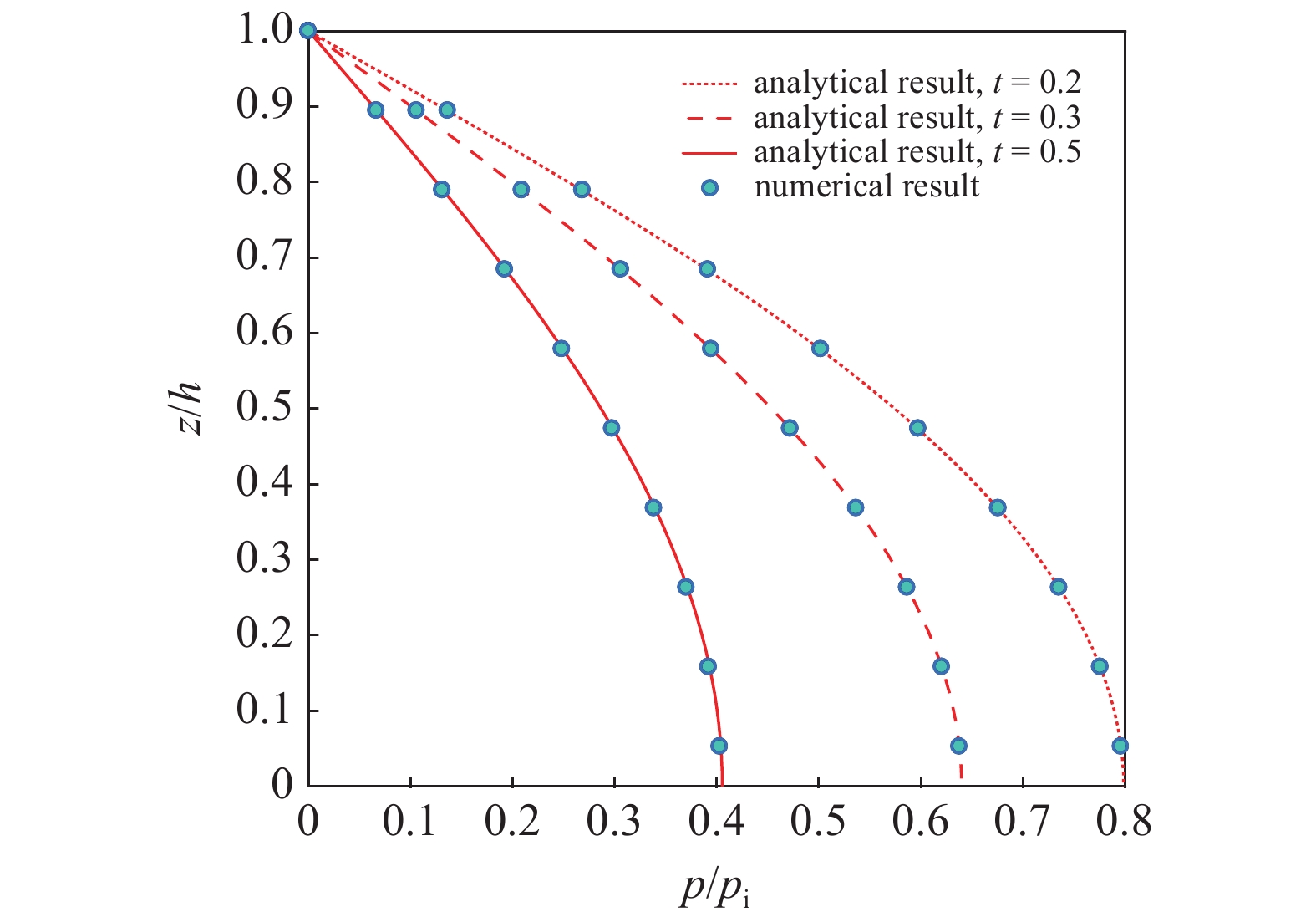
图3为Terzaghi固结问题的理论解[32]和DG有限元数值解的比较. 结果显示, DG有限元计算得到的数值解与理论解吻合较好, 进而验证了间断伽辽金方法在求解流固耦合方程时的可行性和有效性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-177-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
Terzaghi固结问题理论解和数值解的比较



Figure
3.
Comparison of the analytical and numerical results for Terzaghi’s consolidation problem



下载:
全尺寸图片
幻灯片



3.
算例分析



3.1
二维平面两相流固算例


本节利用间断伽辽金方法开展在二维平面应变条件下两相渗流和固体变形耦合数值计算. 在本算例中, 分别选取水和氢气作为湿润相和非湿润相. 模型的几何尺度、初始条件、边界条件和监测线如图4所示. 模型的长度和宽度均设置为10.00 m. 多孔介质的弹性模量和泊松比分别为10.00 GPa和0.30; 渗透率和孔隙度分别设定为$ 1.00times {10}^{-14};{
m{m}}^{2} $和$ 0.20 $. 模拟区域的初始气体压力为4.00 MPa, 初始水饱和度为0.80. 模拟左边界和下边界为位移约束, 在上边界和右边界分别施加$ -1.00;times;{10}^{7} $ MPa (负号表示压应力方向)的垂直和水平应力. 模型左下角为注入边界, 设置注入的氢气压力和水饱和度分别为5.00 MPa和0.80; 右上角为出口边界, 出口气体压力和水饱和度设置为4.00 MPa和0.20.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-177-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
模拟几何尺度、初始和边界条件



Figure
4.
Simulation geometrical configuration with boundary and initial conditions



下载:
全尺寸图片
幻灯片


数值模拟分两个阶段开展. 首先, 开展储层力学和流体平衡的稳态计算. 然后, 将第一步计算得到的应力和孔压等水力信息作为含水层氢气注入模拟算例的初始条件. 整个模拟时间为1500 s, 其他变量的具体数值如表1所示.




表
1
两相流固数值模拟的属性参数



Table
1.
Parameters for two-phase flow simulation



table_type1 ">
ParameterValueUnit
elastic modulus, $ E $$ 30.00 $$ {
m{G}}{
m{Pa}} $
poisson's ratio, $ nu $$ 0.25 $$ - $
permeability, $ k $$ 1.00times {10}^{-14} $$ ;{
m{m}}^{2} $
porosity, $ phi $$ 0.20 $$ - $
water density, $ ;{
ho }_{{
m{w}}0} $		$ 1000.00 $$ {
m{kg}}/{
m{m}}^{3} $
water viscosity, $ ;{mu }_{{
m{w}}} $		$ 1.00times {10}^{-3} $$ {
m{Pa}}cdot {
m{s}} $
water compressibility[32], $ {c}_{{
m{w}}} $		$ 3.84times {10}^{-10} $$ {{
m{Pa}}}^{-1} $
hydrogen density, $; {
ho }_{{
m{n}}{
m{w}}0} $		$ 3.18 $$ {
m{kg}}/{
m{m}}^{3} $
hydrogen viscosity, $; {mu }_{{
m{n}}{
m{w}}} $		$ 9.02times {10}^{-6} $$ {
m{Pa}}cdot {
m{s}} $
hydrogen compressibility[32], $ {c}_{{
m{n}}{
m{w}}} $		$ 7.71times {10}^{-7} $$ {{
m{Pa}}}^{-1} $
entry pressure, $ {p}_{
m{e}} $		$ 1.00times {10}^{4} $$ {
m{Pa}} $
distribution index, $ lambda $$ 0.46 $$ - $
relative permeability variable, $ omega $$ 2.00 $$ - $
variable, $ {omega }_{
m{f}} $		1.00$ - $
penalty factor[27], $ {delta }_{
m{f}} $		1.00$ - $
variable, $ {omega }_{
m{s}} $		0.00$ - $
penalty factor[27], $ {delta }_{
m{s}} $		10.00$ - $





下载:
导出CSV
|显示表格



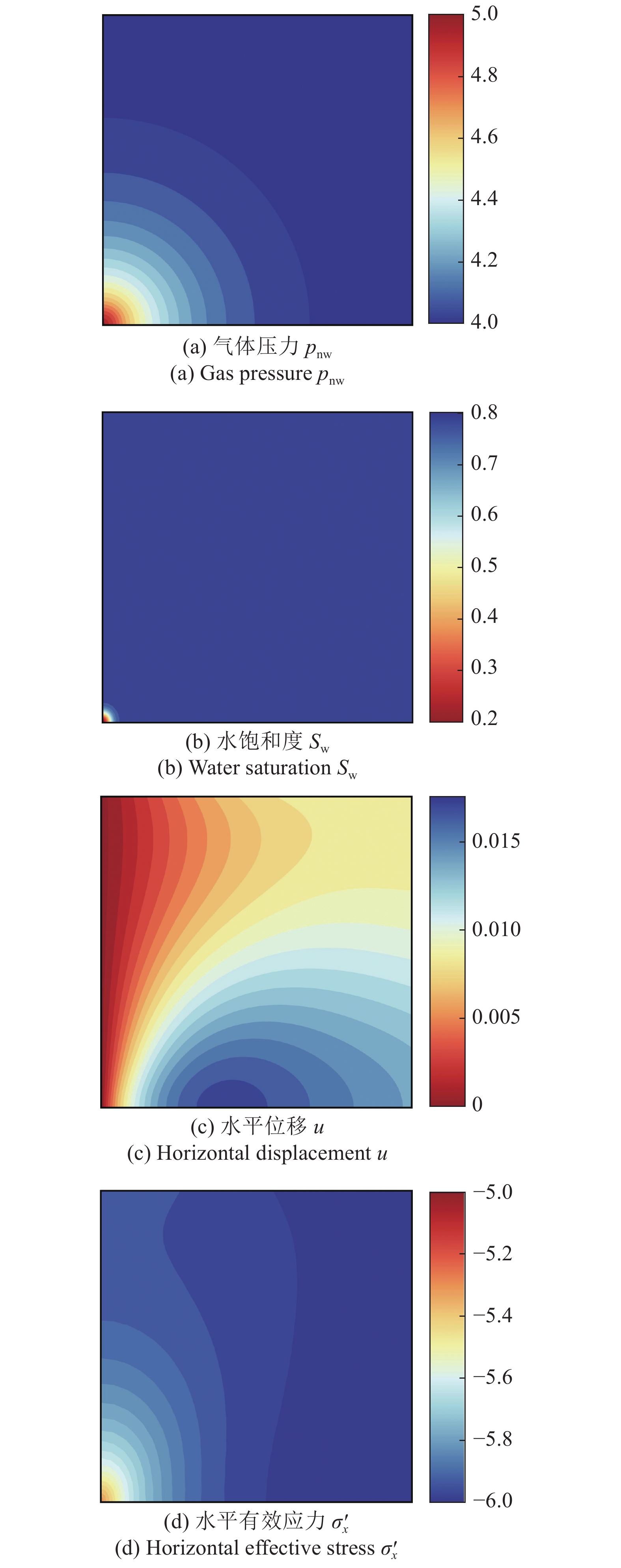
图5和图6分别给出了注气第1500 s气体压力$ {p}_{{
m{n}}{
m{w}}} $、水饱和度$ {S}_{{
m{w}}} $、水平位移$ u $和水平有效应力$ {sigma }_{x}^{{{'}}} $的空间分布云图以及变量沿监测线的分布图. 由图5和图6可知, 随着氢气的持续注入, 气体压力影响范围扩大至距注入边界7 m左右, 并引起固体膨胀变形且变形影响范围扩散至边界处. 究其原因是因为在多孔弹性介质中位移或者应变可传播到压力前沿之前. 受毛细压力和气水两相物理属性差异的共同影响, 氢气主要聚集于注入边界附近. 在多孔介质内孔压在远离注入边界的过程中呈现递减趋势, 而有效应力沿监测线增加.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-177-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
第1500 s气体压力$ {p}_{{
m{n}}{
m{w}}} $、水饱和度$ {S}_{{
m{w}}} $、水平位移$ u $和水平有效应力$ {sigma }_{x}^{{{'}}} $的分布云图



Figure
5.
The distribution of gas pressure $ {p}_{{
m{n}}{
m{w}}} $, water saturation $ {S}_{{
m{w}}} $, horizontal displacement $ u $ and horizontal effective stress $ {sigma }_{x}^{{{'}}} $ at t = 1500 s



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-177-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
第1500 s时气体压力$ {p}_{{
m{n}}{
m{w}}} $、水饱和度$ {S}_{{
m{w}}} $、水平位移$ u $和水平有效应力$ {sigma }_{x}^{{{'}}} $沿监测线的分布



Figure
6.
The profiles of gas pressure $ {p}_{{
m{n}}{
m{w}}} $, water saturation $ {S}_{{
m{w}}} $, horizontal displacement $ u $ and horizontal effective stress $ {sigma }_{x}^{{{'}}} $ along the monitoring line at t = 1500 s



下载:
全尺寸图片
幻灯片



3.2
加罚因子的影响


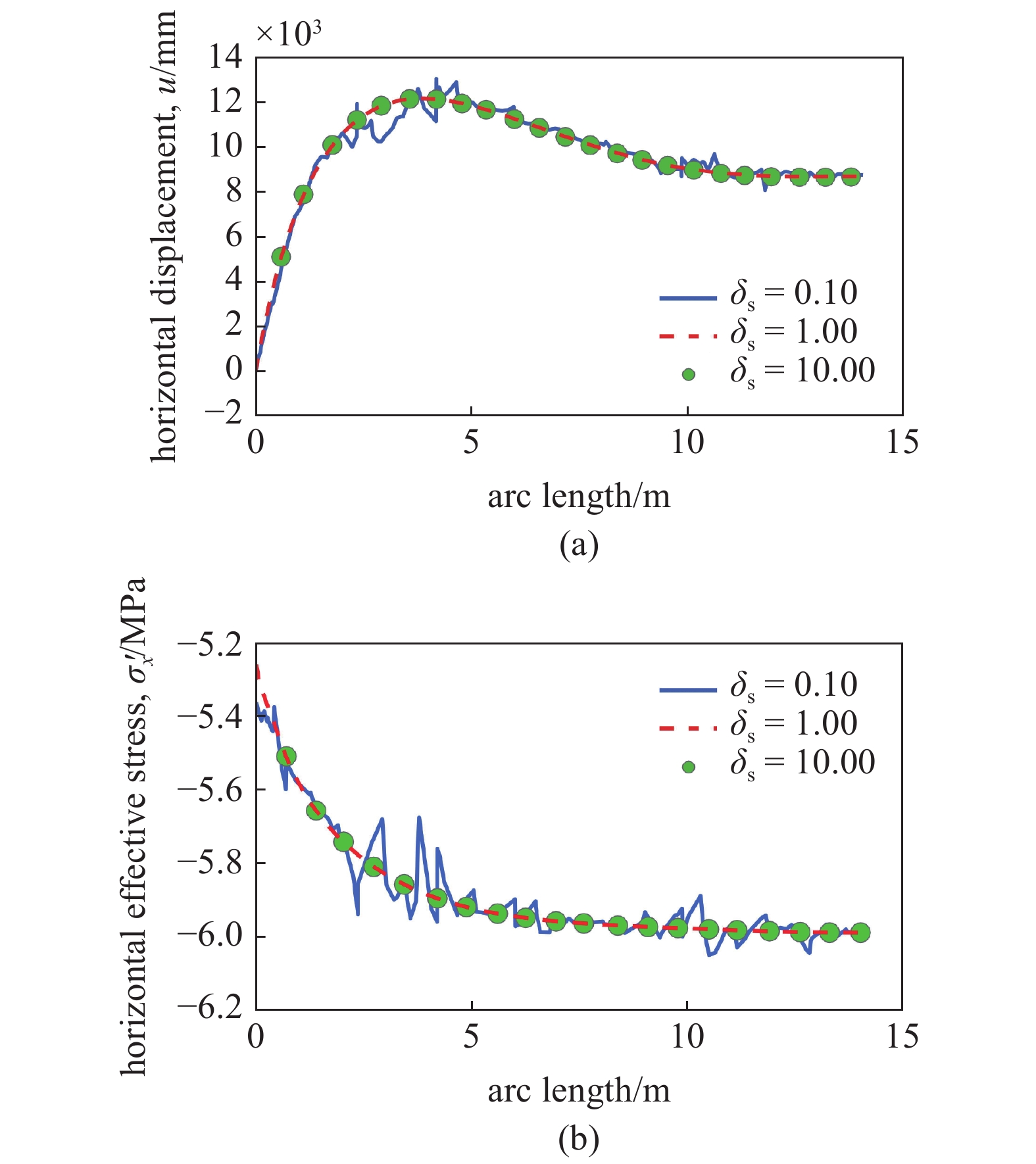
图7给出了$ {delta }_{
m{s}}=0.10 $, 1.00和10.00时水平位移$ u $和水平有效应力$ {sigma }_{x}^{{{'}}} $沿监测线的分布. 图8给出了$ {delta }_{
m{s}}=0.10 $时水平位移$ u $和水平有效应力$ {sigma }_{x}^{{{'}}} $的分布云图. 图9给出了$ {delta }_{
m{f}}=0.01 $, 0.10, 1.00和10.00时气体压力$ {p}_{{
m{n}}{
m{w}}} $、水饱和度$ {S}_{{
m{w}}} $沿监测线的分布. 结果表明, 不同加罚因子条件下, 变量$ u $, $ {sigma }_{x}^{{{'}}} $, $ {p}_{{
m{n}}{
m{w}}} $和$ {S}_{{
m{w}}} $沿着监测线的变化趋势大体保持一致. 在计算固体变形时, 计算结果对加罚因子的选取更为敏感. 当$ {delta }_{
m{s}} $ = 0.10时, 应力和位移均在局部出现明显的波动; 当$ {delta }_{
m{f}} $ = 0.01时, 饱和度在小范围内发生轻微浮动. 这主要由于加罚因子$ {delta }_{
m{s}} $和$ {delta }_{
m{f}} $的降低减少了自变量位移、压力以及饱和度在单元处弱连续性的约束, 造成了变量局部波动的现象. 通过适当提高加罚因子可以加强变量在跨越单元交界面处的连续性, 但是较高的加罚值会引发病态条件矩阵的可能性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-177-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
第1500 s时不同加罚因子$ {delta }_{
m{s}} $条件下水平位移$ u $和水平有效应力$ {sigma }_{x}^{{{'}}} $沿监测线的分布



Figure
7.
The profiles of horizontal displacement $ u $ and horizontal effective stress $ {sigma }_{x}^{{{'}}} $ along the monitoring line at t = 1500 s with different values of penalty parameter $ {delta }_{
m{s}} $



下载:
全尺寸图片
幻灯片




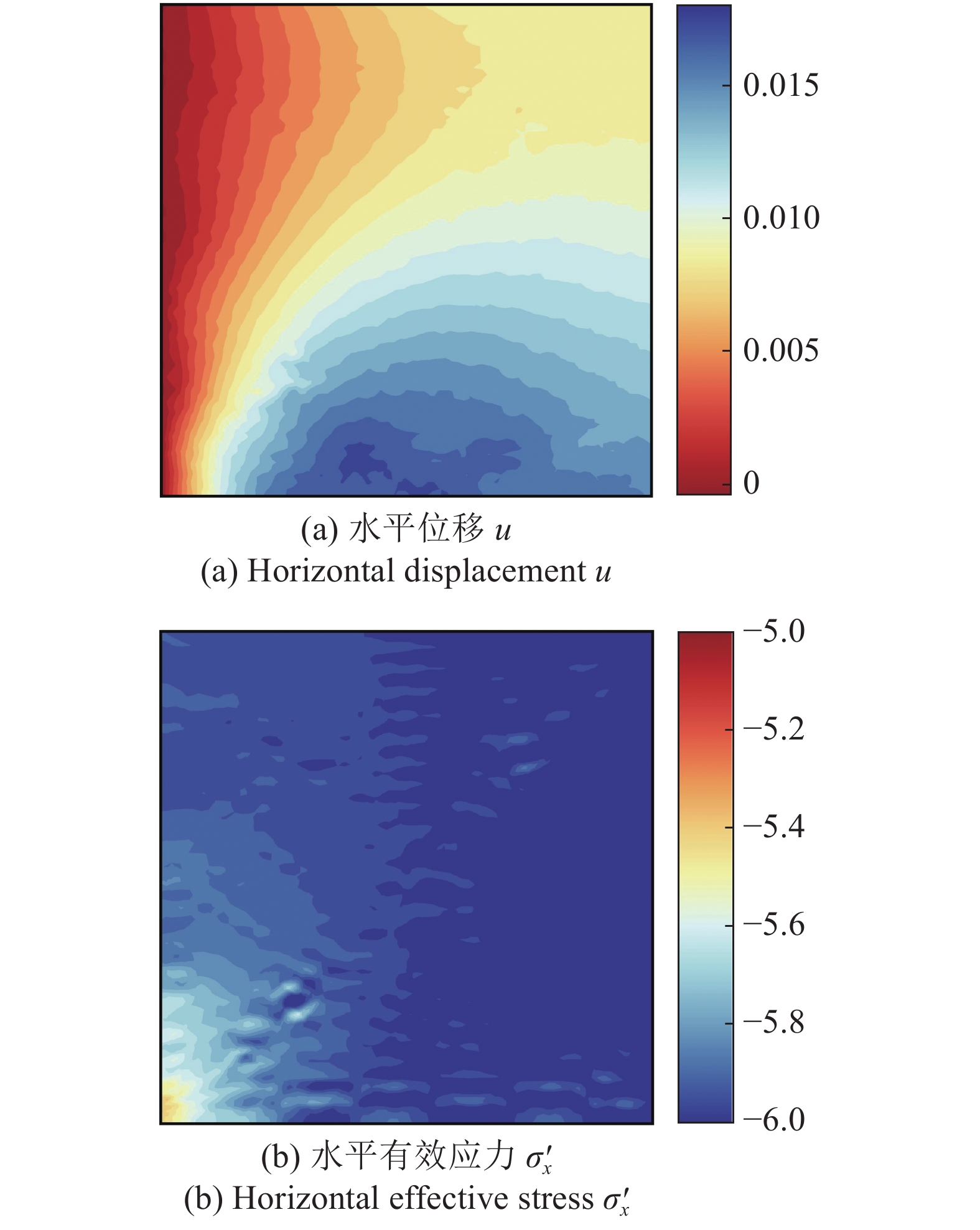onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-177-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
第1500 s时$ {delta }_{
m{s}}=0.01 $水平位移$ u $和水平有效应力$ {sigma }_{x}^{{{'}}} $分布云图



Figure
8.
The distribution of horizontal displacement $ u $ and horizontal effective stress $ {sigma }_{x}^{{{'}}} $ with $ {delta }_{
m{s}}=0.01 $ at t = 1500 s



下载:
全尺寸图片
幻灯片




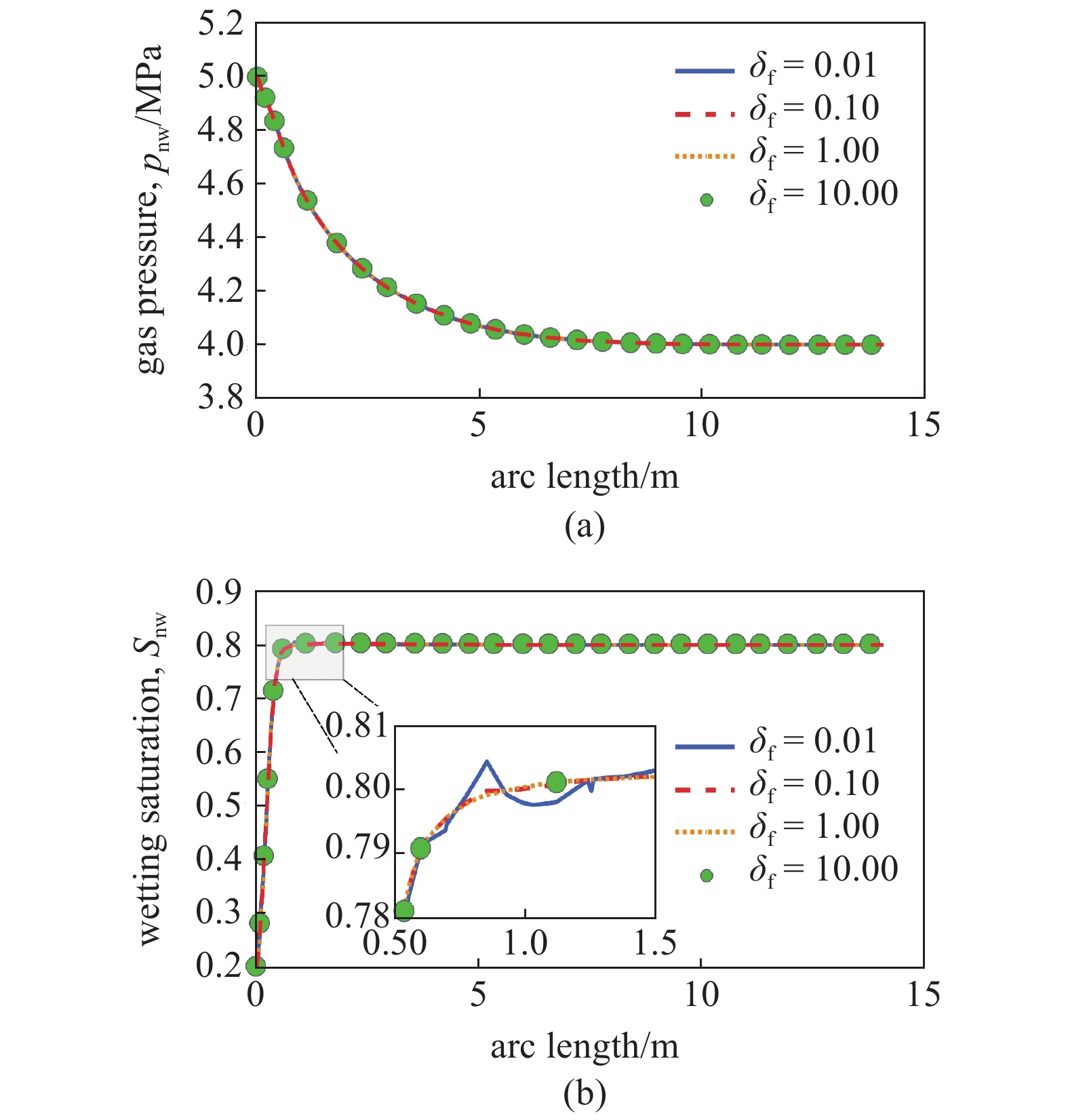onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-177-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
第1500 s时不同加罚因子$ {delta }_{
m{f}} $条件下气体压力$ {p}_{{
m{n}}{
m{w}}} $、水饱和度$ {S}_{{
m{w}}} $沿监测线(0, 0.05)?(10, 9.95)的分布



Figure
9.
The profiles of gas pressure $ {p}_{{
m{n}}{
m{w}}} $ and water saturation $ {S}_{{
m{w}}} $ along monitoring line at t = 1500 s with different values of $ {delta }_{
m{f}} $



下载:
全尺寸图片
幻灯片


值得注意的是, 受流体边界条件、初始条件以及流体方程的非线性特征等因素的影响, 传统有限元方法在求解本节流体模型时无法收敛, 此情况在一定程度上体现了间断伽辽金有限元在求解可压缩两相流固方程上的优越性. 本节将传统有限元的计算结果作为基准方案, 通过比较间断伽辽金有限元和传统有限元两者计算得到的水平位移和水平有效应力之间的相对误差, 分析加罚因子$ {delta }_{{
m{s}}} $对计算结果的影响. 水平位移和水平有效应力的计算误差$ er{r}_{
m{u}} $和$ er{r}_{
m{s}} $的表达式为[33]







$$er{r}_{
m{u}}=sqrt{frac{1}{left|l
ight|{left({Delta }{u}_{{
m{C}}{
m{G}}}
ight)}^{2}}sumlimits_{E}left|h
ight|{left({u}_{{
m{D}}{
m{G}}}-{u}_{{
m{C}}{
m{G}}}
ight)}^{2}}$$
(28)







$$er{r}_{
m{s}}=sqrt{frac{1}{left|l
ight|{left({Delta }{sigma }_{x{
m{C}}{
m{G}}}^{{{'}}}
ight)}^{2}}sumlimits_{E}left|h
ight|{left({sigma }_{x{
m{D}}{
m{G}}}^{{{'}}}-{sigma }_{x{
m{C}}{
m{G}}}^{{{'}}}
ight)}^{2}}$$
(29)

式中, $ l $为几何模型尺度, $ {u}_{{
m{C}}{
m{G}}} $和$ {sigma }_{x{
m{C}}{
m{G}}}^{{{'}}} $分别为有限元方法计算得到的水平位移和水平有效应力, $ {Delta }{u}_{{
m{C}}{
m{G}}} $和$ {Delta }{sigma }_{x{
m{C}}{
m{G}}}^{{{'}}} $分别为$ {u}_{{
m{C}}{
m{G}}} $和$ {sigma }_{x{
m{C}}{
m{G}}}^{{{'}}} $极差, $ {u}_{{
m{D}}{
m{G}}} $和$ {sigma }_{x{
m{D}}{
m{G}}}^{{{'}}} $分别为间断有限元方法计算得到的水平位移和水平有效应力.

图10给出了不同加罚因子$ {delta }_{
m{s}} $条件下间断伽辽金有限元和传统有限元方法计算得到的水平位移和水平有效应力的比较. 结果表明, 随着$ {delta }_{
m{s}} $的增加, 间断有限元与传统有限元计算得到的水平方向的变形和应力的相对误差随之减少, 这说明了加罚项的增加可以有效抑制有限元函数在跨越单元时的不连续性.



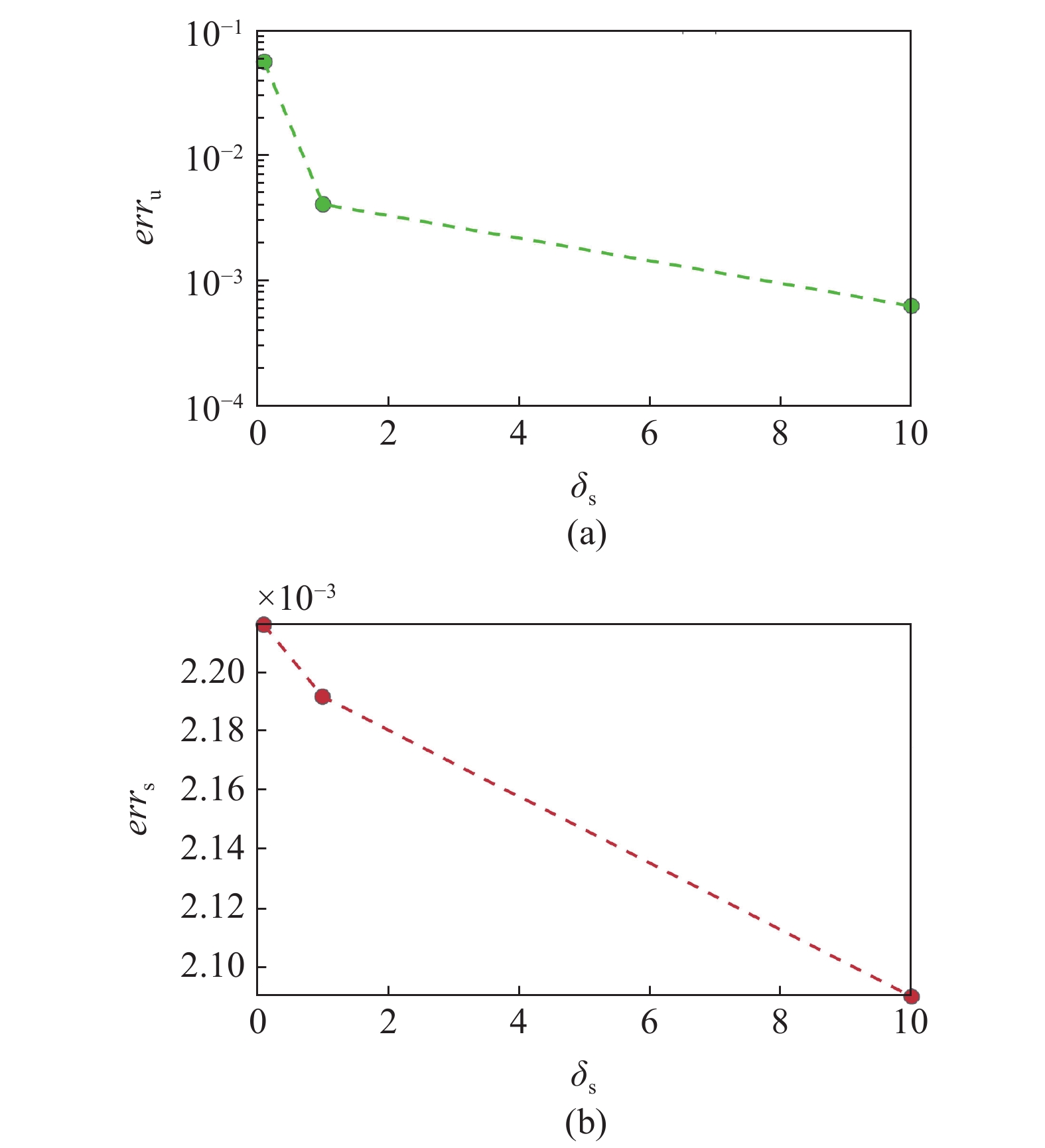onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-177-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
不同加罚因子$ {delta }_{
m{s}} $条件下间断有限元和传统有限元方法计算水平位移和水平有效应力的比较



Figure
10.
Comparison of the horizonal displacement and horizonal effective stress between DG and the CG results with different values of penalty parameter $ {delta }_{
m{s}} $



下载:
全尺寸图片
幻灯片



3.3
考虑重力效应的两相流固三维算例


在本节中, 将开展含水层注氢气的三维数值模拟. 在此算例中, 侧重分析流体重力效应对模拟结果的的影响. 如图11所示, 三维算例的几何尺度为100.00 m×2.00 m×10.00 m. 模拟上边界和右边界为应力边界且${t}_{x}={t}_{z}=;-1.00;times;{10}^{7};{
m{M}}{
m{Pa}}$, 其余边界均设定为位移约束. 氢气从左侧边界注入, 注入率${g}_{{
m{nw}}}= $$ 1.00;times;{10}^{-4};{
m{kg}}/({
m{m}}^{2}cdot {
m{s}})$, 右侧为出口边界, 边界上的气体压力和水饱和度分别为4.00 MPa和0.20, 其余边界则为不流动边界. 整个注气过程持续1 d, 其他变量的数值如表1所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-177-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
三维模型几何尺度以及模拟初始和边界条件



Figure
11.
Geometrical configuration with boundary and initial conditions of 3D case



下载:
全尺寸图片
幻灯片


图12给出了注气1 d后气体压力$ {p}_{{
m{n}}{
m{w}}} $、气体饱和度$ {S}_{{
m{n}}{
m{w}}} $、垂直位移$ w $和水平有效应力$ {sigma }_{x}^{{{'}}} $的分布云图. 图13为在考虑和不考虑重力效应两种情况下点a, b和c处气饱和度$ {S}_{{
m{n}}{
m{w}}} $随时间变化图. 由图12可知, 氢气注入1 d后, 孔压沿着水平x方向传播至距左边界约70.00 m处, 储层边界处气体饱和度和孔隙压力分别增加至约0.52和6.50 MPa, 孔压的增加引起垂直位移的提高和水平有效应力的降低. 在注入过程中, 由于氢气和水两者密度的差异, 引起气体上浮且聚集于模型顶部, 造成顶部点c处气体饱和度要明显高于底部点a处气体饱和度.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-177-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
注气1 d后气体压力$ {p}_{{
m{n}}{
m{w}}} $、气体饱和度$ {S}_{{
m{n}}{
m{w}}} $、垂直位移$ w $和水平有效应力$ {sigma }_{x}^{{{'}}} $的分布图



Figure
12.
The distribution of gas pressure $ {p}_{{
m{n}}{
m{w}}} $, gas saturation $ {S}_{{
m{n}}{
m{w}}} $, vertical displacement $ w $ and horizontal effective stress $ {sigma }_{x}^{{{'}}} $ after 1 day of injection



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-177-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
考虑和不考虑重力效应算例中点a, b和c处气饱和度$ {S}_{{
m{n}}{
m{w}}} $随时间变化图



Figure
13.
The temporal evolution of gas saturation $ {S}_{{
m{n}}{
m{w}}} $ at points a, b and c in the cases with and without gravity



下载:
全尺寸图片
幻灯片



4.
结论


本文建立了考虑毛细压力和重力效应的可压缩两相渗流与孔隙介质变形耦合作用的力学模型. 在此基础上, 分别推导出变形孔隙介质中两相渗流方程的非对称内罚伽辽金弱形式以及固体变形方程的非完全内罚伽辽金弱形式. 主要结论如下:

(1)通过对比一维Terzaghi固结问题的解析解和数值解, 验证了间断伽辽金有限元方法在求解流固耦合问题方面的可行性和准确性;

(2)开展了二维平面应变条件下和考虑重力效应作用的三维两相流固数值算例. 结果显示, 随着气体的注入, 气体饱和度和孔压随之增加, 导致多孔介质膨胀变形和有效应力降低. 由于重力的影响, 气体会上浮聚集于顶部边界;

(3)在二维平面算例中, 讨论了加罚因子对计算结果的影响. 结果表明, 在相同网格条件下, 加罚因子$ {delta }_{
m{f}} $和$ {delta }_{
m{s}} $的降低会导致流体和固体信息在局部出现不同程度的波动. 固体变形参量对加罚因子$ {delta }_{
m{s}} $更为敏感, 提高加罚因子$ {delta }_{
m{s}} $可以有效抑制位移和应力在跨越单元时的不连续性.

相关话题/计算 图片 力学 水力 软件
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 挠性航天器太阳翼全局模态动力学建模与实验研究
    引言随着航天领域的发展,现代大型柔性航天器往往安装有诸如大型太阳翼等柔性结构,为了得到可持续的能源,其尺寸日益增大、结构重量越来越轻,太阳翼的弹性振动不可避免地与航天器主体平台的运动相互耦合,这种耦合效应随着太阳翼尺寸的增大显著增强.此时,单个太阳能帆板的模态(假设模态)并不能准确反映整个太阳翼在系 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 隧道开挖影响下地层-基础体系的接触力学响应分析
    引言在地层条件软弱、周围建筑物繁多的城市环境中进行隧道的施工,不可避免需要穿越和邻近施工,隧道施工扰动将对既有建(构)筑物的力学状态产生较大影响,进而导致建筑物的沉降、变形,甚至发生破坏[1-3].在城市运行高可靠度的要求下,隧道施工引起既有结构的工程响应预测与安全控制问题受到众多专家****与工程 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于T样条的变网格等几何薄板动力学分析
    引言随着柔性轻质结构在航天、汽车以及船舶工程等领域日益广泛的应用,柔性多体系统的动力学分析也愈加重要.然而,以线弹性小变形假设为基础的,将节点位移和转动作为坐标的传统有限单元不适合解决存在大位移、大变形的柔性多体系统的动力学问题.此外,对于传统结构有限元,将几何数据转换为有限元网格数据是困难且耗时的 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于Darcy-Stokes耦合模型的多孔介质颗粒悬浮液等效黏性系数计算
    引言颗粒悬浮液广泛存在于自然界及工程应用领域,其黏性特征对悬浮液的流动行为有着重要的影响[1-4].早在1905年,Einstein[5]就研究了低浓度条件下球形固体颗粒对流体黏性的影响,给出了悬浮液等效黏度系数计算的一个强有力的理论框架,并得到了低浓度球形颗粒悬浮液的著名的Einstein黏性公式 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 新型负刚度吸能结构力学特性分析
    引言在冲击载荷作用下,吸能材料的应用具有重要的工程意义.传统的减振吸能方法主要有两种:其一,利用材料的塑性变形实现能量吸收耗散[1],如汽车保险杠和轻型自行车头盔均是基于这一原理进行结构以及超材料设计,然而破坏性的塑性变形使得材料无法重复利用;其二,利用材料的黏弹特性[2-3],实现重复性的能量吸收 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • DVC中内部散斑质量评价及计算体素点的优化选择
    引言数字体图像相关方法(digitalvolumecorrelation,DVC)是二维数字图像相关方法(two-dimensionaldigitalimagecorrelation,2DDIC)在三维体图像上的拓展.通过比较体成像设备获取的被测试样变形前后数字体图像,该方法可测量物体内部三维全场变 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 一类新型仿生起竖结构设计及其动力学分析
    引言随着科学技术的不断发展,机器人的应用范围越来越广泛,应用场景也越来越多样化.为了进行灾后搜救、管道清理、未知区域探索等任务,机器人需要能在有限的工作空间和不规则的地形下移动并完成任务.于是,许多****以蚯蚓等蠕虫为仿生对象,设计了一系列仿蠕虫机器人[1-8].受到蚯蚓的运动来源于体节的轴向变形 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 不等径颗粒间液桥力学参数及形态的试验研究
    引言作为一种自然界中广泛存在的力,液桥力的研究被广泛运用在制药、结晶提纯、废液中重金属回收、纸张脱墨处理等领域,开展液桥力的研究对工业制造具有积极的作用.对液桥的研究最早可以追溯到20世纪60年代表面科学领域,1925年Hanines率先研究了两等径颗粒间的液桥力的大小.在此基础上,DeBissch ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 颗粒增强复合材料压缩行为的位错动力学模拟1)
    丁一凡,魏德安,陆宋江,刘金铃,康国政,张旭,2)西南交通大学力学与工程学院应用力学与结构安全四川省重点实验室,成都610031DISCRETEDISLOCATIONDYNAMICSSIMULATIONSFORCOMPRESSIONOFPARTICLEREINFORCEDCOMPOSITES1)Di ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于人工弹簧模型的周期结构带隙计算方法研究1)
    冯青松*,杨舟*,郭文杰,*,2),陆建飞&,梁玉雄**华东交通大学铁路环境振动与噪声教育部工程研究中心,南昌330013&江苏大学土木工程与力学学院,江苏镇江212013RESEARCHONBANDGAPCALCULATIONMETHODOFPERIODICSTRU ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.