, 肖湘武DETERMINATION OF DISCRETE ELEMENT MODEL CONTACT PARAMETERS OF NYLON POWDER AT SLS PREHEATING TEMPERATURE AND ITS FLOW CHARATERISTICS1)
TanYuanqiang, Xiaoiangwu中图分类号:TB12
文献标识码:A
版权声明:2019力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (3799KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
选择性激光烧结(selective laser sintering,SLS)通过逐层铺粉、逐层扫描烧结的方式直接制造零件[1].由于SLS具有快捷、方便的特点,能够制造出传统方法难以实现的复杂形状结构的零件[2-3],已成功应用于汽车、航空航天、医疗等领域,是目前得到广泛推广应用的增材制造技术之一[4- 5].
SLS铺粉工艺阶段,铺覆出平整均匀和高密度的粉床是制备性能优良的成型件的前提[6].铺粉质量跟粉体流动特性相关,粉体流动性越好,其铺展特性越好.为了减少烧结成型时所需激光功率,改善烧结件翘曲和残余应力分布,铺粉工艺一般在预热温度下进行[7].预热温度对粉体的流动性有重要影响[8].
目前运用较多的粉体流动性的表征方法有：休止角、流出速度法、Hausner指数法、Carr流动性指数法、剪切法[9- 10],这些参数从不同的角度反映了粉体的流动性.然而现有的测量方法大多数都是在室温的环境下表征粉体的流动性,对高温下粉体流动性表征的研究相对较少.
SLS工艺中,粉体粒径一般小于100 $\mu $m[11],属于细颗粒范畴[12],且粉末在预热温度下为干性物料,颗粒间毛细管力忽略不计,因此,预热温度下尼龙粉末颗粒作用力主要为范德华力和静电力.与细颗粒相关的物理过程受到多种作用力的影响,范德华力属于近程力[13],是引起细颗粒团聚和黏附的主导因素.与范德华力相比,静电力不受作用距离的限制,属于远程力.近些年来,离散元法(discrete element method,DEM)在增材制造粉体流动和铺粉工艺数值模拟的研究受到大家的重视,相关领域的研究人员迅速跟进,成果不断涌现[14- 16]. 而以往数值模拟SLS铺粉工艺的研究对粉体颗粒接触模型的描述,大多仅简单的采用Hertz接触模型,忽略了细颗粒间范德华力和静电力,因此对粉体颗粒接触模型的研究有待进一步深入[17- 19].
本文选取尼龙粉末为原材料,建立了SLS工艺中171${^\circ}$C预热温度下尼龙粉末的DEM模型并对其进行了验证,对加热旋转圆筒中尼龙粉末流动过程进行了DEM数值模拟,研究了粉体粒径对尼龙粉末流动特性的影响规律,以期为增材制造粉体流动性和粉体铺展提供依据.
1 尼龙粉末离散元模型研究
1.1 尼龙粉末离散元模型
本文在Hertz-Mindlin模型基础上,结合SLS铺粉工艺,综合考虑颗粒的重力、颗粒间(颗粒与壁面间)的碰撞力、摩擦力、范德华力、静电力,来描述171${^\circ}$C预热温度下PA3200粉末的接触动力学行为.颗粒流中的粒子可以有两种运动：平移运动和旋转运动.在运动过程中,尼龙粉末可能与其周围的尼龙粉末或壁面相互作用,从而交换动量和能量.单个尼龙粉末的线运动和转动方程给出
$$\label{eq1} {m}_{ i}\frac{{d}v_i }{{d}t} = \sum\limits_j {F_{ij}^{c} } +\sum\limits_k {F_{ik}^{nc}} + F_i^{g}\tag{1}$$
$$I_i \frac{{d}w_i }{{d}t} = \sum\limits_j {M_{ij} }\tag{2}$$
式中,$F_{ij}^{c}$为尼龙粉末之间或者尼龙粉末与墙之间的接触力,$F_{ik}^{nc}$为尼龙粉末之间或者尼龙粉末与墙之间的非接触力,$F_i^{g}$为尼龙粉末$i$的自身重力. $v_i $和$w_i$分别为尼龙粉末$i$平动和转动速度;$M_{ij}$为尼龙粉末间或者尼龙粉末与墙间的转矩.
$F_{ij}^{c} $可以分解为法向接触力$ F_{nc}$ 和切向接触力$F_{tc}$.尼龙粉末$i$在法线方向的接触力$F_{nc}$由法向弹力$F_{{nc,s}} $、法向阻尼力$F_{{nc,d}}$以及接触时的范德华$F_{nc}^{vdw} $和静电力$F_{nc}^{ele} $组成
\begin{equation}\label{eq3} F_{nc} = F_{nc,s} + F_{nc,d} + F_{nc}^{vdw} + F_{nc}^{ele}\tag{3}\end{equation}
基于Hmaker理论计算的范德华力只计入了引力部分. 法向弹力$F_{nc,s} $和法向阻尼力$F_{nc,d} $可以根据Hertz-Mindlin模型得到
$$ \label{eq4} F_{n,s}^{c} = \frac{4}{3}E^\ast \sqrt {R^\ast} \delta _{n} ^{3 / 2}\tag{4}$$
$$F_{n,d}^{c} =-2\sqrt{\frac{5}{6}} \beta \sqrt {S_{n} m^\ast } v_{n}^{\overline{rel} }\tag{5}$$
式中,$E^\ast $为尼龙粉末的等效弹性模量,$R^\ast$为尼龙粉末的等效半径,$m^\ast $为尼龙粉末的等效质量,$\beta$为阻尼系数,$S_{n} $为法向接触刚度,表达式如下
$$E^\ast = \frac{E_{p} }{2(1-\gamma _{p}^2 )}\tag{6}$$
$$\label{eq7} R^\ast = \left[ {\frac{1}{R_i } + \frac{1}{R_j }}\right]^{-1}\tag{7}$$
$$\label{eq8} m^\ast = \left[ {\frac{1}{m_i } + \frac{1}{m_j }}\right]^{-1}\tag{8}$$
$$\label{eq9} \beta = \frac{{In}e}{\sqrt {{In}^2e + \pi^2} }\tag{9}$$
$$\label{eq10} S_{n} = 2E^\ast \sqrt {R^\ast\delta _{n} }\tag{10}$$
式中,$E_{p} $为尼龙粉末的弹性模量,$\gamma _{p}$为尼龙粉末的泊松比,是材料的固有属性;$m_i $和$m_j$分别为尼龙粉末$i$,$j$的质量,$e$为尼龙粉末与尼龙粉末碰撞的恢复系数,$\delta_{n} $为法向重叠量, $v_{n}^{\overline {rel} }$为接触尼龙粉末法向相对速度.
范德华力是细颗粒流中固有特性$^{[20],在研究细颗粒流问题时,经常采用Hamaker理论计算细颗粒间的范德华力[21- 22],可以得到颗粒之间和颗粒与墙面之间的范德华力分别为
$$\label{eq11} F_{PP}^{vdw} =-\frac{\partial U_{PP}^0}{\partial Z_0 } =-\frac{A_{pp} }{12Z_0^2 }\frac{d_i d_j}{d_i + d_j }\tag{11}$$
$$\label{eq12} F_{pw}^{vdw} =-\frac{\partial U_{pw}^0}{\partial Z_0 } =-\frac{A_{pw} d_i }{12Z_0^2 }\tag{12}$$
式中,$d_i $和$d_j $是颗粒$i$和$j$的直径,单位为m;$Z_0$是颗粒间的距离,单位为m;$A_{pp}$是粉末--粉末的Hamaker常数,$A_{pw}$是粉末--墙面的Hamaker常数,单位为eV.
粉体的摩擦带电主要是以粉体的输送为研究对象,涉及粉体与壁面之间以及粉体之间的摩擦带电.两个带电颗粒之间的静电力采用库伦定律来计算
\begin{equation}\label{eq13} F_{pp}^{ele} = \frac{1}{4\pi\varepsilon _0 }\frac{q_i q_j }{r_{ij}^2 } {n_{ij}}\tag{13}\end{equation}
式中,$q_i $和$q_j $ 分别是颗粒$i$和$j$的带电量,单位为C;$r_{ij}$是颗粒$i$和$j$中心之间的距离,单位为m;$\varepsilon _0$是真空介电常数;${n_{ij} } $为颗粒$i$到颗粒$j$的单位矢量.
带电颗粒与导电面之间的静电力应用镜像理论计算[24],可知颗粒与导电平面之间的静电力为
\begin{equation}\label{eq14} F_{pw}^{ele} = \frac{1}{4\pi\varepsilon _0 }\frac{q_i^2 }{\left[ {2\left( {Z_0 + s} \right)}\right]^2}{n_{pw} }\tag{14}\end{equation}
式中,真空介电常数$\varepsilon _0 = 8.85\times 10^{-12}$ F/m.修正因子$s$ = 2.57 nm,$ {n_{pw} } $为单位矢量.
绝缘粒子的摩擦带电是一个相对复杂的过程,在这个过程中,粒子上的电荷量随着接触时间呈指数增长,当电荷量的产生速率与耗散速率相等时,最终达到饱和值.而Greason方程经常被采用来研究绝缘粉末与金属壁面之间的摩擦带电[23]
\begin{equation}\label{eq15} q_i (t) = q_{is} \frac{1}{1 + \beta / \alpha }\left[{1-{e}^{-(\alpha + \beta )t}} \right]\tag{15}\end{equation}
式中,$q_i (t)$是颗粒$i$在摩擦运动过程中$t$时刻的带电量;$\alpha$和$\beta$分别是电荷产生和耗散的时间常数,本文中,模拟时间较短,可以近似认为没有电荷耗散,$\beta$=0;$q_{is} $为颗粒的饱和电荷
\begin{equation}\label{eq16} q_{ is} = q_{m} \pi d_i ^2\tag{16}\end{equation}
式中,$q_{m} $为大气环境下电荷密度常数[24 -25],其值一般取2.66$\times $10$^{-5}$ C$\cdot$m$^{-2}$.将式(15)、式(16)代入式(13)、式(14)中,可得到颗粒之间和颗粒与墙面之间的静电力分别为
$$\label{eq17} F_{pp}^{ele} (t) = \frac{\pi q_{m}^2d_i ^2d_j ^2}{4\varepsilon _0 r_{ij}^2 }(1 -{ e}^{-\alpha t})^2{n_{ij} }\tag{17}$$
$$\label{eq18} F_{pw}^{ele} (t) = \frac{1}{16\varepsilon_0 }\frac{\pi q_{m}^2 d_i ^4}{\left( {s + Z_0 } \right)^2}(1- {e}^{-\alpha t})^2 {n_{pw} }\tag{18}$$
1.2 离散元模型参数标定
1.2.1 Hamaker常数标定本文基于原子力显微镜(atomic force microscopy,AFM)工作原理,将普通AFM 探针制作成胶体颗粒探针[26 -28],通过AFM实验获得Hamaker常数,实验细节可详见文献[28].
颗粒之间的黏附力主要是由范德华吸引力和静电力的共同作用结果,为了减少静电力对黏附力的影响,在进行AFM实验测量之前先对PA3200粉末进行静电中和,此时,可以认为实验结果中的临界黏附力$F_{c}^{pp} = F_{nc}^{vdw}$,代入式(11)可得颗粒之间的Hamaker常数为\begin{equation}\label{eq19} A_{pp} =-\frac{6F_{c} Z^2}{R^\ast }\tag{19}\end{equation}经计算可以求得$A_{pp}$=7.21$\times $10$^{-20}$ J.
PA3200粉末与不锈钢之间的黏附力由范德华吸附力和静电力组成,且静电力不容忽视.颗粒与壁面的临界黏附力为
\begin{equation}\label{eq20} F_{c}^{pw} =-\frac{A_{pw} R_i }{6Z^2} -\frac{{k}_{e} \pi q_{m}^2 R_i^2 }{\varepsilon _0}\tag{20}\end{equation}
式中,$k_{e} $为电荷因子,取值为0.15.在本文中,假设范德华力的作用范围为50 nm,可以求得$A_{pw}$=9.72$\times $10$^{-20}$ J.
1.2.2 弹性模量标定
采用AFM测量了预热温度下尼龙粉末的弹性模量.图1为PA3200粉末微球样品预热温度下的典型载荷--压痕深度曲线.假设载荷直接作用在基面PA3200粉末的顶端,PA3200粉末胶体探针与PA3200粉末之间仅存在单向压缩变形,此时忽略颗粒之间的静电接触力,根据1.1节中尼龙粉末DEM接触模型可知载荷$F_{z}$与压痕深度$\delta$之间的关系如下所示
\begin{equation}\label{eq21} F_z = \frac{4}{3}E^\ast \sqrt {R^\ast } \delta _{n}^{3 / 2}-2\sqrt {\frac{5}{6}} \beta \sqrt {S_{n} m^\ast } v_{n}^{\overline {rel} }-\frac{A_{pp} R^\ast}{6Z^2}\tag{21}\end{equation}
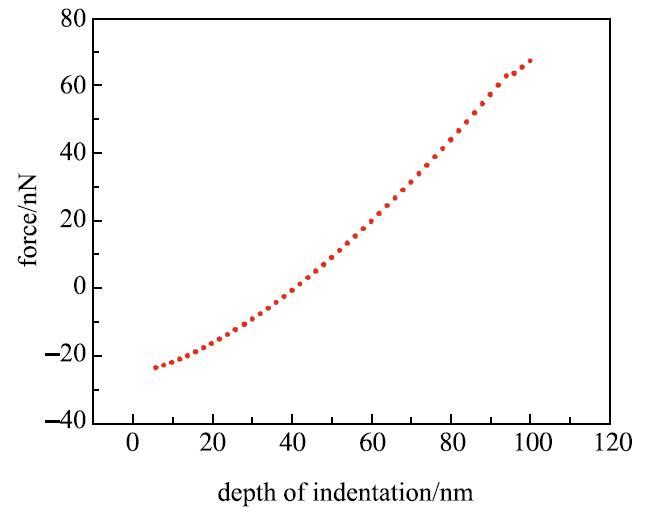显示原图|下载原图ZIP|生成PPT图1预热温度下PA3200粉末载荷--压痕深度曲线...
-->Fig. 1The load-depth of indentation curve of PA3200 powder at preheating temperature
-->
其中,颗粒探针与颗粒的法向相对速度$v_{n}^{\overline {rel} } $认为等于探针靠近颗粒时的速度为1.98$\mu $m/s, 法向阻尼力对载荷的影响非常小,忽略不计,由式(21)可得
\begin{equation}\label{eq22} E^\ast = \frac{3(F + F_{c} )}{4\sqrt {R^\ast }\delta _{n}^{3 / 2} }\tag{22}\end{equation}
结合式(6)可以求得预热温度下尼龙粉末的弹性模量为61.23MPa,此时尼龙粉末的泊松比为0.35.
1.2.3 内摩擦角标定
采用ZJ型应变控制直剪仪、绝缘手套、101-01SB恒温箱、工业电子温度计以及大功率灯管测量预热温度下尼龙粉末的内摩擦特性,获得粉末间、粉末与不锈钢的剪切实验结果如图2和图3所示.经计算,在预热温度下PA3200粉末间内摩擦系数$\mu $}$_{p}$=\ 0.4845、内摩擦角为25.85$^\circ$;PA3200粉末与不锈钢壁面之间的内摩擦系数$\mu$}$_{pw}$=0.512 1、内摩擦角为27.12$^\circ$.
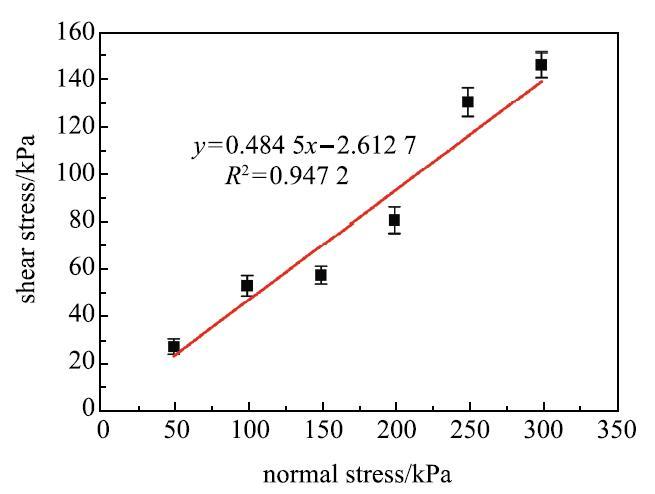显示原图|下载原图ZIP|生成PPT图2PA3200粉末间剪切试验结果...
-->Fig.2Shear test results of PA3200 powder
-->
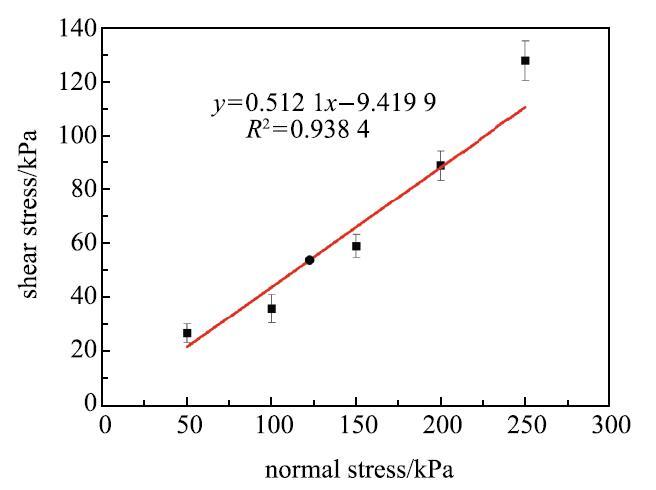显示原图|下载原图ZIP|生成PPT图3PA3200{-}不锈钢壁面剪切试验结果...
-->Fig.3Shear test results between PA3200 powder and stainless steel base surface
-->
1.2.4 电荷生成因子标定
绝缘粒子的摩擦电充电是一个相对复杂的过程,在这个过程中,粒子上的电荷量随接触时间呈指数增长,当产生率等于耗散率时[29- 30],粒子上的电荷量最终达到饱和. 通过式(15)、式(16)可知
$$\label{eq23} Q\left( t \right) = \sum\limits_{i = 1}^{ n} q_{is}\left( {1-{e}^{-\alpha t}} \right)\tag{23}$$
$$\label{eq24} \alpha =-\frac{1}{t}\ln \left( {1-\frac{Q\left(t \right)}{\displaystyle\sum\limits_{i = 1}^{i = n} {q_{m}\pi d_i^2 } }} \right)\tag{24}$$
其中,颗粒的表面积又可以通过比表面积$S_{a}$与质量$M$的乘积求得,所以电荷生成因子可以表示为
\begin{equation}\label{eq25} \alpha =-\frac{1}{t}\ln \left( {1-\frac{Q\left( t\right)}{q_{m} S_{a} M}} \right)\tag{25}\end{equation}
为了测量预热温度下PA3200粉末与不锈钢壁面摩擦带电量,研制了一套电荷测量装置,如图4所示.具体操作方法为：将PA3200粉末填入加热选装圆筒之前先采用高精度天平进行称重,并记录其数值;然后将粉末放入静电消除器中进行静电中和.中和后的粉末在加热旋转圆筒中加热并随着圆筒的低速旋转而流动,这个过程中粉末与筒壁由于不断的摩擦而带电.记录旋转圆筒运动时间,对每组实验进行多次测量,并测量不同运动时间下粉体的带电量.经计算可以得到粉体颗粒电荷质量密度为0.023 $\mu$C/g,电荷生成因子$\alpha $为0.028.
显示原图|下载原图ZIP|生成PPT图4尼龙粉末摩擦带电电荷测量装置...
-->Fig.4The friction charge measuring device for nylon powder
-->
1.3 试验结果与理论模型的比较
为了验证前面建立的预热温度下尼龙粉末DEM模型以及测量得到的力学参数的准确性,对于尼龙粉末间的靠近--接触过程进行离散单元法数值模拟,从而将实验结果与理论模型进行比较,如图5所示.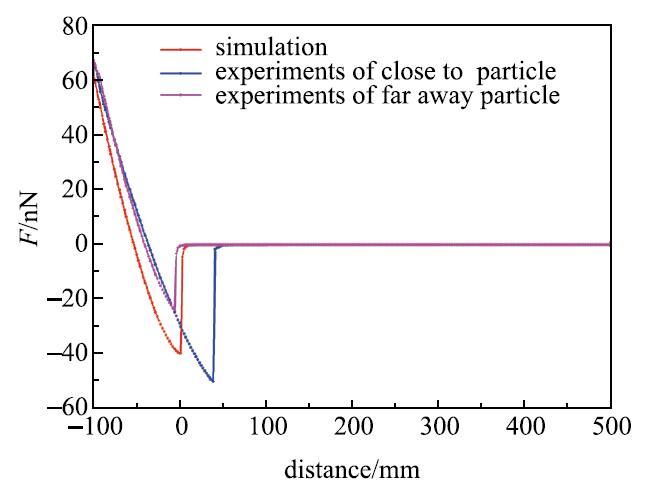
显示原图|下载原图ZIP|生成PPT图5试验结果与理论模型的比较...
-->Fig.5Comparison between experimental results and theoretical model
-->
在墙面上同一位置生成两个颗粒球,探针下移并黏附其中一个颗粒并使之一起上移一段距离,再给颗粒探针一恒定的速度向下靠近墙面上的颗粒,使其距离不断减小并发生接触,重叠量不断增大.获取颗粒探针--颗粒之间力--距离曲线如图5所示.结合DEM仿真分析结果与试验结果进行分析比较,证实模拟和实验结果二者间趋势一致,说明建立的预热温度下尼龙粉末DEM模型以及测量得到的力学参数是可信的.
2 预热温度下尼龙粉末DEM的离散元模拟
2.1 尼龙粉末离散元接触参数的确定
基于漏斗法、圆管提升法安息角实验,建立相应的离散元模型,基于EDEM-API模块编译适用于热温度下尼龙粉末DEM的离散元模拟模型,获取的预热温度下尼龙粉末颗粒DEM接触参数如表1所示.工业应用中经常采用$D_{50}$表征粉体粒径,其中$D_{50}$粒径表示累计粒径分布达到50%点的直径.Table 1
表1
表1预热温度下尼龙粉末颗粒DEM接触参数
Table 1DEM parameters of nylon powder particles at preheating temperature
| Parameters | Values |
|---|---|
| powder density/(kg m-3) | 1000 |
| powder shear modulus/MPa | 61 |
| powder Poisson's ratio | 0.35 |
| roller density/(kgm-3) | 7800 |
| roller shear modulus/GPa | 80 |
| roller Poisson's ratio | 0.3 |
| static friction coefficient of powder-roller | 0.51 |
| rolling friction coefficient of powder-roller | 0.15 |
| Hamaker constant of powder-roller/J | 9.72X10-20 |
| static friction coefficient of powder-powder | 0.48 |
| rolling friction coefficient of powder-powder | 0.24 |
| restitution coefficient of powder-powder | 0.11 |
| Hamaker constant of powder-powder/J | 7.21X10-20 |
| charge generation factor | 0.028 |
| powder D50/^m | 50 |
新窗口打开
2.2 预热温度下尼龙粉末DEM模型的验证
为了验证预热温度下尼龙粉末DEM模型的准确性,对加热旋转圆筒中尼龙粉末流动过程进行了DEM模拟.为了将数值模拟结果和试验结果进行对比,本文设计了一种可实时控温控速的粉体流动性滚筒测量试验台,滚筒试验台的主要工作原理详见参考文献${[31].对预热温度下尼龙粉末在加热旋转圆筒中的流动过程进行试验和DEM数值模拟研究.设置圆筒的转速为10 r/min,尼龙粉末在圆筒中的填充率为0.3.尼龙粉末崩塌角试验与仿真结果图6所示,可知,DEM数值模拟获取的结果能够和实验结果有吻合较好,验证了预热温度下PA3200粉末DEM模型的可靠性和准确性.
显示原图|下载原图ZIP|生成PPT图6PA3200粉末崩塌角实验与DEM仿真结果...
-->Fig.6The avalanche angle experiment and DEM simulation Results of PA3200 powder
-->
2.3 粉体粒径对尼龙粉末流动特性的影响规律
尼龙粉末物性参数(粉末形貌、粉末粒径、粉末粒径分布)都直接影响其流动性能.尼龙粉末物性参数难以控制,采用实验方法难以获取这些参数对粉体流动特性的定量影响.因此,本文采用DEM仿真研究了预热温度下加热旋转圆筒中尼龙粉末粉体粒径对其流动行为的影响规律.不同粒径工况下的DEM数值模拟结果如图7所示.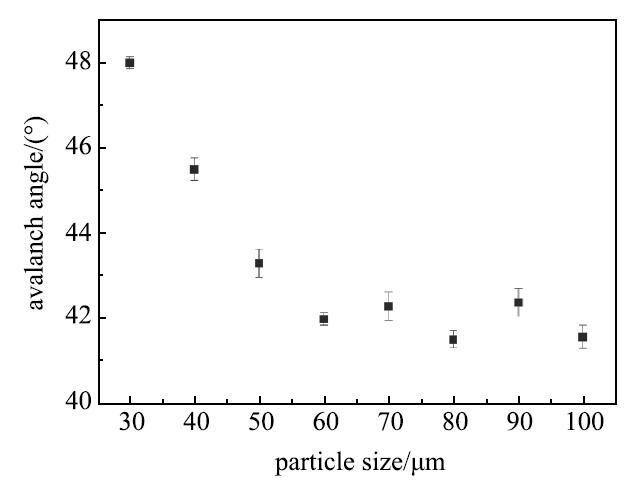
显示原图|下载原图ZIP|生成PPT图7预热温度下PA3200粉粒径对崩塌角的影响...
-->Fig.7Effect of particle size of PA3200 powder on avalanche angle at preheating temperature
-->
从图7中可知：在其他参数条件一定的情况下,随着尼龙粉末粒径的增大,尼龙粉末在加热旋转圆筒中的崩塌角减小,粉体流动特性增强.这主要是因为：位于筒壁附近的粉末颗粒属于被动流,颗粒之间没有相对运动,此时颗粒沿着筒壁上升的高度主要由颗粒与筒壁之间的黏附力决定.当粉体粒径增大时,粉体和筒壁之间的黏附力(范德华力和静电力)增大,颗粒和筒壁的黏附力会促使颗粒沿着筒壁转动而上升.且大颗粒与加热旋转圆筒壁面之间的黏附力较大,故大颗粒靠近加热旋转圆筒壁面,小颗粒会在颗粒中心形成团聚.圆筒中最外层的颗粒属于自由流动层,其对整个粉体颗粒系统的运动起决定作用[32- 33].尼龙粉末之间静电力为斥力,当粉末粒径增大时,粉末间的范德华力和静电力都增大,但是静电力的增大速率要大于范德华吸引力的增大速率,故此时颗粒之间的黏附力会减小,而颗粒之间的黏附力是阻碍颗粒自由流动的主导因素,因此,增大尼龙粉末粒径可以改善其流动性能.
通过对不同粒径分布且$D_{50}$=90mm工况下的尼龙粉末流动特性进行DEM数值模拟,得出粉末粒径分布为均匀分布和高斯分布时的崩塌角分别为40.37$^\circ$$\pm$0.26$^\circ$和42.41$^\circ$$\pm $0.33$^\circ$.尼龙粉末粒径分布均匀时,粉末沿着旋转圆筒壁面上升的最大高度会相对减小,且颗粒间的团聚行为相对减弱,粉末崩塌角也减小,尼龙粉末流动特性增强.因此,减小用于SLS工艺的尼龙粉末粒径分布范围是提高粉末流动特性的有效手段,但是,会增加尼龙粉末制备成本.所以,以提高铺粉质量为目的,通过研究尼龙粉末粒径分布范围较广时的SLS铺粉工艺过程,并试图降低铺粉质量对粉体粒径分布的依赖程度有利于SLS工艺得以顺利推广和铺粉工艺研究中必不可少的关键\环节.
3 结论
本文选取SLS技术中的尼龙粉末为原材料,建立了预热温度下尼龙粉末DEM模型并对其进行了验证,对加热旋转圆筒中尼龙粉末流动过程进行了DEM数值模拟,研究了粉体粒径对尼龙粉末流动特性的影响规律.研究结果表明:(1)对考虑细观作用力的预热温度下尼龙粉末DEM模型进行了研究,基于Hamaker理论模型计算颗粒--颗粒以及颗粒--壁面之间的范德华力,采用库伦定律计算颗粒之间的静电力,并基于镜像力模型计算颗粒--壁面的静电力,并在Hertz-Mindlin模型基础上引入了静电和范德华接触力来描述尼龙粉末的接触动力学行为.
(2)采用实验方法获取了预热温度下尼龙粉末力学特性参数(Hamaker常数、弹性模量、内摩擦角以及电荷生成因子),将这些力学特性参数代入建立的预热温度下尼龙粉末DEM模型中,与实验结果进行对比验证了本模型的合理性.
(3)在加热旋转圆筒中,尼龙粉末崩塌角随着粉体颗粒粒径的增大而减小,粉体流动性增强;相对于粒径为高斯分布的尼龙粉末,均匀分布的尼龙粉末颗粒流动性更强,导致铺粉质量对粉体粒径分布的依赖性较高.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . . |
| [6] | . . |
| [7] | . . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | . |
| [26] | . . |
| [27] | . |
| [28] | . . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | . . |
