何俊¹, 李智^1,2, 吴晓林^1,21 湖南农业大学动物科技学院,中国长沙 410128
2 美国纽勤公司生物信息与生物统计部,美国林肯市 68504

Using Restricted Standardized Linear Regression Model to Estimate Genomic Breed Composition in Composite Breed Animals

HE Jun¹, LI Zhi^1,2, WU XiaoLin^1,21 College of Animal Science and Technology, Hunan Agricultural University, Changsha 410128, China
2 Biostatistics and Bioinformatics,Neogen GeneSeek, Lincoln, NE 68504, USA

责任编辑: 林鉴非
收稿日期:2019-03-1接受日期:2019-05-30网络出版日期:2020-01-01

基金资助:

湖南省科技计划重点项目.2018NK2081 长沙市科技计划重点项目.kq1801014 湖南省****项目和湖南省畜禽安全协同创新中心项目

Received:2019-03-1Accepted:2019-05-30Online:2020-01-01
作者简介 About authors
何俊,Tel：0731-84618176;E-mail：hejun@hunau.edu.cn





摘要
【背景】合成品种是由至少两种纯种（祖先）培育的新品种,旨在兼顾祖先品种的有利遗传特征,并且可以长期保持后代的杂种优势而不需要每个世代都杂交。合成品种的遗传稳定,不同于杂交群体,因而可以像纯种一样繁育。实践中,估计合成品种的祖先品种对每个动物个体基因组的遗传贡献比例,即基因组品种构成（genomic breeding composition, GBC）,在畜禽品种登记、品种培育历史和品种构成分析、品种保护和杂交优势预测等方面有着非常重要的意义。利用基因组SNP基因型数据,采用合适的数学模型和统计方法,可以鉴定现有纯种品种的动物个体或纯种品种在杂交个体基因组的遗传贡献比例,而估计合成品种GBC的方法和研究都较少。【目的】线性回归是估计GBC的常用方法之一,但也存在诸多的问题。本研究旨在提出和评估一种约束的标准化线性回归方法（restricted standardized linear regression, RSLR）,作为传统线性回归方法的改进方法,应用于估计合成品种动物个体的GBC。【方法】采用肉牛王牛（Beefmaster）及其3个祖先品种（婆罗门牛、海福特牛和短角牛）的GGP 50K SNP芯片所测定的基因型数据,通过计算其基因频率和欧氏距离,利用层次聚类分析方法解析了4个动物群体的遗传关系,然后提出了RSLR方法,估计合成品种动物个体GBC的原理和方法。为了检验该方法的估计效果,从基因型数据中选择了均匀分布的分别包含1 000、5 000、10 000、20 000、30 000、40 000个SNP以及3个祖先品种共有的47 900个SNP的7个子集,分别采用RSLR和传统线性回归（linear regression, LR）两种方法估计了4 323头肉牛王牛的GBC,并比较了两种方法的计算结果。【结果】聚类分析的结果与4个品种间的遗传关系相吻合,表明肉牛王牛与婆罗门牛的遗传关系最近,遗传距离小于其与海福特牛和短角牛的遗传距离。LR方法估计的GBC会低估婆罗门牛（0.459—0.462）和短角牛（0.208—0.212）对于肉牛王牛的基因组贡献,同时高估海福特牛（0.326—0.333）的基因组贡献。但RSLR方法估计的肉牛王牛GBC的平均值与3个祖先品种预期的基因组贡献比例比较吻合：婆罗门牛为0.497—0.503,海福特牛为0.262—0.274,短角牛为0.229—0.231。此外,LR方法估计GBC的标准差和变异系数明显大于用RSLR估计的结果。当SNP子集数量在20 000以上时,LR方法估计牛肉王牛的3个祖先品种婆罗门牛、海福特牛和短角牛基因组贡献的标准差分别为0.048、0.032和0.051—0.052,变异系数分别为10.46%—10.50%、9.61%—9.76%和23.94%—25.00%,而RSLR方法估计的标准差,3个祖先品种对应为0.021、0.021—0.022和0.024—0.025,变异系数分别为4.18%—4.20%、7.89%—8.33%以及10.26%—10.68%。【结论】用RSLR方法估计的合成品种肉牛王牛动物个体的GBC,比LR方法的估计结果更加准确,估计的结果比LR方法估计的结果更稳定,且估计的一致性也更好,可以作为线性回归方法的改进,应用于估计合成品种动物个体GBC。
关键词： SNP芯片;线性回归;合成品种;基因组品种构成

Abstract
【Background】A composite breed is made up of two or more purebreds (ancestries), designed to combine advantageous genetic characteristics from the ancestry breeds and to retain heterosis in future generations without crossbreeding. Unlike crossbred populations, composite variety can be maintained as a purebred. In practice, knowing the ratio of genomic contribution of an ancestry breed to individual composite animals, referred to as the genomic breed composition (GBC), is of importance in animal breed registration, tracing breeding history and population structure, breed conservation, and the prediction of heterosis. Using a set of genomic SNP genotype and an appropriate statistical model, GBC of a purebred or crossbred animal can be estimated. So far, studies on statistical methods devote to the estimation of GBC in composite breed are limited. Linear regression (LR) analysis was commonly used to estimated GBC of individual animals, but it had some limitations such as the coefficients of ancestral breeds does not add to 1.【Objective】The purpose of the present study was to propose and evaluate the use of restricted standardized regression analysis, as an improved approach of linear regression analysis to estimate GBC in composite animals. 【Method】The dataset consisted of 4 323 Beefmaster cattle and purebred animals belonging to their ancestry breeds, namely Brahman, Hereford and Shorthorn. All these animals were genotyped by GeneSeek Genomic Profiling (GGP) bovine 50K SNP chips. Allelic frequencies of each SNP and the Euclidean distance between breeds were computed for the four animal populations, and their genetic relationships were revealed by Hierarchical Clustering based on Euclidean distance of SNP allele frequencies among the four populations. Genomic breed composition of the 4 323 Beefmaster cattle were estimated using RSLR and LR, respectively, based on 7 SNP panels(1K, 5K, 10K, 20K, 30K, 40K, and all the common 47 900 SNP). 【Result】The results of the clustering analysis agreed well with the genetic relationships of Beefmaster and the three ancestral breeds, showing that Beefmaster was more related to Brahman than Herdford and Shorhorn. Linear regression analysis underestimated the genomic contribution ratios of Brahman cattle (0.459-0.462) and shorthorn cattle (0.208-0.212) and at the same time overestimated that of Hereford cattle (0.326-0.333) to Beefmaster cattle. In contrast, estimated GBC of the 4 323 Beefmaster cattle obtained by using RSLR agreed well with expected genomic contribution ratios of the three ancestry breeds, which were 0.497-0.503 for Brahman, 0.262-0.274 for Hereford, and 0.229-0.231 for Shorthorn, respectively. Furthermore, the standard deviations (SD) and coefficients of variance (CV) of GBC obtained by using LR were larger than those obtained using RSLR. With 20K or more SNPs as the reference panels, the SD of GBC estimated by using LR were 0.048 (Brahman), 0.032 (Hereford) and 0.051-0.052 (Shorthorn), and the corresponding CV were 10.46%-10.50% (Brahman), 9.61%-9.76% (Hereford) and 23.94%-25.00% (Shorthorn), respectively. Using RSLR, on the other hand, the SD of GBC pertaining to each of the three ancestry breeds were 0.021 (Brahman), 0.021-0.022(Hereford) and 0.024-0.025 (Shorthorn), and the responding CV were 4.18%-4.20% (Brahman), 7.89%-8.33% (Hereford) and 10.26%-10.68% (Shorthorn), correspondingly. 【Conclusion】The RSLR method provided more accurate and consistent estimates of GBC in the 4 323 Beefmaster cattle than the LR approach. It thus provided a new statistical method for the estimation of GBC in composite animals.
Keywords：SNP chip;linear regression;composite breeds;genomic breed composition


PDF (660KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
何俊, 李智, 吴晓林. 约束标准化线性回归法估计合成品种动物基因组品种构成[J]. 中国农业科学, 2020, 53(1): 191-200 doi:10.3864/j.issn.0578-1752.2020.01.018
HE Jun, LI Zhi, WU XiaoLin. Using Restricted Standardized Linear Regression Model to Estimate Genomic Breed Composition in Composite Breed Animals[J]. Scientia Acricultura Sinica, 2020, 53(1): 191-200 doi:10.3864/j.issn.0578-1752.2020.01.018

0 引言

【研究背景】合成品种是综合了两个或更多纯种品种的性状特征而培育的新品种,例如肉牛王牛、布兰格斯牛等。合成品种不同于一般的简单杂交群体,合成品种遗传稳定,可以像纯种品种一样进行本品种内繁育（包括一定程度的近交繁育）。事实上,现在许多的纯种品种,如果追溯到足够久远的年代,也都是合成品种。合成品种兼顾了其祖先品种性状的优势,同时又可以避免这些品种的一些劣势,而不需要继续杂交繁育,因此具有较高的经济价值。通过合成杂交繁育而培育的肉牛、奶牛、绵羊、猪和家禽,已经成为动物商品生产的一个重要方式,为畜禽商品生产提供了优质的种源^[1]。合成品种动物个体的基因组品种构成（genomic breed composition, GBC）,是指祖先品种对于该个体的基因组遗传率,也可以简单理解为合成品种动物个体的基因组与祖先品种基因组的相似性的百分率。例如,布兰格斯牛是安格斯牛和婆罗门牛的杂交后裔。从群体平均而言,布兰格斯牛在遗传上有3/8的婆罗门牛和5/8的安格斯牛血统^[2]。肉牛王牛是20世纪30年代用海福特母牛和短角牛母牛与婆罗门公牛杂交培育而成的肉牛品种,平均含有25%的海福特牛、25%的短角牛以及50%的婆罗门牛血统^[2]。【研究意义】在动物遗传育种中,估计动物个体的GBC具有广泛的应用价值,如了解和评估某动物品种的育成历史和品种纯度、地方品种保种、杂种优势预测以及设计杂交计划和制定杂交育种方案等^[3,4]。【前人研究进展】动物个体的GBC通常可以用系谱资料或基因组分子标记来估计。从理论上讲,后者比前者估计的GBC更准确,因为用基因组分子标记估计GBC,不仅不受系谱错误的影响,还可以反映出实际的遗传抽样导致GBC的偏差。并且,用系谱计算的是平均（期望）GBC,没有反映出孟德尔抽样所导致的亲本遗传贡献率上的偏差^[5],而用基因组标记估计的是真实GBC。因而利用一套全基因组的SNP基因分型数据,采用合适的数学模型和统计方法,可以鉴定现有纯种品种的动物个体,或是估计纯种品种在杂交个体基因组的遗传贡献比例^[6,7,8,9]。采用SNP标记估计动物个体GBC的统计方法很多^{[10,11,12,13]},例如主成分分析方法^[14,15,16]、混合分布方法^[3,8,17-18]、线性回归分析方法^[10,11]。此外,DODDS等^[19]将基因组预测模型（基因组BLUP）方法应用于动物个体基因组品种构成的估计。在这些方法中,线性回归模型的方法比较简便。该方法以参考（祖先）品种的等位基因频率作为自变量,待测动物的基因型为依变量,计算参考群体的基因频率对于每个个体等位基因计数的回归系数。该方法目前已用于估计猪和牛的品种遗传构成^[3,11,20-21]。【本研究切入点】线性回归方法是估计GBC的最常用方法之一。但是,线性回归模型估计的GBC实际上是各祖先的基因频率对于个体动物基因型的回归系数。对于动物个体而言,其多个祖先品种的回归系数之和并不一定等于1,因为回归系数是有理实数,其数值可以超过1,也可以为负数。因此,用传统线性回归模型估计的GBC需要校正,使其和为1^[3,6,8]。【拟解决的关键问题】本研究一是利用约束条件下的标准化变量的线性转换,提出了一个改进的线性回归方法来估计GBC,称为约束的标准化变量线性回归分析（restricted standardized linear regression,RSLR）方法。该方法不需要对所估计的祖先品种的回归系数近似校正,而是直接估计出动物个体的GBC;二是以合成品种肉牛王牛为例,比较了RSLR方法和传统的线性回归方法（linear regression,LR）估计GBC的实际效果,为估计合成品种动物个体的GBC提供更为合适的估计方法。

1 材料与方法

1.1 试验材料

收集了4 323头肉牛王牛,68头婆罗门牛,1 232头短角牛和2 423头海福特牛的GGP 50K SNP基因型数据。基因型数据由美国纽勤GeneSeek公司提供,每个个体有49 463个SNP位点的基因型。缺失基因型通过FImpute软件来填充^[22]。在基因型数据中,删掉Y染色体和线粒体上的SNP基因型,保留芯片共有的47 900个SNP用于后续分析。首先计算了4个品种所有SNP的等位基因频率,利用品种间基因频率的欧氏距离 ^[3,8,23]进行Ward.D2层次聚类分析^[24,25,26],解析了4个品种的群体结构;所有计算和分析过程均采用R及自编的R程序包完成。4个群体的动物数量及GGP 50K SNP的小等位基因频率（minor allele frequency,MAF）的群体均值和标准差列于表1。

Table 1
表1
表14个牛群体的动物个体数目以及GGP 50K SNP芯片的基本信息
Table 1Number of animals and summary information of GGP 50K bovine SNP genotypes for the four experimental cattle populations

	群体 Population	动物数量 Number of animals	SNP数量 Number of SNPs	小等位基因频率 MAF
肉牛王牛 Beefmaster	4323	49463	0.310±0.141
婆罗门牛 Brahman	68	49463	0.248±0.139
短角牛 Shorthorn	1232	49463	0.282±0.145
海福特牛Hereford	2423	49463	0.270±0.150

新窗口打开|下载CSV

1.2 约束的标准化变量线性回归分析方法

通过约束条件下标准化变量的线性转换,改进了传统的线性回归模型估计GBC的方法。该方法提供的标准化线性回归系数可以作为其基因组品种构成的直接估计,因而不再需要对线性回归系数进行校正。该方法的具体过程介绍如下。

设g为一个个体所有M个SNP的基因型向量（M×1）,其中SNP基因型分别用0 (AA)、1 (AB)、2 (BB) 表示。设F=（f₁ … f_T）是一个M×T的参考群体（祖先品种）基因频率的向量,其中f_j为一个M×1的向量,包含第j个参考群体中所有SNP座位的等位基因（例如B等位基因）的频率j=（1,…,T）。因此,GBC可以采用下列的线性回归模型估计：

（1） $g=1\mu +\sum\nolimits_{j=1}^{T}{{{f}_{j}}{{b}_{j}}+e}$
式中,μ是总体均数,b=(b₁ … b_T)′ 是T×1的品种回归系数向量,e 是误差向量。以上即为LR模型估计GBC的方法。理论上,每个动物个体的GBC之和应该为1。但在LR模型中,对每一个动物个体而言,T个品种的回归系数之和并不一定等于1,因此,用LR方法估计GBC需要对回归系数近似校正,使其和为1^[3,6,8]。

如果对上述线性回归模型中的线性变量先标准化,然后约束标准化的（祖先品种）线性回归系数为1,就可以避免对回归系数进行近似校正。因此标准化的（祖先品种）线性回归系数可以直接作为GBC的估计值。

首先计算式（1）的平均值：

（2）$\bar{g}=1\mu +\sum\nolimits_{j=1}^{T}{{{{\bar{f}}}_{J}}{{b}_{j}}}$
因为E(μ)=μ,E(e)=0。然后将线性变量标准化,即将式（1）两边同时减去式（2）两边的相应的平均值,然后再除以g的标准差（σ_g）,这样可得到：


（3）$\frac{g-\bar{g}}{{{\sigma }_{\text{g}}}}=1\times \frac{\mu -\mu }{{{\sigma }_{\text{g}}}}+\sum\nolimits_{j=1}^{T}{\left\{ \frac{{{f}_{j}}-{{{\bar{f}}}_{j}}}{{{\sigma }_{\text{g}}}}\times b{}_{j} \right\}}+\frac{e}{{{\sigma }_{\text{g}}}}
=\sum\nolimits_{j=1}^{T}{\left\{ \frac{{{f}_{j}}-{{{\bar{f}}}_{j}}}{{{\sigma }_{{{f}_{j}}}}}\times \frac{{{\sigma }_{{{f}_{j}}}}}{\sigma {}_{g}}b{}_{j} \right\}}+\frac{e}{{{\sigma }_{\text{g}}}}$

式中,σ_fj为第j个参考群体（祖先品种）的M个SNP的等位基因(例如B)频率的标准差。令$y=\frac{g-\bar{g}}{{{\sigma }_{g}}}$,${{x}_{j}}=\frac{{{f}_{j}}-{{{\bar{f}}}_{j}}}{{{\sigma }_{{{f}_{j}}}}}$,${{p}_{j}}=\frac{{{\sigma }_{{{f}_{j}}}}}{\sigma {}_{g}}b{}_{j}$,$\varepsilon =\frac{e}{\sigma {}_{g}}$,则式（3）可进一步简化为：

（4） $y=\sum\nolimits_{j=1}^{T}{\{{{x}_{j}}}\times {{p}_{j}}\}+\varepsilon$
式中,y为标准化的基因型向量（M×1）,x_j为第j个参考群体（祖先品种）的标准化等位基因频率向量（M×1）,p_j为标准化的回归系数,即通径系数^[27]。

从祖先品种对动物个体基因组遗传贡献的角度看,每个个体的GBC总和应该等于1。因此在$\sum\nolimits_{j=1}^{T}{{{b}_{j}}=1}$的约束条件下做回归变量的线性转换。令${{p}_{T}}=1-\sum\nolimits_{j=1}^{T-1}{{{p}_{j}}}$,则式（4）可变为：

（5） $y-{{x}_{T}}=\sum\nolimits_{j=1}^{T-1}{\{({{x}_{j}}}-{{x}_{T}})\times {{p}_{j}}\}+\varepsilon$
又令 w=y-x_T,z_j= x_j-x_T,c_j= p_j,因此式（5）可以表示如下：

（6） $w=\sum\nolimits_{j=1}^{T-1}{\{{{z}_{j}}}{{c}_{j}}\}+\varepsilon$
式中,c_j为第j个参考品种（群体）的GBC,j = 1, …, T-1。最后一个参考群体（祖先品种）的GBC（c_T）可通过c_T=1-（c₁+…+c_M-1）进行计算。

1.3 SNP子集的选择

使用了7个SNP子集估计肉牛王牛动物个体的GBC,其中6个为从GGP 50K SNP中选择的均匀分布的SNP子集,SNP的数目分别为1 000、5 000、10 000、20 000、30 000和40 000。还有一个SNP子集为包括了数据清理后的全部共有的47 900 SNP。

2 结果

2.1 4个品种的群体聚类分析

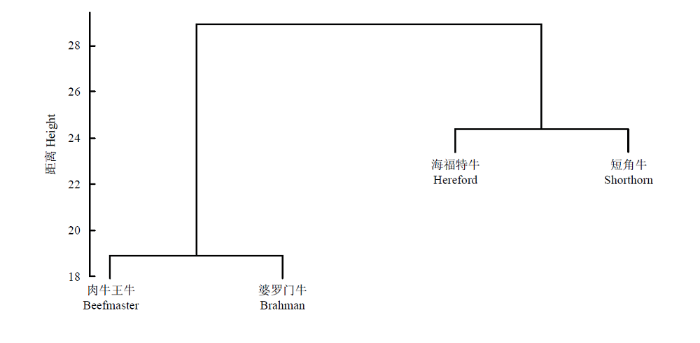
为了了解四个品种的群体结构和遗传背景,对4个群体的聚类分析表明（图1）,肉牛王牛和婆罗门牛先聚成一类,然后和聚成一类的海福特牛和短角牛再聚在一起,这与肉牛王牛的3个祖先品种的血缘构成比例是相符合的,婆罗门牛占血缘构成的50%,所以和肉牛王牛遗传距离最近,其他两个祖先品种各占25%,相对于肉牛王牛而言,它们距离相似,因而聚成一类。

图1

新窗口打开|下载原图ZIP|生成PPT
图1四个品种的群体结构分析

Fig. 1Analysis of population structure of four breeds

2.2 7个子集的SNP在染色体上的分布

选择了6个均匀分布的SNP子集以及数据清理后的全部47 900 SNP,每个SNP子集中的SNP数目从1 000到47 900不等,每个子集中的SNP在每条染色体上的分布数量见表2。

Table 2
表2
表2选择的7个子集中的SNP数量在染色体上的分布
Table 2SNP number distribution in 7 selected SNP panels in each chromosome

染色体 Chromosome	SNP子集 SNP panel
	500	1000	3000	5000	10000	20000	30000	40000	47900
0	35	69	205	341	682	1364	2045	2727	3265
1	26	53	161	268	536	1072	1608	2144	2567
2	24	47	140	235	469	938	1407	1876	2247
3	22	44	133	221	443	886	1330	1772	2123
4	20	40	119	198	396	791	1186	1582	1894
5	22	45	135	225	450	900	1351	1801	2157
6	22	43	129	215	429	859	1288	1718	2057
7	19	39	116	193	386	772	1157	1543	1848
8	19	37	113	189	379	757	1136	1514	1812
9	19	38	113	187	374	748	1123	1497	1793
10	18	36	109	182	364	728	1091	1455	1742
11	18	37	111	186	372	745	1118	1490	1785
12	15	30	88	146	291	581	871	1162	1391
13	16	31	95	159	318	636	954	1272	1523
14	15	31	92	154	308	616	925	1233	1477
15	16	31	93	154	309	618	926	1235	1478
16	13	27	80	133	266	533	800	1067	1279
17	13	26	78	130	260	520	779	1039	1244
18	13	26	80	133	265	530	796	1061	1271
19	13	25	75	126	252	504	755	1007	1205
20	14	28	84	139	279	557	836	1114	1335
21	12	24	72	121	242	484	727	969	1160
22	11	22	64	106	211	423	633	845	1011
23	10	20	62	104	208	416	625	832	998
24	11	23	67	111	223	446	668	892	1067
25	8	15	45	76	152	303	455	606	726
26	9	18	55	91	182	365	547	730	874
27	7	15	45	76	151	301	453	603	722
28	9	17	50	82	164	329	492	657	787
29	8	17	53	89	179	357	537	716	857
X	23	46	138	230	460	921	1381	1841	2205

0号染色体表示该SNP所在的染色体信息未知 Chromosome 0 indicates that the information of the chromosome where the SNP is located is unknown

新窗口打开|下载CSV

2.3 肉牛王牛祖先品种的GBC估计

分别用LR和RSLR方法,估计了4 323头肉牛王牛的GBC（表2）。用LR方法估计的3个祖先品种对于肉牛王牛的GBC分别为：0.457—0.463（婆罗门牛）,0.322—0.338（海福特牛）以及0.208—0.216（短角牛）标准差依次分别为0.048—0.060、0.032—0.054、0.051—0.073。采用RSLR方法估计3个祖先品种对于肉牛王牛的GBC分别为：0.497—0.503（婆罗门牛）、0.262—0.274（海福特牛）和0.229—0.235（短角牛）,3个品种的标准差依次分别为：0.021—0.029、0.021— 0.036、0.024—0.038。可见,用RSLR方法估计的肉牛王牛的GBC比LR方法所估计的GBC更加接近于所期望的群体均值。从所估计的GBC中位数看也是如此（表3）。相比之下,LR方法估计的GBC与期望的GBC偏差较大,特别是低估了肉牛王牛与婆罗门牛的基因组相似性,同时高估了肉牛王牛与海福特牛的基因组相似性。

Table 3
表3
表3两种回归分析方法和7个SNP集分别估计的肉牛王牛祖先品种的GBC
Table 3Estimated GBC for Beefmaster cattle two linear regression methods and seven SNP panels, respectively

方法 Method	SNP子集 SNP panel	婆罗门牛 Brahman					海福特牛 Hereford					短角牛 Shorthorn
		平均数 Mean	标准差 SD	中位数 Median	变异系数CV(%)		平均数 Mean	标准差 SD	中位数 Median	变异系数CV(%)		平均数 Mean	标准差 SD	中位数 Median	变异系数CV(%)
LR	1000	0.462	0.060	0.465	12.99		0.326	0.054	0.327	16.56		0.212	0.073	0.206	34.43
	5000	0.462	0.050	0.465	10.82		0.322	0.037	0.323	11.49		0.216	0.055	0.210	25.46
	10000	0.463	0.049	0.466	10.58		0.322	0.034	0.322	10.56		0.215	0.053	0.206	24.65
	20000	0.459	0.048	0.463	10.46		0.328	0.032	0.328	9.76		0.213	0.051	0.206	23.94
	30000	0.457	0.048	0.461	10.50		0.330	0.032	0.331	9.70		0.213	0.052	0.204	24.41
	40000	0.459	0.048	0.463	10.46		0.333	0.032	0.333	9.61		0.208	0.051	0.200	24.52
	47900	0.459	0.048	0.464	10.46		0.333	0.032	0.333	9.61		0.208	0.052	0.199	25.00
RSLR	1000	0.497	0.029	0.498	5.84		0.274	0.036	0.275	13.14		0.229	0.038	0.227	16.59
	5000	0.501	0.023	0.501	4.59		0.267	0.025	0.267	9.36		0.231	0.027	0.229	11.69
	10000	0.503	0.022	0.504	4.37		0.262	0.023	0.261	8.78		0.235	0.025	0.233	10.64
	20000	0.502	0.021	0.502	4.18		0.264	0.022	0.265	8.33		0.234	0.025	0.231	10.68
	30000	0.500	0.021	0.501	4.20		0.266	0.022	0.267	8.27		0.234	0.024	0.231	10.26
	40000	0.501	0.021	0.501	4.19		0.266	0.022	0.267	8.27		0.233	0.024	0.230	10.30
	47900	0.501	0.021	0.501	4.19		0.266	0.021	0.266	7.89		0.234	0.024	0.231	10.26

新窗口打开|下载CSV

比较了LR和RSLR两个方法用7个不同SNP子集计算的GBC的变异系数（表3）。可以看出：第一,LR方法估计GBC的变异系数（10.46%—34.43%）明显大于用RSLR方法计算的GBC变异系数（4.18%—16.59%）,表明用RSLR方法估计GBC的个体间差异要远小于LR方法。第二,两个方法估计的GBC的变异系数都随着子集SNP数增加而降低,但是,RSLR估计的GBC的变化趋势也要远小于LR估计的GBC的变化趋势。例如,当SNP数由1 000逐步增加到47 900时,用LR估计3个祖先品种的遗传贡献比例分别由12.99%降到10.46%（婆罗门牛）,16.56%降到9.61%（海福特牛）,34.43%降到25.00%（短角牛）。与此相比,RSLR方法在7个SNP子集中,除了1 000 SNP时估计的变异系数稍高,随着SNP数增加,3个祖先品种的变异系数都比较小,而且取值范围都比较接近,分别为4.19%—4.59%（婆罗门牛）,7.89%—9.36%（海福特牛）和10.26%—11.69%（短角牛）。两个方法都表明随着SNP数的增加,GBC估值在个体间的变异呈现降低的趋势。总体而言,用回归模型的方法,GBC估值的变异系数在5 000 SNP以上基本都趋于稳定。

作为初步的研究结果,本研究参考群体（祖先品种）中婆罗门牛的样本数目偏少,因此有必要将来用更大的参考群体样本进行验证。从本研究的结果看,所估计的GBC与预期的GBC基本吻合,表明估计的基因型频率大体上是比较准确的。小样本数据中主要对MAF很低的SNP的基因频率估计偏差比较大（如稀有小等位基因频率位点）,但这些SNP等位基因频率的偏差,对估计GBC的影响非常有限。

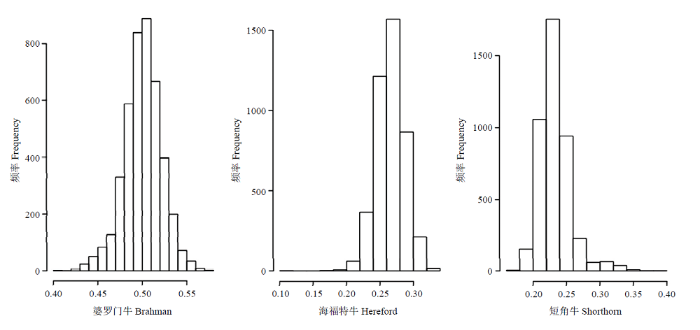
从动物个体看,估计肉牛王牛个体的3个祖先品种的GBC有一定的变化幅度,这是由于在品种繁育过程中实际遗传抽样的结果。如以RSLR方法用全部47 900 SNP估计的结果看,GBC的范围为：[0.401,0.575]（婆罗门牛）、[0.116,0.338]（海福特牛）、[0.167,0.393]（短角牛）;GBC的95%的置信区间为：[0.454,0.541]（婆罗门牛）、[0.223,0.308]（海福特牛）、[0.197,0.302]（短角牛）。RSLR方法用全部47 900 SNP估计肉牛王牛个体的3个祖先品种GBC的分布见图2。

图2

新窗口打开|下载原图ZIP|生成PPT
图2采用RSLR方法用全部47900 SNP估计3个祖先品种GBC的分布

Fig. 2Distribution of genomic breeding composition of three parental breeding estimated in 47900 SNP by RSLR

3 讨论

3.1 用线性回归的方法估计GBC

用线性回归方法估计动物GBC,方法简单实用,是一个非常值得推广的方法。但传统的LR方法估计的GBC实际上是动物个体基因型对于参考群体（祖先品种）相应等位基因频率的回归系数,就数值而言,回归系数可以取任何一个实数数值。因此每个个体的所有祖先品种的回归系数之和不一定等于1。VANRADEN等^[6]提出一个校正品种回归系数的方法,用校正后的回归系数的相对值作为GBC的估计,但是该校正方法在计算上比较繁琐。作者等曾提出了一个简化方法,即将所有负回归系数设为零,然后计算每个个体的参考群体回归系数的相对值作为GBC的估计值^[3,8]。这两个方法在结果上接近,然而这些校正方法是经验式的,没有任何的理论依据。

本研究采用标准化线性变量的约束条件作为LR的改进方法,约束条件是标准化的回归系数之和为1。这样就可以避免对于传统回归系数的校正。当祖先品种间完全没有遗传亲缘关系的时候,这个约束条件是合理的,否则就是近似的。标准化的回归系数,即通径系数。从通径分析的理论看,决定两个变量（个体或群体）间相似性（相关系数）的因素包括它们二者之间的直接通径关系和通过第三个变量（个体或群体）的间接通径关系。当间接通径关系忽略不计的时候,两个变量（个体或群体）间的相关系数,就等于二者之间的直接通径系数^[27]。因此可以合理假设,如果祖先品种间没有遗传亲缘关系,用改进线性回归模型估计的祖先品种的标准化回归系数（通径系数）可以作为每个祖先品种和合成品种动物个体基因组贡献率（或基因组相似程度）的估计。从品种驯化的历史过程看,每个畜禽品种在起源上都可能是相关联的,但在祖先品种间的遗传亲缘关系比较久远的情况下,这个假设是近似成立的。此外,需要说明的是,本研究中约束条件是标准化的回归系数（通径系数）之和为1,这不完全等同于通径分析。就后者而言,所有因素直接通径的决定系数和间接通径的决定系数之和为1,因此,从通径分析的角度,RSLR仍然是一个近似的方法。

3.2 SNP的选择

SNP的选择对GBC的估计结果有一定影响。并且不同的方法对于SNP选择的要求也不尽相同。例如,混合模型方法要求选择信息量高的SNP,这包括群体特有或是群体间差异大的SNP。HULSEGGE等^[12]比较了3个统计指标用以衡量标记信息量的效果,这3个统计指标分别是Delta、Wright的FST以及Weir和Cockerham的FST。笔者通过最大化SNP基因频率的平均欧式距离来筛选SNPs^[8]。除此而外,信息熵^[28,29]和主成分分析^[15,16]中的加载系数 ^[30]也是衡量SNP信息量的指标^[31]。但值得说明的是,回归模型中选择变量（SNP）可能导致选择偏性,特别是对于线性回归的方法。因篇幅所限,本文没有详细讨论这个问题。本研究中没有选择信息含量高的SNP,而是选择均匀分布的SNP。另一方面,线性回归模型一般都需要比较多的SNP数目。在此情形下,使用均匀分布的SNP,可以较好的覆盖整个基因组,使结果更具有代表性^[8]。

降低SNP之间的连锁不平衡也是一个需要考虑的因素。特别是对于混合分布模型,其似然函数的假设前提是SNP之间没有关联。尤其用高密度SNP估计GBC,需要尽量减少或删除处于高度连锁不平衡的SNP。HULSEGGE等^[12]采用LD的r²>0.30作为删除SNP的标准,结果表明在保持相同准确性的前提下,使用这种方法筛选SNP,可以明显降低所需SNP标记的数目。SNP间LD的程度对于线性回归模型而言,没有混合分布模型那样重要。本研究没有选择信息含量高的SNP,也没有作降低SNP之间LD的处理,而是选择均匀分布的SNP。结果表明,对于中、低密度的SNP（50K SNP以内）,在不考虑SNP间LD的情形下,所估计的肉牛王牛的GBC与期望的群体均值也是基本上吻合的。此外,值得一提的是,本研究中当SNP子集为5 000以上时,估计的结果已趋于稳定,在20 000以上时结果已经稳定,说明在不增加实验室检测成本的情况下,利用现有SNP芯片数据筛选可应用于GBC估计的SNP子集是完全可行的,因而当前使用的中低密度芯片数据完全可以满足品种GBC的分析,这是对现有SNP芯片功能的深入开发与拓展,也是对芯片数据的分析和应用的进一步挖掘。

3.3 肉牛王牛的基因组品种构成

肉牛王牛于1954年首次被美国农业部认定为新品种。最初的目的是培育出能够适应德克萨斯州南部环境的一个牛品种。目前的肉牛王牛是一个多用途品种,可用于牛奶和牛肉生产。根据官方数据,肉牛王牛平均包含50%的婆罗门牛、25%的海福特牛以及25%的短角牛的血统。本研究中,RSLR方法估计4 323头肉牛王牛GBC的结果,估计的3个祖先品种的GBC的群体均值分别为：0.501（婆罗门牛）、0.265（海福特牛）和0.234（短角牛）,基本与官方数据相符。肉牛王牛与海福特牛的基因组相似性稍高于25%,而与短角牛则稍低于25%,这个差异可能是由于该品种合成过程中因为选择而产生的偏差。当然,统计方法在估计上的偏差也不能完全排除。对于肉牛王牛的3个祖先品种而言,婆罗门牛是从印度进口的牛品种中繁殖而来的,该品种与海福特牛和短角牛在遗传关系上比较远。相比之下,海福特牛和短角牛都属于原产于英国的牛品种,它们之间可能存在一定的遗传关系。这可能也是导致肉牛王牛与海福特牛和短角牛的基因组相似性产生偏离的原因之一。

用基因组标记估计动物个体GBC,可以反应出个体水平上的遗传抽样,是实现了的个体基因组品种构成的估计值。因此所估计的动物个体GBC在群体中存在一定的变异。本研究用RSLR方法估计肉牛王牛3个祖先品种的基因组贡献率。实践中,GBC的95%的置信区间可以作为肉牛王牛品种登记的分子标记依据,从而可避免由于系谱资料缺失或误差所导致的错误。

4 结论

本研究利用基因组SNP数据,对传统的LR方法进行了改进,提出了RSLR的估计方法估计动物个体GBC。在对合成品种肉牛王牛个体的GBC估计中,与LR方法比较,RSLR方法的估计结果的准确度和一致性更好,可将RSLR方法作为一种估计合成品种GBC的合适方法。若对方法做进一步改进,将需考虑亲本品种间的遗传相关,采用完全的通径分析方法来估计GBC。

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 刘文忠 . 家畜合成群体保留杂种优势的预测与培育效果评价
遗传, 2009,31(8):791-798.
[本文引用: 1]

LIU W Z . Prediction of retained heterosis and evaluation on breeding effects of composite livestock populations
Hereditas(Beijing), 2009,31(8):791-798.(in Chinese)
[本文引用: 1]

[2] MARSHALL B H, BRIGGS D M . Modern Breeds of Livestock. 4th ed
New York: MacMillian Company, 1980.
[本文引用: 2]

[3] 何俊, 钱长嵩, RICHARD G Tait Jr, Stewart Bauck, 吴晓林 . SNP芯片数据估计动物个体基因组品种构成的方法及应用
遗传, 2018,40(4):305-314.
[本文引用: 7]

HE J, QIAN C S TAIT Jr R G, BAUCK S, WU X L . Estimating genomic breed composition of individual animals using selected SNPs
Hereditas (Beijing), 2018,40(4):305-314. (in Chinese)
[本文引用: 7]

[4] WU X L, LIU R Z, SHI Q S, LIU X C, LI X, WU M S . Marker-assisted mating applied in in-situ conservation of indigenous animals in small populations: (1) Choosing mating schemes for maximum heterozygosity
Asian-Australian Journal of Animal Science, 2000,13(4):431-434.
[本文引用: 1]

[5] 杨子博, 王安邦, 冷苏凤, 顾正中, 周羊梅 . 小麦新品种淮麦33的遗传构成分析
中国农业科学, 2018,51(17):3237-3248.
[本文引用: 1]

YANG Z B, WANG A B, LENG S F GU Z Z, ZHOU Y M . Genetic analysis of the novel high-yielding wheat cultivar Huaimai33
Scientia Agricultura Sinica, 2018,51(17):3237-3248.( in Chinese)
[本文引用: 1]

[6] VANRADEN P M, COOPER T A . Genomic evaluations and breed composition for crossbred U.S. dairy cattle
Interbull Bulletin. Orlando,Florida, 2015.
[本文引用: 4]

[7] PRITCHARD J K, STEPHENS M, DONNELLY P . Inference of population structure using multilocus genotype data
Genetics, 2000,155(2):945-959.
[本文引用: 1]

[8] HE J, GUO Y G, XU J, LI H, FULLER A, TAIT R G, WU X L, BAUCK S . Comparing SNP panels and statistical methods for estimating genomic breed composition of individual animals in ten cattle breeds
BMC Genetics, 2018, 19:56.
[本文引用: 8]

[9] GOBENA M, ELZO M A, MATEESCU R G . Population structure and genomic breed composition in an Angus-Brahman crossbred cattle population
Frontier Genetics, 2018,9:90.
[本文引用: 1]

[10] CHIANG C W K, GAJDOS Z K Z, KORN J M, KURUVILLA F G, BUTLER J L, HACKETT R, GUIDUCCI C, NGUYEN T T, WILKS R, FORRESTER T, HAIMAN C A, HENDERSON K D, LE MARCHAND L, HENDERSON B E, PALMERT M R, MCKENZIE C A, LYON H N, COOPER R S, ZHU X F, HIRSCHHORN J N . Rapid assessment of genetic ancestry in populations of unknown origin by genome-wide genotyping of pooled samples
PLoS Genetics, 2010,6(3):e1000866.
[本文引用: 2]

[11] KUEHN L A, KEELE J W, BENNETT G L, MCDANELD T G, SMITH T P L, SNELLING W M, SONSTEGARD T S, THALLMAN R M . Predicting breed composition using breed frequencies of 50,000 markers from the US Meat Animal Research Center 2,000 Bull Project
Journal of Animal Science, 2011,89(6):1742-1750.
[本文引用: 3]

[12] HULSEGGE B, CALUS M P, WINDIG J J, HOVING-BOLINK A H, MAURICE-VAN EIJNDHOVEN M H, HIEMSTRA S J . Selection of SNP from 50K and 777K arrays to predict breed of origin in cattle
Journal of Animal Science, 2013,91:5128-5134.
[本文引用: 3]

[13] AKANNO E C, CHEN L, ABO-ISMAIL M K, CROWLEY J J, WANG Z, LI C, BASARAB J A, MACNEIL M D, PLASTOW G . Genomic prediction of breed composition and heterosis effects in Angus, Charolais, and Hereford crosses using 50K genotypes
Canadian Journal of Animal Science, 2017,97(3):431-438.
[本文引用: 1]

[14] MCVEAN G . A Genealogical Interpretation Of Principal Components Analysis
PLoS Genetics. 2009,5(10):e1000686.
[本文引用: 1]

[15] MA J, AMOS C I . Principal components analysis of population admixture
PLoS ONE, 2012,7(7):e40115.
[本文引用: 2]

[16] LEWIS J, ABAS Z, DADOUSIS C, LYKIDIS D, PASCHOU P, DRINEAS P . Tracing cattle breeds with principal components analysis ancestry informative SNPs
PLoS ONE. 2011,6(4):e18007.
[本文引用: 2]

[17] BANSAL V, LIBIGER O . Fast individual ancestry inference from DNA sequence data leveraging allele frequencies for multiple populations
BMC Bioinformatics, 2015,16:4.
[本文引用: 1]

[18] ALEXANDER D H, LANGE K . Enhancements to the ADMIXTURE algorithm for individual ancestry estima-tion
BMC Bioinform, 2011,12:246.
[本文引用: 1]

[19] DODDS K G, AUVRAY B, NEWMAN N S A, MCEWAN C J . Genomic breed prediction in New Zealand sheep
BMC Genetics, 2014,15:92
[本文引用: 1]

[20] FUNKHOUSER S A, BATES R O, ERNST C W, NEWCOM D, STEIBEL J P . Estimation of genome-wide and locus-specific breed composition in pigs
Translational Animal Science, 2017,1(1):36-44.
[本文引用: 1]

[21] GOBENA M, ELZO M A, MATEESCU R G . Population structure and genomic breed composition in an Angus-Brahman crossbred cattle population
Frontiers in Genetics, 2018,9:90.
[本文引用: 1]

[22] SARGOLZAEI M, CHESNAIS J P, SCHENKEL F S . A new approach for efficient genotype imputation using information from relatives
BMC Genom, 2014,15:478.
[本文引用: 1]

[23] HE J, GUO YG, XU JQ, LI H, FULLER A, RICHARD G JR, WU XL, BAUCK S . Estimating genomic breed composition of individual animals in ten cattle breeds: Comparison of SNP panels and statistical methodology//Proceedings of the 11th World Congress on Genetics Applied to Live-stock Production
New Zealand: Auckland, 2018, 684-687.
[本文引用: 1]

[24] MURTAGH F, LEGENDRE P . Ward's hierarchical agglomerative clustering method: which algorithms implement Ward's criterion?
Journal of Classification, 2014,31(3):274-295.
[本文引用: 1]

[25] LEGENDRE P, LEGENDRE L . Numerical Ecology
3rd ed. Developments in environmental modelling. 2012,24.
[本文引用: 1]

[26] 桑世飞, 王会, 梅德圣, 刘佳, 付丽, 王军, 汪文祥, 胡琼 . 利用全基因组SNP芯片分析油菜遗传距离与杂种优势的关系
中国农业科学, 2015,48(12):2469-2478.
[本文引用: 1]

SANG S F, WANG H, MEI D S, LIU J, FU L, WANG J, WANG W X, HU Q . Correlation analysis between heterosis and genetic distance evaluated by genome-wide SNP chip in Brassica napus
Scientia Agricultura Sinica, 2015,48(12):2469-2478.
[本文引用: 1]

[27] WRIGHT S . Correlation and causation
Journal of Agricultural Research, 1921,20(7):557-585.
[本文引用: 2]

[28] HAN T S, KOBAYASHI K . Mathematics of Information and Coding
Boston, MA,USA: American Mathematical Society, 2001.
[本文引用: 1]

[29] WU X L, XU J Q, FENG G F, WIGGANS G R, TAYLOR J F, HE J, QIAN C S, QIU J S, SIMPSON B, WALKER J, BAUCK S . Optimal design of low-density SNP arrays for genomic prediction: algorithm and applications
PLoS ONE, 2016,11(9):e0161719.
[本文引用: 1]

[30] ABDI H, WILLIAMS L J . Principal component analysis
Wiley Interdisciplinary Reviews Computational Statistics, 2010,2(4):433-459.
[本文引用: 1]

[31] WU X L, XU J Q, FENG G F, WIGGANS G R, TAYLOR J F, HE J, QIAN C S, QIU J S, SIMPSON B, WALKER J, BAUCK S . Optimal design of low-density SNP arrays for genomic prediction: algorithm and applications
PLoS ONE, 2016,11(9):e0161719.
[本文引用: 1]