国外的激波诱导推力矢量控制技术研究最初始于20世纪60年代,主要针对火箭发动机开展了一系列燃气和液体二次喷射矢量控制的技术研究,其中液体二次喷射激波诱导推力矢量控制方案在一些战术导弹上已成功应用[8]。从20世纪90年代开始,美国的NASA Langley实验室开展了针对航空发动机的流体控制推力矢量控制技术的研究工作,取得了较大进展[5]。而国内相关领域研究开展于20世纪90年代末,理论和试验研究资料相对匮乏,只局限于稳态条件下次流喷射角度、喷射位置等几何因素对推力矢量性能影响规律的分析研究。
激波诱导推力矢量喷管的次流气源可以从发动机燃烧室引气,也可以由单独的气源供气。因此,根据气源的不同,次流的种类也不尽相同。而现有研究主要针对主流和次流为同种气体的情况,本文则主要研究了不同工质次流气体条件下喷管的推力矢量性能。通过对喷管内流场进行数值模拟,分析比较次流的渗透高度、喷管的矢量偏转角和推力系数等参数,研究次流的分子质量对推力矢量性能的影响规律,从而选择合适的次流气体,提高矢量喷管的性能。
1 数值方法 喷管内流场为超声速、可压缩气体,密度脉动不能忽略,因此Navier-Stokes方程中的湍流脉动项采用Favre提出的质量加权平均[9]。为使Favre平均Navier-Stokes方程封闭,Favre平均得出的雷诺扩散项和雷诺导热项由梯度扩散假设封闭,其中湍流施密特数(Sc)和普朗特数(Pr)均设为0.9。雷诺应力项由Boussinesq假设封闭,湍流黏性由k-ω SST(Shear Stress Transport)湍流模型方程获得[10]。
依据上述说明,笛卡儿坐标系下多组分守恒型控制方程的形式如下:
 | (1) |
式中:E、H和h分别为总能、总焓和静焓; τij和τij′分别为分子应力张量和湍流应力张量;μ和μt分别为层流黏性和湍流黏性; Ys为各组分质量分数;其余变量定义可参见文献[10]。
气体守恒方程为
 | (2) |
式中:p、ρ和T分别为气体压力、密度和温度;R为理想气体常数;Ms为各组分分子质量。
控制方程的无黏通量向量采用AUSM (Advection Upstream Splitting Method)格式的改进型ASUM+格式进行离散[11]:
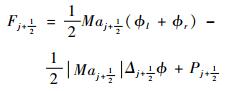 | (3) |
式中:各变量符号说明参见文献[11]。
通过对原始变量进行MUSCL (Monotone Upstream-centred Schemes for Conservation Laws)差值,可提高到二阶精度[12]。黏性通量向量采用中心差分离散。时间推进采用LU-SGS (Low-Upper Symmetric Gauss-Seidel)隐式格式[13]。
2 程序验证及算例 2.1 物理模型 将文献[14]中的氮气垂直喷入超声速空气流场的试验结果来验证程序的准确性。其试验台为500 mm×150 mm×150 mm的三维槽道,其结构平面图如图 1所示。计算网格为318×69×69,在喷射口和壁面处局部加密。表 1给出了主流场中的空气参数和喷射入口处的氮气参数[14]。
 |
| 图 1 氮气喷射试验台几何构型 Fig. 1 Geometry configuration of nitrogen injection testbed |
| 图选项 |
表 1 空气流和氮气流物性参数 Table 1 Physical property parameters for air stream and nitrogen stream
| 参数 | 空气流 | 氮气流 |
| Ma | 3.71 | 1.0 |
| p/MPa | 1.236 | 0.606 |
| T/ K | 301 | 301 |
| YN2 | 0.766 4 | 1 |
| YO2 | 0.233 6 | 0 |
| ??注:Ma—马赫数;YN2—氮气组分质量分数;YO2—氧气组分质量分数。 | ||
表选项
2.2 计算结果 图 2为马赫数等值线,图 3为喷射口附近区域的流线,x、y分别为空气流入方向和氮气注入方向。氮气从喷射口欠膨胀喷出,超声速气流通过Prandtl-Meyer膨胀在喷射口外形成马赫盘。由于喷射气流与主流的交叉干扰作用,在喷射口上游区域形成弓形激波。弓形激波前流场压力升高,致使壁面边界层分离,进而形成了一个与弓形激波相交的分离激波。另外,在喷射口下游区域形成再压缩激波。如图 2和图 3所示,干扰流场复杂的激波结构,马赫盘和分离涡系结构都被数值方法很好的捕捉。
 |
| 图 2 马赫数等值线 Fig. 2 Mach number contour lines |
| 图选项 |
 |
| 图 3 喷射口附近区域流线 Fig. 3 Streamlines near injection orifice |
| 图选项 |
图 4为计算所得壁面压力分布与试验数据结果对比,p∞为空气来流总压,L为氮气喷射孔中心线到入口的距离(即330 mm)。由图 4可见,计算结果与试验数据吻合得很好,只是在喷射口下游计算所得压力的峰值比试验数据略低。
 |
| 图 4 壁面压力分布 Fig. 4 Wall pressure distribution |
| 图选项 |
由上述分析可知,AUSM+格式和k-ω SST湍流模型能够很好地模拟横向喷流的流场结构,计算结果也与试验数据吻合得很好,验证了数值方法的可靠性,因此该方法可以应用到激波诱导推力矢量喷管不同气体喷注时的性能分析研究。
3 不同气体喷注时性能分析 3.1 物理模型 喷管全长为78 mm,喉部直径47 mm,喷管出口面积与喉部面积之比为2.09。由于在相同条件下,矩形注气口的推力矢量性能优于同面积的圆形注气口[15],因此本模型在喷管扩张段开设周向角度40°,宽度3 mm的矩形注气口。该注气口的中心线距喷管入口的距离为喷管全长的0.75,次流方向与喷管轴线夹角为θ。由于几何和流场结构的对称性,沿对称面选取一半作为研究对象。计算模型的网格如图 5所示。
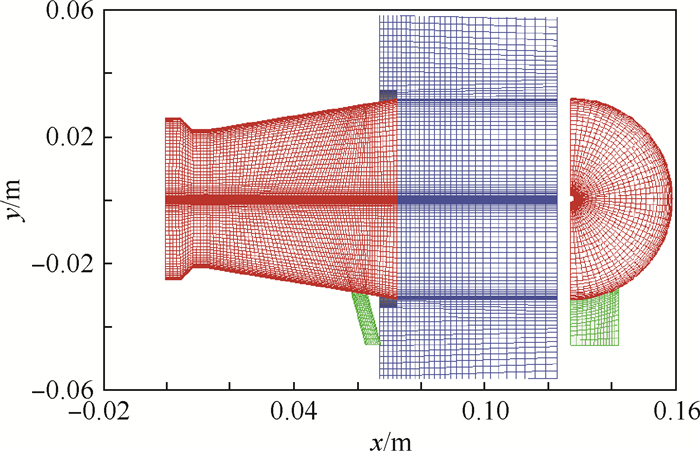 |
| 图 5 激波诱导推力矢量喷管计算网格 Fig. 5 Computational grid of shock thrust vector nozzle |
| 图选项 |
喷管主流气体为空气,其中氮气的质量分数为0.766 4,氧气的质量分数为0.233 6,入口总压为1 MPa和1.5 MPa,出口环境压强为一个标准大气压,则主流落压比(NPR)分别为10和15。次流气体分别为He、N2和CO2气体,其质量分数均为1,次流与主流总压之比(SPR)分别为0.8和1.0,马赫数为1,注气角度θ分别为90°和105°,垂直和逆向主流喷入。主流和次流的总温均为300 K。
3.2 评价标准 通过数值计算可得到喷管矢量偏转角和推力系数作为推力矢量性能指标[16]。
矢量偏转角度为
 | (4) |
式中:FN和FA分别为轴向力和侧向力,可对喷管出口气流积分得到。
推力系数为
 | (5) |
式中:

次流与主流质量流量比为
 | (6) |
式中:Ws和Wp分别为次流和主流的质量流量,可分别对喷管入口和次流入口积分得到。
3.3 计算结果 图 6~图 8所示的状态:次流为He,NPR=10,SPR=1.0,θ=90°。图 6为He注入喷管流场后压强分布。如图 6所示,激波诱导推力矢量喷管的流场结构与第2节中验证模型的流场结构相似,二次流气体喷入喷管扩张段,通过Prandtl-Meyer膨胀在喷射口外形成马赫盘,由于次流的阻碍作用,在喷射口上游形成弓形激波,主流通过弓形激波流动方向发生偏转,在喷管出口产生侧向推力,实现矢量控制。
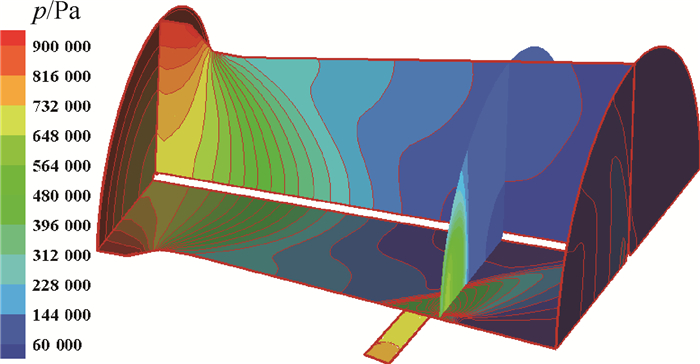 |
| 图 6 流场压强分布 Fig. 6 Pressure distribution of flow field |
| 图选项 |
 |
| 图 7 He质量分数等值线 Fig. 7 Mass fraction contour lines of helium |
| 图选项 |
 |
| 图 8 在对称面x=0.066 m处He和N2的质量分数沿y方向的分布 Fig. 8 Distribution of helium and nitrogen mass fraction along y direction at x=0.066 m on symmetry plane |
| 图选项 |
图 7为He注入喷管流场后在对称面上质量分数等值线图。如图 7所示,He注入喷管流场后渗透到一定高度,压强逐渐降低,y方向速度逐渐减小,受喷管主流的推动作用,然后转弯平行于喷管壁面流动。
图 8为对称面上注气口下游x=0.066 m处,He和喷管主流中的N2沿y方向的质量分数分布曲线。He在靠近壁面处质量分数很低,随着高度的增加质量分数迅速变大,由于受回流涡结构的影响,在y为-0.031~-0.028之间,质量分数的增大趋势变缓,之后随高度增加质量分数又迅速增大,在y为-0.026~-0.023之间达到相对稳定的接近于1的值,然后随着高度的增大又逐渐减小,直至为零。而主流中N2的质量分数变化与He正好相反。
图 9为NPR=10,SPR=1.0,θ=90°和105°时,He、N2和CO2气体在对称面x=0.066 m处沿y方向质量分数分布曲线。由图 9可知,3种气体在此处的质量分数分布情况近似相同,在相同高度上,分子质量大的气体质量分数略高。即分子质量越大,渗透高度越大。这说明,分子质量小的气体由于渗透高度较低对主流的阻碍作用就会相应降低,从而减少推力损失。
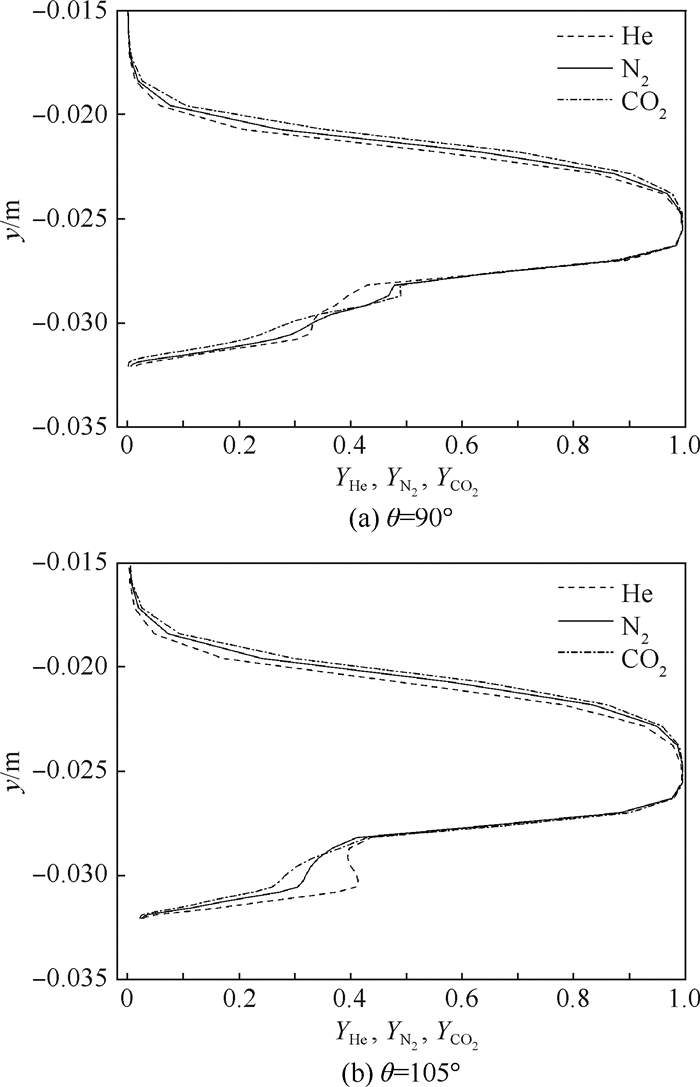 |
| 图 9 在对称面x=0.066 m处不同次流气体的质量分数沿y方向的分布 Fig. 9 Distribution of mass fraction along y direction for different secondary flow gas at x=0.066 m on symmetry plane |
| 图选项 |
表 2为NPR=10,SPR=1.0时,不同注气角度下矢量性能参数对比。由表 2可知,在不同注气角度下,矢量偏转角均随次流气体分子质量的增大逐渐减小。推力系数则近似相等,随分子质量的增大略微减小。分子质量越小,次流与主流的质量流量比ω越小。说明分子质量小的气体在单位质量流量下产生的矢量偏转角更大,而推力损失更小。
表 2 不同注气角度下矢量喷管性能参数对比 Table 2 Comparison of vector nozzle performance parameter under different gas injection angles
| 气体 | θ/(°) | α/(°) | CR, i | ω |
| He | 90 | 4.91 | 0.912 | 0.026 |
| 105 | 5.08 | 0.906 | 0.026 | |
| N2 | 90 | 4.89 | 0.911 | 0.035 |
| 105 | 4.96 | 0.905 | 0.035 | |
| CO2 | 90 | 4.80 | 0.910 | 0.044 |
| 105 | 4.88 | 0.904 | 0.044 |
表选项
表 3为SPR=1.0,注气角度为105°时,不同NPR下矢量性能参数对比。由表 3可知,在不同NPR下,矢量偏转角均随次流气体分子质量的增大逐渐减小。另外,在NPR发生变化时,分子质量小的气体其矢量偏转角变化的程度更大。推力系数则近似相等,随分子质量的增大略微减小。
表 3 不同NPR下矢量喷管性能参数对比 Table 3 Comparison of vector nozzle performance parameter under different NPRs
| 气体 | NPR | α/(°) | CR, i |
| He | 10 | 5.08 | 0.912 |
| 15 | 4.73 | 0.886 | |
| N2 | 10 | 4.96 | 0.911 |
| 15 | 4.66 | 0.885 | |
| CO2 | 10 | 4.88 | 0.910 |
| 15 | 4.61 | 0.884 |
表选项
表 4为NPR=10,注气角度为105°时,不同SPR下矢量性能参数对比。由表 4可知,在不同SPR下,矢量偏转角均随次流气体分子质量的增大逐渐减小。推力系数则近似相等。
表 4 不同SPR下矢量喷管性能参数对比 Table 4 Comparison of vector nozzle performance parameter under different SPRs
| 气体 | SPR | α/(°) | CR, i |
| He | 0.8 | 4.09 | 0.917 |
| 1.0 | 5.08 | 0.912 | |
| N2 | 0.8 | 3.97 | 0.917 |
| 1.0 | 4.96 | 0.911 | |
| CO2 | 0.8 | 3.93 | 0.917 |
| 1.0 | 4.88 | 0.910 |
表选项
4 结论 本文通过在不同注气角度、SPR和NPR条件下求解多组分Navier-Stokes方程,模拟了不同种类次流气体喷注时,激波诱导推力矢量喷管的推力矢量性能。
1) 在相同的物性参数条件下,次流气体的分子质量越小,次流与主流的质量流量比越小,所产生的矢量偏转角越大,推力损失也越小。因此,质量分数小的次流气体有着更高的推力矢量效率。
2) 在进行系统设计时,选用平均分子质量小的气体作为次流气源,或者将从燃烧室引出的高温燃气与分子质量小的气体混合减小其平均分子质量,可以提高激波诱导推力矢量喷管的推力矢量性能。
参考文献
| [1] | DENG R Y, SETOGUCHI T, KIM H D. Large eddy simulation of shock vector control using bypass flow passage[J]. International Journal of Heat and Fluid Flow, 2016, 62: 474-481. DOI:10.1016/j.ijheatfluidflow.2016.08.011 |
| [2] | SHI J W, ZHOU L, WANG Z X, et al. Investigation on flowfield characteristics and performance of shock vector control nozzle based on confined transverse injection[J]. Journal of Engineering for Gas Turbines and Power-Transactions of the ASME, 2016, 138(10): 101502. DOI:10.1115/1.4033140 |
| [3] | 刘辉, 邢玉明. 燃气喷射推力矢量喷管气固两相流数值模拟[J]. 航空动力学报, 2013, 28(1): 151-157. LIU H, XING Y M. Numerical simulation of gas-particle flow in hot gas injection thrust vector nozzle[J]. Journal of Aerospace Power, 2013, 28(1): 151-157. (in Chinese) |
| [4] | 马伟, 杜刚, 金捷, 等. 激波诱导矢量喷管动态数值模拟[J]. 燃气涡轮试验与研究, 2014, 27(5): 30-37. MA W, DU G, JIN J, et al. Dynamic numerical simulation of shock vector control exhaust nozzle[J]. Gas Turbine Experiment and Research, 2014, 27(5): 30-37. DOI:10.3969/j.issn.1672-2620.2014.05.006 (in Chinese) |
| [5] | DEERE K A.Summary of fluidic thrust vectoring research conducted at NASA Langley Research Center: AIAA-2003-3800[R].Reston: AIAA, 2003. |
| [6] | WAITHE K A, DEERE K A.Experimental and computational investigation of multiple injection ports in a convergent-divergent nozzle for fluidic thrust vectoring: AIAA-2003-3802[R].Reston: AIAA, 2003. |
| [7] | DEERE K A, BERRIER B L.Computational study of fluidic thrust vectoring using separation control in a nozzle: AIAA-2003-3803[R].Reston: AIAA, 2003. |
| [8] | 林飞, 王根斌. 固体火箭发动机推力向量控制[M]. 北京: 国防工业出版社, 1981: 121-125. LIN F, WANG G B. Thrust vectoring control for solid rocket motor[M]. Beijing: National Defense and Industry Press, 1981: 121-125. (in Chinese) |
| [9] | FAVRE A. Equations des gaz turbulents compressibles[J]. Journal de Mechanique, 1965, 4: 361-390. |
| [10] | MENTER F R. Two equation eddy viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
| [11] | LIOU M S.Progress towards an improved CFD method: AUSM+: AIAA-95-1701[R].Reston: AIAA, 1995. |
| [12] | VAN LEER B. Towards the ultimate conservative difference scheme V:A second order sequel to Godunov's method[J]. Journal of Computational Physics, 1979, 32(1): 101-136. |
| [13] | YOON S, JAMESON A. Lower-upper symmetric Gauss-Seidel method for the Euler and Navier-Stoker equations[J]. AIAA Journal, 1988, 26(9): 1025-1026. DOI:10.2514/3.10007 |
| [14] | ASO S, OKUYAMA S, KAWAT M, et al.Experimental study on mixing phenomena in supersonic flows with slot injection: AIAA-91-0016[R].Reston: AIAA, 1991. |
| [15] | 刘辉, 邢玉明, 额日其太. 气体二次喷射矢量喷管三维流场计算[J]. 北京航空航天大学学报, 2009, 35(10): 1174-1178. LIU H, XING Y M, ERIQITAI. Computation of three-dimensional flow field in secondary gas injection for thrust vectoring nozzle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(10): 1174-1178. (in Chinese) |
| [16] | DEERE K A.Computational investigation of the aerodynamic effects on fluidic thrust vectoring: AIAA-2000-3598[R].Reston: AIAA, 2000. |
