航空电子设备之间的互联线缆是电磁干扰的重要耦合路径。一方面，航电设备的干扰信号可以通过线缆干扰所联的另一台设备；另一方面，线缆环路本身可以作为天线耦合空间的电磁能量，从而产生沿线缆传播的干扰信号。为了准确建立线缆的电磁干扰耦合模型，分析和解决电磁兼容(EMC)问题，需要在较宽频带内获取线缆终端所联航电设备的共模阻抗^[1-3]。
目前，测试线缆终端共模阻抗的方法主要有2类。第1类方法是在被测系统中接入专用的电路或仪器进行阻抗测量。例如，文献[4]采用电源的功率变换器测量电源阻抗；文献[5]提出了一种基于方波电流注入测量三相交流系统谐波阻抗矩阵的方法, 相较于三相注入法, 降低了硬件实现难度；文献[6]改进了传统的扫频法，提出了分段二叉树阻抗测量方法，可以根据精度要求自动调整测量频点。第2类方法采用电流探头与待测系统线缆间的电磁耦合来测量线缆终端的阻抗。例如，文献[7]从GJB 151A—97^[8]中CS114试验的基本配置出发，采用1个电流探头对线缆注入信号，然后通过1个监测探头测量线缆上的感应电流，最终算出线缆的环路阻抗；文献[9]以2个耦合夹钳分别作为电缆电流注入和感应电流测试的传感器，实现了对飞机电缆屏蔽层环路阻抗的测试；文献[10]采用信号源、频谱分析仪和2个电流探头测试低功耗开关电源的内阻；文献[11]在文献[10]方法的基础上增加了1个电流探头，从而获取了注入电流的相位信息。
第1类方法的共同优点是测量精度较高，但需要在待测系统中接入测量电路或测量仪器，有时不易实现。第2类方法的共同优点是测量过程中对待测系统的完整性没有影响，测量操作较为简便，但测量不确定度相对较大。
受上述文献的启发，针对连接有多条线缆的系统，本文提出了一种采用矢量网络分析仪和电流探头快速测试线缆终端共模阻抗的方法。该方法首先将每条多芯线缆等效为单导体，进而将多条线缆等效为多导体传输线，然后用矢量网络分析仪和电流探头在每条多芯线缆的2个任选位置处分别扫频测量电压反射系数，最后以线缆终端电阻为未知数构造电流探头在各条线缆注入点处的输入阻抗方程组，并采用dogleg算法^[12]求解方程组。本文方法本质上属于第2类方法，由于采用矢量网络分析仪测量电压反射系数在各频点上的驻留时间为毫秒量级，每次扫频可在数秒内完成；在获取各条线缆的电压反射系数后，可以同时计算出各条线缆终端共模阻抗，因此本文方法能够显著提高测试效率。同时，由于在电压反射系数测量过程中引入了线缆之间的互耦效应，符合系统的真实状态，因而有利于提高终端共模阻抗的测量精度。
1 多条平行线缆的等效方法 为便于后续说明与验证，建立了图 1所示的实验模型。该实验模型包括3条长度为2 m的3芯线缆，线缆内每条导体直径为0.000 7 m，将各线缆平行于导电金属板放置，各线缆中轴线距金属板高度为0.025 m。3条线缆相互平行，中间的线缆与左右相邻线缆各相距0.011 m，所有导体终端与金属板之间均接有无源负载，构成线缆终端1和终端2。由于线缆终端共模电流本质上是线缆内各导体共模电流之和，因此可将一条线缆等效为具有相同共模电流的单导体，进而将多条平行线缆等效为多导体传输线。本节分两步将多条线缆等效为多导体传输线。

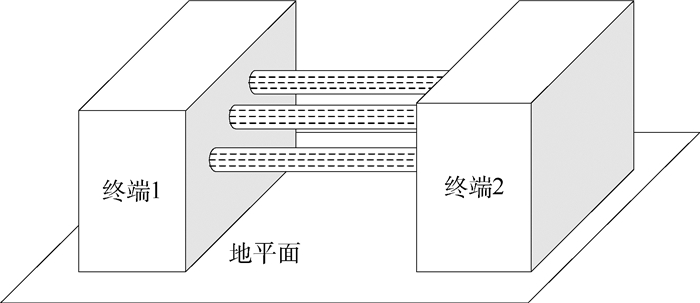图 1 连接2个终端的3条线缆 Fig. 1 Three cables connecting two terminals

图选项

1.1 单根多芯线缆与单导体的等效 如图 2所示，设多芯线缆B内部有n_B根导体，其中导体i距地平面高度为h_i，半径为R_i，导体周围介质的磁导率为μ₀，介电常数为ε，且各导体间距离及介质厚度远小于线缆轴心距地平面高度。设等效导体距地平面高度为h_e，半径为R_e。线缆内导体i与地平面之间单位长度电感l_ii为^[13]

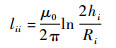(1)

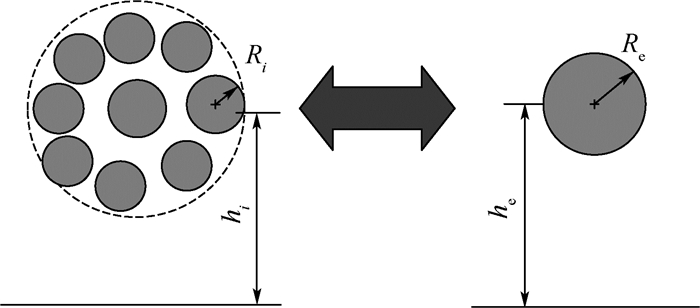图 2 多芯线缆及其等效导体横截面结构尺寸 Fig. 2 Cross section structure of a cable bundle and its equivalent conductor.

图选项

导体i与导体j之间单位长度互感l_ij为

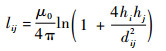(2)

式中：d_ij为导体i与导体j之间的距离。
设线缆B内导体i上存在电流I_i，则单位长度线缆B与地平面间总的磁通ψ_B为

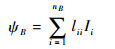(3)

若等效导体通有电流时与地平面间的磁通量为ψ_e，则等效导体与地平面之间的电感l_e满足：

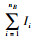
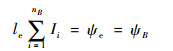(4)

将式(4)代入式(3)可得l_e与l_ij的关系为

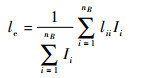(5)

由于多芯线缆内各导体的半径相等且远小于距地平面高度，因此式(5)可近似为

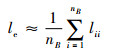(6)

由式(1)可知，对于给定的l_e，等效导体的h_e、R_e不唯一。任取h_e值，可解得R_e为

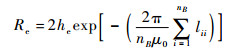(7)

地平面上方导体的对地电感l与对地电容C满足lC=μ₀ε₀，ε₀为真空中的介电常数，因此如果等效导体与线缆的对地电感相同，它们具有相同的共模特征阻抗^[13]。
1.2 平行多芯线缆与平行双导体的等效 在每条线缆与单导体等效的基础上，2条平行线缆间的互耦还应当与2根等效导体间的互耦相同。设2根平行多芯线缆B₁和B₂的轴线距地平面高度分别为h_B1和h_B2，B₁包含导体B_{i, 1}(i=1, 2, …, n₁)，B₂包含导体B_{j, 2}(j=1, 2, …, n₂)，记导体B_{i, 1}、B_{j, 2}间的互感为l_ij。假设线缆B₁内导体i上的电流为I_i，则B₁与B₂内某一导体B_{j, 2}间的磁通量ψ_{B1Bj, 2}为

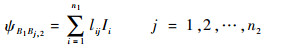(8)

由于线缆B₂内各导体间距离较近，故可用置于在线缆B₂轴心处的等效导体B_{e, 2}取代线缆B₂，则

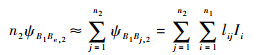(9)

现在以等效导体B_{e, 1}取代线缆B₁，并调整等效导体B_{e, 1}与B_{e, 2}之间的距离，使导体之间的互感l_{Be, 1Be, 2}满足：

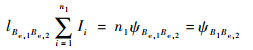(10)

由于线缆内导体间的距离远小于线缆距地平面的高度，将式(10)代入式(9)可得

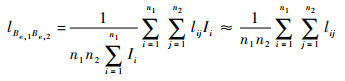(11)

将l_{Be, 1Be, 2}、h_B1和h_B2代入式(2)，即可求得两等效导体间的距离d_ij。对于图 1所示的系统，采用上述方法计算得到如图 3所示的等效多导体传输线。可得各等效导体半径r_e=0.000 35 m，等效导体间距d₁₂= d₂₁=0.01 m，d₁₃=0.02 m，等效导体距地平面高度h₁=h₂=h₃=0.025 m。可将求得的等效导体的参数代入式(1)求出该多导体传输线单位长度电感阵L对角线元素，将等效导体的参数代入式(2)求出L的非对角线元素，进而求得特征阻抗阵。图 3中的z_ia(f)和z_ib(f)分别为各导体左端和右端在频率为f时的阻抗。在本文中，将各等效导体的左端坐标设为x_ia=0，右端坐标设为x_ib=2 m。

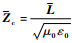
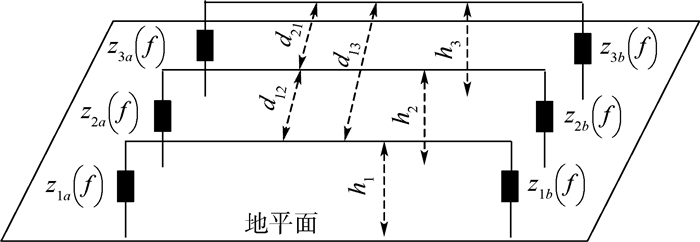图 3 与3条线缆等效的多导体传输线 Fig. 3 Equivalent multi-conductor transmission line of three cables

图选项

2 获取电流注入点处的输入阻抗阵 图 3所示的多导体传输线等效于图 1所示的系统，每根导体等效一根多芯线缆。为求出z_ia(f)和z_ib(f)，需要获取传输线在2个任选位置处的输入阻抗矩阵。测试方法如图 4所示，电流探头与矢量网络分析仪的A通道相联，并将电流探头卡在导体1靠近左端的任选位置x_1sL处。然后令矢量网络分析仪在需测的m个频点上扫频，可得到m个电压反射系数，记为[s_L(f_k, x_1sL)]_1×m，其中s_L(f_k, x_1sL)为在频率f_k时的电压反射系数。将电流探头卡在导体1靠近右端的任选位置x_1sR处，再次进行扫频，可得到另一组电压反射系数，记为[s_R(f_k, x_1sR)]_1×m，其中s_R(f_k, x_1sR)为在频率f_k时的电压反射系数。对导体2、3重复上述过程，可得到电压反射系数矩阵[s_L(f_k, x_isL)]_1×m和[s_R(f_k, x_isR)]_1×m。

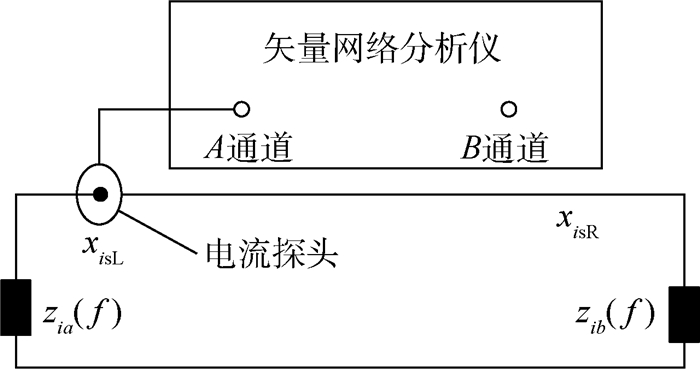图 4 测量导体i在xisL处的电压反射系数 Fig. 4 Measuring voltage reflection coefficient at xisL of conductor i

图选项

为计算等效导体i在x_isL和x_isR处的输入阻抗，需建立电流探头与被测导体的等效电路。将电流探头与被测导体视为电压变换比为α：1的变压器，则图 4中电流探头与导线的等效电路如图 5所示。

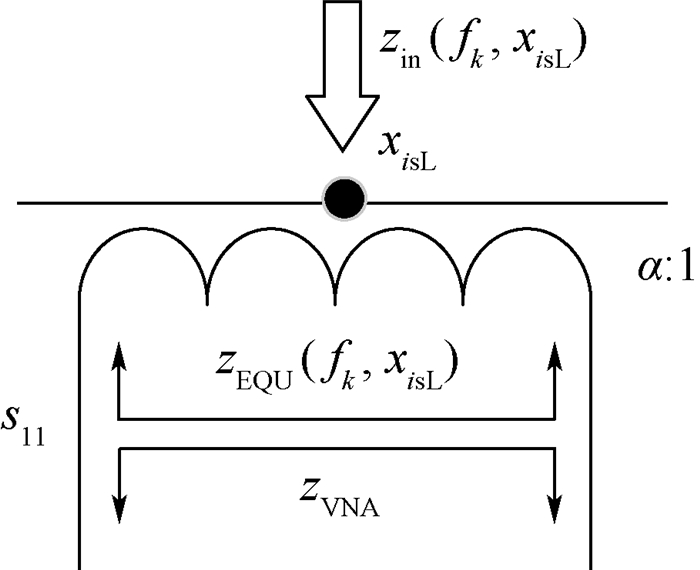图 5 测量导体电压反射系数的等效电路 Fig. 5 Equivalent circuit for measuring voltage reflection coefficient of a conductor

图选项

图 5中，z_VNA为矢量网络分析仪A通道的输入阻抗，z_in(f_k, x_isL)为导体i在x_isL处及频率为f_k时的输入阻抗。根据电路理论，电流探头与矢量网络分析仪连接处的等效阻抗为z_EQU(f_k, x_isL)=α²z_in(f_k, x_isL)，且该处电压反射系数s_L(f_k, x_isL)满足^[13]：

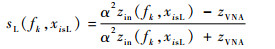(12)

α可由电流探头校准方法得到^[14-15]

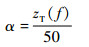(13)

式中：z_T(f)为电流探头的转移阻抗，是由电流探头生产厂家给出的已知量。本文测试中使用的是F-120-6A型电流探头，其电压变换比曲线如图 6所示。

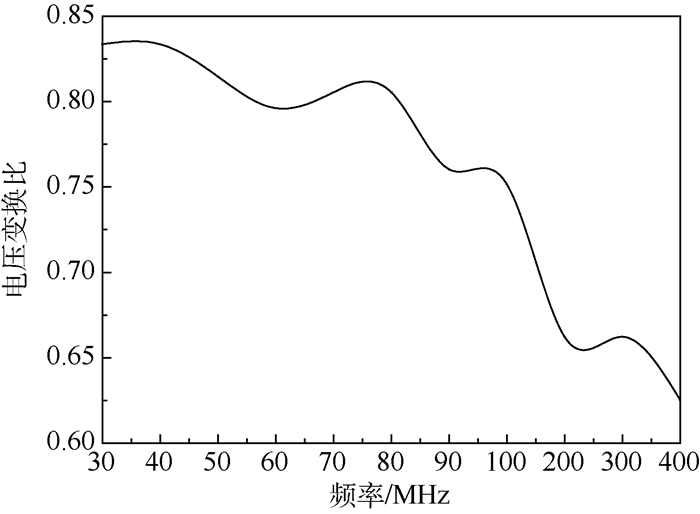图 6 本文所用电流探头的电压变换比曲线 Fig. 6 Voltage conversion ratio curve of current probe used in this paper

图选项

由式(12)变形可得

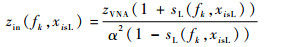(14)

同理，导体在x_isR处输入阻抗计算式为

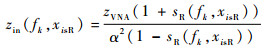(15)

在m个频率上对3根导体分别应用式(14)、式(15)，可得到在X_sL=[x_1sL, x_2sL, x_3sL]^T和X_sR=[x_1sR, x_2sR, x_3sR]^T处的输入阻抗阵:

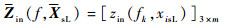(16)

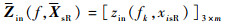(17)

式中:z_in(f_k, x_isL)和z_in(f_k, x_isR)分别为矩阵Z_in(f, X_sL)和Z_in(f, X_sR)矩阵中行列上的元素。
3 计算等效多导体传输线终端阻抗 如图 7所示，当电流探头注入信号的频率为f_k时，设在导体i与地平面的x_sL处向左侧观察时的输入阻抗为z_inL(f_k, x_sL)，向右侧观察时的输入阻抗为z_inR(f_k, x_sL)。在x_sR处向左侧观察时的输入阻抗为z_inL(f_k, x_sR)，向右侧观察时的输入阻抗为z_inR(f_k, x_sR)。当等效多导体传输线导体间距较大时，忽略导体间的互耦，可得它们的求解公式为

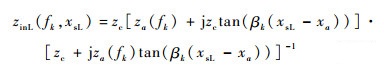(18)

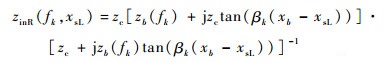(19)

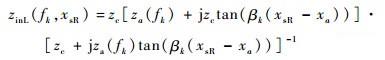(20)

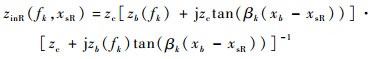(21)

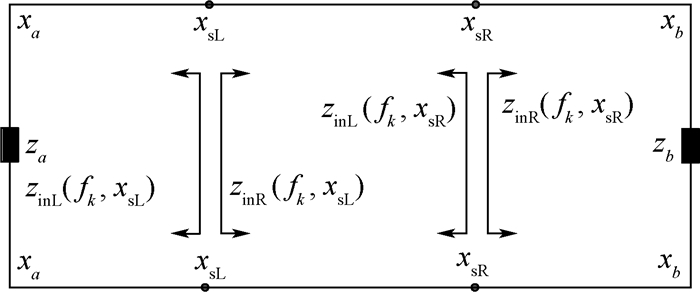图 7 导体与地平面间的4个输入阻抗 Fig. 7 Four input impedances between conductor and ground

图选项

式中：，c为光速；z_c为导体i与地平面间的特性阻抗，可由式(1)计算出对地电感后，乘以获得^[16]。
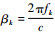
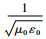
当等效多导体传输线各导体间距离较近时，为引入互耦效应，将式(18)~式(21)拓展到向量空间，得到

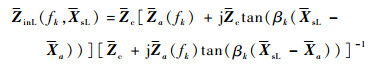(22)

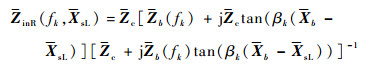(23)

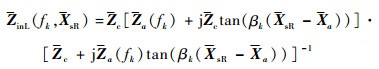(24)

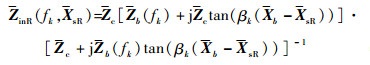(25)

式中：Z_a(f_k)、Z_b(f_k)分别为以待求量z_ia(f_k)、z_ib(f_k)为对角线元素的对角阵(i=1, 2, 3)；X_a=[x_ia]_3×1、X_b=[x_ib]_3×1分别为多导体传输线左、右端点坐标构成的列向量；tan(β_k(X_sL-X_a))、tan(β_k(X_b-X_sL))、tan(β_k(X_sR-X_a))和tan(β_k·(X_b-X_sR))为传输线上观察点与终端之间的相位差正切矩阵，定义如下：

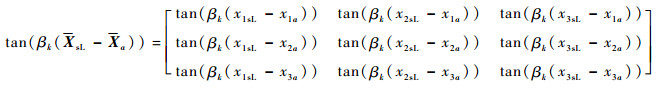(26)

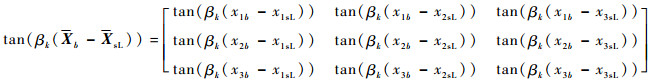(27)

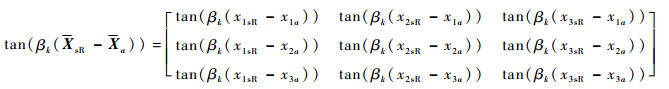(28)

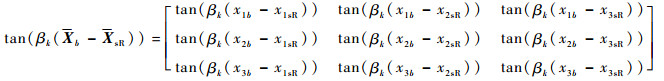(29)

在X_sL处的输入阻抗阵Z_in(f, X_sL)及在X_sR处的输入阻抗阵Z_in(f, X_sR)满足式(30)、式(31)：

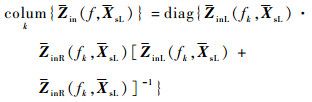(30)

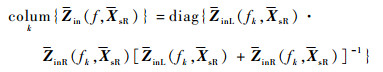(31)

式中: 表示取矩阵第k列元素构成列向量；diag{}表示取括号内方阵对角线上的元素构成列向量。对应每一个k值，式(30)、式(31)构成由6个待求终端阻抗为未知数的方程组。采用信任区域dogleg算法^[12]求解方程组：
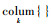
步骤1??令k=1。给待求未知量z_1a、z_2a、z_3a、z_1b、z_2b、z_3b赋大于零的初值。为加快收敛速度，初值不宜过大。本文采用0~10的随机数作为初值。根据式(30)、式(31)构造一个六维列向量方程，其中F₁、F₂分别定义为

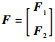
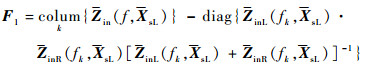(32)

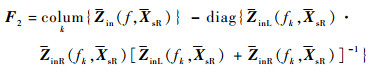(33)

步骤2??将z_1a、z_2a、z_3a、z_1b、z_2b、z_3b代入式(32)、式(33)，得到6维列向量F。
步骤3??计算F的2-范数‖F‖₂，并判断‖F‖₂≤δ是否为真。δ为预先设定的一个很小的正数，作为迭代终止条件，本文设δ=10^-8。若‖F‖₂≤δ成立，则z_1a、z_2a、z_3a、z_1b、z_2b、z_3b为频率f_k时的终端阻抗；否则执行步骤4。
步骤4??应用信任区域dogleg算法对向量方程F迭代一步，得到一组新的z_1a、z_2a、z_3a、z_1b、z_2b、z_3b。返回步骤2。
步骤5??令k=k+1。如果k≤m，返回步骤1；否则循环结束。
4 实验结果 不失一般性，取x_isL=0.2 m，x_isR=1.7 m，按照GJB 151A—97^[8]中CS114扫频频点的计算方法，在30~400 MHz内按相同步长选择130个频率。按照第2节的方法，可测量得到6组电压反射系数(限于篇幅，测试数据未列出)。按照第3节方法，可求得传输线2个3行130列的终端阻抗矩阵。图 8给出用本文方法获取的6个终端阻抗幅值，以及直接采用阻抗分析仪测得的6个终端阻抗幅值。在绝大部分频点上，采用本文方法得到的各终端阻抗值与实测值之间的相对误差小于10%，这说明本文方法的精度能够满足线缆建模需求。同时，由图 8(a)可以看出，各终端阻抗的计算值与测量值随频率起伏振荡较大。这是由于线缆终端等效阻抗并非纯电阻，而是由大量的频变分布电容、电感和电阻构成的复阻抗网络，存在大量的谐振频点。当阻抗网络上的电流频率处于谐振频点时，在该频点上等效阻抗就会出现局部频带内的极大或极小值，从而在阻抗模值曲线上形成局部峰值。

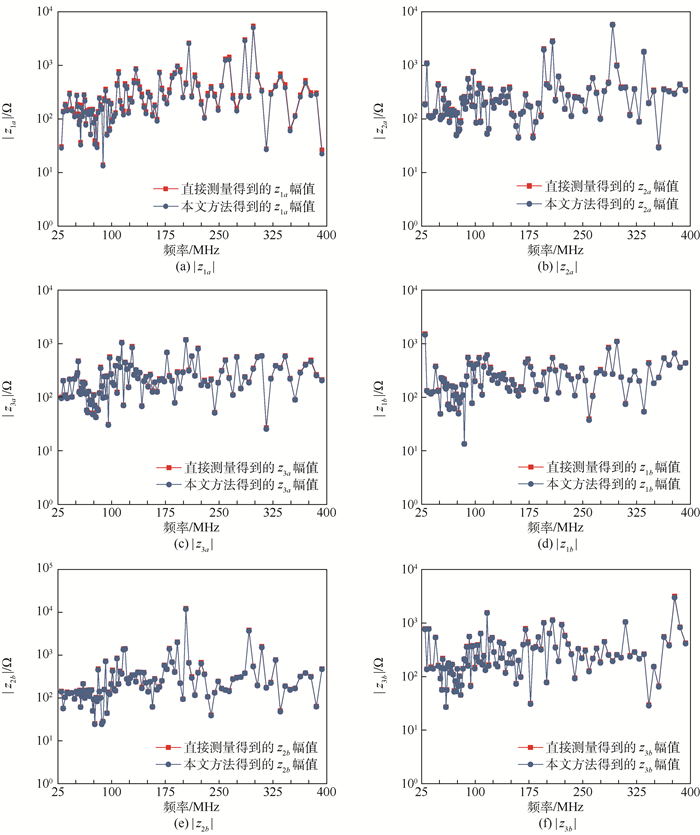图 8 由本文方法和直接测量得到的|z1a|、|z2a|、|z3a|、|z1b|、|z2b|和|z3b| Fig. 8 |z1a|, |z2a|, |z3a|, |z1b|, |z2b| and |z3b| achieved with proposed method and direct measurement

图选项

5 结论 1) 本文根据传输线理论证明，在计算线缆终端共模阻抗时，可将其等效为一根单导体；而对于相邻的平行线缆，可将其等效为多导体传输线。
2) 用矢量网络分析仪和电流探头快速获取线缆的电压反射系数后，能够同时计算出各条线缆终端的等效共模阻抗。而且，本文方法在测试电压反射系数过程中，电流探头与线缆通过空间电磁耦合，因而不会破坏被测系统的完整性。
3) 本文方法得到的结果与采用阻抗分析仪直接测量结果的相对误差只在少数频点上接近10%。考虑到电磁兼容试验的不确定度很少低于3 dB的实际，因而本文方法的测量精度能够满足线缆耦合的建模需求。
4) 本文方法适用于大体上平直的线缆束。对于弯曲线缆束，应用本方法会引入较大误差。对于弯曲线缆束终端共模阻抗的获取，需要在后续的研究加以解决。

参考文献

[1]	苏东林, 谢树果, 戴飞. 系统级电磁兼容性量化设计理论与方法[M].北京: 国防工业出版社, 2015: 125. SU D L, XIE S G, DAI F. The theory and methods of quantification design on system-level electromagnetic compatibility[M].Beijing: National Defense Industry Press, 2015: 125.(in Chinese)
[2]	PAUL C R. Introduction to electromagnetic compatibility[M].2nd edHoboken: Wiley, 2006: 503-557.
[3]	陈穷, 蒋全兴, 周开基, 等. 电磁兼容性工程设计手册[M].北京: 国防工业出版社, 1993: 424-444. CHEN Q, JIANG Q X, ZHOU K J, et al. Electromagnetic compatibility engineering design manual[M].Beijing: National Defense Industry Press, 1993: 424-444.(in Chinese)
[4]	HUANG W, ABU QAHOUQ J A. An online battery impedance measurement method using DC-DC power converter control[J].IEEE Transactions on Industrial Electronics, 2014, 61(11): 5987–5995.DOI:10.1109/TIE.2014.2311389
[5]	杨祯, 章建峰. 基于方波电流注入的正弦调制阻抗测量方法研究[J].陕西电力, 2014, 42(12): 39–43. YANG Z, ZHANG J F. Research on sinusoidal impedance measurement method of square wave current injection based on[J].Shaanxi Electric Power, 2014, 42(12): 39–43.DOI:10.3969/j.issn.1673-7598.2014.12.009(in Chinese)
[6]	岳小龙, 卓放, 张政华, 等. 电力电子系统阻抗测量的分段二叉树法[J].电工技术学报, 2015, 30(24): 76–83. YUE X L, ZHUO F, ZHANG Z H, et al. Measurement of electronic power system impedance section two fork tree[J].Journal of Electric Technology, 2015, 30(24): 76–83.DOI:10.3969/j.issn.1000-6753.2015.24.011(in Chinese)
[7]	孔祥明, 陈中华. 环路阻抗特性确定方法的探讨[J].测控技术, 2014, 33(supplement): 364–370. KONG X M, CHEN Z H. Approach to determination of loop impedance characteristics[J].Measurement and Control Technology, 2014, 33(supplement): 364–370.(in Chinese)
[8]	国防科学技术工业委员会. 军用设备和分系统电磁发射和敏感度要求: GJB 151A-97[S]. 北京: 国防科工委军用标准出版发行中心, 1997. National Defense Science and Technology Industry Committee. Electromagnetic launch and sensitivity requirements for military equipment and subsystems: GJB 151A-97[S]. Beijing: Military Standard Publication and Distribution Center of the National Defense Department, 1997(in Chinese).
[9]	赵宏旭, 王茜, 王家林. 飞机电缆屏蔽层环路阻抗测试系统设计与实现[J].自动化仪表, 2016, 37(12): 40–44. ZHAO H X, WANG Q, WANG J L. Design and implementation of loop impedance measurement system for aircraft cable shield[J].Automation Instrument, 2016, 37(12): 40–44.(in Chinese)
[10]	SEE K Y, DENG J. Measurement of noise source impedance of SMPS using a two probes approach[J].IEEE Transactions on Power Electronics, 2004, 19(3): 862–868.DOI:10.1109/TPEL.2004.826520
[11]	TAN J, ZHAO D, FERREIRA B. A method for in-situ measurement of grid impedance and load impedance at 2k-150 kHz[C]//20159th International Conference on Power Electronics and ECCE Asia. Piscataway, NJ: IEEE Press, 2015: 443-448.http://ieeexplore.ieee.org/document/7167823/
[12]	POWELL M J D. A FORTRAN subroutine for solving systems of nonlinear algebraic equations: AERE-R-5947[R]. Harwell: Atomic Energy Research Establishment, 1968: 142-151.
[13]	PAUL C R. 多导体传输线分析[M]. 2版. 杨晓宪, 郑涛, 译. 北京: 中国电力出版社, 2013: 62-283. PAUL C R. Multi conductor transmission line analysis[M]. 2nd ed. YANG X G, ZHENG T, translated. Beijing: China Electric Power Press, 2013: 62-283(in Chinese).
[14]	陈世钢, 胡景森, 汤仕平, 等. 军用设备和分系统电磁发射和敏感度要求与测量: GJB 151B-2013[S]. 北京: 中国人民解放军总装备部, 2013: 45-49. CHEN S G, HU J S, TANG S P, et al. Requirements and measurements of electromagnetic emission and sensitivity for military equipment and subsystems: GJB 151B-2013[S]. Beijing: General Armament Department of Chinese People's Liberation Army, 2013: 45-49(in Chinese).
[15]	张海东. 解析MIL-STD-461G草案[J].安全与电磁兼容, 2015(6): 25–27. ZHANG H D. Analysis on MIL-STD-461G draft[J].Safety & EMC, 2015(6): 25–27.(in Chinese)
[16]	苏东林, 李冰, 王珺珺. 线缆耦合信号实时监测方法[J].北京航空航天大学学报, 2017, 43(4): 645–653. SU D L, LI B, WANG J J. Real-time monitoring method of cable coupling signal[J].Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(4): 645–653.(in Chinese)