复杂网络[2-3]是在计算机科学取得巨大发展后的技术支持下所发展起来的,是从整体上研究复杂系统特性的理论方法。复杂网络在众多领域的应用都取得了丰硕的成果[4-8]。其中,也有很多****将复杂网络理论与航空航天领域相结合,通过复杂网络来研究现有航空网络在整体规划上的鲁棒性和演化特性[9-14]。Amara等[11]的研究证实了世界航空网(WAN)的小世界属性。Guimera等[12]揭示了WAN中大度值节点并不一定是最具影响的节点,这意味着航空网络中的关键位置可能与高度连接的枢纽不一致。Gautreau等[13]从局部动力特性方面对美国航空网络的进行了研究,并提出了一种动态网络模型来研究网络的统计特性。Chi等[14]对美国航空网络的演化特性进行了分析,发现其具有双幂率分布的特性。Li和Cai[15]对ANC的统计特性进行了相应的研究,揭示了ANC的小世界属性和每个机场的出度与入度的正相关性,以及其与相邻机场度值之间的负相关性。Cai等[16]通过对中国航路网络(CARN)的研究发现其具有与ANC不同的结构特性,且具有同质结构的CARN上的飞行流量分布却是异质的。
然而,仅从拓扑结构来描述网络是不够准确的[17],单纯的结构性分析并不能解释现实中网络大规模的故障现象,如航班的延误多数是受流量的限制,恶劣天气或袭击等造成网络结构性的破坏往往只占网络的小部分,其造成的飞行流量变动所引发的功能性级联失效,才是造成网络功能瘫痪的根本原因。无论是电网中的电流、交通网中的车流、信息网中的信息流还是航空网络中各节点的吞吐量及航线上的飞行流量都可以抽象为复杂网络中的能量,能量才是网络功能的实现行式。Barrat等[18]以节点吞吐量和航距为权重,分析了动态权重和空间约束对航空网络演化的影响。Li和Cai[15]以某天的航班数为基数研究了CAN的效率与连接紧密度成正比。通过研究网络中的能量传递规则可以清楚地了解到整个复杂系统中单元之间的能量交互所存在的隐患和不足[19-20]。
大部分的研究都没有考虑过节点的自恢复能力[21]。功能性级联失效并不影响网络的结构,当过载的能量消退时,节点将恢复其网络功能。由于航空网络结构的无标度性及飞行流量的不均匀性[1, 9, 16],当网络受到攻击或蓄意破坏时,会出现流量的大幅度波动,导致整个航空网络的短暂瘫痪,但波动过后稳定后的网络中能量流将以新的规则发生作用,部分受影响的节点将进行自愈,可自愈的节点反映的是网络应对破坏的弹性恢复能力。因此,自愈后的网络能够更准确地反映网络的鲁棒性。且随着航空网络的发展,大量新增节点及航线必然会通过网络结构的改变影响网络的特性,怎样规划网络的增长机制能够更好地在保证网络鲁棒性的前提下完善网络也有待研究。
本文着眼于航空网络的恢复鲁棒性,从能量的角度出发,考虑网络的自愈能力来分析整个网络在结构和流量分布上的合理性;并针对网络的生长特性,仿真分析了航空网络不同增长机制可能对网络整体自愈特性的影响。本文真实网络数据选择美国航空网,一是由于其经典的复杂网络特性已被许多****所研究证实;二是在于其数据来源的可靠性与便利性,可从美国官方网站[22]直接下载所得;三是已有的研究表明中国的航空网络特性与美国航空网络相接近,如双段幂率及层级结构等[15, 22],且中国未来的航空网络发展可以借鉴其网络规划。因此,研究美国航空网络不同增长机制下的自愈特性可以为中国未来完善航空网络建设提供参考。
本文首先对复杂网络理论在航空方面的研究现状进行了综述,并介绍了网络基本模型及增长机制;然后依据网络能量流动对网络结构进行了划分,并对仿真实现的算法进行了介绍;最后展示了仿真结果,并分析了其原因和影响。
1 网络模型介绍 将机场抽象为复杂网络中的节点,若两机场之间存在飞行安排,则建立连边表示航线。构建图G=(V, E)表示复杂网络,节点集合V=(v1, v2, …, vn)为网络N个节点的集合,连边集合E=(e1, e2, …, em)∈V×V为网络M条连边的集合。
1.1 网络自愈模型 自愈特性指的是在结构未被损坏,但功能受到影响而失效的情况下,当外界因素消失后,功能自主恢复的特性。网络的拓扑结构反映的是网络各节点的关联关系,但造成网络功能缺失的原因不仅仅只有关联关系的断裂。结构未被损坏,但功能受到影响也是网络功能失效的重要原因。在航空网络中,飞行流量控制是航空网络安全的重要因素之一。若将飞行流量看作网络中的能量流动,网络中不恰当的能量流动是造成网络功能缺失和网络无法自愈的主要原因。最初,Motter与Lai提出了经典负载-容量模型(ML模型)[23],以负载表示各节点或链路上流通的能量,以容量表示节点或链路对能量的承载能力,当负载超过容量时,节点或链路失效,负载的重分配将引起新一轮的节点失效,从而导致网络大面积崩溃。在此之后大量的相关模型被提出,不仅弥补了ML模型的缺陷也更加细致地刻画了真实世界复杂系统能量的传递规律。
本文选择Wang等[24]所建立的负载模型Li=kiθ,模型中节点负载L与节点连接度k紧密相关,度值k为与该机场有飞行往来的机场的数目,度值越大表明该机场规模越大,反映了机场的连通性越好,工作流量越大,其中负载参数θ>0。Yang等[25]建立的非线性负载-容量模型为Ci=α+βLi=Li+ΔCi,其中Ci为节点i的容量;α和β均为非线性容量参数;ΔCi为节点冗余容量,表示机场预留的处理突发状况的能力。假设某个节点发生故障,其负载将由其相邻节点共同承担。采用负载择优分配规则[24]实现失效节点负载的重分配,其规则如下:
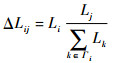 | (1) |
式中:Γi为失效节点i的所有相邻节点集合。式(1)表明负载越大的节点承受的重分配越多。此时,节点j所承受的总的转移能量为ΔLj=
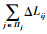
当网络中部分关键点被破坏后,网络功能的缺失将在一段时间内造成网络中能量的巨大波动,从而使得更多的节点受到牵连造成暂时的功能失效,网络将处于崩溃状态。但当这一短暂的波动期过后,恢复稳定的网络将开始自愈。若无外界干扰,自愈的节点将会受到其相邻失效节点的再次能量冲击。若节点j满足ΔLj≤ΔCj,表明节点j可以承受其相邻失效节点能量冲击,自愈后不会再次损坏,能够恢复其网络功能;反之,则说明节点j无法自愈,需要额外手段帮助其处理过量的流量。
1.2 航空网络增长机制 网络增长机制[26]是研究复杂网络不容忽略的重要性质。据统计,目前中国仅1/5城市拥有民用机场,《中国民用航空发展第十三个五年规划》规划到2020年民用机场总数将达到244个,其中2010—2020年将新增78个。网络规模的增长必然带来结构和功能的改变,不恰当的增减很可能使得新的网络结构存在严重缺陷。为了更全面地模拟航空网络的生长特性,文献[18]总结了航空网络增长特点的规律,结合《中国民用航空发展第十三个五年规划》中对新机场建设的需求,本文将网络新增节点分为3个类型,如图 1所示。
 |
| 图 1 新增节点类型划分 Fig. 1 Classification of new nodes |
| 图选项 |
1) 随着城市的发展,在经济和政治的需求下,建立城市群相对应的机场群,为加强城市的运输能力并缓解中心机场的负荷,在其周边另建机场分担客流,这类机场称为分流机场;机场的规模与城市的经济相关,故中心机场和分流机场都属于大负载机场。
a) 分流机场与中心机场距离较近,不设立飞行安排,如上海浦东与虹桥机场,北京首都机场及正在建造的大兴国际机场。
b) 对较为重要的大型机场,两机场均可与其有飞行安排;大型机场之间客流需求较大,两机场共同分担更为合理。如上海浦东和虹桥机场均安排有白云机场的飞行计划。
c) 对度值较小的机场,两机场分工合作,不重复设置飞行安排。小度值机场客流量较少,分工合作可以更合理地利用分流机场和中心机场的职能,减少重叠负载。
2) 为完善航空网络,建设围绕中心机场相对应的机场群,这类机场参照《中国民用航空发展第十三个五年规划》称为续建机场,续建机场多为中型机场。
a) 续建机场的航线安排通常与其自身的经济、地域和所处机场群相关。并没有明确的航线安排特点,但偏向于中大型机场。
3) 为满足相对偏远地区的经济开发和旅游需求而建设的机场称为新兴机场。新兴机场成本较低,故多为小型机场。
a) 新兴机场只与少数机场之间存在飞行安排;机场通常成本不高,所以能力有限,且往往依附其相邻的大机场。如德宏芒市机场的客流大部分由昆明长水国际机场承担。
b) 新兴机场侧重与较大型的机场之间设置飞行安排,与大型机场的连接可以减少网络的最短路径,方便游客的到达。
基于此类特性,在抽象的复杂网络中,对新增节点的拓扑结构按以下规则来建立:
1) 分流节点
采取择优连接的方式构造其拓扑特性,连边数可根据不同需求来设定。同时,为了减少中心节点的度值,将与分流节点连接的节点集合同中心节点的相邻节点集合进行比较,将其中大度值节点以较小概率同原节点断连,以模拟分流机场的建设特点b);将度值较小的节点以较大概率同原节点断连,以模拟分流机场的建设特点c)。但两节点的总负载将超过了原本中心节点的负载以模拟新增机场所带来的更高的新需求。
2) 续建节点
续建节点没有明显的连接特点,但偏向于与大度值节点相连,度值规模可以根据网络拓扑结构在中等规模浮动。本文根据美国航空网络的结构特性设立续建节点度值在1~4倍网络平均度之间。
3) 新兴节点
采取择优连接的方式构造其拓扑特性,新兴机场规模较小,故新兴节点的度值设置为网络平均度的一半。
2 结构划分与算法实现 2.1 结构划分 节点自愈的关键在于其冗余容量能承受其所接收的转移能量。不同的节点对能量冲击有不同的承受能力,每条边所承载的转移能量也各不相同。同时,节点自愈后其对相邻失效节点的转移能量消失,这将减少其相邻节点的负载,有助于其自愈,从而形成新的循环。所以,自愈过程是一个动态过程。
通过对已有文献的学习和思考,本文发现网络拓扑结构和节点负载及容量之间可划分为2种类型的相互作用关系。图 2(a)是一种非耦合结构,节点上的数字表示该节点抵御能量冲击的冗余容量;有向边eij上的数字表示节点i转移到节点j的能量。从这个结构可以看到,出事时只有节点A的冗余容量能够承受相邻失效节点的能量冲击,满足自愈条件。当节点A自愈后,其对节点B和D的转移能量eAB和eAD则消失,此时,节点B接收的转移能量也小于其冗余容量,使得节点B在此时也可以实现自愈,当由节点B造成的转移能量eBC和eBD也消失时,节点C和D也可满足自愈条件。该结构中的失效节点会以A—B—C—D或A—B—D—C顺序自愈,从而恢复网络功能;因此,这种能够实现自恢复的非耦合结构称为自愈结构。图 2(b)的结构形式称为耦合结构,结构内各节点的相互耦合作用形成了一个闭循环,使得该结构内的任何一个节点被修复时,都会由于转移能量大于冗余容量而发生二次失效;因此,该结构不具有自愈特性。耦合结构的存在说明网络的拓扑结构和节点的负载及容量之间不匹配,在网络设计时应尽量避免出现耦合结构。
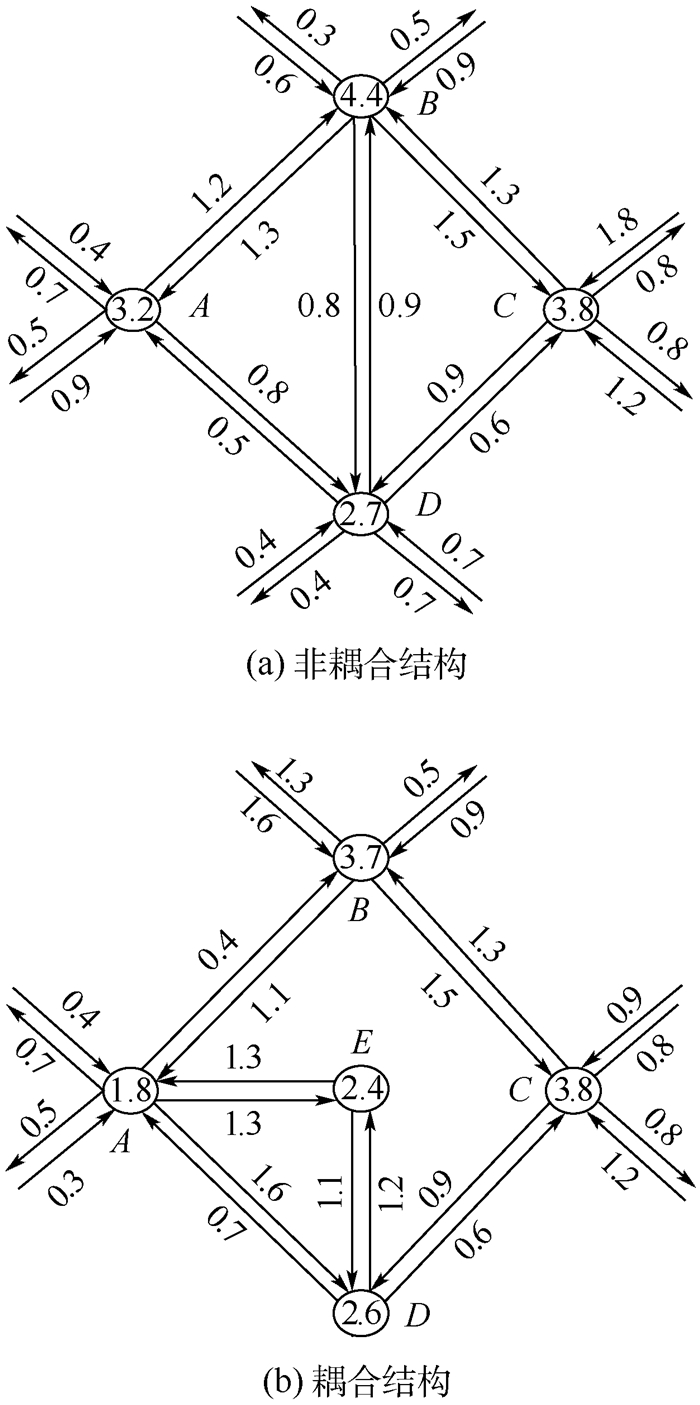 |
| 图 2 失效网络中的网络结构分类 Fig. 2 Classification of network structure in failure networks |
| 图选项 |
2.2 算法实现 为了能够在仿真过程中模拟自愈过程,本文根据网络的自愈特性提出了以下算法流程:
步骤1??将失效节点及其相应链路关系抽取出来构建失效网络,当网络是由单个节点遭受攻击后的级联失效造成的崩溃时,起始失效网络也是连通网络。假设整个失效网络中的失效节点总数为S。
步骤2??依次计算每个节点遭受的重分配负载,当节点i满足ΔLi≤ΔCi,转到步骤3。如果所有节点都不满足上述自愈条件,说明网络中只存在与图 2(b)相似的耦合结构,则自愈过程结束。
步骤3??节点满足自愈条件,自愈后从失效网络中移除节点i及其连边(见图 3)。此时,失效网络的结构发生变化,重返步骤1。
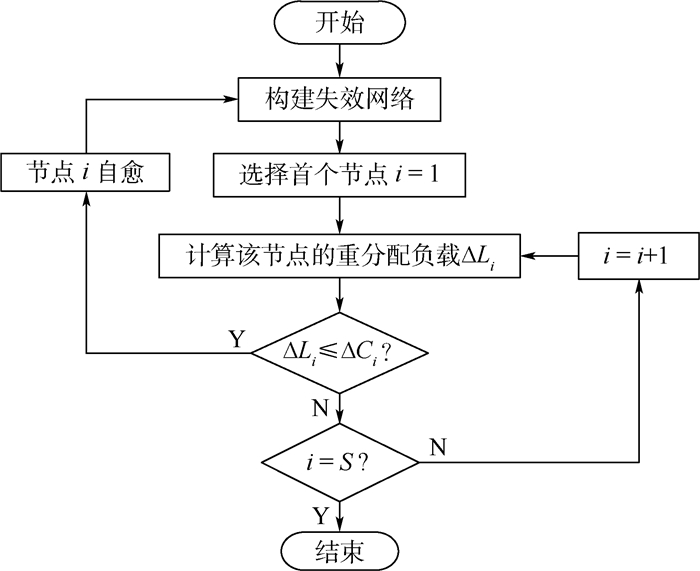 |
| 图 3 自愈流程图 Fig. 3 Self-healing flowchart |
| 图选项 |
3 仿真验证与分析 3.1 网络自愈特性分析 已有的研究表明,大部分的真实网络都具有BA网络的幂率分布特性[26]。为了验证算法的有效性及普适性,构建节点总数为N=500,平均度为〈k〉≈4的无标度网络模型。文献[24]已经证明当网络具有最强鲁棒性时,负载参数要求满足θ=1。对容量参数α(固定β=1.0)和β(固定α=2.5)的影响分别进行仿真计算。定义自愈后的网络节点规模和初始网络规模的比值为网络恢复鲁棒性,记为D,表达式为
 | (2) |
式中:No为网络最初的失效节点数;Nr为网络失效后进行自愈的节点数;Nf为无法自恢复的失效节点数目。
假设失效网络为构建的整个BA网络,即初始时满足No=N=S,运用2.2节算法对失效网络的自愈过程进行仿真,每个值都是20个独立网络下计算所得平均值,其自愈能力和效果如图 4所示。
 |
| 图 4 BA网络自愈特性与容量参数 Fig. 4 BA network self-healing characteristics versus capacity parameters |
| 图选项 |
图 4(a1)和(b1)为BA网络的自愈特性随容量系数变化下的恢复鲁棒性趋势。从图中可以看出,BA网络拥有非常好自愈能力,其网络恢复鲁棒性指标均超过0.95,且随容量系数的增加而增加。仿真结果说明BA网络在受到大振荡导致网络崩溃之后,大部分节点都可以进行自愈而无需采取额外措施。其原因在于BA网络度分布具有幂率特性:BA网络中大部分的节点度值较小,只有极少数的节点具有极大的度值;而度值与负载的正相关性和负载重分配规则的马太效应使得度值较小的节点受到能量冲击也较小,所以更容易满足自愈条件;相反,度值越大的节点其受到的能量冲击也越大,所以越难自愈,但由于大度值数目极少,所以BA网络的大部分节点都可自愈,只有极少数节点形成了耦合结构,需要采取额外手段。图 4(a2)和(b2)为自愈过程结束后,网络中所有未能自愈节点度值的平均值
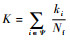
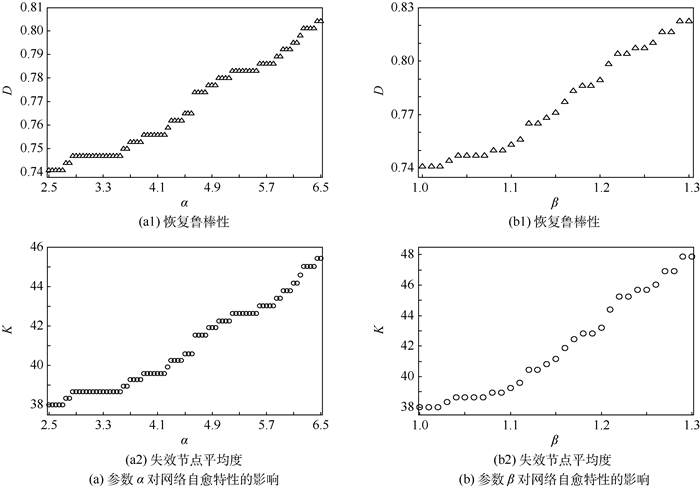
图 5(a1)和(b1)为美国航空网络的自愈特性随容量系数变化下的恢复鲁棒性趋势。美国航空网络具有332个节点,2 126条边,即平均每个机场和12个机场有飞行安排。池丽平[27]研究得出美国航空网与BA网络具有一定的差异性,但都具有幂率特性,且有较强的容错能力和较差的抗攻击能力。仿真结果表明美国航空网络也具有较强的恢复鲁棒性,其中接近80%的机场能够实现功能自愈。图 5(a2)和(b2)说明大度值节点更加容易形成耦合结构,不易进行自恢复,从侧面也反映了度值较大的节点的脆弱性,不仅受到攻击时容易引起网络的级联崩溃,而且瘫痪后也难以自愈。所以重点保护度值较大节点是提高网络安全的一种简单但有效的方法。虽然整个网络中有近八成的节点能够在能量冲击后通过自愈而恢复功能,但如果将无法自愈的节点从网络中移除,网络仍然会分崩离析,这也间接说明耦合结构对网络结构整体上具有较大的影响。
 |
| 图 5 美国航空网络自愈特性与容量参数 Fig. 5 American aviation network self-healing characteristics versus capacity parameters |
| 图选项 |
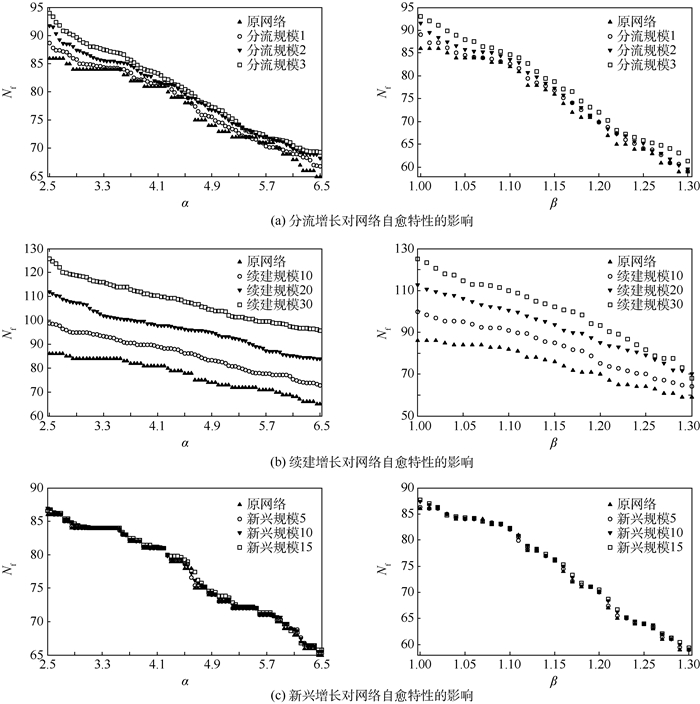
3.2 网络增长机制下自愈特性分析 网络的增长必将使得原网络的结构发生变化,而网络中一个小的缺陷很容易被网络错综复杂的耦合关系所放大,从而造成严重的损失。以美国航空网络为基础,对其生长条件下的自愈特性进行研究。通常作为分流机场而建设的机场类别需求较少,假设只对前1%的大机场(度值大于100的节点)进行分流机场增建,建设数量分别为1、2和3所机场;根据相应的建设需求,续建机场的增建数量分别选择10、20和30;新兴机场选择5、10和15来进行仿真分析。根据2.2节的增长规则对网络进行构建。由于网络增长规模的不同,以恢复鲁棒性作为评估指标不能准确地说明网络自愈能力的变化,因此选择网络中未自愈节点的规模作为评估标准。为了得到随机连接的统计特性,每个数据都是计算20个独立网络后所得平均值,虽存在误差,但能在一定程度上反映相关趋势。仿真结果如图 6所示。
 |
| 图 6 美国航空网络不同增长机制下自愈特性与容量参数的关系 Fig. 6 Relationship between self-healing characteristics and capacity parameters under different growth rules of American aviation network |
| 图选项 |
图 6(a)反映的是增加不同数量的分流机场后,新网络的自愈能力。Nf越大说明网络的自愈能力越差。从图中曲线可以看出,分流机场的增加会降低整个航空网络的自愈能力,且增加的分流机场越多,航空网络的自愈能力越差。图 6(b)反映的是增加不同数量的续建机场对网络自愈能力的影响。续建机场对网络的自愈能力带来的负担超过了分流机场,这是由于续建机场的续建规模远大于分流机场所导致的,相同扩建数量的前提下分流机场的影响力更大。这两类新增机场都具有较大的连接需求,新增航线使拓扑结构很容易形成新的耦合结构,使得整个航空网络的恢复鲁棒性降低。图 6(c)反映的是增加不同数量的新兴机场对网络自愈能力的影响。图中曲线很明显地反映出新兴机场的增建对网络的自愈能力影响微弱,并没有对网络中其他节点的自愈带来太大影响。新增建的机场自身也具有良好的自愈能力,但对原本就未能自愈的节点也未能减缓其压力。总体而言,在现有网络的基础上,增加新兴节点以完善航空网络不会存在降低网络自愈能力的风险。但要构建机场群,在各机场之间开通更多的航线,增加网络密度,将会削弱网络整体的自恢复能力。
4 结论 本文运用复杂网络理论对美国航空网络不同增长机制下的恢复鲁棒性进行了研究,得出以下结论:
1) 美国航空网络中大部分的机场在受到级联失效影响下具有功能自愈能力。
2) 少数大负载机场,由于其易形成耦合结构而无法实现自愈,对网络整体结构的稳定性影响非常大。
3) 为完善航空网络而建立的机场群,由于其较大的连接需求,加大了网络区域密度,复杂了网络拓扑结构,降低了网络的自恢复能力。
4) 新兴机场这一类小型机场的增加不会影响网络整体的自愈能力。
技术的进步和经济的增长使得航空网络的发展步入正轨,其重要地位决定该方向的研究仍会是一个长期且艰巨的过程。本文简化了航空网络的许多特性,用有向加权网络能够更准确地描绘航空网络的特性;结合铁路网等的相依网络模型则能更精细地刻画现实中的客流动向,进而更加准确地反映出机场的建设需求及影响;在后续的研究中将逐步完善模型,以便更贴近客观现实。总体而言,本文的研究结果可以为中国航空发展规划提供一定的理论支持。
参考文献
| [1] | 莫辉辉, 王姣娥. 复杂交通网络:结构、过程与机理[M].北京: 经济管理出版社, 2012: 121-151. MO H H, WANG J E. Complex transport network:Structure, process & mechanism[M].Beijing: Economy and Management Press, 2012: 121-151.(in Chinese) |
| [2] | NEWMAN M E J. Networks:An introduction[M].Oxford: Oxford University Press, 2010: 741-743. |
| [3] | CHEN G R, WANG X F, LI X. Introduction to complex networks:Models, structures and dynamics[M].Beijing: Higher Education Press, 2012: 3-13. |
| [4] | 郑啸, 陈建平, 邵佳丽, 等. 基于复杂网络理论的北京公交网络拓扑性质分析[J].物理学报, 2012, 61(19): 95–105. ZHENG X, CHEN J P, SHAO J L, et al. Analysis on topological properties of Beijing urban public transit based on complex network theory[J].Acta Physica Sinica, 2012, 61(19): 95–105.(in Chinese) |
| [5] | REN T, WANG Y F, LIU M M, et al. Analysis of robustness of urban bus network[J].Chinese Physics B, 2016, 25(2): 1–12. |
| [6] | 蔡君, 余顺争. 一种有效提高无标度网络负载容量的管理策略[J].物理学报, 2013, 62(5): 058901. CAI J, YU S Z. An efficient management strategy for enhancing traffic capacity in scale-free networks[J].Acta Physica Sinica, 2013, 62(5): 058901.(in Chinese) |
| [7] | LIU H R, DONG M R, YIN R R, et al. Cascading failure in the wireless sensor scale-free networks[J].Chinese Physics B, 2015, 24(5): 293–299. |
| [8] | WANG X, WANG Y, ZHU L, et al. A novel approach to characterize information radiation in complex networks[J].Physica A Statistical Mechanics & Its Applications, 2016, 452(1-3): 95–105. |
| [9] | BARRAT A, BARTHELEMY M, VESPIGNANI A, et al. The architecture of complex weighted networks:Measurements and models[J].Proceedings of the National Academy of Sciences of the United States of America, 2003, 101(11): 3747. |
| [10] | COLIZZA V, BARRAT A, BARTHELEMY M, et al. Prediction and predictability of global epidemics:The role of the airline transportation network[J].Proceedings of the National Academy of Sciences of the United States of America, 2015, 103(7): 2015–2020. |
| [11] | AMARA L A N, SCALA A, BARTHELEMY M, et al. Classes of small-world networks[J].Proceedings of the National Academy of Sciences of the United States of America, 2000, 97(21): 11149–11152.DOI:10.1073/pnas.200327197 |
| [12] | GUIMERA R, MOSSA S, TURTSCHI A, et al. Structure and efficiency of the world-wide airport network[J].Polymers & Polymer Composites, 2003, 11(4): 7794–7799. |
| [13] | GAUTREAU A, BARRAT A, BARTHELEMY M, et al. Microdynamics in stationary complex networks[J].Proceedings of the National Academy of Sciences of the United States of America, 2009, 106(22): 8847–8852.DOI:10.1073/pnas.0811113106 |
| [14] | CHI L P, WANG R, SU H, et al. Structural properties of US flight network[J].Chinese Physics Letters, 2003, 20(8): 1393–1396.DOI:10.1088/0256-307X/20/8/362 |
| [15] | LI W, CAI X. Statistical analysis of airport network of China[J].Physical Review E Statistical Nonlinear & Soft Matter Physics, 2004, 69(2): 046106. |
| [16] | CAI K Q, ZHANG J, DU W B, et al. Analysis of the Chinese air route network as a complex network[J].Chinese Physics B, 2012, 21(2): 596–602. |
| [17] | NAKASHIMA S, MITANI T, SENZAKI J, et al. Characterization and modeling of weighted networks[J].Physica A Statistical Mechanics & Its Applications, 2005, 346(1-2): 34–43. |
| [18] | BARRAT A, BARTHELEMY M, VESPIGNANI A. The effects of spatial constraints on the evolution of weighted complex networks[J].Journal of Statistical Mechanics:Theory and Experiment, 2005(5): 799–803. |
| [19] | CHEN S M, XUI Y F, NIE S. Robustness of network controllability in cascading failure[J].Physica A Statistical Mechanics & Its Applications, 2017, 471(1): 536–539. |
| [20] | WANG J W. Robustness of complex networks with the local protection strategy against cascading failure[J].Safety Science, 2013, 53: 219–225.DOI:10.1016/j.ssci.2012.09.011 |
| [21] | MAJDANDZIC A, PODOBNIK B, BULDYREV S V, et al. Spontaneous recovery in dynamical networks[J].Nature Physics, 2014, 10(1): 34–38.DOI:10.1038/nphys2819 |
| [22] | 刘宏鲲, 周涛. 中国城市航空网络的实证研究与分析[J].物理学报, 2007, 56(l): 106–112. LIU H K, ZHOU T. Empirical study of Chinese city airline network[J].Acta Physica Sinica, 2007, 56(l): 106–112.(in Chinese) |
| [23] | MOTTER A E, LAI Y C. Cascade-based attacks on complex networks[J].Physical Review E, 2002, 66(6): 065102.DOI:10.1103/PhysRevE.66.065102 |
| [24] | WANG J W, RONG L L, ZHANG L, et al. Attack vulnerability of scale-free networks due to cascading failures[J].Physica A Statistical Mechanics & Its Applications, 2008, 387(26): 6671–6678. |
| [25] | YANG R, WANG W X, LAI Y C, et al. Optimal weighting scheme for suppressing cascades and traffic congestion in complex networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics, 2009, 79(2Pt2): 026112. |
| [26] | BARABASI A L, ALBERT R. Emergence of scaling in random networks[J].Science, 1999, 286(5439): 509–512.DOI:10.1126/science.286.5439.509 |
| [27] | 池丽平. 遭袭复杂网络的修复策略与关联特性研究[D]. 武汉: 华中师范大学, 2006: 58-69. CHI L P. On the repair strategy and correlation properties of complex networks under attacks[D]. Wuhan: Central China Normal University, 2006: 58-69(in Chinese).http://cdmd.cnki.com.cn/article/cdmd-10511-2006079480.htm |
