结构简单、重量较轻、易于维护及可靠性强的黏弹减摆器现广泛应用于无铰式、无轴承式及星型柔性旋翼直升机桨叶减摆。黏弹减摆器的非线性特性对直升机旋翼/机体耦合动稳定性影响较大，而耦合系统的非线性动稳定性分析一般采用时域分析法，因此建立一种能用于直升机旋翼/机体耦合非线性动稳定性时域分析的黏弹减摆器模型尤为重要。
直升机动力学研究中常用的黏弹减摆器模型有VKS(Voigt-Klevin)模型^[1-3]、ADF(Anelastic Displacement Fields)模型^[4-7]和迟滞非线性模型^[8-11]等。在直升机旋翼/机体耦合动稳定性分析中，一般对黏弹减摆器进行线性化处理后采用特征分析法：Gandhi和Chopra^[12]对黏弹减摆器线性化处理后，分析了其对直升机悬停空中共振的影响；笔者课题组^[13]采用线性化的VKS模型分析了黏弹减摆器对直升机前飞空中共振的影响；王波等^[14]采用线性化的VKS模型分析了黏弹减摆器的不同连接方式对直升机地面共振的影响。而在保留黏弹减摆器非线性情况下进行直升机旋翼/机体耦合动稳定性分析的研究较少，王波等^[15]将基于复模量的非线性VKS模型用于直升机空中共振时域分析；卫丽君等^[16]则将该方法用于分析黏弹减摆器不同连接方式对直升机空中共振的影响。但基于复模量识别的非线性VKS模型不能很好地预估时域响应，而基于时域响应识别的VKS模型却难以描述其幅变特性^[2]。
为了适用较宽的动幅值范围，黏弹减摆器一般引入动幅值变量^[11]，但很难将其用于幅值变化的直升机旋翼/机体耦合动稳定性时域分析。为解决上述问题，对动幅值参量进行改进，并将改进后的黏弹减摆器模型用于直升机地面共振非线性时域分析，验证上述方法的可行性。
1 黏弹减摆器改进模型 现有的黏弹减摆器模型为了适用于宽的动幅值范围，一般在模型中引入动幅值参量δ，如式(1)所示一种双线性迟滞模型，在周期激振x=x₀+δcos(ωt)作用下(x₀为静位移, ω为响应频率，t为时间)，黏弹减摆器恢复力表示为

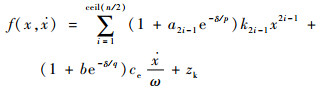(1)

式中：x和分别为减摆器的位移和速度；k_i为第i阶弹性力系数；n为弹性力阶次，实验结果^[11]表明黏弹减摆器弹性力呈明显的奇次性，所以弹性力只取奇次项；c_e为线性阻尼力系数；a_i、p和b、q分别为弹性力和阻尼力随动幅值变化的指数衰减系数；z_k为滑移弹性力，可表示为

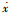
其中：x_s为滑移极限位移；k_s =z_s/x_s为滑移线性刚度，z_s为滑移极限恢复力。
黏弹减摆器的复模量经推导可得

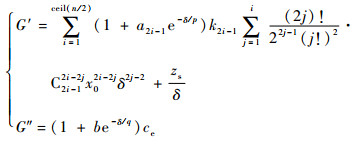(2)

式中：G′和G″分别为储能模量和耗能模量。
在直升机旋翼/机体耦合动稳定性时域分析中，减摆器响应的动幅值一般是变化的，而减摆器刚度会随动幅值变化而变化，这就导致频率也是变化的，采用类似上述包含动幅值及频率参量的模型难以进行时域分析，需要进行改进。
1.1 单频激振条件 减摆器在收敛、中性稳定和发散3种情况下受到扰动后的时域响应如图 1所示。

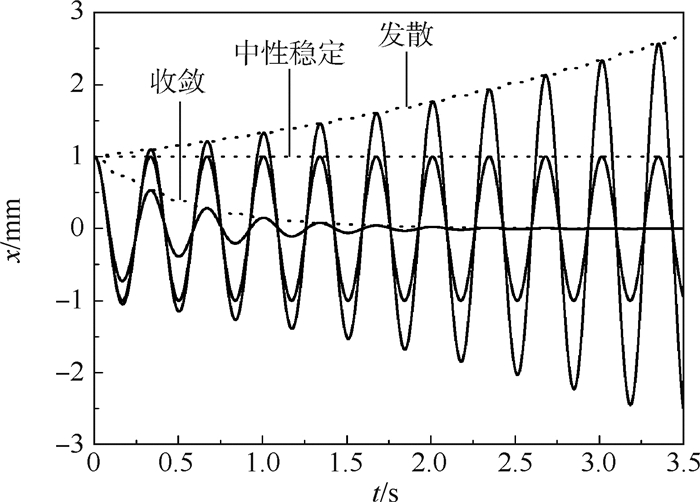图 1 不同稳定情况下的单频时域响应 Fig. 1 Single frequency response in time domain at different stable situations

图选项

减摆器等效线性化后，其响应可表示为

(3)

式中：δ₀为初始幅值；φ_d为初始相位角；ω_d=为阻尼振动频率，ξ为摆振阻尼比，ω_n为摆振固有频率，可表示为

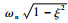
(4)

其中：I_b和S_b分别为桨叶对摆振铰的惯性矩和静矩；k_b为除减摆器外的摆振刚度；e为摆振铰外伸量；Ω为旋翼转速；R_d为摆振铰至减摆器距离。
由式(3)可知，响应振动幅值可表示为

(5)

摆振阻尼较大时，响应很快衰减，没有振荡特性，故暂针对小阻尼情况进行研究。此时，响应振动幅值可近似表示为

(6)

图 1中所示的点线即为采用式(6)计算的振动幅值，结果说明了式(6)计算的准确性。
将式(6)代入式(1)即可消除黏弹减摆器模型中的动幅值及频率参量。
1.2 双频激振条件 直升机前飞或滑跑时，桨叶摆振面由于存在1Ω的哥氏力矩作用，将产生1Ω的强迫振动响应作用于减摆器。因此，黏弹减摆器受到扰动后实际上是处于双频激振条件下，其动态响应可表示为

(7)

式中：x_Ω为强迫振动位移；δ_Ω为强迫振动幅值；φ_Ω为强迫振动初始相位角。
1Ω强迫振动在摆振阻尼较小的情况下，强迫振动幅值可表示为

(8)

式中：M_c为哥氏力矩幅值。
此时，扰动响应振动幅值δ_d可表示为

(9)

完整响应振动幅值可表示为

(10)

式(10)中频率是作用于速度项，因此将其表示成关于强迫振动和扰动运动速度幅值比的指数函数。当δ_Ω=0时，即没有强迫振动的情况下，式(10)与式(6)相同，表示单频条件下的振动幅值。
在1.1节单频激振条件的基础上叠加频率为6 Hz、幅值为1 mm的强迫振动，3种情况下的响应如图 2所示，图中实线表示位移，采用式(10)计算的幅值如点线所示。

图 2 不同稳定情况下的双频时域响应 Fig. 2 Double frequency response in time domain at different stable situations

图选项

由图 2可以看出，式(10)所计算的幅值曲线较好地反映了双频条件下黏弹减摆器响应幅值在时域上的变化趋势。
将式(10)表示的幅值及频率代入式(1)，并结合直升机旋翼/机体耦合动力学模型，便能进行旋翼/机体耦合时域仿真，用于分析耦合系统的非线性动稳定性，具体计算流程如图 3所示，x_t=0和分别为初始位移和初始速度, ζ和分别为摆振角和摆振角速度。

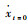
图 3 黏弹减摆器时域响应计算流程 Fig. 3 Calculation flow of elastomeric damper time domain response

图选项

因为幅值计算需要频率参数，而频率又受幅值的影响，因此初始幅值用初始位移与静位移差值的绝对值|x_t=0-x₀|代替。
2 计入黏弹减摆器的地面共振分析 2.1 计入黏弹减摆器的地面共振模型 黏弹减摆器安装在旋翼上主要用于提高桨叶摆振阻尼，计入黏弹减摆器作用后的直升机地面共振当量平面模型为

(11)

式中：c_b为除减摆器外的桨叶摆振阻尼；m_b为桨叶质量；N为桨叶片数；ζ_k和ψ_k分别为第k片桨叶的摆振角和方位角；x_h和y_h分别为桨榖中心纵向和横向位移；m_x和m_y分别为机体当量至桨榖中心纵向和横向的质量；k_x和k_y分别为机体当量至桨榖中心纵向和横向的刚度；c_x和c_y分别为机体当量至桨榖中心纵向和横向的阻尼；f(x_k, )为式(1)计算的第k个减摆器的作用力，x_k=ζ_kR_d和分别为第k个减摆器的位移和速度。
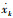
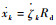
2.2 仿真分析主要参数 某型黏弹减摆器经识别后所得的参数为：a₁=-0.346 2，a₃=-5.087，a₅=-57.83，p=0.798 2 mm，k₁=307.6 N/mm，k₃=11.76 N/mm³，k₅=-0.046 8 N/mm⁵，b=3.103，q=1.367 mm，c_e=541.8 N/mm，z_s=505.6δ N，x_s=0.234 8δ mm。
采用式(2)对静位移为6 mm时，不同动幅值下黏弹减摆器的复模量进行计算，并与实验值对比，结果如图 4所示。

图 4 复模量对比结果 Fig. 4 Comparison of complex modulus

图选项

由图 4可知，采用本文黏弹减摆器双线性迟滞模型计算的复模量与实验值吻合较好，证明了该模型的准确性。后续也将采用静位移为6 mm状态下的黏弹减摆器特性进行计算。
某型直升机旋翼及机体的主要参数如表 1所示，除减摆器外的摆振刚度及阻尼较小，可以忽略不计，即k_b=c_b=0。
表 1 直升机主要参数 Table 1 Main parameters of helicopter

参数	数值
桨叶片数	4
桨叶质量/kg	42.3
桨叶对摆振铰静矩/(kg·m)	123.7
桨叶对摆振铰惯性矩/(kg·m2)	457
摆振铰外伸量/m	0.23
减摆器到摆振铰距离/m	0.35
机体纵向当量质量/kg	2 000
机体纵向固有频率/Hz	1
机体纵向当量阻尼/(N·s·m-1)	1 000
机体横向当量质量/kg	800
机体横向固有频率/Hz	1.5
机体横向当量阻尼/(N·s·m-1)	500

表选项






2.3 地面共振仿真分析 旋翼摆振后退型模态在直升机地面共振分析中较为重要，为分析旋翼摆振后退型模态，首先需要通过对桨叶摆振方向以摆振固有频率施加激振力矩的方式激出旋翼的摆振后退型模态。由图 4可知，黏弹减摆器在不同动幅值下具有不同的复模量，因此采用的激振力矩需要使得激出的桨叶摆振幅值(减摆器振动幅值)与激振频率(减摆器储能模量)符合图 4中的复模量曲线。根据强迫振动理论^[17]可估计需要的激振力矩幅值M_r为

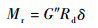(12)

黏弹减摆器取不同动幅值下的复模量确定激振频率，采用式(12)确定激振力矩幅值，激出不同转速下旋翼的摆振后退型模态后，确定模拟出的减摆器响应幅值如图 5所示。

图 5 减摆器响应幅值变化情况 Fig. 5 Response amplitude of damper

图选项

由图 5可知，模拟出的减摆器响应幅值δ_r与最初选择的振动幅值(理论值)基本吻合，虽然个别点由于旋翼摆振后退型模态与机体运动模态耦合引起的误差稍大，但最大误差仍不超过6%，证实了采用式(12)确定激振力矩幅值的可行性。
选取动幅值分别为0.5、2和6 mm的3种情况下对应的复模量状态，针对黏弹减摆器线性化(复模量取常值)的情况，在激出旋翼摆振后退型模态后，采用基于多桨叶坐标变换的阻尼识别法^[18]对瞬态响应进行模态阻尼识别，并与采用特征值法计算的模态阻尼进行对比，具体结果如图 6所示，图中BX和BY分别表示机体的纵横向运动模态，RL表示旋翼摆振后退型模态，f_m和σ分别为模态频率和模态阻尼。

图 6 线性系统的摆振后退型模态特性 Fig. 6 Regressive lagging modal features of linear system

图选项

由图 6可知，在黏弹减摆器取不同复模量的情况下，通过阻尼识别所得的模态阻尼与采用特征值法计算所得的模态阻尼基本吻合，说明所采用的基于多桨叶坐标变换的阻尼识别法的有效性。由图中还可以看出，在旋翼摆振后退型模态与机体模态耦合时，激出旋翼摆振后退型响应的同时也激出了机体响应，使得所识别的摆振后退型模态阻尼误差稍大。
以旋翼转速Ω=300 r/min为例，取黏弹减摆器响应幅值δ=6 mm时的储能模量确定激振频率，以此激振频率激出系统的摆振后退型模态后，计算黏弹减摆器线性化(复模量取常值)和非线性2种情况下的瞬态响应，由于各桨叶减摆器响应仅存在相位差的区别，因此只给出第1个减摆器的位移时域响应和功量图，如图 7、图 8所示。

图 7 第1个黏弹减摆器的位移响应 Fig. 7 Displacement response of the first elastomeric damper

图选项

图 8 第1个黏弹减摆器的功量图 Fig. 8 Force-displacement curves of the first elastomeric damper

图选项

由图 7可以看出，与黏弹减摆器线性化的响应相比，在保留减摆器非线性的情况下，其响应衰减得更快，且振动频率更大。据分析可知，是衰减过程中减摆器阻尼及刚度随响应幅值的减小而增加引起的。
由图 8可见，保留黏弹减摆器非线性的功量图与线性化后差异较大，说明在进行黏弹减摆器载荷计算时不能忽略其非线性的影响。
旋翼摆振后退型模态响应ζ_RL如图 9所示，采用阻尼识别法对旋翼摆振后退型模态阻尼进行识别，其随时间的变化如图 10所示。

图 9 旋翼摆振后退型时域响应 Fig. 9 Time domain response of rotor regressive lagging mode

图选项

图 10 旋翼摆振后退型阻尼随时间变化情况 Fig. 10 Variation of rotor regressive lagging modal damping with time

图选项

由图 10可知，由于减摆器非线性的影响，在响应衰减的过程中，随着黏弹减摆器振动幅值的减小，其耗能模量增加，使得桨叶的摆振阻尼增加，旋翼摆振后退型模态阻尼在时域上呈增加趋势，减摆器线性化后，摆振后退型模态阻尼保持不变，这也就是图 9中保留减摆器非线性后，旋翼摆振后退型响应衰减的更快的原因。
据分析，在图 4所示的黏弹减摆器非线性条件下，系统初始稳定能确保整个过程的稳定。结合图 6的结果可知，减摆器受到的扰动越大，旋翼摆振后退型模态阻尼越小，情况越危险。因此，在地面共振试验或理论分析中应该重点关注大扰动下系统初始阶段的响应及其模态阻尼。
3 结论 1) 针对小摆振阻尼比的情况，给出了单频及双频条件下黏弹减摆器模型中动幅值参量的计算方法，采用该方法计算系统在收敛、中性稳定及发散3种情况下的幅值曲线能较好地反映响应幅值在时域上的变化趋势，说明该方法可使带动幅值参量的黏弹减摆器模型用于直升机旋翼/机体耦合动稳定性时域分析。
2) 给出了计入非线性黏弹减摆器后，激出旋翼摆振后退型模态所需激振力矩的计算方法，在不同转速不同复模量状态下，采用该方法确定的激振力矩对桨叶进行激振激出的响应幅值与预期值误差不超过6%，说明了所述方法的准确性。
3) 将改进后的黏弹减摆器模型用于直升机地面共振时域分析，对摆振后退型响应进行分析可知，系统稳定时，与线性化结果相比，计入黏弹减摆器非线性后，旋翼摆振后退型响应衰减更快，其模态阻尼在时域上呈增加趋势。

参考文献

[1]	FELKER F F, LAU B H, MCLAUGHLIN S, et al. Nonlinear behavior of an elastomeric lag damper undergoing dual-frequency motion and its effect on rotor dynamics[J].Journal of the American Helicopter Society, 1987, 34(4): 45–53.
[2]	KUNZ D L. Influence of elastomeric lag damper modeling on the predicted dynamic response of helicopter rotor systems[C]//Proceedings of 38th Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 1997: 1-11.
[3]	胡国才, 侯志强. 一种基于复模量的黏弹减摆器非线性VKS改进模型[J].工程力学, 2005, 22(Sup.): 73–77. HU G C, HOU Z Q. An improved nonlinear VKS model of elastomeric lag damper based on its complex modulus[J].Engineering Mechanics, 2005, 22(Sup.): 73–77.(in Chinese)
[4]	LESIEUTRE G A. Modeling frequency-dependent longitudinal dynamic behavior of linear viscoelastic long fiber composites[J].Journal of Composite Materials, 1994, 28(18): 1770–1782.DOI:10.1177/002199839402801802
[5]	LESIEUTRE G A, BIANCHINI E. Time domain modeling of linear viscoelasticity using anelastic displacement fields[J].Journal of Vibration and Acoustics, 1995, 117(4): 424–430.DOI:10.1115/1.2874474
[6]	SMITH E C, GOVINDSWAMY K, BCALE M R, et al. Formulation, validation, and application of a finite element model for elastomeric lag dampers[J].Journal of the American Helicopter Society, 1996, 43(3): 257–266.
[7]	BRACKBILL C R, LESIEUTRE G A, SMITH E C, et al. Characterization and modeling of the low strain amplitude and frequency dependent behavior of elastomeric damper materials[J].Journal of the American Helicopter Society, 2000, 47(1): 34–42.
[8]	CAUGHEY T K. Equivalent linearization techniques[J].Journal of the Acoustical Society of America, 1963, 35(11): 1706–1711.DOI:10.1121/1.1918794
[9]	BOUC R. Forced vibration of mechanical system with hysteresis[C]//Proceedings of 4th Conference on Nonlinear Oscillation, 1967: 315-320.
[10]	WEN Y K. Method for random vibration of hysteretic systems[J].Journal of Applied Mechanics, 1976, 102(2): 249–263.
[11]	李冬伟, 白鸿柏, 杨建春, 等. 非线性迟滞系统建模方法[J].机械工程学报, 2005, 41(10): 205–214. LI D W, BAI H B, YANG J C, et al. Modeling of a nonlinear system with hysteresis characteristics[J].Chinese Journal of Mechanical Engineering, 2005, 41(10): 205–214.DOI:10.3321/j.issn:0577-6686.2005.10.040(in Chinese)
[12]	GANDHI F, CHOPRA I. An analytical model for a nonlinear elastomeric lag damper and its effect on aeromechanical stability in hover[J].Journal of the American Helicopter Society, 1994, 39(4): 59–69.DOI:10.4050/JAHS.39.59
[13]	胡国才, 向锦武, 张晓谷. 黏弹减摆器非线性特性对直升机前飞空中共振的影响分析[J].航空学报, 2005, 26(2): 199–202. HU G C, XIANG J W, ZHANG X G. Analysis of the effect of nonlinear characteristics of elastomeric lag damper on helicopter air resonance in forward flight[J].Acta Aeronautica et Astronautica Sinica, 2005, 26(2): 199–202.DOI:10.3321/j.issn:1000-6893.2005.02.015(in Chinese)
[14]	王波, 李书, 徐亚妮. 不同黏弹减摆器连接的直升机地面共振分析[J].振动工程学报, 2007, 20(2): 123–127. WANG B, LI S, XU Y N. Analysis of ground resonance for helicopters with different elastomeric lag damper connections[J].Journal of Vibration Engineering, 2007, 20(2): 123–127.DOI:10.3969/j.issn.1004-4523.2007.02.004(in Chinese)
[15]	王波, 李书, 张晓谷. 非线性叶间黏弹减摆器对直升机空中共振的影响分析[J].航空学报, 2007, 28(3): 550–555. WANG B, LI S, ZHANG X G. Influence analysis of helicopter air resonance with nonlinear inter blade viscoelastic dampers[J].Acta Aeronautica et Astronautica Sinica, 2007, 28(3): 550–555.DOI:10.3321/j.issn:1000-6893.2007.03.008(in Chinese)
[16]	卫丽君, 李书, 王波. 黏弹减摆器结构参数对直升机动稳定性的影响分析[J].南京航空航天大学学报, 2010, 42(3): 303–306. WEI L J, LI S, WANG B. Joint parameter analysis of helicopter dynamic stability with viscoelastic dampers[J].Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(3): 303–306.DOI:10.3969/j.issn.1005-2615.2010.03.008(in Chinese)
[17]	胡海岩. 机械振动基础[M].北京: 北京航空航天大学出版社, 2005: 20-21. HU H Y. Fundamentals of mechanical vibration[M].Beijing: Beihang University Press, 2005: 20-21.(in Chinese)
[18]	胡国才. 直升机旋翼非线性等效阻尼的识别[J].航空学报, 2005, 26(3): 303–307. HU G C. Nonlinear equivalent damping identification for helicopter rotor[J].Acta Aeronautica et Astronautica Sinica, 2005, 26(3): 303–307.DOI:10.3321/j.issn:1000-6893.2005.03.010(in Chinese)