在早期的现场实测中,由于龙卷风发生的地点和时间的不可预测性,以及测量技术的限制,导致实测研究发展很缓慢。Hoecker[1]针对1957年发生的Dallas龙卷风,通过走访目击者以及察看龙卷风的图片和视频资料,指出涡核区域存在下沉气流并给出了龙卷风内部分位置的速度结构。21世纪初,多普勒雷达等的使用大大丰富了数据上的空缺,比较典型的是Alexander和Wurman[2-3]利用移动式多普勒雷达实测了1998年5月30日发生在南达科他州Spencer的龙卷风,并提供了该龙卷风不同高度和时间的速度分布。
相比现场实测,实验研究和数值模拟更加方便易于收集数据。在龙卷风的实验研究中,Chang[4]于1971年率先建立了龙卷风发生装置并测定了龙卷风切向和径向的速度分布特征。基于Chang[4]的研究,Ward[5]于1972年利用蜂窝板消除龙卷风竖向的涡量,建立了著名的Ward模型。此后,许多科研人员又在Ward模型的基础上进行实验并改进建立了诸多模型,其中普渡大学的Church等[6]引入旋转网格栅改进了Ward模型并进行了实验,发现龙卷风的涡可分裂呈现出多涡状态。Jischke和Parang[7]利用Ward模拟器发现了核心半径这一参数的重要性,并提出将涡流比、高宽比和涡流雷诺数作为龙卷风模拟设计的主要参数。上述实验均未考虑龙卷风的横向移动,直到爱荷华州立大学开创了此先河,于2003年建立了可以使龙卷风进行平移运动的模拟发生器。之后Sarkar等[8]利用其对龙卷风进行了风场特性的相关实验研究,并取得了和实测基本一致的结果。
近年来,随着计算机技术和计算流体力学(CFD)相关模拟软件的迅猛发展,对龙卷风的研究更多地转入了数值模拟方面。Hassenzahl[9]采用限制涡流的方式对龙卷风的涡流特性进行了研究。Maruyama[10-11]于2009年应用大涡模拟研究了龙卷风的涡流特性;并于2011年在龙卷风模型中加入碎片,分析了碎片的运动特性,且利用其验证了龙卷风的涡核特性。Natarajan等[12-13]则研究了建筑物表面的粗糙度对龙卷风风场的影响,并于2011年通过数值模拟了Ward-type TVC型、WinDEEE Dome型和AVE型这3种龙卷风发生器形成的龙卷风风场的涡流特性,与实验对比发现Ward-type TVC型与之更相符。徐枫等[14]针对单涡龙卷风的风场特性,分析了切向风速在径向和高度的速度分布规律,并与Rankin涡模型和参数化气旋模型相对比,验证了模拟结果的合理性。
在以往对龙卷风的数值模拟研究中大多都以不可压缩假设处理,忽略了这种极端大气现象中气流可压缩性的影响。与此同时,忽略了温度场内气流之间的热交换。但龙卷风多发于气温很高的夏季时节,而且其内外的温度差很大,气体温度越高其包含的热能越多,在某些情况下,气体所储存的热能可转化为机械能的形式而输出能量做功。北京航空航天大学的高歌教授指出,目前热机做功基本上都是通过膨胀做功的原理来实现,例如拉瓦尔喷管等。但在自然界中所发生的某些现象虽然没有相应的做功机构,但仍然可以达到做功的目的,典型的例子就是龙卷风。显然龙卷风气体自身所具有的巨大热能是龙卷风能够做功的主要动力来源。故本文通过开发计算流体力学软件CFL3D(cfl3d v5 manual)[15]给定了龙卷风初始速度场和边界条件,匹配不同的初始温度场以及龙卷风外围大气温度情况,研究龙卷风风场的发展演化与温度场的关系。
1 数值模拟设置 1.1 数值模拟几何模型 本文龙卷风的初场是给定的,且主要研究的是龙卷风的发展演化,因此其发生区域给定在一尺寸为1 000 m×1 000 m×5 m的长方体内。模型的网格是采用软件Pointwise生成的结构网格,因为参数变化主要集中在核心半径区域,所以在中心加密,从内到外网格由密变疏。网格维数为193×193×5,网格俯视截面图如图 1所示。
 |
| 图 1 龙卷风数值模拟的网格划分 Fig. 1 Mesh generation for numerical simulation of tornado |
| 图选项 |
1.2 控制方程及计算方法 本文选用的控制方程为连续性方程、Navier-Stokes方程以及能量方程。三维非定常流体的连续性方程为
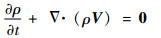 |
式中:ρ为密度;t为时间;?为Nabla算子;V为流体运动速度。
本次模拟采用可压缩流动模拟,故应用于本文的Navier-Stokes方程和能量方程分别为
 |
式中:ρR为单位体积流体所受的质量力,R为质量力;p为黏性流体的动压;τij为黏性应力张量;e为单位质量流体的能量;λ为导热系数;T为流体温度;q为由于热辐射或其他原因在单位时间内传入的热量。
计算方法方面,无黏项空间离散格式采用三阶Roe格式+MUSCL插值,黏性通量空间离散格式为中心差分,时间推进方式采用近似因子分解算法, 双时间步推进实现精确地实时计算。
1.3 初始速度场及边界条件的设置 龙卷风的初始速度场是根据文献[16]中所提供的某种情况下龙卷风的速度剖面图并查找龙卷风相关风强级别后加以修改的,如图 2所示。rc为初始速度场的涡核半径(速度最大处的半径)。在本文的模型中,初始速度场的半径r为140 m,涡核半径rc为50 m,所取最大速度为60 m/s,属于F2级龙卷风速度范围。
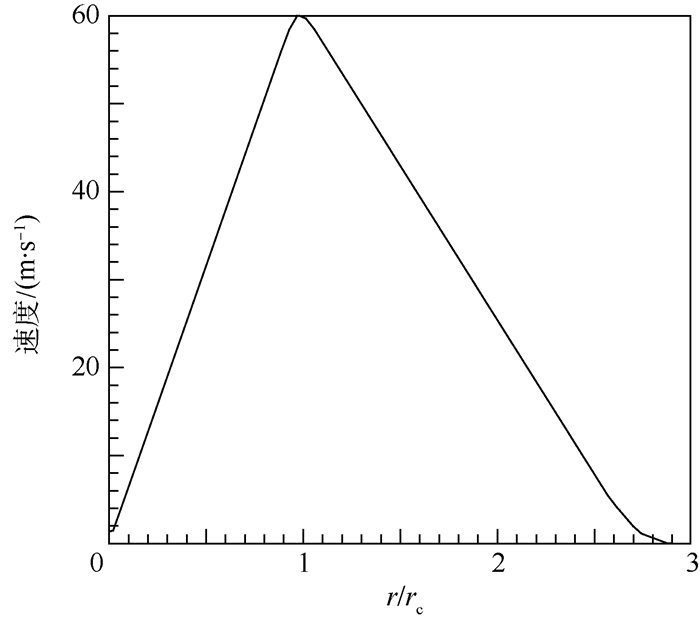 |
| 图 2 初始速度场的速度分布 Fig. 2 Velocity distribution of initial velocity field |
| 图选项 |
本文忽略了龙卷风在水平方向上的移动,输入文件中每一步的时间步长dt为0.1 s,每个步长内迭代5次,计算步数NTSTEP为100、1 000、2 000、4 000和8 000。在数值模拟中边界条件的选择直接关乎到模拟的可信度甚至成败,由于本文研究的是龙卷风内部某一截平面上的变化,相当于是水平截取龙卷风中的一部分,故设置6个面的边界条件均为无黏面(inviscid surface)。
1.4 不同初始温度场的设置 1) 算例1初始温度场为均一的温度场,即场域中初始温度均一样,为288 K。
2) 算例2的初始温度场采用类似于算例1相对稳定后的形式。
2 模拟结果与分析 在龙卷风的发展过程中,气流的旋转运动必然会改变局部气流的参数变化乃至影响到全场。在这些参数中,本文着重关注速度场、温度场、压力场和密度场这4个参数场,通过对比分析来解析龙卷风的发展过程。速度场直观地展现了场中机械动能的大致分布,显示出了龙卷风破坏力最强的地方;温度场的变化则是明确了内能转化为动能的方向以及全场能量变化的趋势;压力场最大的作用是提供足够的压力来抵消气流旋转产生的离心力来维持龙卷风旋转,而且压力主要依托温度和密度存在;密度场的变化主要体现了气流的运动方向,是向某一方向汇聚还是发散,可以说明该状态下龙卷风是被加强还是被削弱。
2.1 算例1 龙卷风的旋转外形是漏斗状的,其风速包含水平运动速度、竖直方向速度、径向速度和切向速度。本文忽略龙卷风水平运动速度,又由于发展演化过程中主要是内外气流的混合过程,所以主要考虑切向速度和径向速度的合速度的变化,即龙卷风在平面上的速度变化。图 3给出了算例1随时间推移在平面上的速度变化曲线。由于在均匀温度场情况下,场内的变量变化并不剧烈,主要集中在初始速度型区域,所以只给出半径为3rc内的变量曲线。由图 3可以看出,速度型随时间虽然是呈整体降低的形式,但降低的程度很小,而且扩散不厉害,也就是说必然有额外的能量提供来抵消动能的耗散。在整个场域中,气流除了有以动能为主的机械能外,就只有气流本身所储存的内能。而气体的内能主要是以温度的形式来体现的。
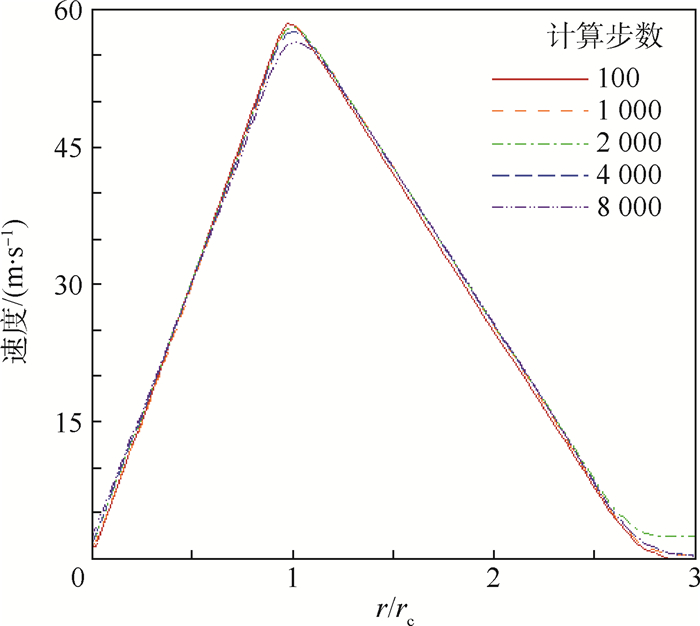 |
| 图 3 不同计算步数下的速度变化曲线(算例1) Fig. 3 Velocity variation curves under different calculation steps (Case 1) |
| 图选项 |
图 4给出了算例1在不同计算步数下的温度变化曲线。从图中可以直观地看出,随着计算步数的增加,即随着时间的推移,中心温度开始降低最终形成中心低温区,而速度型边缘气流温度的变化则是先升高降低到保持为288 K。整个温度场从均一温度场变为有一定梯度的不均一温度场,显然是能量的转化导致了温度的变化,气流的内能在温度降低时将部分能量释放出来转化成了动能。这是气流以一定速度旋转的结果,可以用漩涡管的Ranque-Hilsch效应来解释,即当气流在向心旋流器中,通过向心螺旋通道送入旋涡管产生旋流时,会发生温度分离现象,旋涡管中外围的气流温度比中心的气流温度高且该温差随初始气流温度的升高而升高。
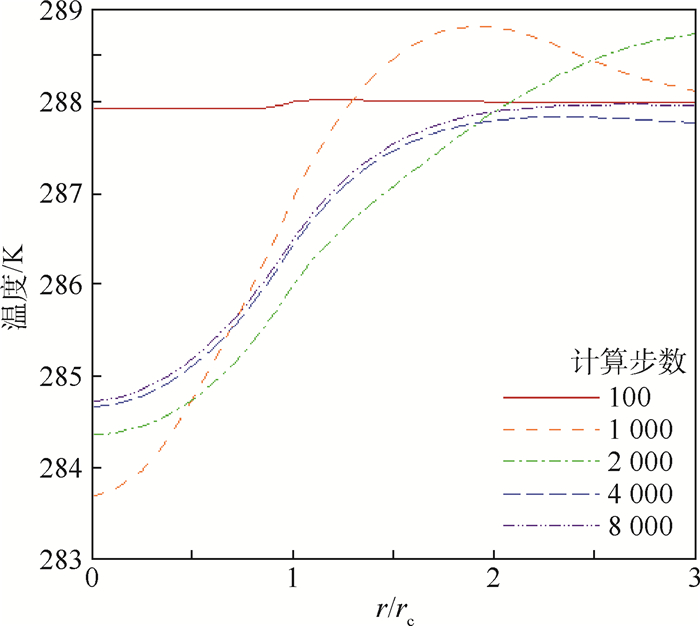 |
| 图 4 不同计算步数下的温度变化曲线(算例1) Fig. 4 Temperature variation curves under different calculation steps (Case 1) |
| 图选项 |
图 5的压力变化曲线和图 6的密度变化曲线应该结合图 4的温度变化曲线分析,因为这3个参数必须满足气体状态方程P=ρRT。从图 5和图 6中参数的变化情况来看,3个参数是符合该状态方程的。从图 5中可以看出,,外围高压区和中心低压区的形成向气流提供了足够的向心力来阻止扩散。从图 6中可以看出,中心密度是先急剧下降之后又回升,是因为刚开始是压力场提供的向心力并不能够抵消气流旋转所产生的离心力,因而中心区域气流会先向外扩散,通过和外围气流挤压换热产生足够强的压力并回流之后,再形成比较稳定的密度场。
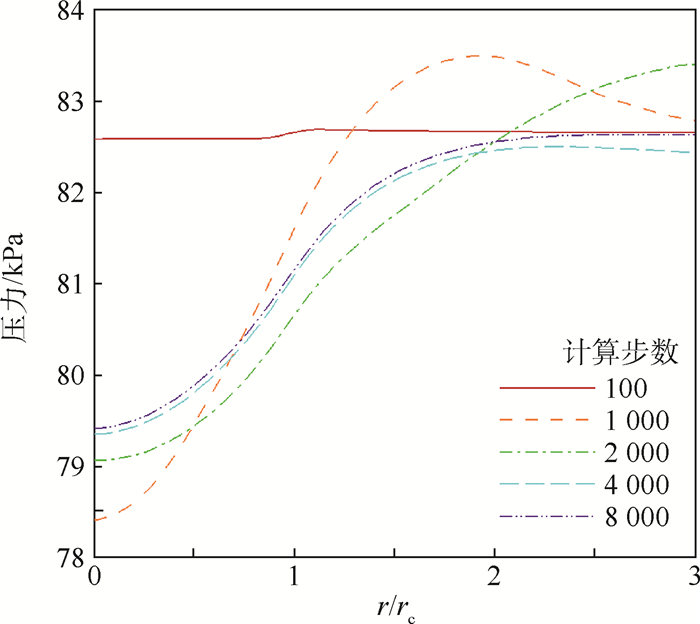 |
| 图 5 不同计算步数下的压力变化曲线(算例1) Fig. 5 Pressure variation curves under different calculation steps (Case 1) |
| 图选项 |
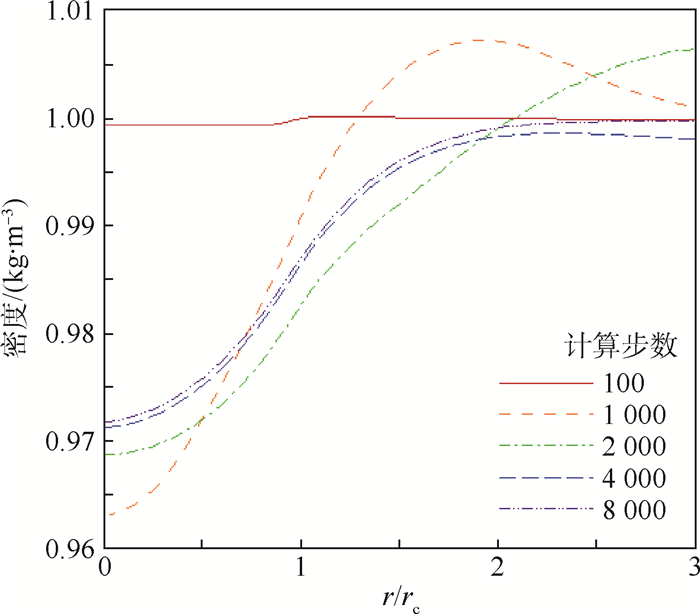 |
| 图 6 不同计算步数下的密度变化曲线(算例1) Fig. 6 Density variation curves under different calculation steps (Case 1) |
| 图选项 |
最终,气流流场内的变量经过一系列的变化形成了一个各个参数互相匹配的新变量场,由此得到的新的旋涡场所具有的各个参数场的形式即为所有稳定的旋涡场所具有的共有特性。
2.2 算例2 由2.1节可知,算例1的数值模拟的理论基础是Ranque-Hilsch效应,通过验证可知漩涡场的旋转会自发的产生一个与之匹配的温度场来维持。而龙卷风也是一个比较特殊的漩涡场,故算例2在算例1的基础上将均一的温度场改为类似于算例1相对稳定后的温度场形式,将其放入原初始速度场中计算并分析结果。这样做的目的是观察加大温度梯度之后,龙卷风风场的变化。
算例2初始温度场为中心低温253 K,到初始速度场边缘处线性升高为303 K,初始速度场外气流温度也为303 K。温度场函数关系式为
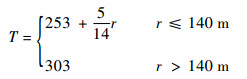 |
在有温度梯度的温度场情况中,场内的变量变化会延伸到部分外围气流,所以给出的都是半径为5rc内的变量曲线图。
图 7给出了算例2随时间推移的速度变化曲线,可以看出在2 000步的时候速度达到最大值,约为62.7 m/s。图 8将算例1中最大速度曲线同算例2中的速度曲线对比,可以发现算例2中速度曲线的各个速度最大值均大于算例1中出现的最大值,说明在算例2中速度在被加强。
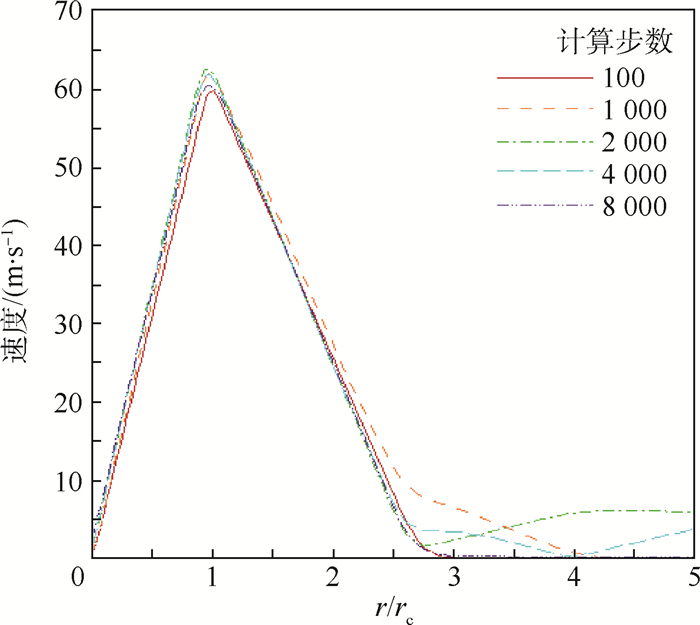 |
| 图 7 不同计算步数下的速度变化曲线(算例2) Fig. 7 Velocity variation curves under different calculation steps (Case 2) |
| 图选项 |
 |
| 图 8 速度变化曲线对比 Fig. 8 Comparison of velocity variation curve |
| 图选项 |
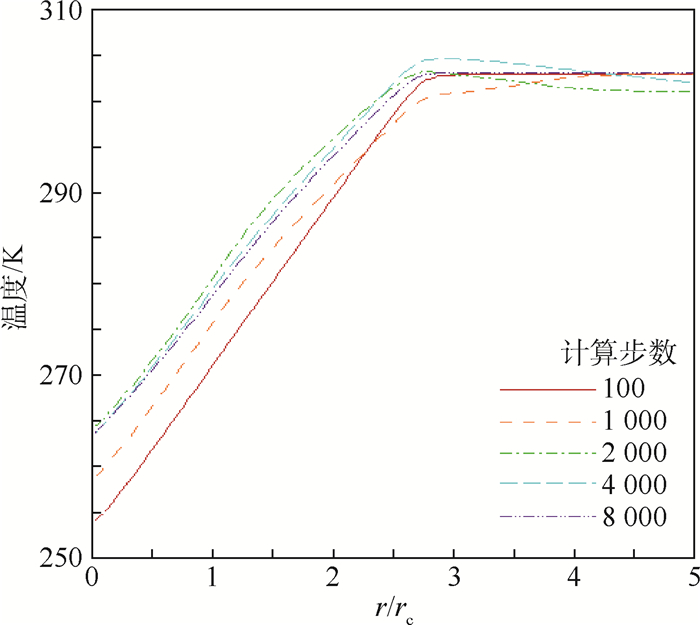
从图 9中可以看出,龙卷风在旋转过程中,中心温度升高减小了内外气流之间的温度差,在2 000步时温差达到最小,同时速度也达到了最大值。在整个变化过程中,温度型都基本保持了相似的形态,仅仅在温差上有变化,说明温度型的选择是正确的。在内外气流之间汇流换热的时候,外部高温气流的热能输运到内部低温气流使其温度升高。此时,内部气流的旋转速度增大则表明外部高温气流提供给内部低温气流的热能并非全部被用来增加内能,而是有部分热能转化为了动能加强了气流的旋转。这是由汇流换热效应所引起的变化。在汇流换热中,根据总压静压的关系:
 | (1) |
 |
| 图 9 不同计算步数下的温度变化曲线(算例2) Fig. 9 Temperature variation curves under different calculation steps (Case 2) |
| 图选项 |
由式(1)以及动量方程
 |
可推导出总温和总压的关系式为
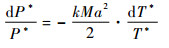 | (2) |
式中:Ma为气流马赫数;k为绝热指数;P*和T*分别为总压和总温,总温代表了热能的大小,总压代表的做功能力的大小。
由式(2)可知,总温的降低会增大总压,而且在此基础上气流马赫数(速度)越高,其温度变化带来的总压变化越大,由热能储存成的机械能增多。高速气流降温、低速气流升温和降温带来的总压增强远大于升温带来的总压损失。显然,图 8中速度的增大与图 9中温度的变化验证了这一点。
因此可以认为,大气中的温差及内外对流是龙卷旋涡形成的前提条件,而使龙卷旋涡得以持续甚至增强的能量则来源于周围的热能。龙卷风外围的热气流与旋涡中心的冷气流形成的有一定温度梯度的温度场,成为把大气热能转化为旋涡流动动能的主要因素。自然界中,龙卷风自转的同时还发生沿地表的平移,那么龙卷风就源源不断地获得环境的热能,从而维持自身旋转。
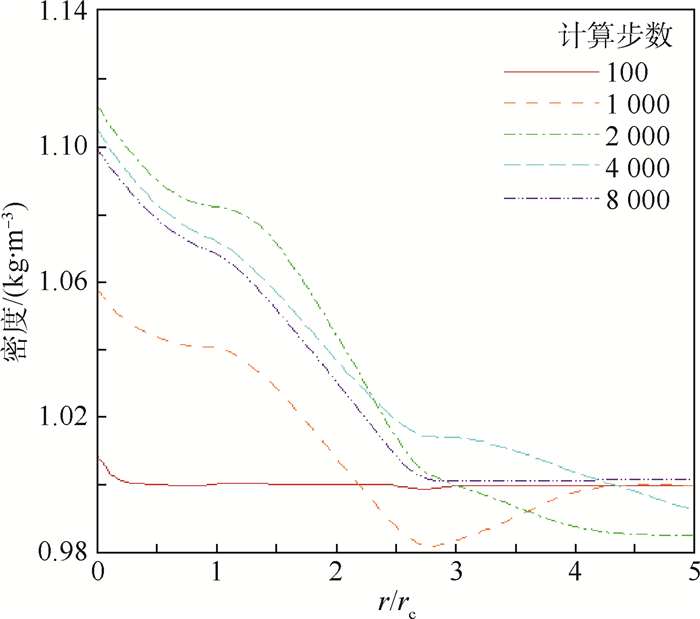
从图 10可以看出,此时算例2中提供的压力要大于算例1中所匹配出来的压力。从图 11中可以更加直观的看出这一结果,对比图 11与图 6发现在相同半径内,算例1中的密度变化曲线所对应的值大都在1以下,而算例2的密度变化曲线所对应的值则大都在1以上,显然在相同半径内算例2的密度积分要远大于算例1的密度积分,也就是说在这一半径内,算例2中包含有更多质量的气流,且这些气流的速度也很高,需要更大的压力来抵制离心力。这些集中在一定范围内的高速高质量的气流所具有的高动能表明该龙卷风的强度被大大加强,进一步说明了算例2的初始温度场加强了龙卷风的破坏能力。由此可以认为以这一温度型为基础,温度梯度越大对龙卷风风场的加强作用越大。
 |
| 图 10 不同计算步数下的压力变化曲线(算例2) Fig. 10 Pressure variation curves under different calculation steps (Case 2) |
| 图选项 |
 |
| 图 11 不同计算步数下的密度变化曲线(算例2) Fig. 11 Density variation curves under different calculation steps (Case 2) |
| 图选项 |
3 结论 1) 均一温度场的旋涡在旋转过程中会发生Ranque-Hilsch效应,产生一个不均一的温度场,通过这个温度场产生过程中气流内能所转化的动能来维持旋转,与此同时引起压力场和密度场的变化,最终这些变量互相匹配成一个新的旋涡变量场。由于新旋涡变量场是自适应生成的,所以其具有的变量场形式可代表所有稳定旋涡的变量场。
2) 特征如算例2的不均一的温度场更加贴近于实际龙卷风的温度场,其通过将气流汇聚到核心区域的加大旋转气流质量的同时加强气流旋转速度,来强化龙卷风旋涡并加剧其破坏力,其是由汇流换热原理所引起的。
3) 通过算例1的引申和算例2的验证,得到龙卷风的生成和强化主要依托于其温度场的变化,温度场梯度的大小在一定程度上决定了该龙卷风的破坏能力。因此,为使龙卷风的强度迅速降低甚至消亡,破坏龙卷风的温度场也许是一种行之有效的方法。
参考文献
| [1] | HOECKER W H. Wind speed and air flow patterns in the Dallas tornado of April 2, 1957[J].Monthly Weather Review, 1960, 88(5): 167–180.DOI:10.1175/1520-0493(1960)088<0167:WSAAFP>2.0.CO;2 |
| [2] | ALEXANDER C R, WURMAN J. The 30 May 1998 Spencer, South Dakota, storm.Part Ⅰ:The structural evolution and environment of the tornadoes[J].Monthly Weather Review, 2005, 133(1): 72–96.DOI:10.1175/MWR-2855.1 |
| [3] | WURMAN J, ALEXANDER C R. .The 30 May 1998 Spencer, South Dakota, storm.Part Ⅱ:Comparison of observed damage and radar-derived winds in the tornadoes[J].Monthly Weather Review, 2005, 133(1): 97–119.DOI:10.1175/MWR-2856.1 |
| [4] | CHANG C C. Tornado wind effects on buildings and structures with laboratory simulation[C]//Proceedings of the Third International Conference on Wind Effects on Buildings and Structures, 1971: 231-240. |
| [5] | WARD N B. The exploration of certain features of tornado dynamics using a laboratory model[J].Journal of the Atmospheric Sciences, 1972, 29(6): 1194–1204.DOI:10.1175/1520-0469(1972)029<1194:TEOCFO>2.0.CO;2 |
| [6] | CHURCH C R, SNOW J T, AGEE E M. Tornado vortex simulation at Purdue University[J].Bulletin of the American Meteorological Society, 1977, 58(9): 900–908.DOI:10.1175/1520-0477(1977)058<0900:TVSAPU>2.0.CO;2 |
| [7] | JISCHKE M C, PARANG M. Properties of simulated tornado-like vortices[J].Journal of the Atmospheric Sciences, 1974, 31(2): 506–512.DOI:10.1175/1520-0469(1974)031<0506:POSTLV>2.0.CO;2 |
| [8] | SARKAR P P, HAAN F L, GALLUS JR W A, et al. A laboratory tornado simulator: Comparison of laboratory, numerical and full-scale measurements[C]//10th Americas Conference on Wind Engineering. Baton Rouge, LA: American Association for Wind Engineering, 2005. |
| [9] | HASSENZAHL H C. Numerical investigations of a tornado vortex using vorticity confinement[D]. Madison: University of Wisconsin Madison, 2007. |
| [10] | MARUYAMA T. A numerically generated tornado-like vortex by large eddy simulation[C]//Proceedings of 7th Asia Pacific Conference on Wind Engineering. Taipei: Wind Engineering, 2009. |
| [11] | MARUYAMA T. Simulation of flying debris using a numerically generated tornado-like vortex[J].Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(4): 249–256.DOI:10.1016/j.jweia.2011.01.016 |
| [12] | NATARAJAN D. Numerical simulation of tornado-like vortices[D]. London: The University of Western Ontario, 2011.https://ir.lib.uwo.ca/etd/89/ |
| [13] | NATARAJAN D, HANGAN H. Numerical study on the effects of surface roughness on tornado-like flows[C]//11th Americas Conference on Wind Engineering(11ACWE). Baton Rouge, LA: American Association for Wind Engineering, 2009. |
| [14] | 徐枫, 肖仪清, 李波, 等. 龙卷风风场特性的CFD数值模拟[J].空气动力学学报, 2013, 31(3): 350–356. XU F, XIAO Y Q, LI B, et al. Study of the adaptive optimal design method based on design variables space[J].Acta Aerodynamica Sinica, 2013, 31(3): 350–356.(in Chinese) |
| [15] | KRIST S L, BIEDRON R T, RUMSEY C L. CFL3D user's manual(version5. 0): NASA-TM-1998-208444[R]. Washington, D. C. : NASA, 1998. |
| [16] | 王锦, 周强, 曹曙阳, 等. 龙卷风风场的试验模拟[J].同济大学学报(自然科学版), 2014, 42(11): 1654–1659. WANG J, ZHOU Q, CAO S Y, et al. Physical study on tornado-like flow based on tornado vortex simulator[J].Journal of Tongji University(Natural Science), 2014, 42(11): 1654–1659.(in Chinese) |
