随着装备对测试性要求的不断提高，故障诊断技术研究日益深入，其被广泛应用在航空、航天和兵器等高精尖的新武器装备故障诊断上。目前大多数故障诊断是在单故障假设下进行的，然而在实际工程中，并非所有的故障都是单个发生的，有些是随机组合或者耦合出现，单故障假设在实际应用中会遇到许多问题。因此研究人员逐渐开展了多故障诊断研究，目前多故障诊断问题是国内外故障诊断研究的热点^[1]。
多故障的处理方法可大致分为多故障直接处理方法和扩展单故障方法。多故障直接处理方法较多，如连可等^[2]基于小波变换和多类支持向量机(SVM)提出了一种多故障诊断方法；杨鹏等^[3]运用布尔逻辑运算生成完备最小碰集，然后用基于信息量启发式算法生成近似最优的多故障隔离策略；赵亮亮等^[4]提出一种基于多色集与概念格的多故障推理方法；Kundu等^[5]通过粒子群算法和多故障注入实现多故障诊断；Issury等^[6]基于一阶逻辑公式和布尔代数工具，利用冲突和诊断的概念创建最小诊断集的方式解决多故障隔离问题；Bartys′^[7-9]提出了基于多故障可隔离矩阵和多故障弱隔离结构剩余集，寻找最优故障隔离结构的方法以及基于二值诊断矩阵和动态二值矩阵进行多故障的诊断和隔离方法。多故障直接处理方法实现的难点在于故障组合的不确定性，无法判断故障组合方式就很难确定最优的诊断算法；另外多故障组合非常多，且以指数形式的增加，多故障直接处理方法必须考虑如何处理“爆炸”的故障组合。扩展单故障的多故障处理方法，如Shakeri等^[10]提出基于扩展单故障和碰集的4种多故障诊断策略，并按照“测试—维修”方式诊断多故障；王子玲等^[11]基于扩展单故障策略，应用附加测试来隔离隐藏故障，并调用单故障策略来隔离冒充故障，从而实现多故障诊断和隔离。扩展单故障的多故障处理方法，单故障测试阶段最优，却无法保证后续扩展阶段是最优的测试序列。多故障算法仍存在诸多问题，但单故障算法已相对成熟，如贪心算法^[12]和AO^*算法^[13]等。
综合上述分析，本文基于测试性D矩阵，研究运用单故障算法处理多故障问题的新方法。首先基于测试性D矩阵元素意义的变化引入析取运算，根据析取运算提出几个基本定义，运用定义和多故障规律判断多故障组合；然后完成多故障单故障化，并将新的单故障集合与原测试集组成新的D矩阵，运用单故障算法对新D矩阵进行处理，得到最优诊断序列，从而得到多故障诊断的最优诊断树；最后将对应的单故障转化为多故障，对多故障集合提出维修策略。
1 析取运算 为便于叙述，引入T={t₁, t₂, …, t_n}表示测试集，C={c₁, c₂, …, c_n}表示对应测试的成本；F={f₁, f₂, …, f_m}为单故障集合；P={p(f₁), p(f₂), …, p(f_m)}为对应单故障的概率；D=[d_ij]_m×n为故障和测试的依赖矩阵，即D矩阵。本文用eval(f_i, t_j)表示故障与测试之间的依赖关系：d_ij=eval(f_i, t_j)。如果t_j可以检测f_i，d_ij=1；否则d_ij=0。
D矩阵的行和列可用向量形式表示：
行向量V_i^f=[eval(f_i, t₁)??eval(f_i, t₂) …eval(f_i, t_n)]=[eval(f_i, t_j)]_1×n(1≤j≤n)，简记为V_i^f=[eval(f_i, T)]。其中，V^f表示行向量，下标i表示第i行。
列向量V_j^t=[eval(f₁, t_j)??eval(f₂, t_j) …eval(f_m, t_j)]^T=[eval(f_i, t_j)]_1×m^T(1≤i≤m)，简记为V_j^t=[eval(F, t_j)]^T。其中，V^t表示列向量，下标j表示第j列。
多故障假设下，D矩阵元素d_ij的意义与单故障假设下不同^[14]，多故障下1和0存在“遮掩”。例如若t_j的测试结果为1时，故障集F中除了满足eval(f_i, t_j)=1的故障f_i可能出现之外，其他的故障虽然满足[eval((F/f_i), t_j)]^T=[0]^T，但也有可能发生故障。
基于上述分析，引入析取运算。析取运算符为“∨”，运算关系如下：
1) D矩阵元素之间的析取运算。设eval(f_i, t_j)=0，eval(f_i, t_r)=0，eval(f_i, t_k)=1，eval(f_i, t_q)=1，其中t_j、t_r、t_k、t_q∈T，则:

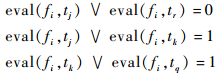2) 假设t_s、t_w∈T，f_i、f_j∈F，则测试向量V_s^t和V_w^t之间，故障向量V_i^f和V_j^f之间的析取运算式分别为

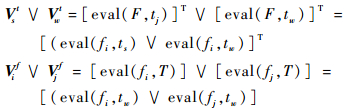3) 测试向量和故障向量连续析取运算式分别为

2 多故障组合的基本定义与规律 多故障单故障化的难点在于多故障的判断，多故障的组合是随机的，对于有m个单故障的系统，将会有2^m-1个组合故障(不含系统无故障状态f₀)，并且以指数的形式增加，这就给多故障诊断带来困难。D矩阵中的测试集有限，能被诊断隔离的故障只是少数，因此从可诊断隔离的故障入手，通过判断故障或者故障集能否被隔离，实现可隔离故障的单故障化。在多故障假设下，单故障、无故障与多故障组合均有可能发生。基于以上分析，提出几个基本定义，并应用文献[10]中具有典型意义的某电路系统D矩阵(见表 1)进行说明，无故障状态f₀的概率为0.62。
表 1 某电路系统的D矩阵^[10] Table 1 D matrix of a circuit system^[10]

故障状态	测试					概率
	t1	t2	t3	t4	t5
f1	0	1	0	0	1	0.014
f2	0	0	1	1	0	0.027
f3	1	0	0	1	1	0.125
f4	1	1	0	0	0	0.068
f5	1	1	1	1	0	0.146

表选项






2.1 单故障的基本定义 单故障假设下，隔离测试和诊断测试共同作用，不分主次^[15]；多故障假设下，故障更多的是依赖隔离测试，诊断测试则是起辅助判断作用。假设测试结果100%可靠。
定义1??在D_m×n中，对于故障f_i，如果存在测试集，满足，1≤q≤m，则称f_i为可隔离单故障。
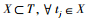
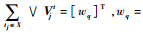
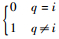
满足定义1的测试集X称为f_i隔离测试集，由X组成的集合记为F_ITⁱ，称为故障f_i隔离测试总集。满足eval(f_i, t_k)=1的测试t_k，称为f_i的诊断测试。
例如表 1中的f₅，没有满足定义1的测试集，那么它不存在故障隔离测试集，也不能被隔离。f₁存在故障隔离测试总集F_IT¹={{t₃, t₁}, {t₄, t₁}}，则f₁是可隔离单故障。
如果故障f_i存在故障隔离测试集，则能被隔离，否则只能够隔离到一组包含f_i的模糊集。f₀只能通过隔离测试进行判断，其故障隔离测试集必定存在。
定义2??在D_m×n中，如果存在测试集Z?T，t_j∈Z，满足，则称Z为f₀故障隔离测试集。由Z组成的集合记为F_IT⁰，称为故障f₀隔离测试总集。
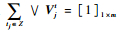
2.2 多故障组合的基本定义 定义3??在D_m×n中，若存在测试集Y?T，，满足

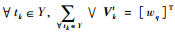
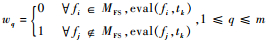则称M_FS为可隔离多故障。
测试集Y称为多故障M_FS的隔离测试集，由测试集Y成组的集合记为F_IT(M_FS)，称为多故障M_FS的故障隔离测试总集。
例如表 1中f₃和f₅组成的多故障，没有满足定义3的测试集，那么它不存在故障隔离测试集，也不能被隔离。f₁和f₄组成的多故障存在故障隔离测试总集F_IT(f₁, f₄)={{t₃, t₄}, {t₄}}，则M_FS(f₁, f₄)是可隔离多故障。
对于组合故障M_fi，若存在M_fj(i≠j)满足，则称M_fi和M_fj征兆相同。
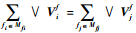
2.3 多故障规律 单故障假设下，能被诊断隔离的故障均可以在诊断树叶子节点上显示。多故障也有相似的规律：
1) 可隔离单故障和可隔离多故障(统称为可隔离故障，记为I_FS)，最终会显示在诊断树的叶子节点上。
2) 显示在叶子节点上的多故障，并不一定表示被完全隔离，其中会隐含一些故障，由于它们之间的“征兆”相同，共用一个叶子节点。
3) 所有故障组合都会在诊断树上出现，但有的故障被其他故障掩盖，无法分辨出。被掩盖的故障可能是隐含故障、伪故障，甚至单故障元素。
另外，多故障F是特例，表示集合F={f₁, f₂, …, f_m}中的所有故障同时发生。F在叶子节点上显示，却不存在隔离测试集。这是因为整体上看多故障F是唯一的故障，对任意测试t_j，若不通过则表示F故障，通过则是f₀，因此不用隔离测试也可以隔离F。
3 基于单故障化的多故障诊断与维修策略 基于单故障化的多故障诊断与维修策略(Multiple Fault Diagnosis and Maintenance Strategy by Translating into Single fault，MFDMSTS)分为单故障化和维修诊断2部分。单故障化阶段考虑多故障单故障化以及测试序列寻优，维修诊断阶段考虑故障集内部的组合以及维修策略。
3.1 单故障化 步骤1??确定可隔离单故障和隔离测试集。根据定义1和定义2确定可隔离的单故障、无故障f₀、F_ITⁱ和F_IT⁰。
步骤2??确定可隔离多故障集和隔离测试集。根据定义3确定可隔离的多故障集合M_FS和F_IT(M_FS)。
步骤3??根据征兆相同的确定可隔离故障集内部的组合数，且不用考虑隐含故障和伪故障等关系。
步骤4??计算可隔离故障集的概率。由步骤1和2得到一组可隔离故障集合F_S={F_S¹, F_S², …, F_S^z, }∪f₀，p(F_Sⁱ)概率计算式为

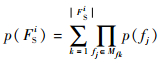(1)

式中：|F_Sⁱ|为F_Sⁱ包含的故障组合数；M_fk为F_Sⁱ的一组故障组合；f_j为M_fk的组成元素。
步骤5??可隔离故障集的概率归一化。步骤4的计算结果会造成整体故障概率大于1，那么需要对故障概率进行归一化处理，概率归一化计算式为

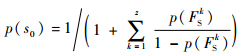(2)

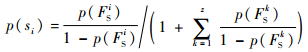(3)

式中：p(s₀)为无故障状态的概率；z为集合F_S的基数；p(s_i)为F_Sⁱ归一化后的概率。
步骤6??可隔离故障集与测试集T组成新的D矩阵，令s₀表示f₀，s_i表示F_Sⁱ，将s₀、S={s₁, s₂, …, s_z}与测试集T组成新的D_(z+1)×n矩阵。
步骤7??用单故障算法处理新D矩阵，得到相应的诊断树，计算诊断树的各项指标，如平均诊断费用、故障诊断率和隔离率等^[16]。
3.2 维修诊断 完成系统的单故障化并得到最优诊断树后，需要对诊断树的各个叶子节点提出合适的维修策略，基于叶子节点内组合数的不同，分为2类维修方式：
1) 组合数为1的叶子节点，表示该叶子节点故障元素是确定唯一的，只需对该叶子节点的所有故障元素进行更换或者维修。
2) 组合数大于1的叶子节点，表示该叶子节点可能存在隐含故障或者伪故障。应该按照叶子节点内部的所有单故障元素之间的概率大小排序，先依次对这些单故障元素进行“测试—维修”^[10]。
例如某叶子节点内部包含多故障{f₅}，{f₂, f₅}，第1个维修的集合为{f₅}，第2个维修的集合为{f₂, f₅}，维修{f₅}后，第2个维修内容只需维修f₂即可。这种方法适用于非耦合故障系统，能有效提高维修的效率。但该方法会引起误修，因此提出误修率的计算公式:

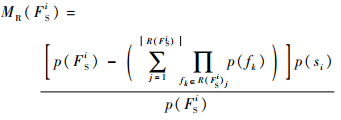(4)

式中：M_R(F_Sⁱ)为可隔离故障集F_Sⁱ的误修率；R(F_Sⁱ)={R(F_Sⁱ)₁, R(F_Sⁱ)₂, …, R(F_Sⁱ)_h}为可隔离故障Fⁱ_S维修诊断树的叶子节点集，R(F_Sⁱ)_j为第j个叶子节点所完成维修的故障集。
维修诊断树中的每个叶子节点可能包含有多个故障集，每个维修诊断树的叶子节点仅有一个故障集被维修，并且该集合包含该叶子节点所有的故障组合情形。
4 实例计算 4.1 电路系统实例
4.1.1 故障诊断及结果对比 在多故障假设下，按照3.1节步骤1~5对表 1系统单故障化处理，得到I_FS、对应的组合数、F_IT、可隔离故障集的概率和归一化后的概率，如表 2所示。
表 2 多故障单故障化的结果 Table 2 Results of translating multiple faults into single fault

IFS	组合数	FIT	故障状态	概率p(FSi)	归一化概率p(si)
f0	1	{{t2, t4}, {t1, t2, t3}, …, {t1, t2, t3, t4, t5}}	s0		0.671 3
f1	1	{{t4, t1}, {t3, t1}}	s1	0.014 000	0.009 5
f2	1	{{t2, t5}, {t2, t1}, {t1, t5}}	s2	0.027 000	0.018 6
f3	1	{{t2, t3}}	s3	0.125 000	0.095 9
f4	1	{{t3, t5}, {t4, t5}}	s4	0.068 000	0.049 0
f1f2	1	{{t1}}	s5	0.000 378	0.000 3
f2f3	1	{{t2}}	s6	0.003 400	0.002 3
f1f4	1	{{t3, t4}, {t4}}	s7	0.000 950	0.000 6
f1f3f4	3	{{t3}}	s8	0.010 400	0.007 0
f2f4f5	5	{{t5}}	s9	0.162 000	0.129 8
f1f2f3f4f5	16		s10	0.022 800	0.015 7
总和	32				1.000 0

表选项






根据步骤6，将s₀、S={s₁, s₂, …, s₁₀}、p(s_i)和测试集T={t₁, t₂, t₃, t₄, t₅}组成新的D_11×5，如表 3所示。
表 3 MFDMSTS得到的新D矩阵 Table 3 New D matrix obtained by MFDMSTS

故障 状态	测试					概率
	t1	t2	t3	t4	t5
s0	0	0	0	0	0	0.671 3
s1	0	1	0	0	1	0.009 5
s2	0	0	1	1	0	0.018 6
s3	1	0	0	1	1	0.095 9
s4	1	1	0	0	0	0.049 0
s5	0	1	1	1	1	0.000 3
s6	1	0	1	1	1	0.002 3
s7	1	1	0	0	1	0.000 6
s8	1	1	0	1	1	0.007 0
s9	1	1	1	1	0	0.129 8
s10	1	1	1	1	1	0.015 7

表选项






根据步骤7，采用文献[13]中的AO^*算法处理表 3的新D矩阵，得到诊断树，如图 1所示。

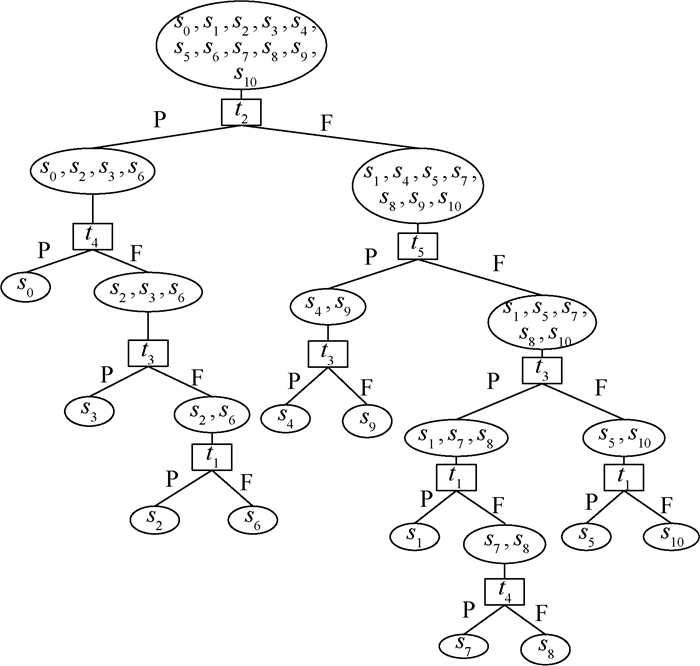图 1 基于MFDMSTS和AO*的新D矩阵诊断树 Fig. 1 Diagnostic tree of new D matrix based on MFDMSTS and AO*

图选项

MFDMSTS方法的故障诊断隔离和维修诊断是分开的。运用文献[10]的Sure3算法对表 1进行多故障处理，为使结果有可比性，按照诊断隔离和“测试—维修”2种方式计算，结果分别用Sure3^*和Sure3表示，并且计算的过程用本文归一化后的概率。通过计算平均诊断费用C_ost、平均诊断步数N_D、故障诊断率FDR和故障隔离率FIR来评价MFDMSTS，计算式分别为

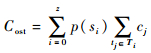(5)

(6)

(7)

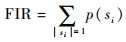(8)

式中：C_ost为平均诊断费用，c_j为对应t_j的费用；N_D为平均诊断步数；T_i为s_i的测试序列，|T_i|为T_i的长度；|s_i|为故障s_i内的组合数。
假设c_j=1，由式(5)~式(8)得MFDMSTS、Sure3^*和Sure3的相应结果，如表 4所示。
表 4 MFDMSTS、Sure3^*和Sure3的诊断结果对比 Table 4 Comparison of diagnosis results among MFDMSTS, Sure3^* and Sure3

算法	Cost	ND	FDR/%	FIR/%
MFDMSTS	2.390	3.727	100	84.75
Sure3*	2.515	3.727	100	84.75
Sure3	2.528	4.154	100	85.46

表选项






由表 4可知，MFDMSTS能有效降低多故障的C_ost，因为单故障化可以对所有可隔离故障集进行测试序列的寻优计算，而Sure3^*与Sure3只是对单故障假设下的诊断树和测试序列进行扩展，忽略了一些概率较大的故障集的顺序；Sure3^*与Sure3的C_ost相差不大是因为维修对象的概率较小，对成本影响较小；在故障诊断阶段，由于Sure3^*和MFDMSTS不存在“测试—维修”，Sure3^*和MFDMSTS的FIR会比较低，两者的N_D也会较小。
在2 G，2.6 GHz的PC机上运用MATLAB运行程序，该电路系统的多故障转化为单故障的计算时间为0.077 0 s。

4.1.2 维修策略 完成故障的诊断后，将对诊断树的叶子节点提出合适的维修策略。本文运用诊断树的形式表现测试诊断过程，用{N|L}的格式表示维修诊断树的节点含义，其中N表示节点内的组合故障数，L表示所包含的故障状态。诊断树叶子节点的维修策略以及与Sure3算法的维修结果对比，如表 5所示，图 2和图 3分别为叶子节点s₉和s₁₀的维修诊断树。
表 5 MFDMSTS与Sure3的维修策略对比 Table 5 Comparison of maintenance strategy between MFDMSTS and Sure3

多故障 状态	组合数	si中的 组合故障	MFDMSTS			Sure3
			维修策略	误修率/%		维修策略	误修率/%
s1, s2, s3, s4, s5, s6, s7	1	f1, f2, f3, f4, f1f4, f2f3	直接维修检测的故障集	0		直接维修检的故障集	0
s8	3	f3f4, f1f3, f1f3f4	维修f3f4，测试，维修f1，结束	0.12		维修f3，测试，维修f1，测试，维修f4	0
s9	5	f5, f4f5, f2 f5, f2f4, f2f4f5	图 2	0.15		维修f2f4f5	12.95
s10	16	f3f5, f1f5, f3 f4 f5, …, f1f2f3f4f5	图 3	0.26		维修f1f2f3f4f5	1.57

表选项

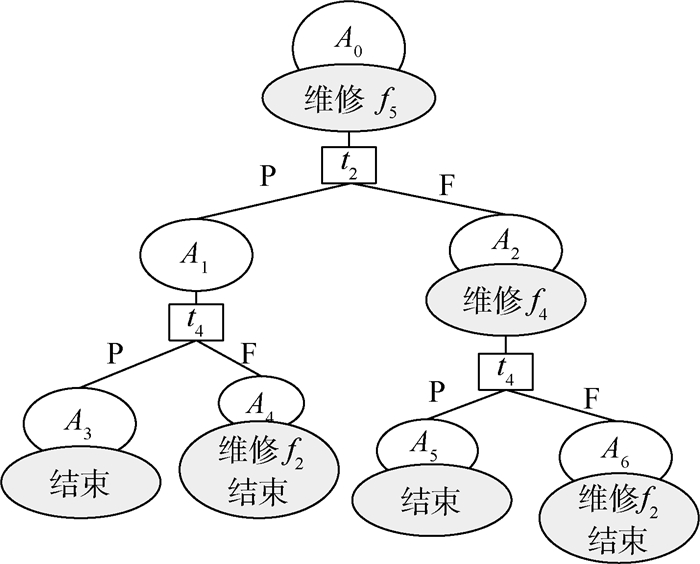图 2 叶子节点s9的维修诊断树 Fig. 2 Maintenance diagnostic tree of leaf node s9

图选项

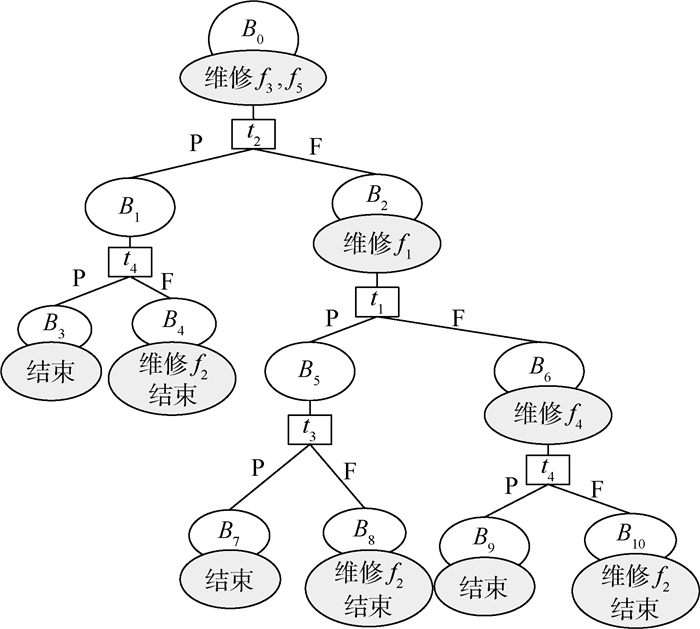图 3 叶子节点s10的维修诊断树 Fig. 3 Maintenance diagnostic tree of leaf node s10

图选项

A₀={5|f₂, f₄, f₅}，A₁={2|f₀, f₂}，A₂={3|f₂, f₄}，A₃={1|f₀}，A₄={1|f₂, f₅}，A₅={1|f₄, f₅}，A₆={2|f₂, f₄, f₅}。叶子节点为A₃、A₄、A₅和A₆，分别表示维修f₅、f₂ f₅、f₄f₅和f₂ f₄ f₅。虽然只有4个多故障被维修，但f₂ f₄ f₅维修过程中包含f₂ f₄，因此5个故障组合被维修策略所包含。
B₀={16|f₁, f₂, f₃, f₄, f₅}，B₁={2|f₀, f₂}，B₂={14|f₁, f₂, f₄}，B₃={1|f₀}，B₄={1|f₂}，B₅={6|f₀, f₂}，B₆={8|f₀, f₂, f₄}，B₇={2|f₀}，B₈={4|f₀, f₂}，B₉={3|f₀}，B₁₀={5|f₀, f₂}。叶子节点为B₃、B₄、B₇、B₈、B₉和B₁₀，分别表示f₃ f₅、f₂ f₃ f₅、f₁ f₃ f₅、f₁ f₂ f₃ f₅、f₁ f₃ f₄ f₅和f₁ f₂ f₃ f₄ f₅的故障组合被维修。至此，16个故障组合被维修策略所包含。
由表 5可知，总共有31个故障组合被维修，包含了多故障假设下所有的故障总数，所有叶子节点的误修率均在0.3%以下，但Sure3算法中有叶子节点的误修率高达12.95%。
4.2 惯导二次电源实例 表 6为某型惯导二次电源的D矩阵，共有9个故障模式(F₁~F₉)，无故障F₀概率为0.74。多故障假设下将会有511个故障模式。
表 6 某型惯导二次电源的D矩阵 Table 6 D matrix for secondary electrical power of an inertial navigation

故障状态	测试						概率
	T1	T2	T3	T4	T5	T6
F1	1	1	1	0	1	1	0.063
F2	0	0	1	0	0	0	0.021
F3	0	1	0	0	0	0	0.013
F4	0	0	1	1	0	0	0.037
F5	0	0	0	0	0	1	0.017
F6	0	0	0	1	0	0	0.023
F7	0	0	0	0	1	1	0.034
F8	1	1	0	0	0	0	0.022
F9	0	0	1	0	1	0	0.030

表选项






现用MFDMSTS对其进行诊断维修，可得到41个可隔离故障，即诊断树有42个叶子结点(限于篇幅，省略故障诊断树和叶子结点的维修树)。同时应用TEAMS软件对惯导二次电源进行建模仿真并将两者结果进行对比(其中单故障算法为Rollout算法)。假设c_j=1，通过计算惯导二次电源诊断树的C_ost、N_D、FDR和FIR评价诊断结果。由于误修率是对诊断树的叶子节点而言，但是叶子节点过多，因此引入平均误修率(M_R-avg)对诊断树所有叶子结点的维修树进行评价。

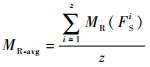(9)

式中:z为可隔离故障个数。
由表 7可知，在C_ost、N_D、FDR和FIR方面，MFDMSTS的结果与TEAMS仿真的结果一致；但是TEAMS没有维修诊断，因此没有误修率的结果，而MFDMSTS的诊断结果中存在11组合数为1的叶子节点和12个组合数为2的叶子节点，这些节点的误修率全为0；同时其余19个叶子节点中有7个叶子节点的故障概率为10^-5，误修率可近似为0，另外有10个叶子节点的误修率约等于0，因此总体的误修率比较小，约为0.012 8%。
表 7 MFDMSTS与TEAMS仿真分析结果对比 Table 7 Comparison of analysis results between MFDMSTS and TEAMS simulation

算法	Cost	ND	FDR/%	FIR/%	MR-avg/%
MFDMSTS	4.22	5.45	100	82.69	0.012 8
TEAMS	4.22	5.45	100	82.69

表选项






在上述运行环境下该型惯导二次电源的多故障转化为单故障的计算时间为0.115 0 s。
5 结论 1) 基于D矩阵元素d_ij的含义、有限的测试，提出了可隔离故障、隔离测试集定义，然后基于隔离测试集和多故障的规律，提出了MFDMSTS。
2) MFDMSTS在故障诊断阶段简化了故障之间的关系如隐含故障、伪故障等，获得了最优的多故障诊断树，与Sure3算法相比能有效降低平均诊断费用和平均诊断步数；该策略的诊断结果与TEAMS软件仿真的结果一致。
MFDMSTS的故障维修阶段是基于叶子节点的内部故障组合以及概率提出的细致维修策略，在维修范围包含所有可能的故障组合基础上，大幅降低了故障的误修率。
3) 本文方法可将大量的多故障转化为数目较少的单故障，被计算处理的故障数目得到了减少，通过对转化的单故障进行故障诊断，并对相应的叶子节点维修，故障维修的精度得以提高。

参考文献

[1]	张可, 周东华, 柴毅. 复合故障诊断技术综述[J].控制理论与应用, 2015, 32(9): 1143–1157. ZHANG K, ZHOU D H, CHAI Y. Review of multiple fault diagnosis methods[J].Control Theory & Applications, 2015, 32(9): 1143–1157.(in Chinese)
[2]	连可, 王厚军, 龙兵. 基于SVM的模拟电子系统多故障诊断研究[J].仪器仪表学报, 2007, 28(6): 1029–1034. LIAN K, WANG H J, LONG B. Study on SVM based analog electronic system multiple fault diagnosis[J].Chinese Journal of Scientific Instrument, 2007, 28(6): 1029–1034.(in Chinese)
[3]	杨鹏, 邱静, 刘冠军. 多故障诊断策略优化生成技术研究[J].兵工学报, 2008, 29(11): 1379–1383. YANG P, QIU J, LIU G J. Research on optimization generation technology for multiple fault diagnostic strategy[J].Acta Armamentarii, 2008, 29(11): 1379–1383.DOI:10.3321/j.issn:1000-1093.2008.11.019(in Chinese)
[4]	赵亮亮, 肖明清, 盛晟, 等. 基于多色集与概念格的多故障推理研究[J].仪器仪表学报, 2014, 35(12): 2690–2699. ZHAO L L, XIAO M Q, SHENG S, et al. Study on reasoning of multi-failure based on polychromatic sets and concept lattice[J].Chinese Journal of Scientific Instrument, 2014, 35(12): 2690–2699.(in Chinese)
[5]	KUNDU S, CHATTOPADHYAY S, SENGUPTA I, et al. Multiple fault diagnosis based on multiple fault simulation using particle swarm optimization[C]//201124th Annual Conference on VLSI Design. Piscataway, NJ: IEEE Press, 2011: 364-369.
[6]	ISSURY I, HENRY D, CHARBONNEL C, et al. A Boolean algebraic-based solution for multiple fault diagnosis:Application to a spatial mission[J].Aerospace Science and Technology, 2013, 28(1): 214–226.DOI:10.1016/j.ast.2012.11.002
[7]	BARTYS' M. Multiple fault isolation algorithm based on binary diagnostic matrix[J].Advances in Intelligent Systems and Computing, 2014, 230: 441–452.DOI:10.1007/978-3-642-39881-0
[8]	BARTYS' M. Diagnosing multiple faults with the dynamic binary matrix[J].IFAC-Papers Online, 2015, 48(21): 1297–1302.DOI:10.1016/j.ifacol.2015.09.704
[9]	BARTYS' M. The weak isolability of the structure of binary residuals of multiple faults[J].Advances in Intelligent Systems and Computing, 2016, 393: 3–11.DOI:10.1007/978-3-319-23923-1
[10]	SHAKERI M, RAGHAVAN V, PATTIPATI K R, et al. Sequential testing algorithms for multiple fault diagnosis[J].IEEE Transactions on Systems, Man, and Cybernetics, Part A:Systems and Humans, 2000, 30(1): 1–14.DOI:10.1109/3468.823474
[11]	王子玲, 许爱强, 王文双, 等. 基于扩展单故障策略的多故障诊断算法[J].海军航空工程学院学报, 2009, 24(6): 695–698. WANG Z L, XU A Q, WANG W S, et al. An extended single-fault algorithm for multiple fault diagnosis[J].Journal of Naval Aeronautical and Astronautical University, 2009, 24(6): 695–698.(in Chinese)
[12]	YANG C L, YAN J H, LONG B, et al. A novel test optimizing algorithm for sequential fault diagnosis[J].Microelectronics Journal, 2014, 45(6): 719–722.DOI:10.1016/j.mejo.2014.03.005
[13]	PATTIPATI K R, ALEXANDRISIS M G. Application of heuristic search and information theory to sequential fault diagnosis[J].IEEE Transactions on Systems, Man, and Cybernetics, 1990, 20(4): 872–887.DOI:10.1109/21.105086
[14]	SHEPPARD J W, BUTCHER S G W. A formal analysis of fault diagnosis with D-matrices[J].Journal of Electronic Testing:Theory and Applications, 2007, 23(4): 309–322.DOI:10.1007/s10836-006-0628-7
[15]	TSAI Y T, HSU Y Y. A study of function-based diagnosis strategy and testability analysis for a system[J].Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2012, 226(1): 273–282.DOI:10.1177/0954406211412017
[16]	石君友. 测试性设计分析与验证[M].北京: 国防工业出版社, 2011. SHI J Y. Testability design analysis and verification[M].Beijing: National Defense Industry Press, 2011.(in Chinese)