目标在飞行过程中,其机动通常是瞬间发生的,而多模型滤波算法的模型概率是一个近似连续的变化过程[4],不同于目标机动发生的突然性。因此在采用IMM滤波算法对机动目标进行跟踪滤波时,通常仅有一个滤波模型起主要作用,该模型能准确描述目标的运动方程,其模型概率近似为1,其余模型的概率近似为0。也就是说,通过IMM滤波算法计算出的模型概率与实际模型所起作用存在一种模糊的非线性关系。基于此,本文依据模糊控制的思想,通过设计模糊逻辑系统,提出了一种基于模糊逻辑的交互式多模型(Fuzzy Logic Interactive Multiple Model, FLIMM)滤波算法来改善传统IMM滤波算法收敛速度慢、滤波精度低的缺点。
1 “蛇形”机动模型 “蛇形”机动模型描述的是一种目标做强机动的情况,目标机动加速度按正弦规律不断变化[5]。其既是一种特殊的转弯运动,又是一种特殊的匀速圆周运动,是多个半圆周运动的叠加,在每个半圆周,角速率变化为相反的方向,同时半径也在不停地改变。本文假设目标的“蛇形”机动发生在水平面上,即在x轴方向上和y轴方向上分别做速度为vx的直线运动和正弦运动,其运动方程为
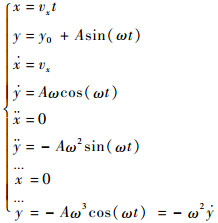 | (1) |
式中:x、?、?和
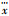
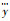
 | (2) |
式中:w1(t)和w2(t)为高斯白噪声。
设采样周期为T,对式(2)进行离散化,有
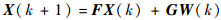 | (3) |
式中:X(k)、X(k+1)分别为k时刻、k+1时刻的状态向量;W(k)为过程噪声;F为状态转移矩阵;G为过程噪声输入矩阵。取值如下:
 |
2 交互式多模型滤波算法 假设机动目标的运动方程由r个数学模型来描述,其模型集可以用集合表示为M={m1, m2, …, mr},描述机动目标运动方程的第j(j=1, 2, …, r)个数学模型表示为[6]
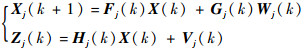 | (4) |
式中:Xj(k+1)为第j个模型的状态向量;Fj(k)为第j个模型的过程矩阵;Gj(k)为第j个模型的过程噪声传递矩阵;Zj(k)为第j个模型的观测向量;Hj(k)为第j个模型的观测矩阵;过程噪声Wj(k)和观测噪声Vj(k)为相互独立的零均值高斯白噪声序列,协方差矩阵分别为Qj和Rj。
IMM滤波算法主要包括输入交互、并行滤波、模型概率更新和输出数据融合4个步骤[7],如图 1所示。
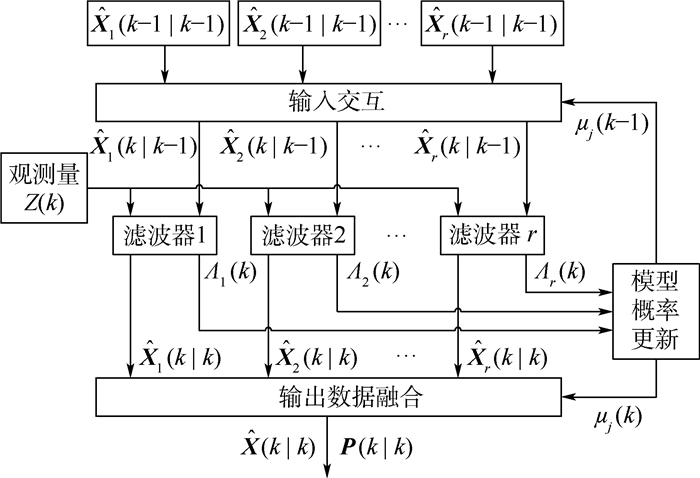 |
| 图 1 IMM滤波算法原理框图 Fig. 1 Principle block diagram of IMM filtering algorithm |
| 图选项 |
假设已知k-1时刻第j个模型的滤波状态估计为
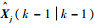
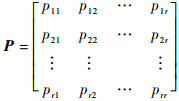 | (5) |
式中:pij表示从模型i到模型j的转移概率,i, j=1, 2, …, r。则IMM滤波算法步骤为:
1) 输入交互
输入交互概率:
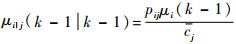 | (6) |
式中:
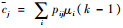
初始状态估计:
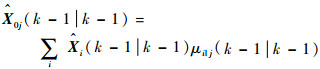 | (7) |
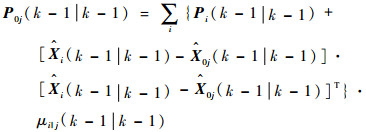 | (8) |
式中:
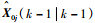
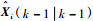
2) 并行滤波
状态预测:
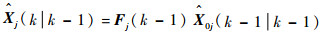 | (9) |
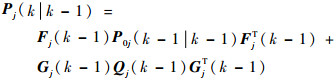 | (10) |
计算残差:
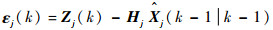 | (11) |
残差协方差矩阵:
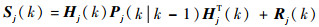 | (12) |
滤波增益:
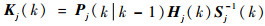 | (13) |
状态更新:
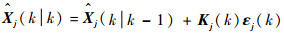 | (14) |
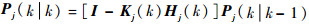 | (15) |
3) 模型概率更新
似然函数:
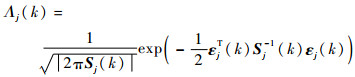 | (16) |
概率更新:
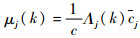 | (17) |
式中:
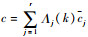
4) 输出数据融合
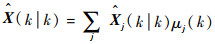 | (18) |
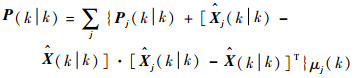 | (19) |
式中:
3 改进的交互式多模型滤波算法 由于目标在进行“蛇形”机动时,存在短暂的匀速运动,引起运动模型频繁切换。在采用IMM滤波算法对其进行跟踪时,模型概率转移时间延迟较长,导致了收敛速度慢,滤波精度低,而且估计误差大,在滤波后期依然存在较大波动。为此,本文基于传统IMM滤波算法,运用模糊逻辑的设计思想[9-10]来改进模型概率更新模块,提出了FLIMM滤波算法。改进后的更新模块结构如图 2所示。
 |
| 图 2 基于模糊逻辑的模型概率更新模块结构 Fig. 2 Structure of model probability updating module based on fuzzy logic |
| 图选项 |
假定目标采用“蛇形”机动与匀速直线运动相结合的运动方式,设滤波器的输入为Λ1和Λ2(Λ1与Λ2是各滤波器的输出),匀速直线运动(设为模型1)的模型概率
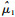
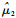
 | (20) |
式中:
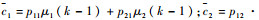
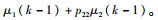
对模型1进行分析,假定模型概率更新模块获得的输入变量是I1和I2,得出的输出变量是u,令
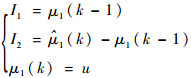 |
1) 输入变量与输出变量的论域
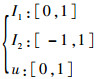 |
2) 输入变量与输出变量的模糊子集
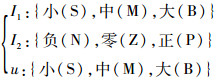 |
3) 确定隶属度函数[11],如图 3~图 5所示。
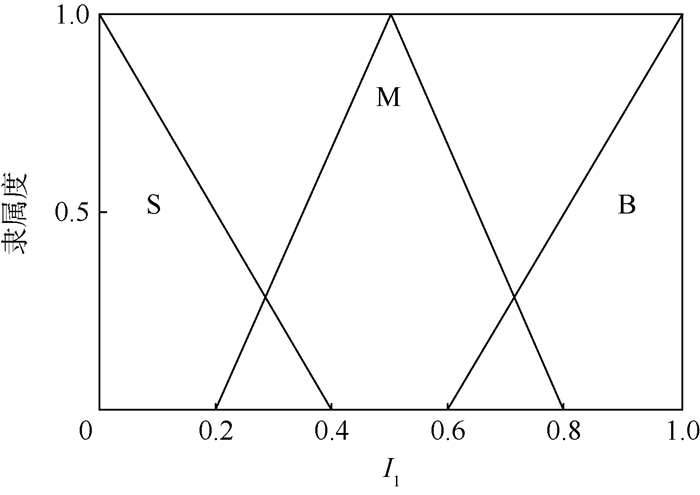 |
| 图 3 I1的隶属度函数 Fig. 3 Membership function of I1 |
| 图选项 |
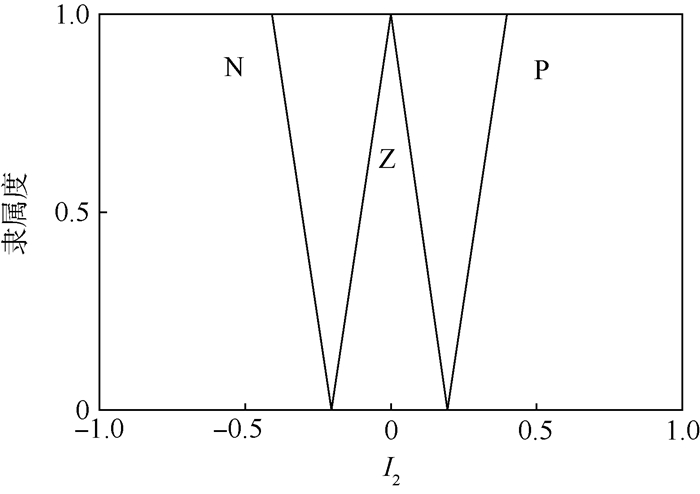 |
| 图 4 I2的隶属度函数 Fig. 4 Membership function of I2 |
| 图选项 |
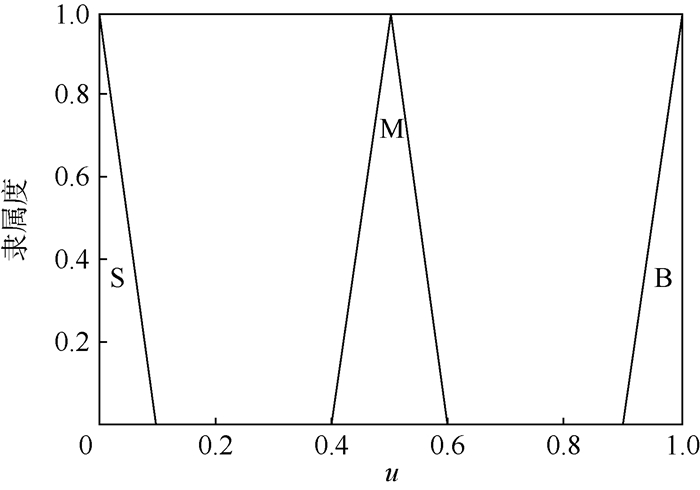 |
| 图 5 u的隶属度函数 Fig. 5 Membership function of u |
| 图选项 |
总结上述过程,可以发现:如果获取的模型概率变化是负值,即I2为N,那么当前模型概率的取值应该小于前一时刻的模型概率I1;如果获取的模型概率变化是零,即I2为Z,那么当前模型概率的取值应该等于前一时刻的模型概率I1;如果获取的模型概率变化是正值,即I2为P,那么当前模型概率的取值应该大于前一时刻的模型概率I1。与之相应的模糊逻辑规则如表 1所示。本文使用中位数法解模糊化,得出模型的实际概率[12-13]。
表 1 模糊逻辑规则 Table 1 Rule of fuzzy logic
| 规则号 | I1 | I2 | u |
| 1 | S | N | S |
| 2 | S | Z | S |
| 3 | S | P | M |
| 4 | M | N | S |
| 5 | M | Z | M |
| 6 | M | P | B |
| 7 | B | N | M |
| 8 | B | Z | B |
| 9 | B | P | B |
表选项
4 仿真分析 在导弹飞行实验的背景下,以导弹为机动目标,采用MATLAB进行仿真分析。导弹的质心运动方程[14-15]为
 | (21) |
式中:机动加速度按正弦规律变化;v为导弹的运动速率;θ为导弹的弹道倾角;ψv为弹道偏角;gx2、gy2、gz2与ax2、ay2、az2分别为重力加速度与导弹过载在弹道坐标系中3个坐标轴方向的分量。弹道坐标系的定义如文献[1]所示:
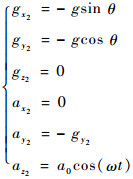 |
目标的初始状态为
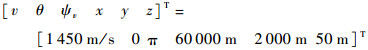 |
对第1节所述的“蛇形”机动模型进行三维扩展,离散状态方程如式(3)所示,取w1(k)、w2(k)、w3(k)为高斯白噪声,式中各项取值依次为
 |
设机动目标在飞行过程中有2种运动方式,第0~15 s,沿x轴负方向进行匀速直线运动,速度为1 450 m/s; 第16~60 s,在水平面上进行“蛇形”机动,x和y方向上的机动加速度是0,目标在z方向的加速度按余弦规律变化,目标机动加速度的幅值为As=2g,机动频率ω=0.2π。
针对目标的运动形式,IMM滤波算法的模型集由匀速直线运动模型(模型1)和“蛇形”机动模型(模型2)组成,采样周期为T=0.015 s,采用球坐标系下的视线角、视距作为观测信息,观测方程为
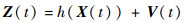 | (22) |
式中:Z(t)为观测向量;V(t)为观测噪声;h(·)为观测函数,取值为
 |
观测噪声协方差阵为
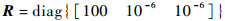 |
过程噪声协方差矩阵为
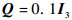 |
式中:I3为3阶单位矩阵。
滤波器的状态估计初始值为
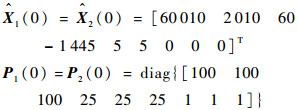 |
模型之间的转移矩阵为
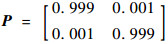 |
模型概率为
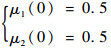 |
为了对比分析,分别采用传统的IMM滤波算法和改进后的FLIMM滤波算法对目标进行跟踪,进行100次Monte Carlo仿真,图 6为目标在铅垂面和水平面内的运动轨迹以及滤波结果。
 |
| 图 6 目标的运动轨迹 Fig. 6 Motion trail of target |
| 图选项 |
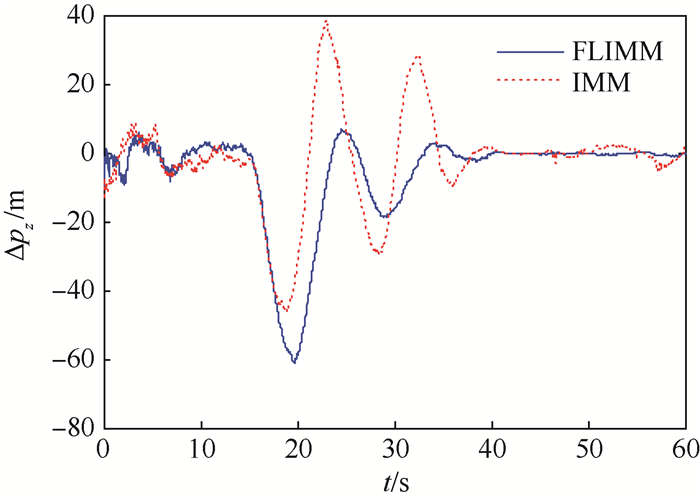
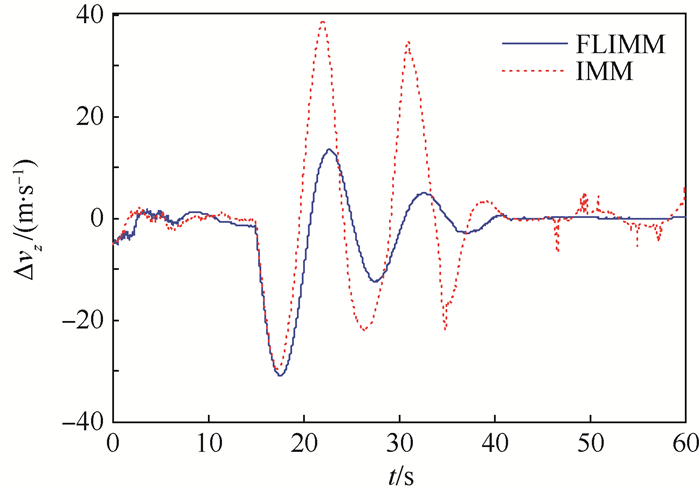
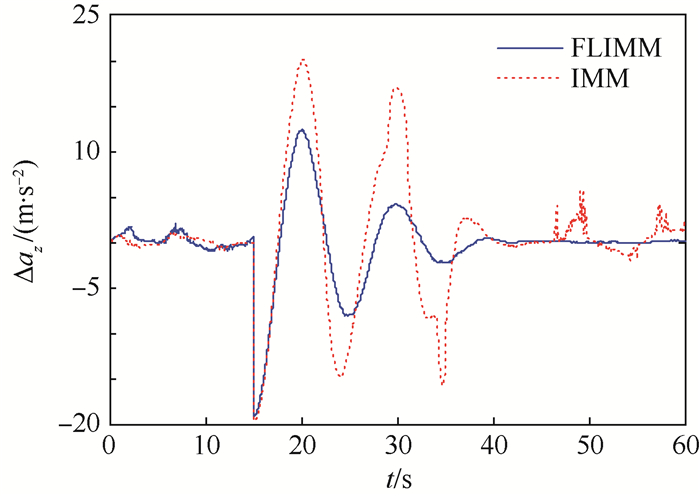
由于目标在x和y方向近似做匀速运动,采用2种算法的估计效果几乎一致,故对z方向的估计误差进行分析,如图 7~图 9所示。图 7为z方向位置估计误差Δpz,前期估计误差一致,当目标发生“蛇形”机动时,FLIMM滤波算法最大估计误差为-61 m,而IMM滤波算法的最大估计误差为-43 m,但是随后FLIMM滤波算法的估计误差迅速收敛,最终两者估计误差在-15~2 m之间。图 8为z向速度估计误差Δvz,最大估计误差均为-30 m/s左右,而FLIMM滤波算法的收敛速度明显较FLIMM滤波算法快,而且稳定后FLIMM滤波算法的估计误差没有发生突变或跳跃,较IMM滤波算法更平稳,FLIMM滤波算法后期估计误差大约为±0.5 m/s,而IMM滤波算法后期估计误差大约为-8~2 m/s之间。图 9为z向加速度估计误差Δaz,最大估计误差均为-20 m/s2,但是FLIMM滤波算法较IMM滤波算法收敛更快、更平稳、精度更高,具有更好的滤波效果,FLIMM滤波算法后期估计误差大约为±0.3 m/s2,而IMM滤波算法后期估计误差大约为-2~4 m/s2之间。
 |
| 图 7 z向位置估计误差 Fig. 7 Estimation error of position in z axis |
| 图选项 |
 |
| 图 8 z向速度估计误差 Fig. 8 Estimation error of velocity in z axis |
| 图选项 |
 |
| 图 9 z向加速度估计误差 Fig. 9 Estimation error of acceleration in z axis |
| 图选项 |
综上所述,当机动目标在0~15 s进行匀速直线运动时,IMM滤波算法与FLIMM滤波算法的估计误差几乎一致,这是因为目标做匀速运动,IMM滤波算法和FLIMM滤波算法都能很快调整模型概率,快速跟踪上目标的运动。当目标在第16 s进行“蛇形”机动后,由于其在x和y 2个方向依然近似是匀速直线运动,故2种算法在这2个方向的估计误差基本无变化;在z方向,由于目标的机动,2种算法均突然产生了较大的跟踪误差,但是由于FLIMM滤波算法能够快速调整模型概率,估计误差收敛速度明显较IMM滤波算法要快,而且FLIMM滤波算法具有一定的鲁棒稳定性,获取的估计误差在后期比较稳定,无突然大幅增加现象,具有比IMM滤波算法更高的估计精度。总体而言,FLIMM滤波算法比IMM滤波算法的滤波效果更好。
5 结论 本文根据模糊逻辑的思想对IMM滤波算法的模型概率更新模块进行改进,提出的FLIMM滤波算法有效地缩短了模型概率转移时间,提高了收敛速度,减小了估计误差,而且滤波过程更加平稳,对“蛇形”机动的跟踪精度更高,对工程实践应用具有一定的借鉴价值。但该算法的观测量获取均是以观测点静止不动为前提的,在实际应用中,存在从拦截弹上获取弹目相对信息的情况,希望在今后的学习中能够将其完善。
参考文献
| [1] | 周荻. 寻的导弹新型导引规律[M].北京: 国防工业出版社, 2002: 11-26. ZHOU D. New type homing missile guidance law[M].Beijing: National Defence Industry Press, 2002: 11-26.(in Chinese) |
| [2] | XING X F, ZUO L L, LEI S. Maneuvering target tracking using real-time input estimation[C]//Proceedings of the 1996 CIE International Conference of Radar Proceedings. Piscataway, NJ: IEEE Press, 1996: 731-734. |
| [3] | BAR-SHALOM Y, LI X R, KIRUBARAJAN T. Estimation with applications to tracking and navigation:Theory algorithms and software[M].New York: John Wiley & Sons.Inc, 2001: 115-178. |
| [4] | JOHNSTON L A, KRISHNAMURTHY V. An improvement to the interacting multiple model (IMM) algorithm[J].IEEE Transactions on Signal Processing, 2001, 49(12): 2909–2923.DOI:10.1109/78.969500 |
| [5] | 周宏仁, 敬忠良, 王培德. 机动目标跟踪[M].北京: 国防工业出版社, 1991: 89-122. ZHOU H R, JING Z L, WANG P D. Maneuver targets tracking[M].Beijing: National Defence Industry Press, 1991: 89-122.(in Chinese) |
| [6] | 刘胜, 张红梅. 最优估计理论[M].北京: 科学出版社, 2011: 102-134. LIU S, ZHANG H M. The optimal estimation theory[M].Beijing: Science Press, 2011: 102-134.(in Chinese) |
| [7] | VASUHI S, VAIDEHI V. Target tracking using interactive multiple model for wireless sensor network[J].Information Fusion, 2016, 27(1): 41–53. |
| [8] | LIU M Y, LI Y, ZHANG X J. A research on the weight of interactive multiple model in maneuvering target tracking[J].Applied Mechanics and Materials, 2014, 568-570: 1008–1011.DOI:10.4028/www.scientific.net/AMM.568-570 |
| [9] | 王立新, 王迎军. 模糊系统与模糊控制教程[M].北京: 清华大学出版社, 2003: 193-244. WANG L X, WANG Y J. The tutorial of fuzzy system with fuzzy logic[M].Beijing: Tsinghua University Press, 2003: 193-244.(in Chinese) |
| [10] | 刘政, 马增强, 柳晓云, 等. 基于模糊推理的改进的交互式多模型算法[J].济南大学学报(自然科学版), 2017, 31(2): 129–135. LIU Z, MA Z Q, LIU X Y, et al. The improved interactive multiple model algorithm based on fuzzy reasoning[J].Journal of University of Jinan(Science and Technology), 2017, 31(2): 129–135.(in Chinese) |
| [11] | 刘杨, 姜礼平, 王炜. 一种结合弹道规律的模糊交互式多模型算法[J].海军工程大学学报, 2015, 27(1): 41–44. LIU Y, JIANG L P, WANG W. A fuzzy interactive multiple model algorithm combined with ballistic rule[J].Journal of Naval Engineering University, 2015, 27(1): 41–44.(in Chinese) |
| [12] | 国强, 贺紫兰. 一种新的模糊控制多模型算法在目标跟踪中的应用[J].哈尔滨工业大学学报, 2016, 48(11): 123–128. GUO Q, HE Z L. The application of a new fuzzy multiple model control algorithm in target tracking[J].Journal of Harbin Institute of Technology, 2016, 48(11): 123–128.(in Chinese) |
| [13] | 付魏, 郑宾. 基于模糊控制交互式多模型粒子滤波的静电机目标跟踪[J].兵工学报, 2014, 35(1): 42–48. FU W, ZHENG B. Electrostatic maneuvering target tracking based on fuzzy interacting multiple model particle filter[J].Acta Armamentarii, 2014, 35(1): 42–48.(in Chinese) |
| [14] | 张翼飞, 邓方林, 顾文锦. 反舰导弹末端机动弹道设计及弹道仿真[J].计算机仿真, 2005, 22(2): 19–22. ZHANG Y F, DENG F L, GU W J. Anti-ship missile terminal maneuver trajectory design and trajectory simulation[J].Computer Simulation, 2005, 22(2): 19–22.(in Chinese) |
| [15] | 李新国, 方群. 有翼导弹飞行动力学[M].西安: 西北工业大学出版社, 2005: 26-63. LI X G, FANG Q. Flight dynamics of winged missile[M].Xi'an: Northwestem Polytechnical University Press, 2005: 26-63.(in Chinese) |
