近年来，随着安全问题的日益严峻，毫米波成像技术在安检领域的应用得到了在全世界范围内科研人员的重视和研究^[1-4]。毫米波成像系统主要分为主动式和被动式。主动式毫米波成像系统向被检物体发射毫米波信号，通过接收目标散射信号并采用算法处理以获得目标毫米波图像^[5-7]。该成像方式得到的信息量更加丰富，因而是一种针对于近程安检成像应用的有效手段。
在主动式毫米波成像系统中，通常采用实孔径阵列或形成虚拟阵列的合成孔径雷达(SAR)方式进行成像。然而在实际应用中，可能会出现被测物体偏移天线阵列中心法向指向的情况。在SAR理论中，此种情况被称为斜视问题，且已有诸多研究及相关成像算法^[8-10]，然而这些成像算法通常具有一定的局限性。一方面，安检应用中，目标距离通常位于单元天线的远场区及阵列的近场区之间，此时称为近程问题。然而大部分斜视成像算法都基于远场条件对传播距离方程进行近似处理，当应用于近程问题时其近似精度远不能满足需求。另一方面，由于成像距离较短，目标短距离移动会造成超过40°的大斜视角情况出现，而SAR斜视算法通常只能应用于0°~30°的斜视角范围。为了满足安检成像的高分辨需求，需要设计满足近程大斜视角情况的高精度成像算法。考虑到SAR成像算法中的距离徙动(Range Migration, RM)算法不加其他近似条件实现无几何形变的完全聚焦^[11]，具有较高的成像精度和准确率^[12-13]，可满足近程成像需求的特点，本文提出一种基于RM成像算法的近程大斜视成像算法，能够在满足近程安检成像分辨率的同时，实现较为快速的成像以及准确聚焦。
RM成像算法通过Stolt插值的方式解决距离徙动引入的误差问题，从而实现较高的成像精度。在RM成像算法中，将目标散射信号通过快速傅里叶变换(FFT)转换到空间域，并进行相位补偿从而实现聚焦目的^[14-15]。在斜视的情况下，目标中心偏移天线阵列中心法向指向，这造成二维波数域的信号谱发生偏移，当偏移超出谱域支持域范围后将发生翻折，造成混叠。此时若直接采用RM成像算法进行处理会造成严重的散焦效果。本文通过目标斜视角或偏移量计算出信号谱偏移量，进而将翻折后的谱进行分块，对不同的部分进行补偿后得到其实际的空间谱，再进行Stolt插值操作及傅里叶逆变换后得到目标图像。仿真分析及实际测量结果验证了本文算法的有效性及实用性。
1 原理推导 1.1 单站SAR距离徙动算法成像原理 考虑单站SAR的等效阵列，令其等效阵元的位置坐标为(x, z)，目标与天线阵列的距离设为d。利用散射中心模型简化目标，令其等效散射点位置坐标为(x₀, z₀)，如图 1所示。

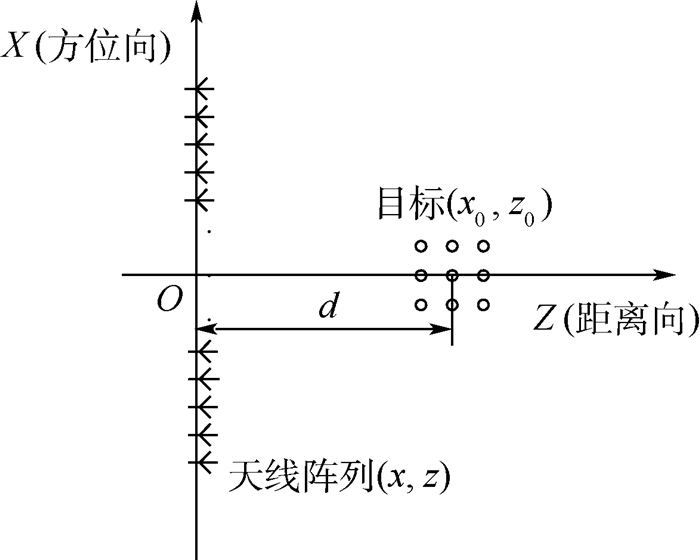图 1 仿真参数设计示意图 Fig. 1 Schematic of simulation parameter design

图选项

为了简化分析，采用理想匹配滤波后的信号进行分析，此时接收信号中仅保留由于传播路径带来的时间延迟，用冲激函数δ表示。接收到的信号空域-时域信号可以表示如下：

(1)

式中：系数2表示单站情况下的双倍传播路径；R(x, t)表示接收到的由目标散射回来的回波信号；s(x₀, z₀)代表可以看作多个散射点组成的目标；c为光传播速度；t为信号传播时间；r为对应的目标到天线的传播距离，可以表示为

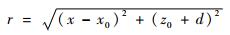(2)

利用傅里叶变换可以将式(1)变换至频域：

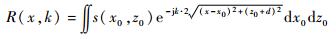(3)

式中：参数k表示波数，，f为频率。从式(3)中可以看出接收信号中仅包含不同频率的传播相位。进一步将接收到的频域信号在阵列维进行傅里叶变换可获得空间谱域-频域的表达：

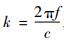
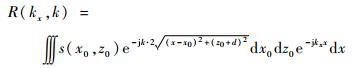(4)

为了对式(4)进一步简化，通过交换积分次序并利用驻定相位原理(Method of Stationary Phase，MSP)，从而式(4)可以转化为

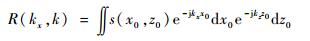(5)

式中：，表示了空间谱的变换。
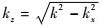
从式(5)可以看出目标散射点分布与接收信号的空间谱域-频域表达呈二维傅里叶变换关系。同时应当注意到，此傅里叶变换关系应将原始信号谱映射到对应的k_x-k_z域上，即RM成像算法中的Stolt插值过程。
1.2 近程斜视成像算法推导 斜视情况下设定目标斜视角为θ，仿真参数设计示意图如图 2所示。

图 2 斜视场景下仿真参数设计示意图 Fig. 2 Schematic of simulation parameter design in squint condition

图选项

当阵列中心与成像区域中心无偏移的时候，信号的传输距离项r′。满足式(2)，而当阵列中心与目标中心存在偏移时，通过引入偏移量x_c，可将距离项重写为

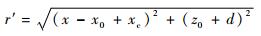式中：x_c=dtan θ。
无偏情况下根据驻定相位原理推导的接收信号如式(5)所示，其中驻相点为k_x= 。在斜视情况下，根据驻定相位原理推导的接收信号为

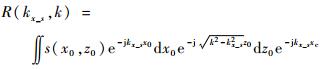(6)

其中：驻相点。
从公式推导中可以看出，目标偏移阵列中心位置使得驻相点发生偏移，因此造成空间谱域的偏移，进而引起翻折混叠，这一点可以直观地从仿真图 3中看出。

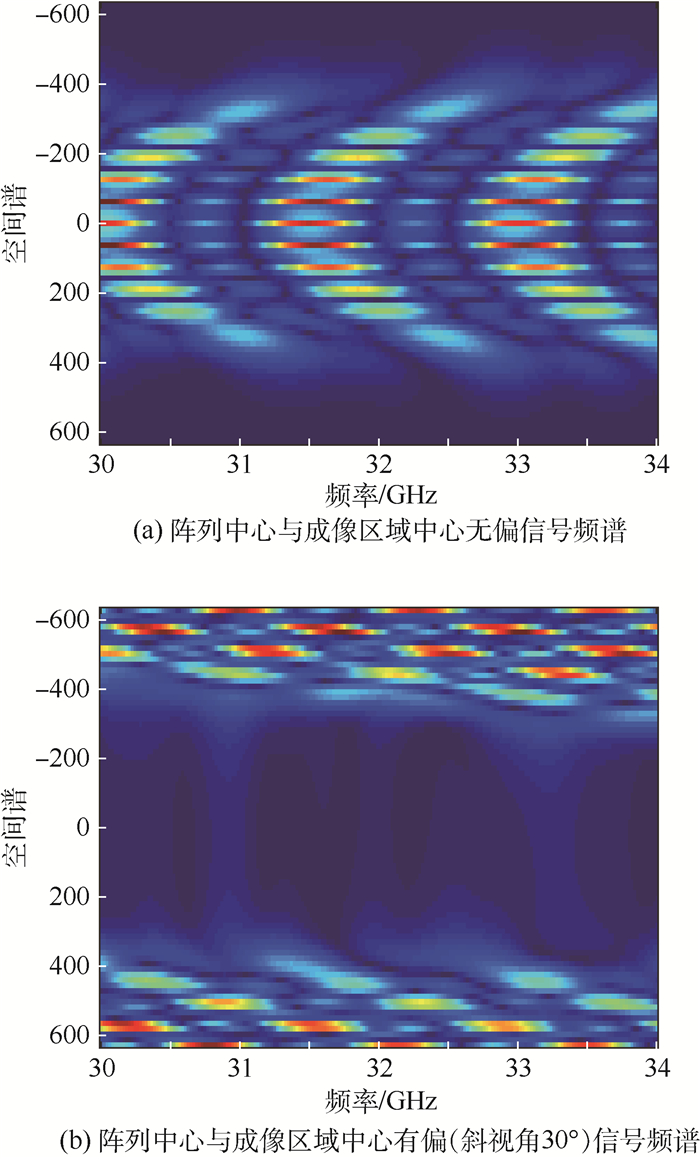图 3 阵列中心与成像区域中心无偏和30°斜视角的频谱对比 Fig. 3 Comparison of spectrum between no squint angle and with squint angle of 30°

图选项

产生的谱域翻折混叠主要由以下2个原因造成：
1) 由于驻相点是接收信号的主要贡献分量，由式(6)可以看出，目标和天线阵元的相对位置决定了目标谱的位置和形状，因此天线阵元的位置决定了谱域的分布，而目标中心与天线阵列中心的偏移决定了目标谱的偏移量，因此斜视情况下目标谱发生偏移。
2) 傅里叶变换后的空间谱域受限于一定范围，由天线阵元间隔决定，为变换后的谱支持域。由离散傅里叶变换的特性可知，当目标谱偏移超出了谱支持域范围将会导致超出支持域范围的目标谱翻折混叠进入谱支持域，造成实际目标谱与谱支持域坐标不对应的问题。
2 算法流程 针对空间谱偏移翻折的问题，可将空间谱支持域内的目标谱分为2个部分：偏移后未发生翻折混叠的部分，发生翻折混叠的部分。因为偏移量可通过已知的目标中心与阵列中心偏移距离计算得出，所以可通过计算还原谱支持域中目标谱的实际位置。
本文算法过程包括为5个步骤：①对接收信号进行二维傅里叶变换。原始接收信号R(x, t)在仿真中为二维矩阵形式，其一维表示不同接收天线的位置，另一维表示时间。对接收信号进行二维傅里叶变换，将其变换到空间谱域-频域上R(k_x, k)。②通过计算谱域中不同区域的翻折次数可对接收信号谱进行区域划分。在大斜视角情况下，式(6)中驻相点k_{x_s}=k(x+x_c-x₀)/ ，代入成像区域中心位置坐标x₀=0，z₀=0，可计算得到目标谱的偏移量。根据离散傅里叶变换原理可知，谱域支持域长度为2π/dx，故翻折次数N为k_{x_shift}/(2π/dx)的整数部分，而其小数部分表示翻折后不同部分的的分界区边界，整理后可得其表达式为：k_{x_shift}-(2N+1)·(π/dx)。根据上述步骤公式计算后可以得到对应区域实际谱域支持域的坐标，并将目标谱在谱域支持域中的实际位置还原出来。③参考函数相乘，如式(6)所示。④Stolt插值处理，此时应在实际谱域支持域的坐标内进行插值。⑤通过二维傅里叶逆变换将信号变回空间位置-时间维，从而实现成像目的。成像处理的流程图如图 4所示。

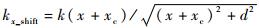
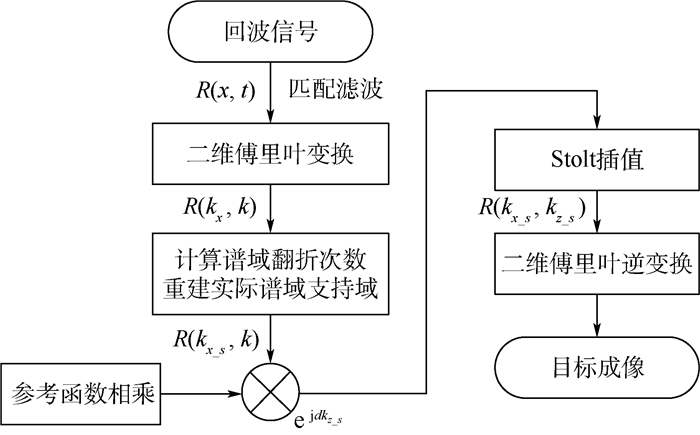图 4 本文算法流程图 Fig. 4 Flowchart of proposed algorithm

图选项

在算法处理过程中，可在原始信号二维傅里叶变换前和谱域信号二维傅里叶逆变换前通过补零的方法提升结果的可视化效果。
3 仿真分析及实验测量结果 3.1 仿真分析 本节通过计算机仿真对本文算法进行验证。仿真分析在MATLAB中进行，仿真场景设置如图 5所示。

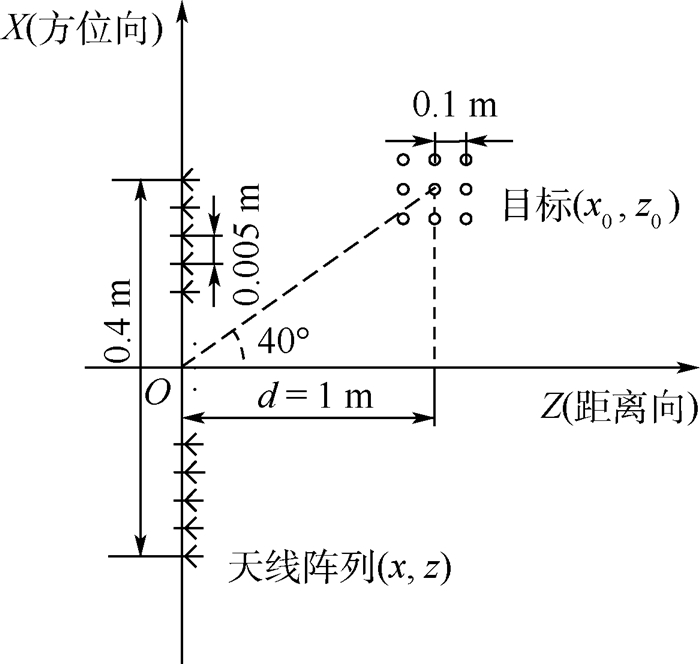图 5 仿真参数设置 Fig. 5 Simulation parameter setting

图选项

图 5显示了仿真场景中天线阵列和目标的位置设定关系，天线阵列的长度设为0.4 m，天线阵元间隔为0.005 m，成像距离设置为1 m。目标设置为0.2 m×0.2 m范围内均匀分布的9个散射点的集合，目标偏移角设为40°。天线发射30~34 GHz的宽带信号，带宽为4 GHz，频点数目为200个采样频点，即每500 MHz一个采样频点，采样间隔遵守奈奎斯特采样定律。计算理论方位向分辨率为0.015 3 m，理论距离向分辨率为0.037 5 m。场景设置满足天线阵列的近场条件。
仿真使用的目标回波信号采用频域表达，可根据式(3)获得，对其沿天线阵列方向作傅里叶变换后可获得频域-空间域的信号，如图 6所示。

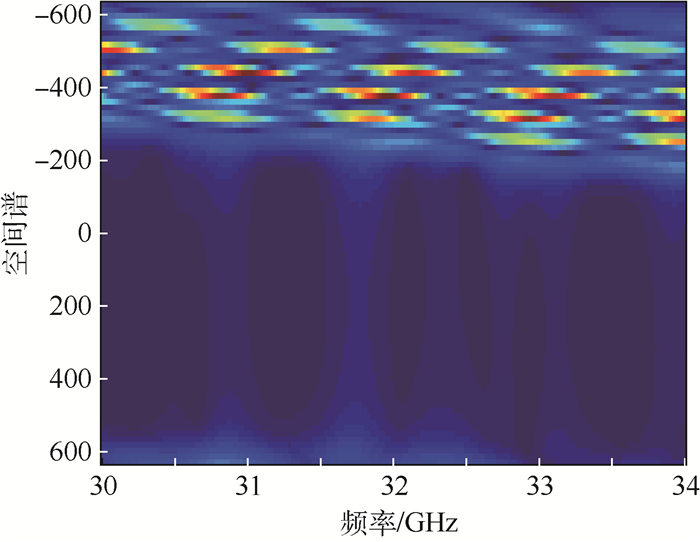图 6 斜视角为40°时接收信号的频谱 Fig. 6 Spectrum of received signal with squint angle of 40°

图选项

从图 6中可以看出，目标谱偏移至谱支持域的上半区域，且有部分目标谱混叠进入谱支持域的下半区域。通过驻定相位原理计算谱域的偏移量，可获得目标谱的翻折次数及混叠区域的划分限，如图 7所示。

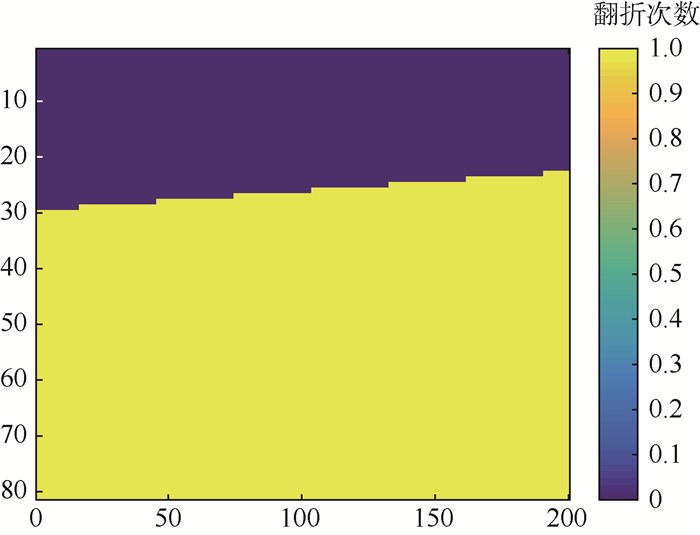图 7 谱域不同部分翻折次数 Fig. 7 Warping and lapping times of differentparts of spectral domain

图选项

图 7中，深色色区域为为目标谱0次翻折后所占区域，而浅色区域表示混叠造成谱域的1次翻折。由此可以针对不同部分计算其实际对应的谱支持域范围，进而进行插值处理。
插值结果如图 8所示，可见经插值后，大斜视角下目标谱的严重弯曲效果被成功的补偿回来。由于目标设置为格点分布形式，因此其真实谱域形状也表现为格点状分布。从图 8的谱域插值结果也可看出，目标谱已被成功恢复出来。

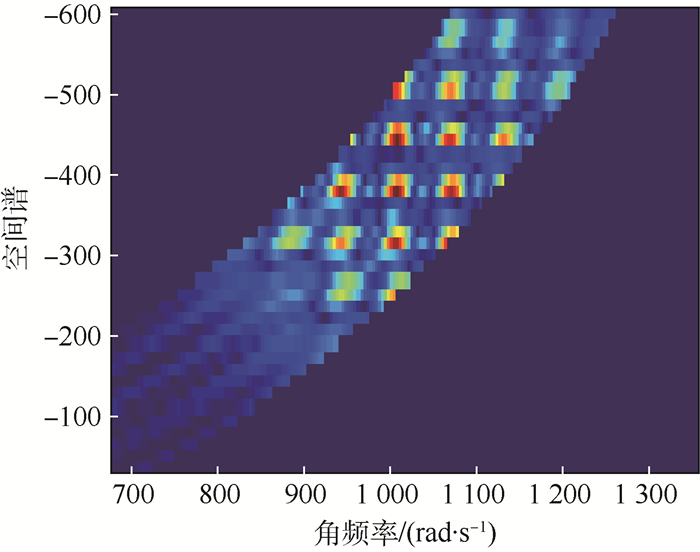图 8 还原后再经插值的信号频谱 Fig. 8 Signal spectrum after restoration and interpolation

图选项

图 9为经二维傅里叶逆变换后获得的目标图像。由图像中可看出，9个目标点均已被正确聚焦。图中右下角目标点所呈现出的波纹状特性是由于补零进行图像平滑的操作所引起，并不影响实际聚焦效果。因为结果并未进行加窗处理，所以通过旁瓣可以看出斜视造成的旁瓣走向旋转，其旋转角度与斜视角一致。在64位操作系统，主频2.50 GHz的Intel i5处理器，6 GB内存的笔记本电脑上，采用MATLAB进行编程并仿真分析，针对实际应用场景该算法运行时间为0.41 s，本算法可基本达到传统RM成像算法的运算效率，可满足实时成像需求。

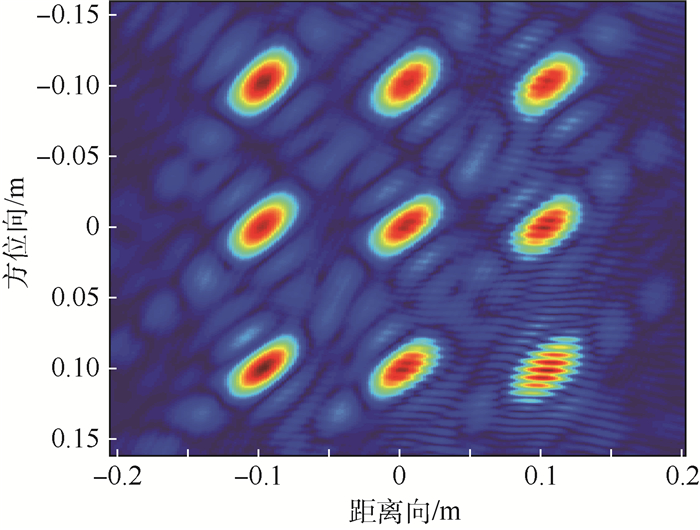图 9 仿真成像结果 Fig. 9 Simulation imaging result

图选项

3.2 实验测量结果 实验系统采用准单站的形式搭建，即一个发射天线和一个接收天线之间设定较近的距离。两天线水平放置可减少天线间的极化耦合现象。通过机械扫描的形式实现单站天线阵列，发射/接收天线以0.01 m的扫描间隔水平扫描60个位置。目标设置为2个标准金属球，斜视角设为60°，放置在距离天线阵列约为0.8 m处。数据发射采集存储利用Agilent 85309分布式系统，发射宽带信号为30~38 GHz，带宽为8 GHz，采样频点个数为201。实际测量场景如图 10所示。

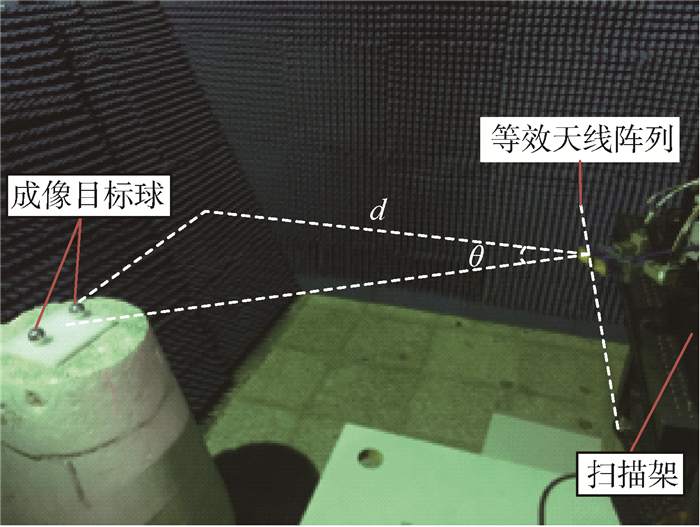图 10 实验测量场景 Fig. 10 Experimental measurement scene

图选项

接收到的信号在处理成像之前应当进行校准，其中包括背景噪声以及系统响应不一致性的消除。应用本文算法进行目标成像，得出结果如图 11所示。

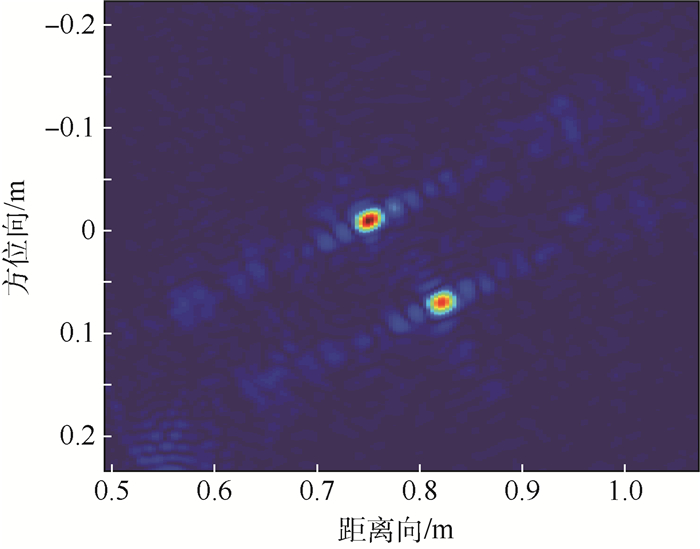图 11 实验测量成像结果 Fig. 11 Actual measured imaging result

图选项

从图 11中可以看出算法能够实现目标区域的精确聚焦，实现近程大斜视角目标成像目的。除此之外，从成像结果仍可看出，旁瓣旋转角度与斜视角一致。图中较为明显的旁瓣拖延现象沿天线指向分布，是由于系统频率响应不能完全精确校准所致。
4 结论 本文在RM算法的基础上进行修正，提出了一种适用于近程大斜视成像场景的改进算法，能保证近程安检成像分辨率要求的同时，实现快速成像以及准确聚焦，该算法主要有以下几个特点：
1) 本文算法基于RM算法的基本理论，具有较高的计算效率。
2) 通过计算机仿真和实际实验测量验证了算法的优势及可行性。成像结果表明该算法能够对目标实现准确聚焦。
3) 由于未引入距离的近似处理，该算法不仅适用于远程斜视成像，也可适用于近程大斜视角场景，以上情况均可实现精确聚焦。

参考文献

[1]	费鹏, 方维海, 温鑫, 等. 用于人员安检的主动毫米波成像技术现状与展望[J].微波学报, 2015, 31(2): 92–95. FEI P, FANG W H, WEN X, et al. Status and prospect of active millimeter-wave imaging technology for personal security inspection[J].Journal of Microwave, 2015, 31(2): 92–95.(in Chinese)
[2]	BHARTIA P, BAHL I J. Millimeter-wave engineering and applications[M].New York: Wiley, 1984: 660-671.
[3]	尚晓舟, 孙鹏, 胡岸勇, 等. 协同体制被动毫米波成像系统天线阵布局优化[J].北京航空航天大学学报, 2015, 41(10): 1842–1847. SHANG X Z, SUN P, HU A Y, et al. Antenna array layout optimization of collaborative passive millimeter-wave imaging system[J].Journal of Beijing University of Aeronauties and Astronautics, 2015, 41(10): 1842–1847.(in Chinese)
[4]	赵自然. 防爆安全检查技术应用及趋势分析——人体安检新技术的分析与探讨[J].中国安防, 2012(3): 32–36. ZHAO Z R. Analysis and discussion on the application and trend analysis of explosion proof safety inspection technology-Analysis and discussion on new technology of human security inspection[J].Journal of China Security, 2012(3): 32–36.(in Chinese)
[5]	KEMP M C. A review of millimetre-wave and terahertz technology for detection of concealed threats[C]//International Conference on Infrared, Millimeter and Terahertz Waves. Piscataway, NJ: IEEE Press, 2008: 1-2.http://ieeexplore.ieee.org/document/4665630/
[6]	SHEEN D M, MCMAKIN D L, COLLINS H D, et al. Near-field millimeter-wave imaging for weapons detection[C]//Applications in Optical Science and Engineering, 1993: 12-16.http://spie.org/Publications/Proceedings/Paper/10.1117/12.142900
[7]	APPLEBY R, ANDERTION R N, PRINCE S, et al. Compact real-time (video rate) passive millimeter-wave imagery[J].Passive Millimeter-wave Imaging Technology Ⅲ, 1999, 3703: 13–19.
[8]	TANG Y, ZHANG B, XING M D, et al. Azimuth overlapped subaperture algorithm in frequency domain for highly squinted synthetic aperture radar[J].IEEE Geoscience and Remote Sensing Letters, 2013, 10(4): 692–696.DOI:10.1109/LGRS.2012.2219033
[9]	YEO T S, TAN N L, ZHANG C B, et al. A new subaperature approach to high squint SAR processing[J].IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(5): 954–968.DOI:10.1109/36.921413
[10]	SUN Y, JING X J, SUN S L, et al. The subaperture secondary range compression algorithm for near space squint SAR[C]//IEEE International Symposium on Signal Processing and Information Techology. Piscataway, NJ: IEEE Press, 2013: 338-343.http://doi.ieeecomputersociety.org/10.1109/ISSPIT.2013.6781904
[11]	保铮, 邢孟道, 王彤. 雷达成像技术[M].北京: 电子工业出版社, 2010: 173-177. BAO Z, XING M D, WANG T. Radar imaging technology[M].Beijing: Electronic Industry Press, 2010: 173-177.(in Chinese)
[12]	CUMMING I G, WONG F H. Digital processing of synthetic aperture radar data:Algorithm and implementation[M].Norwood: Artech House, 2005: 219-244.
[13]	BAMLER R. A comparison of range-Doppler and wavenumber domain SAR focusing algorithms[J].IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(4): 706–713.DOI:10.1109/36.158864
[14]	吴照宪. 合成孔径雷达成像技术研究[D]. 北京: 中国科学院电子学研究所, 2007: 7-10. WU Z X. Research on synthetic aperture radar imaging technology[D]. Beijing: Electronics Institute of Chinese Academy of Sciences, 2007: 7-10(in Chinese).http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1143046
[15]	李峰. SAR成像的ω-k算法研究[J].航空兵器, 2006, 24(6): 10–12. LI F. Research on ω-k algorithm for SAR imaging[J].Journal of Aviation Weapon, 2006, 24(6): 10–12.(in Chinese)