本文针对数字斜波调制实时调整的特点,分析了增益变小时斜波频繁复位的产生及其对死区的影响机理,提出了分离正负向斜波累加区间的滞回复位算法。通过仿真和实验验证了滞回复位算法抑制斜波频繁复位、减小死区的有效性。
1 频繁复位的产生及影响机理 全数字闭环光纤陀螺简化模型如图 1所示[1, 3, 12-13]。图中:Ω和C分别为角速度输入和陀螺数字输出;Ks为萨格奈克效应系数;KD和KF分别为探测通道增益和调制通道增益;KFIL为输出通道滤波器增益。探测通道在每个渡越时间Δτg对A/D转换器采集的信号进行相干解调,得到反映萨格奈克相移?s与反馈相移?f间误差的解调信号e,累加到相位台阶s上,以跟踪?s的变化;累加s产生数字相位斜波r,并通过斜波寄存器自动溢出实现斜波复位[1]。为方便分析,闭环过程可简化为在非复位时?s与?f相等,不存在相位误差;而在复位时斜波自动溢出会引入附加相移,受调制增益漂移影响,?s与?f不仅相差整数倍2π,还存在额外的相位误差[6-10]。设调制增益偏离设计值的比例为ε,相位误差N可表示为
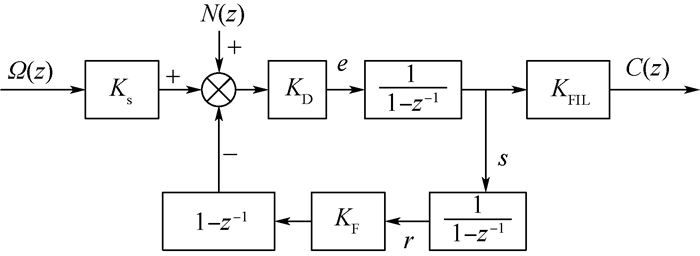 |
| 图 1 方波偏置调制时闭环光纤陀螺简化模型[1, 3, 12-13] Fig. 1 Simplified model of closed-loop fiber optic gyroscope under square wave bias modulation[1, 3, 12-13] |
| 图选项 |
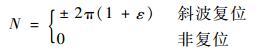 | (1) |
式中:斜波正向溢出复位取“+”,负向溢出复位取“-”。
数字相位斜波溢出复位时,根据相干解调公式可得到解调误差e为[1, 6, 10]
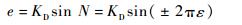 | (2) |
复位时,解调误差仅与斜波溢出的方向和增益漂移有关。ε>0(增益变大)时,解调误差的符号与式(1) 中斜波溢出所取的符号相同,同号解调误差使相位台阶符号不变,相位斜波继续同向累加,不会产生反向复位;而ε < 0(增益变小)时,解调误差的符号与斜波溢出所取符号相反,当解调误差的模大于或等于复位前相位台阶模的2倍时,相位斜波必然反向复位。
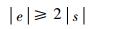 | (3) |
相位斜波反向复位后,在萨格奈克相移作用下恢复同向累加而再次同向复位,会再一次引起反向复位,于是斜波频繁地复位。
将式(2) 及复位前KF(1+ε)s=?s=KsΩ代入式(3),可得斜波频繁复位的条件为
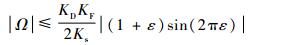 | (4) |
实验所用光纤陀螺的相关设计参数如表 1所示。以调制增益变小1%(ε=-0.01) 为例,解算出数字相位斜波产生频繁复位的输入角速度范围为|Ω|≤0.010 8 rad/s≈2 228 (°)/h。
表 1 实验所用光纤陀螺设计参数 Table 1 Design parameters of experiment fiber optic gyroscope
| 参数 | 设计值 |
| Ks/s | 0.551 6 |
| KD/(LSB·rad-1) | 998.4 |
| KF/(rad·LSB-1) | 1.92×10-4 |
| ??注:LSB(Least Significant Bit)—最低有效位。 | |
表选项
当输入角速度较大时,数字相位斜波复位数次后就会恢复正常累加,频繁复位对光纤陀螺性能参数影响较小。图 2为调制增益变小1%时输入角速度为2228 (°)/h的相位台阶与相位斜波的仿真波形。
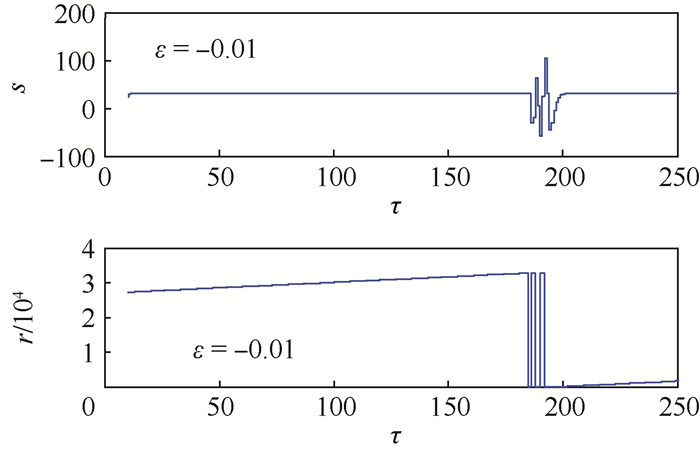 |
| 图 2 输入角速度为2 228 (°)/h时相位台阶与相位斜波仿真波形 Fig. 2 Simulation waveform of phase step and phase ramp when input angular velocity is 2 228 (°)/h |
| 图选项 |
输入角速度的大小会影响数字相位斜波频繁复位的次数。图 3为调制增益变小1%时输入角速度为50 (°)/h的相位台阶与相位斜波仿真波形,数字相位斜波在较长时间内处于频繁复位状态。
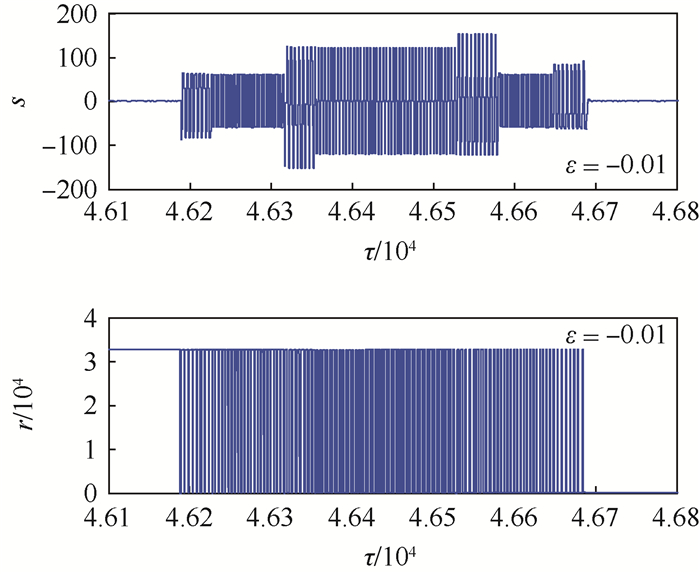 |
| 图 3 输入角速度为50 (°)/h时相位台阶与相位斜波仿真波形 Fig. 3 Simulation waveform of phase step and phase ramp when input angular velocity is 50 (°)/h |
| 图选项 |
通过仿真可得到频繁复位时间占完整斜波累加-复位周期的比例与输入角速度的关系,如图 4所示。当输入角速度为50(°)/h时,频繁复位时间约占斜波周期的0.5%,而输入角速度减小至0.5 (°)/h时,频繁复位时间所占比例已达到约93%。可见,输入角速度越小,数字相位斜波复位次数越多,频繁复位时间所占斜波周期的比例越大。
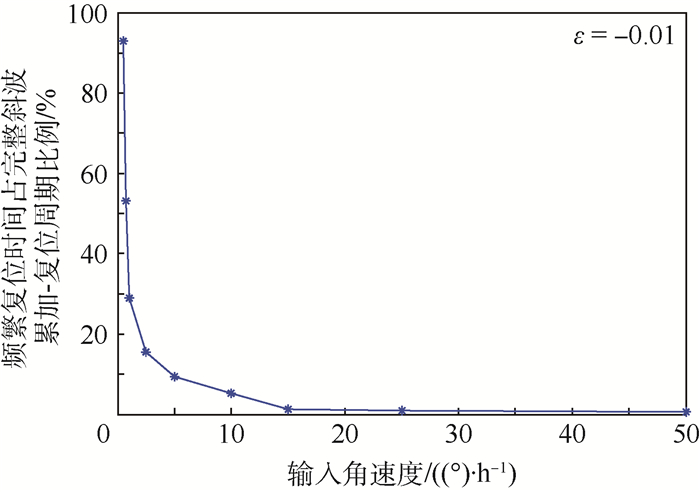 |
| 图 4 频繁复位时间占比与输入角速度的关系 Fig. 4 Relationship between frequent reset time proportion and input angular velocity |
| 图选项 |
当输入角速度继续减小时,数字相位斜波将被“困在”频繁复位状态,斜波不能进行正常累加,频繁复位时间将占整个斜波周期的100%。由式(2) 知,调制增益变小时,不同溢出方向的斜波复位会引入不同符号的复位相位误差,而小角速度时,萨格奈克相移远小于因增益变小而产生的相位误差峰峰值。因此,复位相位误差将主导数字相位斜波的累加与复位,斜波一直处于复位状态,相位斜波和相位误差仿真波形如图 5所示。
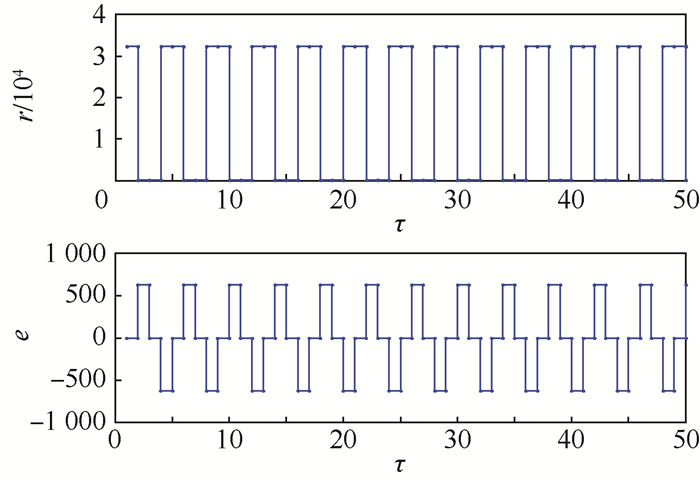 |
| 图 5 斜波频繁复位时相位斜波与相位误差仿真波形 Fig. 5 Simulation waveform of phase ramp and phase error when ramp resets frequently |
| 图选项 |
小角速度输入时,复位相位误差会引起数字相位斜波反向复位,而斜波复位又产生复位相位误差,因此斜波溢出复位与复位相位误差相互促进,从而形成均值为零的相位误差和振荡的相位斜波。与Y波导调制信号-探测器输出信号间电子串扰耦合造成死区机理[14-17]相同,数字相位斜波在复位阈值附近振荡时,光纤陀螺输出为零,产生了“死区”。
2 滞回复位算法 为消除调制增益变小对死区的影响,应设法抑制斜波频繁复位。考虑到自动溢出的复位实现方式,斜波正负向累加区间是重叠的,调制增益变小引起复位后异号的相位台阶使斜波反向溢出而再次复位,因此重叠的累加区间无法实现斜波复位后的反向累加。为抑制反向复位,可把斜波正负向累加区间分离,形成相位斜波滞回复位算法,如图 6所示。设定相位斜波正向累加起点S+为a,正向复位阈值R+为a+2n-1,负向复位阈值R-为b,负向累加起点S-为b+2n-1,a>b>0,从而形成[b, a]和[b+2n-1, a+2n-1]2个滞回区间。
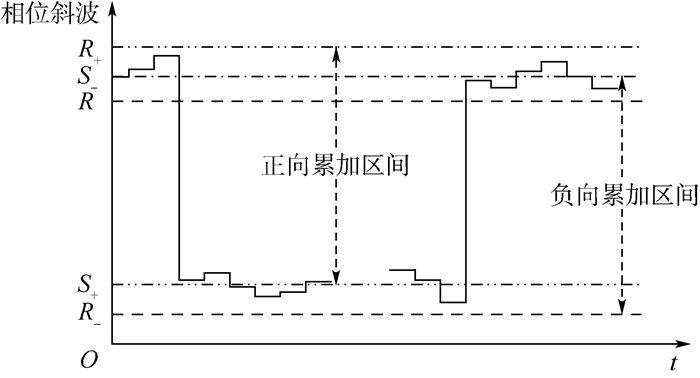 |
| 图 6 滞回复位算法示意图 Fig. 6 Schematic diagram of hysteresis reset algorithm |
| 图选项 |
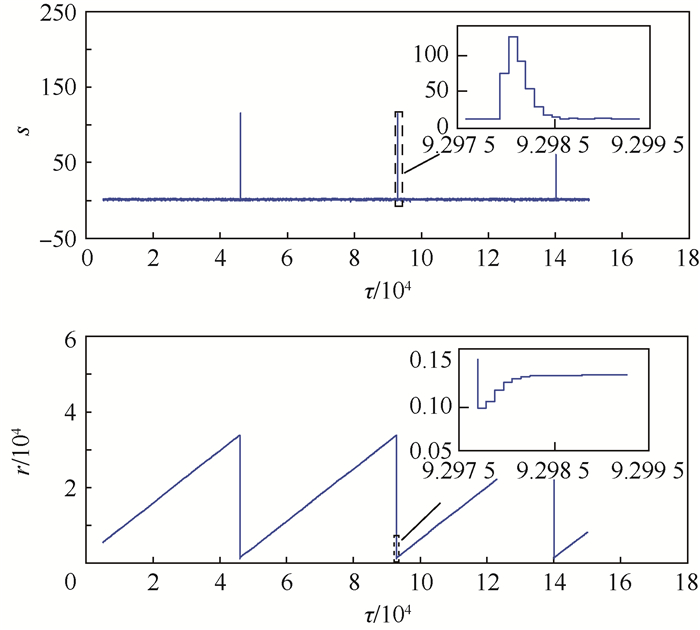
相位斜波同向累加起点与复位阈值间的宽度依旧为2n,借助数字逻辑的灵活性,滞回复位通过寄存器强制溢出来实现[7-8]。调制增益未漂移时,滞回复位算法不会引起额外相位误差,以斜波正向溢出为例,相位台阶和相位斜波的仿真波形如图 7所示。调制增益变大时,复位后相位斜波正常同向累加,正向溢出仿真波形如图 8所示。当调制增益变小时,复位后斜波在滞回区间内反向累加,只要斜波寄存器值不小于b,就不会反向复位,之后恢复同向累加,正向溢出仿真波形如图 9所示,同图 3相比频繁复位有效地被抑制。
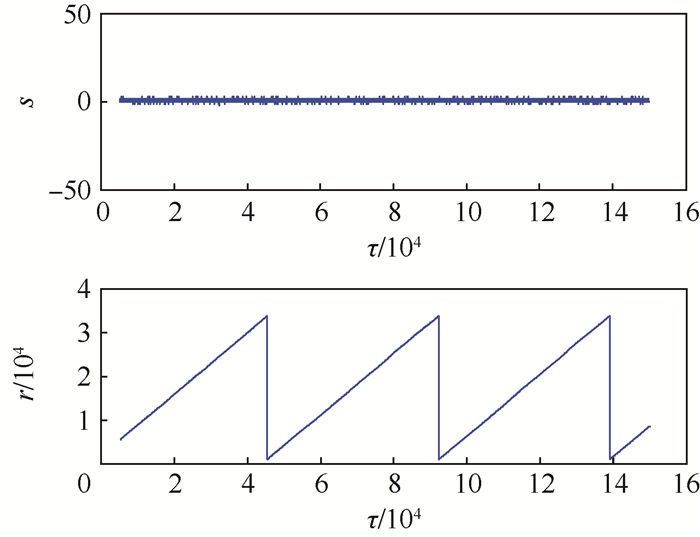 |
| 图 7 调制增益未漂移时斜波滞回复位仿真 Fig. 7 Ramp hysteresis reset simulation with no modulation gain drift |
| 图选项 |
 |
| 图 8 调制增益变大时斜波滞回复位仿真 Fig. 8 Ramp hysteresis reset simulation when modulation gain largens |
| 图选项 |
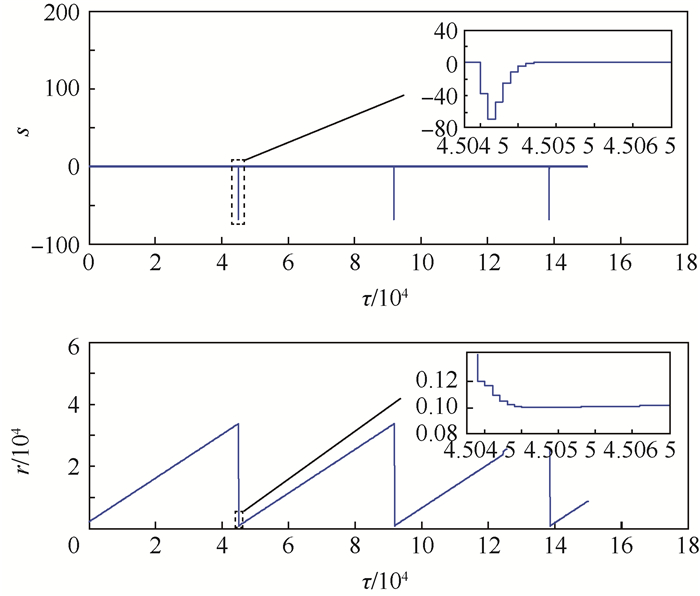 |
| 图 9 调制增益变小时斜波滞回复位仿真 Fig. 9 Ramp hysteresis reset simulation when modulation gain lessens |
| 图选项 |
为保证算法效果,滞回区间宽度应大于复位相位误差对应解调误差绝对值的最大预期值,即
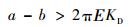 | (5) |
式中:Ε为|ε|可达到的最大预期值,工程中可取解调误差的3倍值6πΕKD。
3 实验验证 3.1 不同调制增益漂移对死区的影响 为验证调制增益变大/变小对死区产生不同的影响,按照GJB 2426A—2004[14]的要求对光纤陀螺进行死区测试。使用安装夹具将陀螺固定在水平速率转台上,陀螺的基准轴在水平面内,以0.01 (°)/s的速率从正北方向顺时针转到一周回到正北方向,采集光纤陀螺的输出[1, 15-16]。同时通过设定调制通道D/A转换器的参考电压以模拟调制增益漂移,以调制增益变大、变小1%(ε=±0.01) 为例,解算出光纤陀螺在死区附近的输入-输出曲线,如图 10所示。
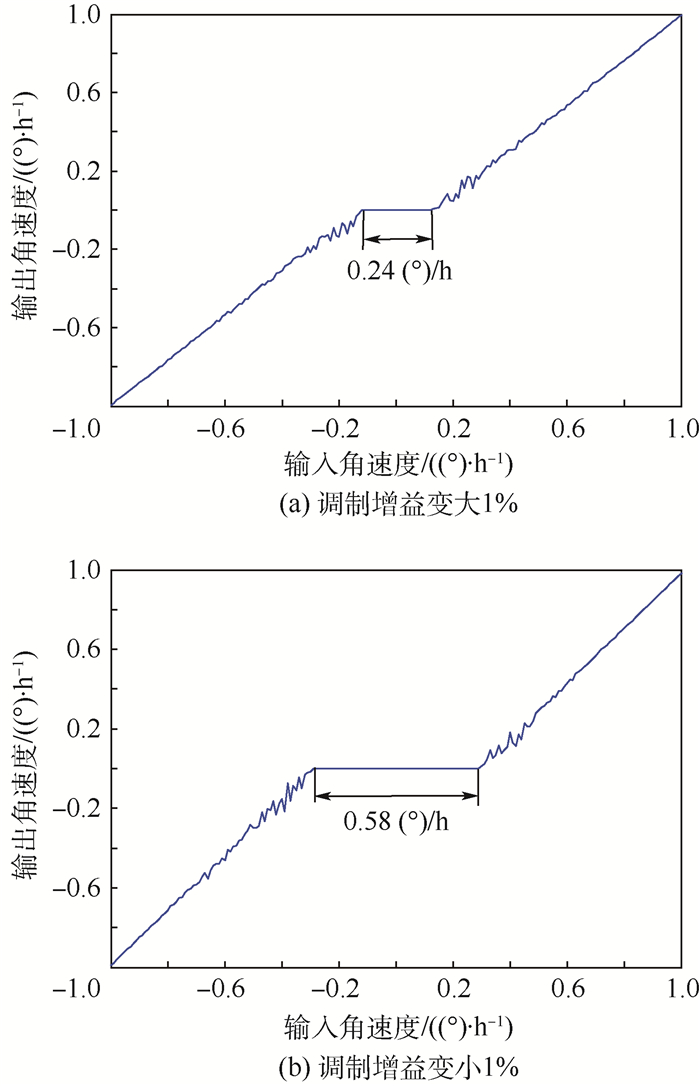 |
| 图 10 调制增益分别变大、变小1%时输入-输出关系 Fig. 10 Relationship between input and output when modulation gain largens or lessens by 1% |
| 图选项 |
实验测得,调制增益变大1%时,光纤陀螺死区范围为±0.12 (°)/h;而增益变小1%时,死区范围为±0.29 (°)/h。一方面,调制增益变大时,光纤陀螺依然存在死区,这是因为实验所用光纤陀螺并未补偿电子串扰耦合等因素造成的死区[15-18];另一方面,调制增益变小时,除电子串扰耦合产生的死区外,数字相位斜波频繁复位也引起了死区,因此调制增益变小时死区范围更大。
3.2 滞回复位算法减小死区 用相同的测试方法获得调制增益变小1%时采用滞回复位算法的光纤陀螺输入-输出关系,如图 11所示。滞回复位算法将死区减小至±0.11 (°)/h,同图 10(b)相比,有效消除了因频繁复位引起的部分死区,改善了光纤陀螺的死区性能。
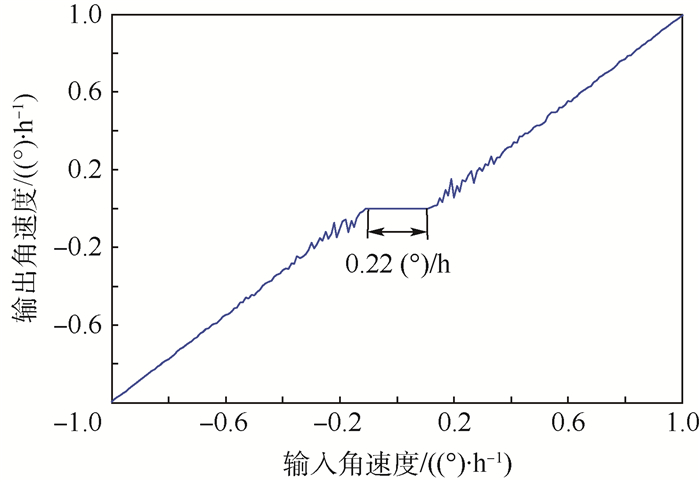 |
| 图 11 调制增益变小1%时采用滞回复位算法的输入-输出关系 Fig. 11 Relationship between input and output with hysteresis reset algorithm when modulation gain lessens by 1% |
| 图选项 |
4 结论 本文分析了数字相位斜波频繁复位对死区的影响,并提出了改进的滞回复位算法。
1) 采用自动溢出复位时,调制增益变小会引起数字相位斜波频繁复位,且输入角速度越小时,频繁复位时间越长。
2) 相位斜波频繁复位增大了死区,恶化了光纤陀螺性能。
3) 通过分离相位斜波正负向累加区间形成滞回复位算法,能够抑制增益变小时斜波频繁复位,将死区从±0.29 (°)/h减小至±0.11 (°)/h。
滞回复位算法只能抑制数字斜波频繁复位,不能改变小角速度输入时复位误差带来的输出波动,需要进一步完善相关算法,消除输出波动对高精度光纤陀螺定位定向应用的影响。
参考文献
| [1] | LEFEèVRE H C. The fiber-optic gyroscope[M].2nd edBoston: Artech House, 2014: 119-150. |
| [2] | LEFEèVRE H C, MARTIN P, MORISSE J, et al.High-dynamic-range fiber gyro with all-digital signal processing[C]//Fiber Optic and Laser Sensors Ⅷ.Bellingham, WA:SPIE, 1996, 1367:72-80. |
| [3] | 金靖, 宋凝芳, 李立京. 干涉型光纤陀螺温度漂移建模与实时补偿[J].航空学报, 2007, 28(6): 1449–1454. JIN J, SONG N F, LI L J. Temperature drift modeling and real-time compensation of interferometric fiber optic gyroscope[J].Acta Aeronautica et Astronautica Sinica, 2007, 28(6): 1449–1454.(in Chinese) |
| [4] | 王海. 光纤陀螺温度影响与误差补偿[J].北京航空航天大学学报, 2007, 33(5): 549–551. WANG H. Affects of temperature and error compensation for fiber optic gyro[J].Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(5): 549–551.(in Chinese) |
| [5] | 张勇, 李绪友, 王南, 等. 高精度数字闭环光纤陀螺的调制增益控制[J].哈尔滨工程大学学报, 2008, 29(11): 1172–1175. ZHANG Y, LI X Y, WANG N, et al. Modulation gain control of high-precision digital closed-loop fiber optic gyroscope[J].Journal of Harbin Engineering University, 2008, 29(11): 1172–1175.DOI:10.3969/j.issn.1006-7043.2008.11.006(in Chinese) |
| [6] | 王妍, 张春熹. 带第二反馈回路的全数字闭环光纤陀螺[J].压电与声光, 2005, 27(4): 348–351. WANG Y, ZHANG C X. All digital closed-loop fiber optic gyroscope with the second feedback loop[J].Piezoelectrics & Acoustooptics, 2005, 27(4): 348–351.(in Chinese) |
| [7] | MA D Y, SONG N F, SONG J M, et al.The novel arithmetic and realization based on FPGA module design for the real time compensation of the reset error in FOG[C]//The 2nd International Conference on Information Science and Engineering.Piscataway, NJ:IEEE Press, 2010:738-741. |
| [8] | MA D Y, SONG N F, PAN X, et al. Binary code compression algorithm used for the real time compensation of the modulation error in miniaturized FOG[J].Optical Fiber Technology, 2011, 17(4): 267–272.DOI:10.1016/j.yofte.2011.04.001 |
| [9] | WANG W, WANG J L, ZHAO Z X. Method to control the gain in modulation chain of closed-loop fiber optic gyroscope with periodical biasing modulation[J].Optical Engineering, 2012, 51(6): 1–5. |
| [10] | LI H, BI L, LI L J, et al. Tracking algorithm for the gain of the phase modulator in closed-loop optical voltage sensors[J].Optics & Laser Technology, 2013, 47(2013): 214–220. |
| [11] | 潘雄, 张春生, 王夏霄, 等. 反馈延迟对光纤陀螺振动误差特性的影响[J].红外与激光工程, 2014, 43(8): 2607–2612. PAN X, ZHANG C S, WANG X X, et al. Impact on vibration error characteristics of FOG with feedback delay[J].Infrared and Laser Engineering, 2014, 43(8): 2607–2612.(in Chinese) |
| [12] | BIELAS M S.Stochastic and dynamic modeling of fiber gyros[C]//Fiber Optic and Laser Sensors Ⅻ.Bellingham, WA:SPIE, 1994, 2292:240-254. |
| [13] | ZHANG Y G, GAO Z X, WANG G C, et al.Modeling and simulation of the second feedback loop for fiber optic gyroscope[C]//International Symposium on Photoelectronic Detection and Imaging 2013:Fiber Optic Sensors and Optical Coherence Tomography.Bellingham, WA:SPIE, 2013, 8914:1-7. |
| [14] | 国防科学技术工业委员会. 光纤陀螺仪测试方法: GJB 2426A-2004[S]. 北京: 国防科工委军标出版发行部, 2004. National Defense Science and Technology Industry Committee.Test methods for fiber optic gyroscope:GJB 2426A-2004[S].Beijing:National Defense Science and Engineering Commission Military Standard Publishing Department, 2004(in Chinese).http://www.doc88.com/p-3899720358953.html |
| [15] | PAVLATH G A.Closed-loop fiber optic gyros[C]//Fiber Optic Gyros:20th Anniversary Conference.Bellingham, WA:SPIE, 1996, 2837:46-60. |
| [16] | 余涛, 卿立, 吴衍记. 光纤陀螺仪死区的原因分析及误差补偿[J].中国惯性技术学报, 2007, 15(3): 363–365. YU T, QING L, WU Y J. FOG deadband reason analysis and error compensation[J].Journal of Chinese Inertial Technology, 2007, 15(3): 363–365.(in Chinese) |
| [17] | CHONG K H, CHONG K T, KIM Y C. Amplitude control of phase modulation for dithered closed-loop fiber optic gyroscope[J].Journal of the Optical Society of Korea, 2012, 16(4): 401–408.DOI:10.3807/JOSK.2012.16.4.401 |
| [18] | 王巍, 付铁刚. 数字闭环光纤陀螺死区机理分析[J].中国惯性技术学报, 2007, 15(1): 105–107. WANG W, FU T G. Analysis on dead-band mechanism of digital closed-loop FOG[J].Journal of Chinese Inertial Technology, 2007, 15(1): 105–107.(in Chinese) |
