2009年,文献[2]首次提出了最优相位恒包络发射最优相位恒包络发射(POCET)技术,以恒包络复用任意路数信号且达到最高复用效率,并建议采用外罚函数法将有约束优化问题转换为无约束优化问题。文献[3]为了减小计算量,对外罚函数法的目标函数做了改进,减少了变量的个数,并建议采用三次插值法确定搜索步长,采用拟牛顿BFGS(Broyden-Fletcher-Goldfarb-Shanno’s)法确定搜索方向。外罚函数法在终止误差较大时能够收敛到局部最优解,但当罚函数的终止误差ε≤1.0×10-4或更小时,随着罚因子的增大,目标函数出现病态,迭代失败。在对相位搜索时,插值法需要计算很多函数值和梯度值,计算量大,当迭代点远离最优解时,有时收敛不到局部最优解,收敛速度较慢;采用直接求解有约束优化问题的复合形法能够消除罚因子的影响,但复合形法适用于变量少的情况[4];文献[5]采用牛顿法实现POCET恒包络调制,当选择的初始点靠近极小点时,该算法是可行的,但牛顿法存在计算量大、二阶导数矩阵可能非正定、当初始点远离最优点时收敛不到局部最优解的缺陷。
本文在已有研究的基础上,针对导航信号最优恒包络复用论证的需求,首先对目标函数进行了适当的改进,引入了增广拉格朗日函数以提高计算精度;然后采用基于Armijo准则的非精确线搜索算法确定搜索步长以减小计算量、保证收敛性[6],对于搜索方向的确定,除了已有的拟牛顿BFGS法和牛顿法之外,还探讨了最速下降法、共轭梯度法和拟牛顿法(对称秩1法)等[6-9],总结了不同算法的特点和适用情况;最后针对BDS B1频段多种信号调制备选方案、待定的信号间功率比和相位约束关系,分别运用合适的改进算法对最优相位表进行了搜索,对合成损耗进行了评估,验证了算法的效果。
1 POCET技术基本原理 POCET技术是一种在保证复用信号的功率和相位关系约束的前提下,通过最优化算法计算调制信号的相位角度和包络幅度,从而保证复用效率最高的相位调制(PM)技术。对于参与复用的二进制基带信号每一码片的不同组合,计算出经过优化的相位表,相位值取决于对复用信号包络值这样一个目标函数在一系列约束条件下的优化结果。信号调制的载波相位按照相位表中的相位进行传输,最后输出的信号满足恒包络要求[2]。
第n路信号在接收机端表现出的平均相关为
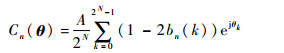 | (1) |
式中:N为参与复用的有用信号路数;bn(k)为第k种码片组合下第n路信号的码片取值;A为复用信号包络的幅度;θk为第k种码片组合情况下信号调制到载波上的相位角;相位角矢量θ=[θ0, θ1, …, θ2N-1]。
信号的功率p的约束条件表示为
 | (2) |
相位?的约束条件表示为
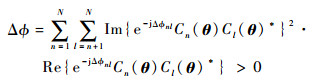 | (3) |
式中:Re{}和Im{}分别表示取实部和虚部;dn2为第n路信号的期望功率;Cl(θ)为第l路信号在接收机端表现出的平均相关;Cl(θ)*为Cl(θ)的复共轭;Δ?nl为第n路信号和第l路信号间的相位差。
N路信号恒包络复用的复用效率表示为
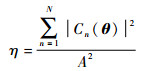 | (4) |
POCET技术在满足功率和相位约束条件下最小化包络幅度A实质是一个有约束的优化问题,可通过最优化理论的数值方法来求解。可采用罚函数方法,即利用问题的目标函数和约束函数构造新的目标函数,把约束最优化问题转化为相应的罚函数的无约束最优化问题来求解。目标函数附加的约束项反映了对落在可行域外(即不满足约束条件)的点的一种惩罚,其作用是在寻优过程中迫使迭代点靠近最优点。构造的目标函数表示为
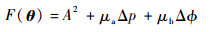 | (5) |
式中:μa、μb为罚因子。
在求解过程中一个主要的问题是搜索到的相位值可能是局部极小值,文献[2]中也给出了获得全局最优解的方法。
2 最优相位搜索的数值算法及其改进 2.1 优化目标函数的改进 在文献[2-3]中,采用外罚函数法把约束最优化问题转化为相应罚函数的无约束最优化问题来求解。文献[3]通过将目标函数中的A2改为1-η以减小计算量。通过仿真可以发现,当罚函数的终止误差ε≤1.0×10-3时,外罚函数法能够收敛到局部最优解;但当终止误差减小,如ε≤1.0×10-4或更小时,一般情况下,迭代过程中会根据优化算法后的结果不断调整罚因子,罚因子的增大会造成罚函数的二阶导数矩阵的接近奇异矩阵,目标函数出现病态,造成迭代失败,无法得到结果。为了克服这一缺陷,本文对目标函数进行了适当的改进,引入了增广拉格朗日函数[7-9]:
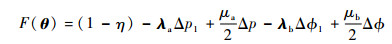 | (6) |
式中:
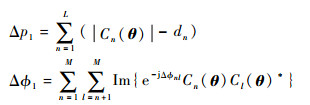 |
λa、λb为乘子向量;L、M对应功率约束条件和相位约束条件的个数。
2.2 搜索步长的确定 文献[3]对调制信号的相位进行数值搜索时,计算搜索步长采用的线搜索算法是精确线搜索算法中的三次插值法[8],在搜索区间中不断地使用三次多项式去近似目标函数,并逐步用插值多项式的极小点去逼近目标函数的极小点。在求解过程中,特别当复用路数多的情况下,等式约束条件数量较多,导致目标函数变量个数较多,式子复杂,需要计算大量的函数值和梯度值,并且当迭代点远离最优解时,有时收敛不到局部最优解,效率很低。对于调制信号的相位搜索,若采用非精确线搜索算法确定搜索步长,则不需要确定包含最佳步长的单谷区间,计算量小,且能够保证收敛[6]。
本文的搜索步长算法采用基于Armijo准则的非精确线搜索算法,Armijo准则是线搜索算法的停止条件,通过不断地更新搜索步长,使目标函数得到可接受的下降量又能使最终形成的迭代序列收敛到最优解[6]。
在Armijo准则中,对于给定参数初始值β∈(0, 1),σ∈(0, 0.5),令搜索步长αk=βmk,其中mk是满足不等式(7) 的最小非负整数。
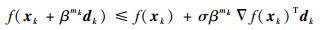 | (7) |
式中:k为迭代步数;dk为xk处的搜索方向;?f(xk)为f(xk)的导数。
通过仿真验证发现,在搜索最优相位问题中,只要搜索方向选择恰当,目标函数沿着搜索方向不一定要达到极小值,只要在每次迭代过程中,目标函数得到可接受的下降量,对求取结果影响不大。改进后的算法减少了计算量,改善了当迭代点远离最优解收敛不到局部极小值的情况。
2.3 搜索方向的确定 已有文献中对搜索方向的论述较简单,采用了拟牛顿BFGS法[3]和牛顿法[5],牛顿法收敛速度快,但该算法需要计算二阶导数矩阵及其逆矩阵,计算量大,并且存在二阶导数矩阵可能非正定、当初始点远离最优点时收敛不到局部最优解的缺陷,并不适用于求解所有的最优相位问题。
当复用路数为N时,目标函数中待求的相位数最少为2N-1-1个,未知量个数很多,不宜采用模式搜索法、单纯形搜索法等直接求解无约束问题的方法,虽然这些方法不需要计算导数,但对于变量多的情况,编写程序复杂,实现困难[9]。其他的无约束优化方法有牛顿法、最速下降法、共轭梯度法、拟牛顿法和信赖域法[9-10]。其中信赖域法需要计算二阶导数矩阵,复用路数较多时,计算量和存储量很大。为了减少算法复杂度,找到搜索相位最优的算法,本文重点探讨了最速下降法、共轭梯度法、拟牛顿法(BFGS法和对称秩1法),表 1列出了上述优化算法的搜索方向、优缺点及其适用性。
表 1 优化算法对比 Table 1 Comparison of optimization algorithms
| 优化算法 | 搜索方向 | 优缺点 | 适用性 |
| 最速下降法[6] | 负梯度方向 | 结构最简单,编程容易,初始点要求不高;收敛速度慢,有时达不到最优解 | 信号路数 < 7路 |
| 共轭梯度法[8-9] | 共轭性与最速下降法相结合,搜索方向满足: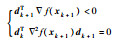 | 收敛速度快,存储量小,稳定性高,对初始点要求不高;相比最速下降法,增加了计算量 | 均适用 |
| BFGS法[8-10] | 近似矩阵的构造: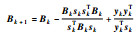 | 相比较前2种算法,收敛速度最快,搜索方向与牛顿法搜索方向近似相同,算法稳定性高,对初始点要求不高 | |
| 对称秩1法[8-10] | 近似矩阵的构造: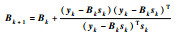 | ||
| 注:?f(xk+1)和?2f(xk+1)—xk+1处的一阶导数和二阶导数;Bk—近似矩阵;位移sk=xk+1-xk;梯度差yk=?f(xk+1)-?f(xk)。 | |||
表选项
上述算法均不需要计算二阶导数矩阵,能够改善牛顿法的缺陷。所采用的算法具有超线性收敛速度和很好的数值稳定性,保证了信号相位优化搜索算法的健壮性和高效性。
3 算法在BDS B1频点最优复用方案论证中的应用 3.1 多种调制方案组合下B1恒包络复用的最优相位数值搜索 在卫星导航系统信号体制论证过程中,各频点各信号往往有多种调制方式备选方案,各信号分量间的功率分配和相位约束关系也有待于分析确定,这些因素都会影响到信号综合性能评估的一个重要指标——复用效率η,或合成损耗10lg(1-η)。本节以BDS B1频点信号为例,说明前述算法在恒包络复用的最优相位表搜索及合成损耗评估中的应用。
中国第二代BDS分为区域系统和全球系统2个阶段逐步完成[11];BDS B1频点区域信号B1I的中心频点在1 561.098 MHz,采用BPSK(2) 调制;B1全球信号的中心频点在1 575.42 MHz,包括公开服务信号B1C和授权服务信号B1A,分别采用MBOC和BOC(14, 2) 调制[12]。目前B1C信号的数据分量调制方式为BOCs(1, 1),导频分量有TMBOC(6, 1, 4/33) 和QMBOC(6, 1, 4/33) 2种备选调制方式[13-14],而B1A信号又有数据和导频时分、数据和导频相分、单导频3种备选调制方式。仅从信号复用效率/合成损耗评估的角度来看,数据和导频时分方式与单导频方式没有差别。因此B1频段信号的恒包络复用有表 2所示的4种方案。其中B1区域信号与全球信号的中心频率相差14.322 MHz,可采用以1 575.42 MHz为中心频点的单边带调制,通过复子载波调制实现区域信号的频移。恒包络基带信号为
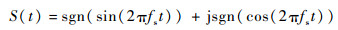 | (8) |
表 2 复用方案 Table 2 Multiplexing scheme
| 复用方案 | B1I | B1C_TMBOC | B1C_QMBOC | B1A_时分 | B1A_相分 | 路数 |
| 方案1 | √ | √ | √ | 5 | ||
| 方案2 | √ | √ | √ | 6 | ||
| 方案3 | √ | √ | √ | 6 | ||
| 方案4 | √ | √ | √ | 7 |
表选项
式中:fs为中心频点;sgn(·)为符号函数。
复子载波调制会引入损耗,即将连续的正余弦子载波转化为二电平子载波的损耗。通过傅里叶级数可以计算出实际上1 561.098 MHz处的功率大约占总功率的81.05%[3]。
要在B1I、B1C、B1A各信号分量间不同的功率比和相位约束关系下,采用POCET技术对表 1中4种复用方案的最优相位表进行数值搜索,不仅仅是消耗大量计算的问题,而且必须保证搜索的收敛性。
具体算法实现流程如下:
1) 设置初始参数,给定x0∈Rn,最大迭代次数M=1×105,λa∈Rl,λb∈Rm分别是2个等式约束条件乘子向量。罚因子μa=1.0,μb=10μa,终止误差值ε≤1.0×10-7,令k=1。
2) 以xk-1为初始点求解无约束优化问题,搜索方向dk由最速下降法、共轭梯度法、拟牛顿法(对称秩1法和BFGS法)确定。采用Armijo准则确定搜索步长,具体见式(7),搜索步长αk=βmk,mk初始值为0,若式(7) 成立,停算,反之,令mk+1=mk+1,直到找到满足式(7) 的最小非负整数。求得无约束优化问题的极小点。
3) 检验终止条件,若满足终止条件即可得到问题的极小点,否则转入下一步。
4) 更新罚因子和乘子向量。μa、μb的更新公式为:μk+1=ημk,λa、λb更新公式分别为
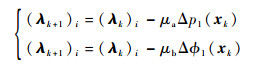 |
令k=k+1, 转第2) 步。
通过仿真分析可以验证:① 目标函数引入拉格朗日函数后,解决了当终止误差减小时矩阵接近奇异、目标函数出现病态、迭代失败的问题,计算精度可达到ε≤1.0×10-7, 且目标函数中的罚因子不需要趋于无穷大,只要求它大于某个整数即可,从而减少了迭代次数;② 采用基于Armijo准则的非精确线搜索算法确定搜索步长,减少了迭代过程中的函数值和梯度值的计算,从而使收敛速度得到提高,改善了迭代点远离最优解有时收敛不到局部最优解的缺陷,算法简单,编程容易。
对4种复用方案进行搜索时,方案1、方案2和方案3中,不同搜索方向的优化算法收敛速度差别不太大,说明当复用路数较少时,上述4种优化算法均可采用。方案4中信号路数较多,4种优化算法的结果如表 3所示。
表 3 4种优化算法的结果 Table 3 Results of four optimization algorithms
| 优化算法 | 迭代次数 | 收敛时间/min | 目标函数值 |
| BFGS法 | 211 | 1 | 0.192 |
| 对称秩1法 | 73 | 1 | 0.192 |
| 共轭梯度法 | 1160 | 5 | 0.192 |
| 最速下降法 | 40 031 | 56 | 0.192 |
表选项
从表 3看出,共轭梯度法和拟牛顿法(对称秩1法和BFGS法)收敛速度较快,拟牛顿对称秩1法的迭代次数最少,在方案4中复用信号路数N=7时,最速下降法的搜索时间很长,不宜采用,该算法适用在复用路数较少的情况。
3.2 不同功率分配下B1复用方案结果分析 上述算法可应用于实际的信号设计,论证在区域信号B1I和全球信号B1C的不同功率比条件下B1频点的最优复用方案。以下分析中假设B1A信号分量的功率占B1信号总功率的1/3,B1I与B1C信号的功率比为待定的γ;B1C信号数据/导频分量功率比为4.77 dB[13]。
当B1C_data与B1C_pilot相位同相或正交时,4种方案合成损耗与功率比的关系如图 1所示。
 |
| 图 1 相位同相和相位正交时4种方案合成损耗与功率比的关系 Fig. 1 Combining loss versus power ratio for four schemes in-phase and in quadrature-phase |
| 图选项 |
从图 1看出,4种方案的合成损耗与信号分量间功率分配和相位约束关系有关,B1C_data与B1C_pilot同相时,TMBOC调制的合成损耗略大于QMBOC调制的合成损耗。B1C_data与B1C_ pilot相位正交时,在方案1和方案2中,即参与复用的B1A只有一路信号分量时,除了在功率比1~3 dB的区间内二者合成损耗基本相同外,其他功率比条件下TMBOC调制比QMBOC调制的合成损耗大,在功率较小时差距尤为显著;在方案3和方案4中,即B1A采用数据和导频相分方式时,却是QMBOC调制比TMBOC调制的合成损耗大。可见随着复用信号路数的增加,合成损耗不一定增大,二者之间没有必然的联系。
根据最优相位表可得到恒包络复用信号的调制星座图,以方案2为例,当B1C_data和B1C_pilot相位正交时,6路信号复用得到恒包络信号的星座图如图 2所示,有64个优化相位。
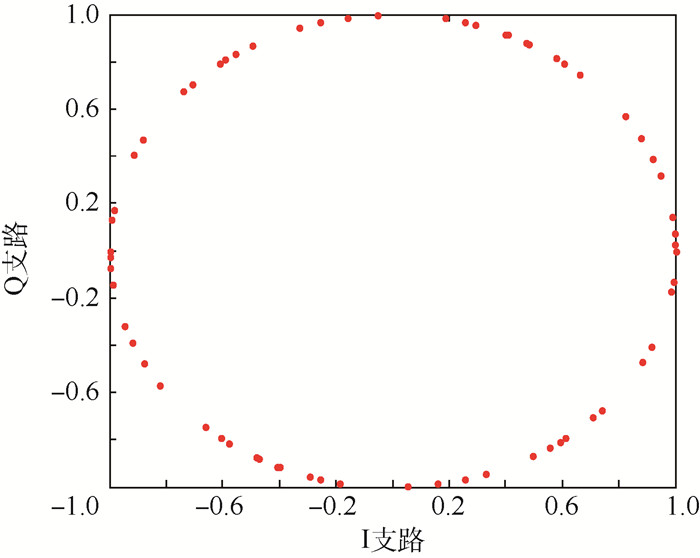 |
| 图 2 方案2复用信号的星座图 Fig. 2 Modulation constellation of multiplexed signal in scheme 2 |
| 图选项 |
利用文献[15]的计算方法可得到对应的恒包络基带信号的解析表达式为
 |
 |
式中:s1(t)、s2(t)、s3(t)、s4(t)、s5(t)、s6(t)分别为SB1I_I(t)、SB1I_Q(t)、SB1C_data(t)、SB1C_pilot11(t)、SB1C_pilot61(t)、SB1A(t)信号。
4 结论 针对已有的POCET最优相位搜索的数值算法计算量大、收敛速度慢、收敛性难以保证等问题,本文在优化目标函数、搜索步长和搜索方向3个方面进行了研究改进:
1) 在目标函数引入拉格朗日函数后,提高了计算精度,解决了当终止误差减小时,目标函数病态,无法收敛到局部最优解的问题。
2) 采用基于Armjio准则下的非精确线搜索算法确定搜索步长,减少了算法的计算量和存储量,解决了当迭代点远离最优解时插值法有时收敛不到局部最优解的问题,提高了收敛速度,程序简单易写。
3) 对于搜索方向的确定,最速下降法、共轭梯度法、拟牛顿法(BFGS法和对称秩1法)均能有效改善牛顿法的不足;其中最速下降法适用于复用路数较少的情况,算法简单;复用信号路数较多时,宜采用拟牛顿法(BFGS法、对称秩1法)或共轭梯度法,收敛速度快。
将上述算法应用于BDS B1频段多种信号调制备选方案、待定信号间功率比和相位约束关系下的最优相位搜索及合成损耗评估,验证了算法的效果,从而为导航信号调制复用体制设计优化提供参考。
参考文献
| [1] | FAN T, LIN V S, WANG G H, et al.Study of signal combining methodologies for future GPS flexible navigation payload (Part Ⅱ)[C]//Proceedings of IEEE/ION on Position, Location & Navigation Symposium.Piscataway, NJ:IEEE Press, 2008:1079-1089. |
| [2] | DAFESH P A, CAHN C R. Phase-optimized constant-envelope transmission (POCET) modulation method for GNSS signals[J].Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation, 2009, 5538(1): 2860–2866. |
| [3] | ZHANG K, ZHOU H W, W F X. Multiplexing performance assessment of POCET method for compass B1/B3 signals[J].Journal of Navigation, 2011, 64(S1): S41–S54.DOI:10.1017/S0373463311000427 |
| [4] | CAI M, XIE J, WANG G.Application study of a phase-optimized constant-envelope transmission(POCET) optimization algorithm for BDS B1 signal[C]//2015 Proceedings of China Satellite Navigation Conference (CSNC):Volume Ⅱ.Berlin:Springer, 2015:491-493. |
| [5] | LIU Y, LI C Z, NIU H F. Research and implementation of POCET constant envelope modulation technique[J].Radio Communications Technology, 2013, 39(5): 85–88. |
| [6] | 马昌凤. 最优化方法及其Matlab程序设计[M].北京: 科学出版社, 2010: 32-55. MA C F. Optimization method and Matlab program design[M].Beijing: Science Press, 2010: 32-55.(in Chinese) |
| [7] | BERTSEKAS D P. Constrained optimization and Lagrange multiplier methods[M].New York: Academic Press, 1982: 280. |
| [8] | 王宜举. 非线性最优化理论与方法[M].北京: 科学出版社, 2012: 30-75. WANG Y J. Nonlinear optimization theory and method[M].Beijing: Science Press, 2012: 30-75.(in Chinese) |
| [9] | 陈宝林. 最优化理论与算法[M].北京: 清华大学出版社, 1989: 300-350. CHEN B L. Optimization theory and algorithm[M].Beijing: Tsinghua University Press, 1989: 300-350.(in Chinese) |
| [10] | NOCEDAL J, WRIGHT S J.Numerical optimization second edition[EB/OL].New York:Springer Science+Business Media, 1999(2012-09-12)[2016-08-02].http://www.doc88.com/p-3837775884985.html. |
| [11] | 谢钢. 全球导航卫星系统原理[M].北京: 电子工业出版社, 2013: 40-43. XIE G. Principles of global navigation satellite system[M].Beijing: Publishing House of Electronics Industry, 2013: 40-43.(in Chinese) |
| [12] | TAN S S, ZHOU B, GUO S T, et al. Studies of compass navigation signals design[J].Scientia Sinica, 2010, 40(5): 514–519. |
| [13] | LU M Q, SHEN J.Optimized modulation and multiplexing for COMPASS B1C signal[C]//Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2012).Piscataway, NJ:IEEE Press, 2012:1876-1904. |
| [14] | YAO Z, LU M, FENG Z M. Quadrature multiplexed BOC modulation for interoperable GNSS signals[J].Electronics Letters, 2010, 46(17): 1234–1236.DOI:10.1049/el.2010.1693 |
| [15] | ZHANG K, LI Y, ZHOU H, et al.Analytical transmission model of POCET technique for compass B1 and B3 signals[C]//Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation.Piscataway, NJ:IEEE Press, 2012:277-285. |
