传统的光纤F-P传感器的解调方法有强度解调法[7-9]和相位解调法[10-12]。传统的强度解调法,可以实现高速解调,但F-P传感器的腔长变化限定在±λ/8(λ为波长)以内,测量范围十分有限,且解调精度低。传统相位解调法,采用宽谱光源,测量范围大,解调精度高,但解调速度慢,不适合高速测量,不能满足对发动机等监测的高速要求。1999年,Schmidt等设计三波长数字相位解调法[13-14](以下简称三波长法),用宽谱光通过耦合器入射至F-P腔,再经滤波器分为3个光波进行探测。该解调方法是基于强度解调的原理而设计的,在保持传统强度解调法解调速度快的同时,利用相位实时补偿的方式扩大了F-P腔长的动态测量范围,而且通过引入三路光强,减小了光源波动与光纤传输损耗等对输出结果的影响,从而使得解调精度也有所提高。而基于相位解调原理设计的解调方法中的三波长相位解调法[15],通过已知三波长对应的初始相位信息和经过光谱仪获取的经过传感后的三波长的相位信息进行解调,该解调方法能够实现大动态范围的精准测量,而且能够解决环境干扰导致的随机漂移和电路引入的直流漂移的影响,但是其解调速度慢,不能满足对发动机高速监测的要求。在目前的研究中,尚未见对基于强度解调原理设计的三波长法解调的误差及影响因素的分析报道。本文在详细推导三波长法解调原理的基础上,分析了三波长法理论误差,对三波长法的解调影响因素进行了详细的说明。
1 解调原理 三波长法是在双波长正交解调法(以下简称双波长法)的基础上发展和改进而来的[16]。双波长法[17]利用双光源的相位差与对应光强的关系进行腔长的解调。双波长法采用的实验设置和产生正交信号的方式如图 1所示[17]。宽谱光源(BBS)经F-P腔加载信号反射后,分别由环形器两端光纤布拉格光栅(FBG)选频,反射得到两束窄带光,两束光的相位差等于π/2的奇数倍,利用两束光的正交相位关系,对腔长进行解调。图中:C为耦合器;D为探测器。
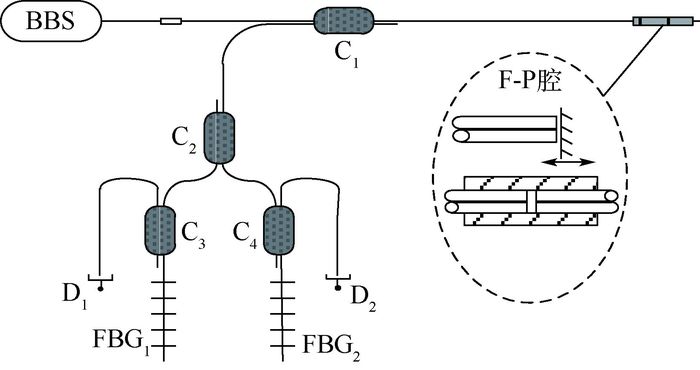 |
| 图 1 双波长正交法原理图[17] Fig. 1 Schematic of two-wavelength orthogonal method[17] |
| 图选项 |
采用低细度的F-P腔,由F-P腔的理论可知,在低细度的情况下,反射光强信号可近似看成双光束干涉形成的,这样更有利于构造出正交关系。2个相位正交光源的反射光强可以表示为
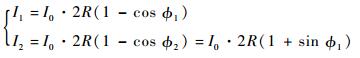 | (1) |
式中:I1和I2分别为第1、2束窄带光光强;R为光纤反射率;?1和?2分别为第1、2束窄带光相位。
将式(1) 中两式变形相除得到
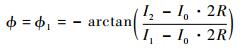 | (2) |
式中:I0为初始光强。
通过相位与腔长的关系可以得到腔长改变量
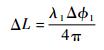 | (3) |
式中:λ1为第1束光的光波长; Δ?1为第1束光波的相位差。
三波长法借鉴双波长法的解调理论,增加一路光强信号,通过整理和变换,构造出类似双波长法中的正切关系,进而求取腔长的变化值。
三波长数字相位解调系统的结构如图 2所示,由超发光二极管(Super-Luminescent Diodes, SLD)光源、环形器、光纤F-P传感器、耦合器、解调模块和数据处理模块组成。同样,三波长法采用的也是低细度的光纤F-P腔,考虑到光源的有限光谱宽度会影响干涉条纹的可见度,设光源符合高斯光谱分布,中心波长为λi,得到三路光波的输出信号为
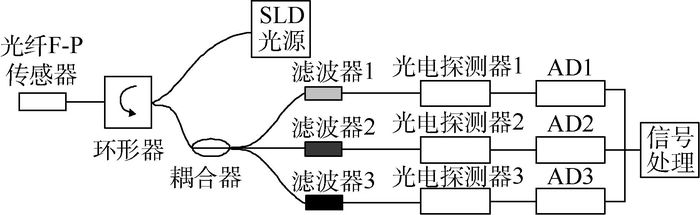 |
| 图 2 三波长数字相位解调系统结构简图 Fig. 2 Simplified structure of three-wavelength digital phase demodulation system |
| 图选项 |
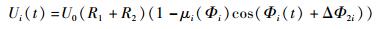 | (4) |
式中:Ui为第i束光强;U0为初始光强;μi(Φi)为条纹对比度, Φi为第i束光相位;R1和R2为光纤端面的反射率;ΔΦ2i为第2束和第i束光的相位差。通过调节滤波器(格林透镜)选择合适的波长,选取的波长需满足正交关系:
 | (5) |
利用式(5),将得到的三路输出信号的表达式进行整理:
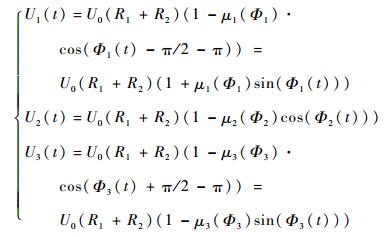 | (6) |
对式(6) 三路信号进行整理合并,以构造出类似于式(1) 的关系:
 | (7) |
当光源带宽较窄时,条纹对比度差异较小,可认为近似相等,即μ1(Φ1)≈μ2(Φ2)≈μ3(Φ3)。又腔长变化量相比较与腔长很小(约为腔长的1/50),所以可认为相位一直满足正交条件,则相位变化近似相等,即Φ1(t)≈Φ3(t)≈Φ2(t),则有sin(Φ1(t))≈sin(Φ3(t))≈sin(Φ2(t)),则式(7) 可简化为
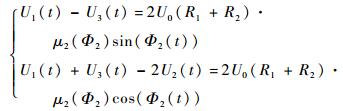 | (8) |
式(8) 中两等式相除,则可得出中间波长的相位公式:
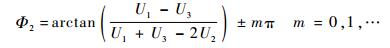 | (9) |
由式(9) 和式(2) 对比,可以看出:双波长法相位公式中,I0为已知量不受附加偏置的影响,项数的相减和除法不能消除附加偏置带来的误差与线性误差的影响;三波长法相位公式中所有量均为测量值,相同项数的减法消除了附加偏置带来的误差,而除法消除了线性误差的影响。因此相较于双波长法,三波长法的解调更加精准,测量环境要求更低,也更易于实现。
如图 3所示,通过对相位值正负进行连续监测的方式可实现腔长解调范围的扩展:在相位跳变处通过加减mπ实现相位的补偿(因arctan Φ取值范围是-π/2~π/2)。通过以上的推导,计算相位前后的变化差值ΔΦ,再根据相位与腔长的关系计算就可以得到腔长变化量ΔL的值:
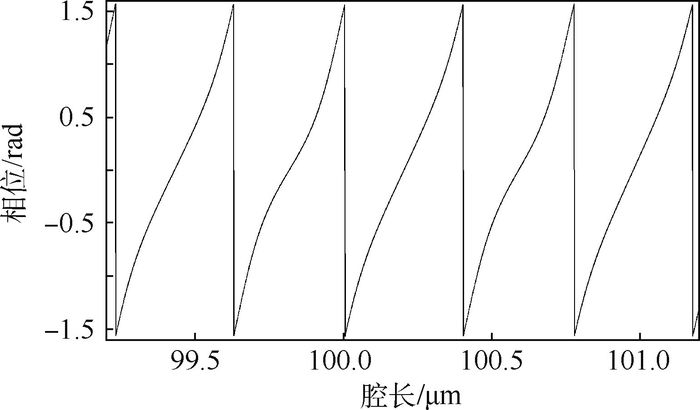 |
| 图 3 相位变化与腔长关系 Fig. 3 Relationship between phase variation and cavity length |
| 图选项 |
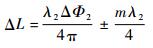 | (10) |
2 解调影响因素分析 三波长数字相位解调的实质是强度解调,三路光波的光强将直接影响着解调的精度。在三波长法的解调理论中存在着对低细度、条纹对比度和相位变化等的近似处理,其处理结果直接影响着光强,是其解调原理的理论误差来源,即三波长法解调的影响因素。三波长法解调的影响因素,不仅决定着解调方法的理论精度,更影响着三波长法的应用。因此,研究三波长法的影响因素是非常重要的。
2.1 低细度近似影响 EFPI光纤传感器是基于光学中F-P干涉仪的原理。图 4为F-P干涉仪的原理示意图。
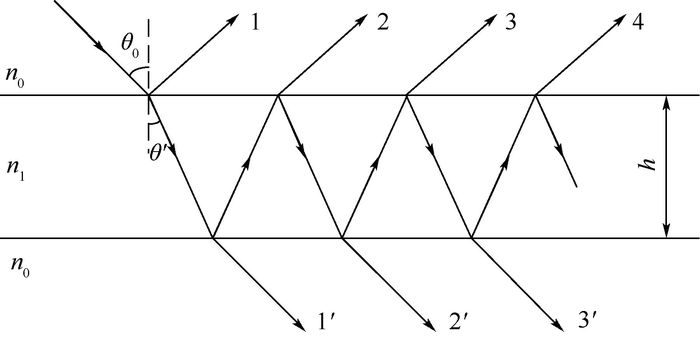 |
| 图 4 F-P干涉仪的原理 Fig. 4 Principle of F-P interferometer |
| 图选项 |
平行的反射光束之间相互叠加干涉,不考虑光束在光学平面间传输损耗的情况下,反射光强可以表示为
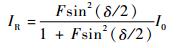 | (11) |
式中:δ为两信号的相位差;F为F-P干涉仪的细度,定义为F=4R/(1-R)2,在低细度的EFPI光纤传感器中平整光纤端面的石英玻璃与空气界面上,可以认为反射率R?1,在此情况下有
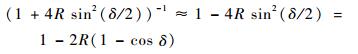 |
因此
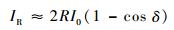 | (12) |
在三波长法的解调理论中,反射光强表达式认为是在低细度情况下的近似双光束干涉的结果。但实际光强是多光束的干涉。当F-P腔光纤端面的反射率R≈0.04时,反射光强的实际值(由式(11) 计算得出)与理论值(由式(12) 计算得出)的对比关系如图 5所示。两者随腔长的变化趋势是一致的,变化周期基本相同,在光强变化的波谷处由于光强很弱,两者的差异很小;但在光强的波峰附近两者的差异显著,在波峰处的光强误差大于8%。
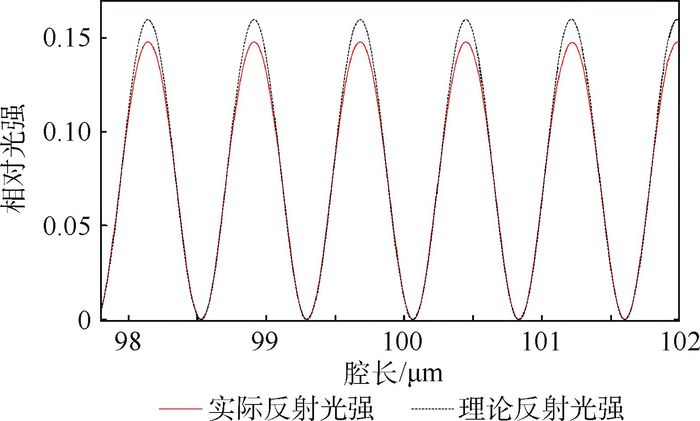 |
| 图 5 实际与理论反射光强对比 Fig. 5 Comparison between actual reflected light intensity and theoretical reflected light intensity |
| 图选项 |
利用式(11) 和式(12) 计算得出的实际光强和理论光强,通过式(9) 可得出实际相位解调值和理论相位解调值。图 6为实际相位解调值和理论相位解调值的对比关系图。在相位连续变化区间,实际和理论的相位解调值基本一致;但在相位跳变处,实际和理论的相位解调值误差较大,跳变位置有着明显的偏移。理论的相位解调值的变化周期与实际的变化周期不一致,两者的误差达到14 nm。
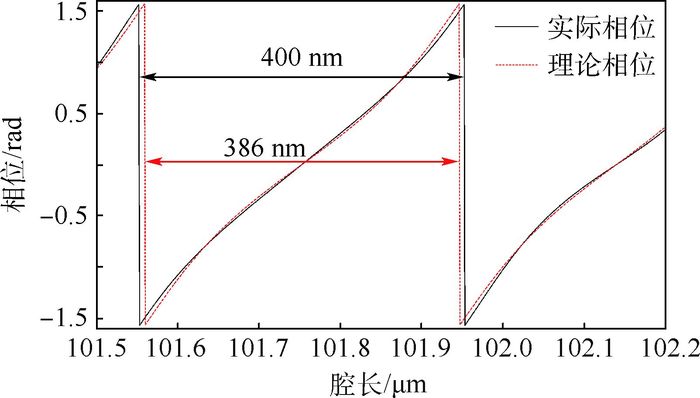 |
| 图 6 实际与理论解调相位的对比 Fig. 6 Comparison between actual demodulated phase and theoretical demodulated phase |
| 图选项 |
通过实际反射光强和理论反射光强解调出腔长变化量并计算其解调误差如图 7所示,误差在腔长变化区间内不大于3.56 nm,其大小与腔长变化无相关关系。
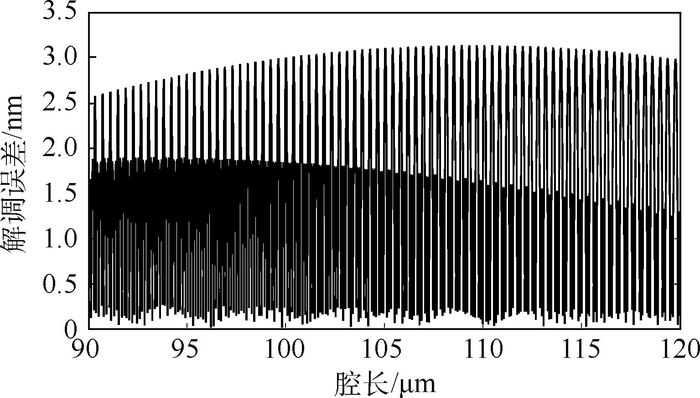 |
| 图 7 双光束近似引起的解调误差 Fig. 7 Demodulation error caused by approximation of two beam interference |
| 图选项 |
2.2 对比度近似影响 条纹对比度表征了干涉场中某处条纹亮暗反差的程度[18],其定义为
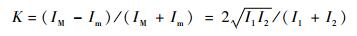 | (13) |
式中:IM和Im分别为干涉场中参考位置附近的最大光强和最小光强。由此双光束干涉强度分布公式可表示为
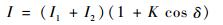 | (14) |
由式(14) 可知,干涉光强的调制度即是条纹的对比度。影响干涉条纹对比度的主要因素是两相干光束的振幅比、光源大小和光源的非单色性。
在三波长法中,干涉条纹对比度主要受到相干光束的振幅比和光源的非单色性的影响。光源的初始光强相同,所以影响光束振幅的因素是F-P腔两反射面的反射率;光源的非单色性则是考虑光源的有限光谱宽度的影响,设光源符合高斯光谱分布。则得条纹对比度表达式:
 | (15) |
光源的相干长度对条纹对比度有重要的影响。采用宽谱光源,相干长度较小,条纹对比度较小;实际应用中,通常采用3个独立的激光光源代替宽谱光源,激光光源相干长度大,条纹对比度可以接近于1。条纹对比度随着腔长变化的关系如图 8所示。
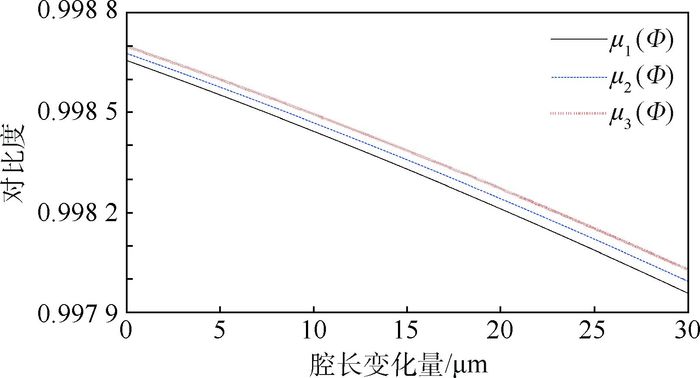 |
| 图 8 对比度随腔长变化量的关系 Fig. 8 Variation of fringe visibility factors with cavity length |
| 图选项 |
从图 8中可知,条纹对比度随着腔长变化量的增大而减小,且不同波长对应的条纹对比度之间的差异随着腔长变化量的增大而呈现增大的趋势。但是在腔长变化30 μm范围内,对比度的变化不超过0.001,变化十分微小。忽略条纹对比度的差异而引起的解调误差如图 9所示。
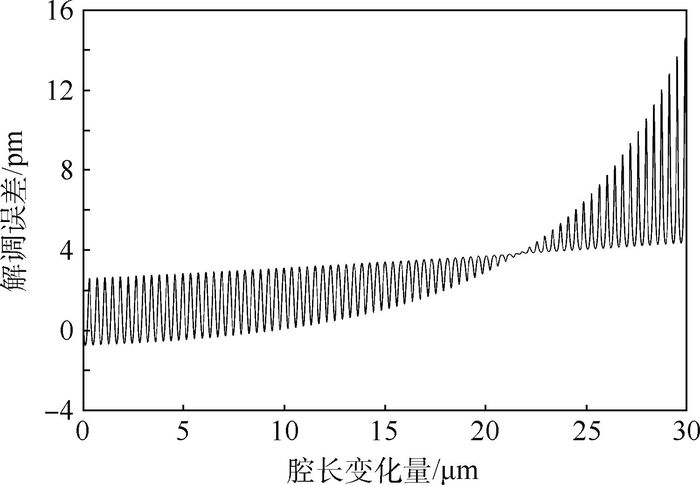 |
| 图 9 忽略对比度差异引起的解调误差 Fig. 9 Demodulation error caused by ignoring differences of fringe visibility factors |
| 图选项 |
从图 9中可知,随着腔长变化量的增加,误差呈现增大的趋势,但误差量级很小,在腔长变化25 μm范围内,解调误差不超过16 pm,对解调不会产生明显的影响,可以忽略不计。
2.3 相位变化影响 在三波长法中,要求相位满足彼此正交关系,即满足ΔΦ12=ΔΦ23=(2n+1)π/2。因此相位需满足:
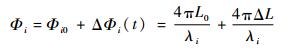 | (16) |
式中:L0为初始腔长;λi为第i光路的光波长值。
两信号间的初始相位差是由波长不同引起的λi, λj=λi+Δλ(Δλ为波长差),初始相位差为
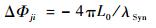 | (17) |
式中:λSyn为综合波长,λSyn=λiλj/Δλ,由正交关系条件ΔΦji=(2N+1)π/2(N=0, 1,…)可知反射路径,即正交腔长为
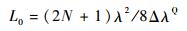 | (18) |
式中:ΔλQ为波长差的平均值。
相位的正交条件与腔长的关系如图 10所示。当腔长在正交腔长L0附近变化时,相位变化较小,可认为相位满足正交关系;但当腔长不在正交腔长附近时,相位变化大,相位已经不满足正交关系。
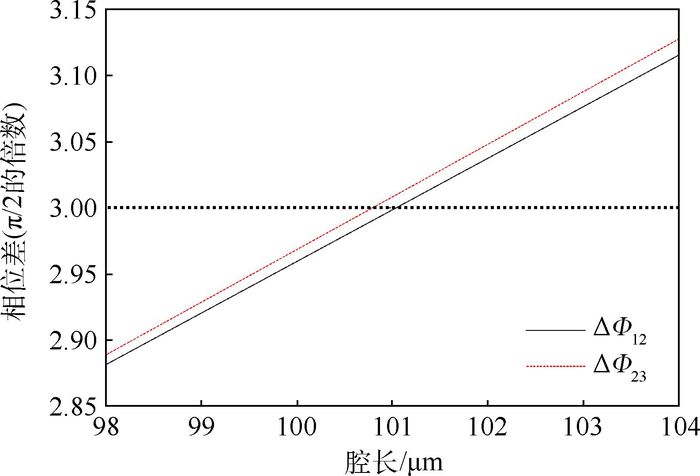 |
| 图 10 相位的正交关系 Fig. 10 Orthogonal relationship of phase |
| 图选项 |
从图 10中可以看出,在正交腔长(L0=100.8 μm)附近,相位变化较小,相位差ΔΦ12和ΔΦ23是π/2的3倍关系,认为满足正交关系;当腔长偏离正交腔长时,相位变化大,相位差不满足π/2的3倍关系,即已不满足正交关系。腔长不在正交腔长附近,由式(9) 和式(16) 分别获得的中间相位的解调值和真实值之间的对比如图 11所示。
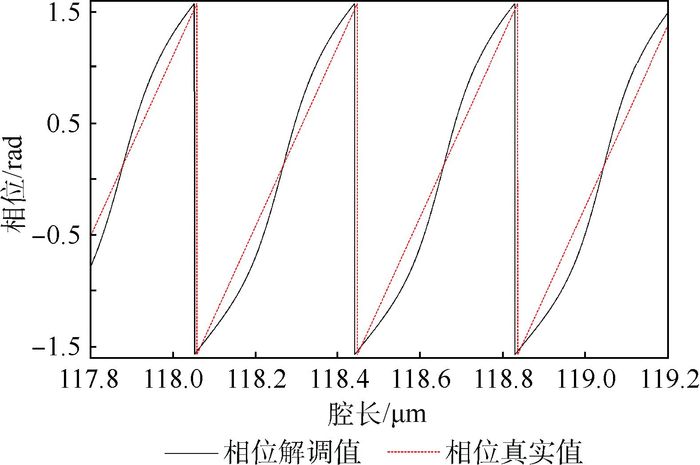 |
| 图 11 偏离相位正交关系 Fig. 11 Deviation from orthogonal relationship of phase |
| 图选项 |
从图 11可以看出,解调值与真实值的变化周期相同,但是在腔长连续变化区间,两者有着明显的差异,说明解调已存在明显的误差。偏离相位正交关系引起的解调误差如图 12所示。
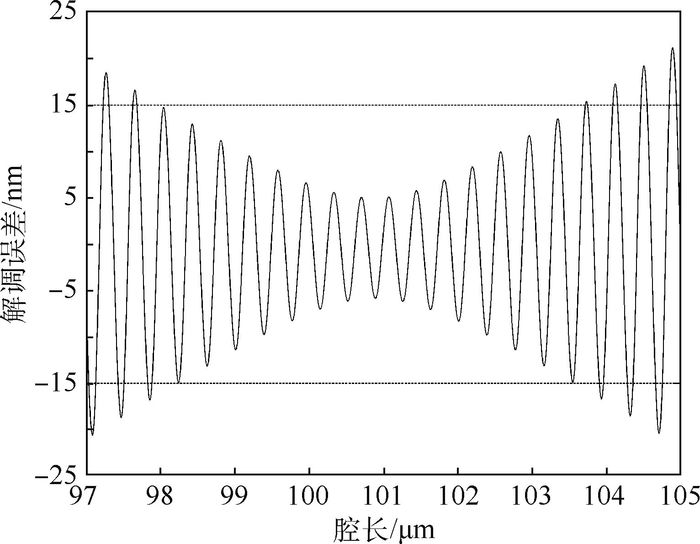 |
| 图 12 偏离相位正交关系引起的解调误差 Fig. 12 Demodulation error caused by deviation from orthogonal relationship of phase |
| 图选项 |
从图 12可以看出,F-P腔长与解调误差的关系中,在偏离正交腔长2 μm的变化范围内,解调误差小于15 nm;当腔长变化超过2 μm时,解调误差会迅速增大,很快会超过20 nm。相位偏离正交关系,即腔长偏离正交腔长会引起解调误差的增大,且误差会随着偏离的增大而迅速的增大。随着腔长偏离正交腔长,三波长法的解调误差增大,精度降低。
3 实验 理论解调系统,通过SLD光源获得宽谱光源,再经滤波器获得满足正交关系的三路光波信号,三路信号包含了传导光路中的所有信息;为了简化解调系统,将SLD光源和滤波器替换成满足正交关系的3个DFB激光器的激光信号,在保障激光器初始光强相等的情况下,三路信号包含了传导光路中的所有信息,保障了解调系统的精度和灵敏度。
通过设计静态解调实验和瞬间释压实验以验证解调系统在正交腔长附近的解调能力和解调稳定性。实验中,利用精度为1 nm的光纤F-P解调仪SM125标定静态腔长,并与解调腔长进行对比。
3.1 静态解调实验 采用油压装置给F-P腔施压,对分别处在2、4、6、8和10 MPa压力下的静态腔长进行解调,并与利用SM125在对应压强下的标定值进行对比,其结果如表 1所示。
表 1 标定腔长与解调腔长对比 Table 1 Comparison between calibration cavity length and demodulation cavity length
| 压力/MPa | 标定腔长/μm | 解调腔长/μm | 误差/nm |
| 2 | 100.614 | 100.622 | 8 |
| 4 | 100.418 | 100.429 | 11 |
| 6 | 100.231 | 100.243 | 12 |
| 8 | 100.043 | 100.052 | 9 |
| 10 | 99.859 | 99.865 | 6 |
表选项
从表 1数据可以看出:在不同的压力作用下,腔长的变化量接近1 μm,且在1 μm的变化范围内,解调腔长均值与标定腔长值能够很好地吻合,解调的最大误差小于12 nm,满足解调误差小于15 nm。从图 13标定、解调与仿真的对比图中可以看出,解调值与仿真结果基本相符,且解调值和标定值均呈现线性关系。
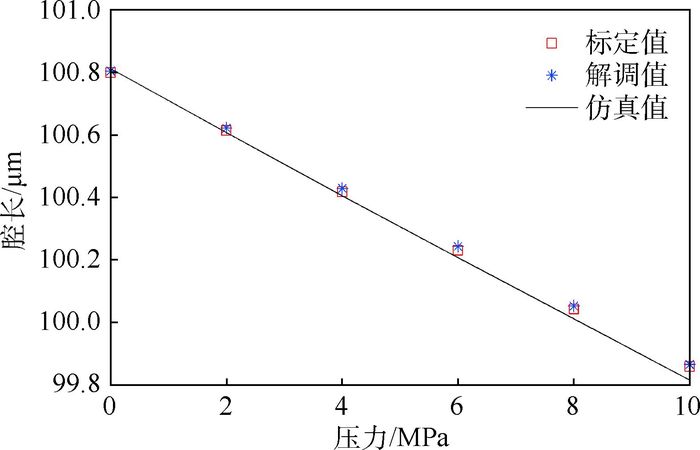 |
| 图 13 标定、解调与仿真对比关系图 Fig. 13 Comparison of calibration, demodulation and simulation |
| 图选项 |
3.2 瞬间释压实验 在不同的初始压力下,瞬间释放压强至无压状态,通过解调稳定后的腔长与标定的初始腔长(100.800 μm)进行对比,判断解调的稳定性。
在初始压力分别为2、4、6、8和10 MPa情况下,F-P腔瞬间释放至无压状态,腔长很快恢复到加压前的初始状态。解调稳定后的腔长均值,并与标定的初始腔长进行对比,得到的误差如表 2所示。
表 2 解调的重复性误差 Table 2 Repeatability error of demodulation value
| 初始压力/MPa | 解调均值/μm | 误差/nm |
| 2 | 100.800 | 0 |
| 4 | 100.794 | 6 |
| 6 | 100.809 | 9 |
| 8 | 100.791 | 9 |
| 10 | 100.799 | 1 |
表选项
从表 2数据可以看出:在不同压力下瞬间释压后,腔长均恢复至初始值,解调均值与标定值的最大误差小于10 nm,即重复性误差小于10 nm,说明解调系统具有很好的稳定性。
4 结论 本文详细推导了针对EFPI解调的三波长数字相位解调法的解调原理。仿真分析了三波长法中低细度、条纹对比度近似和相位变化对解调方法的限制影响,并对解调方法的解调能力和解调稳定性进行了实验验证。仿真和实验结果表明:
1) 仿真分析表明低细度、条纹对比度近似和相位变化都会引起解调误差。低细度下双光束干涉近似引起的解调误差与F-P腔长无关,在腔长变化范围内误差小于3.56 nm;条纹对比度近似引起的解调误差随腔长变化的增大而增大,但误差量级为pm级,可以忽略不计;相位变化引起相位偏离正交条件是限制三波长法应用的最主要因素,当腔长变化大于正交腔长2 μm变化范围时,解调误差将大于20 nm,解调精度大大降低。
2) 静态解调实验表明在正交腔长附近1 μm变化范围内,解调误差小于12 nm,与仿真结果相符,满足误差小于15 nm。瞬间释压实验表明解调的重复性误差小于10 nm,解调稳定性良好。
本文对三波长法的解调影响因素进行了详细的分析,为三波长法应用提供了有效参考,并为三波长法的优化提供了重要依据。
参考文献
| [1] | SEN M B, BHATIA V, MURPHY K A.Recent advances in the fiber extrinsic Fabry-Perot interferometric strain sensor development[C]//Lasers and Electro-Optics Society Meeting, 1994.Piscataway, NJ:IEEE Press, 1994, 2:253-254. |
| [2] | 张磊, 于清旭. 光纤F-P腔与FBG复用传感器精确解调方法研究[J].光电子·激光, 2009, 20(8): 1008–1011. ZHANG L, YU Q X. An improved demodulation method for F-P and FBG multiplexing system[J].Journal of Optoelectronics Laser, 2009, 20(8): 1008–1011.(in Chinese) |
| [3] | 李春成, 王鸣, 夏巍, 等. 基于F-P腔强度解调的微位移传感器[J].光学学报, 2014, 34(6): 0628001. LI C C, WANG M, XIA W, et al. A novel Fabry-Perot micro-displacement sensor based on intensity demodulation method[J].Acta Optica Sinica, 2014, 34(6): 0628001.(in Chinese) |
| [4] | GANDER M J, MACPHERSON W N, BARTON J S, et al. Embedded micromachined fiber-optic Fabry-Perot pressure sensors in aerodynamics applications[J].IEEE Sensors Journal, 2003, 3(1): 102–107.DOI:10.1109/JSEN.2003.810099 |
| [5] | 李坤, 文泓桥, 李慧. 光纤法布里-珀罗结构的微型应变传感器的研制[J].光学学报, 2009, 9(12): 3282–3285. LI K, WEN H Q, LI H. A study on miniature interferometer strain sensor based on EFPI[J].Acta Optica Sinica, 2009, 9(12): 3282–3285.(in Chinese) |
| [6] | SHAN N, SHI Y K, LIU X. Detecting crack of aircraft engine blade based on optical fiber F-P sensor[J].Nodestructive Testing, 2009, 31(3): 206–207. |
| [7] | BHATIA V, MURPHY A, CLAUS R O, et al. Recent developments in optical-fiber-based extrinsic Fabry-Perot interferometric strain sensing technology[J].Smart Materials and Structures, 1995, 24(4): 246–251. |
| [8] | YU Q X, ZHOU X L. Pressure sensor based on the fiber-optic extrinsic Fabry-Perot interferometer[J].Photonic Sensors, 2011, 1(1): 72–83.DOI:10.1007/s13320-010-0017-9 |
| [9] | MA C, DONG B, GONG J, et al. Decoding the spectra of low-finesse extrinsic optical fiber Fabry-Perot interferometers[J].Optics Express, 2011, 19(24): 23723–23742. |
| [10] | MACPHERSON W N, KIDD S R, BARTON J S, et al. Phase demodulation in optical fiber Fabry-Perot sensors with inexact phase steps[J].IEEE Proc-Optoelectron, 1997, 144(3): 130–133.DOI:10.1049/ip-opt:19971092 |
| [11] | JIANG Y. Fourier transform white-light interferometry for the measurement of fiber-optic extrinsic Fabry-Perot interferometric sensors[J].IEEE Photonics Technology Letters, 2008, 20(2): 75–77.DOI:10.1109/LPT.2007.912567 |
| [12] | ZHANG X M, LIU Y, BAE H, et al. Phase demodulation with micromachined resonant mirrors for low-coherence fiber-tip pressure sensors[J].Optics Express, 2009, 17(26): 23965–23974.DOI:10.1364/OE.17.023965 |
| [13] | SCHMIDT M, FURSTENAU N. Fiber-optic extrinsic Fabry-Perot interferometer sensors with three-wavelength digital phase demodulation[J].Optics Letters, 1999, 24(9): 599–601.DOI:10.1364/OL.24.000599 |
| [14] | SCHMIDT M, WERTHER B, FURSTENAU N. Fiber-optic extrinsic Fabry-Perot interferometer strain sensors with < 50pm displacement resolution using three-wavelength digital phase demodulation[J].Optics Express, 2001, 8(8): 475–480.DOI:10.1364/OE.8.000475 |
| [15] | 张佩. 基于光纤F-P传感器的动态解调算法的研究[D]. 武汉: 武汉理工大学, 2013. ZHANG P.Study on methods of the dynamic demodulation for optical fiber Fabry-Perort sensors[D].Wuhan:Wuhan University of Technology, 2013(in Chinese).http://d.wanfangdata.com.cn/Thesis/Y2504382 |
| [16] | SONG N F, CUI R Q, YANG Y J, et al.Fiber-optic extrinsic Fabry-Perot interferometer sensors with multi-wavelength intensity demodulation[C]//Mechanical Engineering, Materials Science and Civil Engineering Ⅱ.Zurich-Durnten:Trans Tech Publications Ltd., 2013:630-635. |
| [17] | MURPHY K, GUNTHER M, VENGSARKER A, et al. Quadrature phase-shifted extrinsic Fabry-Perot optical fiber sensors[J].Optics Letters, 1991, 16(4): 273–275.DOI:10.1364/OL.16.000273 |
| [18] | 郁道银, 谈恒英. 工程光学[M].2版北京: 机械工业出版社, 2011: 310-313. YU D Y, TAN H Y. Engineering optics[M].2nd edBeijing: China Machine Press, 2011: 310-313.(in Chinese) |
