1 计算方法 1.1 控制方程与离散方法 三维可压缩Naiver-Stokes方程可以写为
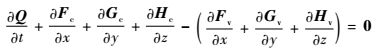 | (1) |
式中:Q为守恒变量;t为时间;x、y和z为三方向坐标;Fc、Gc和Hc为对流通量;Fv、Gv和Hv为黏性通量。当仅考虑对流通量时,方程简化为Euler方程。
方程式(1) 的半离散形式可写为
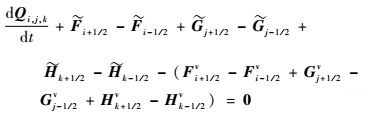 | (2) |
其中:
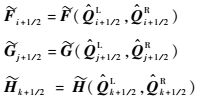 |
下标i、j、k分别代表x、y和z三方向的离散节点,i±1/2、j±1/2、k±1/2分别表示对应节点左右半节点;
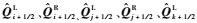
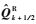
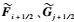
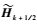
1.2 插值格式 为了表述简洁,以下对插值格式的描述均以偏左插值(即求解
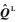
通过Taylor展开法[16],可以获得五阶显式线性迎风格式:
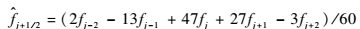 | (3) |
式中:fj为j点处某个原始变量分量的值;
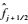
同样的,可以推导出五阶紧致迎风格式:
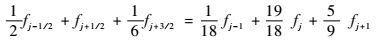 | (4) |
Lele[2]的研究表明,紧致格式具有类谱方法的优秀频谱特性。但因需要联立求解代数方程组,其计算量略大于显式线性迎风格式。
线性格式在间断附近会产生振荡,进而导致计算结果发散。五阶WENO格式采用低阶格式非线性加权的方式,光滑区域使加权结果近似于五阶显式线性迎风格式(式(3)),间断区域则减小跨间断模板的权重,从而既保证了计算的无振荡,又确保了计算精度。其具体形式详见文献[5]。
同样的,可以利用非线性权系数,以紧致迎风格式为基础,获得五阶紧致型非线性激波捕捉格式——CRWENO[10]。利用五阶紧致迎风格式的网格模板可以拆分出3个三阶迎风紧致格式,即
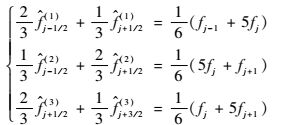 | (5) |
当权系数为C1=1/5, C2=1/2, C3=3/10(即理想权系数)时,式(5) 中3个格式即可加权成式(4)。为了使流场间断处的模板权系数降低,可以利用光滑因子βn(n=1, 2, 3)[5], 其定义为
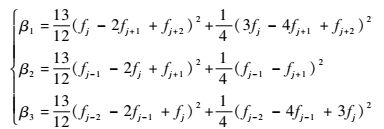 | (6) |
获得非线性权系数
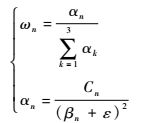 | (7) |
式中:ε为确保分母不为0的小量,本文取10-6。
这样,将式(5) 中的低阶格式与式(7) 中的非线性权系数对应相乘并相加,就能获得五阶紧致型非线性激波捕捉格式——CRWENO,即
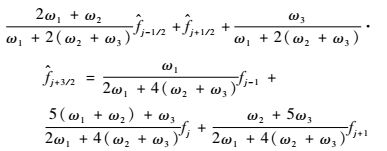 | (8) |
光滑区域非线性权系数蜕化成理想权系数Cn时,式(8) 退化成紧致迎风格式(式(4))。
当使用非周期边界条件时,为了使方程组封闭,在边界处使用五阶WENO格式。
2 数值性能分析 为表述简便,以下将五阶显式线性迎风格式、五阶紧致迎风格式、五阶WENO和五阶CRWENO分别记为UW5、compact5、WENO5和CRWENO5。
2.1 精度测试 首先检验格式是否达到预期精度并对程序进行校验,选取Euler方程精确解为
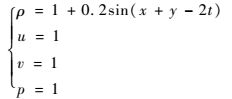 | (9) |
式中:ρ、p、u和v分别为密度、压强、x和y方向速度。计算域为[-π, π]×[-π, π],采用周期边界条件,计算网格共5组:10×10, 20×20, 40×40, 80×80以及160×160,时间步长(无量纲)Δt=(Δx)3,Δx为网格间距,无量纲时间推进至t=0.2。
此处考虑密度误差,用2-范数(L2) 误差表示。计算结果如图 1所示(h5为五阶精度的参考斜率)。图中可见,4种格式均能达到预期精度。从量值上看,2种线性格式的误差量值均比所对应的非线性格式(compact5与CRWENO5、UW5与WENO5相比)小约一个量级,紧致型格式误差量值明显小于相应显式格式(compact5与UW5、CRWENO5与WENO5相比)。CRWENO5的误差较接近UW5。结果表明,即使对于光滑流动,格式的非线性权系数也难以完全蜕化成理想权系数,因此非线性格式的数值误差绝对量值较大。格式的紧致特性则能减小数值误差,从而一定程度上弥补非线性权系数对计算精度的影响。
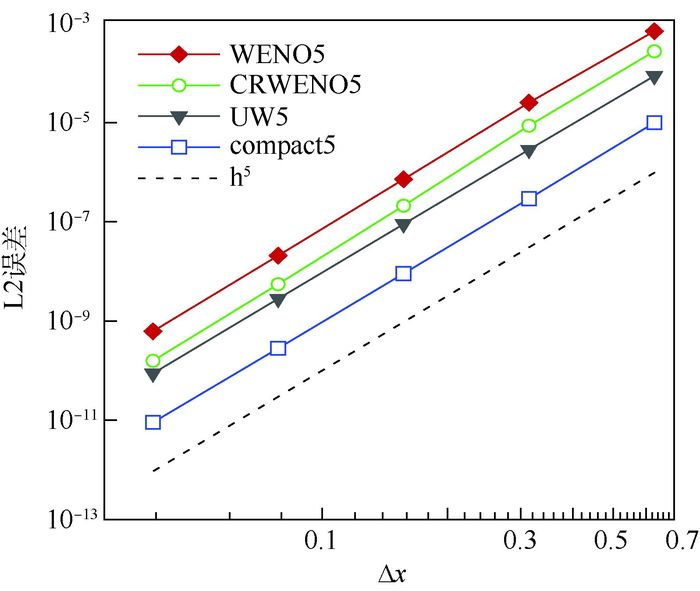 |
| 图 1 4种格式精度测试结果(密度误差) Fig. 1 Accuracy test results of four schemes (density errors) |
| 图选项 |
2.2 Fourier分析 数值精度阶数代表了网格足够密时数值格式的精度,分辨率则能体现网格分辨率有限情况下格式的精度[16]。格式分辨率可通过Fourier分析获得的修正波数反映。对于线性格式,能够获得修正波数的解析解,而对于非线性格式,修正波数只能通过数值方法近似得到。本文采用Fauconnier和Dick提出的非线性谱分析(NSA)方法[17]对4种格式的分辨率进行分析。计算结果如图 2(spectral为谱方法结果)。图中横坐标为波数w与最大波数wmax的比值,纵坐标分别为修正波数w′的实部Re(w′)、虚部lm(w′)与wmax的比值。从图 2中可以看出,非线性格式的色散和耗散误差均大于线性格式,其中compact5最优,UW5其次,CRWENO5优于WENO5。这说明非线性权系数的引入对格式的色散和耗散性能均有明显影响。此外,紧致型格式的频谱特性均优于对应的显式格式。
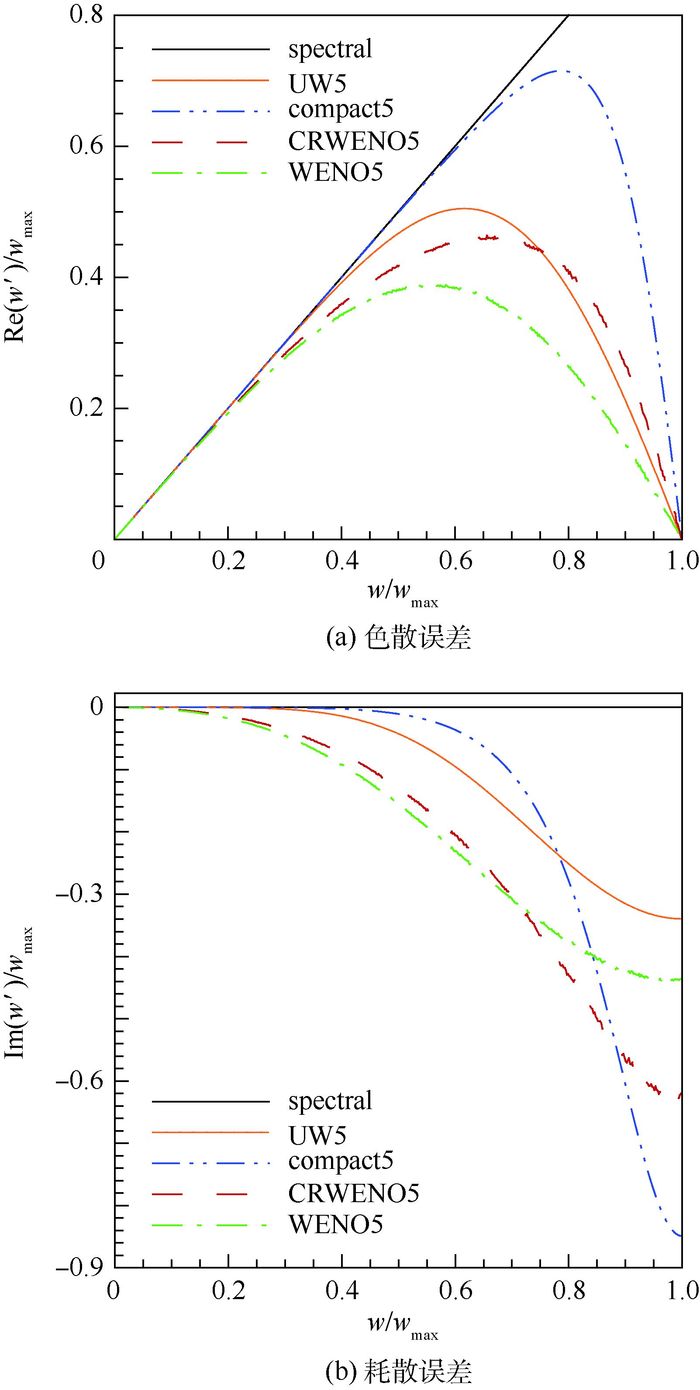 |
| 图 2 4种格式的色散和耗散误差 Fig. 2 Dispersion and dissipation errors of four schemes |
| 图选项 |
3 数值试验和结果分析 3.1 一维Sod激波管 本算例求解Euler方程。初始条件为[18]
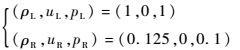 | (10) |
式中:带下标R和L的ρ、u、p分别为间断左右两边的密度(无量纲)、速度和压强。计算区域为[0, 1],网格点数100,计算截止至无量纲时间t=0.2。
图 3给出了4种格式的密度分布曲线及局部放大图(exact为精确解),可见,线性格式在所有间断处均会出现振荡,而2种非线性激波捕捉格式能保持稳定,仅在接触间断附近出现轻微过冲(见图 3中局部放大3)。此外,本算例中CRWENO5和WENO5的间断分辨能力相近。
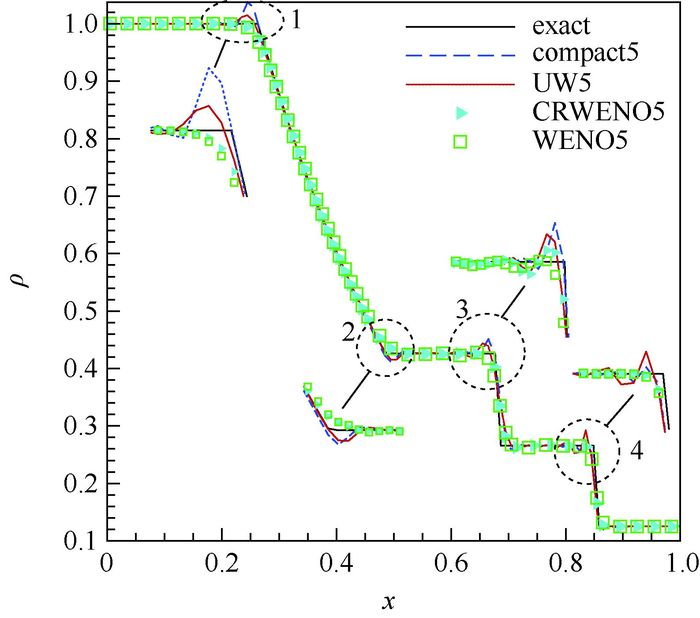 |
| 图 3 Sod激波管不同格式的密度分布曲线 Fig. 3 Density distribution curves of Sod shock tube with different schemes |
| 图选项 |
3.2 前向台阶绕流 计算模型[19]为在一洞长为3个洞宽的风洞中设一前向台阶,台阶位于距入口0.6个洞宽处,高度为洞宽的1/5。初始流场为自左面流入的马赫数为3的均匀超声速气流。风洞壁面均设为无反射边界条件,风洞入口和出口分别设入口/出口边界条件。本算例求解Euler方程,模拟的截止无量纲时间为t=4。计算网格等距划分,网格线与壁面平行或正交,网格间距为Δx=1/320(以洞宽为1)。
本算例流场具有较强的压缩性,线性格式无法保持计算的稳定性,仅采用2种激波捕捉格式进行计算,以检验CRWENO5在强压缩性流场中的计算性能。计算结果如图 4所示。
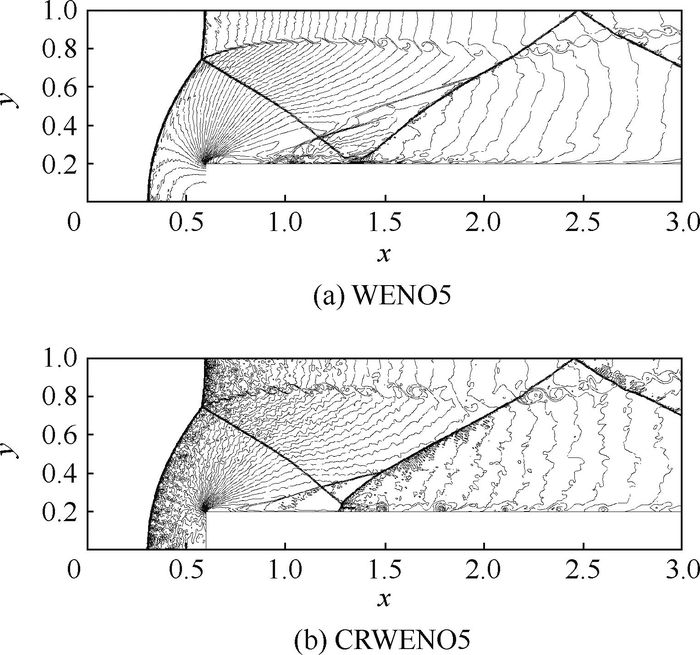 |
| 图 4 Δx=1/320时,前向台阶密度等值线图 Fig. 4 Density contours at forward facing step at Δx=1/320 |
| 图选项 |
从图 4中可以看出,CRWENO5在此算例中能够稳定、清晰地捕捉激波结构,其间断分辨能力与WENO5相当。因CRWENO5耗散相对较小,在强压缩性流场中稳定性稍逊色,具体表现为密度等值线抖动更剧烈。相对地,CRWENO5结果中的流动细节更丰富。
3.3 泰勒-格林涡 本算例模拟了流动从近似无黏到转捩再到湍流的过程[20],能够全面反映数值格式对多尺度流动结构的模拟能力。初始流场为[20]
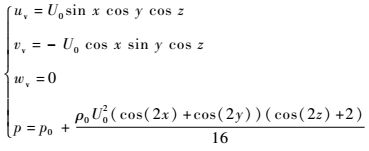 | (11) |
式中:uv、vv、wv分别为x、y、z方向速度;U0=1;p0、ρ0分别为初始时刻的压强和密度。雷诺数Re=ρ0U0L/μ,本文取1 600,L为参考长度,μ为动力黏性系数;马赫数Ma=U0/c0,本文取0.1,c0为声速,由c02=γp0/ρ0算出,γ为比热比,取1.4。模拟区域为一边长为2πL的立方体,本文取L=1,采取周期边界条件。计算网格等距划分,网格间距为Δx=2π/128。本文对2种线性格式和2种非线性格式均进行了模拟,以研究格式的非线性对纯光滑流动结构的捕捉能力。模拟截止于无量纲时间t=20。各时均量和能谱的计算方法分别参见文献[20]和文献[16]。
图 5给出了流场平均动能(K)及动能耗散率(ε1)随时间变化曲线,DRP5123为参考解[20]。图 5(a)中随着时间推移,模拟结果与参考解出现偏差。相比而言,2种线性格式,尤其是compact5与参考解最为接近。而由于流场逐渐出现尺度相差较大的流动结构,非线性权系数的作用逐渐显著,2种非线性格式的平均动能衰减较明显,尤其WENO5与参考解的偏差最大,CRWENO5因其紧致型特征耗散略小。该结果与Fourier分析的结果相近。图 5(b)中看出,WENO5的动能耗散率过早达到峰值,这是格式耗散过大、分辨率不足的表现[21],其他3种格式的曲线则更接近参考解,compact5的曲线峰值出现时间最为接近。
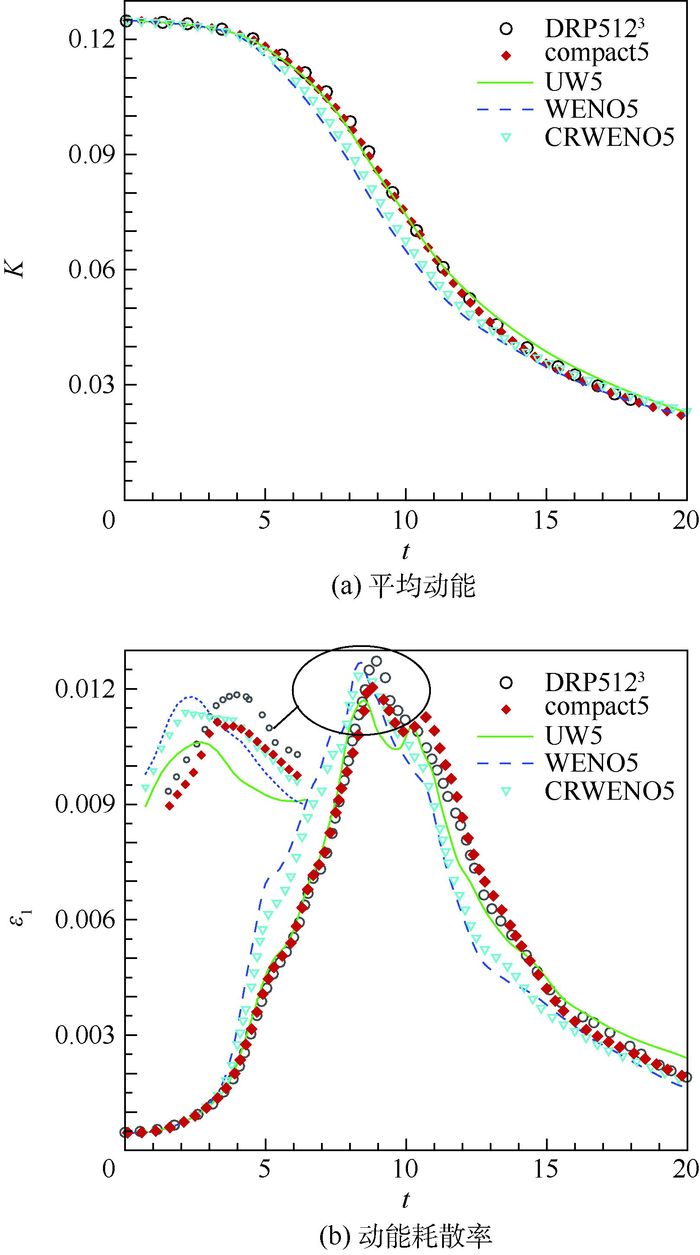 |
| 图 5 泰勒-格林涡平均动能及其动能耗散率随时间变化曲线 Fig. 5 Variation of kinetic energy and kinetic energy dissipation rate of Taylor-Green vortex with time |
| 图选项 |
研究表明[21],t=9时流场已为完全湍流。图 6给出该时刻各格式获得的能谱分布曲线(spectral为参考解[22],同时给出斜率-5/3次幂的w-5/3作参考)。低波数时,4种格式能谱均与参考解吻合较好。随着波数增大,4种格式的动能衰减逐渐增大,其中compact5能吻合的波数范围最广,WENO5发生偏离的位置最早,UW5与CRWENO5结果相近,UW5略好。
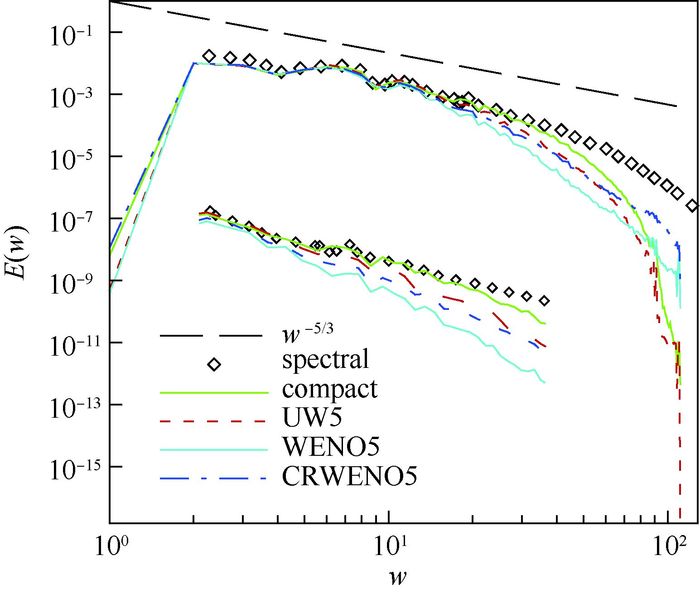 |
| 图 6 t=9时泰勒-格林涡能谱分布曲线 Fig. 6 Energy spectrum distribution curves of Taylor-Green vortex at t=9 |
| 图选项 |
3.4 可压缩各向同性衰减湍流 计算域为[-π, π]×[-π, π]×[-π, π],周期边界条件,网格间距Δx=2π/128。给定初始条件[23]:湍流能谱E(w)=Aw4e (-2w2/w02),其中A=0.000 13,k0=8;湍流马赫数Mat=0.3,Taylor微尺度雷诺数Reλ=72。
本算例用于测试激波与多尺度流动结构相互干扰流场中各格式的计算性能。由于初始流场中存在局部激波,线性格式无法稳定计算,仅给出WENO5和CRWENO5的计算结果(见图 7~图 9)。图中横坐标t/τ为实际时间t与初始时刻大涡翻转时间τ之比。图 7(a)为两格式获得的实际动能K(t)与初始时刻动能K0之比随时间变化规律,可见CRWENO5的动能耗散小于WENO5。从图 7(b)(拟涡能与初始拟涡能之比ζ随时间变化曲线)中能看出,CRWENO5所得的最大拟涡能大于WENO5,说明CRWENO5能捕捉到更多小尺度流动结构。能谱分布曲线图 8中亦能得到相似结论。
 |
| 图 7 不同时刻动能与初始动能之比及拟涡能与初始拟涡能之比随时间变化曲线 Fig. 7 Variation curves of ratio of kinetic energy to initial kinetic energy and ratio of enstrophy to initial enstrophy at different moments with time |
| 图选项 |
 |
| 图 8 2种格式在t/τ=4时刻的能谱分布曲线 Fig. 8 Energy spectrum distribution curves of two schemes at t/τ=4 |
| 图选项 |
图 9给出了t/τ=2时瞬时流场的密度分布曲线。可以看出,2种格式均能准确捕捉激波。相比而言,WENO5的稳定性略好,CRWENO5对激波的捕捉更锐利。
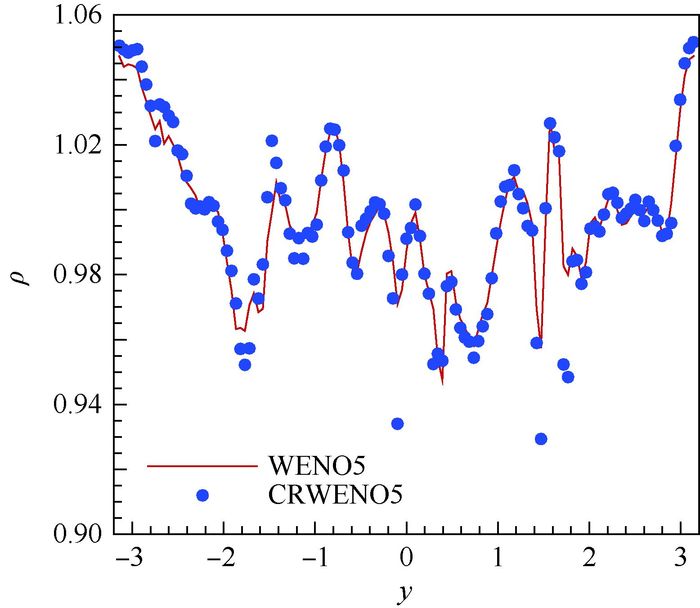 |
| 图 9 瞬时流场在t/τ=2时刻密度分布曲线 Fig. 9 Instantaneous flow field density distribution curves at t/τ=2 |
| 图选项 |
4 结论 1) 紧致型格式的分辨率优于显式格式,非线性情况下也如此;相对地,紧致型格式的稳定性略逊于显式格式。
2) 即使在流场光滑的情况下,非线性格式的耗散仍大于对应的线性格式,频谱特性也较逊色,这是因为非线性权系数难以完全蜕化成理想权系数;紧致型格式的低耗散特性能够一定程度上弥补该缺陷。
3) CRWENO5格式具备与WENO5相当的激波捕捉能力,在强压缩性流场中能够稳定清晰地捕捉激波。
4) 在网格分辨率一定的情况下,紧致型特性能够弥补非线性权系数带来的耗散过大的缺陷,使CRWENO5的频谱分辨范围优于WENO5格式,数值耗散也较小。
总之,紧致型激波捕捉格式CRWENO既具备稳定捕捉激波的能力,又继承了紧致型格式耗散较小、频谱特性较好的优点,在可压缩多尺度流动数值模拟中具有优势。其构造方法则为今后高分辨率激波捕捉格式的构造和改进提供思路。
参考文献
| [1] | 屈峰, 阎超, 于剑, 等. 高精度激波捕捉格式的性能分析[J].北京航空航天大学学报, 2014, 40(8): 1085–1089. QU F, YAN C, YU J, et al. Assessment of shock capturing methods for numerical simulations of compressible turbulence with shock waves[J].Journal of Beingjing University of Aeronautics and Astronautics, 2014, 40(8): 1085–1089.(in Chinese) |
| [2] | LELE S K. Compact finite difference schemes with spectral-like resolution[J].Journal of Computational Physics, 1992, 103(1): 16–42.DOI:10.1016/0021-9991(92)90324-R |
| [3] | VAN LEER B. Towards the ultimate conservation difference scheme Ⅴ:A second-order sequal to Godunov's method[J].Journal of Computational Physics, 1979, 32(1): 101–136.DOI:10.1016/0021-9991(79)90145-1 |
| [4] | HARTEN A. High resolution schemes for hyperbolic conservation laws[J].Journal of Computational Physics, 1983, 49(3): 357–393.DOI:10.1016/0021-9991(83)90136-5 |
| [5] | JIANG G S, SHU C W. Efficient Implementation of weighted ENO schemes[J].Journal of Computational Physics, 1996, 126(1): 202–228.DOI:10.1006/jcph.1996.0130 |
| [6] | GEROLYMOS G A, SéNéCHAL D, VALLET I. Very-high-order WENO schemes[J].Journal of Computational Physics, 2009, 228(23): 8481–8524.DOI:10.1016/j.jcp.2009.07.039 |
| [7] | MARTIN M P, TAYLOR E M, WU M, et al. A bandwidth-optimized WENO scheme for the effective direct numerical simulation of compressible turbulence[J].Journal of Computational Physics, 2006, 220(1): 270–289.DOI:10.1016/j.jcp.2006.05.009 |
| [8] | HENRICK A K, ASLAM T D, POWERS J M. Mapped weighted essentially non-oscillatory schemes:Achieving optimal order near critical points[J].Journal of Computational Physics, 2005, 207(2): 542–567.DOI:10.1016/j.jcp.2005.01.023 |
| [9] | ACKER F, BORGES R B D R, COSTA B. An improved WENO-Z scheme[J].Journal of Computational Physics, 2016, 313: 726–753.DOI:10.1016/j.jcp.2016.01.038 |
| [10] | GHOSH D, BAEDER J. Compact reconstruction schemes with weighted ENO limiting for hyperbolic conservation laws[J].SIAM Journal on Scientific Computing, 2012, 34(3): A1678–A1706.DOI:10.1137/110857659 |
| [11] | GHOSH D, MEDIDA S, BAEDER J D. Application of compact-reconstruction weighted essentially nonoscillatory schemes to compressible aerodynamic flows[J].AIAA Journal, 2014, 52(9): 1858–1870.DOI:10.2514/1.J052654 |
| [12] | GHOSH D, CONSTANTINESCU E M, BROWN J. Efficient implementation of nonlinear compact schemes on massively parallel platforms[J].SIAM Journal on Scientific Computing, 2015, 37(3): C354–C383.DOI:10.1137/140989261 |
| [13] | PENG J, SHEN Y. Improvement of weighted compact scheme with multi-step strategy for supersonic compressible flow[J].Computers & Fluids, 2015, 115: 243–255. |
| [14] | ROE P L. Approximate Riemann solvers, parameter vectors and difference schemes[J].Journal of Computational Physics, 1981, 43(2): 357–372.DOI:10.1016/0021-9991(81)90128-5 |
| [15] | GOTTLIEB S, SHU C. Total variation diminishing Runge-Kutta schemes[J].Mathematics of computation of the American Mathematical Society, 1998, 67(221): 73–85.DOI:10.1090/mcom/1998-67-221 |
| [16] | 傅德薰, 马延文, 李新亮, 等. 可压缩湍流直接数值模拟[M].北京: 科学出版社, 2010: 34-36. FU D X, MA Y W, LI X L, et al. Direct numerical simulation of the compressible turbulences[M].Beijing: Science Press, 2010: 34-36.(in Chinese) |
| [17] | FAUCONNIER D, DICK E. On the spectral and conservation properties of nonlinear discretization operators[J].Journal of Computational Physics, 2011, 230(12): 4488–4518.DOI:10.1016/j.jcp.2011.02.025 |
| [18] | SOD G A. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws[J].Journal of Computational Physics, 1978, 27(1): 1–31.DOI:10.1016/0021-9991(78)90023-2 |
| [19] | WOODWARD P, COLELLA P. The numerical simulation of two-dimensional fluid flow with strong shocks[J].Journal of Computational Physics, 1984, 54(1): 115–173.DOI:10.1016/0021-9991(84)90142-6 |
| [20] | DEBONIS J R.Solutions of the Taylor-Green vortex problem using high resolution explicit finite difference methods:AIAA-2013-0382[R].Reston:AIAA, 2013. |
| [21] | BULL J R, JAMESON A. Simulation of the compressible Taylor-Green vortex using high-order flux reconstruction schemes[J].AIAA Journal, 2015, 53(9): 2750–2761.DOI:10.2514/1.J053766 |
| [22] | DE WIART C C, HILLEWAERT K, DUPONCHEEL M, et al. Assessment of a discontinuous Galerkin method for the simulation of vortical flows at high Reynolds number[J].International Journal for Numerical Methods in Fluids, 2014, 74(7): 469–493.DOI:10.1002/fld.v74.7 |
| [23] | SAMTANEY R, PULLIN D I, KOSOVIC B. Direct numerical simulation of decaying compressible turbulence and shocklet statistics[J].Physics of Fluids, 2001, 13(5): 1415–1430.DOI:10.1063/1.1355682 |
