目标散射特性的评估方法可以分为2种:理论预估和试验测量[3]。理论预估主要通过各种电磁场的解析或者数值分析方法实现;试验测量既可以在室内开展也可以在室外进行。在长期的发展中,2种方法各有优劣。理论预估方法使用灵活、方便,可根据目标选择不同计算方法[4-13],时间周期短,但算法会受模型复杂程度、网格划分、计算机硬件等影响,精度及稳定性有待提高;试验测量[14-18]在结果准确性、可靠性方面具有优势,但需要设计、加工相应的试验模型,试验需要的缩比比例、模拟精度、重量限制等均对模型提出了较高要求,所需成本较高,周期较长。
当前缺陷类目标电磁散射特性的计算方法有:高低频混合方法,如迭代物理光学法(IPO)与矩量法(MOM)[6]、物理光学法(PO)、物理绕射理论(PTD)与有限元法(FEM)[7]等;低频数值方法,如多层快速多极子算法(MLFMA)[8-10]或时域有限差分方法(FDTD)[11-12]等。其中,混合方法的计算精度主要取决于3个方面,即高频近似、低频数值方法本身的精度以及目标表面各部分间相互耦合的处理效果,只有对上述3个方面全面兼顾才能得到满意的分析效果。低频数值方法则存在计算时间长、占用内存大的问题,不能及时有效地进行大规模计算分析。
为了满足工程使用要求,研究者发展了缺陷类目标散射特性的试验测量技术,具有更实用、有效的优点。当前对缺陷类目标的试验测量方法可根据载体不同而分为2类:① 采用竖直放置的平板作为缺陷载体,制作一系列不同物理特征的缺陷类目标[14-15],进行大量试验;② 采用水滴形、杏仁体、钻石体等低散射体作为基础载体,制作可替换的部件来表征缺陷类目标[16-18]进行试验。这些载体都在一定条件下具有低散射特性,如在一定频率下,竖直放置的平板在30°~90°方位角内的雷达散射截面积(Radar Cross Section, RCS)均值可达-35 dBsm,水滴形载体和杏仁体在0°~30°方位角内的RCS均值可达-40 dBsm。通过对比含缺陷目标与光滑表面(即不含缺陷目标)载体散射曲线,得到缺陷目标的部分散射特性。但是,这2种测试方法得出的结果受到载体本身的散射影响,某些角度范围内的缺陷类目标散射被载体的强散射覆盖,无法获得全角域范围内缺陷类目标的散射特性,准确性需要提高。
为了得到完整的缺陷类目标散射特性,本文提出一种改进的散射特性试验方法,采用矢量对消排除缺陷类目标评估中的载体影响,提取出完全独立于载体之外的全角域范围的缺陷类目标散射特性,得到更为完整、精确的缺陷类目标散射特性,改进当前试验测量技术的不足。
1 基本定义与原理 1.1 散射特性基本定义 目标的电磁散射特性常用RCS来衡量,用符号σ来表示,其是一个假想面积,通常是基于平面板照射下目标各向同性散射的概念,与目标到雷达的距离无关,用以描述在给定方向上的散射场功率流密度强弱,它的理论定义式[1]可以表示为
 |
式中:Ei、Hi分别为入射雷达波在目标处的电、磁场强度;Es、Hs分别为目标散射波在雷达处的电、磁场强度;R为目标到雷达天线的距离。
RCS是下列因素的函数:① 目标结构,即目标的形状、尺寸和材料的电参数;② 入射波的频率和波形;③ 雷达天线的极化方向(天线所发射的电场方向及天线可接收的电场方向);④ 目标相对于入射方向和雷达接收方向的姿态角(对于单站雷达,只受入射姿态角的影响)。
1.2 紧缩场目标测试原理 在紧缩场中进行目标RCS测量时,被测目标(如飞机模型)通过低散射泡沫支架或低散射金属支架置于静区中。在紧缩场静区中,电磁波以平面波形式传播,不随距离变化发生衰减,在这种情况下,替代定标法很方便。以金属球作为定标体为例,测量目标前,首先进行背景电平测量,然后在目标支架上放置金属球进行定标体测量,最后再架设目标进行目标测量,即可得到被测目标的散射特性。
不考虑系统噪声因素,对于目标RCS宽带扫频测量,目标和定标体的信号可以表示为
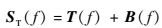 | (1) |
 | (2) |
式中:f为频率;ST(f)和SC(f)分别为测目标和测定标体时雷达接收到的回波信号,包含杂波背景;T(f)为目标真实回波;C (f)为定标体真实回波;B (f)为由目标支架及测试场其他杂散回波构成的背景回波。上述回波信号均为复数矢量。
为提高RCS测量精度,一般在定标中采用背景矢量场相减技术处理[19],目标散射函数的定标方程为
 | (3) |
式中:σT(f)为目标散射函数,是需要测量和定标的量;σC(f)为定标体的散射函数,是可通过精确理论计算得到的已知量。
由式(3) 可见,当背景回波B (f)能够被测得并通过背景矢量场相减技术处理后,就能消除其对目标RCS测量与定标的影响,实现对目标RCS的精确测量与定标。
1.3 缺陷类目标特点 缺陷类目标使得飞行器上存在表面的不连续结构,其电磁散射机理可以分为2种情况[20]:① 雷达波掠入射时,在飞行器表面产生爬行波,在其传播路径上如果存在不连续的缺陷类目标,将会在不连续边界上激发二次散射场;② 不同形式和结构的缺陷类目标自身对入射雷达波的直接响应,如缝隙、台阶和螺钉在雷达波照射时产生的反射、折射和绕射等。
缝隙、台阶等缺陷类目标与其他散射源的主要区别在于其不能独立存在,一定是依附于某种类型的载体上。例如,对于缝隙板,其对应的无缝平板就是缝隙的载体。
在理论计算中,载体可以无限大,此时缺陷类目标可等效为表面电磁流,用低频精确算法如矩量法进行求解,得到的结果即认为是缺陷类目标自身的散射(实际上是整个目标结果)。但实际建模和计算中,需要评估的缺陷类目标是依附于有限尺寸载体的,计算结果包含了目标表面各部分间相互耦合。
目前对缺陷类目标的测试采用的是常规测试方法,以含缺陷类目标的载体和光滑表面载体为被测目标,进行对比试验来获得缺陷类目标的散射特性。
此时,采用计算或试验方法得到的总散射可视为3部分[21]:① 缺陷类目标本身的散射;② 载体的散射;③ 载体边缘与缺陷类目标的耦合。这一散射特点导致了缺陷类目标散射结果很难真实地被反映出来。
2 缺陷类目标评估改进方法 2.1 方法原理 根据缺陷类目标的散射特点,在紧缩场中进行测量时,其目标信号可以表示为
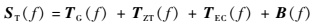 | (4) |
式中:TG(f)为缺陷类目标本身回波;TZT(f)为载体回波信号;TEC(f)为载体边缘与缺陷类目标耦合产生的回波。上述回波信号均为复数矢量。
式(4) 中,4种信号是矢量叠加的关系,载体回波信号TZT(f)和背景回波B (f)处于同等地位。载体相当于缺陷类目标的存在环境,但是研究缺陷本身的散射时又希望排除载体本身的散射。
为了得到更为完整、精确的缺陷类目标散射特性,提出一种基于矢量场相减理论的改进方法:把载体散射作为缺陷类目标的背景,也采用矢量对消的方式进行消除。
用Eθ、Eφ表示含缺陷类目标载体的电场分量,Eθ1、Eφ1表示无缺陷类目标载体的电场分量,则矢量对消公式可以写为
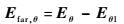 | (5) |
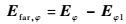 | (6) |
通过2组复数矢量的对消,得到不包含载体散射贡献的新的分量Efar, θ和Efar, φ。
通过RCS的定义公式可得到对消后缺陷类目标的散射值,表示如下:
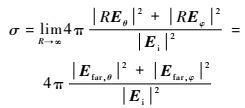 | (7) |
2.2 方法实施步骤 改进方法在紧缩场中进行试验测量的具体实施步骤描述如下:
步骤1?按照常规RCS测量方法,测量包含目标支架在内的微波暗室背景,获得测试场地环境杂波信号B (f)。
步骤2?在目标支架上放置标准体,如金属球,进行标准体测量,获得标准体回波信号SC(f),用于RCS测量的定标。
步骤3?将载体置于目标支架上,将可替换的缺陷类目标区域用光滑表面替代,或者粘贴铝箔,确保该区域基本不产生散射。由于缺陷类目标不存在,此时也不存在载体边缘与缺陷类目标的耦合。在这种情况下,测量获得用于载体对消处理的目标背景信号为
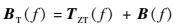 | (8) |
步骤4?保持载体姿态不变,将替换的光滑表面区域更换为缝隙、台阶等缺陷类被测目标,测量获得目标信号,见式(4)。
步骤5?定标处理中,采用背景矢量场相减技术时,对目标信号和标准体信号分别应用各自对应的背景信号,新的目标散射函数的定标方程为
 | (9) |
由式(9) 可见,当把载体作为目标背景进行测量时,可以分别获得场地背景回波B (f),以及包括载体在内的背景回波BT(f),在进行背景对消和定标处理后,可以得到缺陷类目标的散射,排除了载体本身的散射。
改进方法把载体作为目标背景进行测量,并通过矢量场相减技术处理后,就能消除其对目标RCS测量的影响,从而实现对缝隙等缺陷类目标RCS的精确测量。
需要说明的是,这一结果包含载体边缘与缺陷类目标的耦合散射。由于载体边缘属于弱散射源,与缺陷类目标的耦合进一步减弱,可以认为该结果是单独缺陷类目标的散射特性。
2.3 方法优点 从方法的精度上看,矢量对消方法将测量载体作为目标背景看待,将不含缝隙、台阶等缺陷类目标的载体测量数据作为背景数据,通过背景对消实现缝隙、台阶等缺陷类目标和载体的散射分离,显著提高了缺陷类目标的测量精度。
从测试目标上看,载体做为背景存在,摆脱了对于超低散射载体的依赖,不需要将载体设计成水滴形、橄榄形等标准体形状,使得模拟缺陷类目标的区域不再受限于低散射载体有限的表面尺寸,从而有效地增加被测缝隙、台阶等缺陷类目标的尺寸,扩展了研究对象的范围。
从成本上看,传统方法采用的标准体形状特殊,对设计加工以及精度要求高,本文方法对载体的形状、复杂程度以及精度等要求较低,有效降低了时间及经济成本。
3 改进方法验证 3.1 单直缝隙目标分析验证 根据文献[14]建立如图 1所示的单直缝隙模型来进行测试,以验证本文方法的准确性。模型包括含单直缝隙的正方形金属平板、不含缝隙的正方形金属平板;缝隙长度为200 mm,宽度为5 mm,入射频率为10 GHz,极化方式为水平极化(HH)。
 |
| 图 1 单直缝隙测试模型[14] Fig. 1 Single-slit test model[14] |
| 图选项 |
通过测试得到含有单直缝隙和不含缝隙的正方形金属平板的RCS值,然后通过矢量对消得到缝隙的散射特性曲线,如图 2实线所示,虚线为文献[14]对应的测试曲线。
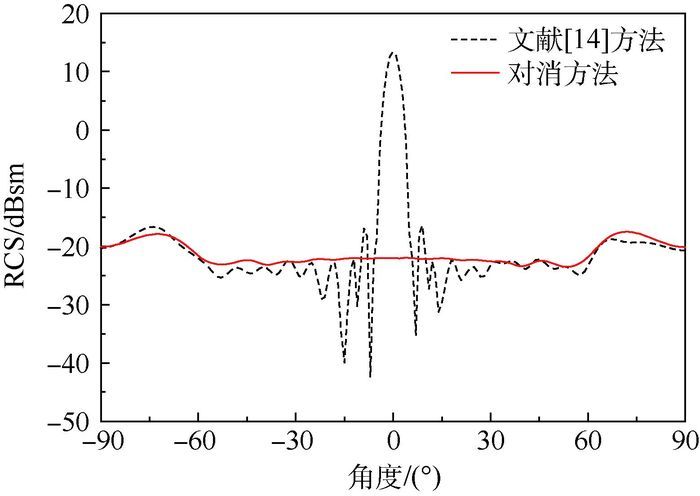 |
| 图 2 2种方法单直缝隙散射结果对比 Fig. 2 Comparison of single-slit scatteringresults between two methods |
| 图选项 |
从散射原理上分析,在正入射附近(入射角-30°~30°)范围内,传统方法测试得到的散射是缝隙目标和载体的共同耦合作用,文献[14-15]认为缝隙本身的散射被载体的镜面散射所淹没,仅能间接观察分析。而改进方法将载体散射与缝隙散射分离开,并通过矢量对消方法抵消了载体的影响,得到了缝隙在此角域内的真实RCS值,即图 2中较为平缓的散射曲线。
在侧向角域(±30°~±90°),缝隙散射强于载体的散射,特别是±60°~±90°范围内,缝隙引起的行波散射比无缝金属平板更强,此角域内载体散射对缝隙的干扰最小。文献[14-15]认为能够通过对比该范围的散射变化,得出缝隙在侧向带来的散射贡献;而图 2中2种方法得到的散射曲线基本吻合,仅在入射角±75°左右,缝隙与金属平板边缘耦合作用使得实线与虚线吻合度出现波动;这表明在较大角域内,改进方法得到的测试结果与传统方法的结果是一致的,均不含载体散射。
通过上述对比可知,本文方法得到的结果可靠,并提取出了缝隙在正向角域(-30°~30°)内的精确散射曲线,将缝隙散射数据扩展到了全角域,满足深入研究的需要。
3.2 单直台阶目标分析验证 为了验证本文方法对复杂非标准体载体的适用性,建立了大尺寸非标准体载体模型,如图 3所示。
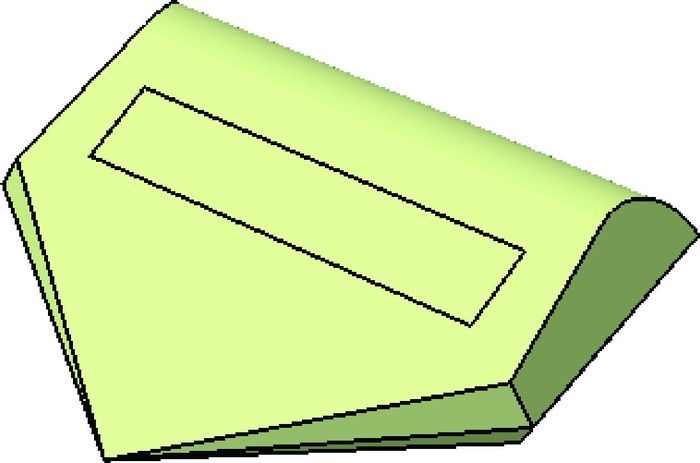 |
| 图 3 大尺寸载体模型 Fig. 3 Large-size carrier model |
| 图选项 |
在模型上表面设置可替换的大尺寸不同高度单直台阶目标,长度为900 mm,宽度为130 mm,高度分别为5 mm和10 mm。采用矢量对消方法对该模型进行测试,从而得到不同高度单直台阶的散射曲线,如图 4所示。
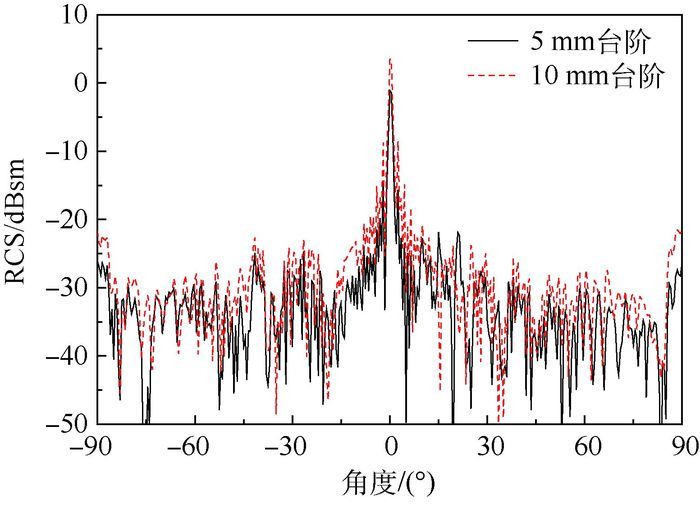 |
| 图 4 不同高度单直台阶散射结果对比 Fig. 4 Comparison of single-step scattering results with different heights |
| 图选项 |
分析图 4可知,首先从散射对称性上看,台阶散射曲线关于0°入射角呈现弱对称性;其次,随台阶高度增加,曲线变化更加剧烈,散射明显增强。文献[8]采用平板载体对单直台阶散射特性进行了试验分析,其结论与本文是一致的。可见采用矢量对消方法测试台阶等缺陷类目标时,复杂外形的非标准载体与平板等低散射载体相比,测试结果基本吻合。通过矢量场对消,载体的影响作为目标背景从总体散射中分离出去,载体的外形及其复杂程度对缺陷类目标散射测量没有影响。
表 1给出了长度为900 mm的不同高度单直台阶目标的散射均值。可知,±10°角域内台阶散射最强,这是由台阶目标的二面角散射决定的;全向范围内的台阶散射保持在一个相对大的量级上;台阶高度增加带来了约5 dB的散射增幅。
表 1 不同高度单直台阶电磁散射均值(HH极化) Table 1 Average value of single-step electromagnetic scattering with different heights (HH polarization)
| 台阶高度/mm | 散射均值/dBsm | |||
| -10°~10° 角域 | -30°~30° 角域 | -90°~-30° 角域 | -90°~90° 角域 | |
| 5 | -13.21 | -17.71 | -32.08 | -22.21 |
| 10 | -8.52 | -13.12 | -29.26 | -17.68 |
表选项
表 1的数据说明,在载体形状不受限制的条件下,矢量对消方法可以得到较大尺寸缺陷类目标较为准确的散射结果。
4 结论 1) 缺陷类目标的散射机理较为复杂,传统测试方法采用低散射目标作为载体,对有无缺陷类目标的测试结果进行对比,获得缺陷类目标产生的散射增幅,从而分析其散射特性。该方法受载体的影响大,无法获取全角域范围的缺陷类目标散射特性,也不适合较大尺寸的缺陷类目标。
2) 本文提出的矢量对消方法在测试中将载体视为目标背景的一部分,通过矢量场对消将载体从散射结果中分离出来,得到单纯的缺陷类目标的散射结果。该方法包含了全角域结果,且测试结果、目标尺寸均不受载体限制,具有精确度高、成本低的优点。
3) 随着低散射设计技术的发展,缺陷类目标的散射将成为减缩的重点,矢量对消方法将为设计者提供有效的分析手段。
参考文献
| [1] | 阮颖铮. 雷达截面与隐身技术[M].北京: 国防工业出版社, 1998. RUAN Y Z. Radar cross section and stealth technology[M].Beijing: National Defence Industry Press, 1998.(in Chinese) |
| [2] | 朱劲松, 于洋, 王宝发. 飞行器结构缝隙电磁散射问题的研究[J].北京航空航天大学学报, 1999, 25(1): 99–102. ZHU J S, YU Y, WANG B F. Research on electromagnetic scattering for aircraft structural slot[J].Journal of Beijing University of Aeronautics and Astronautics, 1999, 25(1): 99–102.(in Chinese) |
| [3] | 何国瑜, 卢才成, 洪家才, 等. 电磁散射的计算和测量[M].北京: 北京航空航天大学出版社, 2006. HE G Y, LU C C, HONG J C, et al. The computation and test for RCS[M].Beijing: Beihang University Press, 2006.(in Chinese) |
| [4] | 袁宁, 聂小春, 梁昌洪. 有限厚导电平板上任意缝隙的耦合特性分析[J].电波科学学报, 1999, 14(3): 261–267. YUAN N, NIE X C, LIANG C H. Analysis of coupling properties of an arbitrary slit in a thickconducting plate[J].Chinese Journal of Radio Science, 1999, 14(3): 261–267.(in Chinese) |
| [5] | 黄沛霖, 马冬立, 武哲. 低RCS齿形挂架参数选择研究[J].北京航空航天大学学报, 2001, 27(3): 293–296. HUANG P L, MA D L, WU Z. Research on parameter selection of low RCS serrated pylon[J].Journal of Beijing University of Aeronautics and Astronautics, 2001, 27(3): 293–296.(in Chinese) |
| [6] | 聂小春, 葛德彪, 阎玉波, 等. 计算开槽电大目标电磁散射的IPO-MOM混合法[J].西安电子科技大学学报, 1999, 26(1): 13–17. NIE X C, GE D B, YAN Y B, et al. The hybrid method of IPO-MOM for scattering by large bodies with cracks[J].Journal of Xidian University, 1999, 26(1): 13–17.(in Chinese) |
| [7] | 丁卫平, 徐金平. 带有腔体或槽缝的电大尺寸目标电磁散射特性分析[J].电子学报, 2002, 30(6): 815–818. DING W P, XU J P. Evaluation of electromagnetic scattering by electrically large bodies with cracks and cavities on their surfaces[J].Acta Electronica Sinica, 2002, 30(6): 815–818.(in Chinese) |
| [8] | 刘战合, 黄沛霖, 武哲. MLFMA分析表面不连续特征散射特性[J].合肥工业大学学报(自然科学版), 2009, 32(9): 1430–1435. LIU Z H, HUANG P L, WU Z. Analysis of scattering characteristics of surface discrete characters with MLFMA[J].Journal of Hefei University of Technology(Natural Science), 2009, 32(9): 1430–1435.(in Chinese) |
| [9] | 刘战合, 黄沛霖, 高旭, 等. MLFMA用于不连续特征多频散射特性研究[J].空军工程大学学报(自然科学版), 2009, 10(2): 60–65. LIU Z H, HUANG P L, GAO X, et al. Multi-waves scattering characteristic of gaps in aircraft surface with MLFMA[J].Journal of Air Force Engineering University(Natural Science Edition), 2009, 10(2): 60–65.(in Chinese) |
| [10] | 刘战合, 蒋胜矩, 姬金祖, 等. 基于MLFMA的表面台阶多频散射特性[J].探测与控制学报, 2009, 31(z1): 20–24. LIU Z H, JIANG S J, JI J Z, et al. Multi-frequencies scattering characteristic of steps in surface based on MLFMA[J].Journal of Detection & Control, 2009, 31(z1): 20–24.DOI:10.3969/j.issn.1008-1194.2009.z1.007(in Chinese) |
| [11] | 王钢林, 武哲. FDTD算法中的时空匹配问题及其解决方法研究[J].航空学报, 2007, 28(5): 1116–1121. WANG G L, WU Z. Problem of space and time matehing in FDTD algorithm and research on solving it[J].Acta Aeronautica et Astronautica Sinica, 2007, 28(5): 1116–1121.(in Chinese) |
| [12] | 李元新, 张俏梅, 龙云亮. 基于FDTD的微带漏波天线分析的新方法[J].电波科学学报, 2007, 22(4): 637–640. LI Y X, ZHANG Q M, LONG Y L. New method for analysis of microstrip leaky wave antenna based on FDTD[J].Chinese Journal of Radio Science, 2007, 22(4): 637–640.(in Chinese) |
| [13] | 段洪, 李建周, 侯婷. 任意形状带隙结构电磁散射特性的精确分析[J].电子测量技术, 2009, 32(12): 52–55. DUAN H, LI J Z, HOU T. Accurate analysis of the scattering characteristics from abitrary slits structure[J].Electronic Measurement Technology, 2009, 32(12): 52–55.DOI:10.3969/j.issn.1002-7300.2009.12.015(in Chinese) |
| [14] | 黄沛霖, 刘战合. 飞行器表面缝隙电磁散射特性研究[J].航空学报, 2008, 29(3): 675–680. HUANG P L, LIU Z H. Research on elect romagnetic scattering characteristics of slit s on aircraft[J].Acta Aeronautica et Astronautica Sinica, 2008, 29(3): 675–680.(in Chinese) |
| [15] | 高旭, 刘战合, 武哲. 缝隙目标电磁散射特性试验[J].航空学报, 2008, 29(6): 1497–1501. GAO X, LIU Z H, WU Z. Experiment on scattering characteristics of serrate gap[J].Acta Aeronautica et Astronautica Sinica, 2008, 29(6): 1497–1501.(in Chinese) |
| [16] | 桑建华, 张宗斌, 王烁. 低RCS飞行器表面弱散射源研究[J].航空工程进展, 2012, 3(3): 257–262. SANG J H, ZHANG Z B, WANG S. Research on the radar cross section of weak scatterers on stealth vehicle[J].Advances in Aeronautical Science and Engineering, 2012, 3(3): 257–262.(in Chinese) |
| [17] | 柴建忠, 高旭, 刘学强, 等. 几种载体表面缝隙对雷达目标特性的影响[J].南京航空航天大学学报, 2014, 46(4): 567–572. CHAI J Z, GAO X, LIU X Q, et al. Effect of gaps in different surfaces on radar target characteristic[J].Journal of Nanjing University of Aeronautics and Astronautics, 2014, 46(4): 567–572.(in Chinese) |
| [18] | 桑建华, 周海. 飞行器表面电磁缺陷及雷达吸波材料应用[J].航空材料学报, 2003, 23(2): 51–55. SANG J H, ZHOU H. The electromagnetic discontinuities of the aircraft surface and an application of the radar absorbing materials[J].Journal of Aeronautical Materials, 2003, 23(2): 51–55.(in Chinese) |
| [19] | 庄钊文, 袁乃昌, 莫锦军, 等. 军用目标雷达散射截面预估与测量[M].北京: 科学出版社, 2007. ZHUANG Z W, YUAN N C, MO J J, et al. Calculation and measurement of radar cross section of military targets[M].Beijing: Science Press, 2007.(in Chinese) |
| [20] | 桑建华. 飞行器隐身技术[M].北京: 航空工业出版社, 2013. SANG J H. Low-observable technologies of aircraft[M].Beijing: Aviation Industry Press, 2013.(in Chinese) |
| [21] | 张振利, 倪维立. 缝隙及其与边缘的相互作用对目标散射的影响[J].电波科学学报, 2001, 16(3): 301–305. ZHANG Z L, NI W L. The scattering by gaps and the multiple scattering between gaps and edges[J].Chinese Journal of Radio Science, 2001, 16(3): 301–305.(in Chinese) |
