在近红外光谱技术的发展中,化学计量学的发展与应用起到十分重要的作用。目前,常用的近红外光谱定量回归分析方法有偏最小二乘法(PLS)、支持向量机(SVM)以及BP神经网络(BP-ANN)等。PLS是一种多元数据分析方法,建立在主成分分析和回归基础上,主要适合于数据量少、各变量内部高度线性相关的模型,不适应动态多变量建模[2]。SVM是基于风险最小化的统计学习理论,可解决标准的优化问题,对小样本、非线性及高维数据具有很强的泛化能力,一经提出,便得到了广泛应用[3-4]。但SVM不适用于大规模数据样本,会耗费机器大量内存资源。BP-ANN是一种按误差逆传播算法训练的多层前馈网络,其以良好的泛化能力、容错能力以及自学习、自适应能力获得了国内外****广泛关注。但随着应用范围的扩大,BP-ANN也暴露出不少缺点,如需要人为设置大量网络参数,网络结构模型不单一,容易陷入局部优化,而且参数需迭代调整,训练效率不高,容易出现过拟合现象[5]。
2004年,南洋理工大学黄广斌等[6]提出一种人工神经网络模型训练新算法——极限学习机(Extreme Learning Machine,ELM),该算法输入层与隐含层之间的连接权值和阈值均随机产生,而且在模型训练过程中无需对参数进行调整,只需对隐含层神经元个数进行设置,便可避免陷入局部的最小值,从而获得唯一最优解。与传统方法相比具有简单易用、学习速度快及泛化性好的特点。此后,不少****开始运用并不断改进ELM算法。Masri等[7]运用ELM对土壤的近红外光谱进行建模分析,并用非洲土壤属性预测数据库验证模型,获得了较好的预测性能。Guo等[8]采用偏最小二乘支持向量机(LS-SVM)和ELM建立近红外光谱桃品种的聚类分析模型,预测准确率高达100%。Huang和Chen[9]先后提出了核极限学习机(K-ELM)、增强增量极限学习机(EI-ELM)和凸增量的极限学习机(Cl-ELM)等改进极限学习机算法。Jin等[10]提出了用于交叉特性学习的多任务聚类ELM,实现了人脸特性识别。Alexandre等[11]采用遗传算法优化ELM对交通噪声进行分类,改进后算法分类准确性由改进前的74.83%提高至93.74%。陈媛媛等[12]采用遗传算法改进ELM,用于NO与NO2混合气体的定量分析,实验结果表明,改进后的模型能够快速、准确地预测混合气体各组分浓度。de Oliveira和Ludermir[13]采用鱼群算法改进ELM用于聚类分析,经过与标准数据库对比实验验证,改进后的算法具有更好的准确性和泛化性能。
本文基于小样本氨水近红外光谱数据,采用粒子群优化极限学习机(PSO-ELM)算法建立了氨水浓度定量分析模型,优化了ELM输入层与隐含层之间的连接权值和偏差,对比了BP-ANN、SVM、ELM以及PSO-ELM算法模型的精度和泛化性能。通过实验验证,改进后的PSO-ELM算法氨水浓度定量分析模型的稳定性、精度和泛化性能较传统方法均有显著提高。
1 近红外光谱理论 近红外光是介于可见光和中红外之间的电磁辐射波,美国材料检测协会将近红外光谱区定义为780~2 526 nm的区域。近红外光谱区主要反映的是有机分子中含氢基团(C—H、O—H、N—H)振动的合频和各级倍频的吸收谱线信息[14]。通过扫描样品的近红外光谱,可以得到样品分子含氢基团的特征信息。
图 1所示为氨分子(NH3)振动模式。NH3为C3v对称性分子,具有对称伸缩振动、非对称伸缩振动、对称弯曲振动以及反对称弯曲振动4种振动形式,会产生4个基频特征谱带。气态氨一级倍频和二级倍频均为尖吸收峰,分别在6 520 cm-1(1 534 nm)和9 650 cm-1(1 046 nm)附近。NH3的倍频、组合频吸收峰较多,通常选择6 609 cm-1(1 513 nm)、5 084 cm-1(1 967 nm)和4 417 cm-1(2 264 nm)处吸收强度较大的吸收峰建模[14]。
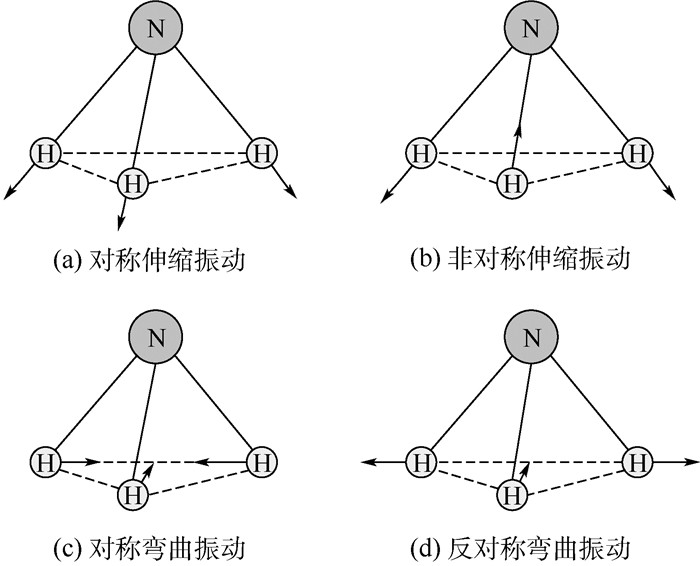 |
| 图 1 氨分子振动模式 Fig. 1 Vibration modes of ammonia molecule |
| 图选项 |
氨呈弱碱性,在水中主要以NH3形式存在。水是近红外定量分析的主要干扰因素,在近红外谱区有较强的吸收峰,而且谱带较宽[15]。如图 2所示为实际测得氨水近红外光谱图,氨水样本光谱在4 484 cm-1(2 203 nm)、4 892 cm-1(2 044 nm)、5 962 cm-1(1 706 nm)和6 024 cm-1(1 660 nm)出现较强吸收峰。由于近红外光谱峰位容易受到诱导效应、共轭效应、氢键效应、空间效应以及外部条件等多种因素的影响,氨水近红外光谱相比气态氨峰位有较大移动。
 |
| 图 2 氨水近红外吸收光谱 Fig. 2 Near infrared absorption spectrum of ammonia |
| 图选项 |
2 算法理论 2.1 极限学习机(ELM) ELM是南洋理工大学黄广斌教授提出的一种人工神经网络模型训练新算法,该算法针对单隐含层前馈神经网络(Single-hidden Layer Feedforward Neural Network,SLFN),改进了传统训练方法训练速度慢、容易陷入局部极小值以及学习率选择敏感等缺点[6]。
图 3所示为典型的单隐含层前馈神经网络结构图。图中:x1,x2,…, xm为输入;y1, y2, …, ym为输出;o1, o2, …, om为隐含层节点;w=[wij]为输入层与隐含层的连接权值;β=[βjk]为隐含层与输出层的连接权值。
 |
| 图 3 典型单隐含层前馈神经网络结构 Fig. 3 A typical single-hidden layer feedforward neural network structure |
| 图选项 |
设样本数为Q,训练集的输入矩阵为X,输出矩阵为Y:
 | (1) |
设隐含层神经元的激活函数为g(x),则网络输出T为
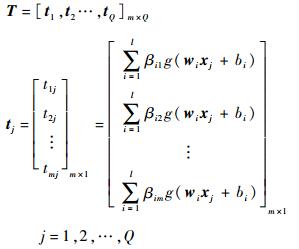 | (2) |
式中:wi=[wi1, wi2, …, win]; xj=[x1j, x2j, …, xnj]T。
则式(2) 可表示为
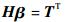 | (3) |
式中:TT为矩阵T的转置;H为神经网络的隐含层输出矩阵,其具体形式可表示为
 | (4) |
在文献[16]算法的基础上,Huang等[6]证明:在任意区间范围内,给定无限可微的激活函数g:R→R和任意小误差ε>0,则总存在一个含有K(K≤Q)个隐含层神经元的单隐含层神经网络模型,在任意赋值wi∈Rn和bi∈R的情况下,有||HN×M βM×N-TT|| < ε。
因此,当存在无限可微的激活函数g(x)时,单隐含层神经网络模型中的参数都无需调整,只需在训练前,通过随机的方法确定参数w和b,则求下列方程组的最小二乘解便可得到隐含层与输出层间的连接权值β:
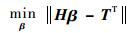 | (5) |
其解为
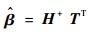 | (6) |
式中:H+为隐含层输出矩阵H的Moore-Penrose广义逆。
ELM算法实现分为以下3个步骤[17]:
1) 设置隐含层神经元个数,输入层与隐含层间的连接权值w和隐含层偏差b可以通过随机数产生。
2) 选择无限可微的隐含层神经元激活函数,计算输出矩阵H。
3) 通过求解
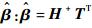
2.2 粒子群优化算法 粒子群优化(Particle Swarm Optimization,PSO)算法由Kennedy和Eberhart[18]提出。该算法从鸟群捕食特征中得到启发。初始化一个种群,种群中的个体称为粒子。种群中的每个粒子都具有3个特征,即速度、位置和适应值,且随着粒子的更新和迭代不断改变。在可解空间中,每个粒子都可能是问题的一个最优解。个体粒子的位置更新取决于个体极值和群体极值,通过跟踪极值来确定在解空间中的运动方向。
假设确立了一个D维搜索空间,空间中有由n个粒子组成的种群Xp =(X1, X2, …, Xn),则在D维搜索空间中第i个粒子的位置,可能是问题的一个潜在的最优解,可用一个D维的向量Xi=(xi1, xi2, …, xiD)T表示。设每个粒子位置为Xi,则根据目标函数可以算出对应的适应度值。第i个粒子的速度为Vi=(Vi1, Vi2, …, ViD)T,其个体极值为Pi=(Pi1, Pi2, …, PiD)T,种群的全局极值为Pg=(Pg1, Pg2, …, PgD)T。速度和位置更新公式如下:
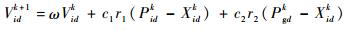 | (7) |
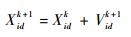 | (8) |
式中:ω为惯性权重;k为当前的迭代次数;d=1,2,…,D;i=1,2,…,n;Vid为粒子的速度;c1和c2为加速度因子,为非负常数;r1和r2为分布于[0, 1]之间的随机数。为防止粒子盲目搜索,一般将其速度和位置限制在一定的区间[-Vmax,Vmax]、[-Xmax,Xmax]内[19]。
2.3 粒子群优化极限学习机(PSO-ELM)算法 由于ELM的隐藏节点参数(输入权值和偏差)随机产生,相比于很多传统的算法需要更多的隐层节点才能达到理想的精度[20]。在ELM中,输出权值矩阵由输入权值矩阵和偏差计算得到,可能会存在很多无效的隐含层节点,影响ELM的泛化性能。因此,要提高ELM的性能,主要目标是寻找最优的隐含层节点个数,选择恰当的隐含层节点参数。
针对上述问题,本文提出一种PSO-ELM算法,采用PSO优化ELM的输入层权值和隐含层偏差。流程图如图 4所示。
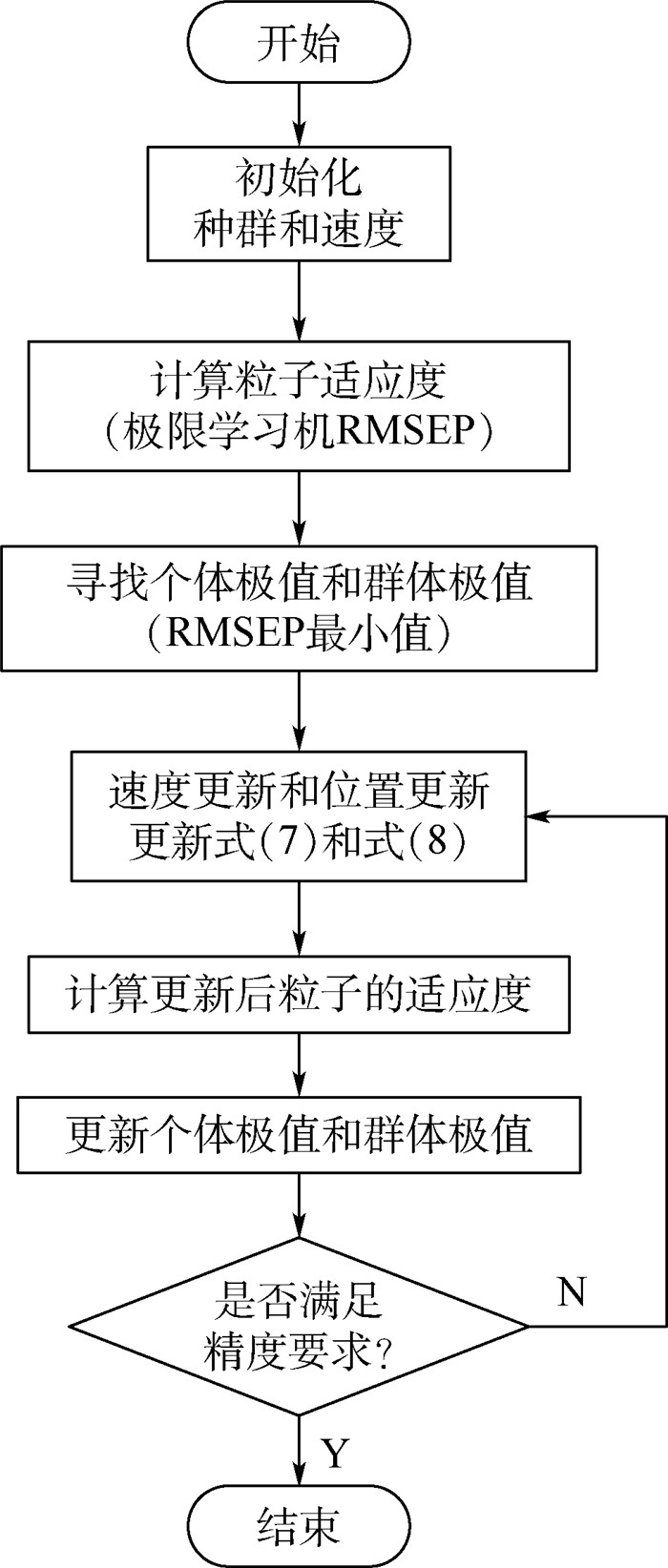 |
| 图 4 PSO-ELM算法流程图 Fig. 4 Flowchart of PSO-ELM algorithm |
| 图选项 |
PSO-ELM具体实现步骤如下:
1) 初始化种群。种群规模P设为200,设隐含层节点数为h,输入层神经元数为m,则粒子长度L=h(m+1),种群个体即粒子,由输入权值和隐含层偏差构成。
2) 计算每个粒子的适应度。采用ELM算法对初始化种群中的粒子进行训练,计算出每个粒子的预测集均方根误差(RMSEP),将其作为粒子群优化算法的适应度值。
3) 寻找个体极值和群体极值。每次迭代后,将计算出的适应度值PMSEP和粒子的个体极值、群体极值进行比较,如果较好即RMSEP值较小,则将其作为个体极值和群体极值。
4) 适当选取速度参数c1和c1,将位置和速度限制在ELM隐含层节点参数取值范围[-1, 1]内,根据式(7) 更新粒子速度,式(8) 更新粒子位置。
5) 判断结果是否满足训练目标精度,不满足则转到步骤2)。迭代结束时,全局最优粒子所在位置便是最优解。
3 实验设计 3.1 仪器设备 实验的检测设备是德州仪器公司生产的DLP? NIRscanTM Evaluation Module (EVM)[21]近红外光谱仪,该仪器配置有基于DLP的光谱仪光学引擎。光源为频带从可见光到红外光的钨卤素灯,探测器为单元件扩展型InGaAs探测器,可探测长范围为1 350~2 450 nm。
3.2 样本材料 实验样本材料为实验用滴定标准氨水溶液。氨水溶液采用高纯氨气和蒸馏水按体积比进行配置。氨水样本浓度范围为0~0.25,浓度梯度为0.01。每个样本浓度取样3次。每次取样样本用光谱仪重复扫描3次,建模样本光谱取3次扫描和3次取样的平均值。样本数共计26,将样本分为预测集和训练集。为使样本具有代表性,将样本按照浓度梯度顺序等分为5份,随机选取每份中任意一个浓度点作为预测集样本,其余为训练集样本。预测集样本数为5,训练集样本数为21。
3.3 模型建立与评价 本文采用PSO-ELM算法建立定量分析模型。将处理后的光谱分为训练集和预测集,训练集用于建立模型,预测集用于验证模型。采用MATLAB 2009a进行模型建立和分析。程序分为5个部分,产生训练集/预测集、数据归一化处理、模型训练、模型测试以及结果分析。
本文采用训练集相关系数(correlation coefficient of calibration)Rc、训练集均方根误差(Root Mean Square Error of Calibration,RMSEC)、预测集相关系数(correlation coefficient of prediction)Rp和RMSEP对模型性能进行评价[22]。
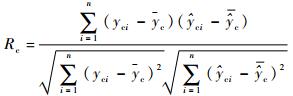 | (9) |
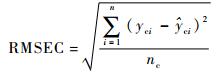 | (10) |
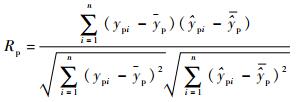 | (11) |
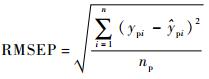 | (12) |
式中:nc和np分别为训练集和预测集的样本个数;
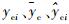
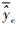
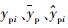
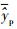
4 结果分析 4.1 光谱预处理 氨水样本的原始近红外光谱图如图 5(a)所示,图中各样品的近红外光谱谱峰严重重叠,且谱带较宽,无法直接进行定量分析建模,需对光谱进行预处理。
 |
| 图 5 氨水近红外光谱预处理前后对比 Fig. 5 Comparison of ammonia near infrared spectrum before and after preprocessing |
| 图选项 |
光谱仪得到的光谱信号中含有叠加的随机误差,信号平滑是消除噪声的最常用的方法。本文采用S-G(Savitzky-Golay)滤波器对光谱进行平滑处理。S-G滤波器是一种在时域内基于局域多项式最小二乘法拟合的滤波方法,其最大特点在于在滤除噪声的同时能够确保信号的形状、宽度不变,可尽可能保留光谱特征[23]。对原始光谱采用25点平滑滤波,平滑后的光谱如图 5(b)所示。氨水样本光谱吸收强度随着浓度增大逐渐增强。
4.2 建模结果分析 选择光谱吸收特征明显的1 600~2 100 nm谱段建立模型,用预测集对模型进行验证。为了更好地验证算法性能,本文将PSO-ELM建模结果与传统的BP-ANN和SVM算法建模结果进行对比。
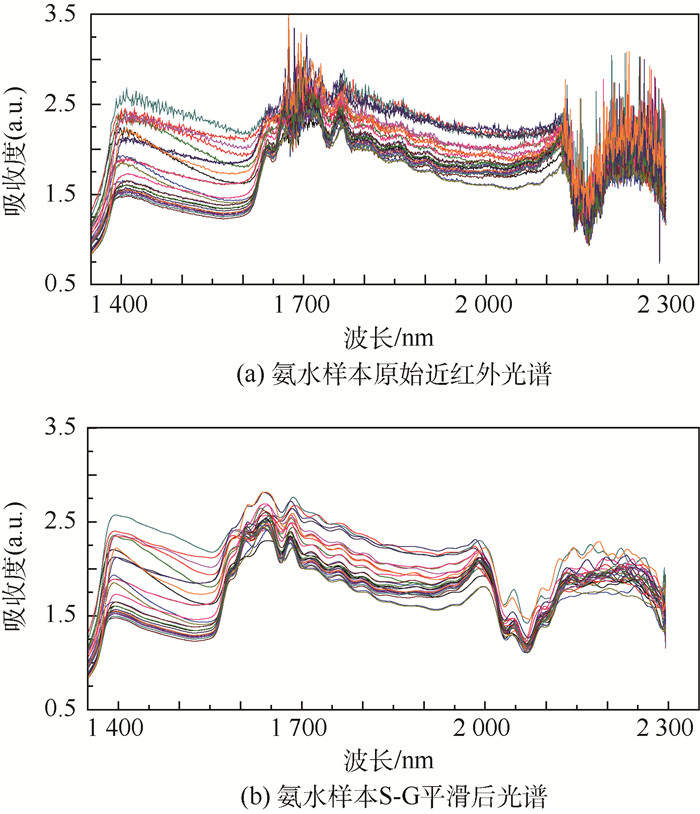
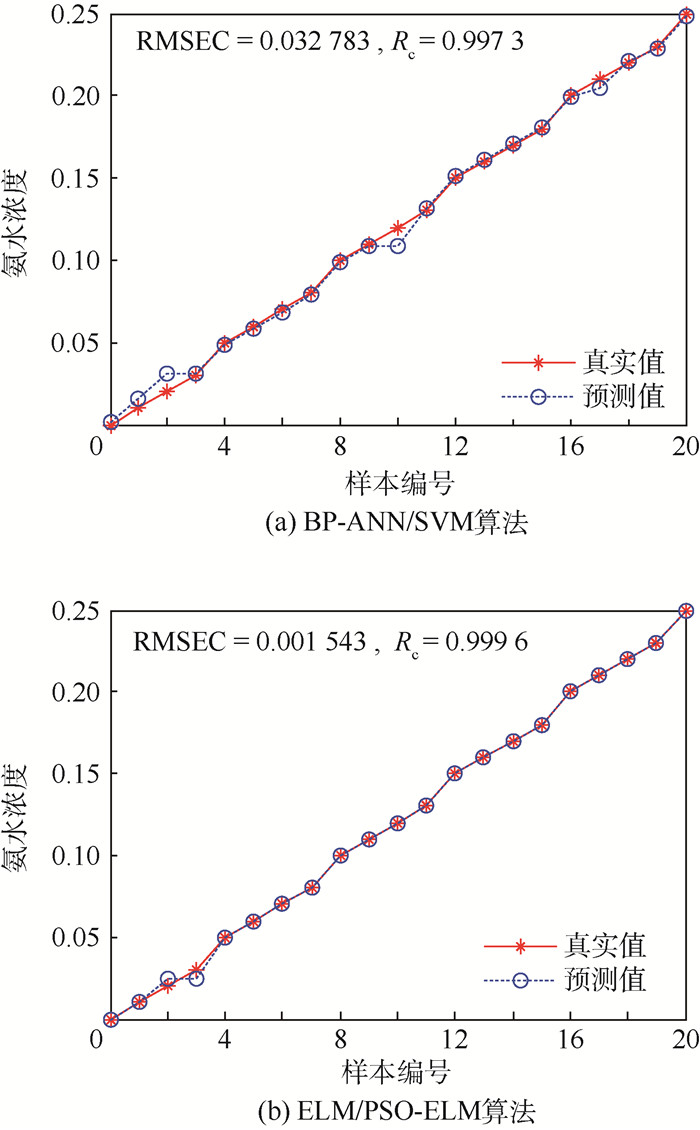
表 1和图 6为BP-ANN/SVM和ELM/PSO-ELM训练集拟合结果对比。表 1中ELM/PSO-ELM训练集均方根误差RMSEC为0.001 543远远小于BP-ANN/SVM训练集均方根误差0.032 783。拟合相关系数相差0.002 3,但均接近1。图 6为训练集拟合曲线,横坐标为样本编号,总共21个训练集样本,纵坐标为氨水体积浓度。对比图 6(a)和图 6(b)可知,ELM/PSO-ELM对样本的利用率更高,训练集拟合效果优于BP-ANN/SVM。
表 1 训练集拟合效果对比 Table 1 Comparison of imitative effects of training sets
| 算法类型 | RMSEC | Rc |
| BP-ANN/SVM | 0.032 783 | 0.997 3 |
| ELM/PSO-ELM | 0.001 543 | 0.999 6 |
表选项
 |
| 图 6 4种算法训练集拟合结果 Fig. 6 Imitative effects of training sets of four algorithms |
| 图选项 |
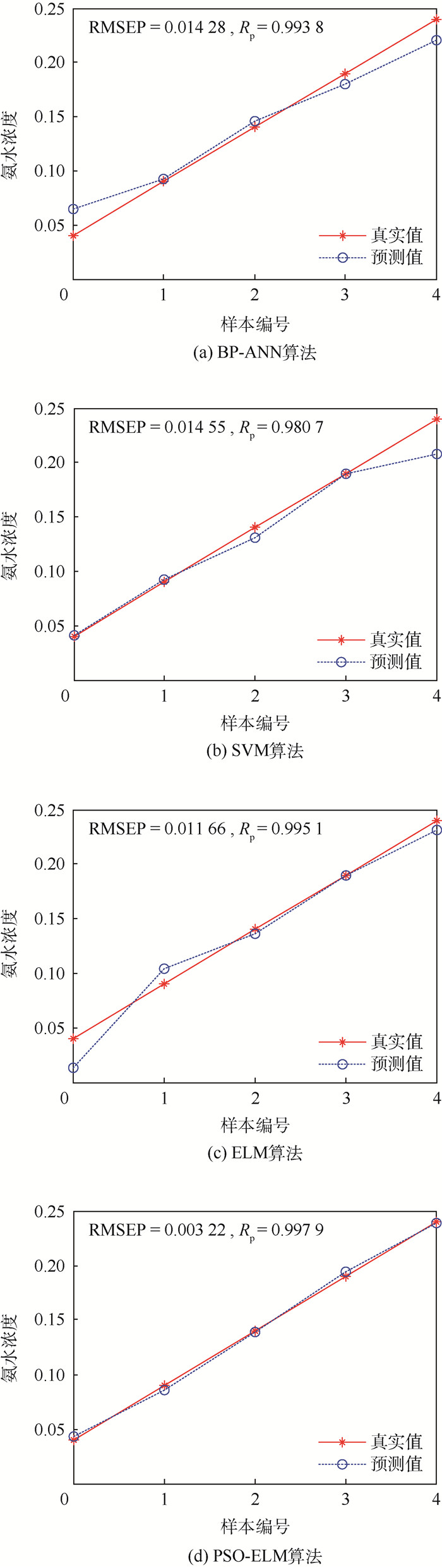
表 2和图 7为BP-ANN、SVM、ELM和PSO-ELM 4种算法预测结果对比。表 2中真实值是预测集氨水样本的体积浓度,未参与训练集拟合建模。预测值为建模拟合的结果,真实值与预测值之差即为误差值。PSO-ELM算法建模的拟合最大误差的绝对值为0.004 61,RMSEP值为0.003 22,均小于其他3种算法,Rp值为0.997 9,大于其他3种算法,拟合效果最好。图 7(a)~图 7(d)分别为BP-ANN、SVM、ELM以及PSO-ELM预测集建模拟合结果。比较可知,图 7(d)中预测值和真实值误差最小、精度最高、拟合线性度最好。4种算法拟合效果顺序为:PSO-ELM>ELM>BP-ANN>SVM。
表 2 4种算法建模结果对比 Table 2 Comparison of modeling results among four algorithms
| 算法类型 | 氨水浓度 | 浓度误差 | RMSEP | Rp | |
| 真实值 | 预测值 | ||||
| BP-ANN | 0.04 | 0.064 23 | 0.024 23 | 0.014 28 | 0.993 8 |
| 0.09 | 0.092 75 | 0.002 75 | |||
| 0.14 | 0.145 53 | 0.005 33 | |||
| 0.19 | 0.179 77 | -0.010 23 | |||
| 0.24 | 0.220 36 | -0.019 64 | |||
| SVM | 0.04 | 0.040 84 | 0.000 84 | 0.014 55 | 0.980 7 |
| 0.09 | 0.092 72 | 0.002 72 | |||
| 0.14 | 0.130 62 | -0.009 38 | |||
| 0.19 | 0.189 76 | -0.000 24 | |||
| 0.24 | 0.207 74 | -0.032 26 | |||
| ELM | 0.04 | 0.013 72 | -0.026 28 | 0.011 66 | 0.995 1 |
| 0.09 | 0.103 68 | 0.013 68 | |||
| 0.14 | 0.136 14 | -0.003 86 | |||
| 0.19 | 0.189 76 | -0.000 24 | |||
| 0.24 | 0.231 55 | -0.008 45 | |||
| PSO-ELM | 0.04 | 0.042 64 | 0.002 64 | 0.003 22 | 0.997 9 |
| 0.09 | 0.085 39 | -0.004 61 | |||
| 0.14 | 0.138 42 | -0.001 58 | |||
| 0.19 | 0.194 34 | 0.004 34 | |||
| 0.24 | 0.238 40 | -0.001 60 | |||
表选项
 |
| 图 7 4种算法预测集拟合结果 Fig. 7 Imitative effects of prediction sets of four algorithms |
| 图选项 |
5 结论 本文提出了基于小样本数据的粒子群改进极限学习机算法,建立了氨水浓度的定量分析模型,可实现允许误差范围±0.005的氨水浓度预测。
1) PSO-ELM算法优化了ELM算法中随机产生的输入权值和隐含层偏差,减小了建模结果的随机性,提高了建模精度。
2) PSO-ELM和ELM算法训练集拟合效果明显优于BP-ANN和SVM算法,提高了训练集数据点的利用率,有利于提高模型预测精度。
3) PSO-ELM算法相比传统的SVM、BP-ANN算法,对于小样本数据具有更好的泛化性能和更高的回归拟合精度。
本文研究中,ELM和PSO-ELM算法的隐含层节点个数和激活函数均选用经验值得出的最佳参数,未来的研究中,可结合实际样本和需求,选取出性能更好的建模参数。
参考文献
| [1] | 王海莲, 万向元, 胡培松, 等. 稻米脂肪含量近红外光谱分析技术研究[J].中国农业科学, 2005, 38(8): 1540–1546. WANG H L, WAN X Y, HU P S, et al. Quantitative analysis of fat content in brown rice by near infrared spectroscopy (NIRS) technique[J].Scientia Agricultura Sinica, 2005, 38(8): 1540–1546.(in Chinese) |
| [2] | 吴琼, 原忠虎, 王晓宁. 基于偏最小二乘回归分析综述[J].沈阳大学学报, 2007, 19(2): 33–35. WU Q, YUAN Z H, WANG X N. Summary of partial least squares regression[J].Journal of Shenyang University, 2007, 19(2): 33–35.(in Chinese) |
| [3] | CORTES C, VAPNIK V. Support-vector networks[J].Machine Learning, 1995, 20(3): 273–297. |
| [4] | SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J].Neural Processing Letters, 1999, 9(3): 293–300.DOI:10.1023/A:1018628609742 |
| [5] | HEERMANN P D, KHAZENIE N. Classification of multispectral remote sensing data using a back-propagation neural network[J].IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(1): 81–88.DOI:10.1109/36.124218 |
| [6] | HUANG G B, ZHU Q Y, SIEW C K.Extreme learning machine:A new learning scheme of feedforward neural networks[C]//2004 IEEE International Joint Conference on Neural Networks, 2004.Piscataway, NJ:IEEE Press, 2004, 2:985-990. |
| [7] | MASRI D, WOON W L, AUNG Z.Soil property prediction:An extreme learning machine approach[C]//22nd International Conference on Neural Information Processing, ICONIP 2015.Berlin:Springer, 2015:18-27. |
| [8] | GUO W, GU J, LIU D, et al. Peach variety identification using near-infrared diffuse reflectance spectroscopy[J].Computers and Electronics in Agriculture, 2016, 123(C): 297–303. |
| [9] | HUANG G B, CHEN L. Enhanced random search based incremental extreme learning machine[J].Neurocomputing, 2008, 71(16): 3460–3468. |
| [10] | JIN Y, LI J, LANG C, et al. Multi-task clustering ELM for VIS-NIR cross-modal feature learning[J].Multidimensional Systems and Signal Processing, 2016, 28(3): 1–16. |
| [11] | ALEXANDRE E, CUADRA L, SALCEDO-SANZ S, et al. Hybridizing extreme learning machines and genetic algorithms to select acoustic features in vehicle classification applications[J].Neurocomputing, 2015, 152: 58–68.DOI:10.1016/j.neucom.2014.11.019 |
| [12] | 陈媛媛, 张记龙, 赵冬娥. 基于极限学习机的混合气体FTIR光谱定量分析[J].中北大学学报(自然科学版), 2011, 32(5): 636–641. CHEN Y Y, ZHANG J L, ZHAO D E. Quantitative analysis of mixed gas FTIR spectrum based on extreme learning machine[J].Journal of North University of China (Natural Science Edition), 2011, 32(5): 636–641.(in Chinese) |
| [13] | DE OLIVEIRA J F L, LUDERMIR T B.Homogeneous ensemble selection through hierarchical clustering with a modified artificial fish swarm algorithm[C]//2011 23rd IEEE International Conference on Tools with Artificial Intelligence (ICTAI).Piscataway, NJ:IEEE Press, 2011:177-180. |
| [14] | WORKMAN J, WEYER L. 近红外光谱解析实用指南[M]. 褚小立, 许育鹏, 田高友, 译. 北京: 化学工业出版社, 2009: 6-17. WORKMAN J, WEYER L. Practical guide to interpretive near-infrared spectroscopy[M].CHU X L, XU Y P, TIAN G Y, translated.Beijing:Chemical Industry Press, 2009:6-17(in Chinese). |
| [15] | 严衍禄. 近红外光谱分析基础与应用[M].北京: 中国轻工业出版社, 2005: 128-130. YAN Y L. Near infrared spectrum analysis and application[M].Beijing: China Light Industry Press, 2005: 128-130.(in Chinese) |
| [16] | POGGIO T, GIROSI F. A theory of networks for approximation and learning[M].Cambridge: Massachusetts Institute of Technology, 1989: 25-39. |
| [17] | 陈林伟. 基于极限学习机的骨髓细胞识别技术研究[D]. 杭州: 中国计量学院, 2014: 44-49. CHEN L W.Research on recognition of bone marrow cells based on extreme learning machine[D].Hangzhou:China Jiliang University, 2014:44-49(in Chinese). |
| [18] | KENNEDY J, EBERHART R. Particle swarm optimization[J].Swarm Intelligence, 2007, 1(1): 33–57.DOI:10.1007/s11721-007-0002-0 |
| [19] | 石山, 刘德鹏, 李成茂. 基于改进粒子群优化算法的飞机作动系统功率调度[J].北京航空航天大学学报, 2016, 42(10): 2024–2030. SHI S, LIU D P, LI C M. Power dispatch of actuator of aircraft based on improved particle swarm optimization algorithm[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(10): 2024–2030.(in Chinese) |
| [20] | 李永强. 基于粒子群优化的极限学习机的XML文档分类中的研究与应用[D]. 沈阳: 东北大学, 2013: 27-33. LI Y Q.Research and application of XML classification based on extreme learning machine with particle swarm optimization[D].Shenyang:Northeastern University, 2013:27-33(in Chinese). |
| [21] | PRUETT E.Techniques and applications of programmable spectral pattern coding in Texas Instruments DLP spectroscopy[C]//Proceedings of SPIE-The International Society for Optical Engineering.Bellingham, WA:SPIE, 2015. |
| [22] | 刘小丽. 红外光谱在药物分析中的应用研究[D]. 西安: 西北大学, 2013: 6-8. LIU X L.The application of infrared spectroscopy in pharma-ceutical analysis[D].Xi'an:Northwest University, 2013:6-8(in Chinese). |
| [23] | GORRY P A. General least-squares smoothing and differentiation by the convolution (Savitzky-Golay) method[J].Analytical Chemistry, 1990, 62(6): 570–573.DOI:10.1021/ac00205a007 |
