一些高可靠、长寿命的产品,性能退化量不会马上呈现出下降趋势,而是在一段时间内平稳退化。Tseng等[3]在研究日光灯的退化数据时,将前期没有退化趋势的数据舍去进行分析研究,但这样损失了大量关于产品寿命的有用信息。因此,融合不同退化阶段的分阶段模型得到了发展。Bae等[4-5]提出了带变点的分段线性回归模型来拟合产品的性能退化轨迹,随后又提出了一种分层的贝叶斯变点回归模型。这些分阶段模型的提出,由于信息量增加,提高了模型的准确性和性能预测的精度。国内针对多阶段模型的研究中,黎明[6]假设多阶段变点是随机的,且服从正态分布,通过求取分阶段模型的似然函数,估计出随机变点的取值,但随机变点受采样周期影响很大,且在小样本情形下,对随机变点的正态性假设具有主观性,不适合单机变点的选取。鄢伟安等[7]对液力耦合器的两阶段退化过程进行可靠性建模及评估,运用Schwarz信息准则对某台液力耦合器进行变点估计,但此方法只能用于单一变点的多阶段建模。刘君强等[8]提出了基于多阶段性能退化模型预测航空发动机剩余寿命的方法,但变点的选取是通过预先设置阈值给定的,没有充分考虑具体产品的性能退化曲线。基于以上分析可以看到,综合考虑平稳阶段与退化阶段的退化信息,可以增大信息量的获取,提高模型精度,但多阶段的变点选取受到多种制约因素的影响,变化较大,是一个难点问题;且在分阶段建模中,多以线性模型为主,没有充分考虑模型的非线性特点。
实际产品的性能退化过程常常具有一定的非线性,退化过程的非线性建模成为近年的研究热点。在产品性能退化轨迹的建模研究中,文献[9]利用非线性回归模型拟合产品的退化轨迹;文献[10]提出了误差项相关的非线性回归退化模型;徐正国和周东华[11]对一组疲劳裂纹增长数据建立非线性退化轨迹模型并进行可靠性评估。在基于随机过程的退化建模中,Si等[12]基于非线性Wiener过程模型进行剩余寿命估计;Wang等[13]针对非线性退化情形下的产品进行了剩余寿命的研究。
针对机载燃油泵性能退化过程中压力信号具有多阶段与非线性的特点,引入平滑转换自回归(Smooth Transition Auto-Regression,STAR)模型进行分析。STAR能较好地捕捉到时间序列机制转换的动态过程,将呈现多阶段、非线性特点的压力退化序列看做一个整体进行研究。文献[14-15]对STAR模型进行了深入的探讨。
本文运用STAR模型中具有良好特性、获得广泛研究的逻辑平滑转换自回归(Logistic Smooth Transition Auto-Regression,LSTAR)模型进行机载燃油泵性能退化过程的建模,将多阶段退化模式联合分析,依据参数估计结果与转换函数值分析性能退化轨迹的特点,成功完成了机载燃油泵的性能退化建模,为机载燃油泵的在线性能分析和健康管理提供了理论依据。
1 机载燃油泵 燃油泵由油泵和电机两部分组成。工作过程主要分3个流程,即电机流程—传动流程—泵流程。电机流程与一般交流电动机工作流程相似,输油过程中,燃油泵应保证系统的流量和压力要求。燃油泵主要失效形式为流量和压力不足。
燃油泵正常运行需要各个流程持续稳定工作且各个部件共同配合来完成,直接从燃油泵出发很难分析其退化趋势。笔者所在课题组在前期研究中发现机载燃油泵的出口压力信号与机载燃油泵的健康状态有着密切关系[16],因此选取机载燃油泵的出口压力信号作为研究性能退化的指标。
2 STAR模型 文献[14]提出改进的单方程平滑转换回归(Smooth Transition Regression,STR)模型,形式为
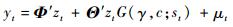 | (1) |
式中:Φ=(Φ0, Φ1, …, Φp)′,Θ=(θ0, θ1, …, θp)′为系数向量;μt为正态分布白噪声序列,即μt~i.i.d.N(0, σ2);G(γ, c; st)为转换函数;zt为需要考察的自变量,可以是时间,也可以是包括yt的滞后值。如果zt只包含yt的滞后值,则STR模型称为STAR模型,此时
 |
根据转换函数的形式不同,STR模型可以分为3种形式[17]。其中,最常用的就是LSTAR模型和指数平滑转换自回归(Exponential Smooth Transition Auto-Regression,ESTAR)模型。
本文主要讨论LSTAR模型的应用,其中G(γ, c; st)的形式为
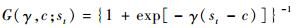 | (2) |
式中:γ为斜率参数,要求γ > 0;st为转换变量;c为位置参数。
转换函数G(γ, c; st)是取值在[0, 1]上的连续函数。当G(γ, c; st)=0时,式(1) 变为
 |
称为状态“0”,yt处于低机制,取值较小。当G(γ, c; st)=1时,式(1) 变为
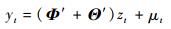 |
称为状态“1”,yt处于高机制,取值较大。当转换变量st随时间变化时,转换函数逐步变化,体现了线性与非线性过程的交互变化。γ较小时,从状态“0”向状态“1”转化速度较慢,当γ较大时,转换速度较快。通过转换速度γ,可以反映2种状态之间的转换快慢。
3 机载燃油泵性能退化建模 根据文献[18]提出的基于STAR的建模步骤,针对机载燃油泵压力退化序列多阶段、非线性的特点,提出基于LSTAR模型的机载燃油泵出口压力退化序列建模方法如下:
1) 对压力退化序列yt建立求和自回归模型[19]:
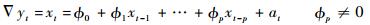 | (3) |
式中:▽为差分算子;Φj(j=0, 1, …, p)为模型系数;at~i.i.d.N(0, σ2)。
对自回归模型式(3),借助偏自相关系数的截尾性质,进行延迟阶数的选择。偏自相关系数λk可以按照如下方法计算:
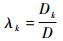 | (4) |
式中:
 |
其中:自相关系数ρk的估计值为
 |
式中:T为观测点数目。
2) 计算式(3) 残差平方和的估计值SSR0。
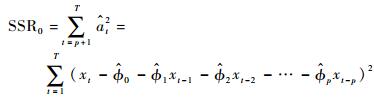 |
用三阶泰勒多项式[18]建立辅助回归函数:
 | (5) |
残差平方和估计值SSR为
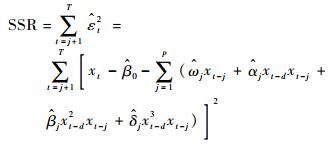 |
式中:xt-d为转换变量, d=1, 2, …, p;ωj、αj、βj和δj为模型系数。
进行模型式(5) 的非线性检验:原假设为αj=βj=δj=0, j=1, 2,…, p。检验统计量为
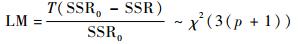 |
依据统计量大小与显著性概率进行非线性检验,确定建立LSTAR模型的合理性。
3) 用非线性最小二乘法对LSTAR模型的参数进行估计。即对于未知参数Ψ=(Φ′, Θ′, γ, c)实现:
 |
4) 依据步骤1)~步骤3),依次选择不同的转换变量xt-1, xt-2, …, xt-p进行LSTAR模型拟合,并计算不同转换变量下的拟合优度R2与AIC(Akaike Information Criterion)值。
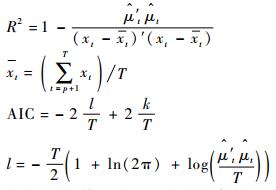 |
式中:k为模型式(1) 中未知参数的个数;l为对数似然函数值;
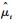
5) 根据最终建立的LSTAR模型的残差,借助LB(Ljung-Box)统计量进行白噪声检验[19]:
 |
运用J-B(Jarque-Bera)统计量对残差进行正态性检验[20],S为偏度,K为峰度。
 |
从而完成模型的适应性分析。
4 应用 4.1 数据获取 在实验室对某型机载燃油泵进行循环电压下的试验,一个循环为3个过程:① 电压207~209V,频率420~422Hz,工作0.5h;② 电压185~187V,频率378~380Hz,工作0.5h;③ 电压192~202V,频率398~402Hz,工作9h。试验过程中,记录机载燃油泵出口压力传感器的输出值。本文在设备开始工作后的195个循环中第3个工作电压时各进行一次压力值采集,共1950h的压力传感器信号值。图 1为压力信号值随时间的退化曲线。
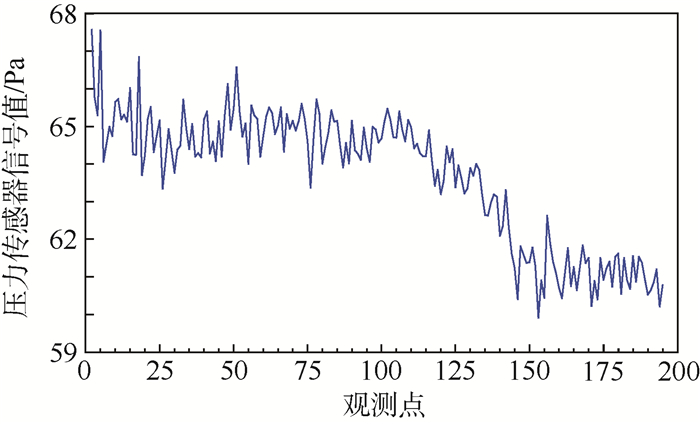 |
| 图 1 机载燃油泵压力退化曲线 Fig. 1 Curves of airborne fuel pump pressure degradation |
| 图选项 |
通过初始序列图可以看到,在1950h的观测中,机载燃油泵压力信号呈现出多阶段的退化模式,第1阶段平稳退化,之后有下降退化趋势,之后又趋于平稳退化。
4.2 基于LSTAR的机载燃油泵压力信号值退化曲线建模 令yt为压力信号退化序列,此序列有明显的趋势,是一个非平稳序列。对yt进行差分运算,则退化增量xt=▽yt=yt-yt-1, t=2, 3, …, 195,如图 2所示。
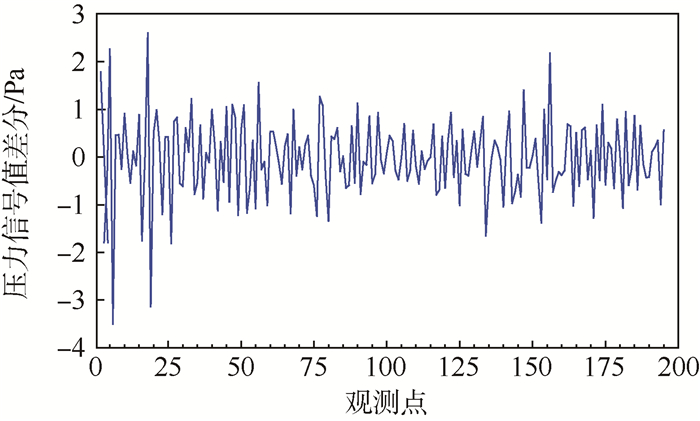 |
| 图 2 机载燃油泵压力退化增量值 Fig. 2 Incremental value about pressure degradation of airborne fuel pump |
| 图选项 |
根据PP单位根检验[19] (Phillips-Perron unit-root test),对自回归模型xt=Φ1xt-1+Φ2xt-2+…+Φpxt-p+at,令ρ=Φ1+Φ2+…+Φp-1,σ2表示残差的方差。修正后的统计量为
 |
式中:
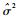

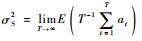
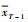
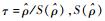
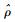
表 1 PP检验 Table 1 PP test
| 压力序列 | 统计量 | 显著性概率 |
| yt | -2.438 | 0.132 6 |
| xt | -72.745 | 0.000 1 |
表选项
通过差分运算,xt在显著性水平5%的条件下拒绝了单位根假设,退化增量序列呈现出整体平稳性。由式(4) 计算各阶模型偏自相关系数估计值和AIC值,如表 2所示。
表 2 模型定阶 Table 2 Model order determination
| λk | 偏自相关系数估计值 | AIC值 |
| λ1 | -0.405 | 2.277 |
| λ2 | -0.392 | 2.117 |
| λ3 | -0.154 | 2.105 |
| λ4 | -0.234 | 2.044 |
| λ5 | -0.157 | 1.950 |
| λ6 | -0.003 | 1.948 |
表选项
综合考虑偏自相关函数的截尾性与模型的AIC值最小,最终建立自回归模型为
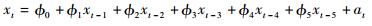 | (6) |
用最小二乘法进行参数估计,得到自回归模型为
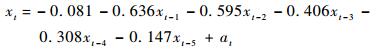 |
计算非线性检验统计量为
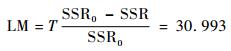 |
显著性概率为0.009,因此,机载燃油泵压力信号退化曲线存在着明显的非线性特征,建立LSTAR模型是合理的。
对于转换变量xt-d(d=1, 2, …, 5),备选非线性模型为
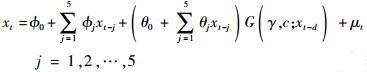 | (7) |
为了避免参数γ的过度估计,利用
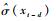
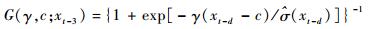 |
计算不同转换变量xt-d(d=1, 2, …, 5) 时模型式(7) 的拟合优度值及AIC值,如表 3所示,基于拟合优度最大与AIC值最小选择xt-3为转换变量。
表 3 拟合优度和AIC值 Table 3 Goodness of fit and AIC value
| 转换变量 | 拟合优度 | AIC值 |
| xt-1 | 0.379 | 1.969 |
| xt-2 | 0.377 | 1.972 |
| xt-3 | 0.435 | 1.873 |
| xt-4 | 0.374 | 1.976 |
| xt-5 | 0.366 | 1.989 |
表选项
运用非线性最小二乘估计,得到模型式(7) 的参数估计结果为:Φ0=-1.172;Φ1=-1.202;Φ2=0.119;Φ3=-1.202;Φ4=-0.851;5=-0.057;θ0=1.133;θ1=0.653;θ2=-0.729;θ3=0.794;θ4=0.659;θ5=-0.035;γ=6.402;c=-0.904;
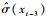
得到转换函数为
 |
γ=6.402说明在机载燃油泵的性能退化过程中,从一种状态向另外一种状态的转换是一个缓慢、连续的过程,可考虑为累积失效。
转换函数值如图 3所示。通过转换函数取值,可见压力退化曲线从状态1到状态0的变化非常频繁,根据退化趋势选取转换函数R的阈值为0.2[22],则整个退化过程具有多个变点。说明机载燃油泵的退化过程是线性与非线性频繁交替的过程,通过选择固定的变点进行分阶段建模是不可行的。所以文献[4-8]提出的依据变点进行分段的模型,如Bae和Kvam[4]提出的带变点的分段线性回归模型和分层的贝叶斯变点回归模型[5]等不适合对机载燃油泵的退化过程进行建模分析。
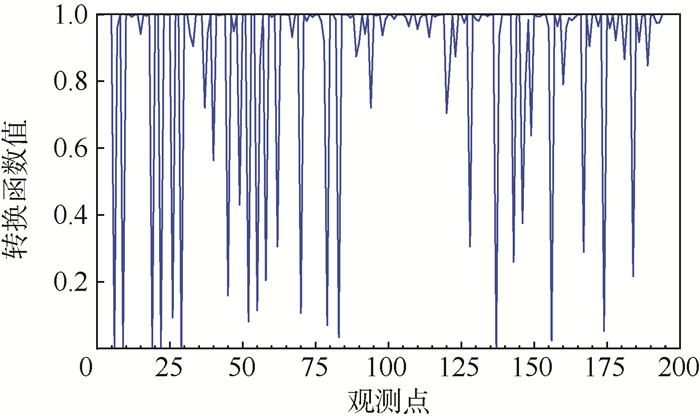 |
| 图 3 转换函数值 Fig. 3 Transition function values |
| 图选项 |
因此,通过LSTAR模型,融合退化过程的多个阶段,体现非线性时间序列的动态特征,对退化特征的压力传感序列联合建模。
通过图 3可以看出,选取R为0.2,在前840h之内,从状态1到状态0的转换十分频繁,退化序列yt表现为平稳退化阶段,中间一段时间以靠近状态1为主,退化序列yt表现为下降退化阶段,在测点137(1 370 h)之后又开始较为频繁地转换,退化序列yt表现为平稳退化阶段。转换函数的取值反映了压力退化序列从一种状态1向另外一种状态0的转换过程,表明机载燃油泵性能退化过程是线性与非线性交替发生的过程。
对LSTAR模型拟合的残差序列计算LB统计量并进行白噪声检验,结果如表 4所示,在显著性水平为5%的水平下,延迟1~5阶的显著性概率均远大于0.05,即残差为白噪声序列,表明所建立的模型是成功的。
表 4 白噪声检验 Table 4 White noise test
| 延迟阶数 | LB统计量 | 显著性概率 |
| 1 | 0.1671 | 0.683 |
| 2 | 0.8955 | 0.639 |
| 3 | 1.4921 | 0.684 |
| 4 | 1.8461 | 0.764 |
| 5 | 1.8668 | 0.867 |
表选项
运用LSTAR模型进行预测,可得拟合曲线如图 4所示,可见基于LSTAR模型的机载燃油泵退化建模效果较好。
 |
| 图 4 机载燃油泵压力退化预测值 Fig. 4 Predictive values for airborne fuel pump pressure degradation |
| 图选项 |
4.3 LSTAR模型与AR模型的对比 自回归(Auto-Regressive,AR)模型是广泛使用的一种时间序列模型[23]。计算自回归模型式(6) 的残差,与LSTAR模型式(7) 的残差进行对比,结果如表 5所示。LSTAR模型的误差平方和小于AR模型。且LSTAR模型的J-B统计量显著性概率为0.521,接受残差服从正态分布的原假设,AR模型在0.1水平下拒绝了正态分布的原假设,可知LSTAR模型更符合实际退化曲线。
表 5 LSTAR模型与AR模型对比 Table 5 Comparison of LSTAR and AR models
| 模型 | 误差平方和 | J-B统计量 | 显著性概率 |
| LSTAR | 66.867 | 1.305 | 0.521 |
| AR | 82.529 | 4.619 | 0.099 |
表选项
以C1表示LSTAR模型的残差,C2表示AR模型的残差,做残差分布的Q-Q(Quantile-Quantile)图,如图 5所示。可见, C1更靠近对角线,与正态分布更为接近,即LSTAR模型较AR模型提高了模型精度。
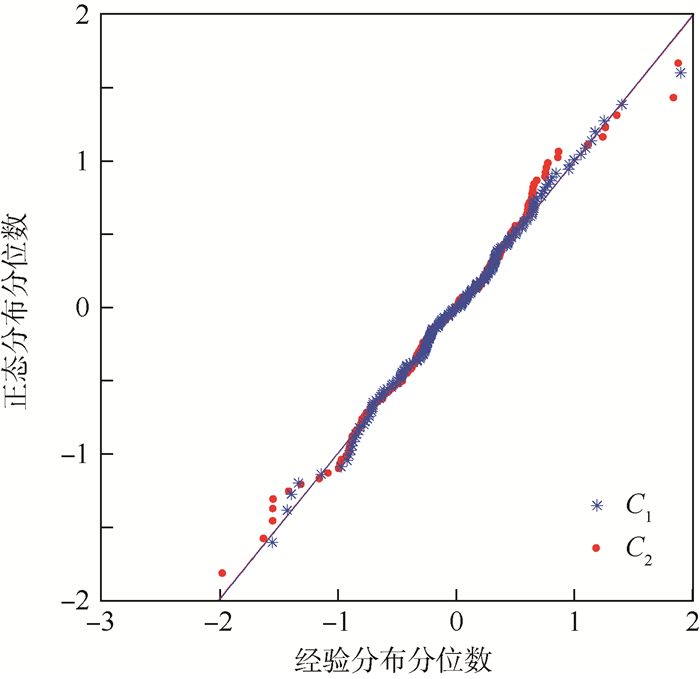 |
| 图 5 LSTAR模型与AR模型残差Q-Q图 Fig. 5 Residual Q-Q diagram about LSTAR and AR models |
| 图选项 |
5 结论 本文针对机载燃油泵性能退化的非线性、多阶段特性,区别于现有的先确定拐点再进行多阶段建模方法,研究了基于LSTAR模型的退化数据建模方法,应用平滑转换自回归项驱动的方法解决了多阶段建模问题,具有思路清晰、方法简单和精度高的优点,对指导实际工程应用具有重要意义。
1) 根据转换函数的斜率参数,证明机载燃油泵的性能退化过程是一个缓慢的过程。
2) 建立了机载燃油泵性能退化的LSTAR模型,根据转换函数值证明机载燃油泵的性能退化是一个非线性、多阶段过程。
3) 针对实测的机载燃油泵性能监测数据,验证了本文研究的基于LSTAR模型的非线性、多阶段退化模型明显优于线性自回归模型。
参考文献
| [1] | 冯威, 于劲松, 袁海文. 机载燃油系统在线实时健康管理[J].北京航空航天大学学报, 2013, 39(12): 1639–1643. FENG W, YU J S, YUAN H W. Online real-time health management for aerial fuel delivery system[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(12): 1639–1643.(in Chinese) |
| [2] | 景博, 杨洲, 迟小泉, 等. 系统健康管理及其在航空航天领域的应用[M].北京: 国防工业出版社, 2014: 3-7. JING B, YANG Z, CHI X Q, et al. System helath management with aerospace application[M].Beijing: National Defence Industry Press, 2014: 3-7.(in Chinese) |
| [3] | TSENG S T, HAMADA M S, CHIAO C H. Using degradation data to improve fluorescent lamp reliability[J].Journal of Quality Technology, 1995, 27(4): 363–369. |
| [4] | BAE S J, KVAM P H. A change-point analysis for modeling incomplete burn in for light displays[J].ⅡE Transaction, 2006, 38(6): 489–498. |
| [5] | BAE S J, YUAN T, NING S, et al. A Bayesian approach to modeling two-phase degradation using change-point regression[J].Reliability Engineering and System Safety, 2015, 134(2): 66–74. |
| [6] | 黎明. 带随机拐点的退化失效建模与分析方法研究[D]. 长沙: 国防科学技术大学, 2009. LI M.Reserch on the degradation-failure modeling and analysis methods of degradation path with random change-points[D]. Changsha:National University of Defense Technology, 2009(in Chinese). |
| [7] | 鄢伟安, 宋保维, 段桂林, 等. 基于两阶段维纳退化过程的液力耦合器可靠性评估[J].系统工程与电子技术, 2014, 36(9): 1882–1886. YAN W A, SONG B W, DUAN G L, et al. Reliability evaluation of LCD based on two-phase Wiener degradation process[J].Systems Engineering and Electronics, 2014, 36(9): 1882–1886.DOI:10.3969/j.issn.1001-506X.2014.09.34(in Chinese) |
| [8] | 刘君强, 谢吉伟, 左洪福, 等. 基于随机维纳过程的航空发动机剩余寿命预测[J].航空学报, 2015, 36(2): 564–574. LIU J Q, XIE J W, ZUO H F, et al. Residual lifetime prediction for aeroengines based on Wiener process with random effects[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(2): 564–574.(in Chinese) |
| [9] | LU C J, MEEKER W O. Using degradation measures to estimate a time-to-failure distribution[J].Technometrics, 1993, 35(2): 161–174.DOI:10.1080/00401706.1993.10485038 |
| [10] | BAE S J, KVAM P H. A nonlinear random-coefficients model for degradation testing[J].Technometrics, 2004, 46(4): 460–469.DOI:10.1198/004017004000000464 |
| [11] | 徐正国, 周东华. 基于马尔可夫链蒙特卡罗的实时可靠性预测方法研究[J].机械强度, 2007, 29(5): 765–768. XU Z G, ZHOU D H. Real-time reliability prediction method based on Markov chain Monte Carlo[J].Journal of Mechanical Strength, 2007, 29(5): 765–768.(in Chinese) |
| [12] | SI X S, WANG W, HU C H, et al. Remaining useful life estimation based on a nonlinear diffusion degradation process[J].IEEE Transactions on Reliability, 2012, 61(1): 50–67.DOI:10.1109/TR.2011.2182221 |
| [13] | WANG X L, BALAKRISHNAN N, GUO B. Residual life estimation based on a generalized Wiener degradation process[J].Reliability Engineering & System Safety, 2014, 124(4): 13–23. |
| [14] | TERASVIRTA T. Specification estimation, and evaluation of smooth transition autoregressive models[J].Journal of the American Statistical Association, 1994, 89(425): 208–218. |
| [15] | TERASVIRTA T, TJ?STHEIM D, GRANGER C W J. Modelling nonlinear economic time series[M].Oxford: Oxford University Press, 2010: 37-40. |
| [16] | 李娟, 景博, 羌小清, 等. 基于样本分位数的机载燃油泵故障状态特征提取及实验研究[J].航空学报, 2016, 37(9): 2851–2863. LI J, JING B, QIANG X Q, et al. Fault states feature extraction and experimental study for airborne fuel pumps based on sample quantile[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(9): 2851–2863.(in Chinese) |
| [17] | SANDBERG R. Critical values for linearity tests in time-varying smooth transition autoregressive models when data are highly persistent[J].The Econometrics Journal, 2008, 11(3): 638–647.DOI:10.1111/ectj.2008.11.issue-3 |
| [18] | LUNDBERGH S, TERASVIRTA T, VAN DIJK D. Time-varying smooth transition autoregressive models[J].Journal of Business and Economic Statistics, 2003, 21(1): 104–121.DOI:10.1198/073500102288618810 |
| [19] | 王燕. 应用时间序列分析[M].北京: 中国人民大学出版社, 2008: 88-89. WANG Y. Applied time series analysis[M].Beijing: China Renmin University Press, 2008: 88-89.(in Chinese) |
| [20] | 张晓峒. 计量经济学基础[M].3版天津: 南开大学出版社, 2001: 274-277. ZHANG X T. Basic econometrics[M].3rd edTianjin: Nankai University Press, 2001: 274-277.(in Chinese) |
| [21] | MACKINNON J G. Approximate asymptotic distribution functions for unit-root and cointegration tests[J].Journal of Business & Economic Statistics, 1994, 12(2): 167–176. |
| [22] | AGENOR P R, MCDERMOTT C J, PRASAD E S. Macroeconomic fluctuations in developing countries:Some stylized facts[J].The World Bank Economic Review, 2000, 14(2): 251–285.DOI:10.1093/wber/14.2.251 |
| [23] | 刘大同, 周建宝, 郭力萌, 等. 锂离子电池健康评估和寿命预测综述[J].仪器仪表学报, 2015, 36(1): 1–16. LIU D T, ZHOU J B, GUO L M, et al. Survey on lithium-ion battery health assessment and cycle life estimation[J].Chinese Journal of Scientific Instrument, 2015, 36(1): 1–16.(in Chinese) |
