在任意曲面射线寻迹研究领域,国内外****近年来开展了大量的研究工作,文献[3]采用LOS-Floyd算法对光滑与非光滑凸曲面结构进行了射线寻迹研究,基于视距的搜索算法未考虑光线传播方向,射线为非光滑折线。文献[4]采用了动态规划法和遗传算法求解短程线,需要遍历所有点,对采样点分辨率要求较高。文献[5]提出了一种新颖的最小夹角的曲面寻迹方法,未考虑射线初始传播方向,复杂曲面易因多个夹角相等而陷入局部最优,造成射线“绕圈”现象。近年来文献[6-9]结合非均匀有理B样条(NURBS)曲面采样点离散化后局部区域寻优的方法开展了寻迹研究,极大程度上发展了任意曲面的寻迹方法及其在UTD上的应用,但对由大量参数面片组成的复杂结构采用NURBS寻迹方法时,难以精确解决射线在相邻参数片面的过渡问题,数值精度同样取决于采样精度,对于非光滑曲面及难以用NURBS表达的结构求解困难,因此面向工程实用的UTD方法仍然存在发展空间。
考虑到网格数据优越的几何构造、路径表达及分析能力,基于网格的UTD数值分析算法可望为任意曲面的射线寻迹问题提供解决途径。文献[10]提出了基于投影的三角网格寻迹方法,仅解决了球体寻迹问题。经典的节点搜索方法多采用Dijkstra类似方法[11-12],该方法在寻迹过程中搜索面积过大,对于电大尺寸的求解目标易导致寻迹速度很慢,不利于工程分析,此外这些方法没考虑剖分形成三角平面片产生的“虚假边缘”带来的噪声。本文基于三角网格模型,构造了支持快速搜索及拟合的任意曲面的网格数据链表,采用切割面自适应调整的短程线几何代数算法,遵循广义费马原理,对任意曲面寻优,在提高搜索精度的同时可有效避免局部最优问题,然后结合曲率对任意2个点曲线拟合求弧长,进而消除三角片的剖分带来的累积误差,之后结合射线亮区场与绕射场模型,实现了三角网格几何绕射(TM-UTD)方法,基于典型模型对算法进行了验证。
1 相关定义与模型 1.1 射线寻迹问题描述 研究基于网格的UTD射线寻迹之前,首先对射线寻迹进行描述。UTD是一种电大尺寸目标高频求解技术,其本质是源点到观测点的不同射线的寻迹问题,包含了直射线、反射线、绕射线、曲面绕射线、边缘绕射线及尖端绕射线等。其中直射线和反射线能到达的区域称为明区,绕射线及其组合能到达的区域称为暗区,以复杂结构为例,各型射线的示意如图 1所示。
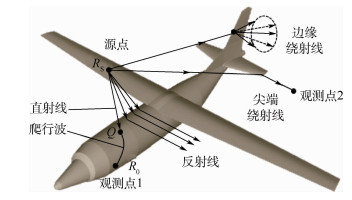 |
| 图 1 射线寻迹问题描述 Fig. 1 Description of ray tracing problem |
| 图选项 |
UTD理论应用到工程问题中一般分为两步:第1步,射线寻迹;第2步,计算各类射线的并矢绕射系数。其中射线寻迹问题是最为关键的一步。射线寻迹问题的描述,如图 1所示,射线类型包括了直射线、爬行波、反射线、尖端绕射线和边缘绕射线,其中传统UTD方法对于直射线、反射线、边缘绕射线、尖端绕射线研究较多,因为这些射线都是考虑的直线与面或点之间的几何关系,利用费马原理可相对容易地求解。而对于爬行波的求解,则由于曲面的表达式未知而寻迹困难。射爬行波求解问题的核心是求短程线,如图 1所示:从源点RS点到观察点R0点,两点之间只有一条曲线能保证其路径长度为最小值,这条特定的曲线称为短程线,需要在机身一定范围内寻找一组切点[Q1, Q2, …],之后寻找各个切点沿着掠入射方向到观察点的短程线QiR0,射线RSR0=RSQi+QiR0,因此Qi点及曲线QiR0的求解即射线寻迹的核心问题。
1.2 网格模型的链表设计 本文算法基于.NAS网格数据文件,该文件是由网格数据和拓扑结构两部分构成的,用M表示求解对象的三角网格模型,它是由三维空间中的三角片通过边和顶点连接而成的分片线性曲面。M=(V, E),V为M中所有顶点的集合,E为M中全部边的集合。为了便于算法实现,本文设计了数据存储链表。
网格模型的数学几何表达如图 2所示。假设v为顶点, Av为E中所有与顶点v相连的边,Pv为Av中所有与顶点v相连点的顶点v的集合,Tv为所有与顶点v相连三角片的集合,P为顶点v及其相关属性Pv、Av和Tv的集合,Pv、Av、Tv和P的定义分别为
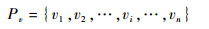 | (1) |
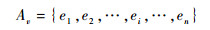 | (2) |
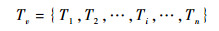 | (3) |
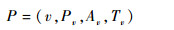 | (4) |
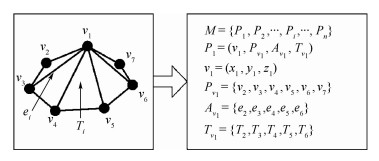 |
| 图 2 三角网格模型的数学几何表达 Fig. 2 Mathematic and geometrical expression of triangle mesh model |
| 图选项 |
1.3 爬行波射线场模型 凸曲面爬行波示意图如图 3所示。直射线及反射线对应的直射场和反射场可采用文献[13-14]提出的PO模型。
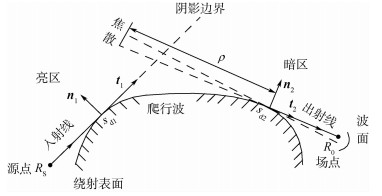 |
| sd1,sd2-入射采样点和出射点;ni-顶点连接的第i个三角片的单位法矢;t1,t2-初始传播方向和出射方向;ρ-射线焦散距离。 图 3 凸曲面爬行波示意图 Fig. 3 Schematic diagram of convex surface creeping wave |
| 图选项 |
本文主要考虑相对复杂的暗区场,爬行波射线是其主要的贡献,考虑阴影边界后的UTD公式可表示为
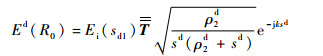 | (5) |
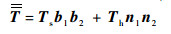 | (6) |
式中:Ed(R0)为R0点处的场强值;Ei(sd1)为第1个绕射点处的场强值;
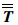
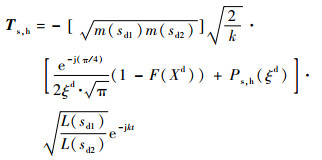 | (7) |
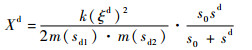 | (8) |
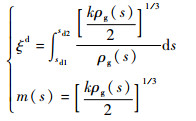 | (9) |
式中:F(Xd)为Fock函数,Xd为Fock函数变量;Ps, h(ξd)为Pekeris函数,ξd为Pekeris函数变量;

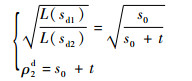 | (10) |
将式(7)和式(8)代入式(5),则有
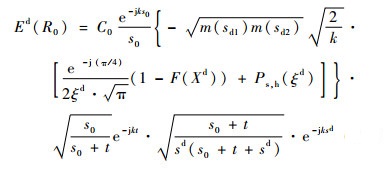 | (11) |
式中:C0为源点RS的初始场强值;s0为源点RS到一个绕射点sd1的欧式距离,对于入射波为平面波; ρg(s)为测地线上任意一点在切向方向上的曲率半径,其表达式为
 | (12) |
测地线上的采样点足够密(
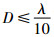
2 射线寻迹算法设计与实现 2.1 爬行波寻迹算法流程 如图 3所示,按照费马原理,从源点RS出发的射线会沿曲面的切线方向t1到达曲面后,被限制在沿曲面上测地线轨迹sd1sd2前进到达出射点sd2,最后沿着出射方向t2到场点R0,测地线sd1sd2也称为短程线,该射线的计算流程如下:
1)?采用式(1)~式(4),生成求解目标的网格链表矩阵。
2)?计算入射方向下,可能的入射采样点。
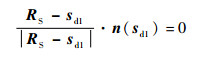 | (13) |
 | (14) |
式中:n(sd1)和n(sd2)分别为sd1和sd2的法向量。
式(13)称为入射候选点条件,式(14)称为出射候选点基本条件。
3) ?筛选入射采样点。对采样点逐一判断是否存在遮挡,如果存在遮挡,则剔除该点作为采样点的资格。
4) ?对入射采样点采用适用于任意凸曲面射线寻迹算法求短程线。
5)?依据法向量和曲率拟合短程线弧长。
因此,寻迹方法依赖于3个技术点,离散点法矢求解、遮挡判别和适用于任意凸曲面射线寻迹算法,其实现方法见2.2节。
2.2 离散点曲面高精度法矢求解 从式(9)可知,离散点的法向信息及曲率对场强计算结果影响较大,因此需要对三角网格数值模型的离散点法矢精确计算,传统方法采用面积加权[15],即以面积作为加权因子,对与离散点相接的面的法向量加权获得法矢,研究表明该方法法矢计算精度不足以满足场计算的精度,这并未考虑顶点邻近域的三角形的形状,会造成计算偏差,为减小法矢的计算偏差,本文采用面积-内角率加权法求解法矢,法矢表达式为
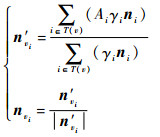 | (15) |
式中:n′vi为vi点法矢;nvi为vi点单位法矢;Ai为顶点连接的第i个三角片的面积;γi为顶点所在的第i个三角形的内角占内角和(180°)的比率。
以半径为1 m的球体为例进行该方法的准确性验证,按照f=300 MHz,
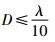
表 1 法矢计算精度对比 Table 1 Computation precision of normal vector
| 参量 | x/m | y/m | z/m | 模长/m |
| 理论 | -0.0074 | 0.1002 | 0.9877 | 1 |
| 本文算法 | -0.0016 | 0.1222 | 0.9925 | 0.99999165 |
表选项
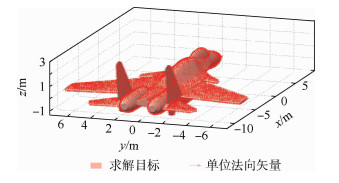 |
| 图 4 复杂结构法矢计算 Fig. 4 Normal vector computation for complex structure |
| 图选项 |
2.3 采样点遮挡判断 点源入射时遮挡示意图如图 5所示。采用式(13)可求得一组采样点,还需要判断源点与采样点的连接线段是否与除该采样点邻域面外的其他三角面相交,若相交则该采样点不是合理的采样点。这里采用的算法是:如果在源点RS和采样点sd1之间连一条线,则RS指向sd1的方向就是来波方向,考察线段RSsd1和组成散射体的其他面片是否有交点,若存在交点DS,则认为当前面片被遮挡。
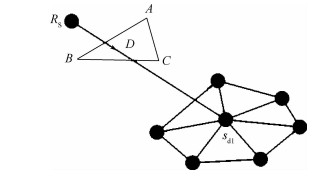 |
| 图 5 点源入射时遮挡示意图 Fig. 5 Schematic diagram of shelter from a point source incidence |
| 图选项 |
假设组成散射体的任意一个面片的3个顶点为A、B和C,源点的坐标向量为S, 采样点坐标向量为R,3个顶点向量为A、B和S,ABC组成的面片上任意点可以表示为
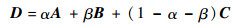 | (16) |
若α、β及1-α-β均在区间[0, 1]内,则表示点D就在三角形ABC内部,否则在三角形外面。线段RSsd1上任意一点的向量表达式为
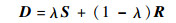 | (17) |
式中:λ为点S到点R的距离。若λ在[0, 1]内,则表示该点在线段上面,将式(17)代入式(16), 则可求解交点D。
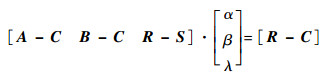 | (18) |
det[A-C? B-C? R-S]=0时,方程无解,即射线未被遮挡,否则依次求解α、β、1-α-β及λ,有任意一个参数不在区间[0,1]内时,则线段未被该面片遮挡,依次循环,完成该采样点的存在性判别。
2.4 切割面自适应寻迹方法 在顶点处作一个以这些虚平面的法向量平均值为法向的基平面,垂直该平面且经过始末两点(源点和场点)的直线的平面称为切割面,应用切割面与网格曲面依次相交, 交线称为短程线,文献[16]率先应用该方法。
这种近似方法并未考虑曲面法向突变及短程折线对真实结果的影响,本文依据当前点法平面的几何信息不断地自适应调整切割面, 直至满足出射条件,后利用细微三角形3个顶点及其法矢拟合多项式,消除网格剖分过程中产生的“虚假边缘”误差。自适应切割面调整的算法流程如下:
1) ?记入射点为S1,加入测地线S′向量,采用(RS-sd1)/|RS-sd1|计算切向传播方向d1。
2) ?由式(15)求S1点的法向量nS1。
3)?计算由d1和nS1构成的平面与前向三角形的交点记为S2。
4)?采用步骤2)和步骤3)的方法,逐渐调整传播方向和切割面,依次求解测地线上的离散点S3, …, Si, Si+1。
寻迹结束条件为以下之一:①到达网格的边界;②测地线长度到达给定值;③测地线自交了;④离散点切向可达场点。符合条件④则为一条合格的备用测地线。
备用测地线是基于三角网格的,因三角网格顶点真实但存在“虚假边缘”,由此会带来测地线累积误差。本文利用相邻测地点间法矢特征,弧面拟合减弱剖分误差。切割面调整寻迹方法示意图,如图 6所示。如果备用测地点非网格顶点,则将备用测地顶点按矢量方向投影到圆弧,获取真实测地顶点,求测地线间弧长的方法如下:
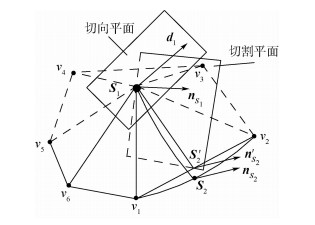 |
| S′2-未修正的传播交点;n′S2-未修正传播交点的法向量。 图 6 切割面调整寻迹方法示意图 Fig. 6 Schematic diagram of cutting surface adjustment tracing method |
| 图选项 |
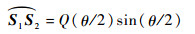 | (19) |
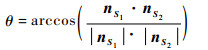 | (20) |
式中:Q为测地点间的欧式距离;θ为两相邻测地点间法向量的夹角。
3 算法验证及应用 以下计算选用的硬件资源配置如下:内存4G,CPU2.3G,集成显卡(NVIDIA GT550M)。首先采用不可展曲面对寻迹算法的准确性进行验证,后对球、柱、锥及复杂飞机结构进行寻迹。之后利用UTD爬行波模型,对场强仿真结果进行验证,进一步说明寻迹算法的准确性。
3.1 不可展凸曲面爬行波寻迹精度验证 采用本文提出的TM-tracing算法对不可展球体进行爬行波寻迹,目标球体半径为1m,掠入射方向为(1,1,0),入射点为(0,0,1),出射点为(0.0485,0.0468,-0.9976),将寻迹结果与基于三角网格的最小夹角法[5]和理论方法进行对比,对比结果如图 7与表 2所示。
 |
| 图 7 球体上短程线寻迹 Fig. 7 Geodesic tracing on a sphere |
| 图选项 |
表 2 球体上短程线寻迹结果对比 Table 2 Comparison of geodesic tracing results on a sphere
| 方法 | 长度/m | 偏差/m | 误差/% | 时间开销/s |
| 理论方法 | 3.1237 | 0.0496 | 1.61 | 2.8 |
| 最小夹角法[5] | 3.6925 | 0.6184 | 20.11 | 1.2 |
| 本文算法 | 3.0741 |
表选项
从图 7及表 2可知,本文算法与理论方法能较好地吻合,误差仅为1.61%,相对于最小夹角法,本文算法射线传播方向和法矢不断调整,可良好逼近理论的爬行波,又因“变测地线段为测地弧线”的思想,使得爬行波射线长度也与实际偏差较小。
但不可否认的是本文算法相对于最小夹角法时间开销增大了1倍,其主要原因本文算法需要在以下3个技术点增加开销:①为保证精度,本文算法的射线不严格走三角网格边,需要实时计算行走各点的法矢与曲率;②需要对每一节点向曲面映射;③对射线节点矩阵变折线为弧线,向真实目标表现逼近。考虑到速度与精度的平衡,本文算法的寻迹速度是合理、工程可接受的。
3.2 不可展凸曲面爬行波寻迹收敛性验证 进一步选取椭球体验证本文算法的收敛性,椭球体3轴分别为2、1和1 m,采用本文算法以及最直测地线算法[16]对不可展椭球体进行爬行波寻迹,入射点为(-2,0,0),掠入射方向为(1,2,2),射线寻迹对比结果如图 8和表 3所示。
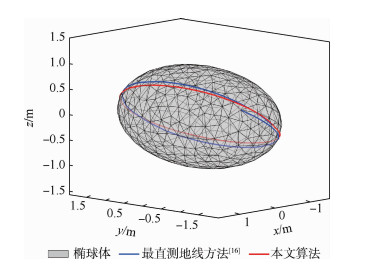 |
| 图 8 寻迹结果收敛性对比 Fig. 8 Tracing result convergence comparison |
| 图选项 |
表 3 椭球体上测地线的结束点与长度对比 Table 3 Finishing point and length of geodesic on ellipsoid
| 寻迹结果 | 数值 | |
| 起点 | (-1.9904, 0.0581, 0.0791) | |
| 初始方向 | (1, 2, 2) | |
| 结束点 | 理论方法 | (-1.9904, 0.0581, 0.0791) |
| 本文算法 | (-1.9672, 0.0381, 0.0238) | |
| 最直测地线方法[16] | (-1.8932, 0.1692, -0.1424) | |
| 长度/m | 理论方法 | 5.141 6 |
| 本文算法 | 5.230 8 | |
| 最直测地线方法[16] | 5.420 1 | |
| 寻迹时间/s | 本文算法 | 2.85 |
| 最直测地线方法[16] | 2.75 | |
表选项
对比结果表明,本文算法相对于最直测地线方法在寻迹结束点及长度与理论值较好地吻合,爬行波寻迹可根据当前节点法矢和3.1节点传播方向而动态调整切割面,而最直测地线方法因忽略目标曲率变化对射线传播方向的扭矩效应,出现了不稳定,导致射线不闭合。从表 3可知,由于采用了更高效的网格链表结构,本文算法与最直测地线方法在寻迹时间上相差不大。
图 9(a)~图 9(d)分别为应用本文算法对可展曲面、不可展曲面、带边界的可展曲面和复杂曲面等常见结构的寻迹结果,其中发射点位于表面,向四周爬行波寻迹,寻迹结果表明本文提出的精确法矢下切割面自适应的凸曲面爬行波寻迹方法除了对球、柱、锥等初等几何体适用外,对任意复杂的凸曲面也适用。
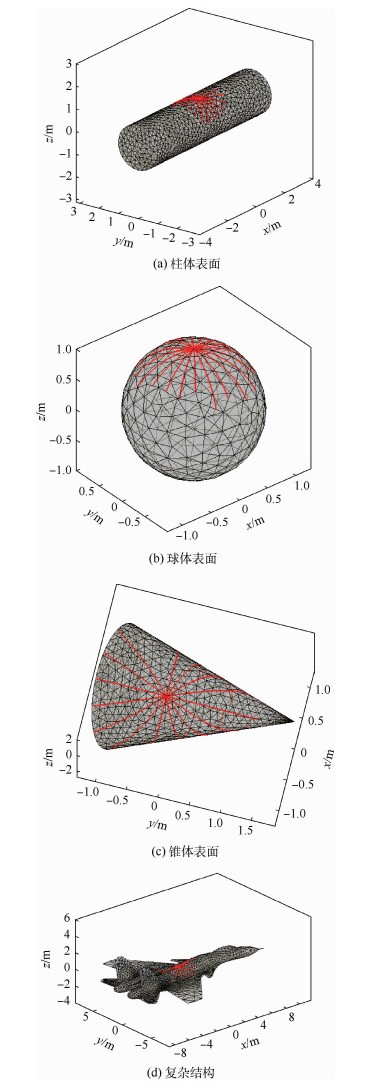 |
| 图 9 柱体表面、球体表面、锥体表面及复杂结构爬行波寻迹 Fig. 9 Creeping wave tracing on cylinder surface, sphere surface, cone surface and complex structure |
| 图选项 |
3.3 凸曲面寻迹方法在UTD中的应用 为进一步验证本文提出的爬行波射线寻迹方法的准确性,对平面波入射下柱体阴影区的场强分布进行计算。阴影区场的求解配置如图 10所示。仿真参数如下:入射的平面波电场强度E=1 V/m, 垂直极化,圆柱体半径r=1 m,球坐标体系下,场点观测角度为(-30°,30°),场点到圆心半径β=2 m。TM-UTD圆柱体阴影区场强值与理论值的对比结果如图 11所示。
 |
| 图 10 理想导体圆柱面绕射场求解配置图 Fig. 10 Configuration diagram of diffraction field solve on a perfect electric conductor cylinder surface |
| 图选项 |
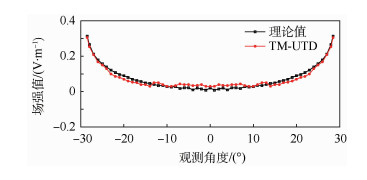 |
| 图 11 圆柱阴影区场强值对比 Fig. 11 Comparison of shadow field strength on a cylinder |
| 图选项 |
圆柱体阴影区场强值的求解结果表明:基于三角网格的任意凸曲面射线寻迹算法的场强计算值与理论值能较好地吻合,这也从射线寻迹的应用层次验证了本文方法对爬行波寻迹的准确性。
4 结论 针对工程中电大尺寸目标难以用简单解析式表达,导致高频电大尺寸求解困难的现状。本文采用工程中较易获取的网格数据,针对性提出了:①满足快速多边搜索条件的任意数值网格存储链表;②基于面积-角率加权的高精度法矢求解方法;③基于切割面自适应拟合的凸曲面爬行波寻迹方法。
并通过典型球、柱、椎、飞机上爬行波寻迹的算例,验证了:
1) ?本文所提出的爬行波寻迹方法具有较高的精度和速度,寻迹偏差小于1.61%,1万网格的寻迹速度约为2.8 s。
2) ?本文算法可适用于任意数值凸曲面的射线寻迹问题。
本文算法可进一步应用于电大尺寸目标加载条件下的装机方向图和装机天线间隔离度计算,这也是下一步的研究工作。
参考文献
| [1] | 苏东林, 谢树果, 戴飞, 等. 系统级电磁兼容性量化设计理论与方法[M].北京: 国防工业出版社, 2015: 115.SU D L, XIE S G, DAI F, et al. The theory and method of quantification design on system-level electromagnetic compatibility[M].Beijing: National Defense Industry Press, 2015: 115.(in Chinese) |
| [2] | FU S, ZHANG Y H, HE S Y, et al. Creeping ray tracing algorithm for arbitrary NURBS surfaces based on adaptive variable step euler method[J].International Journal of Antennas and Propagation, 2015, 2015: 604861. |
| [3] | JONATHAN R P, ERIC L S. Exact geodesics and shortest paths on polyhedral surfaces[J].IEEE Transactions on Pathtern Analysis and Machine Intelligence, 2009, 31(6): 1006–1015.DOI:10.1109/TPAMI.2008.213 |
| [4] | 王冰切, 苏东林, 张晓雷. 飞机表面绕射射线的寻迹方法[J].北京航空航天大学学报, 2007, 33(7): 785–788.WANG B Q, SU D L, ZHANG X L. Discrete ray path tracing on aircraft[J].Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(7): 785–788.(in Chinese) |
| [5] | 陈志贤, 苏东林, 刘焱, 等. 任意曲面上射线的寻迹方法[J].北京航空航天大学学报, 2013, 39(5): 665–669.CHEN Z X, SU D L, LIU Y, et al. Ray path tracing on discrete surface[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(5): 665–669.(in Chinese) |
| [6] | WANG N, DU X X, WANG Y, et al. Double diffraction and double reflection in NURBS-UTD method[J].Microwave and Optical Technology Letters, 2013, 55(7): 1549–1553.DOI:10.1002/mop.27652 |
| [7] | CHEN X, HE S Y, YU D F, et al. Geodesic computation on nurbs surfaces for UTD analysis[J].IEEE Antennas and Wireless Propagation Letters, 2013, 12: 194–197.DOI:10.1109/LAWP.2013.2245291 |
| [8] | WANG N, LIANG C H, YUAN H B. Calculation of pattern in UTD method based on NURBS modeling with the source on surface[J].Microwave and Optical Technology Letters, 2007, 49(10): 2492–2498.DOI:10.1002/mop.22727 |
| [9] | CHEN X, HE S Y, YU D F, et al. Ray-tracing method for creeping waves on arbitrarily shaped nonuniform rational B-splines surfaces[J].Journal of the Optical Society of America A, 2013, 30(4): 663–670.DOI:10.1364/JOSAA.30.000663 |
| [10] | RUAN Y C, ZHOU X Y, JESSIE Y C, et al.The UTD analysis to EM scattering by arbitrarily convex objects using ray tracing of creeping waves on numerical meshes[C]//IEEE Antennas and Propagation Society International Symposium.Piscataway, NJ:IEEE Press, 2008:1-4. |
| [11] | SURAZHSKY V, SURAZHSKY T, KIRSANOV D, et al. Fast exact and approximate geodesics on meshes[J].ACM Transactions on Graphics, 2005, 24(3): 553–560.DOI:10.1145/1073204 |
| [12] | FRANK W. Ray tracing with PO/PTD for RCS modeling of large complex objects[J].IEEE Transactions on Antennas and Propagation, 2006, 54(6): 1797–1806.DOI:10.1109/TAP.2006.875910 |
| [13] | PATHAK P H, BURNSIDE W D, MARHEKA R J. A uniform GTD analysis of the diffraction of electromagnetic waves by a smooth convex surface[J].IEEE Transactions on Antennas and Propagation, 1980, 28(5): 631–642.DOI:10.1109/TAP.1980.1142396 |
| [14] | 汪茂光. 几何绕射理论[M].西安: 西安电子科技大学出版社, 1994: 198-210.WANG M G. Geometrical theory of diffraction[M].Xi'an: Xidian University Press, 1994: 198-210.(in Chinese) |
| [15] | 神会存, 周来水. 基于离散曲率计算的三角网格模型优化调整[J].航空学报, 2006, 27(2): 318–324.SHEN H C, ZHOU L S. Triangular mesh regularization based on discrete curvature estimation[J].Acta Aeronautica et Astronautica Sinica, 2006, 27(2): 318–324.(in Chinese) |
| [16] | MARTINEZ D, VELHO L, CARVALHO P C. Computing geodesics on triangular meshes[J].Computers & Graphics, 2005, 29(5): 667–675. |
