当钝头细长旋成体大攻角飞行时，其背风面会出现非对称涡结构，且其方向具有随机性^[1]。对于采用钝头细长前体的战术导弹而言，这种大攻角绕流的非对称性所诱导出的偏航力矩甚至大于导弹方向舵的控制能力，严重降低导弹的可控性，使其偏离飞行轨道，致使任务失败。因此，作为当前空气动力学领域的研究热点和难点，国内外对细长体大攻角非对称性问题开展了大量研究^[2-5]。一方面研究有效的人工干预手段，以推迟非对称流动出现的起始攻角，减小甚至消除非对称涡引起的侧向力和偏航力矩。另一方面，以利用非对称流动所引起的侧向力和偏航力矩为目的，针对消除非对称涡结构的随机性进行研究，进而通过控制流动的非对称结构，得到确定的侧向力和偏航力矩并加以利用。为了消除非对称涡结构的随机性，国内外尝试了吹气、边条、鸭舌翼、开槽、粗糙带等多种手段进行控制^[6-8]，并取得了不同程度的效果。其中，Moskovitz等^[9]通过实验方法，在细长旋成体头部引入微粒作为人工扰动，成功地得到了确定的、可重复的侧向力。所以，通过头部施加人工微扰动的方法可以确定钝头细长旋成体的非对称涡结构。但是人工微扰动对非对称涡结构起主控作用的机理还并不清楚，其中人工微扰动形状对非对称涡结构是否存在影响及影响形式并不明确。
本文利用数值模拟的方法，在雷诺数Re_D=1.54×10⁵条件下，分别在钝头体头部同一扰动位置(周向角θ=90°，子午角γ=10°)施加半球形、D型、方形3种形状的微扰动块，计算并分析攻角α=50°时人工微扰动形状对钝头细长旋成体非对称涡结构的影响。
1 研究方法 1.1 数值方法 本文针对钝头体整机模型进行研究，对于其大攻角下复杂的非对称背涡结构，需要选择合适的湍流方程。对于钝头体大攻角的流动分离现象的研究，湍流的动量输运作用可使流动依附于壁面。层流模型对于湍流的输运作用估计过小，流动分离现象发生过于频繁^[10]。而κ-ε两方程模型对于湍流的输运作用估计过度，使得流动分离过分推迟，甚至不发生分离。因此本文采用工程上应用广泛的κ-ω SST混合湍流模型^[11]。因为对于κ-ε两方程湍流模型，可以很好地模拟远离壁面的而充分发展的湍流流动，而κ-ω两方程湍流模型则可以更好地模拟各种压力梯度下的边界层问题。Menter^[12]结合2种模型的特点提出的κ-ωSST混合湍流模型，在近壁面保留原始的κ-ω模型特点，远离壁面的地方应用κ-ε湍流模型。
离散方程采用有限体积法，求解方法采用SIMPLEC算法，远场采用压力远场条件，物面满足无滑移边界条件。计算风速V_∞=35 m/s，基于钝头体直径的雷诺数Re_D=1.54×10⁵，模型攻角为α=50°。为保证计算准确性，计算网格数量为500万，且第一层网格尺寸满足y⁺＜1。
1.2 物理模型 计算模型如图 1(a)所示为钝头旋成体，其头部为球体的一部分，且其钝度B=80%(钝度=头部圆弧半径/模型后体等值段半径)，总体长度为X=1 060 mm，后体直径D=66 mm，即总长细比X/D=16。

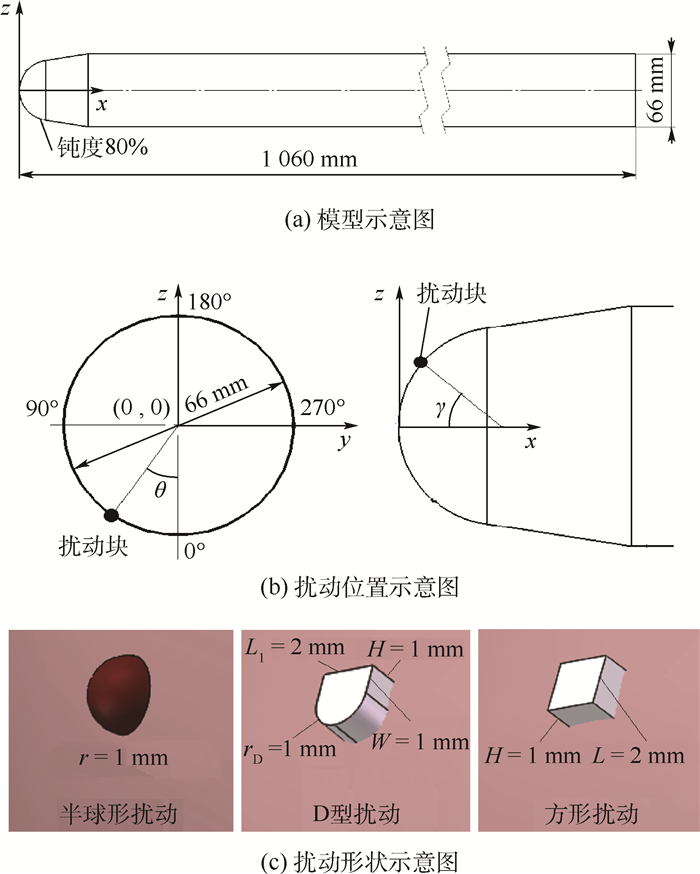图 1 模型与人工扰动 Fig. 1 Model and artificial perturbation

图选项

人工扰动位置定义如图 1(b)所示，其周向位置用周向角表示，定义为从模型尾端向前看，扰动位置到x轴的垂线与z轴负方向的顺时针夹角θ。扰动轴向位置用子午角表示，其定义为扰动位置到钝头球心的连线与x轴负向的夹角γ。本文计算模型为固定扰动位置周向角θ=90°、子午角γ=10°。
本文针对3种扰动块形状进行研究，如图 1(c)所示，分别为半球形扰动、D型扰动和方形扰动。半球形扰动为半径r=1 mm的半球形，其球心落在钝头体头部扰动位置周向角θ=90°、子午角γ=10°处。D型扰动高H=1 mm，如图 1(c)所示，由半柱体和长方体组合而成，其长方体长度L₁=2 mm，宽度W=1 mm，柱体半径r_D=1 mm，其柱体轴心在钝头体头部扰动位置周向角θ=90°、子午角γ=10°处，且半圆弧中点指向钝头体头部顶点。方形扰动高H=1 mm，其垂直于高的截面为边长L=2 mm的正方形，其正方形中心落在钝头体头部扰动位置周向角θ=90°、子午角γ=10°处。其中定义半球形扰动为无棱边的扰动块，D型扰动为半棱边扰动块，方形扰动位全棱边扰动块，3种扰动形式的选择依据为从半球体的无棱形式向方体的多棱形式的一个演化过渡。
1.3 数值方法验证 通过试验数据对计算结果进行验证，确定计算结果的可靠性。对比计算数据和试验数据的条件为风速V_∞=35 m/s，基于钝头体直径的雷诺数Re_D=1.54×10⁵，模型攻角为α=40°。扰动块为半径r=1 mm的半球扰动，扰动位置周向角θ=90°、子午角γ=40°。试验风洞的来流湍流度为0.08%，开口试验段尺寸为：2.5 m×1.5 m×1.5 m。图 2给出了计算数据与试验数据的对比结果，从图 2(a)所示的截面法向力C_Ns沿轴向的变化曲线可以看出，其变化规律基本保持一致，截面x/D=2之后存在一定误差, 主要是因为钝头体大攻角飞行时，其多涡系背涡结构非常复杂，很难完全模拟出相同涡系结构。图 2(b)为截面x/D=1的压力分布C_p曲线的计算结果和试验结果对比，从图中数据可见，计算结果与试验数据吻合较好(图中θ_s为截面周向角)。综合判断，计算方法对于模拟钝头旋成体大攻角非对称背涡结构是可行的，其计算结果可信。

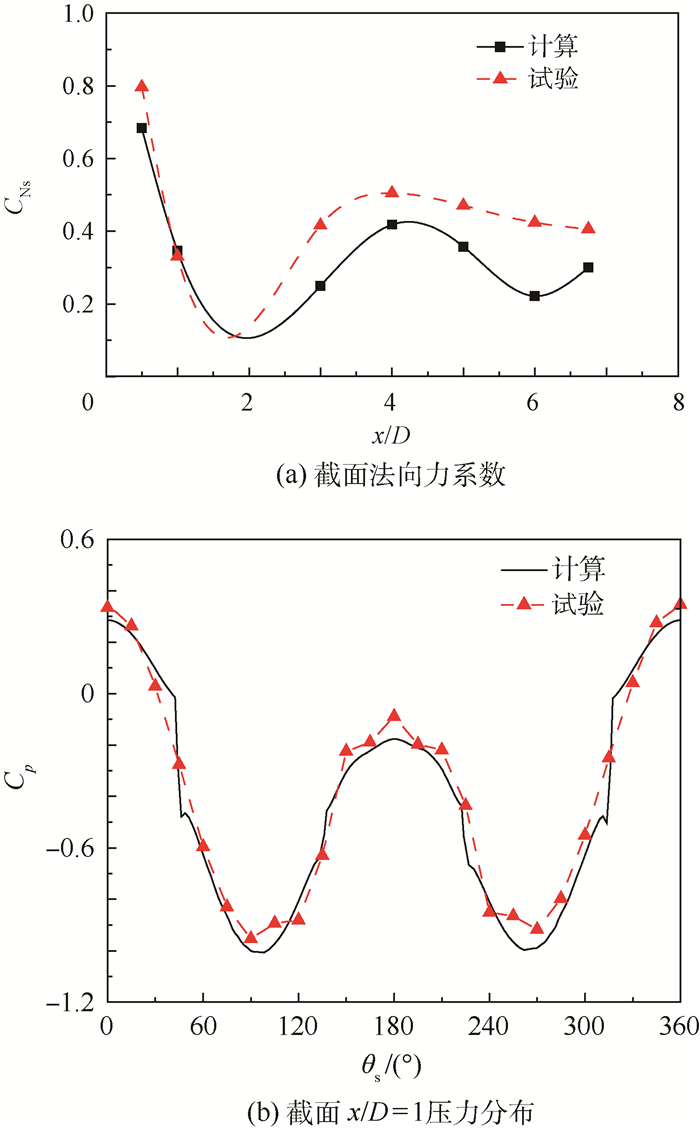图 2 数值方法验证(V∞=35 m/s，α=40°，θ=90°，γ=40°，ReD=1.54×105) Fig. 2 Verification of numerical simulation method (V∞=35 m/s, α=40°, θ=90°, γ=40°, ReD=1.54×105)

图选项

2 结果与分析 2.1 扰动形状对表面压力分布的影响 因为钝头体非对称涡结构主要受到头部影响^[13]，所以本文中，扰动形状对表面压力分布的影响主要针对模型头部的压力分布进行讨论。图 3所示为来流风速V_∞=35 m/s，模型攻角α=50°，扰动位置为θ=90°，γ=10°的条件下，3种不同扰动块形状的钝头体头部的表面压力分布情况。从图中可以看出，3种扰动形式下头部表面的压力分布基本相同，但在扰动块周围存在差异(见图 4)。

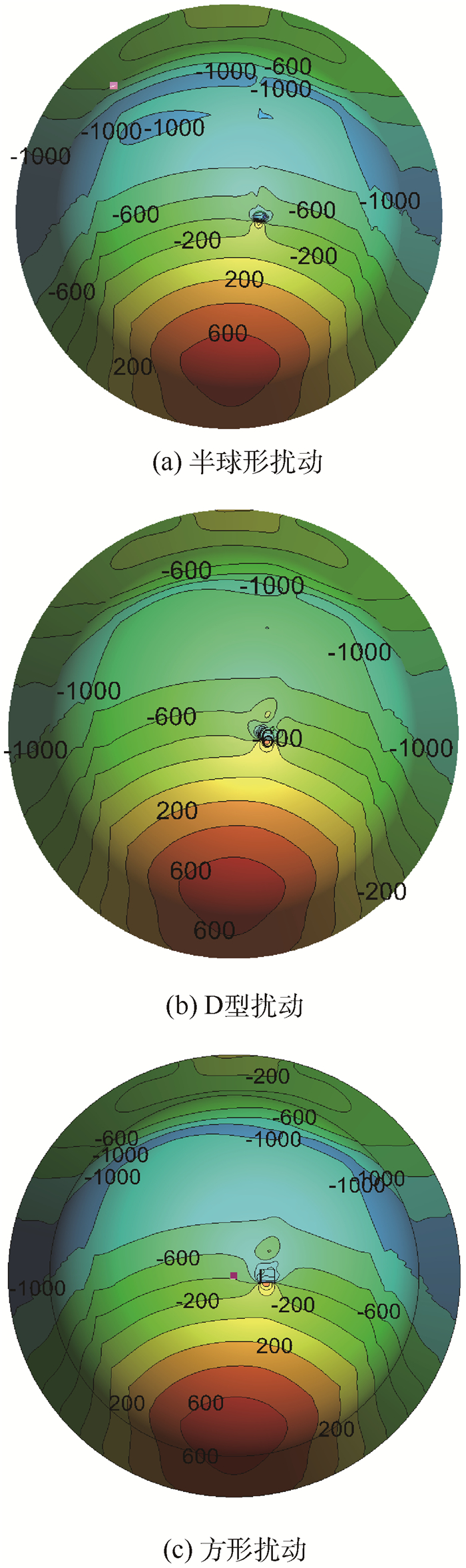图 3 3种扰动块下钝头体头部压力分布(V∞=35 m/s，α=50°，θ=90°，γ=10°，ReD=1.54×105) Fig. 3 Nose pressure distribution of blunt body for three perturbations (V∞=35 m/s, α=50°, θ=90°, γ=10°, ReD=1.54×105)

图选项

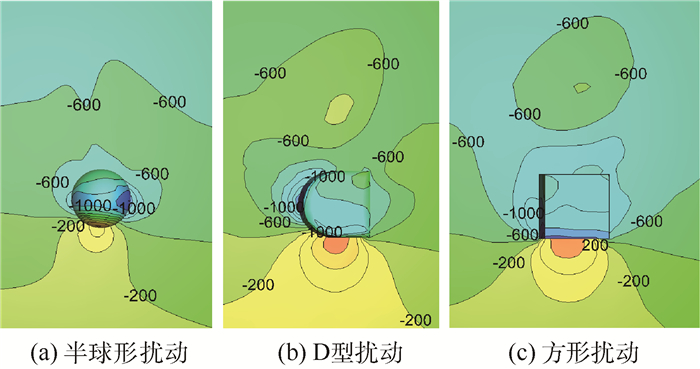图 4 3种扰动块下扰动位置的压力分布(V∞=35 m/s，α=50°，θ=90°，γ=10°，ReD=1.54×105) Fig. 4 Locational pressure distribution for three perturbations (V∞=35 m/s, α=50°, θ=90°, γ=10°, ReD=1.54×105)

图选项

从图 4中可以看出，对于3种不同扰动块形状，扰动块周围的模型表面压力分布存在不同。截取扰动块下游的模型截面(见图 5)进行分析，如图 6所示为3种不同扰动块下截面x/D=0.017和x/D=0.17的表面压力系数沿周向的分布。当来流刚刚流经扰动块时，从图 6(a)可以看出，半球形扰动的情况下，截面的周向位置θ_s=120°时，出现壁面压力增大现象，主要是流体经过半球扰动时在半球体表面依附通过，而在半球扰动的背风区域流体速度减小，所以出现压力增加现象。对于D型和方形扰动块，流体不能依附其表面通过，所以截面的周向位置θ_s=110°出现的表面压力下降的峰值。相比较于半球形扰动，其背风区域的流体速度更低，所以在截面的周向位置θ_s=130°出现了压力增加的峰值。

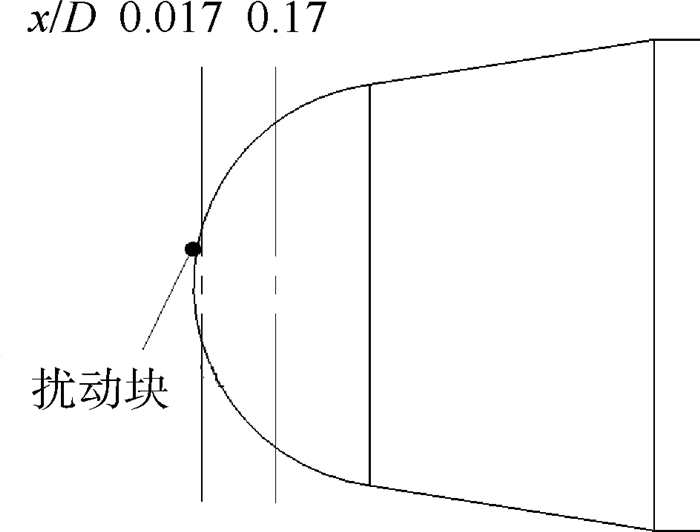图 5 模型头部压力分析截面 Fig. 5 Nose sections of model for pressure analysis

图选项

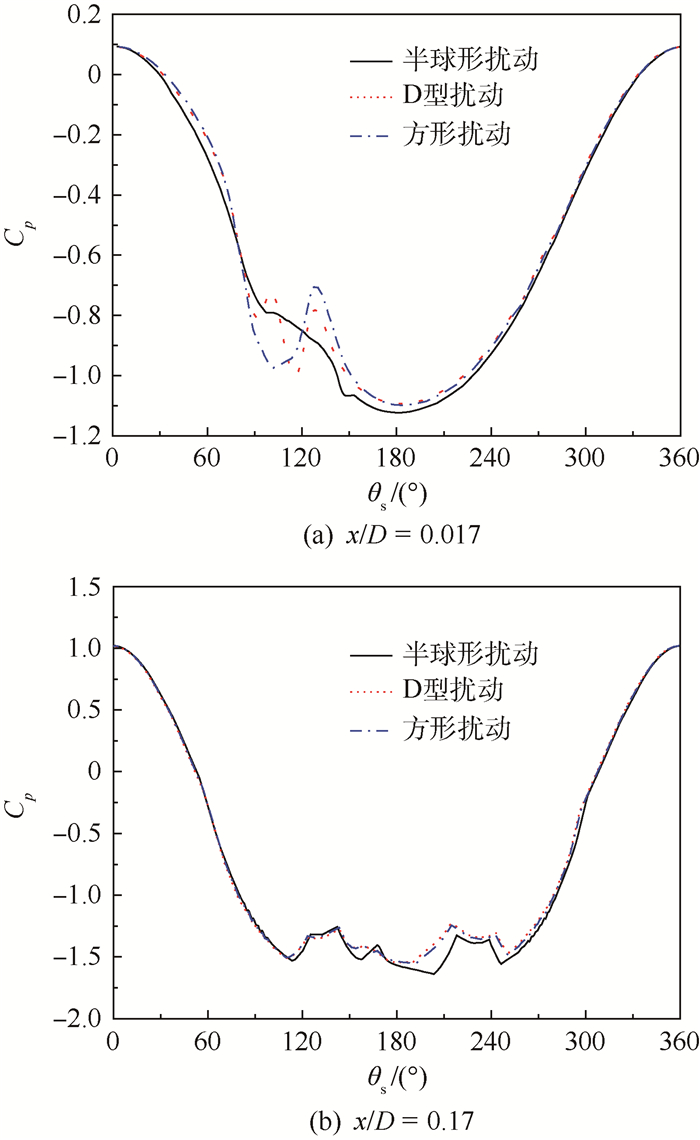图 6 3种扰动块下模型头部截面的压力系数分布(V∞=35 m/s，α=50°，θ=90°，γ=10°，ReD=1.54×105) Fig. 6 Sectional pressure coefficient distribution of model nose for three perturbations (V∞=35 m/s, α=50°, θ=90°, γ=10°, ReD=1.54×105)

图选项

随着流体沿着轴向继续向下游发展，图 6(b)的表面压力系数沿周向的分布曲线可以发现，在截面x/D=0.17处D型和方形扰动块下的压力系数分布曲线已经重合，3种扰动形状在该截面处均发展出了非对称性。
2.2 扰动形状对流场结构的影响
2.2.1 扰动形状对钝头体非对称流场的影响 因为钝头体头部扰动块对其大攻角流动的非对称性有主控作用^[9]，所以本节针对扰动块引起的微流动对整个钝头体非对称流动的影响进行分析。
为了分析扰动块引起的微流动对钝头体非对称流动的影响，图 7显示了3种不同扰动块下的截面x/D=2.5的压力分布曲线，可以发现对于半球形扰动，截面x/D=2.5的压力曲线呈现右涡型，即此截面非对称涡中的右涡处于靠近物面的低位(见图 8(a))。而对图 7中的D型扰动而言，截面x/D=2.5的压力曲线则呈现左涡型，即此截面非对称涡中的左涡处于靠近物面的低位(见图 8(b))。此外，图 7中的方形扰动块下的截面x/D=2.5的压力分布曲线显示出不明显的非对称性。根据坐标轴定义，规定绕x轴顺时针旋向的涡向为正，逆时针旋向的涡向为负，即如图 8所示，左涡为x轴正旋向涡，右涡为x轴负旋向涡。

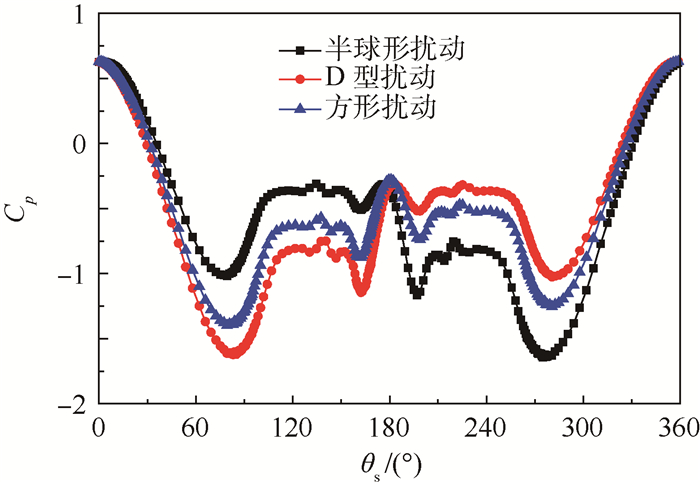图 7 3种扰动块下截面x/D=2.5的压力系数分布(V∞=35 m/s，α=50°，θ=90°，γ=10°，ReD=1.54×105) Fig. 7 Pressure coefficient distribution for three perturbations at section x/D=2.5 (V∞=35 m/s, α=50°, θ=90°, γ=10°, ReD=1.54×105)

图选项

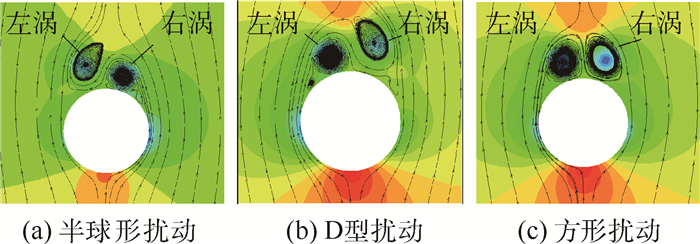图 8 3种扰动块下截面x/D=2.5的压力分布与流线(V∞=35 m/s，α=50°，θ=90°，γ=10°，ReD=1.54×105) Fig. 8 Pressure distribution and streamlines for three perturbations at section x/D=2.5 (V∞=35 m/s, α=50°, θ=90°, γ=10°, ReD=1.54×105)

图选项

1)半球形扰动对流场结构的影响
对于半球扰动情况，从图 8(a)中可以发现在截面x/D=2.5处，左涡为高涡。如图 9(a)所示，左涡先抬升，离开物面。图 9(b)中可以发现，左涡的抬升流线起始于半球扰动，近壁流动流经半球扰动时，分成两股半球两侧的扰动微流动，在E点会合并向左侧发展，促使左涡从物面抬升。因此半球扰动促进了涡从物面分离，使得左涡成为高涡。而扰动引起的微流动在E点的转向主要取决于其在E点处的x轴旋涡的旋向，如图 9(c)所示，当来流绕过半球形扰动时，A点形成x轴负旋向涡，而B点形成x轴正旋向涡，同时C和D点分别出现负压区的新生涡为x轴负旋向涡和x轴正旋向涡。因为扰动块的位置在θ=90°，γ=10°，其B侧的负压区大于A侧，则其产生的D点涡量强于C点涡量，之后A、C、D点的3个涡交错后流向点E(见图 9(b))，在E点为涡量大小为72 s^-1的x轴正旋向涡，而B点的流动到E点为涡量大小为932 419 s^-1的x轴正旋向涡。因为左涡为x轴正旋向涡，所以两股流动在E点向左转向，使左涡成为高涡。

图 9 半球形扰动对背涡结构的影响 Fig. 9 Effect of hemispherical perturbation on vortex structure

图选项

2) D型扰动对流场结构的影响
图 8(b)所示D型扰动下，截面x/D=2.5处右涡为高涡。从图 10(a)中可以看出右涡线先抬升，离开物面。根据扰动块引起的微流动流场(见图 10(c))可以看出，当来流通过扰动块时，从扰动块的两侧流过，流过棱1时发生分离流动，为x轴正旋向涡。而另一侧，当流动沿弧面流动时，被分为两股流动形式，一股沿弧面的切向向前流动，如图 10(c)中的流动1，在A点形成x轴负旋向涡。而另一股流动2沿着弧面到棱2处发生分离流动并与棱1的分离流动合并，即C点的x轴负旋向涡融入E点的x轴正旋向涡，使得合并流动的涡量减弱，至F点(见图 10(b))为涡量为221 s^-1的x轴正旋向涡。而从图 10(b)中可以看出，扰动块弧面上分离出来的流动1发展到F点处，为涡量为161 224 s^-1的x轴负旋向涡，转向右侧涡结构中，促进了右涡从物面上抬升成为高涡，因此使得D型扰动下的截面x/D=2.5处的压力曲线呈现左涡型。

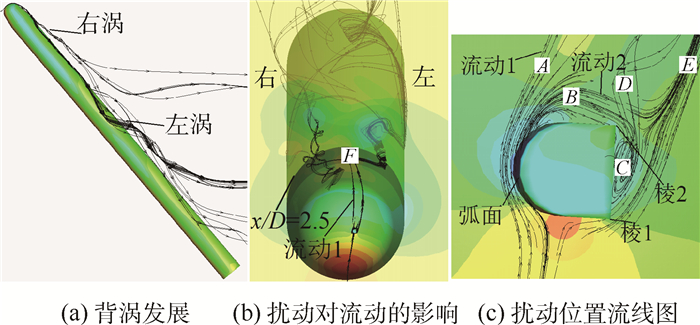图 10 D型扰动对背涡结构的影响 Fig. 10 Effect of D-type perturbation on vortex structure

图选项

3)方形扰动对流场结构的影响
图 8(c)所示方形扰动下，截面x/D=2.5处右涡为高涡，但相比于左涡并没有明显抬升。图 7中方形扰动下的截面x/D=2.5处的压力分布还没有形成明显的非对称性。从图 11(a)中可以看出，右涡先于左涡从物面上发生缓慢的抬升。根据扰动块引起的微流动流场(见图 11(c))可以发现，当流动流经方形扰动块时，从扰动块两侧通过，分别在A、B点形成x轴负旋向涡和x轴正旋向涡。当流动经过扰动块棱3时发生分离流动，形成流动1继续向前流动。另一侧当流动经过扰动块棱2时，被分为两股流动，一股与物面分离形成流动2，在C点处形成x轴负旋向涡，最终与流动1在D点形成的x轴正旋向涡合并流动，使流动1的涡量减弱。而棱1分离出来的另一股流动3贴近壁面在棱2处发生流动分离，也与流动1合并，且两股流动同样方向相反，流动1的涡量强度被再一次减弱。从图 11(b)中可以看出当合并流到达E点，为涡量为5 696 s^-1的x轴正旋向涡，所以向左发展，使得左涡成为高涡位，但对比于半球扰动块和D型扰动块引起的为流动发展至拐点位置所具有的涡量，其涡量值较低，所以高涡发展相对较慢。

图 11 方形扰动对背涡结构的影响 Fig. 11 Effect of square perturbation on vortex structure

图选项

2.2.2 扰动形状对钝头体表面流动的影响 因为扰动块微流动形式影响到钝头体非对称流动结构，反映到钝头体表面上即为左右两边分离线的非对称性受扰动块形状的影响。如图 12所示为3种不同扰动形状下，物面的分离线情况。

图 12 物面分离线 Fig. 12 Separation lines of model surface

图选项

图 12(a)和图 12(b) 分别为半球形扰动下，模型两侧的物面分离线形式。因为半球扰动时，左视图的物面分离线先发展到轴对称线以下，表示左涡先发生抬升成为高涡。而此处的模型右视图中分离线在轴对称线以上，表示右涡没有从物面抬升，成为低涡。根据2.2.1节中分析可知，其主要原因为扰动微流动主控了钝头体非对称流动，导致了物面分离线的发展形式。
图 12(c)和图 12(d)分别为D型扰动下，模型两侧的物面分离线形式。其与半球扰动下的分离线形式刚好相反，其右视图的物面分离线先发展到轴对称线以下，表示右涡先发生抬升成为高涡。而左视图中分离线在轴对称线以上，表示左涡没有从物面抬升而成为低涡，其发展形势也是主要受到扰动块的影响。对于图 12(e)和图 12(f)所显示的方形扰动，两侧分离线发展结构相似，其背涡非对称性不明显，也是主要受到了方形扰动块所引入的微流动的影响。
3 结论 本文针对3种不同扰动块形状对钝头体大攻角下的非对称流动进行研究，得到以下结论：
1) 3种扰动块形状对于钝头体的头部表面压力分布影响主要集中于扰动块周围的背风区域，随着流动向下游发展，其对头部靠近下游的位置影响减小。
2)扰动块对钝头体大攻角的非对称流动有主控作用，且扰动块所引起的微流动的x轴涡旋向决定钝头体的非对称的左、右涡模态；微流动的涡量决定非对称程度的大小。
为了更好地研究扰动块与非对称背涡之间的响应关系，需要得到稳定的扰动块微流动，因此应尽量将扰动块的形状简单化，且表面平滑过渡。

参考文献

[1]	王刚, 梁新刚, 邓学蓥. 细长体大迎角绕流的滚转角特性[J].实验流体力学, 2004, 18(4): 11–14.WANG G, LIANG X G, DENG X Y. Effects of roll angle on side force distribution over slender bodies of revolution at high angle of attack[J].Experiments and Measurements in Fluid Mechanics, 2004, 18(4): 11–14.(in Chinese)
[2]	ERICSSON L E, BEYERS M E.Fluid mechanics considerations for successful design of forebody flow control:AIAA-2000-2320[R].Reston:AIAA, 2000.
[3]	张涵信, 冉政. 细长锥体有攻角绕流对称流态到非对称流态的结构稳定性研究[J].空气动力学学报, 1997, 15(1): 20–26.ZHANG H X, RAN Z. On the structural stability of the flows over slenders at angle of attack[J].Acta Aerodynamica Sinica, 1997, 15(1): 20–26.(in Chinese)
[4]	程克明, 范召林, 尹贵鲁. 大攻角流动非对称性成因与对策[J].南京航空航天大学学报, 2002, 34(1): 17–21.CHENG K M, FAN Z L, YIN G L. On cause and research strategy of flow asymmetry in high-alpha flows[J].Journal of Nanjing University of Aeronautics and Astronautics, 2002, 34(1): 17–21.(in Chinese)
[5]	LAMONT P J, HUNT B L. Prediction of aerodynamic out-of-plane forces on ogive-nosed circular cylinders[J].Journal Space-craft and Rockets, 1997, 14(1): 38–44.
[6]	WILLIAMS D A.A review of forebody vortex control scenarios:AIAA-1997-1967[R].Reston:AIAA, 1997.
[7]	MALOCOLM G N.Forebody vortex control-A progress review:AIAA-1993-3540[R].Reston:AIAA, 1993.
[8]	王元靖, 范召林, 侯跃龙, 等. 粗糙带对细长体大迎角流动非对称性的影响[J].空气动力学学报, 2005, 23(3): 284–288.WANG Y J, FAN Z L, HOU Y L, et al. Effects of grid strip on flow asymmetry over a slender revolution body at high angles of attack[J].Acta Aerodynamica Sinica, 2005, 23(3): 284–288.(in Chinese)
[9]	MOSKOVITZ C A, HALL R M, DEJARNETTE F R.Effects of nose bluntness, roughness and surface perturbations on the asymmetric flow past slender bodies at large angles of attack:AIAA-1989-2236[R].Reston:AIAA, 1989.
[10]	DRIVER D M.Reynolds shear stress measurements in a separated boundary layer:AIAA-1991-1787[R].Reston:AIAA, 1991.
[11]	周宇, 钱炜褀, 邓有奇, 等. κ-ω SST两方程湍流模型中参数影响的初步分析[J].空气动力学学报, 2010, 28(2): 213–217.ZHOU Y, QIAN W Q, DENG Y Q, et al. Introductory analysis of the influence of menter's κ-ω SST turbulence model's parameters[J].Acta Aerodynamica Sinica, 2010, 28(2): 213–217.(in Chinese)
[12]	MENTER F R.Zonal two equation κ-ω turbulence models for aerodynamic flows:AIAA-1993-2906[R].Reston:AIAA, 1993.
[13]	邓学蓥, 刘沛青, 孔繁美. 旋成体非对称背涡特性及其形成机理的研究[J].空气动力学学报, 2000, 18(S1): 121–126.DENG X Y, LIU P Q, KONG F M. Investigation on characteristics of asymmetric vortices and mechanism[J].Acta Aerodynamica Sinica, 2000, 18(S1): 121–126.(in Chinese)