近场测量法[6]通过探头对围绕阵列闭合面上电场的采样,经过数值计算获得远场方向图和各单元通道的幅相分布。该方法测量精度高,可用于各种体制的阵列天线,但只能在微波暗室中进行,对测量仪器的同步性要求高、扫描时间长,数据量大,测量效率低。
旋转矢量法[7-9]通过测量和信号幅度随单个天线单元相位变化的正弦曲线,就可计算出每个单元通道的幅相值,而无需矢量测量仪器。但在实际应用中,若阵列单元数较多,则单个单元造成的曲线变化不明显,且需要校准的时间也较长。
互耦校准法[10-12]是基于大型阵列的阵中相邻单元的互耦系数是相同的这一基本原理,通过对阵列中相邻单元进行收发测试,由测试数据计算出各有源通道的幅相信息,再根据理想分布进行阵列校准。互耦校准法虽然无需外场测量装置,测试过程简单,但其仅适用于收发共口面的相控阵天线,且辐射单元之间的隔离度不能太大。
换相测量法[13-15]的基本思想是在相控阵天线和测量探头均保持固定的情况下,测量相控阵天线不同配相状态下探头的接收信号幅相,然后用数学算法对实验数据进行处理即可确定任意配相状态下各通道激励的幅相,进而根据试验结果复原所有的方向图。其不足之处在于,一般情况下系数矩阵不满秩,在解测量方程时,必须引入其他的先验知识,这样也会导致其测量时间较长,测试效率不高。
以上测量方法的测量速度都不够快,一般用于相控阵天线研制阶段的验证校准工作,不能满足大量工程需求的测量校准。而针对大规模的工程应用,需要一种更快、更稳健的校准方法。
1 四相幅度校准法原理 鉴于上述原因,本文提出了一种相控阵天线快速校准方法,该方法无需矢量测量仪器,仅仅测量幅度值,即可快速、稳健地实现相控阵天线单元通道初始相位的校准。其校准原理如下。
假设在相控阵天线的远场处有一频率为f的单载波信号,则相控阵天线的第n个天线单元接收到的信号为
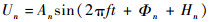 | (1) |
式中,An、Φn和Hn分别为第n个天线单元接收信号的未知幅度、未知的固有相位以及已知的相位分布, n=1, 2, …, N, N为天线单元的数量。
假设n=1的天线单元所在的通道为参考通道,参考通道的相位记为Φ1=0,则Φn为在H1=0和Hn=0条件下,第n(n≠1)个通道相对于参考通道的相位差。此时,相控阵天线接收到的信号功率和可表示为
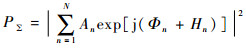 | (2) |
由式(2)可以看出,该式中含有2N-1个未知数,其中和N个未知幅度An(n=1, 2, …, N),N-1个未知相位差Φn (n=2, 3,…, N)。
由欧拉公式,式(2)可表示为
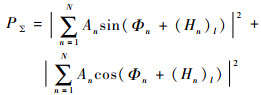 | (3) |
式中:(Hn)l为第n个通道在数字移相器的第l个状态下的相位分布值,l=1, 2, …, L, L为数字移相器的最大二进制状态数,如若采用6位数字移相器,则L=26。
下面以五元阵为例,来详细说明四相幅度校准法的原理。
以n=1天线单元所在的通道作为参考通道,则其初始相位Φ1=0,H1=0。首先进行第1轮测量:将被测通道的相位值设置为(Hn)1=π,其余N-2个通道的相位值分别设置为(Hn)1-π,如表 1所示,则此时测得的和信号功率为Pi(i=2, 3, 4, 5):
表 1 第1轮相位分布下的和信号功率测量 Table 1 Power measurement under the first round phase distribution
| 相位分布/rad | P∑/dBm | ||||
| 通道1 | 通道2 | 通道3 | 通道4 | 通道5 | |
| 0 0 0 0 | π 0 0 0 | 0 π 0 0 | 0 0 π 0 | 0 0 0 π | P2 P3 P4 P5 |
表选项
 | (4) |
然后进行第2轮测量:将被测通道的相位值设置为(Hn)1=0,其余N-2个通道的相位值分别设置为(Hn)1-π,如表 2所示。则此时测得的和信号功率为P′i(i=2, 3, 4, 5):
表 2 第2轮相位分布下的和信号功率测量 Table 2 Power measurement under the second round phase distribution
| 相位分布/rad | P∑/dBm | ||||
| 通道1 | 通道2 | 通道3 | 通道4 | 通道5 | |
| 0 0 0 0 | 0 π π π | π 0 π π | π π 0 π | π π π 0 | P′2 P′3 P′4 P′5 |
表选项
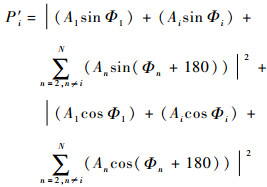 | (5) |
接着进行第3轮测量:将被测通道的相位值设置为(Hn)1=π/2,其余N-2个通道的相位值分别设置为(Hn)1-π,如表 3所示。则此时测得的和信号功率为Pi(i=2, 3, 4, 5):
表 3 第3轮相位分布下的和信号功率测量 Table 3 Power measurement under the third round phase distribution
| 相位分布/rad | P∑/dBm | ||||
| 通道1 | 通道2 | 通道3 | 通道4 | 通道5 | |
| 0 | π/2 | 3π/2 | 3π/2 | 3π/2 | P2 |
| 0 | 3π/2 | π/2 | 3π/2 | 3π/2 | P3 |
| 0 | 3π/2 | 3π/2 | π/2 | 3π/2 | P4 |
| 0 | 3π/2 | 3π/2 | 3π/2 | π/2 | P5 |
表选项
 | (6) |
最后进行第4轮测量:将被测通道的相位值设置为(Hn)1=3π/2,其余N-2个通道的相位值分别设置为(Hn)1-π,如表 4所示。则此时测得的和信号功率为P′i(i=2, 3, 4, 5):
表 4 第4轮相位分布下的和信号功率测量 Table 4 Power measurement under the fourth round phase distribution
| 相位分布/rad | P∑/dBm | ||||
| 通道1 | 通道2 | 通道3 | 通道4 | 通道5 | |
| 0 | 3π/2 | π/2 | π/2 | π/2 | P′2 |
| 0 | π/2 | 3π/2 | π/2 | π/2 | P′3 |
| 0 | π/2 | π/2 | 3π/2 | π/2 | P′4 |
| 0 | π/2 | π/2 | π/2 | 3π/2 | P′5 |
表选项
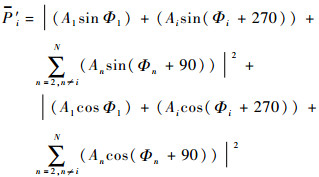 | (7) |
若式(7)减式(6)、式(5)减式(4), 则可得
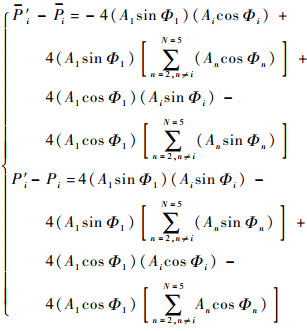 | (8) |
进一步化简,可得
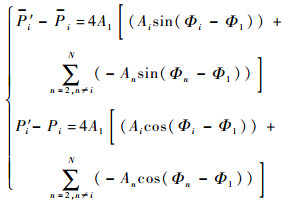 | (9) |
分别对式(9)中的2个等式进行运算,可得式(10)和式(11):
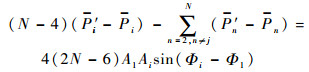 | (10) |
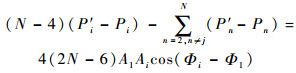 | (11) |
式(10)除以式(11),可得
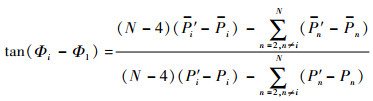 | (12) |
其中:Φ1=0,即有
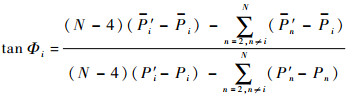 | (13) |
考虑到反正切函数的多值性,应在单值区间[-90°, 90°]内求解Φi。
2 四相幅度校准法时间性能分析 由校准算法原理可得,完成N个阵元的相控阵天线所有通道的一个频点校准所需的时间Ttol由下列时间组成:
1)将校准信号发生器调谐到频率f的时间T1。
2)将校准功率测量仪器调谐到频率f的时间T2。
3)将移相器置于所要求状态的时间T3。
4)幅度测量时间T4。
5)传送控制指令的时间T5。
6)相位差计算时间T6。
则总共需要的时间为
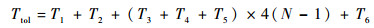 | (14) |
对于大型相控阵天线的一个频点而言,T1、T2和T6所花费的时间远远小于(T3+T4+T5)×4(N-1)所需时间;而T3、T4、T5中,由于测量仪器的反应速度受限,功率测量时间T4的量级最大,为ms量级;指令传输时间T5为μs量级;移相器动作时间为ns量级。
可见,上述校准算法的时间主要取决于功率测量仪器的响应时间。以ROHDE & SCHWARZ公司的频谱分析仪FSV作为功率测量仪器,频谱分析仪的扫描带宽设置为5 kHz,分辨带宽设置为100 Hz,扫描时间为500 ms,则对于一个N元相控阵天线,则校准一个频点所需时间约为2(N-1) s。
此外,若采用四相幅度法校准相控阵天线单元通道的初始相位,则需要采样4(N-1)次;若采用6位数字移相器的旋转矢量法,则需要采样26×N次;若采用4位数字移相器的旋转矢量法,则需要采样24×N次。因此可得出结论:若采用相同的测量设备校准一个大型相控阵天线(N较大),采用四相幅度校准法所需时间仅约相当于采用6位数字移相器的旋转矢量法所花费时间的1/16。
3 实验验证 3.1 测量步骤 如图 1所示,待测相控阵天线为接收天线,则具体测量步骤如下:
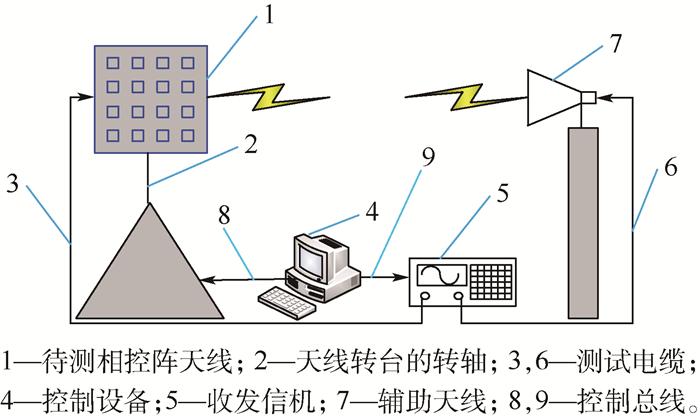 |
| 图 1 相控阵天线测量框图 Fig. 1 Measurement diagram of phased array antenna |
| 图选项 |
1)调整待测相控阵天线1和辅助天线7的相对位置,使其满足远场条件。
2)利用控制设备4控制天线转台的转轴2,使待测相控阵天线1和辅助天线7的物理中心对齐;收发信机5的发射端口通过测试电缆6连接到辅助天线7的馈源端口上;待测相控阵天线1的接收端经过测试电缆3进入收发信机5的接收端口。
3)控制设备4通过控制总线9控制收发信机5打开开关,并设置好所需校准的频点,使收发信机5的发射端口发出功率,且使收发信机5的接收端口处于接收状态。
4)以N=1的天线单元作为参考通道,控制设备4通过控制总线8控制参考通道的相位为0°,被测通道按照算法原理设置为相应的相位分布,然后测量收发信机5的接收端口测得的功率值。经过算法处理,即可完成相位测量校准。
3.2 测量结果
3.2.1 校准Ku频段一维相控阵天线 根据上述测量步骤,分别采用矢量网络分析仪直接校相法、4位数字移相器的旋转矢量法(REV-4 bit法)、6位数字移相器的旋转矢量法(REV-6 bit法)和四相幅度校准法(FPC法),对图 2所示的10个阵元的Ku频段一维相控阵天线的初始相位进行了校准,校准结果如表 5所示。
 |
| 图 2 Ku频段一维相控阵天线 Fig. 2 One-dimensional phased array antenna in Ku band |
| 图选项 |
表 5 4种校准方法校准结果 Table 5 Calibration results with four calibration methods
| 单元编号 | 相位/(°) | |||
| 直接校相法 | REV-4 bit法 | REV-6 bit法 | FPC法 | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 268 | 261.58 | 261.09 | 267.81 |
| 3 | 115 | 110.45 | 112.44 | 114.81 |
| 4 | 7 | 353.70 | 354.70 | 0.49 |
| 5 | 236 | 230.87 | 229.33 | 233.19 |
| 6 | 29 | 20.37 | 22.48 | 23.99 |
| 7 | 265 | 256.48 | 256.08 | 260.84 |
| 8 | 341 | 342.64 | 343.13 | 345.98 |
| 9 | 160 | 159.33 | 162.70 | 165.06 |
| 10 | 34 | 28.48 | 30.11 | 29.91 |
表选项
由表 5可以看出,FPC法的精度可以跟采用REV-6 bit法的精度相比拟。
3.2.2 校准S频段二维相控阵天线 根据3.1节测量步骤,分别采用REV-4 bit法、REV-6 bit法和FPC法,对图 3所示的19个阵元的S频段二维相控阵天线的初始相位进行了校准,校准前后的方向图对比如图 4所示。
 |
| 图 3 S频段二维相控阵天线 Fig. 3 Two-dimensional phased array antenna in S band |
| 图选项 |
 |
| 图 4 校准前后不同方法方向图对比 Fig. 4 Radiation patterns before and after calibration with different methods |
| 图选项 |
由图 4可以看出,FPC法的校准精度优于REV-4 bit法,稍逊于REV-6 bit法。
4 结论 该校准方法为全波法,校准时所有的射频通道均处于工作状态,因此天线单元之间的互耦、天线单元的匹配状态均考虑在内。且该方法无需矢量测量仪器,只需改变某些单元通道的相位,通过测量和信号随天线单元通道相位变化4(N-1)次的和信号幅度值,经过算法演算,就可计算出每个天线单元通道的相位。该校准方法具有如下特点:
1)幅度测量相对于相位测量更加稳定可靠,且工程实现相对简单,因此该方法相对稳健。
2)当相控阵天线的某些通道发生故障时,通过该校准方法获得的其他通道的相位差依然有效,不易发生故障扩散,因此该校准方法具有较强的鲁棒性。
3)由校准算法原理可知,该校准算法所需采样点少,占用系统开销少,因此该方法具有快速性。
4)目前相移器件多采用数字移相器,数字移相器的量化误差必然会影响该方法的测量精度,但随着数字移相器位数的增多以及移相精度的提高,该方法的测量精度会进一步提高。
参考文献
| [1] | TORU T, YOSHIHIKO K, SHIGERU M. Fast measurement technique for phased array calibration[J].IEEE Transactions on Antennas and Propagation, 2008, 56(7): 1888–1899.DOI:10.1109/TAP.2008.924682 |
| [2] | LIU M G, FENG Z H.Combined rotating-element electric-field vector (CREV) method for nearfield calibration of phased array antenna[C]//International Conference on Microwave and Millimeter Wave Technology.Piscataway, NJ:IEEE Press, 2007:1-4. |
| [3] | YAHYA R S, ARTHUR C D. Technology trends and challenges of antennas for satellite communication system[J].IEEE Transactions on Antennas and Propagation, 2015, 63(4): 1191–1203.DOI:10.1109/TAP.2014.2366784 |
| [4] | GU Q, DAI C G, ZHANG C F.Analysis of amplitude-phase error of phased array calibration in mid-field[C]//3rd Asia-Pacific Conference on Antennas and Propagation, APCAP 2014.Piscataway, NJ:IEEE Press, 2014:280-283. |
| [5] | LONG R, OUYANG J, YANG F, et al.Calibration method of phased array based on near-field measurement system[C]//2014 IEEE Antennas and Propagation Society International Symposium.Piscataway, NJ:IEEE Press, 2014:1161-1162. |
| [6] | JI B, YANG Y. Online gain and phase calibration for phased array radar[J].Telecommunication Engineering, 2014, 54(5): 621–625. |
| [7] | TAKAHASHI T, KONISHI Y, CHIBA I. A novel amplitude-only measurement method to determine element fields in phased arrays[J].IEEE Transactions on Antennas and Propagation, 2012, 60(7): 3222–3230.DOI:10.1109/TAP.2012.2196961 |
| [8] | 刘明罡, 冯正和. 分组旋转矢量法校正大规模相控阵天线[J].电波科学学报, 2007, 22(3): 380–384.LIU M G, FENG Z H. Combined rotating-element electric-field vector method for calibration of large-scale phased array antenna[J].Chinese Journal of Radio Science, 2007, 22(3): 380–384.(in Chinese) |
| [9] | FAN X J, LI C W, CHEN Z H.The application of REV method for missile-borne phased array antenna calibration[C]//2012 International Conference on Microwave and Millimeter Wave Technology.Piscataway, NJ:IEEE Press, 2012:241-242. |
| [10] | 高铁, 王金元. 大型有源相控阵校准的MCM法及其误差分析[J].微波学报, 2002, 18(1): 6–10.GAO T, WANG J Y. MCM of large active phased array calibration and tolerance analysis[J].Journal of Microwaves, 2002, 18(1): 6–10.(in Chinese) |
| [11] | BAO J, HUANG Q, WANG X, et al. An improved method for mutual coupling calibration with application in wide-angle direction-of-arrival estimations[J].Electromagnetics, 2015, 35(2): 101–111.DOI:10.1080/02726343.2014.987638 |
| [12] | HUANG Q, ZHOU H, BAO J, et al. Accurate calibration of mutual coupling for conformal antenna arrays[J].Electronics Letters, 2013, 49(23): 1418–1420.DOI:10.1049/el.2013.2258 |
| [13] | 尚军平, 傅德民, 徐平. 基于控制电路编码算法的相控阵天线快速测量[J].电波科学学报, 2010, 25(1): 73–76.SHANG J P, FU D M, XU P. Fast measurement of the phased array antennas based on control circuit encoding algorithm[J].Chinese Journal of Radio Science, 2010, 25(1): 73–76.(in Chinese) |
| [14] | HE C, LIANG X L, GENG J P. Parallel calibration method for phased array with harmonic characteristic analysis[J].IEEE Transactions on Antennas and Propagation, 2015, 62(10): 5029–5036. |
| [15] | LIU K, LI Y Q, WANG H. Calibration method to characterize the accuracy of phase-shifting point diffraction interferometer[J].Review of Scientific Instruments, 2011, 82(3): 33105–33110.DOI:10.1063/1.3560072 |
