从20世纪80年代后期,我国在装备研制中开始全面推广可靠性工程技术,这些技术来源于20世纪五六十年代国外(以美国为主)形成的定性分析与定量评估相结合的工程方法[3-5],在设计上主要依赖设计准则(基于工程经验的定性设计)、裕度设计(预留安全系数)[6]和余度设计(增加冗余备份)等提高产品可靠性,然后基于可靠性统计试验定量评估产品可靠性水平。这种方法的认识基础是产品故障具有不可归因的随机特性,理论基础是概率论与数理统计,工程实施中更多关注产品故障的结果数据,不能关注产品的故障过程。这就导致在设计分析方面,只能采取“事后”改进的方法,而对故障原因缺乏认知,针对高可靠长寿命需求的产品,面临改进无方向的弊端[7-9]。综上所述,面对高可靠长寿命的技术要求,需要研究建立一种基于故障过程认知的可靠性技术来设计和分析产品的可靠性水平。
产品的故障行为模型能够描述系统或单元在复杂应力条件下,多种故障机理综合作用的故障规律[10-11]。从本质上看,故障行为模型属于确定性模型,即在一组给定的输入条件下,系统或单元的故障行为是确定的,故障时间可以由故障行为模型进行预测。但是,实际使用中的产品,所经历的使用条件和环境条件等外因条件的差异是很大的。另一方面,即使采用同样的设计方法,同一批次生产出的同一批产品,由于材料性质、工艺条件等内因方面的不可能完全相同,产品的性能也存在着差异性[12]。
本文在前人研究成果的基础上,充分考虑引起产品寿命分散性的内因和外因的不确定性,在产品功能模型或数字样机模型的基础上,结合产品的故障行为模型,建立一种基于产品故障行为模型的产品寿命分析方法。在该方法中,内因参数与外因参数的分散性分别可以用相应的概率密度函数p(I)和p(E)来表示,其中I和E分别为内因参数向量和外因参数向量。在故障行为模型中,将内因参数、外因参数分别视为来自这两个分布的随机变量,就可以通过数理统计的方法估计产品在实际使用条件下的平均无故障间隔时间(Mean Time to Failure,MTTF)。由于概率密度函数p(I)和p(E)是通过对实际使用情况和生产条件的估计得到的,因此,按照这种方法评估得到的MTTF,能够弥补基于故障物理的可靠性预计方法无法体现产品正常使用条件的不足。
1 产品寿命分析方法 1.1 原理与流程 基于故障行为模型的产品寿命分析方法首先在进行内因和外因的特征参数提取及分布规律确定的基础上,利用相应的概率密度函数来表示故障行为模型中的内因参数和外因参数的分散性;其次,在故障行为模型中,将内因参数、外因参数分别视为来自这两个分布的随机变量,通过数理统计的方法估计产品在实际使用条件下的故障行为,确定产品的敏感故障机理和理论寿命,为产品的设计改进提供支撑。具体分析原理与流程如图 1所示。
 |
| 图 1 产品寿命分析原理与流程 Fig. 1 Principle and process of life analysis for products |
| 图选项 |
1.2 机理分析流程 机械类产品在寿命周期内主要表现出耗损型失效机理,机理分析根据给定的载荷谱或任务剖面,结合产品的组成、结构、原理,定性分析,确定产品每个单元对应的耗损型失效机理以及对应的敏感应力。机理分析的主要工具是故障模式、机理和影响分析(Failure Mode,Mechanisms and Effects Analysis,FMMEA)[13-14],机理分析流程如图 2所示。
 |
| 图 2 机理分析流程 Fig. 2 Process of mechanism analysis |
| 图选项 |
1.3 故障行为分析方法 故障行为分析是指在产品性能模型或数字样机模型的基础上,考虑产品内外因参数分散性,利用故障行为模型进行产品应力分析和寿命分析的过程。以下以产品的MTTF的计算为例介绍产品的故障行为分析方法。
MTTF的计算是利用故障行为模型,综合考虑产品内因参数和外因参数的分散性,对产品的寿命指标进行预计。指标计算的原理如式(1)所示:
 | (1) |
式中:Bt(I,E)表示以故障时间表征的故障行为模型。
对于内因参数与外因参数取值为离散的情况,式(1)可以表示为
 | (2) |
式中:p(I=Ii)和p(E=Ej)分别为内因参数、外因参数的分布律。
故障行为分析的具体实施步骤如图 3所示。
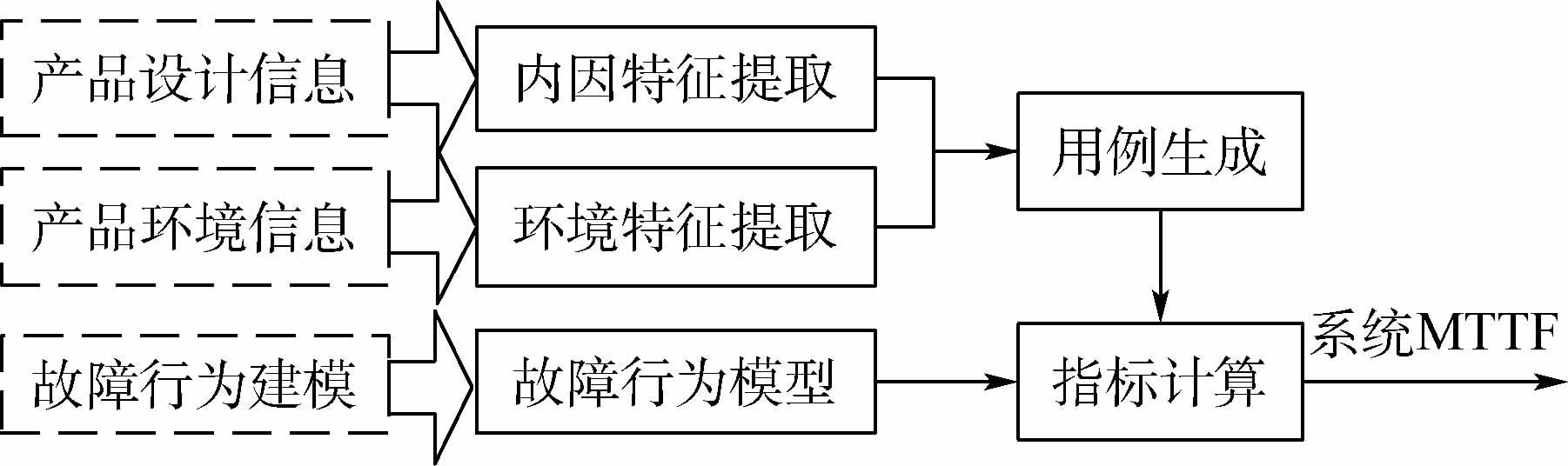 |
| 图 3 MTTF分析步骤 Fig. 3 Analysis procedure of MTTF |
| 图选项 |
1) 建立故障行为模型
采用故障时间表述方式,建立产品的故障行为模型:
 | (3) |
式中:T为产品的寿命。
2) 内因特征参数提取
分析确定式(3)中的内因集合中的参数可能产生的分散性,用分布律或者密度函数的形式表示,即p(I)。内因参数中的分散性主要来源于生产、制造等过程。
3) 环境特征参数提取
分析确定式(3)中的外因集合中的参数可能产生的分散性,用分布律或者密度函数的形式表示,即p(E)。外因参数中的分散性主要产品使用环境的不同,可以由产品寿命周期中的环境剖面和使用剖面转化获得。
4) 按照式(1)或式(2)计算产品的MTTF
当故障行为模型较为复杂时,则可以通过仿真的方法计算式(1)或式(2)的值:首先,通过环境特征提取确定能够表征实际使用环境的内因参数、外因参数分布p(I)和p(E);然后,进行分析用例生成,即按照p(I)和p(E)仿真生成n组测试条件,分别按照式(1)或式(2)计算故障时间。对n个故障时间求取算术平均值,即得到所需评估的MTTF指标。
1.4 分析用例生成方法 对于形式复杂的故障行为模型,式(1)或式(2)的解析解往往是无法求得的,此时需要通过数值模拟的方法进行MTTF的评估。其中,一个重要的环节即为分析用例生成。
分析用例生成是指从给定的内因、外因概率密度函数p(I)和p(E)中,生成一组样本量为N的随机样本。利用这些样本,可以通过蒙特卡罗方法,进行MTTF的估计。生成随机样本的方法有很多种,例如,直接抽样法(反函数法)、挑选抽样法、复合抽样法等。以下以直接抽样法为例,示意测试用例生成的方法[15]。
对于任意给定的分布函数F(x),直接抽样法的流程如下:首先,生成一组样本量为N的服从区间[0,1]均匀分布的伪随机数,记为ξ1,ξ2,…,ξN。然后,按照式(4)确定服从F(x)的随机序列。
 | (4) |
对于离散型分布F(x)=$\sum\limits_{{{x}_{i}} <x}{{{P}_{i}}}$,其中,x1,x2,…为相应的分布函数间断点,P1,P2,…为相应的概率,则直接抽样法可以表示为
 | (5) |
对于连续型分布,如果分布函数F(x)的反函数F-1(y)存在,则直接抽样法可以表示为
 | (6) |
1.5 机理敏感性分析方法 机理敏感分析的目的是通过分析确定系统的薄弱环节或主机理,从而为系统的设计改进提供方向。薄弱环节,是针对系统而言的,指的是系统中最容易发生故障的单元;主机理,是针对单元而言的,指的是单元最容易出现的故障机理。由于二者从分析方法上是相同的,故以下仅以主机理分析为例进行说明。
假定某一单元的故障行为模型的时间表示为式(3)所示,该单元共有n种潜在的故障机理,其机理模型为式(7),给定环境条件Eg,则满足式(8)的第j种机理称为环境条件Eg下的敏感机理。
 | (7) |
 | (8) |
式中:Ti为第i个机理对应的寿命值。
通常,机理之间的关系表现为时间竞争关系,即
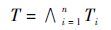 | (9) |
此时,式(8)简化为
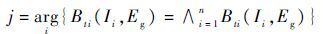 | (10) |
假设产品实际使用的环境条件可以用密度函数p(E)来表示,按照p(E)随机生成m种环境条件,对每一种环境条件分别求取敏感机理,则成为敏感机理次数最多的故障机理即为该单元的主机理。主机理分析的实施步骤如下:
1) 建立故障行为模型,如式(3)或式(7)所示。
2) 通过环境特征提取的方法,获得表征产品实际工作条件的环境应力分布,记为p(E)。
3) 按照p(E)随机生成m组环境条件,分别按照式(8)确定每一种环境条件下的敏感机理。称敏感机理次数最多的故障机理即为主机理。
4) 在通过分析确定主机理或薄弱环节之后,应该针对主机理或者薄弱环境,进行相应的设计改进,从而提高产品的可靠性水平。
2 案例分析 本节将以某航空液压柱塞泵为应用案例,综合运用上述方法,开展基于故障行为模型的寿命分析。该柱塞泵是利用发动机提供的动力作为输入,为液压系统各部件提供一定压力、流量的液压能。某柱塞泵机理分析结果如表 1所示。
表 1 某柱塞泵机理分析结果 Table 1 Results of mechanism analysis for piston pump
| 序号 | 薄弱环节单元 | 主机理 |
| 1 | 滑履、卡盘 | 磨损 |
| 2 | 转子 | 疲劳 |
| 3 | 内轴、传动轴 | 接触疲劳 |
| 4 | 弹簧 | 应力松弛 |
| 5 | 四氟塑料圈 | 老化 |
| | | |
表选项
根据机理分析结果,选择相应的寿命模型,计算各耗损性失效机理的失效时间,式(11)~式(13)为建立的滑履-卡盘磨损寿命模型[16]:
 | (11) |
 | (12) |
 | (13) |
式中:R1为滑履下表面内圈直径,mm;R2为滑履上表面外圈直径,mm;R3为滑履上表面内圈直径,mm;H为材料硬度(布氏硬度),MPa;h0为油膜厚度,mm;hmax为最大允许磨损深度,mm;f为摩擦系数;F为法向载荷,N;I为滑履绕自身中心轴线转动惯量,kg·m2;μ为油液的动力黏度,Pa·s;R为柱塞分布圆半径,mm;n为转子转速,r/min;t0为从启动至额定转速所需时间,s;ω0为滑履自转角速度,rad/s。
利用式(11)~式(13)的寿命计算模型计算滑履-卡盘磨损机理的理论寿命值,模型参数表如表 2所示,可得滑履-卡盘的磨损寿命为1 413 h。
表 2 滑履-卡盘磨损寿命模型参数 Table 2 Parameters of wear life model forslipper and chuck
| 序号 | 参数 | 数值 |
| 1 | F/N | 34.1 |
| 2 | R1/mm | 5.15 |
| 3 | R2/mm | 7.2 |
| 4 | R3/mm | 5.5 |
| 5 | hmax/mm | 1 |
| 6 | f | 0.075 |
| 7 | H/MPa | 500 |
| 8 | I/(10-7kg·m2) | 1.927 |
| 9 | μ/(Pa·s) | 0.006 63 |
| 10 | R/mm | 21.5 |
| 11 | n/(r·min-1) | 4 000 |
| 12 | t0/s | 20 |
| 13 | h0/mm | 0.085 |
表选项
通过上述方法可以计算出所有最低约定层次单元的理论寿命计算结果如表 3所示。
表 3 最低约定层次单元理论寿命计算结果 Table 3 Calculation results of theoretical life for the lowest level units
| 序号 | 薄弱环节单元 | 主机理 | 模型名称 | 寿命/h |
| 1 | 滑履、卡盘 | 磨损 | 滑履-卡盘磨损寿命计算模型 | 1 413 |
| 2 | 转子 | 疲劳 | 名义应力(时域法)寿命计算模型 | 1 742 |
| 3 | 内轴、传动轴 | 接触疲劳 | 渐开线花键接触疲劳寿命计算模型 | 5 512 |
| 4 | 弹簧 | 应力松弛 | 弹簧应力松弛寿命计算模型 | 3 200 |
| 5 | 四氟塑料圈 | 老化 | 塑料老化寿命计算模型 | 4 786 |
| | | | | |
表选项
根据确定性寿命模型,考虑寿命模型参数的不确定特征,进行内因参数提取并确定其分布特性;同时根据全寿命周期载荷谱,确定其载荷的特征参数及分布特性。
对每个内因参数和外因参数进行蒙特卡罗抽样,将每次抽样值代入寿命模型计算得到每个失效机理的若干个寿命值。然后对每个失效机理的所有寿命值进行分布曲线拟合,得到每个失效机理对应的寿命分布,确定每个失效机理在给定置信度下的寿命区间。
下面以滑履-卡盘磨损寿命区间计算为例说明求解过程。
为了方便计算,本案例采取内因参数、外因参数和变异系数皆取为0.01。根据上述步骤,确定抽样次数为1 000次,将每次抽样值代入寿命模型计算得到1 000个寿命值,通过分布曲线拟合得到寿命服从的正态分布,最后通过分析寿命分布特点确定置信度为95%的滑履-卡盘磨损寿命区间为[1 236,1 606]h。
同理,可对所有最低约定层次单元寿命区间进行计算,计算结果汇总如表 4所示。
表 4 最低约定层次单元寿命区间计算结果 Table 4 Calculation results of life interval for the lowest level units
| 序号 | 单元名称 | 机理 | 模型名称 | 寿命均值/h | 寿命区间/h |
| 1 | 滑履、卡盘 | 磨损 | 滑履-卡盘磨损寿命计算模型 | 1 413 | [1 236,1 606] |
| 2 | 转子 | 疲劳 | 名义应力(时域法)寿命计算模型 | 1 742 | [1 533,2 054] |
| 3 | 内轴、传动轴 | 接触疲劳 | 渐开线花键接触疲劳寿命计算模型 | 5 512 | [5 021,6 102] |
| 4 | 弹簧 | 应力松弛 | 弹簧应力松弛寿命计算模型 | 3 200 | [2 713,3 518] |
| 5 | 四氟塑料圈 | 老化 | 塑料老化寿命计算模型 | 4 786 | [4 205,5 432] |
| | | | | | |
表选项
考虑柱塞泵的各机理竞争失效机制,采取短板原则,给出柱塞泵的整寿命区间的计算方法。在表 4的基础上,分别对每个失效机理对应的理论寿命分布进行蒙特卡罗抽样,通过取小原则确定的每次抽样的理论寿命最小值作为当次抽样的柱塞泵整体寿命,抽样确定的理论寿命最小值对应的失效机理为柱塞泵的敏感机理,敏感机理对应的单元为柱塞泵的薄弱环节。
对表 4确定的理论寿命分别进行1 000次仿真抽样则有1 000个取小值,则得到柱塞泵整体寿命值的1 000个计算结果,然后通过分布曲线拟合可认为柱塞泵整体寿命服从正态分布,最后基于寿命分布计算得到柱塞泵的敏感机理为滑履-卡盘磨损机理,薄弱环节为滑履和卡盘,最终确定的柱塞泵置信度为95%的寿命区间为[1 219,1 540]h。
3 结 论 本文充分考虑了引起产品寿命分散性的内因和外因的不确定性,在产品功能模型或数字样机模型的基础上,结合产品的故障行为模型,提出了一种基于产品故障行为模型的产品寿命分析方法。具体创新点如下:
1) 在产品功能模型或数字样机模型的基础上,系统地提出了一种基于故障行为模型的产品寿命分析方法,为具有长寿命指标产品的设计改进提供了技术支撑。
2) 给出了综合考虑内因和外因分散性的故障行为分析方法,内因参数与外因参数的分散性分别用相应的概率密度函数来表示,并且从实际使用情况和生产条件的估计得到,为准确评估产品在正常使用工况下的故障行为提供了方法支撑。
3) 提出了机理敏感性的分析方法,确定了产品的寿命薄弱环节和敏感机理,为具有长寿命指标产品的设计改进指明了方向。
参考文献
| [1] | SALEH J H, MARAIS K. Highlights from the early(and pre-) history of reliability engineering[J].Reliability Engineering and System Safety, 2006, 91(2): 249–256.DOI:10.1016/j.ress.2005.01.003 |
| [2] | MCLINN J. A short history of reliability[J].Journal of Reliability Data Analysis Center, 2011, 54(1): 8–15. |
| [3] | MEEKER W Q, ESCOBAR L A. Statistical methods for reliability data[M].Hoboken: John Wiley & Sons, 2014: 350-420. |
| [4] | ZACKS S. Introduction to reliability analysis:Probability models and statistical methods[M].Berlin: Springer Science & Business Media, 2012: 100-150. |
| [5] | GNEDENKO B V, BELYAYEV Y K, SOLOVYEV A D. Mathematical methods of reliability theory[M].Manhattan: Academic Press, 2014: 300-500. |
| [6] | ZHOU T,DONG J B,PENG L X,et al.Designing method research of generalized reliability margin for complex system[C]//IEEE Conference on Prognostics and System Health Management (PHM).Piscataway,NJ:IEEE Press,2012:1-4.http://cn.bing.com/academic/profile?id=1990568362&encoded=0&v=paper_preview&mkt=zh-cn |
| [7] | MEEKER W Q, HAMADA M. Statistical tools for the rapid development and evaluation of high-reliability products[J].IEEE Transactions on Reliability, 1995, 44(2): 187–198.DOI:10.1109/24.387370 |
| [8] | 邓爱民.高可靠长寿命产品可靠性技术研究[D].长沙:国防科学技术大学,2006:1-7.DENG A M.Research on reliability technology of high-reliability and long-lifetime products[D].Changsha:National University of Defense Technology,2006:1-7.http://epub.cnki.net/kns/detail/detail.aspx?QueryID=0&CurRec=1&FileName=2007141020.nh&DbName=CDFD9908&DbCode=CDFD&pr= |
| [9] | 陈云霞,赵安,康锐.非电产品寿命分析和试验方法研究[C]//中国运筹学会可靠性分会第九届可靠性学术会议论文集.长沙:中国运筹学会,2013:205-211.CHEN Y X,ZHAO A,KANG R.Research on life analysis and test method for non-electric products[C]//The Reliability of the Operational Research Society of China,the Ninth Session of the Reliability Academic Conference.Changsha:Operations Research Society of China,2013:205-211(in Chinese). |
| [10] | ZENG Z G, CHEN Y X, KANG R. Failure behavior modeling:Towards a better characterization of product failures[J].Chemical Engineering Transactions, 2013, 33(2): 571–576. |
| [11] | ZENG Z G,KANG R,CHEN Y X.A physics-of-failure-based approach for failure behavior modeling:With a focus on failure collaborations[C]//Proceedings of Annual European Safety and Reliability Conference (ESREL2014).Piscataway,NJ:IEEE Press,2014:1-9.http://cn.bing.com/academic/profile?id=2494320972&encoded=0&v=paper_preview&mkt=zh-cn |
| [12] | 陈云霞.性能与可靠性一体化建模和分析方法研究[D].北京:北京航空航天大学,2004:22-24.CHEN Y X.Study on method of modeling and analysis for integrating performance and reliability[D].Beijing:Beihang University,2004:22-24(in Chinese). |
| [13] | MATHEW S, ALAM M, PECHT M. Identification of failure mechanisms to enhance prognostic outcomes[J].Journal of Failure Analysis and Prevention, 2012, 12(1): 66–73.DOI:10.1007/s11668-011-9508-2 |
| [14] | CHEN Y X, JING H L, LIAO X, et al. Methods to determine stress profile in ALT based on theoretical life models[J].Chinese Journal of Aeronautics, 2015, 28(3): 729–736.DOI:10.1016/j.cja.2015.04.004 |
| [15] | 杨振海, 程维虎. 非均匀随机数产生[J].数理统计与管理, 2006, 25(6): 750–756.YANG Z H, CHENG W H. The common method of generating random number for the non-uniform distribution[J].Jouranl of Applied Statistics and Management, 2006, 25(6): 750–756.(in Chinese) |
| [16] | LIAO X,CHEN Y X.Research on the wear life of slipper in aero-hydraulic pump based on Archard wear model and liquid friction work[C]//2013 International Conference on Quality,Reliability,Risk,Maintenance,and Safety Engineering(QR2MSE).Piscataway,NJ:IEEE Press,2013:930-934.http://cn.bing.com/academic/profile?id=2331413225&encoded=0&v=paper_preview&mkt=zh-cn |
