齿轮系统完整的振动特性分析包括模态计算和激励-响应特性分析。在齿轮系统模态特性有限元研究方面,目前已积累了大量研究成果[2-4]。齿轮系统的动态激励包括内部激励和外部激励,其中齿轮的内部激励必然存在,这是齿轮系统与一般机械系统的主要区别。齿轮内部激励按照其产生机理不同,可分为刚度激励、误差激励和啮合冲击激励。长期以来,国内外****采用集中参数法和有限元法研究齿轮啮合的3种内部动态激励及其作用下的系统响应特性,取得了大量研究成果[5-10]。然而,在齿轮系统实际啮合过程中各种动态激励共同作用,因此应将齿轮啮合作为一个连续、弹性、动态和接触的过程来研究。
目前,国内外****开始利用接触有限元分析理论模拟齿轮动态啮合过程。Parker等[11]首先采用接触有限元分析方法,研究了二维行星齿轮副的动态响应特性。国内,唐进元和彭方进[12]基于接触动力学和显式有限元分析方法,研究得出准双曲面齿轮的啮合接触冲击特性、齿面接触区域和齿轮应力等在动态啮合过程中的变化规律。吴勇军等[13-14]通过建立精确的齿轮副啮合有限元模型,提出一种可综合考虑齿轮副连续弹性啮合过程中多种影响因素的接触有限元分析方法。在实验研究方面,Li[15]利用循环加载实验台,研究了薄壁直齿轮的共振特性。上述研究对分析齿轮动态啮合特性具有重要意义,但利用数值模拟方法对薄壁直齿轮动态啮合过程的振动特性研究依然较少。
因此,本文以文献[15]中的实验齿轮为研究对象,建立其精确的有限元分析模型,基于LS-DYNA软件,模拟齿轮的动态啮合过程。根据数值模拟的计算结果,分析腹板厚度、轮缘厚度及腹板中心偏移距离对齿轮振动响应的影响,研究齿轮共振条件和共振判定方法。
1 薄壁直齿轮啮合系统有限元分析模型 齿轮系统振动分析是典型的动力学问题,动力学问题的基本运动方程为
 | (1) |
式中:F、M、C和K分别为系统结构的载荷向量、质量矩阵、阻尼矩阵和刚度矩阵;
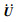
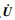
LS-DYNA软件采用显式中心差分法,求解动力学问题的运动微分方程。中心差分法的本质是以差分代替微分,即
 | (2) |
将式(2)代入动力学微分方程式(1),整理可得线性方程组为
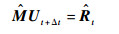 | (3) |
式中:
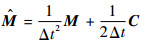
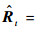
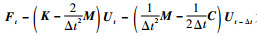
LS-DYNA显式计算的时间步长受单元尺寸的限制。理论与实践均表明,有限元分析模型对计算效率及结果有重要影响。因此,建立合理、精确的齿轮啮合有限元分析模型是本文研究工作的基础。根据文献[15]中实验齿轮的参数(见图 1),建立其精确的有限元分析模型,如图 2所示。两齿轮的其他结构参数为:两齿轮的齿数zA/zB=50/50,模数m=4 mm,齿宽W=40 mm, 压力角为20°,两齿轮按标准中心距安装。由图 1中参数可计算出两齿轮的腹板厚度T1、轮缘厚度T2及腹板中心偏移距离L,其中齿轮B的腹板厚度T1=4 mm,轮缘厚度T2=5 mm,腹板中心偏移距离L=11 mm。齿轮材料牌号为SCM415,其材料参数选为:密度ρ=7 850 kg/m3,弹性模量E=210 GPa,泊松比μ=0.3。
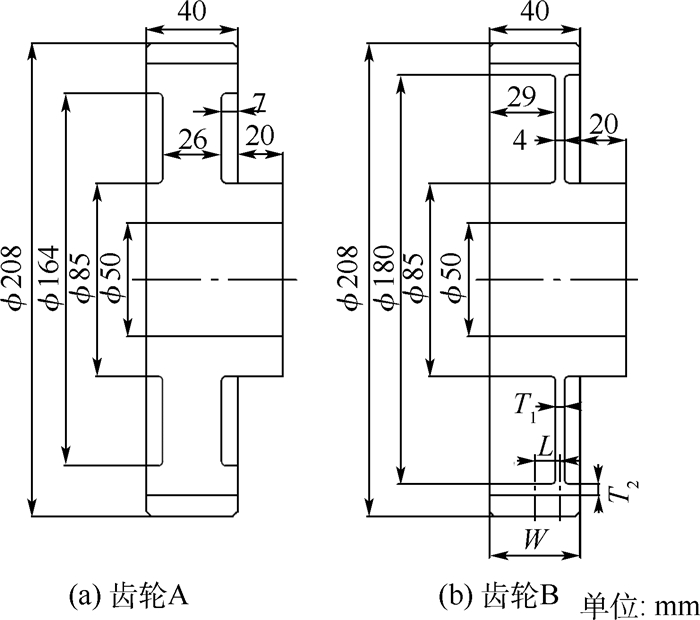 |
| 图 1 实验直齿轮的结构参数[15] Fig. 1 Structure parameters of experimental spur gears[15] |
| 图选项 |
采用六面体单元对齿轮结构进行离散,建立两齿轮的有限元分析模型,如图 2所示,该模型中共计实体单元92 200个。此外,为了便于施加载荷和约束,在两齿轮的轮毂内侧,各建立一圈壳单元并将其刚化。
 |
| 图 2 啮合齿轮的有限元分析模型 Fig. 2 Finite element analysis model of meshing gears |
| 图选项 |
根据JIS B 1721[16]中对薄壁齿轮的定义,当齿轮的结构参数满足式(4)时,齿轮可以称为薄壁齿轮。
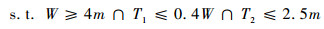 | (4) |
式中:m为齿轮模数。
由此可知,齿轮A为厚壁齿轮,其作为主动齿轮;齿轮B为薄壁齿轮,其轮缘及腹板均较薄,且其腹板位置偏离齿宽中心。本文不考虑齿轮轴及支承等因素对齿轮动态特性的影响,约束两齿轮轮毂内侧刚性壳单元绕轴转动自由度之外的全部自由度,并在主动齿轮A的刚性壳单元上施加不同的驱动转速,在从动齿轮B的刚性壳单元上施加负载扭矩。
根据上述建立的齿轮有限元分析模型,定义单元类型为SOLID186,利用节点耦合法[3],即通过将两齿轮模型中处于啮合线附近节点的沿啮合方向的位移耦合,模拟两齿轮间的啮合耦合关系。在不考虑预应力的情况下,计算齿轮B在啮合状态下的振动模态,其计算结果与实验结果[15]的对比如表 1所示。可以看出,齿轮B的模态计算结果与实验结果有较好的一致性,计算误差均低于5%。由此可以说明,本文所建立的齿轮有限元分析模型是可靠的。
表 1 齿轮B的固有频率 Table 1 Natural frequency of gear B
| 振型 | 计算频率/Hz | 实验频率/Hz | 误差/% |
| 轮缘1弯 | 694.66 | 663 | 4.78 |
| 轮缘2弯 | 1 062.70 | 1 088 | -2.33 |
| 轮缘3弯 | 2 752.90 | 2 700 | 1.96 |
| 轮缘4弯 | 4 483.80 | 4 425 | 1.33 |
| 腹板2节径 | 5 936.80 | 5 950 | -0.22 |
| 腹板3节径 | 7 693.10 | 7 625 | 0.89 |
表选项
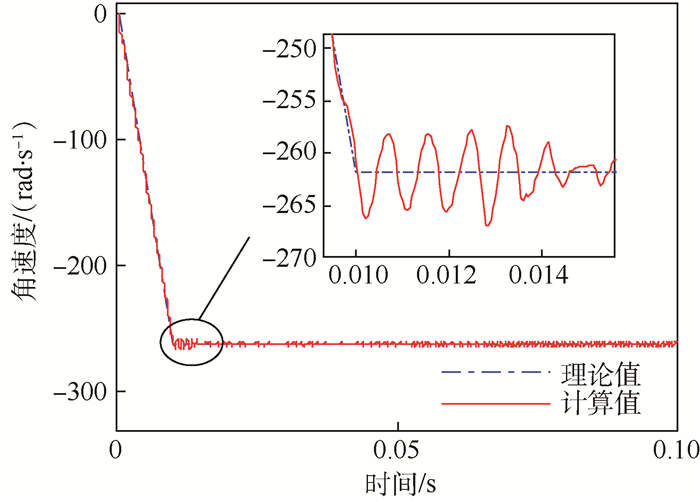
2 齿轮动态啮合过程时域响应特性分析 采用第1节建立的齿轮接触有限元分析模型,定义齿间接触为自动面-面接触,齿间滑动摩擦系数设置为0.1,黏滞阻尼系数设置为20 N·s/mm。在齿轮A上施加不同的驱动转速,即500~3 000 r/min,在齿轮B上施加相同的负载扭矩为297 N·m。在施加转速及负载时,为避免突然加载引起的冲击问题,加载过程存在0.01 s的过渡时间,在这段时间内加载量由零增大到最大值。以下以2 500 r/min计算转速为例,根据其计算结果分析齿轮A-B动态啮合过程的时域响应特性。据计算结果,提取从动齿轮B的输出角速度,如图 3所示。
 |
| 图 3 齿轮B角速度输出 Fig. 3 Angular velocity output of gear B |
| 图选项 |
由图 3可以看出,从动齿轮B的角速度输出在理论值附近呈现明显的波动,这是由齿轮啮合过程中轮齿弹性变形及啮合位置变化等因素造成的。
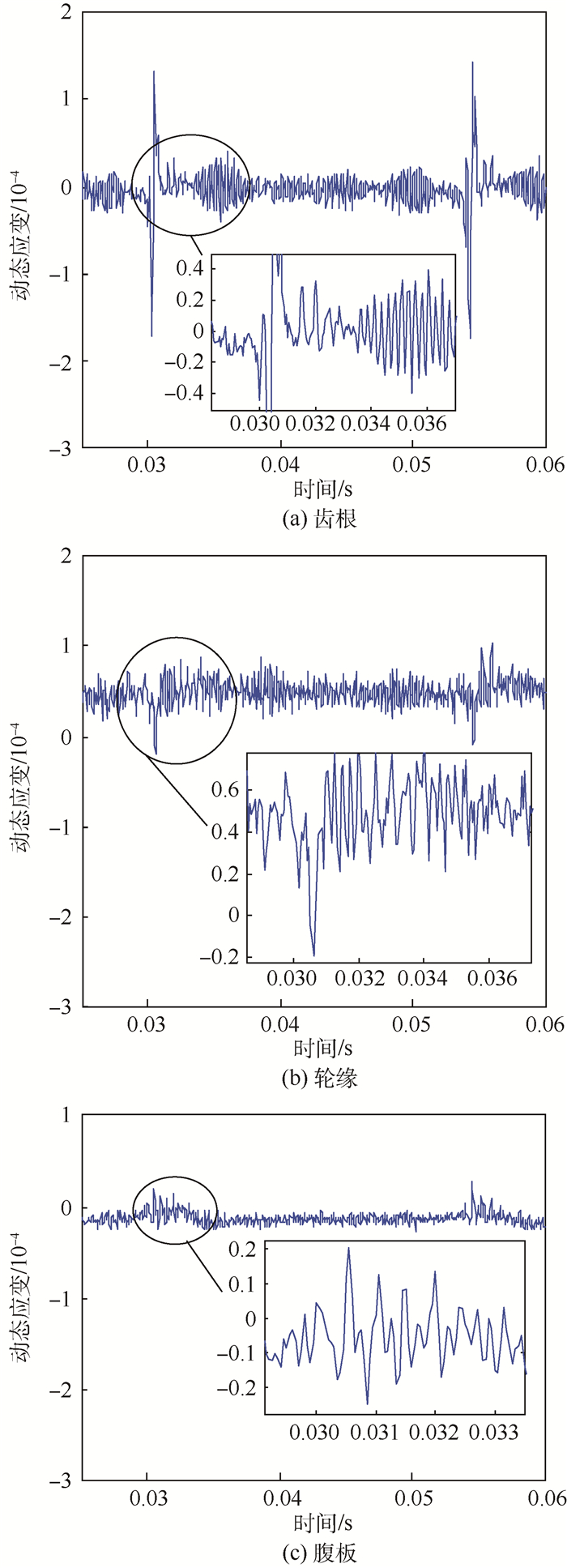
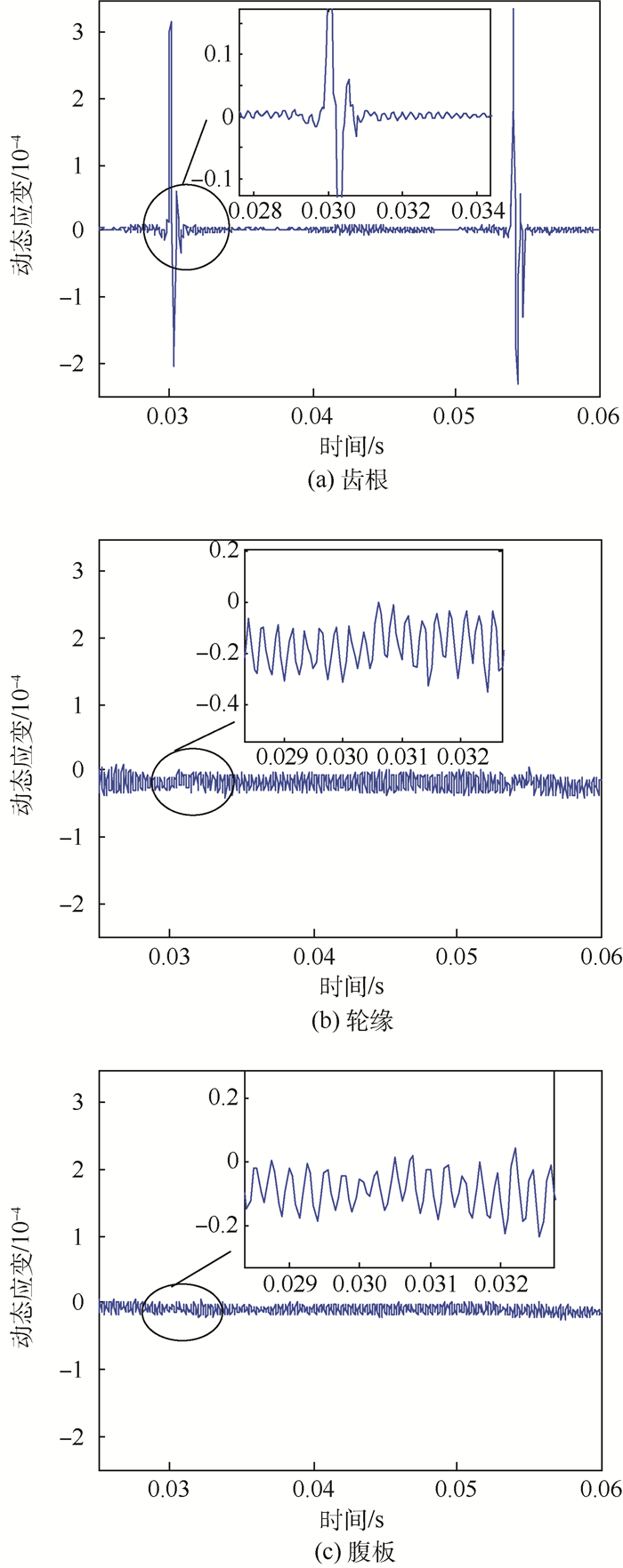
为分析两齿轮动态啮合过程的时域响应特性,提取薄壁齿轮B位于齿根圆角、轮缘内侧以及腹板中心位置的3个单元的拉-压应变时域响应,截取稳定加载阶段0.025~0.060 s间的动态应变,如图 4所示。同时,提取厚壁齿轮A对应位置处的单元响应,如图 5所示。
 |
| 图 4 齿轮B齿根、轮缘及腹板动态应变 Fig. 4 Dynamic strain of gear B root, rim and web |
| 图选项 |
 |
| 图 5 齿轮A齿根、轮缘及腹板动态应变 Fig. 5 Dynamic strain of gear A root, rim and web |
| 图选项 |
对比分析图 4和图 5可得:①在对应轮齿处于啮合状态时,齿根应变信号存在明显峰值,薄壁齿轮B轮缘及腹板处的应变存在较低的啮合峰值,而厚壁齿轮A轮缘及腹板处的应变响应没有明显的啮合峰值。这表明增加齿轮轮缘、腹板的厚度,会减弱轮齿载荷对轮缘及腹板的作用。②比较图 4(a)与图 5(a),发现厚壁齿轮的齿根应变峰值远大于薄壁齿轮的齿根应变峰值。这是因为齿轮啮合载荷由轮齿、轮缘及腹板共同承担,增加轮缘及腹板厚度,会使轮齿承担的啮合载荷比重增加。③在对应轮齿处于非啮合状态时,相对于厚壁齿轮A,薄壁齿轮B 3处应变的稳定值较大,且波动也大,这表明薄壁齿轮更易产生结构振动。④比较3处应变稳定值发现,齿轮轮缘内侧的应变稳定值大于齿根及腹板的应变值,并且降低轮缘及腹板的厚度,这种差别更加明显,这意味着薄壁齿轮的轮缘振动显著。上述分析结论与文献[15]中的实验结论相一致。
3 齿轮动态啮合过程频域响应特性分析 为了进一步研究齿轮动态啮合过程中振动产生的机理,需对齿轮动态响应进行频域响应特性分析。本节仍主要以2 500 r/min转速计算结果为例,分析齿轮动态啮合过程的频域响应特性。
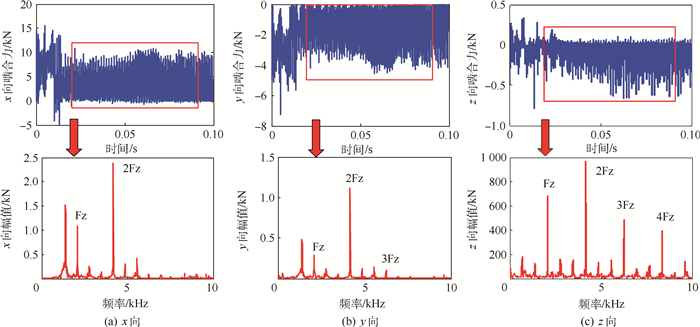
动态啮合力是齿轮啮合系统的主要激励,其频率成分对齿轮动态响应的频域特性具有重要影响。提取齿轮B在x、y、z 3个方向上的动态啮合力,经傅里叶变换得到加载稳定阶段(0.02~0.09 s)啮合力在3个方向上分力的幅-频特性曲线,如图 6所示。图中:Fz为啮合频率,即啮合1倍频;2 Fz为2倍啮合频率,即啮合2倍频。
 |
| 图 6 x、y、z向啮合力 Fig. 6 x、y、z direction meshing force |
| 图选项 |
由图 6可以看出,齿轮啮合力在x方向分力最大(均值为3 266.8 N),而在z方向(轴向)分力最小(均值为47.75 N),但不为零,表明在该对直齿轮啮合过程中存在轴向激振力。这主要是因为齿轮B腹板位置不在齿宽中心,导致轮齿啮合沿齿宽方向不均匀分布,从而产生轴向分力。由啮合力3个方向分力的幅-频特性曲线可以看出,啮合力的频率成分主要包含齿轮的啮合频率及其倍频,其他频率成分则是两齿轮该工作状态下的振动频率,其与齿轮是固有振动频率相关。此外,由图 6还可以看出,啮合2倍频对应的幅值最大,由以下分析可知,这是因为啮合2倍频的激振力激起了齿轮A的共振。
根据第2节中分析齿轮拉-压应变时域响应特性得出的结论④,分别提取两齿轮轮缘内侧某单元在x、y、z方向上的平均有效应变,并给出它们的幅-频特性曲线,如图 7和图 8所示。图 7分别为薄壁齿轮B轮缘内侧3个方向动态应变的幅-频特性曲线。可以看出,2 500 r/min工况下,齿轮B的振动频率成分较多,存在多个频率峰值,表明此时齿轮B的振动是多个振动的耦合,各频率峰值既包括齿轮的固有频率,又包括组合频率。所谓的组合频率,是指齿轮振动为多种振动的耦合时出现的位于齿轮固有频率与啮合倍频之间的振动频率。图 8为对应厚壁齿轮A轮缘内侧3个方向动态应变的幅-频特性曲线。可以发现,齿轮A 3个方向的振动存在相同且较为单一的频率峰值(4 110 Hz),表明齿轮A此时处于共振状态,其对应的共振频率为4 110 Hz。
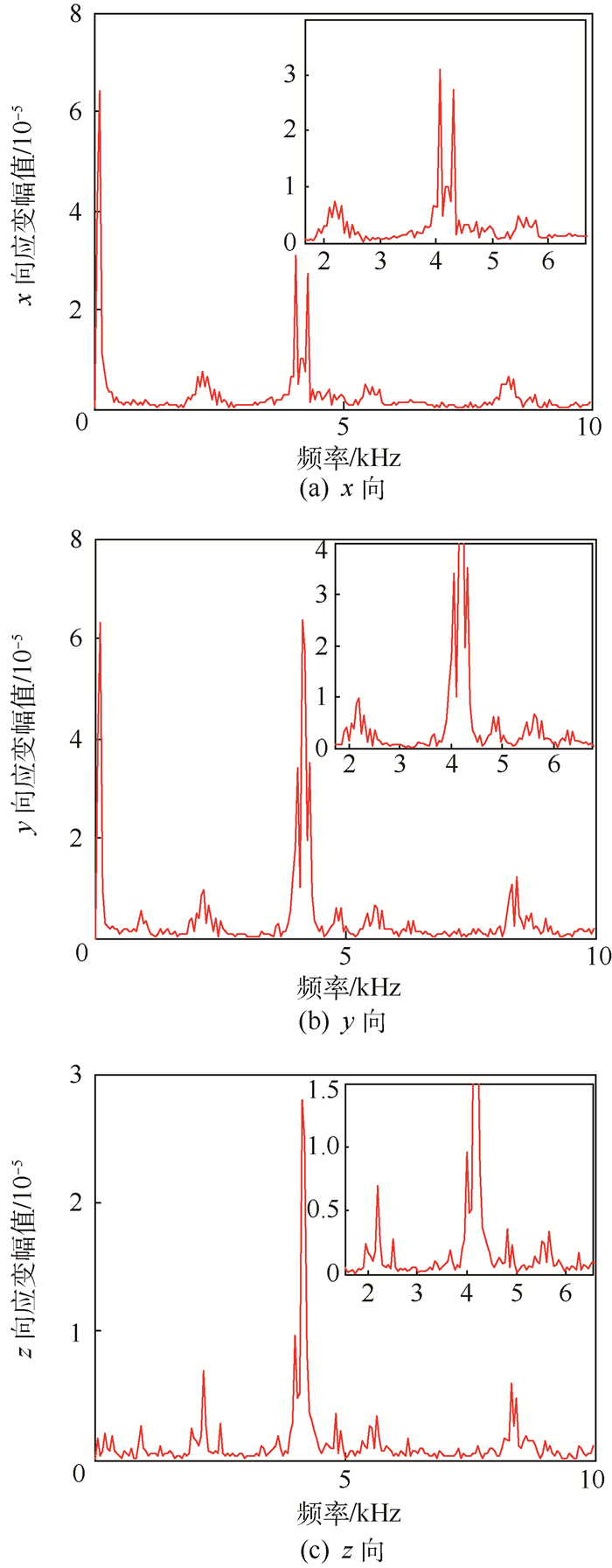 |
| 图 7 齿轮B轮缘x、y、z向动态应变 Fig. 7 x、y、z direction dynamic strain of gear B rim |
| 图选项 |
 |
| 图 8 齿轮A轮缘x、y、z向动态应变 Fig. 8 x、y、z direction dynamic strain of gear A rim |
| 图选项 |
为了进一步确定在2 500 r/min工况下,齿轮A是否发生共振,特提取齿轮A-B啮合系统模态计算中模态频率接近4 110 Hz的模态振型,如图 9所示,其模态计算结果显示此时的振型为齿轮A的2节径振动,对应的模态频率为4 165.4 Hz,该频率与啮合2倍频激振频率非常接近。同时提取齿轮动态啮合过程中某一时刻齿轮A的z向位移响应云图,如图 10所示。可知,此时齿轮A的响应振型与模态振型相一致,均为轮缘-腹板2节径振动的振型。
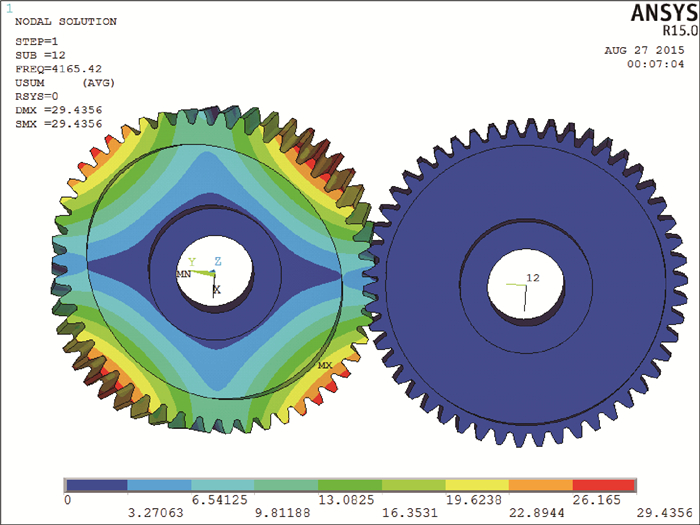 |
| 图 9 齿轮A模态振型 Fig. 9 Modal shape of gear A |
| 图选项 |
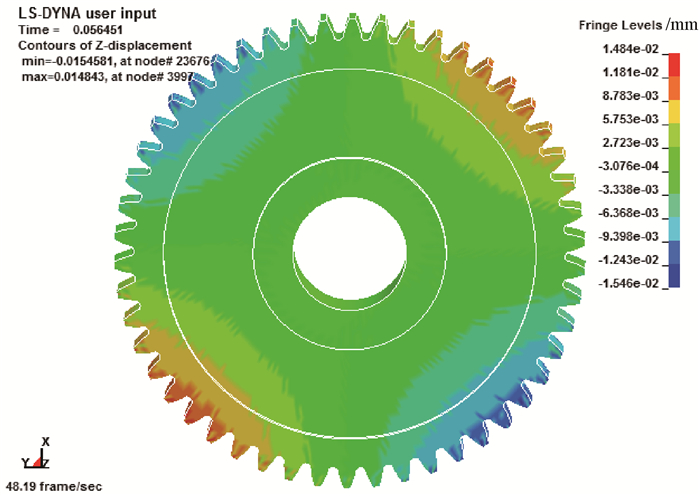 |
| 图 10 齿轮A轴向位移云图 Fig. 10 Axial direction displacement contour of gear A |
| 图选项 |
此外,根据不同转速下齿轮动态啮合过程的计算结果,可得到齿轮A轮缘内侧动态应变的Campbell图,如图 11所示。可以看出,2 500 r/min为2倍啮合激振频率与4 110 Hz固有频率相交共振点对应的共振转速。
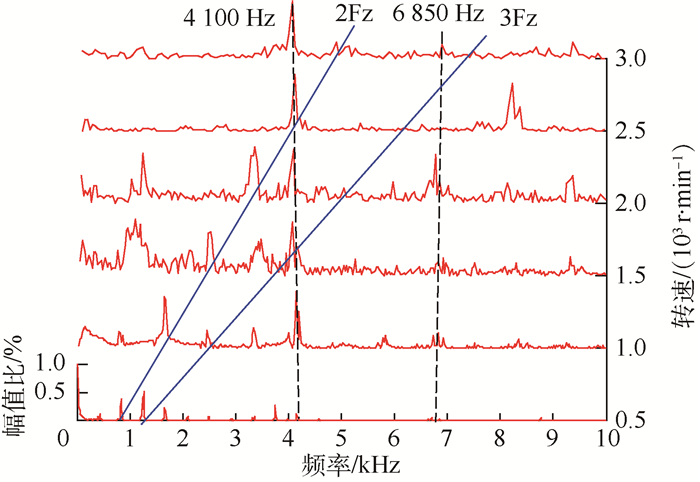 |
| 图 11 齿轮A轮缘应变Campbell图 Fig. 11 Rim strain Campbell diagram of gear A |
| 图选项 |
综上所述,齿轮A-B啮合系统在2 500 r/min工况下,齿轮A会发生频率为4 110 Hz的轮缘-腹板2节径振动的共振。由分析可得,齿轮在啮合过程中产生共振的必要条件是:啮合力中存在能激起齿轮某一方向振动的分力,且该分力的某一频率成分(啮合频率及其倍频)与该方向齿轮振动的某一固有频率相吻合。
4 结论 1)通过建立精确的齿轮啮合有限元分析模型,根据接触有限元分析方法,利用LS-DYNA显式计算可以高保真地模拟齿轮连续弹性动态啮合过程,为齿轮啮合系统动态特性的研究提供很好的研究平台。
2)齿轮轮缘及腹板的厚度对齿轮的结构振动具有重要影响。降低齿轮轮缘及腹板的厚度,会使轮缘、腹板的响应应力增加,而让齿根应力降低,同时也会使得齿轮的轮缘振动变得显著。
3)齿轮腹板位置的偏移,会导致直齿轮啮合过程中产生轴向啮合分力。此外,由于结构振动和弹性变形,直齿轮啮合过程中必然产生轴向啮合力。齿轮啮合激励和动态响应之间存在相互耦合的关系,动态啮合力会激起齿轮的振动,这反过来又会引起齿轮动态啮合力的变化。
4)齿轮动态啮合系统中,齿轮产生共振的必要条件是:啮合力中存在能激起齿轮某一方向振动的分力,且该分力的某一频率成分(啮合频率及其倍频)与该方向齿轮振动的某一固有频率相吻合。通过分析齿轮响应的频域特性及响应振型,或通过齿轮响应Campbell图分析,可以判定某一工况下的齿轮是否处于共振状态。
5)齿轮啮合力的频率成分包括啮合频率及其倍频,以及齿轮工作状态下的产生的振动频率,该振动频率与齿轮固有频率相关。除齿轮共振之外,齿轮的结构振动多为多个振动的耦合,各频率峰值对应齿轮的固有频率值及组合频率。
参考文献
| [1] | 李润方, 王建军. 齿轮系统动力学[M].北京: 科学出版社, 1997.LI R F, WANG J J. Gear system dynamics[M].Beijing: Science Press, 1997.(in Chinese) |
| [2] | 陶泽光, 李润方, 林腾蛟. 齿轮系统有限元模态分析[J].机械设计与研究, 2000(3): 45–46.TAO Z G, LI R F, LIN T J. Finite element modal analysis of gear system[J].Machine Design & Research, 2000(3): 45–46.(in Chinese) |
| [3] | 周立峰.基于ANSYS的行星齿轮系统参数化建模与模态分析研究[D].南京:南京航空航天大学, 2009.ZHOU L F.Parameterized modeling and mode analysis of planetary gear train based on ANSYS[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2009(in Chinese).http://cdmd.cnki.com.cn/article/cdmd-10287-2010081603.htm |
| [4] | 吴文光, 朱如鹏. 基于Workbench的斜齿轮固有特性分析[J].机械传动, 2010, 34(4): 54–56.WU W G, ZHU R P. Analysis on natural vibration characteristics of helical gear based on Workbench[J].Journal of Mechanical, 2010, 34(4): 54–56.(in Chinese) |
| [5] | 林腾蛟, 杨妍妮, 李润方, 等. 弧齿锥齿轮传动内部动态激励数值仿真[J].重庆大学学报, 2009, 32(6): 609–613.LIN T J, YANG Y N, LI R F, et al. Numerical simulation of the internal dynamic excitation of a spiral bevel gear transmission[J].Journal of Chongqing University, 2009, 32(6): 609–613.(in Chinese) |
| [6] | 常乐浩, 刘更, 郑雅萍, 等. 一种基于有限元法和弹性接触理论的齿轮啮合刚度改进算法[J].航空动力学报, 2014, 29(3): 682–688.CHANG L H, LIU G, ZHENG Y P, et al. A modified method for determining mesh stiffness of gears based on finite element method and elastic contact theory[J].Journal of Aerospace Power, 2014, 29(3): 682–688.(in Chinese) |
| [7] | 李亚鹏, 孙伟, 魏静, 等. 齿轮时变啮合刚度改进计算方法[J].机械传动, 2010, 34(5): 22–26.LI Y P, SUN W, WEI J, et al. Study on the improved algorithm of the time-varying meshing stiffness of gear[J].Journal of Mechanical, 2010, 34(5): 22–26.(in Chinese) |
| [8] | HE S, GUNDA R, SINGH R. Effect of sliding friction on the dynamics of spur gear pair with realistic time-varying stiffness[J].Journal of Sound and Vibration, 2007, 301(3-5): 927–949.DOI:10.1016/j.jsv.2006.10.043 |
| [9] | HE S, ROOK T, SINGH R. Construction of semianalytical solutions to spur gear dynamics given periodic mesh stiffness and sliding friction functions[J].Journal of Mechanical Design, 2008, 130(12): 122601.DOI:10.1115/1.2988478 |
| [10] | LIN T, OU H, LI R. A finite element method for 3D static and dynamic contact/impact analysis of gear drives[J].Computer Methods in Applied Mechanics and Engineering, 2007, 196(9-12): 1716–1728.DOI:10.1016/j.cma.2006.09.014 |
| [11] | PARKER R G, AGASHE V, VIJAYAKAR S M. Dynamic response of a planetary gear system using a finite element/contact mechanics model[J].Journal of Mechanical Design, 2000, 122(3): 304–310.DOI:10.1115/1.1286189 |
| [12] | 唐进元, 彭方进. 准双曲面齿轮动态啮合性能的有限元分析研究[J].振动与冲击, 2011, 30(7): 101–106.TANG J Y, PENG F J. Finite element analysis for dynamic meshing of a pair of hypoid gears[J].Journal of Vibration and Shock, 2011, 30(7): 101–106.(in Chinese) |
| [13] | 吴勇军, 梁跃, 杨燕, 等. 齿轮副动态啮合特性的接触有限元分析[J].振动与冲击, 2012, 31(19): 61–67.WU Y J, LIANG Y, YANG Y, et al. Dynamic meshing characteristics of a gear pair using contact finite element method[J].Journal of Vibration and Shock, 2012, 31(19): 61–67.(in Chinese) |
| [14] | WU Y J, WANG J J, HAN Q K. Contact finite element method for dynamic meshing characteristics analysis of continuous engaged gear drives[J].Journal of Mechanical Science and Technology, 2012, 26(6): 1671–1685.DOI:10.1007/s12206-012-0416-5 |
| [15] | LI S T. Experimental investigation and FEM analysis of resonance frequency behavior of three-dimensional, thin-walled spur gears with a power-circulating test rig[J].Mechanism and Machine Theory, 2008, 43(8): 934–963.DOI:10.1016/j.mechmachtheory.2007.07.009 |
| [16] | Japanese Industry Standards.Shape and dimensions of spur gears for general engineering:JIS B 1721[S].Tokyo:Japanese Standard Association, 1984. |
