双β衰变是β衰变的一种特殊形式，分为两类：一类是放出中微子的双β衰变，简称为2vββ衰变；另一类是不放出中微子的双β衰变，简称为0vββ衰变^[1-2]。双β衰变一直以来都是核物理理论和实验研究的热点课题。近期，任月皎和任中洲^[3-4]发现了一个简单实用的描述2vββ衰变半衰期的唯象公式。该唯象公式形式非常简单，仅需要两个参数就能够依据衰变能计算双β衰变的半衰期，并且计算结果与实验数据十分接近，对于与双β衰变有关的理论和实验研究都有一定的参考意义。
本文在任月皎和任中洲^[3-4]工作的基础上，分析并且改进了关于描述2vββ衰变半衰期的唯象公式，希望能对未来与双β衰变有关的工作有所借鉴。
1 双β衰变半衰期的唯象公式 通过分析双β衰变半衰期与衰变能实验数据，任月皎和任中洲^[3-4]发现，双β衰变半衰期与衰变能之间存在一个对数反比关系，在考虑了库仑势与核结构的修正之后，得出了一个简单实用的描述双β衰变半衰期与衰变能关系的唯象公式：

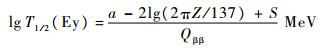(1)

式中: T_1/2为2vββ过程的半衰期; Ey表示10¹⁸年；Q_ββ为双β衰变的衰变能；常数a为与弱相互作用强度有关的项，通过拟合双β衰变半衰期的实验数据确定其值为a=5.843；Z为母核的电荷数；S为一个描述壳相互作用的物理量，当母核的中子数等于幻数时S=2，其他情况S=0。
利用唯象公式(1)得到的计算结果和实验半衰期以及衰变能的数值在表 1给出^[3-12]。可以看到，对于不同的原子核，式(1)仅含有两个变量，因此应用起来十分方便。与其他一些双β衰变的理论计算方法比较^[13-16]，式(1)的计算简便，适用范围广(理论上对于所有能发生双β衰变的原子核都适用)。因此有必要对它进行进一步的研究。
表 1 双β衰变的半衰期与衰变能^[3-12] Table 1 Double-beta decay half-lives and decay energy^[3-12]

原子核	实验半衰期的对数	衰变能/MeV	理论半衰期的对数
			文献[3-4]]的唯象公式	本文改进后的唯象公式
48Ca	1.643	4.267	1.865	1.890
76Ge	3.265	2.039	2.702	2.774
82Se	1.964	2.966	1.822	1.870
96Zr	1.371	3.349	1.578	1.631
100Mo	0.851	3.034	1.738	1.127
116Cd	1.447	2.813	1.834	1.174
128Te	6.279	0.866	5.872	6.040
130Te	2.845	2.528	2.013	2.070
136Xe	3.362	2.458	2.871	2.930
150Nd	0.960	3.371	1.473	1.516
238U	3.301	1.144	4.015	4.142

表选项






2 相空间因子对双β衰变半衰期的影响 从式(1)可看出，双β衰变的半衰期的对数与衰变能之间存在一个反比关系。纵观物理学发展史，一种奇特的物理现象的背后都蕴藏着更深的物理含义。例如氢原子的线状光谱是由分离的原子能级所导致的。因此，下面本文从理论的角度分析双β衰变，试图找到双β衰变的半衰期的对数与衰变能之间的反比关系所蕴含的物理规律。
理论上计算2vββ过程半衰期的公式为^[17]

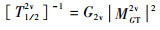(2)

式中:G_2v为一个与4个费米子相关的相空间因子；M_GT^2v为2vββ过程的核矩阵元。
这里可以发现，要计算双β衰变的半衰期，需要计算相空间因子与矩阵元两项。对于相空间因子，无论终态有几个粒子，计算方法都大同小异。而对于矩阵元，采取不同的理论，结果可能大相径庭。除此之外，矩阵元的计算一般比较复杂，需要用到比较高深的量子力学知识。按照从易到难的思想，首先考虑相空间因子的影响。如果不能在相空间因子的方向有所收获，再去考虑矩阵元的影响。下面给出推导相空间因子的一般过程。
双β衰变过程在弱相互作用中是一个二阶过程。它的计算方法可以类比β衰变过程。0⁺ 态到0⁺态的2vββ过程的微分几率为^[17]

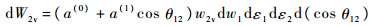(3)

式中：ε₁和ε₂为电子的能量; w₁和w₂为中微子的能量; θ₁₂为2vββ过程释放出来的两个电子之间的夹角; w_2v的定义如下^[17]：

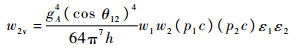(4)

式中：p₁和p₂为中微子的动量；c为光速；a⁽⁰⁾和a ⁽¹⁾为所有中间态的贡献之和，依赖于奇奇核中间态的激发能以及核矩阵元, 其具体形式为

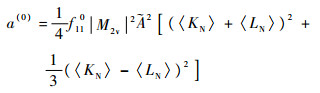(5)

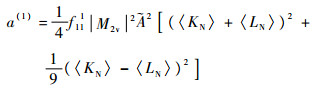(6)

其中：〈L_N〉和〈K_N〉是两个缩写，具体形式如下：

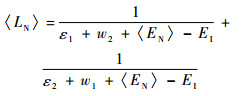(7)

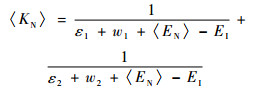(8)

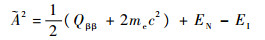(9)

式中：E_N为2vββ过程中中间核的激发能；E_I为母核的能量；m_e为电子的质量。〈E_N〉是一个适当选择的偶偶核激发能的近似。由于〈E_N〉同时通过〈K_N〉与〈L_N〉出现在分母项，且通过?²出现在分子项，因此衰变概率对于〈E_N〉的依赖很弱。这里的M_2v是核矩阵元, f ₁₁⁰和f₁₁¹是电子径向波函数的产物，由于它们的形式比较复杂，这里就不再列举，具体形式可以参见文献[17]。
在所有参数的意义已经明确后，将它们代入式(3)并积分，借助一定的近似，可以在半衰期中将相空间因子与矩阵元的影响分离开来，即^[17]

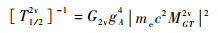(10)

其中，相空间因子的部分为

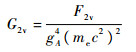(11)

式中：

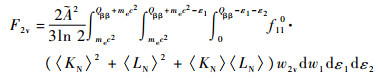(12)

核子的轴矢量耦合常数g_A已经重整化以便于从相空间因子中分离出来。
仔细观察式(12)很容易发现，相空间因子式(11)无法得到解析解，只能得到数值解。这与本文初衷，即得到相空间因子对半衰期的具体影响的形式多少有些出入。但是，无法得到相空间因子的解析解对本文的研究影响并不大，仍然可以将已有的实验数据(如衰变能)代入式(11)求得不同原子核的相空间因子的数值。从式(10)中可以看出，双β衰变的半衰期与相空间因子成反比，假若相空间因子的数值解的对数与所对应的核子的衰变能成正比，那么就可以认为双β衰变的半衰期的对数与衰变能的反比关系是由相空间因子造成的。
将式(12)积分并代入式(11)后可得到相空间因子的数值解，表 2是具体的结果^[17]。
表 2 双β衰变的相空间因子与衰变能的比较^[17] Table 2 Comparison between phasespace factor and decay energy of double-beta decay^[17]

原子核	相空间因子/ (10－21a－1)	衰变能/ MeV	相空间因子的对数
48Ca	15 550	4.267	4.192
76Ge	48.17	2.039	1.683
82Se	1 596	2.996	3.203
96Zr	6 816	3.349	3.834
100Mo	3 308	3.034	3.520
116Cd	2 764	2.813	3.441
128Te	0.268 8	0.866	-0.570
130Te	1 529	2.528	3.184
136Xe	1 433	2.458	3.156
150Nd	36 430	3.371	4.561
238U	14.57	1.144	1.163

表选项






表 2中列出了发生双β衰变原子核相空间因子及其对数和衰变能。观察表 2中第3列与第4列的数据，可以清楚发现双β衰变的衰变能与相空间因子的对数是正相关的，至于是否是成正比关系，可以进行如下检验。
图 1给出了双β衰变相空间因子的对数与衰变能的关系。从中可以发现，基本上所有的数据点都在趋势线的附近。对数据点进行线性拟合得到的相关系数的平方(R-square)为0.843。所有的数据点与趋势线的平均偏离为0.285。偏离最小的¹⁰⁰Mo，为0.003 4，偏离最大的⁴⁸Ca，为0.828。其中偏离大于0.3的共有4个核，分别是⁴⁸Ca，偏离为0.828；¹²⁸Te，偏离为0.323；¹³⁶Xe，偏离为0.351；²³⁸U，偏离为0.454。总的来说，可以认为双β衰变的衰变能与相空间因子的对数之间存在较强的正比关系。而式(10)中已经指出，双β衰变的半衰期与相空间因子是成反比的，也就是说双β衰变的半衰期的对数与衰变能存在反比关系。这与从双β衰变半衰期与衰变能的实验数据中观察到的现象不谋而合。至此，可以得出结论，任月皎和任中洲^[3-4]所发现的双β衰变半衰期的对数与衰变能的近似反比关系可以认为是在忽略双β衰变的核矩阵元随衰变能变化的情况下(核矩阵元不仅仅与Q 值有关，而且依赖于原子核的结构。正因为如此，半衰期的对数与Q值的反比关系才不严格成立。然而，考虑这些问题不仅超出了提出简单唯象公式的目的，也超出了本文的研究范畴)，由双β衰变的相空间因子导致的。

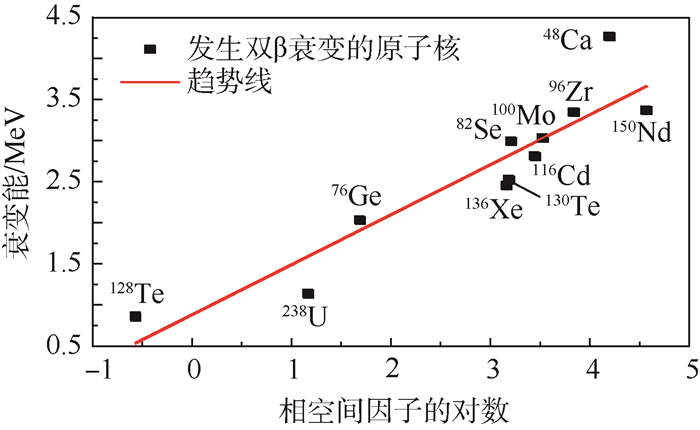图 1 双β衰变衰变能与相空间因子关系 Fig. 1 Relationship between phasespace factor and decay energy of double-beta decay

图选项

3 对唯象公式所做的改进 任月皎和任中洲^[3-4]通过观察双β衰变半衰期与衰变能的实验数据以及合理的分析，得到了描述双β衰变半衰期的唯象公式(1)。利用唯象公式计算所得到的双β衰变的半衰期与实验数据之间的平均偏差只有0.486 (定义平均偏差，其中x_i和y_i分别为半衰期的对数的计算值与实验值) ^[3]。这说明唯象公式可以较好地描述现有实验数据。然而，虽然大部分的计算结果与实验的数据比较吻合，还是有少量原子核的计算结果与实验数据的偏差较大，比如¹⁰⁰Mo核。接下来，探索改进该唯象公式，使其能够更加精确地描述双β衰变半衰期。
首先仔细分析¹⁰⁰Mo核的特点。¹⁰⁰Mo是⁹⁶Mo的一种同位素，质子数是42，中子数是58，半衰期为7.1Ey，衰变能是3.034 MeV。虽然¹⁰⁰Mo不是幻数核，但是依据壳模型理论，它的中子数恰好填满2f_7/2这个亚壳层。之前我们在对唯象公式添入壳模型修正这一项时是当母核的中子数等于幻数时令S=2，其他情况时令S=0。假设中子数填满亚壳层时，S也不为0(其值可以通过拟合表 1的实验数据得到)，或许能够对唯象公式做出改进。
表 3是所有发生双β衰变的原子核的质子数、中子数以及对应的壳修正项的关系表。即当母核中子数等于幻数时，S′=2；母核中子数恰好填满亚壳层时, S′=-2 (对于母核中子数填满亚壳层的原子核, 其S′的取值是通过拟合实验数据得到的近似整数，其真实的拟合值为-1.973)；其他情况时，S′=0。
表 3 双β衰变原子核的质子数、中子数以及对应的壳效应修正项的数值 Table 3 Number of protons, neutrons and corresponding shell corrections for double-beta decay nuclei

原子核	质子数	中子数	质量数	改进后的壳效应修正项
48Ca	20	28	48	2
76Ge	32	44	76	0
82Se	34	48	82	0
96Zr	40	56	96	0
100Mo	42	58	100	-2
116Cd	48	68	116	-2
128Te	52	76	128	0
130Te	52	78	130	0
136Xe	54	82	136	2
150Nd	60	90	150	0
238U	92	146	238	0

表选项






从表 3中可以看到，改进后的壳效应修正项不仅对¹⁰⁰Mo核有影响，对¹¹⁶Cd核也有影响，而对其他的原子核无影响。利用表 1的实验数据拟合公式：

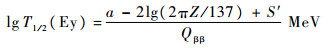(13)

得到的新的参数的数值为a=5.989。
图 2是改进后的从⁴⁸Ca到²³⁸U 11个偶偶核的双β衰变的半衰期的计算结果与改进前计算结果的对比。图中：“■”为改进前半衰期的计算结果与实验数据的偏差；“●”为相应的改进后的计算结果与实验数据的偏差。

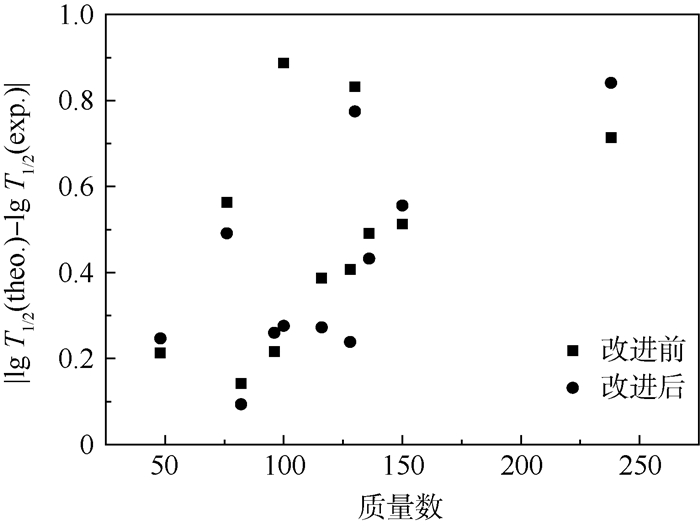图 2 双β衰变半衰期的对数的计算值与实验值的偏差 Fig. 2 Deviation between calculated and experimental values of logarithms of double-beta decay half-lives

图选项

观察图 2很容易发现，改进后的壳修正效应所作用的两个核子¹⁰⁰Mo与¹¹⁶Cd的计算结果与实验值的偏差比利用原本的唯象公式(1)所得到的计算值与实验值的偏差要小。不仅如此，从整体来看，图 2中有7个改进后的数据点(●)比改进前的数据点(■)要更接近横轴。也就是说，按照改进后的唯象公式(13)所计算的双β衰变的半衰期要比改进前的唯象公式(1)所给出的结果更接近于实验值。从⁴⁸Ca到²³⁸U 11个偶偶核的双β衰变的半衰期对数的计算值与实验值之间的平均偏差lg T_1/2(theo.)-lg T_1/2(exp.)也从原本的0.486下降到了0.408。总之，无论是从个别还是从整体来说，改进后的唯象公式都要比改进前的能更好地描述双β衰变的半衰期。
此外研究发现，对唯象公式(1)中其他项做改动难以有效地改进其对实验数据的描述。
4 结论 1)?在忽略核矩阵元影响的情况下，可以认为任月皎和任中洲所发现的双β衰变的唯象公式中衰变半衰期的对数与衰变能的反比关系是由双β衰变的相空间因子所造成的。
2)?在任月皎和任中洲工作的基础上，本文用新的壳效应修正项替换了原本的修正项。替换之后双β衰变的半衰期的对数的理论值与实验值之间的平均偏差从原本的0.486下降到了0.408。
致谢    
感谢李凯文、周丹、崔二亮和陆俊旭有益的讨论。此工作是在任中洲教授作客北京航空航天大学物理科学与核能工程学院《物理与核科学大家谈》的启发下完成的，在此对任月皎和任中洲表示诚挚的谢意。
参考文献

[1]	卢希庭. 原子核物理[M].修订版北京: 原子能出版社, 2001: 144-145.LU X T. Nuclear physics[M].Revised edBeijing: Atomic Energy Press, 2001: 144-145.(in Chinese)
[2]	ALFONSO K, ARTUSA D R, Avignone F T, et al. Search for neutrinoless double-beta decay of 130Te with CUORE-0[J].Physical Review Letters, 2015, 115(10): 102502.DOI:10.1103/PhysRevLett.115.102502
[3]	REN Y J, REN Z Z. Systematic law for half-lives of double-β decay with two neutrinos[J].Physical Review C, 2014, 89(6): 064603.DOI:10.1103/PhysRevC.89.064603
[4]	REN Y J, REN Z Z. Half-lives of double β+-decay with two neutrinos[J].Nuclear Science and Techniques, 2015, 26(2): S20510.
[5]	SAAKYAN R. Two-neutrino double-beta decay[J].Annual Review of Nuclear and Particle Science, 2013, 63(1): 503–529.DOI:10.1146/annurev-nucl-102711-094904
[6]	WANG M, AUDI G, KONDEV F G, et al. NUBASE2012 evaluation of nuclear properties[J].Chinese Physics C, 2012, 120(12): 6–7.
[7]	ACKERMAN N, AHARMIM B, AUGER M, et al. Observation of two-neutrino double-beta decay in 136Xe with the EXO-200 detector[J].Physical Review Letters, 2011, 107(21): 212501.DOI:10.1103/PhysRevLett.107.212501
[8]	GANDO A, GANDO Y, HANAKAGO H, et al. Measurement of the double-β decay half-life of 136Xe with the KamLAND-Zen experiment[J].Physical Review C, 2012, 85(4): 045504.DOI:10.1103/PhysRevC.85.045504
[9]	ARNOLD R, AUGIER C, BAKER J, et al. Measurement of the ββ decay half-life of 130Te with the NEMO-3 detector[J].Physical Review Letters, 2011, 107(6): 062504.DOI:10.1103/PhysRevLett.107.062504
[10]	BARABASH A S. Precise half-life values for two-neutrino double-β decay[J].Physical Review C, 2010, 81(3): 035501.DOI:10.1103/PhysRevC.81.035501
[11]	RADUTA A A, RADUTA C M. Double beta decay to the first2+ state within a boson expansion formalism with a projected spherical single particle basis[J].Physics Letters B, 2007, 647(4): 265–270.DOI:10.1016/j.physletb.2007.02.007
[12]	AUNOLA M, SUHONEN J. Systematic study of beta and double beta decay to excited final states[J].Nuclear Physics A, 1996, 602(2): 133–166.DOI:10.1016/0375-9474(96)00087-5
[13]	TOIVANEN J, SUHONEN J. Study of several double-beta-decaying nuclei using the renormalized proton-neutron quasiparticle random-phase approximation[J].Physical Review C, 1997, 55(5): 2314–2323.DOI:10.1103/PhysRevC.55.2314
[14]	STOICA S, MIHUT I. Nuclear structure calculations of two-neutrino double-beta decay transitions to excited final states[J].Nuclear Physics A, 1996, 602(2): 197–210.DOI:10.1016/0375-9474(96)00122-4
[15]	BARABASH A S, HUBERT F, HUBERT P, et al. New limits on the ββ decay of 130Te to excited states of 130Xe[J].The European Physical Journal A, 2001, 11(2): 143–145.DOI:10.1007/s100500170079
[16]	HIRSCH J G, CASTANOS O, HESS P O, et al. Double-beta decay of 100Mo:The deformed limit[J].Physical Review C, 1995, 51(4): 2252–2255.DOI:10.1103/PhysRevC.51.2252
[17]	KOTILA J, IACHELLO F. Phase space factors for double-β decay[J].Physical Review C, 2012, 85(3): 034316.DOI:10.1103/PhysRevC.85.034316