Web服务是网络化应用软件开发的基础,随着互联网、云计算、移动计算和大数据等技术的快速发展,面向海量终端用户的互联网软件服务不断涌现,由它们组合而成的网络化软件已经逐渐成为软件的重要形态和发展趋势。面向服务计算的体系结构能够无缝地把各种在线Web服务和API组合起来,形成新的增值服务来满足用户需求。然而,随着互联网产业突飞猛进的发展,在线Web服务和API的数量正在飞速增长,如何从大量的网络服务中快速有效地选择出满足用户功能性和非功能性要求的服务已经成为服务计算领域面临的一个重要问题,目前解决这一问题的主要技术途径是服务推荐。
主流的服务推荐系统在为用户进行服务推荐时,主要考虑的是用户偏好、服务应用场景和服务质量(Quality of Service,QoS)等因素。其中,QoS作为一系列用户可以感知和监测到的非功能属性,实际上成为了众多服务推荐系统进行服务选择和推荐的核心依据。大多数服务推荐系统使用协同过滤算法对用户观察到的QoS属性信息进行挖掘,找到与当前用户服务体验相似的用户,为当前用户预测其未使用过的服务QoS属性值,并以此进行服务推荐。近年来,基于QoS的服务推荐技术受到学术界广泛关注[1-2]。
Al-Masri和Mahmoud[3]构建的服务检索系统通过定期对系统内所有的服务进行监测,获取相应的QoS属性的数值,并根据用户选择的QoS属性预测值,对服务进行检索。基于这些预测数据进行服务间相似度的计算,给出检索和推荐结果。另外,该类系统中使用的QoS值通常与用户自身感受存在一定差异。
香港中文大学的郑子彬等[4]提出了一个基于用户反馈的协同过滤算法的Web服务推荐系统,该系统对两个可测量的QoS属性(响应时间和失败率)进行用户反馈信息的收集,使用协同过滤算法对QoS值进行预测,为提交反馈的用户提供符合用户偏好的服务推荐列表。该系统也存在着使用协同过滤算法而导致的推荐系统的局限性,即稀疏数据严重影响QoS预测准确性的问题。
“混合式”协同过滤的双向服务推荐算法[5],同时对用户之间和服务之间的相似度进行计算,向用户和服务供应商双方同时提供推荐信息。与传统的协同过滤推荐算法通过用户评价矩阵来分析用户之间相似程度不同的是,这种“混合式”协同过滤同时考虑了结合用户间的相似度和服务间的相似度。文献[6]还提出了更加优化的“混合式”协同过滤算法,通过计算用户、服务和全局平均评分偏差的加权来同时得到用户、服务的预测分,从而产生更高质量的推荐。
文献[3-6]使用的方法存在共同不足:在服务QoS属性值的模型设计方面,都假定服务的QoS是静态不变的,推荐算法都是在{用户-服务}二维矩阵模型基础上设计的。而真实环境中服务的QoS受多种因素影响,具有动态性,与用户地理位置和服务调用时间具有时空相关性。
为了解决上述问题,本文考察了在传统推荐领域中的一些先进的推荐预测算法,文献[7]在服装、鞋子等商品的销售趋势预测方面引入了张量的概念提出了带时间信息的推荐预测算法。该算法将时间信息加入到原有的{商品-用户}二维矩阵模型,使之扩展为{商品-用户-时间}三维张量模型,相应的张量分解(Tensor Factorization,TF)算法使得推测算法的准确率和计算效率有了很大的提高。 受此启发,本文将服务QoS从{用户-服务}二维静态模型扩展为{用户-服务-时间}三维动态模型,并充分利用这3种元素之间存在的有用信息,使用基于张量分解的协同过滤算法对服务的QoS进行预测,结合QoS值的非负特性,本文提出用非负CP(NNCP)分解方法来提高服务的QoS预测准确率。
1 基础知识 本节主要介绍本文用到的相关技术,首先介绍传统的服务推荐算法,其次介绍张量相关知识以及张量分解相关技术。
1.1 传统服务推荐算法 服务推荐系统中的预测模型和预测算法是服务推荐系统的核心组成部分,WSRec服务推荐算法[4]是本领域近年来非常经典的算法。该算法结合了user-to-user和item-to-item两种基于记忆的协同过滤算法给出推荐。服务推荐系统中的用户通过提交自己观测到的QoS属性,为系统提供训练数据。服务推荐算法分为如下几步:
1) 相似度计算。WSRec服务推荐算法分别计算用户间的相似性和 Web 服务间的相似性,对于目标用户a,该算法使用改进的皮尔逊相关系数(PCC)计算目标用户与其他用户的相似性。
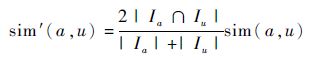 | (1) |
式中:sim(a,u)为用户a和u的PCC相似度;Ia和Iu分别为用户a和u评价过的Web服务集合。对于两个服务i和j,算法中两个 Web 服务间的相似性为
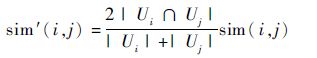 | (2) |
式中: sim(i,j)为使用PCC计算服务i和j的相似度; Ui和Uj分别为提交过Web服务i和j的QoS属性的用户集合。
2) 选择邻居。对于当前用户a,选取与其正相关(相似性大于零)的用户为用户邻居,其定义为
S(u) = {u|u∈U,sim′(a,u)>0,u≠a}
式中:U为所有用户的集合。
对于Web服务i,选取与其正相关(相似性大于零)的服务作为服务邻居,其定义为
S(i) = {j|j∈S,sim′(i,j) >0,i≠j}
式中:S为所有服务的集合。
3) 产生预测值。算法对当前用户a所有未使用过的服务QoS进行预测,并选取预测值最好的服务推荐给用户。对于用户a未使用过的Web服务i,算法分别计算基于user-to-user和item-to-item协同过滤算法产生的预测值。
基于user-to-user的预测方法产生的预测值为
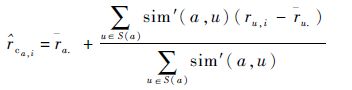 | (3) |
式中: r a.为用户a提交的QoS属性均值; S(a)为用户a的相似用户集合;ru,i为用户u对服务i的真实值; u.为用户u对所有服务的平均值。
基于item-to-item的预测方法产生的预测值为
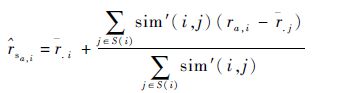 | (4) |
式中:r .i为服务i获得QoS属性的均值;S(i)为与其似的Web服务集合;ra,i为用户a对服务i的真实值; .j为服务j对于所有用户的平均值。
算法分别计算信心指数conc和cons,conc为对user-to-user方法预测结果的信心指数,cons为对item-to-item方法预测结果的信心指数,其定义分别为
 | (5) |
 | (6) |
最终QoS预测值的计算方法为
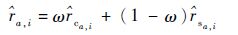 | (7) |
式中:ω=
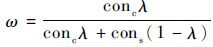
WSRec算法结合了相似用户和相似服务两种预测方式,并通过调节参数λ决定两个算法预测结果对最终结果的影响,在一定程度上解决了单一方法在矩阵过于稀疏时预测不准确的缺点。
1.2 张量基础 数据沿着一个相同的方向排列称为一路阵列。标量是零路阵列的表示,行向量和列向量分别是数据沿着水平和垂直方向排列的一路阵列,矩阵是数据沿着水平和垂直两个方向排列的二路阵列。向量是下标集为一维的数列,矩阵是下标集为二维的数列,多维数列,可以用张量来表示。因此张量可以视为向量和矩阵在多维空间中的推广,一维张量即为向量,二维张量则是矩阵。例如,一个三维张量可以表示为三维数列 ∈ R I×J×K,I、J和K分别为用户数量、服务数量和时间点数。其元素沿着不同的下标方向,在实际中可以表示不同的意义。图 1为一个一般的三维张量及其下标集。
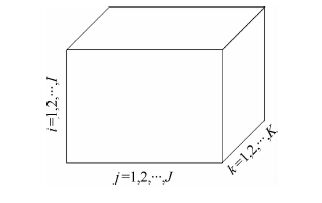 |
| 图 1 三阶张量及其下标集 Fig. 1 3 order tensor and subscript indexes |
| 图选项 |
为了进行张量的信息挖掘,需要对张量进行分解,张量分解是张量研究的主要方面。张量分解是在奇异值分解(Singular Value Decomposition,SVD)的概念上的延伸。文献中提出的张量分解主要有两大类模型:Tucker模型[8]和CP模型[9]。CP分解模型将张量表现为一系列秩为1的矩阵相乘的形式。与此不同,Tucker分解模型是一种高维主成分分析的方式,把一个张量表现成了一个核心张量和各个维度上的因子矩阵相乘的形式。有关张量分解及其应用方面的综述,可以参考Kolda和Bader[10]的研究,详细介绍了张量的各种分解模型及其在不同领域的实际应用。
1.3 CP分解 本文在CP分解的基础上设计服务推荐的预测算法。一个三阶张量 A ∈ R I×J×K 的CP分解就是寻找向量 u i∈ R I,s j∈ R J,t k∈ R K,使得
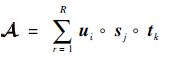 | (8) |
式中:“。” 表示向量的外积运算;R为张量的秩。
图 2为CP分解三阶示意图。
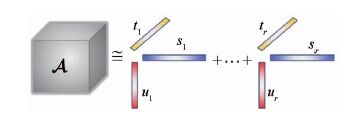 |
| 图 2 三维张量的CP分解 Fig. 2 CP decomposition of a 3-dimensional tensor |
| 图选项 |
对于三阶张量的CP分解问题,可以从优化问题考虑解决:
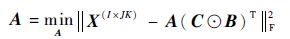 | (9) |
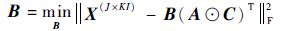 | (10) |
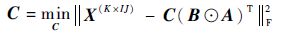 | (11) |
式中: A ∈ R I×R、 B ∈ R J×R、 C ∈ R K×R 为因子矩阵; X 为原始张量转换后矩阵。
它们的最小二乘解(Alternating Least Squares,ALS)分别为
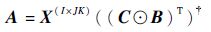 | (12) |
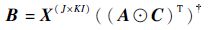 | (13) |
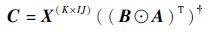 | (14) |
利用Khatri-Rao积的Moore-Penrose广义逆矩阵的性质
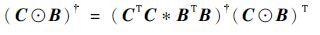 | (15) |
可求得因子矩阵 A 的最小二乘解,同理可得因子矩阵 B 和 C 的最小二乘解为
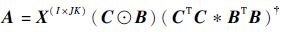 | (16) |
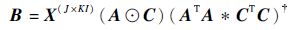 | (17) |
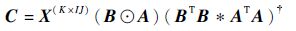 | (18) |
算法:CP分解的交替最小二乘算法[11]
输入:张量χ的水平展开矩阵 X (I×JK)、 X (J×KI)及因子个数R。
输出:因子矩阵 A ∈ R I×R,B ∈ R J×R,C ∈ R K×R。
初始化:矩阵 B 0和 C 0。
步骤1?对k=1,2,…,K执行以下更新:
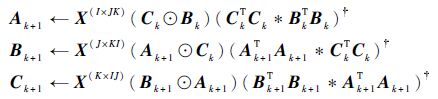 |
步骤2?收敛条件检验:若对某个误差常数ε>0,收敛条件为
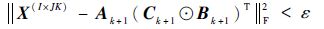 | (19) |
满足,则停止迭代,输出因子矩阵 A 、 B 、 C ;否则,返回步骤1,继续迭代,直至收敛。
交替最小二乘算法的主要优点是简单、容易实现,主要缺点是有可能迭代过程徘徊不止,不能收敛;或者因为迭代过程陷入泥沼之中,使得需要经过漫长迭代,最终才能收敛。
1.4 时间感知的服务推荐算法 传统的服务推荐算法在过去的研究中取得了一些成就,但是这些算法大多都假定服务的QoS属性固定不变,但在实际环境中,服务的QoS属性受到多种因素的影响,时刻发生着变化。在真实的网络环境中,服务用户的上下文信息包括时间、地点以及当时所在网络的实际情况等信息,都能够影响服务的QoS属性。因此,本文建立能够描述多种影响因素的服务QoS模型,将传统{用户-服务}二维模型User×Service→QoS扩展为多维模型D1×D2×…×Dn→QoS,D1,D2,…,Dn为维度,本系统主要多考虑了影响服务QoS的时间因素,模型为:User×Service×Time→QoS。然后,将服务QoS的用户、服务和时间信息构建为{用户-服务-时间}三维张量,并通过张量分解的算法得到服务在不同时间点上的QoS预测值,进而为用户做出符合需求的个性化推荐。
2 基于QoS的服务推荐算法 如图 3所示为现有基于协同过滤算法的研究工作中服务推荐算法的一般模型,图中QoS数据采用矩阵的形式,按照用户和服务两个维度描述每一个数值,“”表示已有的QoS数据,“”表示缺失的QoS数据,接下来,算法将数据矩阵分解(Matrix Factorization,MF)为两个低维因子矩阵相乘的形式,一个因子矩阵由用户组成,一个因子矩阵由服务组成,然后用这两个因子矩阵的乘积结果来逼近原始的QoS数据矩阵,该结果是一个全值矩阵,与原矩阵对应位置的数据可以用来预测“”所代表的缺失的QoS数据。考虑到这类算法的不足和缺陷,在这类协同过滤算法的基础上,引入张量和张量分解来改进服务的QoS描述模型以及预测算法。
 |
| 图 3 现有研究中的协同过滤预测算法 Fig. 3 Collaborative filtering method for prediction inexisting research |
| 图选项 |
使用张量数据结构,可以从多个维度上描述对服务的QoS数据产生影响的因素,如图 4所示,引入了时间因素,对不同时间段的QoS数据综合分析,构造三阶张量数据结构,充分利用数据的相互关系作出更加准确地预测结果。通过扩展基于矩阵分解的协同过滤算法,不仅考虑{用户-服务}所构成的二维数据矩阵,同时加入了时间因素这个维度的数据,将以前的服务推荐系统从{用户-服务}这种二维数据,扩展到{用户-服务-时间}的三维数据,并充分利用张量分解算法构造出新的预测算法。
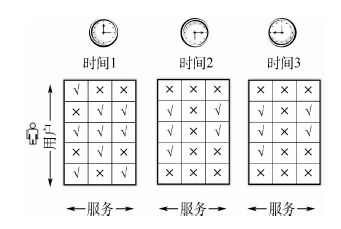 |
| 图 4 时间序列上的QoS矩阵 Fig. 4 QoS matrices in time sequence |
| 图选项 |
3 基于QoS的Web服务推荐系统 从一个Web服务调用的应用场景出发,分析在实际应用中遇到的用户无法得到满意服务的问题来源,然后引出一种能够涵盖更多维度数据的服务QoS预测模型,最后提出一个带时间信息的基于QoS预测的服务推荐系统框架的思路,先给一个简单的应用实例的场景。
这里本文假设一个基于QoS的Web服务推荐应用的场景,该场景的用户需要查找具有最佳QoS值的Web服务。处在不同地理位置的服务用户在不同的时间向Web服务推荐系统提交他们的服务调用请求,当然这些服务用户指定了一些他们所需要的服务的QoS参数要求(响应性、可用性和吞吐量等)。服务推荐系统通过采取综合分析这些用户和服务的调用上下文信息来返回一个具有最佳QoS表现的Web服务的列表呈现给用户。然后,这些被推荐出来的Web服务或者API可以被服务用户用于开发组合服务。
如图 5所示,在本文假设的情景中,身处北京、伦敦、洛杉矶和纽约的一些服务用户分别在不同的时间调用Web服务。现在服务推荐系统需要考虑用户调用服务的时间信息对Web服务的QoS值进行预测。通过预测具有相同功能的服务QoS属性值,面向服务的体系结构系统设计人员可以在组合Web服务时作出更明智的选择。因此,为了解决在不同的时间点上预测服务的QoS属性值这个问题,本文提出了一个在时域上的QoS感知的Web服务推荐系统框架。该服务推荐系统的主要目标是在不同时间点上预测,处在不同位置的用户调用服务时的QoS属性值。
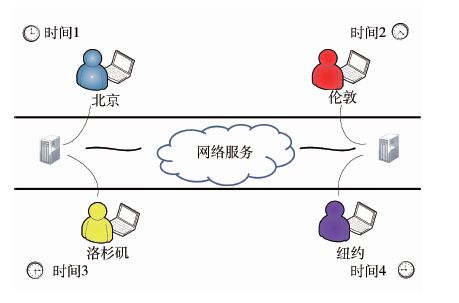 |
| 图 5 服务调用的应用场景 Fig. 5 A motivating scenario of Web service invocation |
| 图选项 |
在本场景中,用来描述服务QoS属性值的{用户-服务}这样的二维关系模型经常被表示为二维矩阵,这种的模型的推荐算法在以前的研究中都有提及[12-16]。为了涵盖更多的QoS影响因素,更充分地利用有限且有用的数据信息,本文使用张量的数据模型来描述QoS属性值,即将以前的二元关系表示模型扩展为{用户-服务-时间}这样的三元张量表示模型,同时,提出了一些张量分解[17]的算法来解决本文所要预测的服务QoS属性。本文的关键是用考虑时间因素之后的三维张量分解算法替代现有研究中的二维矩阵分解,{用户-服务-时间}这3个维度的关系在预测缺失的QoS属性的时候能够提供更多的相关信息,使得预测结果更加准确。同时考虑到这些QoS属性都是非负的数值,因此本文在张量分解的基础上,加入了非负性的限制,提出了使用非负张量分解(Nonnegative Tensor Factorization,NTF)[18]的方法来建立服务推荐系统的预测模型。
3.1 构造QoS张量 将一个带时间信息的Web服务的QoS值在三维张量中的下标信息表示为一个三元组
每一个Web服务在某个时间点被服务用户调用的QoS信息就可以通过这个
每当一个服务用户调用Web服务的时候,推荐系统都会收集被调用服务相应的QoS值。经过一段时间的收集以后系统就积累出一个庞大的数据集,这个数据集里的每一个数据,本文都用一个四元组来描述:
为了将这些服务的QoS信息值构建为本文提出的三维张量,设计了如下算法将服务器中的文件信息构建为一个三维张量。它的输入是由Web服务的QoS属性值组成的四元组的集合<u,s,t,r>,输出为一个时域三维张量 Y ∈ R I×J×K。算法总结如下:
算法1 构造带时间信息QoS值的三阶张量
输入:一个全部都是由Web服务的QoS属性值组成的四元组的集合<u,s,t,r>。
输出:一个时域三维张量 ∈ R I×J×K。
// 构造K个时间段的连接矩阵 U
a. 加载所有的四元组,组成一个{用户-服务}矩阵;
b. for each k∈K do {
c. 将所有四元组<u,s,t,r>构成一系列连续的 U (t)矩阵,该矩阵的元素为四元组中的r值,构造一个第t个时间段的矩阵,表示所有的I个用户作为行,所有的J个用户作为列。
}
// 构造时域三阶张量
d. 得到K个时间段的联合矩阵 U
e. 将矩阵 U 如图 6所示,按照不同的时间段将矩阵 U (t)构造成三维张量 Y ∈ R I×J×K
f. return: Y ∈ R I×J×K
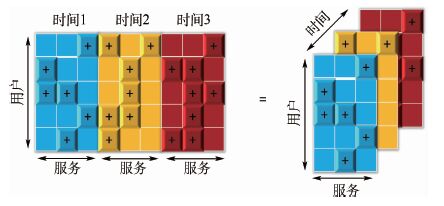 |
| 图 6 将时间序列上的{用户-服务}矩阵转换为时域张量 Fig. 6 Transformation of slices of time-specific matriceswith users and services into a temporal tensor |
| 图选项 |
3.2 基于时间信息的服务推荐系统 对于服务用户而言,由服务供应商声明的服务QoS性能,由于种种原因,这些数据并不完全准确。为了获得每个服务用户准确的调用Web服务时的QoS值,本文开发了带时间信息的QoS感知的Web服务推荐框架来预测缺失的服务QoS值。如图 7所示,本文开发的基于时间信息的QoS感知服务推荐系统收集不同服务用户调用的Web服务的QoS信息。如果服务用户信息的贡献超过阈值,服务用户就可以通过本文的推荐系统获得服务的QoS值的预测。服务QoS信息的贡献越多,QoS值的预测精度就会越高。在实际系统中本文搜集了大量的服务QoS信息,根据实际情况本文设定了一些实验数据的挑选规则 ,最后筛选出了一些质量比较优秀的QoS值作为训练数据来生成服务推荐系统的预测模型。
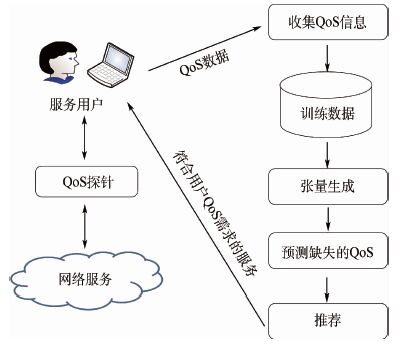 |
| 图 7 基于时间信息的Web服务推荐系统 Fig. 7 Framework of temporal QoS-aware Web service recommendation system |
| 图选项 |
该推荐系统主要分为6个主要的步骤:
1) QoS探针。在Planet-Lab实验床上部署该软件服务中间件,它将根据本文使用网络爬虫技术抓取到的Web服务的信息(例如WSDL、XML文件等)调用对应的Web服务,并将各种QoS信息记录在本地文件中。
2) 收集QoS信息。在服务推荐系统的服务器端,每天定时从各个PlanetLab切片上,将QoSProbe捕获的QoS信息取回并存储在文件系统中,作为原始的服务QoS数据。
3) 训练数据。在上面得到的大量原始QoS数据中,由于各种原因造成有些服务被调用的次数为0或者有的用户调用的服务为0,通过一定的筛选规则,剔除一些不够健全的数据,本文将剩下的一部分资质优秀的服务QoS数据作为服务推荐系统的训练数据。
4) 生成预测模型。在得到的大量训练数据的基础上,服务推荐系统使用各种不同的算法,经过反复训练得到预测模型。
5) 预测缺失的QoS。得到预测模型以后,根据服务推荐系统要求对缺失的QoS属性值进行预测。
6) 推荐。按照用户的需求,将QoS值最接近的一个或几个Web服务推荐给用户。
4 基于张量分解的服务推荐算法 4.1 非负张量分解 一个全部元素为非负实数的张量称为非负张量。给定一个N阶非负张量 Y ∈ R I1×I2×…×IN的非负CP分解:
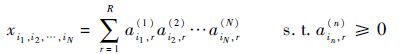 | (20) |
并使得重构误差平方
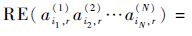
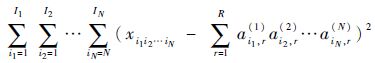
 | (21) |
因此,结合服务QoS的非负特性,本文将前面介绍的CP分解的交替最小二乘算法推广为的非负张量CP分解的交替最小二乘算法来预测缺失的服务QoS值。算法总结如下:
算法: CP非负交替最小二乘算法CP-NALS( χ ,R)
输入:N阶张量 及因子个数R。
输出: 因子矩阵 A (n)∈ R In×R,n=1,2,…,N。
初始化: A 0(n) ∈ R In×R,n=1,2,…,N,并令k=0。
步骤1?将N阶张量水平展开为矩阵 X (n),其中n=1,2,…,N。
步骤2?计算式(22)。
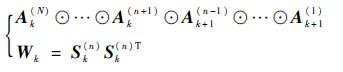 | (22) |
步骤3?更新因子矩阵 A (k+1)(n)= X (n) S k(n) W k。
步骤4?若收敛条件满足或已达到某个预先规定的最大迭代次数,则输出 A (1),A (2),…,A (N);否则,令k←k+1,并返回步骤2,重复以上运算,直到收敛条件满足或者达到最大迭代步数。
4.2 QoS预测表达式 利用在4.1节得到的非负CP分解预测算法,将它应用到本文得到的三阶张量数据集上,最终得出Web服务QoS属性值的预测公式为
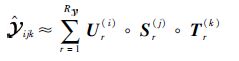 | (23) |
式中:
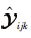
5 实验验证 本文在MATLAB程序中运行第4节描述的非负张量分解算法,构建基于时间信息的QoS值所组成的三阶张量和非负CP分解算法并预测缺失的服务QoS值。这里用到了MATLAB Tensor Toolbox工具包[19]。
5.1 实验数据集 为了在真实环境中的Web服务上评估本文所提出的QoS预测算法性能,本文实现了一个ServiceXchange网站[20]和QoSDetecter探针工具。ServiceXchange是一个平台,通过网络爬虫在互联网中抓取了超过20 000个可以公开访问的Web服务及其相关的信息。同时,本文把QoSDetecter部署在600多个分布式试验床Planet-Lab[21]的切片上,这是一个全球性的研究网络,支持部署新的网络服务的开发。本文过滤出一些优秀的适合做测试的切片,也就是已成功地调用了至少50个Web服务的切片,以便有足够的观测值是分裂的培训不同比例和测试设置本文的评价。最后,343个切片被选定为在Web服务用户,5 817个公众可访问的真实的Web服务持续被每个切片监测。其他的1万多个收集到的Web服务被排除在实验之外的原因主要有:①要求有调用该服务的认证资格;②被服务提供者拒绝(例如,Web服务是由一个私人高尔夫球俱乐部所提供,要求本文停止调用他们的服务);③永久性故障的调用失败(例如,提供该Web服务的机器已关机)。
实验中,343个Planet-Lab切片持续调用服务列表里的这5 000多个Web服务。实验数据集是由这些Web服务的QoS值构成的,这些服务调用发生在连续的4 d中,并且每间隔3 h就调用一次,从2013年的7月26日一直持续到29日,一共32个时间段。
从这个系统中收集尽可能多的实验数据,然后构建用于进行服务推荐的三维张量数据集,其中每个数据都可被一个四元组表示为<u,s,t,r>。这个数据集里面有超过1 900万个这样的四元组,其中包括343个服务用户,5 817个Web服务和32个时间段。最终本文构建了两个343×5 817×32的由用户、服务和时间3个维度构成的三维张量,它们分别对应响应时间和吞吐量两种属性,Web服务总体QoS值的数据统计如表 1所示。表 1中所示的响应时间的均值为0.684 0 s,吞吐量的均值为7.244 5 kb/s。95%的响应时间小于1.6 s,99%的吞吐量小于100 kb/s。关于实验数据集的更多细节,已经发布在ACT实验室云平台网站上[20]。虽然本实验只统计了响应时间和吞吐量,但是如果将NNCP的方法用来预测其他的QoS属性也是适用的(例如,失败率、可用性等)。
表 1 服务QoS值的统计信息 Table 1 Statistical information of Web service QoS value
| 统计信息 | 响应时间/s | 吞吐量/( kb·s -1) |
| 范围 | 0~200 | 0~1 000 |
| 均值 | 0.684 0 | 7.244 5 |
表选项
5.2 评价标准 推荐算法的准确性使用统计精度进行度量,此方法通过计算预测值与真实值之间的差别来衡量推荐结果的准确性。因为推荐系统总是采用具有最好的QoS预测值的Web服务作为推荐结果提供给用户,所以预测的准确性越高,推荐的准确性越高。本文实验中使用的评价指标平均绝对误差(Mean Absolute Error,MAE)是最常使用的度量标准,其定义为
 | (24) |
式中: | T |为需要预测的QoS值的个数。另外,还使用了均方根误差(Root Mean Squared Error,RMSE)统计标准,其定义为
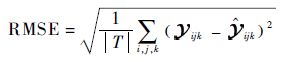 | (25) |
5.3 对比算法 为比较本文的算法在预测准确性方面的表现,选择常见的UMean、IMean算法以及协同过滤算法UPCC、IPCC、WSRec和MF进行比较。参与该对比实验的基本算法如下:
1) UMean。将当前活跃用户调用其他服务时所观察到的QoS表现的平均值视作为当前用户预测的当前未调用过服务的QoS属性值。
2) IMean。将其他用户调用该服务时所观察到的该服务的QoS表现的平均值作为当前活跃用户对该服务的QoS预测值。
3) UPCC。邻居(KNN)模型通常也被称为 k-最近邻模型,其可以获得精确的推荐结果并为结果给出合理的解释,它们是 协同推荐系统中最早被使用也是直至目前最流行的一类模型[22]。
4) IPCC。该方法是对基于产品的(item-based)的 KNN模型的研究[23]。这类 KNN模型假设一个用户现在保持着和过去相近的兴趣,也就是如果某个产品和用户过去喜欢的产品相似,那么此产品现在也很有可能被用户所喜欢。
5) WSRec。提出改进的协同过滤服务QoS预测算法,同时综合了相似用户与相似服务的信息,在两部分结果的融合方式上引入权重的概念,得出预测结果,在一定程度上提升了预测的准确性。
6) MF。一般表达形式为 R ≈ PQ T,其中 P ∈ R U×K和 Q ∈ R M×K分别为用户和服务的潜在因子矩阵,该因子模型通常被称为矩阵分解模型。Webb[24]利用该分解算法解决Netflix Prize中的推荐问题。
5.4 预测准确性对比 在给定相同的训练集和测试集的情况下,5.3节中6种基本算法与本文的NNCP算法的预测准确率做对比。由于基本算法不能直接应用于本文提出的带时间特性的预测问题,本文给这些算法进行了一些特殊的改造,使得它们可以与NNCP算法进行比较。本文把三维张量视作矩阵在多个时间段上的一组切片的集合。首先,本文将三维张量沿着时间轴压缩成矩阵,即该矩阵中的每个数值都是服务用户在这些时间段上调用Web服务的QoS属性值的平均值。在这个矩阵上,应用对比算法来预测缺失的QoS值。其次,本文计算这些基本算法的MAE和RMSE值,并与NNCP算法做比较。
在现实世界中,数据集通常是很稀疏的,因为真实的服务用户通常只调用很少一部分的Web服务。因此,本文从QoS数据中随机取出一些数据来稀疏数据集,并且将这些稀疏数据集按照不同的张量密度从5%~25%,以每次5%递增,作为本文的实验训练数据集。例如,张量密度为5%意味着本文随机分离后的数据集中QoS值的密度是5%,将这5%的数据作为训练数据,其他被分离的QoS值作为测试数据。将NNCP算法中的参数,因子矩阵的维数设置为20。本实验的比较结果示于表 2~表 5中,可以观察到本文的NNCP算法显著提高了预测精度,在不同的矩阵密度的情况下,无论是在响应时间还是在吞吐量方面都获得了较小的MAE和RMSE值。吞吐量的MAE和RMSE值均远远大于响应时间,是因为吞吐量的取值范围为0~1 000 kb/s的,而响应时间的范围仅为0~20 s。随着张量密度从5%增加至25%,NNCP算法的MAE和RMSE值是逐渐变小的,因为更大张量密度的数据集为缺失的QoS值预测提供了更多的有用信息。显然,本文设计的NNCP算法实现了比基本算法更好的预测性能。但是,表 4和表 5也存在一些不和谐的因素,基本算法的MAE和RMSE并没有在严格意义上随着矩阵密度的增加而减小。这种波动的原因是基本算法的预测值仅有一层,而测试集的数值是在32个时间段中随机抽取的,因此增加了预测的不确定性。从表中的数据可以计算出NNCP的预测结果在MAE方面比基本算法降低了20%~50%,这种现象可以解释为:基础算法只考虑用户和服务两方面的关系,而NNCP考虑了更多一维的因素——时间,同时也引入了大量的有用信息,所以为数据预测的性能提高带来了很大的帮助。
表 2 不同张量密度下响应时间预测的MAE Table 2 MAE of response time prediction withdifferent tensor densities
| 算法 | 响应时间预测的MAE | ||||
| 5% | 10% | 15% | 20% | 25% | |
| UMean | 0.815 6 | 0.724 7 | 0.716 1 | 0.675 8 | 0.636 1 |
| IMean | 0.570 8 | 0.491 9 | 0.498 8 | 0.415 8 | 0.408 3 |
| IPCC | 0.686 1 | 0.797 2 | 0.514 6 | 0.601 4 | 0.407 3 |
| UPCC | 0.596 5 | 0.662 7 | 0.662 5 | 0.601 4 | 0.543 5 |
| WSRec | 0.513 5 | 0.5252 | 0.526 8 | 0.394 7 | 0.371 7 |
| MF | 0.916 2 | 0.837 5 | 0.816 8 | 0.808 8 | 0.780 0 |
| NNCP | 0.483 8 | 0.358 9 | 0.325 4 | 0.317 8 | 0.314 8 |
表选项
表 3 不同张量密度下吞吐量预测的MAE Table 3 MAE of throughput prediction withdifferent tensor densities
| 算法 | 吞吐量预测的MAE | ||||
| 5% | 10% | 15% | 20% | 25% | |
| UMean | 8.369 6 | 8.426 2 | 8.082 7 | 7.771 3 | 7.711 3 |
| IMean | 6.794 7 | 7.043 3 | 6.460 6 | 5.735 6 | 5.203 3 |
| IPCC | 8.252 1 | 8.650 8 | 8.141 3 | 8.817 9 | 8.341 6 |
| UPCC | 8.053 3 | 7.725 9 | 7.110 3 | 7.343 7 | 7.048 6 |
| WSRec | 6.313 9 | 6.260 8 | 5.965 6 | 5.922 2 | 4.787 9 |
| MF | 9.642 9 | 8.988 5 | 7.599 8 | 5.626 1 | 5.103 0 |
| NNCP | 6.000 7 | 5.488 9 | 4.985 9 | 4.500 1 | 4.038 5 |
表选项
表 4 不同张量密度下响应时间预测的RMSE Table 4 RMSE of response time prediction withdifferent tensor densities
| 算法 | 响应时间预测的RMSE | ||||
| 5% | 10% | 15% | 20% | 25% | |
| UMean | 2.380 7 | 1.958 9 | 1.993 7 | 1.622 9 | 1.421 7 |
| IMean | 2.334 4 | 2.026 4 | 2.414 6 | 2.087 8 | 1.721 6 |
| IPCC | 3.851 1 | 3.833 6 | 3.377 0 | 2.512 9 | 1.918 8 |
| UPCC | 2.342 4 | 1.884 3 | 1.933 1 | 1.512 9 | 1.267 1 |
| WSRec | 2.183 8 | 2.020 7 | 2.153 3 | 1.714 4 | 1.297 5 |
| MF | 6.697 0 | 5.228 4 | 3.809 9 | 4.958 1 | 3.641 9 |
| NNCP | 1.147 0 | 1.068 5 | 1.050 2 | 1.043 4 | 1.039 9 |
表选项
表 5 不同张量密度下吞吐量预测的RMSE Table 5 RMSE of throughput prediction withdifferent tensor densities
| 算法 | 吞吐量预测的RMSE | ||||
| 5% | 10% | 15% | 20% | 25% | |
| UMean | 32.742 4 | 35.373 2 | 32.841 3 | 44.491 8 | 40.974 9 |
| IMean | 33.544 7 | 34.525 0 | 25.668 7 | 22.790 3 | 19.372 1 |
| IPCC | 41.441 1 | 40.969 3 | 37.409 6 | 48.987 7 | 42.647 1 |
| UPCC | 31.868 7 | 32.908 9 | 29.623 8 | 29.261 4 | 25.100 4 |
| WSRec | 23.017 1 | 24.622 3 | 22.438 4 | 22.370 9 | 17.958 0 |
| MF | 23.592 8 | 25.417 2 | 20.369 5 | 19.747 8 | 19.942 0 |
| NNCP | 10.809 8 | 10.173 8 | 9.570 85 | 8.987 22 | 8.430 47 |
表选项
5.5 算法参数对实验结果分析 1) 张量密度的影响。为了调查张量密度对本文算法的预测准确率的性能影响,本文分5个密度阶段来对算法进行考察,分别为5%、10%、15%、20%和25%,实验结果如图 8和图 9所示。图 8为不同张量密度下响应时间的MAE和RMSE值,图 9为不同张量密度下吞吐量的MAE和RMSE值。本文可以看到随着张量密度的增加NNCP算法在响应时间和吞吐量这两种QoS属性方面的性能都有明显提升,这也暗示了更多的数据能带来更好的预测结果。
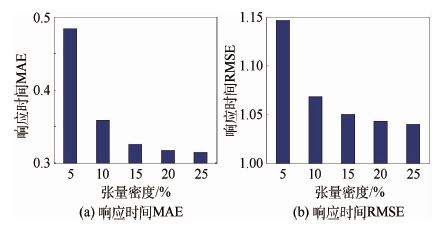 |
| 图 8 张量密度对响应时间的影响 Fig. 8 Impact of tensor density on response time |
| 图选项 |
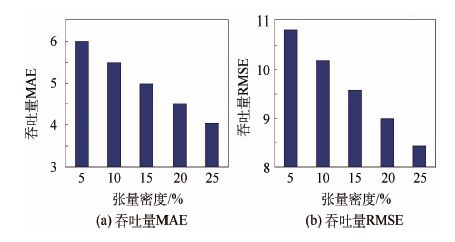 |
| 图 9 张量密度对吞吐量的影响 Fig. 9 Impact of tensor density on throughput |
| 图选项 |
2) 因子矩阵维度的影响。为了调查张量分解算法中的因子矩阵的维度对最终的算法预测准确率的性能影响,本文将张量密度设定为25%,因子矩阵的维度从1变化到20,实验结果如图 10、图 11所示。图 10为不同维度下响应时间的MAE和RMSE值,图 11为不同维度下吞吐量的MAE和RMSE值。本文可以看到随着因子矩阵维度的增加NNCP算法在响应时间和吞吐量这两种QoS属性方面的性能都有明显提升,这也暗示了更多的因子矩阵维度能带来更好的预测结果。但是也要注意过拟合的问题,当因子矩阵维度过高的时候,预测性能会有所下降。
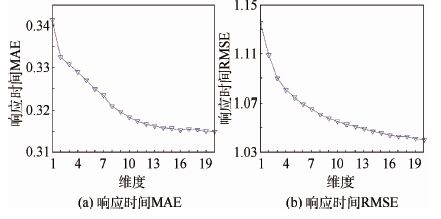 |
| 图 10 因子矩阵维度对响应时间的影响 Fig. 10 Impact of factor matrices dimensionality onresponse time |
| 图选项 |
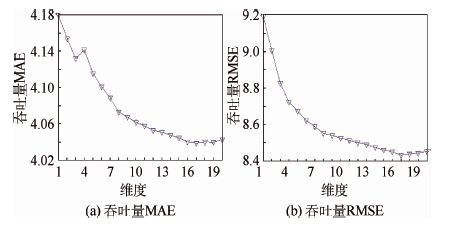 |
| 图 11 因子矩阵维度对吞吐量的影响 Fig. 11 Impact of factor matrices dimensionality onthroughput |
| 图选项 |
6 结 论 在服务推荐领域中,矩阵分解算法是一种非常流行的协同过滤算法,但是矩阵的二维模型不足将对服务的QoS产生影响的多种因素全部涵盖进来。于是,本文提出了新的模型:
1) 新模型将二维矩阵模型扩展成多维的张量模型,并利用张量分解的算法对服务的QoS属性值进行预测。本文虽然只考虑了{用户-服务-时间}这种三维模型,但是其他的影响服务QoS的因素可以很容易地加入到这个模型中来。
2) 使用非负CP分解算法有效解决了缺失的QoS预测问题。本文将现有服务推荐系统中的预测算法作为文中实验对比的基本算法,从对比实验结果得出的结论可以看到,非负CP张量分解算法很好地提高QoS的预测精度,改善预测结果的有效性,其中在MAE方面比6种基本算法降低了20%~50%。
3) 在分析非负CP分解算法的参数影响时,首先分析实张量的密度对实验的预测准确性的影响,结论是张量的密度越大,预测的准确率越高;其次分析非负CP分解中因子矩阵的维度对预测结果的影响,结论是随着因子矩阵维度的增加,预测准确率会上升,但是随着维度不断增大,会出现过拟合现象,不过由于本实验的计算机物理硬件的限制,未能将实验进行至过拟合的情况。
在未来工作方面,主要考虑结合神经网络领域的算法,对Web服务未来时刻的QoS值做出预测:将神经网络中的前向网络或者反馈神经网络的方法与本文的张量预测结果想结合,后者作为前者的样本信息,对未来时间上的QoS数值作出预测。
参考文献
| [1] | ?STRUNK A.QoS-aware service composition:A survey[C]//Proceedings of 8th IEEE European Conference on Web Services(ECOWS).Piscataway,NJ:IEEE Press,2010:67-74. |
| [2] | HADDAD J, MANOUVRIER M, RUKOZ M. TQoS:Transactional and QoS-aware selection algorithm for automatic Web service composition[J].IEEE Transactions on Services Computing, 2010, 3(1): 73–85.DOI:10.1109/TSC.2010.5 |
| [3] | AI-MASRI E,MAHMOUD Q H.Identifying client goals for Web service discovery[C]//IEEE International Conference on Services Computing,2009.Piscataway,NJ:IEEE Press,2009:202-209. |
| [4] | ZHENG Z B,MA H,LYU M R,et al.WSRec:A collaborative filtering based Web service recommender system[C]//Internationnal Conference on Web Services.Piscataway,NJ:IEEE Press,2009:437-444. |
| [5] | SUNG H H. Helping online customers decide through Web personalization[J].IEEE Intelligent Systems, 2005, 17(6): 34–43. |
| [6] | ZHENG Z, MA H, LYU M R, et al. QoS-aware Web service recommendation by collaborative filtering[J].Services Computing, 2011, 4(2): 140–152.DOI:10.1109/TSC.2010.52 |
| [7] | XIONG L,CHEN X,HUANG T K,et al.Temporal collaborative filtering with Bayesian probabilistic tensor factorization [C]// Proceedings of the 10th SIAM International Conference on Data Mining,SDM 2010.Philadelphia:Society for Industrial and Applied Mathematics,2010:211-222. |
| [8] | TUCKER L R. Some mathematical notes on three-mode factor analysis[J].Psychometrika, 1966, 31(3): 279–311.DOI:10.1007/BF02289464 |
| [9] | HARSHMAN R A. Foundations of the PARAFAC procedure:Models and conditions for an "explanatory" multi-model factor analysis[J].UCLA Working Papers in Phonetics, 1970(16): 1–84. |
| [10] | KOLDA T G, BADER B W. Tensor decompositions and applications[J].SIAM Review, 2009, 51(3): 455–500.DOI:10.1137/07070111X |
| [11] | ACAR R, YENER B. Unsupervised multiway data analysis:A literature suervey[J].IEEE Transactions on Knowledge and Data Enginerering, 2009, 21(1): 6–20.DOI:10.1109/TKDE.2008.112 |
| [12] | CHEN X, ZHENG Z, YU Q, et al. Web service recommendation via exploiting location and QoS information[J].IEEE Transactions on Parallel and Distributed Systems, 2014, 25(7): 1913–1924.DOI:10.1109/TPDS.2013.308 |
| [13] | LO W,YIN J,DENG S,et al.Collaborative Web service QoS prediction with location-based regularization[C]//2012 IEEE 19th International Conference on Web Services (ICWS).Piscataway,NJ:IEEE Press,2012:464-471. |
| [14] | ZHENG Z, MA H, LYU M R, et al. Collaborative Web service QoS prediction via neighborhood integrated matrix factorization[J].IEEE Transactions on Services Computing, 2013, 6(3): 289–299.DOI:10.1109/TSC.2011.59 |
| [15] | CHEN X, ZHENG Z, LIU X, et al. Personalized QoS-aware Web service recommendation and visualization[J].IEEE Transactions on Services Computing, 2013, 6(1): 35–47.DOI:10.1109/TSC.2011.35 |
| [16] | WU C,QIU W W,ZHENG Z B.QoS prediction of Web services based on two-phase K-means clustering[C]//2015 IEEE International Conference on Web Services(ICWS).Piscataway,NJ:IEEE Press,2015:161-168. |
| [17] | KOLDA T G.Multilinear operators for higher-order decompositions:SAND 2006-2081[R].Livermore,CA:Sandia National Laboratores,2006. |
| [18] | WELLING M, WEBER M. Positive tensor factorization[J].Pattern Recognition Letters, 2001, 22(12): 1255–1261.DOI:10.1016/S0167-8655(01)00070-8 |
| [19] | KOLDA T G,BADER B W,SUN J M,et al.MATLAB tensor toolbox version 2.5[CP/OL].(2012-02-01)[2015-08-08].http://www.sandia.gov/~tgkolda/TensorToolbox/index-2.5.html. |
| [20] | [2015-08-08].http://www.service4all.org.cn/servicexchange/. |
| [21] | [2015-08-08].http://www.planet-lab.org/. |
| [22] | HERLOCKER J,KONSTAN J,BORCHERS A,et al.An algorithmic framework for performing collaborative filtering[C]//Proceedings of the 22nd Annual International ACM SIGIR Conference on Researsh and Development in Information Retrieval (SIGIR-99).New York:ACM Press,1999:230-237. |
| [23] | SALAKHUTDINOV R, MNIH A. Probabilistic matrix factorization[J].Advances in Neural Information Proceeding Systems, 2008, 20: 1–8. |
| [24] | WEBB B.Netflix update:Try this at home (2006) [EB/OL].[2015-08-08].http://sifter.org/~simon/journal/20061211.html. |
