集束型设备群是半导体制造系统的核心和关键设备，主要用于晶圆的蚀刻、光刻以及离子注射等处理过程。由于其调度问题的重要性以及复杂性^[1]，近年来受到了业界和学术界的广泛关注。
目前关于集束型设备群调度研究尚处于初始阶段。大多数有关其调度文献集中于同种晶圆在稳态模式下的周期性调度的研究。Yi等^[2]将集束型设备群调度问题分解为多个单集束型设备调度问题建模分析，并求解出晶圆无驻留约束条件下调度的基本周期下界(lower-bound fundamental period)。Chan等^[3-4]将机械手搬运时间假定为固定常数，对2种不同结构的集束型设备群进行研究，以最小循环周期为目标，提出了一种基于资源的集束型设备群分析建模方法。Ding等^[5]利用关键路径松弛法对具有固定动作顺序的单种晶圆集束型设备群调度进行研究，并给出了具有固定动作顺序机械手调度方案，但该方法不能保证其松弛调度结果最优。Liu和Zhou^[6]在单臂集束型设备群中同时考虑晶圆驻留约束和多晶圆流，提出了基于时间约束集的逐级回溯算法。文献[1-6]均未考虑集束型设备群实际工程应用中普遍存在的带并行处理腔的调度。
并行腔广泛存在于晶圆制造过程加工时间相对较长的处理模块，通过平衡不同工序之间负荷，可提高系统有效产出。已有****已对于带并行腔的单集束型设备调度问题进行了研究^[7-12]。但对于具有多机械手同时作业的集束型设备群，由于系统中各单集束型设备间的耦合和相互间的依赖增加其调度复杂性，使得传统单集束型设备的调度方法无法直接应用^[13]，同时目前对此类调度问题的研究鲜有报道，仅有Kumar等^[14]研究了与集束型设备群结构类似但缓冲连接不同的多机械手制造单元的调度，但并未考虑驻留约束。因此，对于问题规模更加复杂的此类调度问题亟需探索有效的解决方法。
本文对带并行腔双集束型设备调度问题进行研究，在问题域中考虑晶圆多品种加工和驻留约束，建立调度模型，提出了基于产能约束资源(Capacity Constraint Resource, CCR)的启发式算法。
1 问题描述 典型带并行腔的双集束型设备如图 1所示。图中：C₁、C₂为在双集束型设备群的2个单集束型设备；R₁、R₂为对应的搬运模块；M_h,j^P为第h个集束型设备中的第j个处理模块；M_h,j(k)^P为模块M_h,j^P的第k个加工腔(若k=1，可省略)，且k≤K_h,j，处理模块M_h,j^P共有K_h,j个并行腔；M_h,j^B为用于连接C_h和C_h+1的缓冲模块。模型中用坐标集X表示晶圆加工路径。X={x₁, x₂,…,x_i,…,x_φ}，x_i=(h, j)为晶圆第i步工序处理模块序号坐标，φ为晶圆加工工序总数；系统并行腔数集合P_n={K₁, K₂,…,K_i,…,K_φ}，K_i为M_xi^P含有的并行腔数目。

图 1 带并行腔的双集束型设备群示意图 Fig. 1 Schematic of double-cluster tools with parallel chambers

图选项

晶圆按照其工艺路径从输入卡闸模块M_a^C进入系统，依次经过位于各个集束型设备中的处理模块(processing module)，连接相邻集束型设备的缓冲模块(buffer module)，最终加工完成后存放在输出卡闸模块M_b^C，晶圆在不同模块间的转移通过搬运模块(robotic module)完成。
晶圆调度有关符号与变量定义如下:S_xi(w)为晶圆w进入M_xi^P的时间；L_xi(w)为晶圆w离开M_xi^P的时间；B_h,j^S(w)为晶圆w进入M_h,j^B的时间；B_h,j^L(w)为晶圆w离开M_h,j^B的时间；t_M为机械手单次搬运时间，t_M=t_l+t_u+t_m，t_l、t_u和t_m分别为机械手装载、卸载以及移动时间；P(w)为晶圆w在所有处理模块的加工时间集合P(w)={P_x1(w), P_x2(w),…,P_xi(w),…,P_xφ(w)}，其中P_xi(w)为晶圆w在M_xi^P的加工时间(若P_xi(w)=0，表示晶圆不经过该模块加工，反之则需经过，不同种晶圆具有不同加工路径)；U(w)为晶圆w驻留时间集合U(w)={U_x1(w), U_x2(w),…,U_xi(w),…,U_xφ(w)}，U_xi(w)为晶圆w在M_xi^P加工完成后允许的最大驻留时间；P_M^B为晶圆w在M_h,j^B的加工时间；U_M^B为晶圆w在M_h,j^B的驻留时间；f_xi(w)为晶圆w在M_xi^P中的实际停留时间；d_xi(w)为晶圆w在M_xi^P加工完成后实际驻留时间；P_xi^C(t)为t时刻在M_xi^P进行加工的晶圆数量；T_R,h(w)为对晶圆w调度时R_h的可用时间区间集，T_R,h(w)={t_R,h,1(w), t_R,h,2(w),…,t_R,h,φt(w,h)(w)}，包含φt(w,h)个区间，q为T_R,h(w)的第q个可用时间区间。
为有效描述带并行腔的双集束型设备群调度问题，作如下假设：①晶圆从M_a^C进入系统，处理完后存放在M_b^C中，且只进入每个模块一次，不考虑重入，即晶圆路径坐标集为X={(1,1), (1,2),…,(h,j),…,(1,n)}(包含所有加工模块)；②晶圆搬运模块采用单臂机械手，每次只能搬运一片晶圆，且晶圆在不同模块间的搬运时间固定；③相邻的集束型设备用2个缓冲模块连接，其中一个用于暂存进入集束型设备的晶圆，另一个用于暂存离开集束型设备的晶圆。M_h,j^B仅对晶圆起到缓冲作用，不作任何处理，驻留时间无限；④晶圆在处理模块内驻留时间有上限限制，即驻留约束，超过该时间上限，晶圆变成次品；⑤同一处理模块的并行腔在同一个集束型设备中，不跨集束型设备存在；⑥同类型晶圆在同一M_h,j^P并行腔的处理时间和驻留时间相同；⑦同一批(lot)中含有不同种类的晶圆，不同种晶圆在各处理腔的加工时间不同。
根据假设前提，建立问题模型：
由假设②可知：晶圆搬运模块采用单臂机械手，则

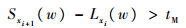(1)

连续晶圆进入同一模块的时间差大于t_M。

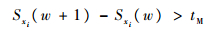(2)

同理，缓冲模块：

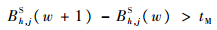(3)

由假设②可知：搬运必须发生在机械手可用时间集内。

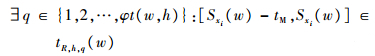(4)

由假设③可知：

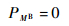(5)

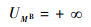(6)

由假设④可知，驻留约束：

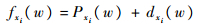(7)

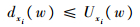(8)

由假设⑤可知：M_xi^P共有K_i个并行腔。则

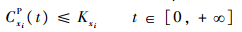(9)

晶圆离开M_xi^P的必要条件是下一工序存在未被占用的加工腔：

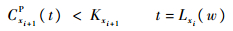(10)

调度目标是晶圆的总加工完成时间(makespan)最小，即最小化最后一片晶圆W进入M_b^C的时间：

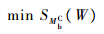(11)

综合上述，本文对应的调度问题是以式(11)为目标函数，以式(1)~式(10)为约束条件的非线性规划问题。
2 算法构建 为了解决综合考虑多品种加工、晶圆驻留和资源约束等条件下的带并行腔集束型设备群调度问题，结合上述数学模型，构建基于CCR的调度算法，采用逐次计算设备平均活跃时间的方式进行产能约束资源识别，并在产能约束资源前后采用拉动和递推分段调度的优化策略，以达到提高资源利用率的目的。同时为了优化机械手作业顺序，对产能约束资源采取锁定-收紧-松弛(Locking-Tightening-Loosening, LTL)策略。
根据Roser等^[15]的研究内容，对带并行腔的集束型设备群CCR作如下定义。
定义1 集束型设备群中，CCR是平均活跃时间a_xi最长的处理模块或设备。其计算公式为

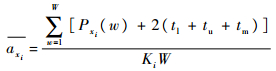(12)

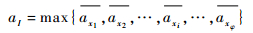(13)

式中：a_I为CCR的设备的活跃时间，I为CCR的设备编号,I±i为CCR前(后)第i个处理模块。
定义2 模块饱和状态，在带有K_i个并行腔的M_xi^P，满足C_xi^P(t)=K_i时，该状态称为饱和状态。
定理1 若含有K_i(K_i≥2)个并行腔的M_xi^P可达到其饱和状态，则须满足P_xi≥(K_i-2)·t_M。
证明 (反证法)假设M_xi^P处于饱和状态，且P_xi<(K_i-2)·t_M。根据递推，易得第j片晶圆进入设备时间满足：

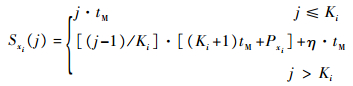(14)

式中：

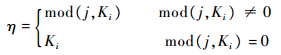(1)

因为P_xi<(K_i-2)·t_M，则易推出?t∈[0, +∞]，P_xi^C(t)<K_i，则假设不成立，定理1得证。
引理1 根据定理1和约束理论可得，当M_xi^P为CCR，且P_xi<(K_i-2)·t_M时，增加并行腔数量对throughput提升无影响(3.3节结果可说明)。
定义3 对于在M_xi^P进行加工的晶圆w，定义3种基本操作：①锁定(Locking)，令L_xi^ξ(w)=S_xi^ξ(w)+P_xi(w)，即d_xi^ξ(w)=0；②收紧(Tightening)，令S_xi^ξ+1(w)=S_xi^ξ(w)+1或L_xi^ξ+1(w)=L_xi^ξ(w)-1，即d_xi^ξ+1(w)=d_xi^ξ(w)-1；③松弛(Loosening)，令S_xi^ξ+1(w)=S_xi^ξ(w)-1或L_xi^ξ+1(w)=L_xi^ξ(w)+1，即d_xi^ξ+1(w)=d_xi^ξ(w)+1(“1”为一单位时间，ξ为变量的更新次数)。
本文算法的核心思想包括4个阶段：①CCR识别；②CCR调度；③CCR前模块调度；④CCR后模块调度。首先，根据定义1确定系统的CCR。然后对CCR实施Locking操作，最大限度使其处于活跃状态。再以CCR为界，在CCR之前模块实施拉动调度，在驻留时间范围内，优化机械手作业时间，若出现不可行时间区间，则返回上一阶段对CCR实施Loosening操作，重新搜索机械手可行作业时间，直至完成CCR之前所有模块调度。然后对CCR之后模块，采用基于Tightening策略下的推式调度，使完成加工的晶圆尽早离开处理模块，减少晶圆驻留时间，逐级推动，直至完成晶圆在所有模块的调度。
具体算法步骤如下。
步骤1 CCR识别。
步骤1.1 录入加工参数数据。
步骤1.2 根据式(12)计算加工腔平均活跃时间。
步骤1.3 根据式(13)识别CCR处理模块I。
步骤2 CCR调度。
步骤2.1 初始化各参数，当前调度的晶圆为w，令ξ=1。
步骤2.2 计算晶圆w在CCR第k个并行腔的开始加工时间S_I(k)(w)，k∈[1, K_i]。
若式(15)成立，令ξ=ξ+1，按式(16)逐次叠加，直至式(17)成立；若式(17)成立，按式(18)计算S_I(k)(w)。

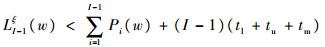(15)

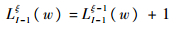(16)

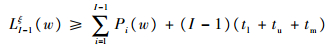(17)

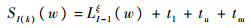(18)

步骤2.3 判断机械手是否空闲。
判断式(19)是否成立，若不成立，令ξ=ξ+1，按式(16)更新，直至成立；否则，读取当前各参数：

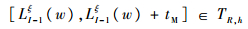(19)

步骤2.4 对CCR实施Locking操作，根据式(20)计算L_I(k)(w):

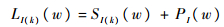(20)

步骤2.5 判断式(21)是否成立，若不成立，令ξ=ξ+1，按式(22)更新，直至式(21)成立。

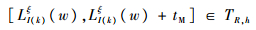(21)

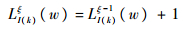(22)

步骤2.6 根据Locking策略计算晶圆w+1的S_I(w+1)，L_I(w+1)。
若C_I^P(t)<K_I且w<K_I，则

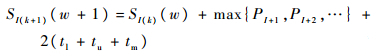(23)

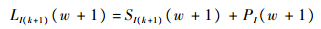(24)

否则

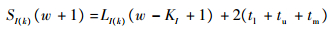(25)

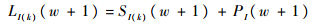(26)

步骤2.7 根据上述完成CCR调度。
步骤3 CCR前模块调度。
步骤3.1 初始化参数d_c(w)(实际驻留时间)、c(当前被调度的处理模块编号)。
步骤3.2 判断是否满足驻留约束，如果满足，继续下一步；否则，对CCR执行一次Loosening操作，返回步骤2。
步骤3.3 计算。

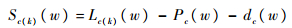(27)

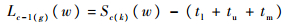(28)

步骤3.4 判断机械手是否空闲，若机械手空闲，则继续下一步; 若机械手忙碌，则执行一次Loosening操作，返回步骤2。
步骤3.5 判断当前处理模块是否空闲

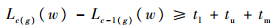(29)

步骤3.6 更新参数，判断是否完成所有CCR前处理模块的调度，如果已完成即进入下一阶段，否则返回步骤3.2。
步骤4 CCR后模块调度。
步骤4.1 初始化参数d_c(w)、c。
步骤4.2 判断是否满足驻留约束，若满足，则执行一次Tightening操作，继续下一步；否则：若当前处理模块为CCR，则返回前一处理模块，按式(16)更新，返回步骤2.2。若当前模块为非CCR，则增加一单位驻留时间，返回步骤4.2。
步骤4.3 计算。

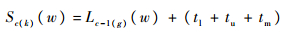(30)

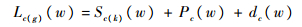(31)

步骤4.4 判断处理模块是否繁忙，如式(32)，若繁忙，增加一单位驻留时间，并返回步骤4.2；否则，记录各参数。

(32)

步骤4.5 更新参数，判断是否完成CCR后的所有模块调度，若未完成，返回步骤4.2，否则计算结束，完成晶圆w的调度。
步骤5 重复上述步骤1~步骤4，直至完成所有晶圆调度，算法结束。
以图 1 所示集束型设备群为例，运用基于CCR的TLT算法对其中6个不同种类的晶圆(w₁~w₆)进行调度，调度结果的甘特图如图 2所示。

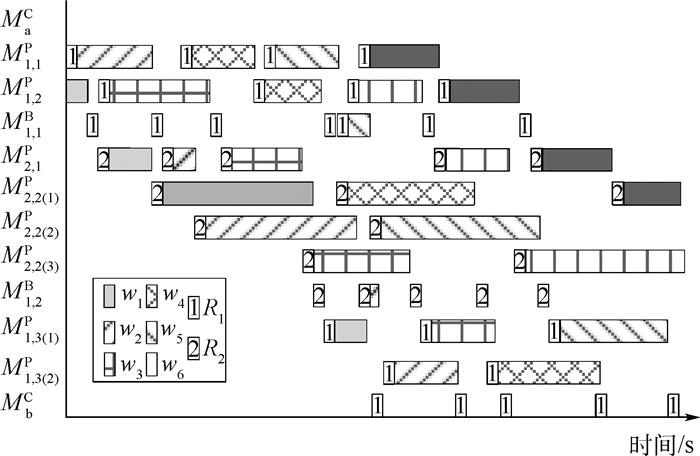图 2 计算实例甘特图 Fig. 2 Gantt chart of calculative example

图选项

3 仿真实验与分析 为有效评价本文算法，选取无驻留约束条件下带并行腔单集束型设备调度最优策略——LCM策略进行比较，并以Kumar等^[14]提出的算法作为Benchmark。
现将相关符号与变量定义如下：R=×100%，该值越大，表明调度得到的制造期相对C_LCM的提升越大，即算法的性能越好，C_TLT为本文提出的LTL策略下算法的制造周期，C_LCM为基于LCM策略算法的制造周期；F^C=为设备因子(cluster factor)，表征集束型设备群中机械手繁忙程度的函数，其值越大，机械手完成一次搬运所需时间与最大处理时间的比例越大，即机械手越繁忙，反之越空闲，max P为晶圆在集束型设备中各个处理模块的最大处理时间，M^H为每个集束型设备中的处理模块数目。
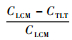
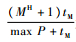
实验用C++编程实现，仿真的环境为主频为2.13 GHz、内存为8 GB的笔记本电脑。实验中的数据，均为10次相同实验的平均结果。
3.1 运算时间 假设晶圆在各处理模块的处理时间服从P～N(40,10)；在各处理模块的驻留约束时间服从U～N(20,5)；搬运时间t_M=2 s；每个集束型设备所含的处理模块的数目M^H=4；每个处理模块并行腔数集合P_n={1,2,1,3,1,1,1,1}。仿真运行结果如图 3所示。

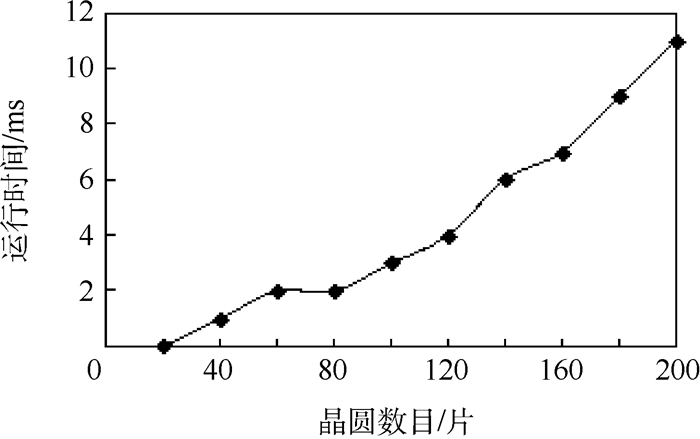图 3 算法运行时间分析 Fig. 3 Running time analysis of algorithm

图选项

图 3显示，算法在晶圆数目较少时(小于20片)，运行时间几乎为0，算法的运行时间随着晶圆数目的增加大体上呈正相关，当晶圆数目为200片，算法运行时间仍未超过0.2 s，由此可见，算法响应速度极快，适合于晶圆实时调度。
3.2 加工时间对调度的影响 令M^H=4；t_M=2；P_n={1,2,1,3,1,1,1,1}；晶圆在各个处理模块的处理时间服从期望μ=40，方差σ=0,1/8,1/4,1/2均值的正态分布；驻留约束时间分别服从U～N(20,5)。仿真运行的结果如图 4所示。由图 4可见，随着加工晶圆的数量增加，R值逐渐增加，说明在加工批量越大的情况下本文算法的调度结果相对于Benchmark的提升越大。同时，图 4中的4条不同曲线的走向趋势基本一致，且在σ的较大的情况下，本文算法的优化结果更为明显，说明了算法对不同处理时间波动的适应性。

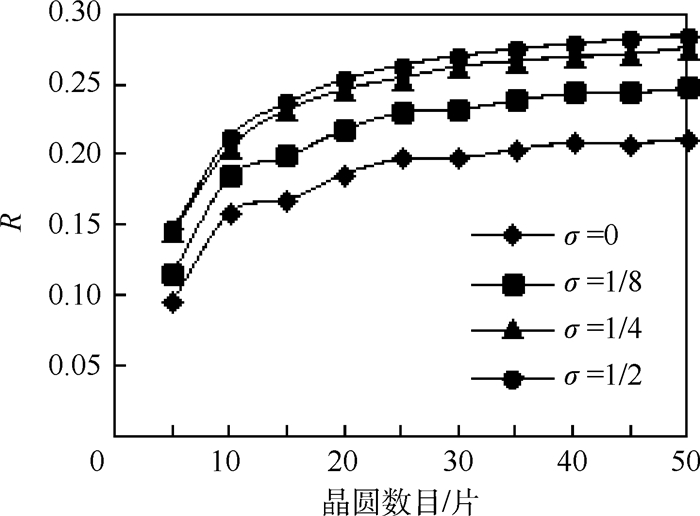图 4 不同方差下R值与晶圆数目的关系 Fig. 4 Relationship between R value and number of wafer with different variance

图选项

3.3 CCR并行腔对调度的影响 令M^H=4，t_M=2 s；晶圆在各个处理模块的处理时间服从P～N(40,10)；驻留约束时间分别服从U～N(20,5)；CCR模块的并行腔数目K_I=1,2,…,7。仿真运行的结果如图 5所示。

图 5 CCR并行腔对调度的影响 Fig. 5 Effect of parallel chambers at CCR on scheduling

图选项

图 5显示了在CCR并行腔数目不同的情况下，本文算法的调度makesapn均小于基于LCM的调度结果，并且CCR设备的利用率也相对较高。同时，随着CCR并行腔数目的增多，可以看出makespan不断减小，设备利用也相对降低，这是TOC理论下对CCR不断改善的结果，当CCR并行腔数超过6时，增加并行腔数目，makespan不再下降，说明此时CCR发生转移。
3.4 机械手对调度的影响 令M^H=4，t_M=2 s，Pⁿ={1,2,1,3,1,1,1,1}；晶圆在各个处理模块的处理时间服从P～N(40,10)；驻留约束时间分别服从U～N(20,5)；分别令F^C=1,2,…,6。仿真运行的结果如图 6所示。

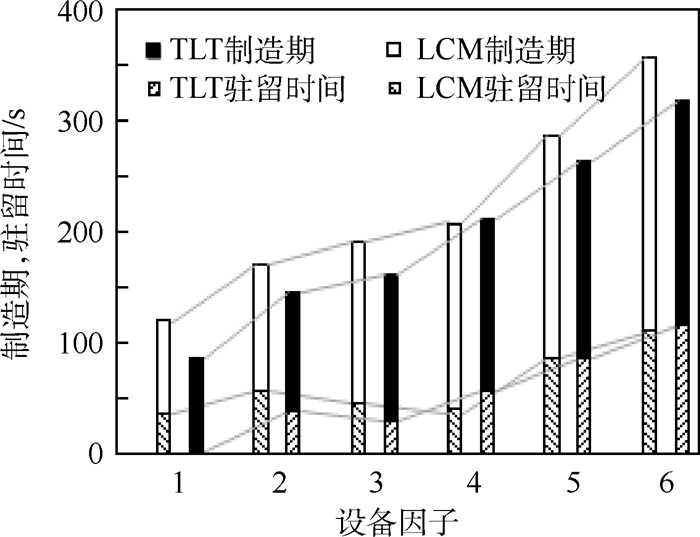图 6 机械手对调度的影响 Fig. 6 Effect of manipulator on scheduling

图选项

图 6显示了不同机械手繁忙程度下2种算法累计驻留时间和makespan的关系。随着F^C的增加，makespan趋向于线性增加，且本文算法调度结果均优于Benchmark。在一般情况下，累计驻留时间越短，则调度可得到的makespan越小，图中的时间比例也说明这种关系。同时，算法在获取较短驻留时间方面也存在优势。
4 结 论 1) 算法可以有效解决在集束型设备群的调度过程中普遍存在的带并行腔多品种加工的问题，特别在减少驻留提升CCR设备利用率方面有明显优势。
2) 在晶圆批量较小(每批少于20片)的情况下，得出算法的仿真运行时间几乎为零，可有效地进行实时调度，即使批量较大(每批达到200片)也能满足调度的要求，证明了算法的高效性。
3) 随着晶圆数目和σ增大，R值不断增加，表明本文算法相对于LCM算法的提升效果明显，且在并行腔数目和设备因子变化的情况下，也能获得较优的调度结果。
4) 算法对于晶圆加工时间波动性、并行腔数目和机械手繁忙程度的仿真证明算法对不同的加工数据和设备具有非常好的适应性。
针对此类问题的优化，今后可不仅考虑makespan最小这一个目标，还可以引入拖期时间最少、设备利用率最高等其他因素，采用多目标优化技术。此外，通过甘特图看到调度结果还有进一步优化的空间，因此今后可以考虑以启发式算法作为初始解，采用迭代搜索算法进行进一步的优化。

参考文献

[1]	PERKINSON T L, MCLARTY P K, GYURCSIK R S, et al. Single-wafer cluster tool performance: An analysis of throughput[J].IEEE Transactions on Semiconductor Manufacturing, 1994, 7(3): 369–373.DOI:10.1109/66.311340
[2]	YI J, DING S, SONG D, et al. Steady-state throughput and scheduling analysis of multi-cluster tools: A decomposition ap-proach[J].IEEE Transactions on Automation Science and Engineering, 2008, 5(2): 321–336.DOI:10.1109/TASE.2007.906678
[3]	CHAN W K, YI J, DING S. Optimal scheduling of multi-cluster tools with constant robot moving times, Part I: Two-cluster analysis[J].IEEE Transactions on Automation Science and Engineering, 2011, 8(1): 5–16.DOI:10.1109/TASE.2010.2046891
[4]	CHAN W K, DING S, YI J, et al. Optimal scheduling of multicluster tools with constant robot moving times, Part II: Tree-like topology configurations[J].IEEE Transactions on Automation Science and Engineering, 2011, 8(1): 17–28.DOI:10.1109/TASE.2010.2046893
[5]	DING S, YI J, ZHANG M T, et al. Performance evaluation and schedule optimization of multi-cluster tools with process times uncertainty[C]//Proceeding of the 2006 IEEE International Conference on Automation Science and Engineering. Piscataway, NJ: IEEE Press, 2006: 7-10.
[6]	LIU M X, ZHOU B H. Modeling and scheduling analysis of multi-cluster tools with residency constraints based on time constraint sets[J].International Journal of Production Research, 2013, 51(16): 4835–4852.DOI:10.1080/00207543.2013.774490
[7]	PERKINSON T L, GYURCSIK R S, MCLARTY P K. Single-wafer cluster tool performance: An analysis of the effects of redundant chambers and revisitation sequences on throughput[J].IEEE Transactions on Semiconductor Manufacturing, 1996, 9(3): 384–400.DOI:10.1109/66.536110
[8]	GEISMAR H N, DAWANDE M W, SRISKANDARAJAH C. Robotic cells with parallel machines: Throughput maximization in constant travel-time cells[J].Journal of Scheduling, 2004, 7(5): 375–395.DOI:10.1023/B:JOSH.0000036861.28456.5d
[9]	ZHENG X H, YU H B, HU J T. A general throughput model for parallel cluster tools[C]//International Conference on ICCE2011, AISC 110. Berlin: Springer Press, 2011: 215-222.
[10]	卢睿, 李林瑛. 有晶滞留时间约束的集束型装备调度问题研究[J].控制仿真学报, 2014, 26(8): 1775–1780.LU R, LI L Y. Research on scheduling problem of cluster tools with residency time constraints[J].Journal of System Simulation, 2014, 26(8): 1775–1780.(in Chinese)
[11]	WIKBORG U, LEE T E. Noncyclic scheduling for timed discrete-event systems with application to single-armed cluster tools using pareto-optimal optimization[J].IEEE Transactions on Automation Science and Engineering, 2013, 10(3): 699–710.DOI:10.1109/TASE.2012.2217128
[12]	ZHANG J, FANG X, QI L. LCM cycle based optimal scheduling in robotic cell with parallel workstations[C]//2014 IEEE International Conference on Robotics and Automation (ICRA). Piscataway, NJ: IEEE Press, 2014: 1367-1373.
[13]	DING S, YI J. An event graph based simulation and scheduling analysis of multi-cluster tools[C]//Proceedings of 2004 Winter Simulation Conference. Piscataway, NJ: IEEE Press, 2004: 1915-1924.
[14]	KUMAR S, RAMANAN N, SRISKANDARAJAH C. Minimizing cycle time in large robotic cells[J].IIE Transactions, 2005, 37(2): 123–136.DOI:10.1080/07408170590885279
[15]	ROSER C, NAKANO M, TANAKA M. A practical bottleneck detection method[C]//Proceedings of Winter Simulation Conference, 2001. Piscataway, NJ: IEEE Press, 2001, 2: 949-953.