PN由于其简单实用得到最广泛的研究和发展,形成了纯比例导引(PPN)和真比例导引(TPN)两大基础类型及其改良变种[7],前者设定拦截弹控制力垂直于速度方向,拦截弹恒速飞行;而TPN则设定控制力垂直于弹目视线,飞行速度可变; Yang等[8]统一了PN的框架和数学分析方法。拦截弹飞行中控制力来源于气动力或发动机推力,气动控制力垂直于导弹的速度方向,是PPN等比例制导方案的基础设定依据;而对于大气层外和有动力加速行为的拦截弹,控制力主要由推力矢量调整获得,改变速度方向的同时也会带来速度大小的变化[9]。由于拦截弹在实际飞行过程中速度很难保持恒定,以恒速假设为前提的制导率不可避免会由于假设速度与实际速度的偏差而降低制导的精度[10],影响对其目标有效拦截范围的设定[11-14]。
本文针对高速目标的拦截问题,结合大气层外拦截弹的飞行特点选用TPN的基本设定和思想[15-17]作为研究出发点,分析比例制导下顺、逆轨拦截的形成机理和成功条件,将速度前置角的变化引入控制力导引计算,结合正负比例制导的优势提出全向拦截的概念,设计了可拦截高速非机动目标的全向真比例制导律(Omnidirectional True Proportion Navigation,OTPN)。OTPN综合了对正负比例制导机理的认识和研究成果,以单一制导律同时满足高速目标拦截的顺、逆轨导引需求,具备了全向拦截制导能力,且在拦截时间、总控制量以及捕获范围方面均优于经典PN和RPN。为进一步研究OTPN的制导特性,对OTPN捕获能力与比例系数及控制加速度限制之间的关系进行了仿真研究和分析。
1 相对运动方程 为便于分析,将拦截弹和目标看作平面运动中的质点,忽略重力对目标和拦截弹的影响,拦截弹除控制力外不受其他外力作用。因拦截对象为高速目标,故拦截弹初始位置需要位于目标飞行方向的前方,即目标的前半球。拦截弹M和目标T在平面的相对运动几何关系如图 1所示。图中: R 为拦截弹与目标之间相对距离, Vt 为目标速度, Vm 为拦截弹速度,?为目标速度与参考线之间的夹角, λ 为拦截弹与目标之间的视线(LOS)与参考线的夹角, γ 为拦截弹速度倾角,拦截弹速度前置角 θ 为拦截弹速度 Vm 与视线之间的夹角,定义控制加速度 ac 垂直于视线方向。
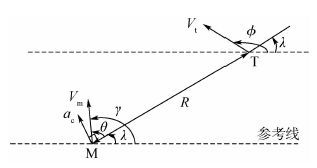 |
| 图 1 拦截弹与目标的相对运动几何关系 Fig. 1 Geometry of the relative motion between interceptor and target |
| 图选项 |
根据图 1列出拦截弹与目标的相对运动方程:
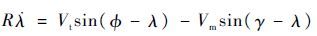 | (1) |
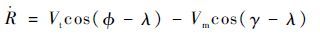 | (2) |
比例制导的实质是通过对目标视线旋转的抑制,使得拦截弹在制导飞行中速度矢量的转动角速率与目标视线的旋转角速率保持为设定的比例关系,在比例制导的过程中,拦截弹速度倾角 γ 与弹目视线角 λ 的关系[18]为
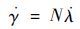 | (3) |
式中: N 为比例导引系数,经典的PN设定 N 为大于2的正整数,取值范围通常为3~7之间;比例导引的各种变种(如真比例导引(TPN)、纯比例导引(PPN)、广义比例导引(GPN)、扩展比例导引(APN)和理想比例导引(IPN)等)基本沿用经典PN对比例导引系数 N 的定义,将 N 设定为大于2的正值[18];2012年,Prasanna和Ghose[5]提出RPN,使用负比例系数以顺轨模式对目标进行拦截,加速度方向与经典PN相反。2.1节将详细分析PN设计中比例系数的符号问题, N 的符号不影响运动方程和公式的推导。
由图 1知,拦截弹的速度前置角为其速度倾角与视线角的差[19],即
 | (4) |
式(4)两边微分后将式(3)代入,有
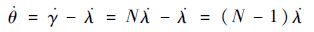 | (5) |
对式(2)两边微分:
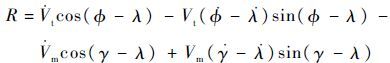 | (6) |
式中: V·m 为拦截弹的控制加速度 ac 在速度方向上的分量。
将式(5)代入式(6):
 | (7) |
结合式(1),可得
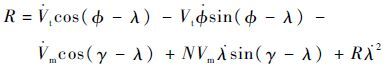 | (8) |
由于拦截弹的控制力垂直于视线方向,有 R¨-R2=0 [16-18],因此有
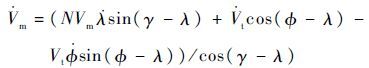 | (9) |
对于目标速度恒定且无规避行为的情况,式(9)中 V·t=0、?·=0 ,式(9)变为
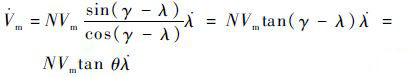 | (10) |
V·m 不为0时使拦截弹飞行速度 Vm 改变,因此 ac 在速度方向的分量 aV=V·m 为制导过程中拦截弹所受合外力在速度方向的有效增量,由式(10)和式(3)得到拦截弹的控制加速度:
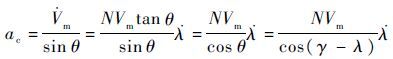 | (11) |
将拦截弹所能得到的最大加速度设为控制加速度 ac 的约束条件,即
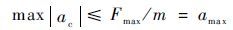 | (12) |
式中: Fmax 为拦截弹可获得最大合外力; m 为拦截弹质量。通过式(12)可实现拦截过程中拦截弹的制导指令约束。考虑到拦截弹所受合外力最大值的限制,比例制导中的控制加速度方程写为
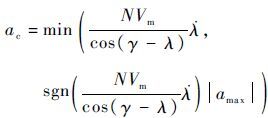 | (13) |
对式(13), cos(γ-λ)≠0 ,即
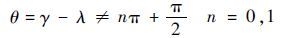 | (14) |
对制导过程中由于 cos θ 取零值而导致制导控制方程式(13)无意义的情况,即 θ=π/2 或 θ=3π/2 处出现奇点的问题,在控制方程中加入开关判定来处理:将奇点处的控制加速度设为零或延用上一时刻的控制加速度,奇点消除后继续用式(13)制导。因此,对恒速非机动目标实施拦截的比例制导控制加速度方程为
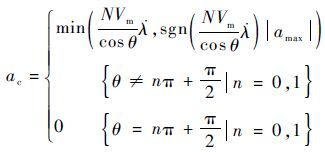 | (15) |
2 导引比例系数分析与OTPN设计 2.1 导引比例系数分析 TPN设定控制加速度 ac垂直于LOS,因 ac 与 Vm 非正交,故控制加速度在速度方向的分量会导致拦截弹的速度大小发生变化,制导过程中 Vm 为变量。对给定初始弹目视线角的拦截情况,拦截弹在相同速度前置角 θ 下对目标实施拦截的控制力方向和拦截路径如图 2所示:垂直于视线存在2种方向相反的控制加速度,如图中红色和蓝色 ac所示,不同方向的控制加速度将拦截弹导引至不同的制导终点A、B。此外,初始 θ 角与视线垂线的相对位置会使得拦截弹在相同方向的加速度下产生不同的速度方向变化。
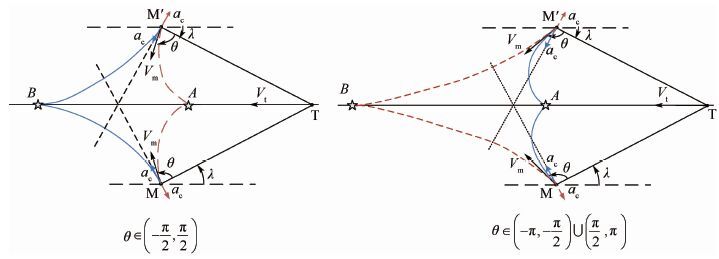 |
| 图 2 速度前置角 θ 下拦截比例导引示意图 Fig. 2 Interception by proportional navigation guidance law at velocity lead angle θ |
| 图选项 |
将 ac在拦截弹的速度坐标系进行分解,得到导致速度大小改变的分量 V·m 和速度方向改变的分量 Vm 。由图 2可以看出,在同样的初始速度前置角 θ 的情况下,由于控制加速度 ac的方向相反,使得拦截弹速度方向的变化趋势相反,速度大小的变化也相反,因而拦截轨迹发生变化。
拦截弹在比例导引下达到 =0 或成功拦截目标在交汇点处 Rf→0 这2种情况下,式(1)变为
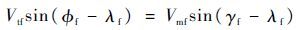 | (16) |
定义目弹速度比 β 为目标与拦截弹速度的比值:
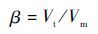 | (17) |
将初始时刻的目弹速度比记为 β0 ,拦截终点的目弹速度比记为 βf ,对于高速目标 β >1 。将式(17)代入式(16)有
 | (18) |
取反三角运算:
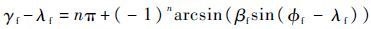 | (19) |
故拦截弹在与目标交会时刻的速度倾角:
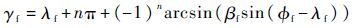 | (20) |
考虑到 γ 和 λ 的实际意义和取值范围,式(20)中 n 取0、1,因此有
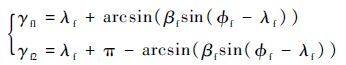 | (21) |
要使式(21)中 arcsin(βsin( -λ)) 有意义,因 β >1 ,由函数 arcsin x 的定义域知必有 -1≤βfsin(?f-λf)≤1 ,即
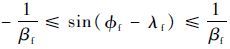 | (22) |
求得在区间 (-π/2,π/2) :
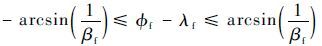 | (23) |
在区间 (π/2,3π/2) :
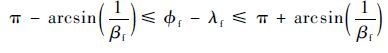 | (24) |
由式(23)和式(24)求得最终视线角 λf 与最终目标速度倾角 f 和目弹速度比 βf 之间的关系。
在区间 (-π/2,π/2) :
 | (25) |
在区间(π/2,3π/2):
 | (26) |
由式(25)和式(26)可知,对于给定的最终目标速度倾角 f 和最终目弹速度比 βf ,在(-π/2,π/2)和(π/2,3π/2)区间内分别存在一个 λf 可以满足成功拦截条件。图 3为在最终目标速度倾角为0的情况下,由目弹速度比 β 决定的最终视线角范围。
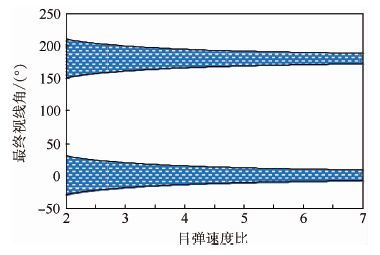 |
| 图 3 不同目弹速度比取值的最终视线角范围(?f=0 ) Fig. 3 Range of final LOS angle of different velocity ratios between target and interceptor(?f=0 ) |
| 图选项 |
最终目标速度倾角及最终目弹速度比对最终弹目视线角仅为弱约束条件,即由式(25)、式(26)仅可确定最终视线角所在的范围,并不是满足该条件的角均可能成为拦截成功的最终视线角。
当 arcsin(βfsin( f-λf)) 为±π/2时,式(21)的2个值相同:
 | (27) |
此时有
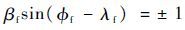 | (28) |
则
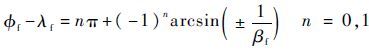 | (29) |
由式(21)可知,对给定的目标速度倾角 f 、最终弹目视线角 λf 和最终目弹速度比 βf ,存在满足成功拦截的条件的2个不同的拦截弹最终速度倾角 γf1 和 γf1 ,如图 4所示。
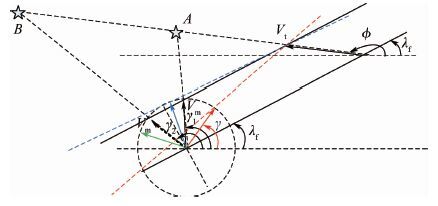 |
| 图 4 拦截弹以不同的速度倾角完成对目标拦截示意图 Fig. 4 Geometry of interceptor and target engaged in successful interception by different final velocity angles |
| 图选项 |
目标与拦截弹在给定的最终接近视线角 λf 和碰撞时刻速度比 βf 的约束下,达成拦截的末端速度倾角存在 γ1 和 γ2 2种情况,即式(21)中 γ 的2个取值。对照图 4分析比例导引过程中拦截弹初始速度倾角 γ0 取值范围与目标视线角速率 之间的关系:
当γ <γ1 时,由图 2可知有λ >λf,即λ>0 ,通过比例导引使γ→γ1,则γ>0,因此式(3)中N>0 。
当 γ>γ2 时,由图 2可知有 λ>λf ,即>0 ,通过比例导引使 γ→γ2 ,则<0 ,因此式(3)中 N<0 。
对 γ1<γ<γ2 的情况,由图 2可知此时 λ<λf ,即 <0 ,若通过比例导引使 γ→γ1 ,则 <0 ,因此式(3)中 N>0 。
同样对于 γ1<γ<γ2 的情况, λ<λf , <0 ,此时也可以通过比例导引使 γ→γ2 ,则>0 ,此时式(3)中 N<0 。
综合以上分析,使用比例导引进行拦截制导时,将拦截弹速度倾角 γ 导向 γ1 ,比例导引系数 N 为正;以 γ2 作为导引目标,比例导引系数 N 为负。
2.2 OTPN设计 以?、 β 和 λ 为约束,拦截弹能以2种不同的末端速度倾角 γ 完成对目标的拦截。 γ1 与 γ2 的关系由图 4和式(21)可知:
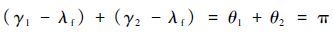 | (30) |
即 θ1 和 θ2 在视线的法线( θ=π/2 )两侧对称分布。在比例导引中,比例系数取正时,拦截弹速度倾角趋于 γ1 ,为逆轨拦截;比例系数取负时,拦截弹速度倾角趋于 γ2 ,为顺轨拦截。因此拦截导引的比例系数可正可负,按照就近原则,设定在拦截弹初始速度前置角|θ|<π/2 时,比例系数 N 取正;当拦截弹初始速度前置角|θ|>π/2 时,比例系数 N 仍取正值,在其制导方程中加入负号,则式(3)变为
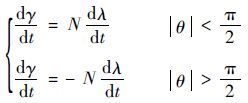 | (31) |
取式(31)和式(15)作为控制方程得到兼具顺轨和逆轨拦截能力的新的制导律,与传统拦截制导律相比,新的制导律对起始约束条件的要求宽,能覆盖顺、逆轨拦截需求,有利于提高拦截范围和效能。该制导律延续了TPN中控制力垂直于视线的设定,可在任意拦截弹初始速度倾角下,自动调整比例系数的正负,实现全平面内的拦截制导,故称为OTPN。OTPN的完整导引方程为
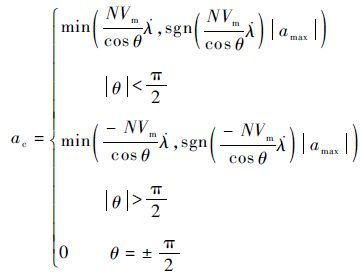 | (32) |
3 制导仿真与验证 3.1 基本参数设定 仿真目的:针对高速目标拦截任务,使用MATLAB进行计算机制导仿真,将OTPN方法与经典PN方法以及适用于顺轨拦截的RPN方法进行对比,验证OTPN的正确性及其拦截性能。
仿真环境及参数设置:使用MATLAB2014a软件,仿真步长设定为0.002 s。设拦截弹的视场足够大,拦截弹在距离目标30 m内失盲后保持导引参数最终值,有效拦截设定为拦截弹与目标的最小距离(即脱靶量)小于10 m。
仿真初始条件设定:初始拦截弹与目标距离R0=10 000m;初始弹目视线角λ0=10°;目标初始位置为 (xt,yt)= (10 000,10 000)m;拦截弹的位置由 R0,λ0,(xt,yt) 之间的几何关系确定;目标速度Vt=1 500 m/s,目标初始速度倾角?0=180°,目标恒速运动,即 at=0 ;拦截弹初始速度Vm0=600m/s。
3.2 制导方案设计 1) RPN拦截方案
RPN[5]应用于顺轨拦截,定义导弹速度倾角 γ 的变化率与导弹至目标的视线角 λ 的变化率之间的比例系数为负值,导引微分方程为
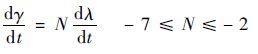 | (33) |
拦截弹所需的控制加速度 ac为
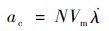 | (34) |
由于RPN导引结果为顺轨拦截,故用RPN制导方案对比研究顺轨拦截模式下OTPN的可行性及其制导特性。设置RPN制导方案中拦截弹初始速度倾角γ0=130°,则速度前置角θ0=γ0-λ0=120°,比例导引系数 N=-6 ,加速度上限amax=30g。
2) 经典PN拦截方案
经典的PN[20]定义拦截弹速度倾角 γ 的变化率与拦截弹至目标的视线角 λ 的变化率成正比,制导微分方程为
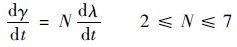 | (35) |
拦截弹所需的控制加速度 ac为
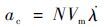 | (36) |
由于PN对高速目标的拦截结果只能为逆轨,因此使用PN制导方案对比研究逆轨拦截模式下OTPN的可行性及其制导特性。
3) OTPN拦截方案
OTPN可根据拦截弹初始速度前置角的不同对拦截弹分别实施顺轨和逆轨2种拦截制导,能同时满足2种拦截模式的制导需求。其导引微分方程定义如式(31),拦截弹的控制方程如式(32)。为适应与PN制导方案和RPN制导方案的参数设置,拦截弹初始速度倾角分别设定与PN和RPN制导方案相同。
共计4种制导方案进行仿真,其中顺轨拦截采用RPN制导方案作为对比方案,逆轨拦截采用经典PN制导方案为对比方案,OTPN分别对应RPN和经典PN制导方案的初始条件进行拦截导引仿真,各方案代号和主要设定参数见表 1。
表 1 拦截制导仿真方案参数 Table 1 Parameters of interception guidance schemes for simulation
| 方案代号 | 制导律 | λ0/(°) | γ0/(°) | θ0/(°) | 拦截成功条件 |
| 1 | RPN | 10 | 130 | 120 | <10m |
| 2 | OTPN | 10 | 130 | 120 | <10m |
| 3 | PN | 10 | 40 | 30 | <10m |
| 4 | OTPN | 10 | 40 | 30 | <10m |
表选项
3.3 仿真结果及分析 表 2列出各方案制导仿真结果关键指标参数,图 5给出了表 1中所列4种拦截制导方案的仿真结果。仿真结果表明,4种拦截制导方案在给定的初始参数下均能成功拦截目标。
表 2 仿真制导方案结果比较 Table 2 Results comparison of guidance schemes for simulation
| 方案代号 | 末端脱靶量/m | 最大加速度/g | 末端视线角/(°) | 总控制量/(m·s-1) | 拦截总时间/s |
| 1 | 0.136 3 | 9.729 3 | 2.223 9 | 488.580 2 | 10.450 0 |
| 2 | 0.131 5 | 19.037 1 | 6.407 5 | 332.634 2 | 8.539 8 |
| 3 | 0.193 0 | 12.808 2 | 8.198 7 | 115.036 4 | 4.958 2 |
| 4 | 0.046 2 | 1.676 7 | 8.900 2 | 77.970 2 | 5.008 6 |
表选项
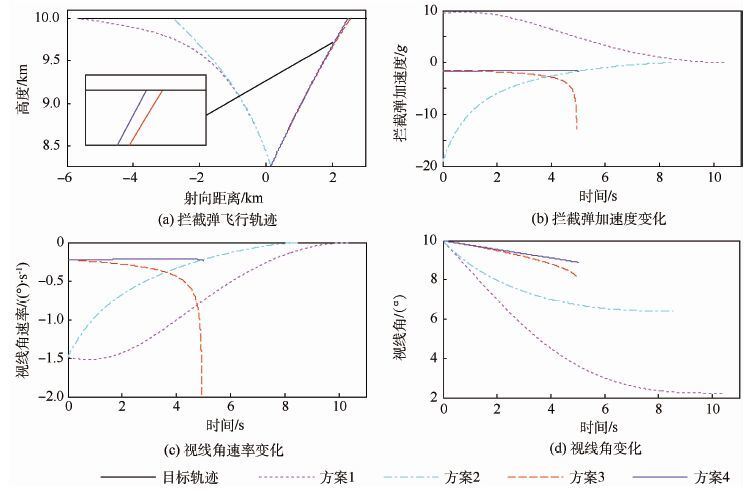 |
| 图 5 高速非机动目标拦截制导仿真结果 Fig. 5 Guidance simulation results for interception of nonmaneuvering high-speed targets |
| 图选项 |
通过图 5以及表 2对4种拦截制导方案的仿真结果进行分析比较:
1) 由于逆轨拦截时间较短,图 5(a)中OTPN与经典PN拦截轨迹区分不明显,但在图 5(b)中可明显区分两者的控制加速度以及视线角变化率;在顺轨拦截制导仿真中,OTPN与RPN轨迹区别明显,两者的最终视线角也存在差异,末端脱靶量基本相同。
2) 图 5(a)的拦截轨迹显示OTPN制导轨迹较经典PN更平直,拦截点位置与PN不重合;通过表 2可看出方案3和方案4的拦截时间基本相同,但OTPN在末端脱靶量、总控制量以及最大控制加速度需求方面均有优势。
3) 图 5(b)和图 5(c)显示,因逆轨拦截中相对速度较高、距离较近,OTPN与PN均未在碰撞前达成平行接近,PN在导引末端视线角速率突增,引起控制加速度绝对值急剧增大直至进入失盲区,与经典PN导引在进入盲区前未达到平行接近,导致末端大幅机动的特征相吻合[20];而OTPN在整个拦截制导中对控制加速度的需求,与PN相比初期表现基本相同,中、后期则相对稳定。
4) 从图 5(d)和表 2看出,在拦截达成时刻,OTPN的视线角变化量小于经典PN和RPN,这是由于OTPN的控制加速度垂直于视线方向,其在拦截弹速度方向的分量改变了拦截弹的速度大小,从而改变了目标与拦截弹的速度比,因此OTPN的末端视线角与经典PN和RPN不同。
5) 由图 5(b)看出,在拦截制导过程中OTPN的总控制量比经典PN小,最大控制加速度需求小于经典PN。因此,OTPN进行拦截制导时拦截弹对动力系统的要求小于经典PN,从另一个方面看,对于特定的拦截弹,采用OTPN进行拦截制导将可以获得较经典PN制导律更大的机动范围。
6) 由图 5(b)、图 5(c)、图 5(d)以及表 2中数据可看出,OTPN制导的拦截时间较RPN缩短19%,总控制量需求较RPN缩小32%,制导中OTPN的视线角速率收敛较RPN制导更快,但控制加速度的最大绝对值较RPN大。
7) OTPN可以完成对高速非机动目标的拦截导引,仿真结果显示脱靶量、拦截时间及总控制量等关键参数满足拦截制导需求,式(32)所列导引方程有效,使用OTPN进行全向拦截制导的方案可行。
3.4 OTPN捕获能力研究 仿真目的:通过仿真在不同初始条件下OTPN对高速目标拦截的捕获范围,研究控制加速度上限和比例导引系数取值对OTPN拦截制导的影响。
仿真初始条件设定:同3.1节。
设定比例导引系数 N=6 ,初始速度前置角 θ 从0°变化至360°,变化步长为5°;最大控制加速度上限设定为30g,脱靶量小于10 m为有效拦截。仿真结果显示在此条件下仅有γ0=100° 时无法成功拦截,其余初始速度倾角均可在OTPN导引下成功拦截目标,仿真拦截轨迹见图 6。
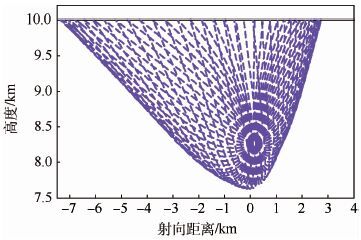 |
| 图 6 速度前置角0°~360°OTPN制导成功拦截轨迹 Fig. 6 Trajectory of successful interception guided by OTPN at 0°-360° velocity lead angle |
| 图选项 |
按照相同的仿真初始设定,分别使用经典PN和RPN进行拦截制导仿真,结果显示仅在10°≤γ0≤75°范围内PN制导能够成功拦截目标(见图 7);而RPN能够成功拦截的初始速度倾角范围为60°≤γ0≤210°(见图 8)。
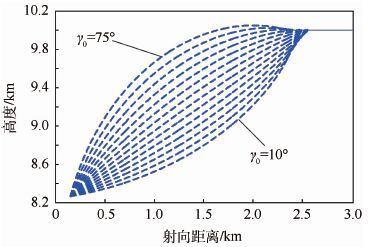 |
| 图 7 速度前置角0°~360°经典PN成功拦截轨迹 Fig. 7 Trajectory of successful interception guided by classic PN at 0°-360° velocity lead angle |
| 图选项 |
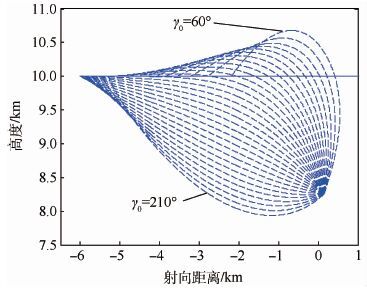 |
| 图 8 速度前置角0°~360° RPN制导成功拦截轨迹 Fig. 8 Trajectory of successful interception guided by RPN at 0°-360° velocity lead angle |
| 图选项 |
为精确研究OTPN的捕获能力,将初始速度倾角变化步长缩小为0.1°,其他设定不变,仿真结果显示OTPN无法成功拦截的初始速度倾角范围为[99.0°,100.0°]∪[280.1°,284.8°]。由图 9可以看出,同样的初始条件下,OTPN拦截制导对高速目标的捕获能力大于经典PN和RPN。
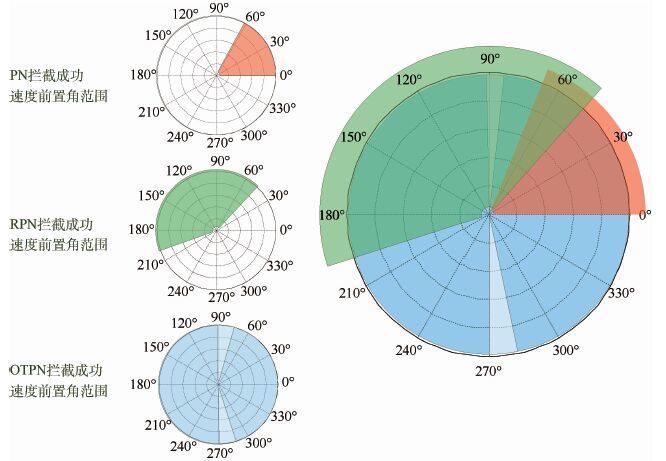 |
| 图 9 相同初始条件下OTPN、RPN和经典PN捕获范围对比 Fig. 9 Comparison of capture region for guidance of OTPN,RPN and classic PN under same initial conditions |
| 图选项 |
1) 控制加速度上限 amax 对OTPN捕获区域的影响
设定比例导引系数 N=6 ,初始弹目视线角 λ0 为0°,初始弹目速度前置角 θ 从0°变化至360°,变化步长为0.1°;最大控制加速度上限分别设定为30g、20g、15g和10g,设定脱靶量小于10 m为有效拦截,通过仿真研究控制加速度上限变化对OTPN拦截制导的捕获区域的影响,仿真结果见图 10。
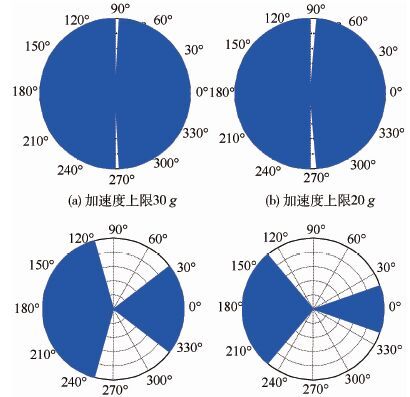 |
| 图 10 不同加速度上限OTPN成功拦截初始速度倾角范围 Fig. 10 Range of initial velocity angle for OTPN’s successful interception with different acceleration limits |
| 图选项 |
由图 10可以看出,随着控制加速度上限的缩小,OTPN无法成功拦截的初始速度倾角范围逐渐增大,即OTPN拦截制导的捕获范围随着控制加速度上限的减小而减小。在本文所用的仿真实例中,加速度上限达到20g时OTPN可实现在除奇点附近任意初始速度倾角的情况下,对高速非机动目标实施成功拦截。
2) 比例导引系数 N 对OTPN捕获区域的影响
设定最大控制加速度上限为30g,初始弹目视线角 λ0 设定为0°,初始速度前置角 θ 从0°变化至360°,变化步长为0.1°;比例系数分别设定为3、4、5、6,脱靶量小于10 m为有效拦截,通过仿真研究比例导引系数变化给OTPN拦截制导的捕获区域带来的影响,仿真结果如图 11所示。
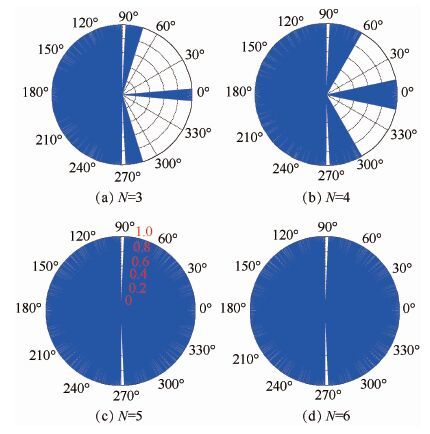 |
| 图 11 不同比例系数下OTPN成功拦截初始速度倾角范围 Fig. 11 Range of initial velocity angle for OTPN’s successful interception with different navigation ratios |
| 图选项 |
由图 11可知:①比例系数N越大,OTPN进行拦截制导的捕获范围越大;②OTPN在拦截高速目标时,顺轨模式较逆轨模式的捕获范围更大,因此在条件许可的情况下,高速目标的拦截采用顺轨拦截模式可以减小对拦截弹初始条件的约束范围;③比例系数N在大于5之后,捕获范围的增加有限,而比例导引中N值增大会造成制导噪声的增加,因此OTPN的比例系数应根据实际拦截情况适当设置。
4 结 论 1) 通过对高速目标拦截问题的分析和研究,发现了对高速目标进行比例导引拦截时,2个相对于视线垂直方向对称分布的制导目标,导致导引比例关系的正负和拦截模式的不同。
2) 在制导律的设计中突破拦截弹恒速假定,综合控制加速度约束及正负比例制导切换,完成了全向真比例制导律OTPN的设计。OTPN拦截制导具备顺轨和逆轨2种拦截能力,通过自动调整比例系数的正负实现对高速目标的全向拦截。
3) 数值仿真表明OTPN能根据初始条件自主选择顺/逆轨拦截模式,在同等条件下拦截时间、最大控制力以及总控制量需求等参数较经典PN和RPN制导方案更具优势;OTPN的捕获范围比经典PN和RPN更大,具备在更大的初始速度倾角范围内对高速目标的拦截制导能力;OTPN的捕获能力会受到拦截弹的加速度上限和比例系数取值影响。
参考文献
| [1] | SHIMA T, GOLAN O M. Head pursuit guidance[J]. Journal of Guidance,Control,and Dynamics,2007, 30(5): 1437–1444. |
| Click to display the text | |
| [2] | LIN Y P, LIN C L, LI Y H. Development of 3-D modified proportional navigation guidance law against high-speed targets[J]. IEEE Transactions on Aerospace and Electronic Systems,2013, 49(1): 677–687. |
| Click to display the text | |
| [3] | 李超勇, 荆武兴, 齐治国, 等. 空间微分几何制导律应用研究[J]. 宇航学报,2007, 28(5): 1235–1240.LI C Y, JING W X, QI Z G, et al. Application of the 3D differential geometric guidance commands[J]. Journal of Astronautics,2007, 28(5): 1235–1240.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [4] | 熊俊辉, 唐胜景, 郭杰, 等. 基于模糊变系数策略的迎击拦截变结构制导律设计[J]. 兵工学报,2014, 35(1): 134–139.XIONG J H, TANG S J, GUO J, et al. Design of variable structure guidance law for head-on interception based on variable coefficient strategy[J]. Acta Armamentarii,2014, 35(1): 134–139.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | PRASANNA H M, GHOSE D. Retro-proportional-navigation:A new guidance law for interception of high speed targets[J]. Journal of Guidance,Control,and Dynamics,2012, 35(2): 377–386. |
| Click to display the text | |
| [6] | 闫梁, 赵继广, 沈怀荣, 等. 带末端碰撞角约束的三维联合偏置比例制导律设计[J]. 航空学报,2014, 35(7): 1999–2010.YAN L, ZHAO J G, SHEN H R, et al. Three-dimensional united biased proportional navigation guidance law for interception of targets with angular constraints[J]. Acta Aeronautica et Astronautica Sinica,2014, 35(7): 1999–2010.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [7] | SHUKLA U S, MAHAPATRA P R. The proportional navigation dilemma-pure or true?[J]. IEEE Transactions on Aerospace and Electronic Systems,1990, 26(2): 382–392. |
| Click to display the text | |
| [8] | YANG C D, YANG C C. Unified approach to proportional navigation[J]. IEEE Transactions on Aerospace and Electronic Systems,1997, 33(2): 557–567. |
| Click to display the text | |
| [9] | LI K, CHEN L, TANG G. Improved differential geometric guidance commands for endoatmospheric interception of high-speed targets[J]. Science China:Technological Sciences,2013, 56(2): 518–528. |
| Click to display the text | |
| [10] | VISWANATH D,DEB D.A new nonlinear guidance law formulation for proportional navigation guidance[C]//Proceedings of IEEE International Workshop on Variable Structure Systems.Piscataway,NJ:IEEE Press,2012:190-195. |
| Click to display the text | |
| [11] | DHANANJAY N, GHOSE D. Accurate time-to-go estimation for proportional navigation guidance[J]. Journal of Guidance,Control,and Dynamics,2014, 37(4): 1378–1383. |
| Click to display the text | |
| [12] | HELLER C, YAESH I, BEN-ASHER J Z. Engineering notes:Optimal setting of the proportional-navigation gain[J]. Journal of Guidance,Control,and Dynamics,2013, 36(3): 888–891. |
| Click to display the text | |
| [13] | GOLDAN O, GUTMAN S. Adjoint stability and miss distance in proportional navigation[J]. Journal of Guidance,Control,and Dynamics,2012, 35(4): 1089–1093. |
| Click to display the text | |
| [14] | FENG T. Capture region of a 3D PPN guidance law for intercepting high-speed targets[J]. Asian Journal of Control,2012, 14(5): 1215–1226. |
| Click to display the text | |
| [15] | YANG C D, YANG C C. Analytical solution of three-dimensional realistic true proportional navigation[J]. Journal of Guidance,Control,and Dynamics,1996, 19(3): 569–577. |
| Click to display the text | |
| [16] | GHOSE D. True proportional navigation with maneuvering target[J]. IEEE Transactions on Aerospace and Electronic Systems,1994, 30(1): 229–237. |
| Click to display the text | |
| [17] | DHAR A, GHOSE D. Capture region for a realistic TPN guidance law[J]. IEEE Transactions on Aerospace and Electronic Systems,1993, 29(3): 995–1003. |
| Click to display the text | |
| [18] | 钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M].北京: 北京理工大学出版社, 2006: 2-64.QIAN X F, LIN R X, ZHAO Y N. Flight dynamics of missiles[M].Beijing: Beijing Institute of Technology Press, 2006: 2-64.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [19] | 黎克波, 陈磊, 张翼. 真比例导引律的降维分析方法[J]. 国防科技大学学报,2012, 34(3): 1–5.LI K B, CHEN L, ZHANG Y. Dimension-reduction method of true proportional navigation guidance law[J]. Journal of national university of Defense Technology,2012, 34(3): 1–5.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [20] | SIOURIS G M. Missile guidance and control systems[M].New York: Springer, 2004: 142-173. |
| Click to display the text | |
