对于上述基于ML准则的多径参数估计算法,为了进一步降低算法复杂度,一个直接有效的努力方向是增大搜索步进、减小搜索次数,但这样做难免会牺牲估计精度和分辨率,且对于多径延迟量接近或小于观测间距(即搜索步进)的多路多径信号,易出现参数估计错误。在保证参数估计精度和分辨率的前提下,为了尽量降低搜索次数,同时能够避免Turbo-DLL中无法跟踪短时延多径信号的缺陷,且相比于Turbo-DLL和CADLL,能获得更好的多径参数估计精度。本文在ML估计的基础上对MEDLL算法的搜索策略进行了优化,提出了基于树状分级结构的搜索方法,并分析了其相比于传统的盲搜索策略所能简化的计算复杂度,最后通过全球定位系统(GPS)信号模拟器和软件接收机对其参数估计精度和抗多径效果进行了测试验证。
1 MEDLL算法 用户接收信号的表达式为
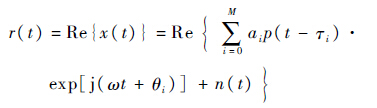 | (1) |
式中:i=0为直达信号,i=1~M为M路多径信号;p(t)为基带信号;ω为载波角频率;信号幅度ai、码延迟量τi和相位θi为待估的信号参量;Re{}为取{}内表达式的实数部分;j为虚数单位;n(t)为噪声,t为时间。
建立似然函数:
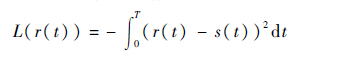 | (2) |
式中:s(t)为由直达和多径信号参量估计值(τi,ai,θi)构造的本地信号;T为积分周期。为了求解方程式(2),只需令似然函数L(τi,ai,θi)的偏导为0,可得M+1路待估信号的参数,其中第i(0≤i≤M)路信号的参数表达式为[1]
 | (3) |
 | (4) |
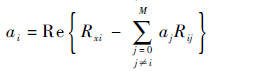 | (5) |
式中:
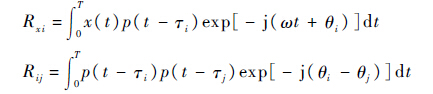 |
由式(3)~式(5)可知,参数求解的核心部分是对各路信号码延迟量的估计;对于每一假设的多径路数M,需要多次迭代得到对应的τi,θi,ai估计值(i=0,1,…,M)。由式(3)可知,求信号的码延迟估计量,实质为在需搜索的码相位范围内一系列离散的相关值观测点中寻找相关峰的位置;为了获得更高的分辨率,必须减小相关器本地码相位搜索步进、增加搜索次数(即相关器个数)。在算法实现中一般以±1.5 chip为搜索范围、以多径延迟估计分辨率d为搜索步进[12]。
无论是提高分辨率,还是提高参数估计精度,都必须缩小搜索步进,这无疑会增加算法计算量[13-14]。因此,在实际工程应用中,往往不得不在分辨率/估计精度和计算复杂度这一对矛盾量之间进行折中考虑。
2 树状分级结构T-MEDLL 2.1 T-MEDLL算法原理 为了在保证分辨率和估计精度的同时尽量减少计算量,本文提出树状分级结构的MEDLL(记为T-MEDLL),即采用树状分级结构的搜索路径,分阶段多分辨率逐级精细化地对参数进行估计。首先在全局范围内(搜索范围为±1.5 chip,记为d0=1.5)依靠第1级搜索单元(FSU)实现低分辨率搜索(搜索步进记为d1,d1<d0),粗略估算直达信号和多径信号的参数,以估计的信号路数M1+1作为第2级搜索单元(SSU)的个数,以所估计的多径信号延迟量[AKτ^]i作为每个SSU搜索延迟量的中心,各单元的搜索范围为FSU的搜索步进d1的2倍。
在MEDLL和T-MEDLL算法中,对于多径信号路数的估计,是利用接收信号和本地伪码的相关波形,与未发生畸变的标准相关波形进行匹配,并对比其残值比(SRR)。因此,对于在FSU中出现多径信号被遗漏的现象,可分成2种情况讨论:①多径信号太弱,相关波形畸变不严重;②由于FSU分辨率太低,多条多径信号被误当作一条合信号。对于情况①,说明此时多径信号对于相关波形的影响不大,可以忽略其对环路的影响;对于情况②,未被监测出的多径信号将在分辨率更高的下一级单元被估计出,因此也避免出现Turbo-DLL和CADLL中多径信号路数的估计完全依赖于MMU单元的情况。同时可进一步增加树状结构的分级数,以新的参数估计值作为下一级搜索单元的先验信息,逐级提高分辨率。另外,为了进一步节约计算资源,可根据实际需求为下一级搜索单元数设置上限,仅对功率大的多径信号进行精细的参数估计;对跟踪环路影响小的多径信号由分辨率较低的FSU负责参数估计即可,不再参与下一级的精细估计。
图 1为三级结构T-MEDLL的框图。图中:搜索步进d即为子单元内离散观测点的观测间距,单位为码片(chip);nh为在第h级子单元的搜索范围内的观测点个数,h=1,2,3为采用分级结构的层级数量;M1、M2和M3表示三级搜索分别得到的多径信号路数。T-MEDLL在前期盲搜索阶段,利用搜索步进较大的FSU来完成粗略的参数估计,最后利用分辨率更高的SSU,甚至是第3级搜索(TSU)完成最终的估计算法,因此能够在确保分辨率的前提下,降低搜索次数,节约计算资源。
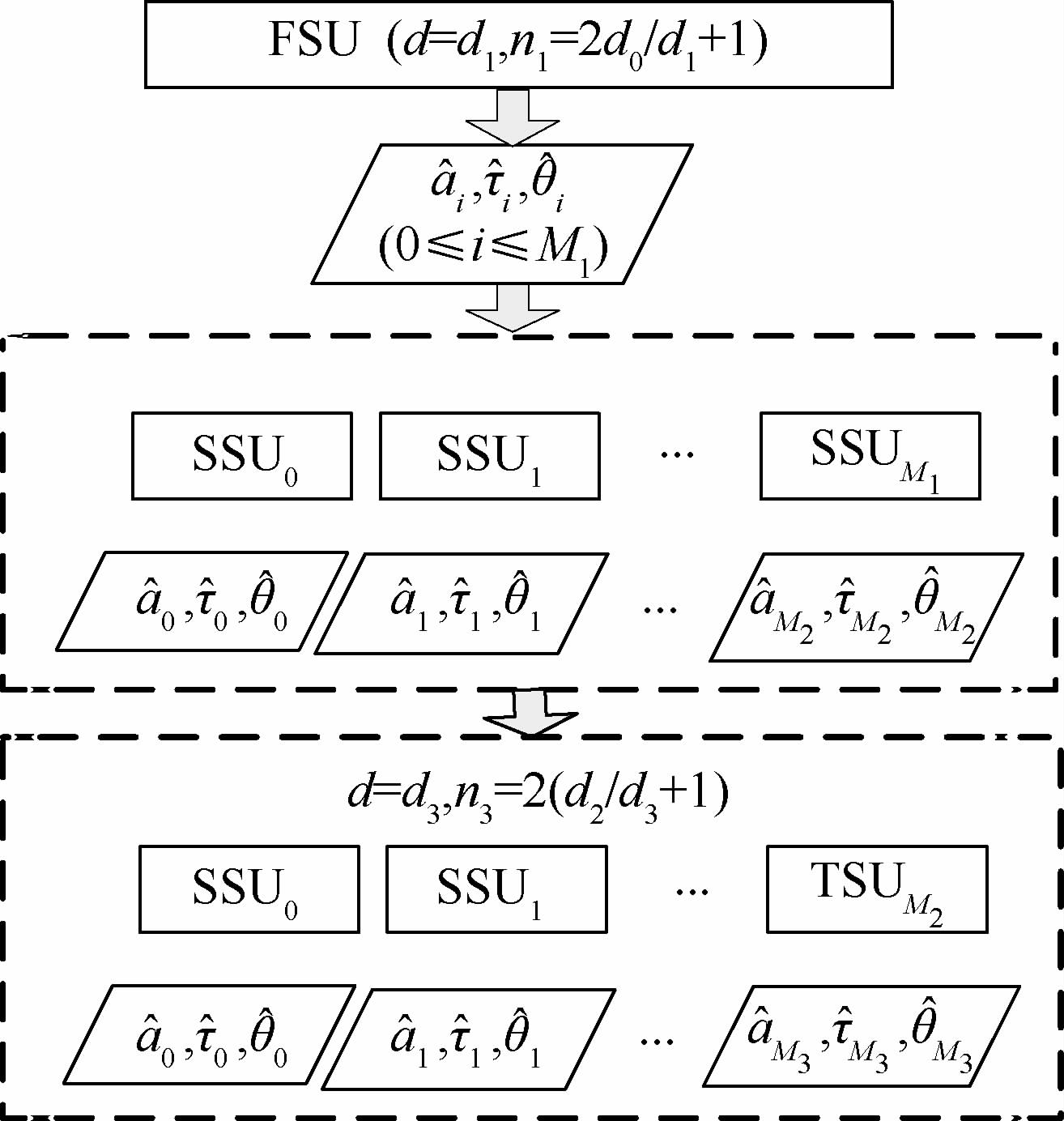 |
| 图 1 三级结构T-MEDLL框图 Fig. 1 Block diagram of three hierarchical structures of T-MEDLL |
| 图选项 |
2.2 T-MEDLL算法的计算复杂度 为了进一步说明T-MEDLL的执行过程,图 2以T-MEDLL的第2级搜索为例,给出了参数估计算法的流程图,并标明了其中每个步骤所需的ML估计次数,每一次ML估计需完成一次式(3)~式(5)的运算,其中步骤1)中的包括直达和多径共(M1+1)路信号参数为上一级搜索(FSU)的估计结果。步骤2)中的参数迭代,是为了基于FSU输出的估计值在搜索步进更小的SSU范围内,进一步提高估计精度,N为迭代次数。第1次估计第i路多径信号的延迟量τi,必须遍历M1+1个SSU单元中的所有观测点,完成一次ML估计。第2次执行迭代过程是为了使新获得的i+1路信号的参数估计值收敛至正确解,在迭代过程中各路信号只需在各自的SSU内搜索最大似然解,本次迭代过程需要执行的ML估计次数为(i+1)N。为了保证在完成前后两次迭代后

当多径信号路数为i时,求取其中第j路信号参数值所需的计算量(即在第j路信号对应的SSU单元内执行一次ML估计所需的计算量)为
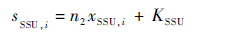 | (6) |
式中:xSSU,i为在单个离散的观测点上实现式(3)中中括号内的式子所需的计算量,下标i表示在观测点上需要减掉除第j路外的其余i路信号分量;KSSU则表示在SSU内继续完成式(3)和式(4)并得到
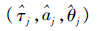
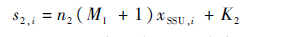 | (7) |
K2的意义与KSSU类似,只是其执行范围从单个的SSU扩大到M1+1个SSU单元。
图 2中SRR的引入是为了正确估计多径信号的路数,SRR(i)表示多径信号路数为i时的信号残值比[14]:
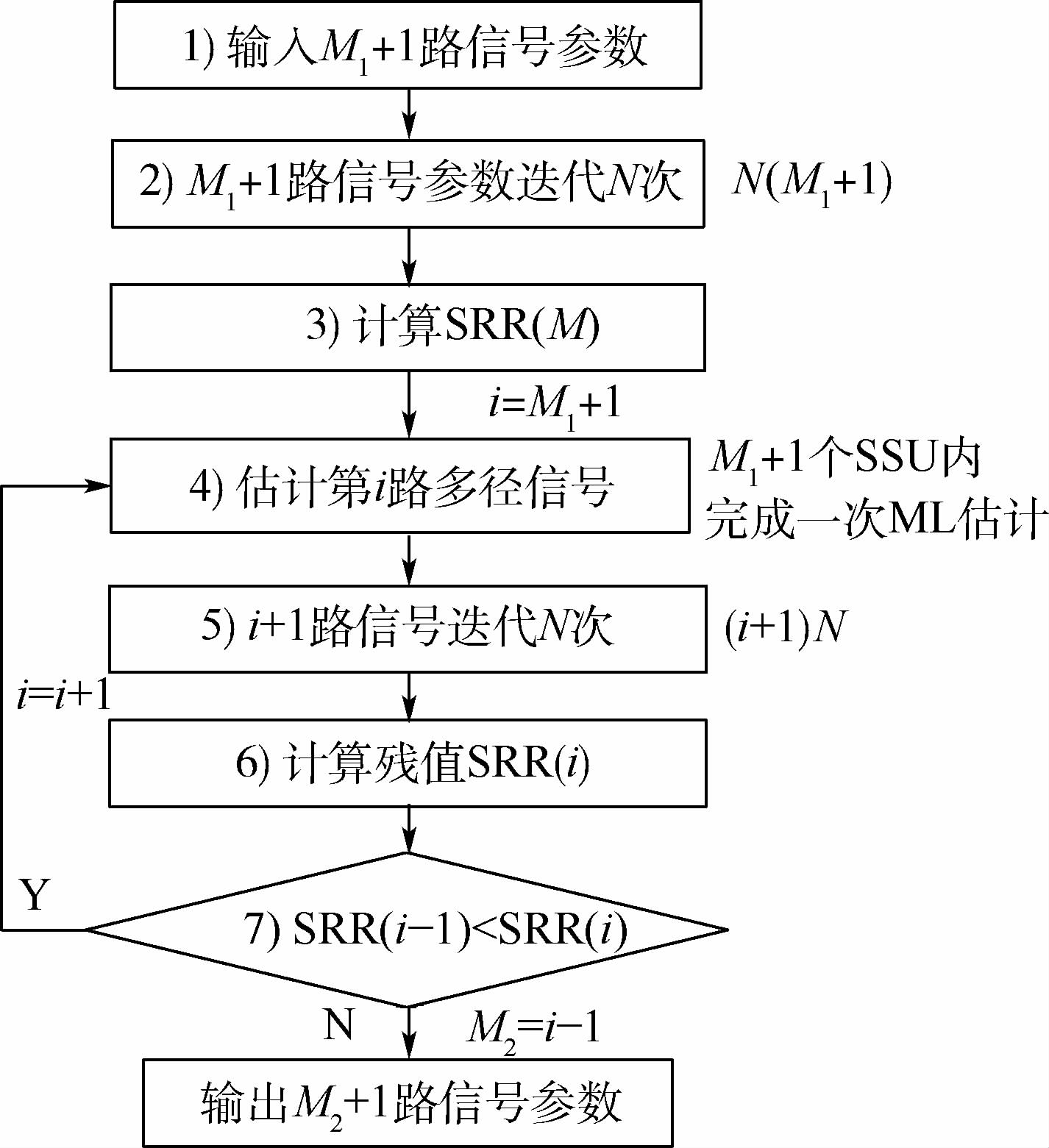 |
| 图 2 第2级参数估计算法流程图 Fig. 2 Flowchart of the second-level parameter estimation algorithm |
| 图选项 |
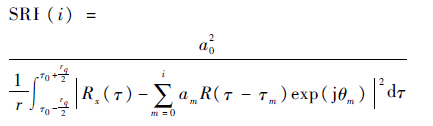 | (8) |
式中:rq为全局搜索范围,本文中r=3chip。如图 2所示,当信号残值比变小,即SRR(i)<SRR(i-1)时,停止计算并输出M2=i-1时的直达信号与多径信号的参数估计值,否则继续估计第i+1路多径信号。由此可见,当只存在i-1路多径信号时,实际是估计至第i路多径信号。
式(9)给出了执行步骤6)和步骤7)所需的计算量表达式:
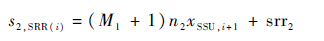 | (9) |
式中:(M1+1)n2xSSU,i+1完成所有离散点上的残值计算;srr2为获得单点残值后计算SRR(i)以及执行SRR(i-1)<SRR(i)所需的计算量。
由式(9)可见,在各步骤中都涉及了对观测点的残值计算,在实际算法实现中,应合理利用计算资源,避免重复计算,比如在步骤4)中,可利用步骤3)得到的各观测点残值直接进行ML估计,因此对式(7)进行修正得到实际计算量为s2,i=K2;式(9)中xSSU,i+1的计算,也只需在之前获得的各点残值中减去新估计得到的信号分量,因此对式(9)修正得到s2,SRR(i)=(M1+1)n2·xSSU,1+srr2。
表 1列出了xSSU,i、KSSU和srr2计算量的具体情况,包括各运算类型的执行次数。
表 1 计算量 Table 1 Computation complexity
| 计算量 | 执行次数 | |||||
| +/- | ×/÷ | sin/cos | arctan2 | ≥ | ||
| xSSU.i | 2i+1 | 4i+2 | ||||
| KSSU | 1 | 2 | 1 | n2-1 | ||
| K2 | 1 | 2 | 1 | (M1+1)n2-1 | ||
| srr2 | (M1+1)n2-1 | 2 | ||||
表选项
结合图 1和图 2,当采用两级搜索时,其中第2级搜索所消耗的计算量表达式为
 | (10) |
以此类推,可得其余各级搜索的参数估计流程和计算量表达式。为了得到第1级FSU的搜索结构,只需修改图 2中的前2个步骤为输入直达信号的参数初始值,且后续的ML估计过程在FSU范围内执行;为了得到第3级搜索结构的参数估计流程,只需将图 2中的输入值改为由第2级处理获得的M2+1信号参数值,并将子单元由SSU改为TSU即可。
式(11)给出第1级搜索FSU完成多径信号参数估计所需的计算量表达式,这也是采用盲搜索法的传统MEDLL算法的计算量表达式:
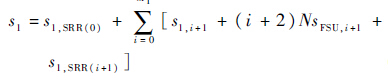 | (11) |
式(12)为第3级搜索TSU的计算量表达式:
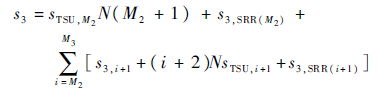 | (12) |
MEDLL和T-MEDLL算法的本质为在一组离散的观察点上进行ML估计,因此对于算法计算复杂度的分析,还必须包括获取观测点的相关值,即不同相位偏移下本地复制信号与接收信号之间的相关累加结果。当采样率为fs,相关积分时长为Tcoh时,为了获取每个观测点的相关值需要在I、Q通道内各完成fsTcoh个采样点的相关累加运算,其计算量记为scor。
因此,采用分级搜索的T-MEDLL算法进行多径信号的参数估计,消耗的计算量可用式(13)表示,M0=0。
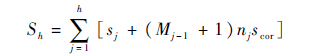 | (13) |
为了更直观地对比传统盲搜索MEDLL和T-MEDLL算法的计算复杂度,以存在一路多径信号、采样率fs=100 MHz、相关积分时长Tcoh=20 ms为例,表 2列出了达到0.01 chip时延分辨率的4种不同搜索策略各自所需的计算量。
表 2 MEDLL与T-MEDLL计算复杂度对比示例 Table 2 Illustration of computation complexity of MEDLL and T-MEDLL
| 搜索方案 | FSU/chip | SSU/chip | TSU/chip | 不同运算类型的复杂度 | ||||||||
| d1 | 范围 | d2 | 范围 | d3 | 范围 | +/- | ×/÷ | sin/cos | arctan2 | ≥ | ||
| 盲搜索 | 0.01 | 3 | 804 066 819 | 804 131 844 | 52 | 104 | 52 | 15 600 | ||||
| 两级T-MEDLL | 0.1 | 3 | 0.01 | 0.2 | 292 011 625 292 031 732 | 103 | 206 | 103 | 2 601 | |||
| 0.2 | 3 | 0.01 | 0.4 | 392 009 662 | 392 018 922 | 103 | 206 | 103 | 2 861 | |||
| 三级T-MEDLL | 0.5 | 3 | 0.1 | 1 | 0.01 | 0.2 | 284 008 779 | 284 017 288 | 154 | 308 | 154 | 1 874 |
表选项
MEDLL与T-MEDLL计算复杂度对比示例如表 2所示。相比于传统盲搜索的MEDLL,采用分级结构的T-MEDLL能大幅减少加减、乘除和比较运算的运算次数;由于加减和乘除运算的次数远远多于其余的运算类型,尽管开根号和三角函数运算次数有所增加,其对总计算量的影响仍是可以忽略的。由表 2可知,不同分级搜索策略的T-MEDLL算法计算复杂度将下降至传统盲搜索的35%~50%;相同分级、不同搜索步进的复杂度也有所不同;两级搜索相对于盲搜索的计算复杂度下降比较显著,但三级搜索相对于两级搜索的计算复杂度仅降低10%左右。
3 测试结果及分析 为了验证分级结构的T-MEDLL算法的多径参数估计性能,以及对伪距多径误差的修正效果,本文通过自研的数字中频GPS信号模拟器和软件接收机平台对T-MEDLL和MEDLL进行闭环测试。数字中频模拟器的相关设置为:选择GPS L1 C/A信号为测试信号,载波噪声比:C/N0=50 dB·Hz,C为载波,N0为噪声,并关闭除多径和噪声外的其余测距误差项。接收机的相应设置为:码环等效噪声带宽BL=1 Hz;DLL的超前支路和滞后支路的相关间距分别为D=1 chip和D=0.2 chip;相关积分时长Tcoh=20 ms,不需要考虑数据位跳变对测试的影响。为了使分辨率达到0.01 chip,采用两级搜索,第1级FSU的搜索步进d1=0.2 chip,第2级SSU的搜索步进d2=0.01 chip。
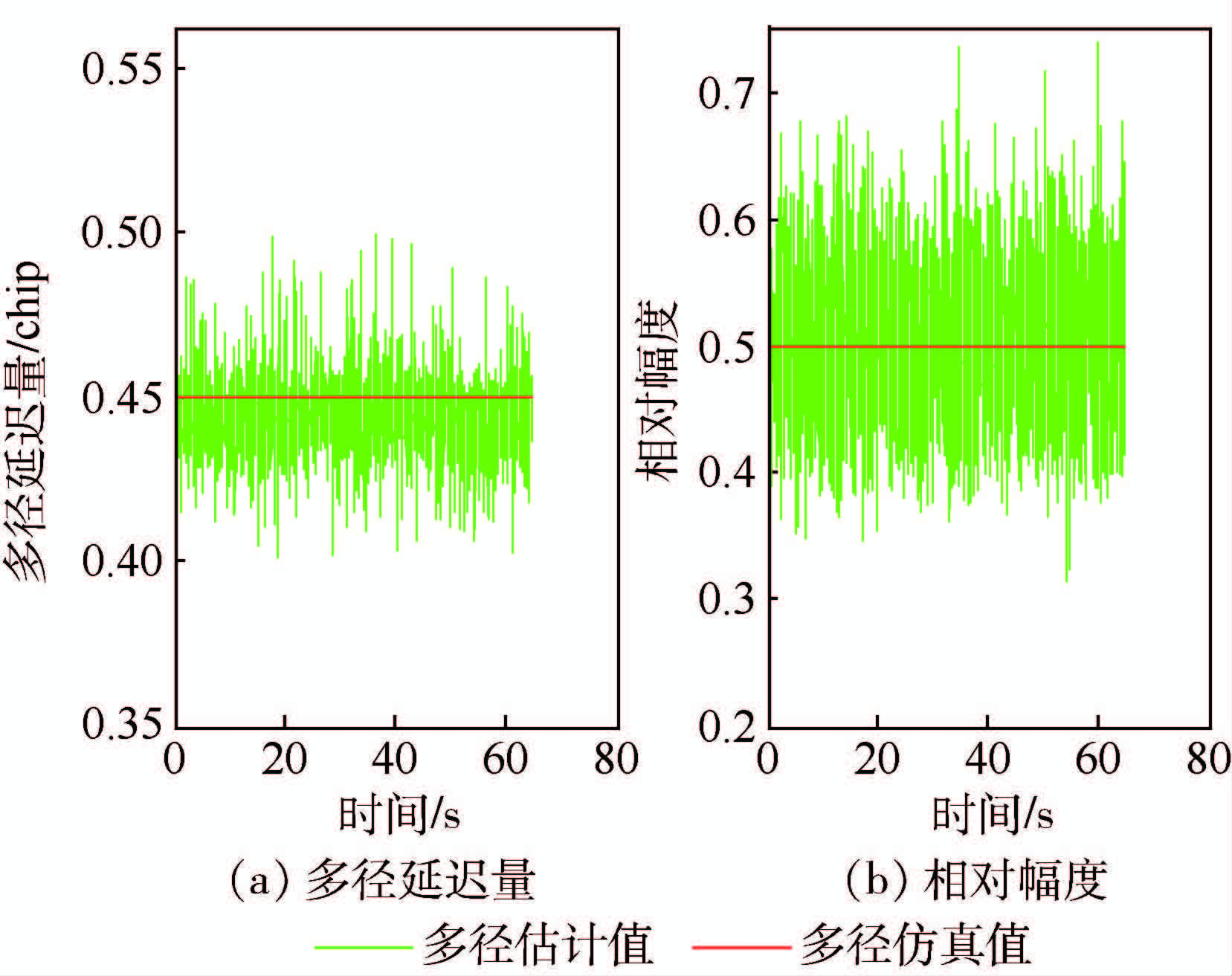
3.1 一路多径测试 数字中频软件模拟器产生的GPS L1 C/A信号中存在一路多径信号,相对于直达信号,其码延迟τ1=0.45 chip,相对幅度c1=a1/a0=0.5,载波相位偏差为θ1=π/6。接收机分别采用T-MEDLL及不同相关间距的普通DLL进行处理。
图 3给出了T-MEDLL的多径参数估计结果。T-MEDLL算法下多径信号相对于直达信号的多径延迟量估计结果
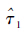
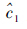
 |
| 图 3 T-MEDLL的多径参数估计结果 Fig. 3 Multipath parameter estimation results using T-MEDLL |
| 图选项 |
由图 3可见,参数估计值围绕仿真设置值波动。图中数据的更新率为50 Hz,即接收机T-MEDLL算法估计多径参数时直接利用了每20 ms得到的相关结果而非更长时间(如1 s或更长)平均的结果,因而噪声对信号的参数估计值尤其是多径相对幅度估计值的影响比较明显。
表 3对多径参数估计结果进行了统计分析,由表中可见,在存在一路多径信号(多径1)的条件下,采用T-MEDLL算法,能够完成对多径信号参数的估计,多径信号延迟量的估计误差均值仅为0.006 2 chip,可以达到0.01 chip的分辨率。
表 3 多径1的参数估计统计值 Table 3 Statistical values of parameter estimation of a single multipath
| 多径信号 | 多径延迟量/chip | 相对幅度 | ||
| 均值 | 标准差 | 均值 | 标准差 | |
| 多径1 | 0.443 8 | 0.009 8 | 0.503 8 | 0.056 2 |
表选项
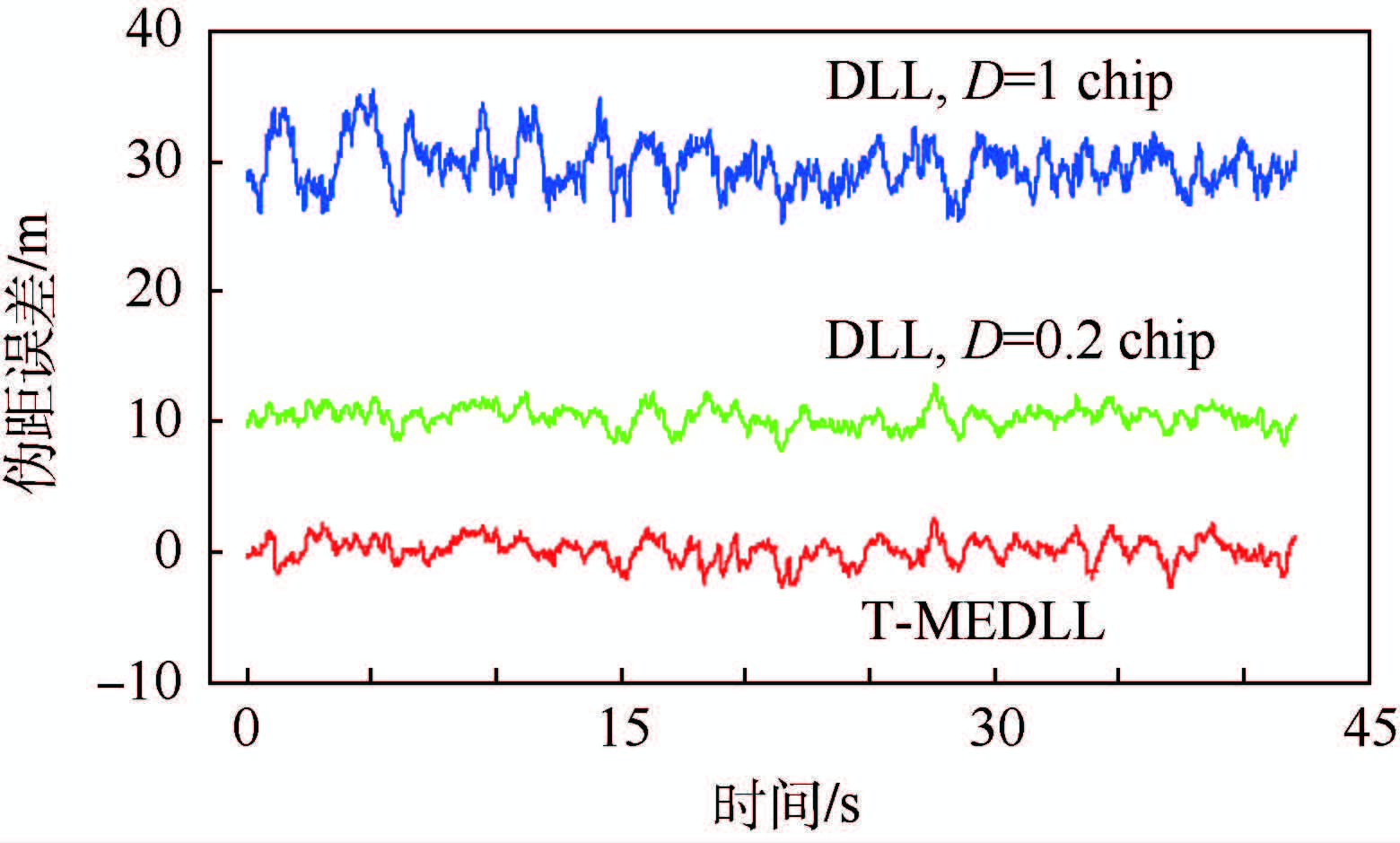
图 4为利用T-MEDLL及不同相关间距D的普通DLL,接收机输出的伪距值与模拟器仿真伪距值之差(伪距误差)。表 4为图 4中伪距误差统计值。
 |
| 图 4 DLL和T-MEDLL伪距误差 Fig. 4 Statistical values of pseudo-range error |
| 图选项 |
由图 4和表 4结果可见,虽然可以通过减少相关间距D来减少多径误差,但窄相关技术的抗多径性能依然不够理想,而采用T-MEDLL算法则能大大降低多径误差。
表 4 伪距误差统计值 Table 4 Statistical values of pseudo-range error
| 统计值 | DLL,D=1 chip | DLL,D=0.2 chip | T-MEDLL |
| 误差均值/m | 29.676 9 | 10.323 2 | 0.107 7 |
| 误差标准差/m | 1.829 3 | 0.794 3 | 0.904 8 |
表选项
理论上,对于一路多径的情况,可以根据多径参数计算出普通DLL的伪距多径误差包络值[15]。另外,当无多径或多径信号被完全消除后,由热噪声引起的伪距测量标准差可作为伪距测量误差的下限[16-17]:
 | (14) |
在π/6的载波相位偏差下,本次实验一路多径下普通DLL测得的伪距偏差约为理论多径误差包络的0.866,与理论预期吻合;而采用T-MEDLL则能将多径下的伪距偏差降低至0.107 7 m。根据式(14)可算得完全消除多径后的码跟踪误差标准差应为0.165 1 m;而实际采用T-MEDLL测得的伪距误差标准差为0.904 8 m。可见,尽管T-MEDLL较之普通DLL能更好地抑制多径干扰,但是由于MEDLL算法对于噪声较敏感[13],因此无法完全消除多径误差。
3.2 两路多径测试 数字中频软件模拟器产生的L1 C/A信号中存在两路多径信号,相对于直达信号,其码延迟量分别为τ1=0.4 chip,τ2=0.6 chip,相对幅度c1=0.5,c2=0.3,其他参数不变。
图 5为利用搜索步进d=0.2 chip的单级MEDLL得到的多径信号参数估计结果。低分辨率MEDLL只能检测到一路多径信号,估计均值τ=0.476 5 chip,c=0.722 3。可见,当两路多径信号码延迟量之差接近算法本身分辨率时(τ2-τ1≈d=0.2 chip),MEDLL算法无法正确估计其多径参数。当遇到此类情况时,为得到正确的多径参数估计结果,必须进一步精细搜索,以提高分辨率。
 |
| 图 5 MEDLL的多径参数估计结果(d=0.2 chip) Fig. 5 Multipath parameter estimation results using MEDLL (d=0.2 chip) |
| 图选项 |
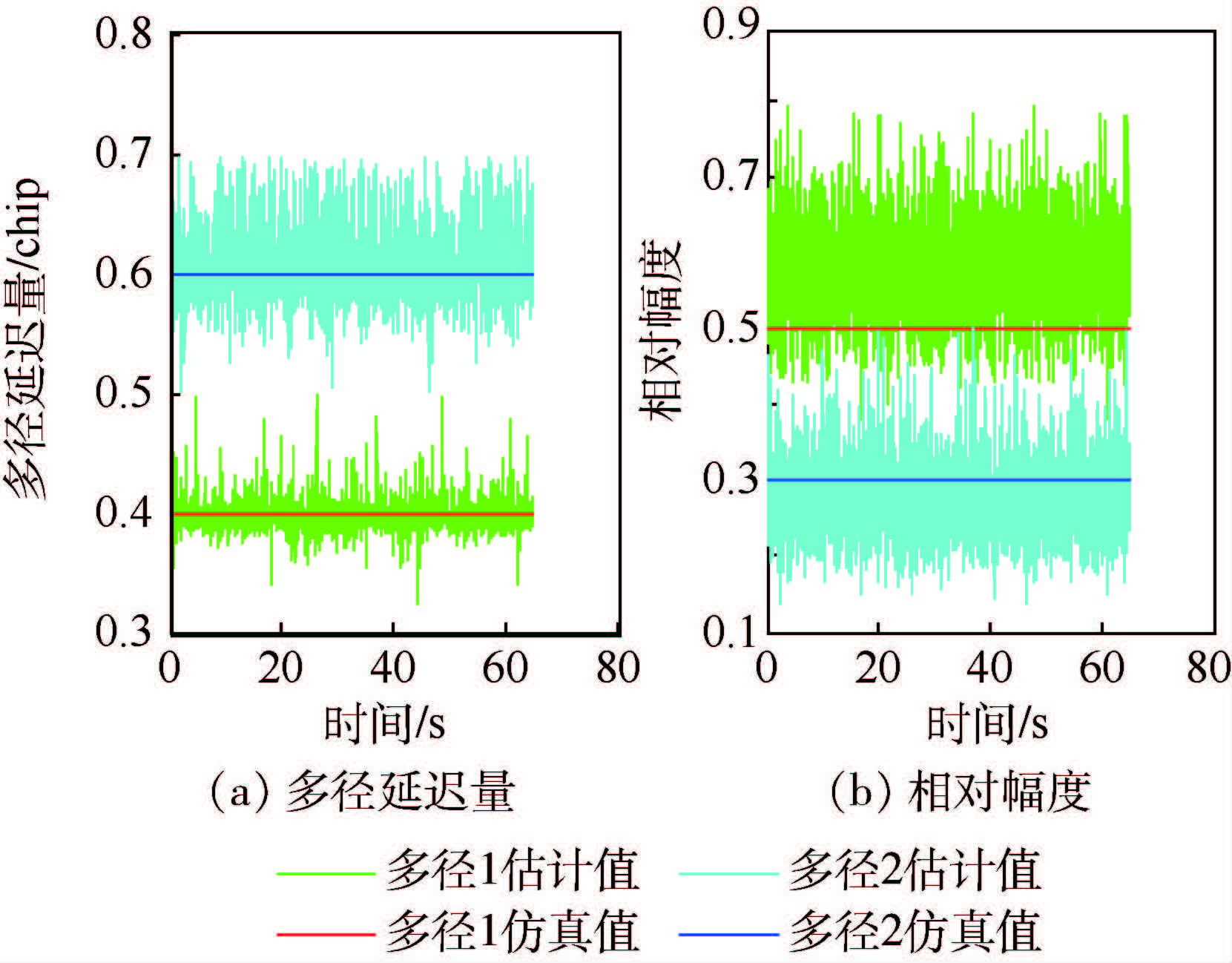
图 6为利用搜索步进d=0.01 chip的单级MEDLL得到的多径信号参数估计结果。可见,采用高分辨率的MEDLL,能够完成两条多径信号的参数估计。类似图 3的情况,参数估计值受噪声影响围绕仿真值波动,且相对幅度比多径延迟量的估计更易受噪声影响。
 |
| 图 6 MEDLL的多径参数估计结果(d=0.01 chip) Fig. 6 Multipath parameter estimation results using MEDLL(d=0.01 chip) |
| 图选项 |
表 5为对图 6中多径参数估计统计值。对比图 5可见,将观测间隔由0.2 chip缩小为0.01 chip之后,以计算量增大为原来20倍的代价,实现了两路多径信号的参数估计,且达到了0.01 chip的多径延迟分辨率。图 7给出了两级T-MEDLL对多径参数的估计结果,可见采用T-MEDLL同样能够完成对两路多径信号的参数估计。
表 5 参数估计统计值(d=0.01 chip) Table 5 Statistical values of parameter estimation(d=0.01 chip)
| 多径信号 | 多径延迟量/chip | 相对幅度 | ||
| 均值 | 标准差 | 均值 | 标准差 | |
| 多径1 | 0.397 2 | 0.011 7 | 0.577 7 | 0.060 5 |
| 多径2 | 0.603 3 | 0.026 9 | 0.277 2 | 0.048 1 |
表选项
 |
| 图 7 两级T-MEDLL的多径参数估计结果(d1=0.2 chip,d2=0.01 chip) Fig. 7 Multipath parameter estimation results using secondary T-MEDLL (d1=0.2 chip,d2=0.01 chip) |
| 图选项 |
表 6为对图 7中多径参数估计统计值。对比图 6,T-MEDLL在降低了一半复杂度的同时,能够保持基于盲搜索的传统MEDLL的参数估计性能。
表 6 参数估计统计值(d1=0.2,d2=0.01 chip) Table 6 Statistical values of parameter estimation (d1=0.2 chip,d2=0.01 chip)
| 多径信号 | 多径延迟量/chip | 相对幅度[ | ||
| 均值 | 标准差 | 均值 | 标准差 | |
| 多径 1 | 0.404 4 | 0.013 2 | 0.562 1 | 0.065 1 |
| 多径2 | 0.602 6 | 0.026 6 | 0.269 8 | 0.047 3 |
表选项
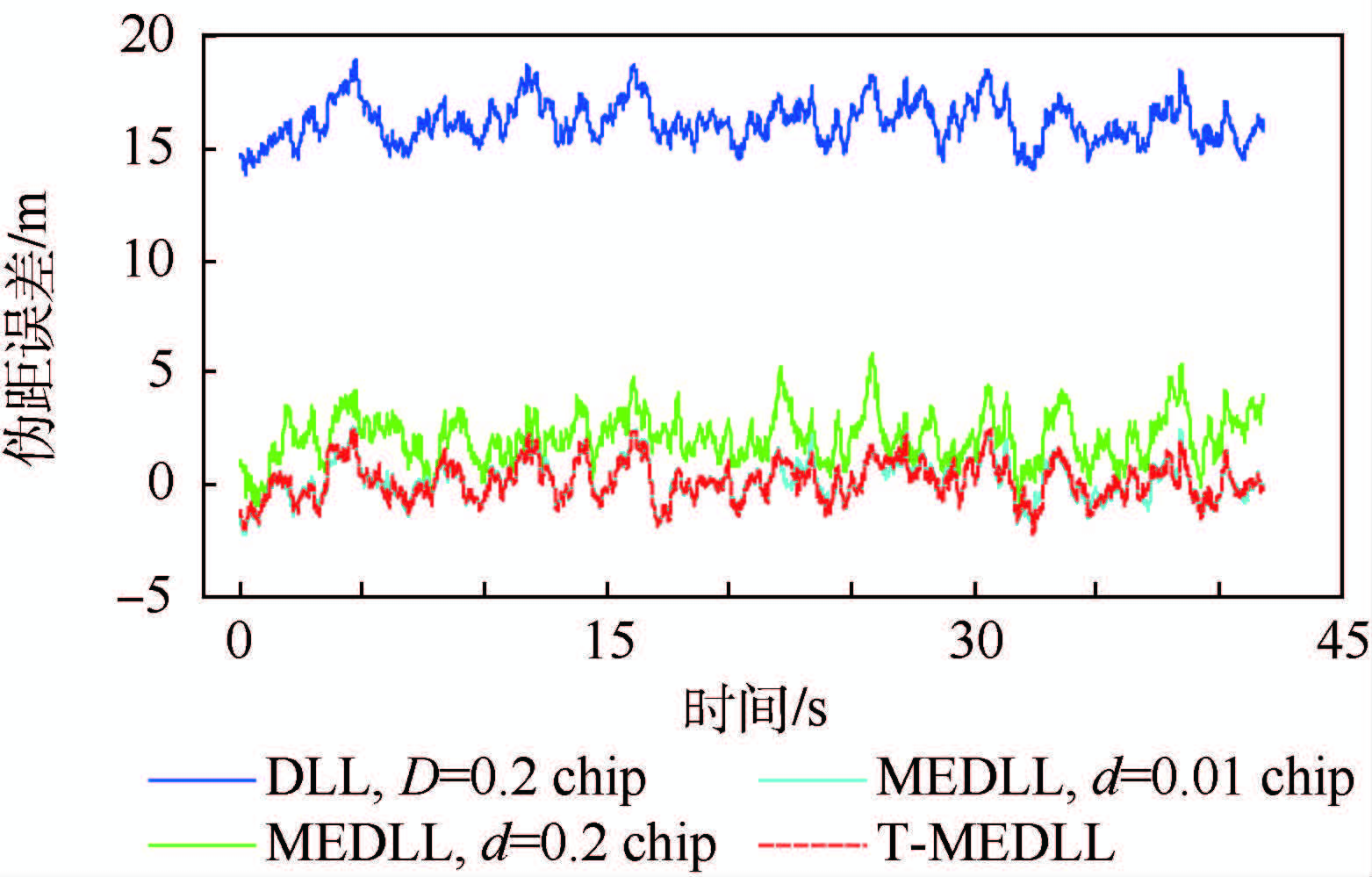
图 8为分别采用窄相关技术的DLL(D=0.2 chip)、MEDLL(d1=0.2 chip, d2=0.01 chip)和T-MEDLL时测得的伪距误差。可见参量式抗多径算法MEDLL和T-MEDLL的抗多径性能明显优于非参量式的窄相关技术;分辨率为0.01 chip的MEDLL(蓝线)与T-MEDLL(红线)伪距误差基本重合,对多径误差的修正效果优于分辨率为0.2 chip的MEDLL(绿线),大大优于窄相关DLL(紫线)。
 |
| 图 8 DLL、MEDLL和T-MEDLL的伪距误差 Fig. 8 Pseudo-range errors for DLL,MEDLL and T-MEDLL |
| 图选项 |
表 7为对图 8中伪距误差的统计结果。可见,采用两级搜索的T-MEDLL在参数估计精度和修正伪距测量误差的性能上,能够继承采用盲搜索的高分辨率MEDLL的优势。
表 7 伪距误差统计值 Table 7 Statistical values of pseudo-range error
| 算法 | 误差均值/m | 误差标准差/m |
| DLL,D=0.2 chip | 16.200 3 | 0.932 8 |
| MEDLL,d=0.2 chip | 2.092 2 | 1.093 7 |
| T-MEDLL | 0.133 4 | 0.869 5 |
表选项
4 结 论 在参量估计式基带抗多径算法中,需要折中考虑参数估计精度的提高和计算复杂度的降低。本文基于经典的MEDLL算法,提出了一种树状分级结构的最大似然估计抗多径算法T-MEDLL,其优势如下:
1) 算法计算复杂度较MEDLL显著降低。根据文中推导的计算复杂度表达式,若将分辨率从0.2 chip提高至0.01 chip,传统盲搜索法的计算量将增加20倍;而以估计一路多径信号为例,同等分辨率T-MEDLL算法的计算量仅为盲搜索的30%~50%。
2) 能够保持同等分辨率经典MEDLL的多径参数估计精度和修正伪距测量精度;上述结论通过了基于自研的软件GPS接收机和数字中频模拟器的测试验证。
参考文献
| [1] | VAN NEE D J R.The multipath estimating delay lock loop[C]//Proceedings of the IEEE 2nd International Symposium on Spread Spectrum Techniques and Applications.Piscataway,NJ:IEEE Press,1992:39-42. |
| Click to display the text | |
| [2] | VAN NEE D J R,SIEREVELD J.The multipath estimating delay lock loop-approaching theoretical accuracy limits[C]//Proceeding of IEEE Position Location and Navigation Symposium.Piscataway,NJ:IEEE Press,1994,4:246-251. |
| Click to display the text | |
| [3] | SAHMOUDI M, AMIN M G. Fast iterative maximum-likelihood algorithm (FIMLA) for multipath mitigation in the next generation of GNSS receivers[J]. IEEE Transactions on Wireless Communications,2008, 7(11): 4362–4374. |
| Click to display the text | |
| [4] | KAISER J F.On Teager's energy algorithm and its generalization to continuous signals[C]//Proceedings of the 4th IEEE Digital Signal Processing Workshop.Piscataway,NJ:IEEE Press,1990:30-35. |
| Click to display the text | |
| [5] | HU Y, SONG M Z, MENG B, et al. An efficient method for GPS multipath mitigation using the Teager-Kaiser-operator-based MEDLL[J]. Radio Engineering,2013, 22(4): 1202–1210. |
| Click to display the text | |
| [6] | WEILL L R.Multipath mitigation using modernized GPS signals:How good can it get?[C]//Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation.Fairfax,VA:ION,2001:493-505. |
| Click to display the text | |
| [7] | FLEURY B H, TSCHUDIN M, HEDDERGOTT R, et al. Channel parameter estimation in mobile radio environments using the SAGE algorithm[J]. IEEE Journal on Selected Areas in Communications,1999, 17(3): 434–450. |
| Click to display the text | |
| [8] | BHUIYAN M Z H, LOHAN E S, RENFORS M. Code tracking algorithms for mitigating multipath effects in fading channels for satellite-based positioning[J]. EURASIP Journal on Advances in Signal Processing,2008, 2008(1): 17. |
| Click to display the text | |
| [9] | DOVIS F,PINI M,MULASSANO P.Turbo dll:An innovative architecture for multipath mitigation in GNSS receivers[C]//Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation.Fairfax,VA:ION,2001:1-7. |
| Click to display the text | |
| [10] | CHEN X, DOVIS F, PINI M, et al. Turbo architecture for multipath mitigation in global navigation satellite system receivers[J]. IET Radar,Sonar & Navigation,2011, 5(5): 517–527. |
| Click to display the text | |
| [11] | CHEN X,DOVIS F,PINI M.An innovative multipath mitigation method using coupled amplitude delay lock loops in GNSS receivers[C]//Position Location and Navigation Symposium (PLANS).Piscataway,NJ:IEEE Press,2010:1118-1126. |
| Click to display the text | |
| [12] | VAN NEE D J R.Method of estimating a line of sight signal propagation time using a reduced-multipath correlation function:US,5615232[P].1997-03-25. |
| Click to display the text | |
| [13] | DELGADO N,NUNES F.Theoretical performance of the medll algorithm for the new navigation signals[C]//Proceedings of the 7th Conference on Telecommunications (ConfTele 09).Piscataway,NJ:IEEE Press,2009,1:1-4. |
| Click to display the text | |
| [14] | 刘亚欢, 田宇, 李国通. 基于最大似然估计的GPS多径估计[J]. 宇航学报,2009, 30(4): 1466–1471.LIU Y H, TIAN Y, LI G T. GPS multipath estimation based on maximum likelihood estimation[J]. Journal of Astronautics,2009, 30(4): 1466–1471.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [15] | RAY J K.Mitigation of GPS code and carrier phase multi-path effects using a multi-antenna system[D].Calgary:University of Calgary,2000:27-35. |
| Click to display the text | |
| [16] | 谢钢. GPS原理与接收机设计[M].2版北京: 电子工业出版社, 2009: 317-319.XIE G. Principles of GPS and receiver design[M].2nd edBeijing: Publishing House of Electronics Industry, 2009: 317-319.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [17] | KAPADIA S.Cramèr-Rao lower bound and maximum likelihood estimation for multipath propagation of GPS signals[D].Cincinnati:University of Cincinnati,2013:32-35. |
| Click to display the text | |
