区别于传统数据驱动方法建立系统退化过程的全局模型,基于相似性的寿命预测方法,利用参考样本建立基于个体的退化模型,然后用每个退化模型的局部估计加权平均给出最终的预测结果,这种方法更符合复杂系统多退化模式的特点[7-8]。
相似性方法的基本假设是:如果服役样本与参考样本具有相似的退化性能,它们就会有相似的RUL[7]。其中服役样本是正在运行且尚未失效的样本,参考样本是与服役样本相同型号,运行在相同工况下且已经失效的历史样本。
工况是指设备运行所处的环境或操作条件等。在实际设备的初始到失效的运行过程中,设备不可能完全处于相同工况条件,例如飞机处于起飞、爬升、巡航、降落等不同阶段或不同的外界环境时,对系统部件的退化有显著不同的影响[8]。因此忽略工况影响的传统相似性寿命评估不能满足实际系统运行的评估需求,同时真实实验中获得大量相同工况下的参考样本成本巨大。那么相似性预测方法是否能利用变工况模式下的参考样本进行预测、将工况因素加入到剩余寿命预测中是否能提升预测的准确度,这是本文主要研究的2个问题。已有的基于相似性方法虽在相似性基础架构[7, 9]、相似性度量方法[10]、预测效果检验[11]等方面进行了深入研究,但目前尚未将变工况问题纳入其中。本文对基本相似性方法进行了如下改进:①建立区分工况的退化模型,以描述不同工况对退化的差异化影响;②在预测中,依据服役样本实时的工况,运用参考样本对应的工况模型进行工况的匹配预测,从而模拟变工况对退化的差异化影响,完成更符合实际工程的预测。
为检验算法性能,本文采用2008 PHM Data Challenge 国际竞赛提供的一套商用涡轮发动机数据[12]验证,竞赛中采用基于相似性的剩余寿命预测方法的评估结果获得了冠军。本文在相同数据集上测试算法性能并与冠军方法[13]进行比较。同时在原有方法基础上进行传感器特征集的优化。多组实验结果表明加入工况影响的预测方法具有更好的预测性能。
1 算法框架 文献[7]中详细介绍了相似性方法的基本思想,也被引用在文献[9-11, 13]中。已知相似性方法应用步骤为:首先进行特征提取,在每个参考单元上建立一个对应的平均退化模型,将多种工况影响平均在退化模型中,在预测中同样平均各工况对服役样本的影响,然后运用定义的相似性测度函数S(·)和时间测度τ完成与参考模型的相似性计算获得评估结果。其中相似性测度函数S(·)用于度量服役样本与参考样本的相似性,而时间测度τ用于定义服役样本的待测范围。平均的处理方案无法准确反映变工况的差异影响,因此本文方法在基础方法的各环节进行更符合变工况问题的改进:①在特征提取阶段,进行工况特征的提取;②在建模阶段对各参考样本建立分工况的退化模型;③在剩余寿命预测阶段对服役样本进行工况的识别,完成相应工况模型的相似性匹配预测。
设参考样本包含N个全寿命单元,每个单元包含M路监测信号。变工况条件下的基于相似性的RUL预测算法框架如图 1所示。图中I为初始状态个数,P为提取的特征个数,F为失效状态个数,HI为健康指数。记参考样本的总工况类型集合为OC,包含的工况总数记为nOC,服役样本工况为OC*,工况总数记为nOC*。本方法可以使用的前提为OC*?OC,即要求参考集包含足够多先验信息用于进行服役单元的预测。通过3个阶段融入工况的影响,算法可以实现对变工况条件下参考样本的建模训练,完成对不同工况运行规律的服役样本的基于相似性方法的RUL预测。
 |
| 图 1 变工况下基于相似性的RUL预测方法框架 Fig. 1 Framework of similarity-based RUL estimation method under varying operational conditions |
| 图选项 |
2 算法原理 2.1 特征提取 获得参考样本原始信号后,首先进行信号的预处理去除噪声和野值影响,然后进行工况信息的分类提取。若运行中各采样点的操作条件已知,样本的工况集合直接可得;若操作信息未知,需根据多路信号数据进行聚类,评估可能的工况类型。在实际应用中,面对可能出现的未知工况,通过计算新工况和已知工况的特征相似性关系,可以近似评估出其对退化的影响,建立对应模型用于预测;同时通过不断在线更新各工况退化模型,建立更丰富的先验知识库,随着学习样本的丰富,算法性能可以持续得到改进。完成工况集的建立,多路传感器信号可依据工况进行分类,这样原始包含N个单元各采样时间的信号的二维数据(N×M)就增加了一维工况信息(N×M×nOC)。
完成工况特征的提取后,需要在各工况下进行与退化相关的特征信号提取。本文在时域上运用观察法选择特征传感器,在实际应用中需根据信号特性选择适合方法。设完成提取后各工况下都会获得P个特征可以建立参考特征空间(N×P×nOC),服役样本的特征提取依据参考样本的提取规则完成获得对应的P个特征。
最后模型的建立需要对退化的初始状态和失效状态进行描述。依据各参考样本的失效位置建立包含P个特征和OC中各工况的F个失效状态的样本失效空间(F×P×nOC),同理提取参考样本的初始位置获得包含I个初始状态的样本初始空间(I×P×nOC)。
2.2 退化模型建立 完成特征提取工作后,需要建立特征空间到设备退化状态的映射关系,去定量地描述系统的健康状态,即建立系统的健康指标。通用的健康指标一般要求HI(t)∈[0,1],0表示系统完全失效,1表示系统的初始健康状态[14]。样本失效空间中的值对应HI目标定义为0,样本初始空间对应的HI目标值定义为1。然后通过回归就能获得系统各时刻健康状态。为最大程度保留样本原有的退化信息,本文采用线性回归方法用多维传感器信号建立一维HI指标如式(1)所示:
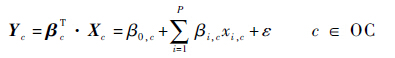 | (1) |
式中:Yc为健康指标序列;βc=(β0,c,β1,c,β2,c,…,βP,c)为P+1维的回归参数;Xc=[e x1,c x2,c … xP,c]为c工况下P+1维的特征矩阵,e[WTBZ]为单位向量,xp,c为c工况下第p个特征向量;ε为噪声项。服役样本各已知采样点在对应工况下的HI建立可依据参考样本的βc完成。这样就可在各工况下建立参考样本的HI序列(N×nOC)。
下一步就是基于HI序列进行退化过程的建模。传统相似性方法运用所有样本数据得到平均多种工况的退化模型,但这样无法充分考虑不同工况作用在退化过程中的差异化影响,如图 2所示。其中多工况平均的退化曲线与工况1、工况5、工况6下的十分接近,工况2~4下的退化特征无法充分反映在多工况平均的退化曲线中。因此本文对于每个参考样本k建立各工况c的退化模型Mk,c:
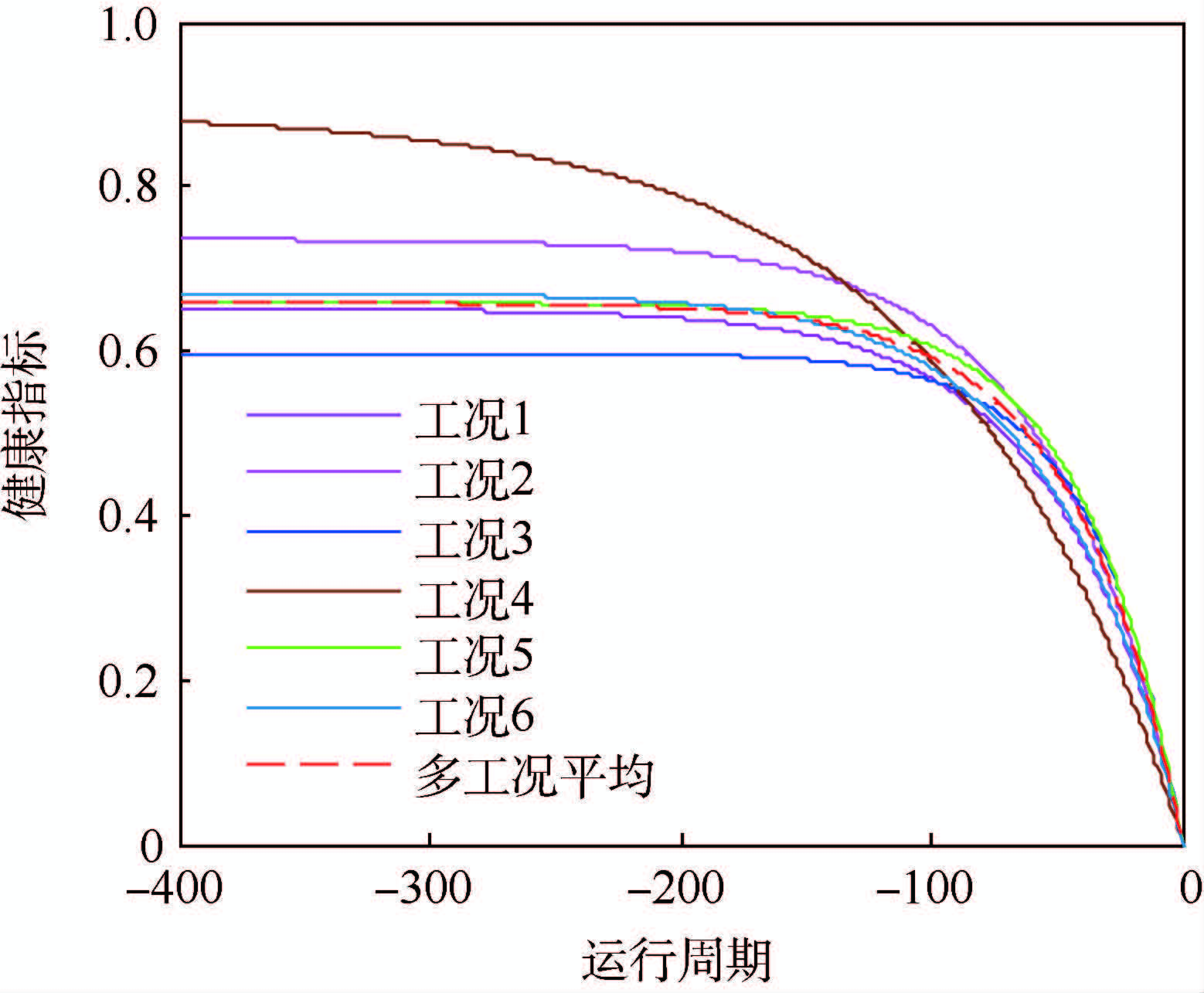 |
| 图 2 单工况和多工况条件下的设备退化曲线 Fig. 2 Device degradation curves under single operational condition and mutilple operational conditions |
| 图选项 |
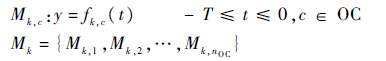 | (2) |
式中:y为模型输出;fk,c(t)为对应t时的模型方程;T为模型的时间限制;Mk模型集中包含样本k各工况下的退化模型。使用样本k的模型进行预测时根据服役样本对应的工况选择对应的模型Mk,c。考虑到参考样本在初始阶段包含差异的初始误差,例如现实中元件开始使用时的加工精度和初始制造参数存在分散性,所以利用负向时间轴建立退化模型,t=0表示失效,t<0表示未失效,这种方法可以将不同参考样本的初始差异加入建模的考量中,建立绝对失效、相对初始的模型。
2.3 RUL预测 获得参考样本的退化模型集后,就可用服役样本的健康指标与参考模型集合进行相似性度量以评估模型与服役样本的相似性。对于相似性的度量需要定义相似性测度函数S(·)去量化服役样本与参考模型的相似程度。本文采用最通用的欧式距离函数进行相似性测量。加入工况影响后,相似性度量过程需要在匹配中实时进行工况判断以实现变工况下的寿命预测。对于已获得的整段服役样本数据,首先提取服役样本HI中各工况的原时间位置向量Tc和对应的HI值Yc,对于当前待测参考样本k的模型Mk={Mk,1,Mk,2,…,Mk,n}采用整段滑动度量的方法,完成工况匹配的相似性度量,如图 3所示。其中每条曲线对应一种特定工况下的退化模型,服役样本的HI依据工况表示为不同颜色的点,基于时间位置转换的方法可以并行完成匹配工况的相似性度量,如式(3)和式(4)所示,相较逐点匹配,这种匹配测量可以大幅提升运算效率。
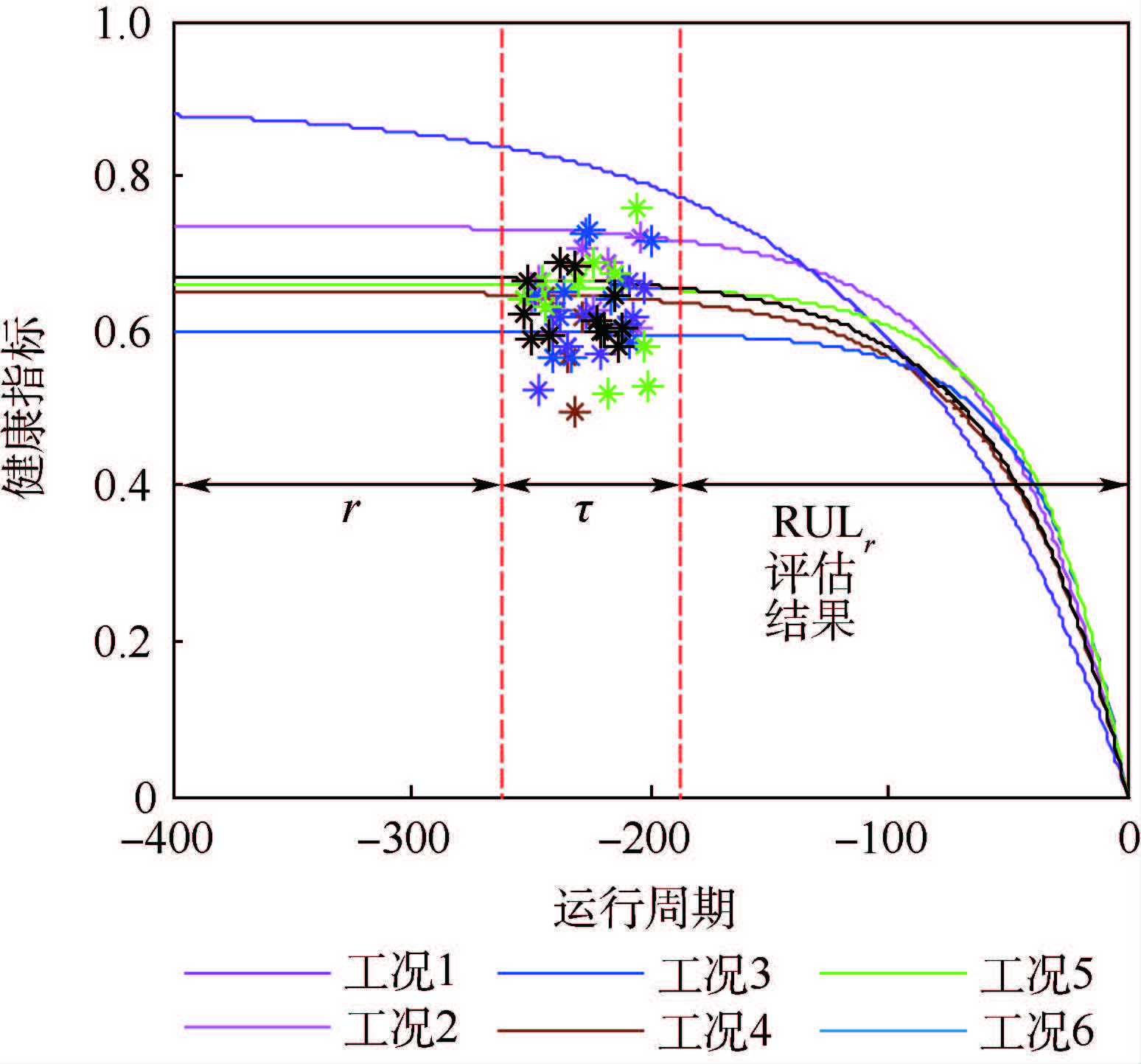 |
| 图 3 变工况下RUL预测方法滑动评估过程 Fig. 3 Moving estimation process of RUL under varying operational conditions |
| 图选项 |
方法的时间测度为服役样本总时长τ,滑动时间位置转换方法为
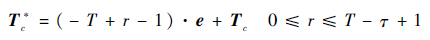 | (3) |
式中:T*c为转换后的新时间位置向量;r为服役样本在参考模型上的滑动窗距离。这样就可以获得相应r下的相似性测量结果。在向量计算中欧式距离等价于向量二范数,因此相似度函数可表示为
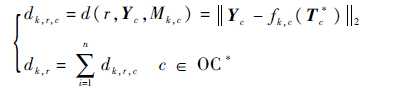 | (4) |
这样就完成了对第k个参考样本与服役样本在滑动窗位置为r时的相似性度量,结果为dk,r,数值越小说明相似性越好,进而在参考样本k上最好的相似性结果为
 | (5) |
最终在参考样本k上的最佳预测结果为
 | (6) |
获得各参考模型的最佳剩余寿命预测估计值后,需要根据相似度Dk进行排序,提取相似性高的部分结果作为评估候选集,用于最终的加权平均。基于相似性方法基本假设,模型的相似性越高,相应模型的剩余寿命预测值与真实值越接近,因此候选集的建立不仅可以过滤不一致模型的预测值,也能够避免仅选取相似性最好的预测值可能存在的过拟合问题。基于训练样本,采用交叉检验方法在全集中搜索最优的候选集边界。完成筛选后就可对候选集中的结果进行加权平均完成样本的RUL预测,如式(7)所示:
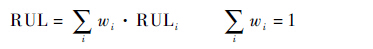 | (7) |
3 算例分析 运用2008 PHM Data Challenge国际竞赛提供的数据验证本文数据驱动方法的有效性,并与竞赛冠军方法[13]进行对比。同时对文献[13]提出的传感器特征集进行优化。
3.1 2008 PHM Data Challenge数据介绍 数据驱动方法不依赖特定对象,无需机理模型,适用于尤以航空航天领域为代表的大型系统。但大量初始到失效的训练数据是方法使用的前提。而对于大型系统,获取足够训练数据成本较大。为解决这一矛盾,2008 PHM Data Challenge提出了解决方案。竞赛主办方提供一套基于效率与流量方程建立的商用涡轮发动机的热力学仿真模型数据[14],仿真数据较准确地呈现了发动机多种故障模式下的退化规律,该数据源在预测问题研究中得到了广泛的应用[15-17],具有很好的方法检验价值。数据集由多维时间序列组成,包含218组参考样本数据和218组待测服役样本数据。数据结构包括样本编号,运行周期,三路操作设置信息和21路传感器信息。3路操作参数作用于对象,可以划分为6种工况,如图 4所示。传感器测量值也自动地依据工况进行了划分,如图 5(a)所示。为清晰观测退化规律,可在单一工况下观测信号走势,如图 5(b)所示。比赛要求应用这些已知信息完成对待测服役样本的剩余寿命预测。
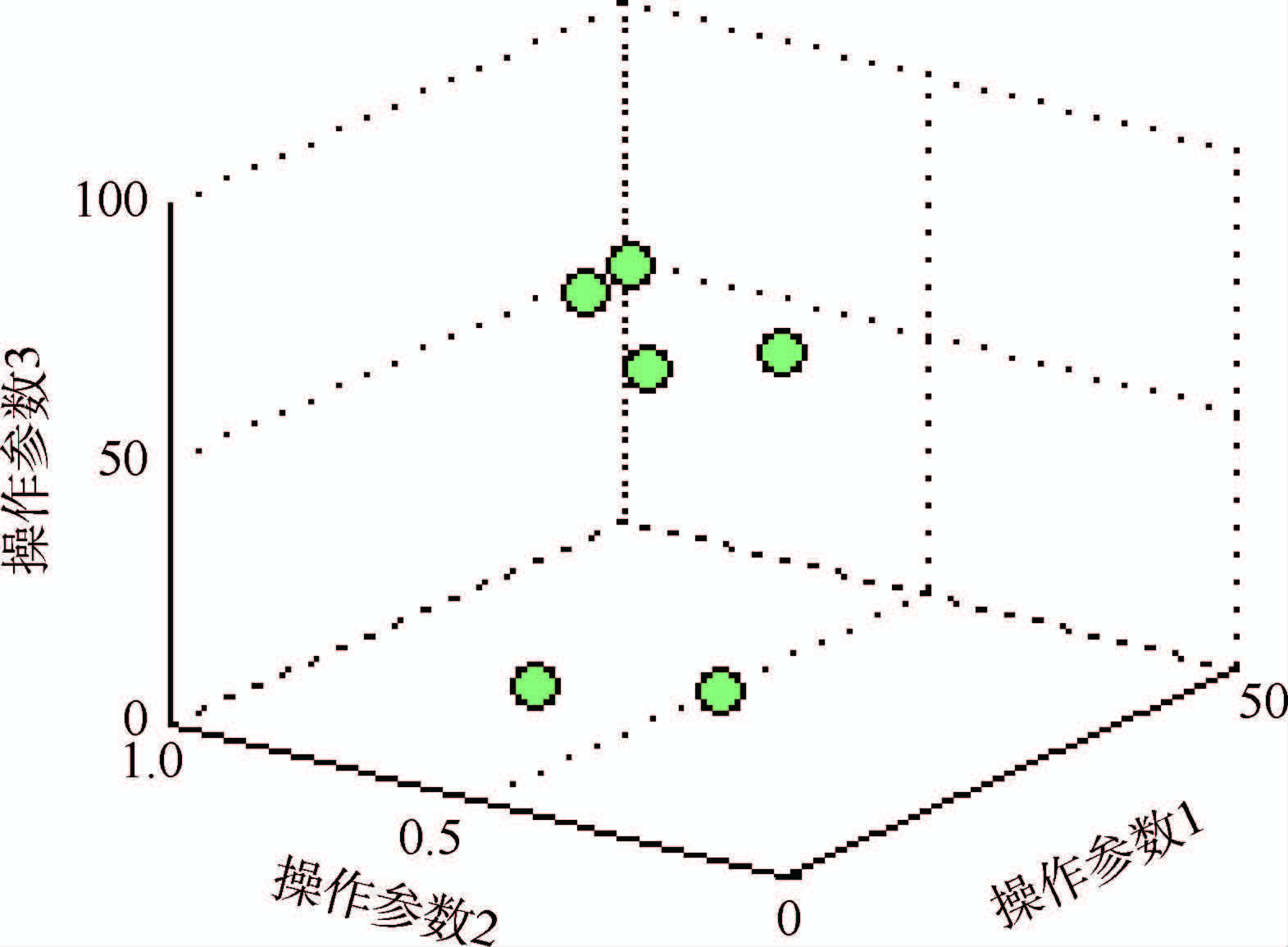 |
| 图 4 6种不同工况的划分 Fig. 4 Six different operational conditions partition |
| 图选项 |
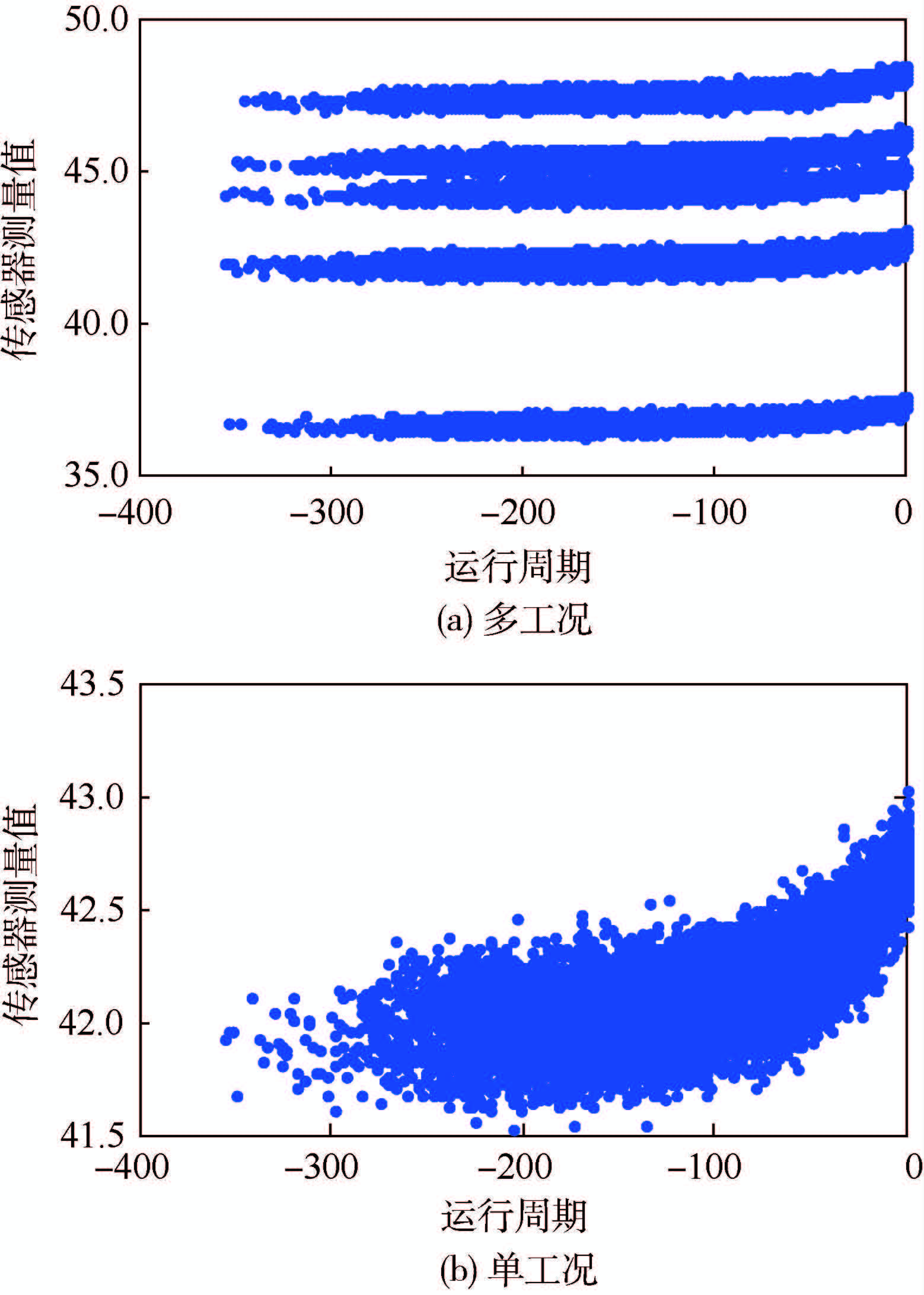 |
| 图 5 218个训练单元的第11号传感器测量数据 Fig. 5 Sensor measurements of sensor 11 for 218 training units |
| 图选项 |
比赛的评分方式对于预测值超出实际寿命的滞后型预测给出更大的惩罚分数。这种评分方法能够选出具备更好超前预测能力的方法,但对预测的准确度的评价不够准确,因此本文增加均方误差(MSE)的评价方法综合完成对预测性能的考量。评分方法和均方误差方法如式(8)所示:
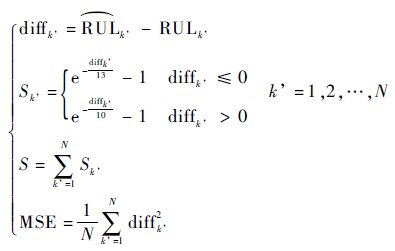 | (8) |
式中:k’为待测服役单元编号;
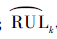
3.2 模型训练过程 训练阶段需要在参考样本上完成特征提取和模型建立。本数据集的数据是在相同采样时间下获取的时域传感器信号,采用观察法完成特征选择。提取单工况传感器测量值,可观察到不同传感器测量值随时间的变化规律:整体呈上升和下降趋势的传感器可明显反映出设备的退化过程;表现为常值或发散趋势的传感器信号无法给出准确表征。因此选择对退化敏感的传感器信号建立健康指标。观察发现传感器的特性在不同工况下具有相似规律,所以在各工况下采用相同传感器组合。传感器的基本集为2,3,4,7,11,12,15,21。文献[11]中使用的传感器组合为2,3,4,7,11,12,15,其中也提及传感器组合的选择应该被进一步优化,因为优化的传感器组合有助于预测性能的提高。因此本文运用训练数据进行交叉检验在传感器的基本集中进行遍历搜索寻找预测性能最好的传感器组合。
获得了提取特征的训练样本,需要在其中选出样本初始状态集合Ω0和样本失效状态集合ΩF以对应健康状态的1和0。如2.2节所述,采用负向的时间轴可以将样本起始状态差异纳入退化的影响因素中,更符合工程实际。数据中的时间不是具体时刻而是运行周期数,各参考样本的寿命即为经历的运行周期总数。依据参考样本全集的寿命分布统计,建立Ω0和ΩF如式(9)所示:
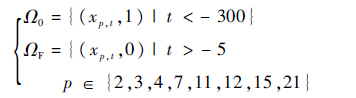 | (9) |
式中:t为坐标转换后运行周期在时间轴上的对应位置;p为选择的传感器编号;xp,t为当前运行周期t、传感器p的信号值。
在参考样本全集上找出Ω0和ΩF后,按6种工况将集合划分为Ω0={Ω0,1,Ω0,2,…,Ω0,6}和ΩF={ΩF,1,ΩF,2,…,ΩF,6}。基于各工况的初始集合和失效集合就可通过式(1)求得建立HI需要的6种工况下的参数集β={β1,β2,…,β6}。这样就可以建立每个参考样本各工况下的HI指标去定量地描述该样本的退化过程。基于对HI的分析和经验方法研究,选择指数回归模型建立样本的退化模型。文献[11]运用各参考样本不区分工况的全部HI值建立每个参考样本退化模型,本文选择依据不同工况的HI分工况建立退化模型,将原有模型在工况维度上进行了扩充,将工况影响加入预测评估中来,指数模型如式(10)所示:
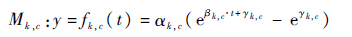 | (10) |
式中:(αk,c,βk,c,γk,c)为参考样本k在工况c上的模型参数可通过与已获得的样本目标HI的非线性回归方法计算求得。这样就可以在每个参考模型上获得其中各工况的样本模型集。
3.3 剩余寿命预测过程 这一阶段需要完成待测服役样本与参考样本模型的相似性匹配以实现对设备剩余寿命的预测。首先依据训练样本的健康指标回归参数β求得服役样本的HI序列。然后在每个参考样本模型Mk上进行服役样本HI序列匹配工况的滑动寻优,以二范数作为相似性测度函数,找出本模型相似性Dk最小的位置对应求得该模型上的最优预测结果RULk。在各参考模型上重复操作最终可建立全部参考模型的评估结果集。在评估结果全集中筛选建立候选集用于最终的加权平均结果,有利于提高预测性能。图 6展示了候选集在预测中的作用,候选集的选取参数设计流程为:首先在评估结果全集中选中最高的相似度min Dk,然后候选集的选择边界为Dk≤(1/θ)·min Dk,θ为候选集参数范围为(0,1),0表示选入全部结果,1表示仅选择相似性最高结果。性能最好的评估出现在θ=0.9时,其取值既覆盖了相似性好的评估结果又避免了仅取最好结果存在的过拟合问题,因此性能最佳。候选集参数实验是在训练集上运用交叉检验完成,获得最优θ后将其应用于待测服役单元的预测中。
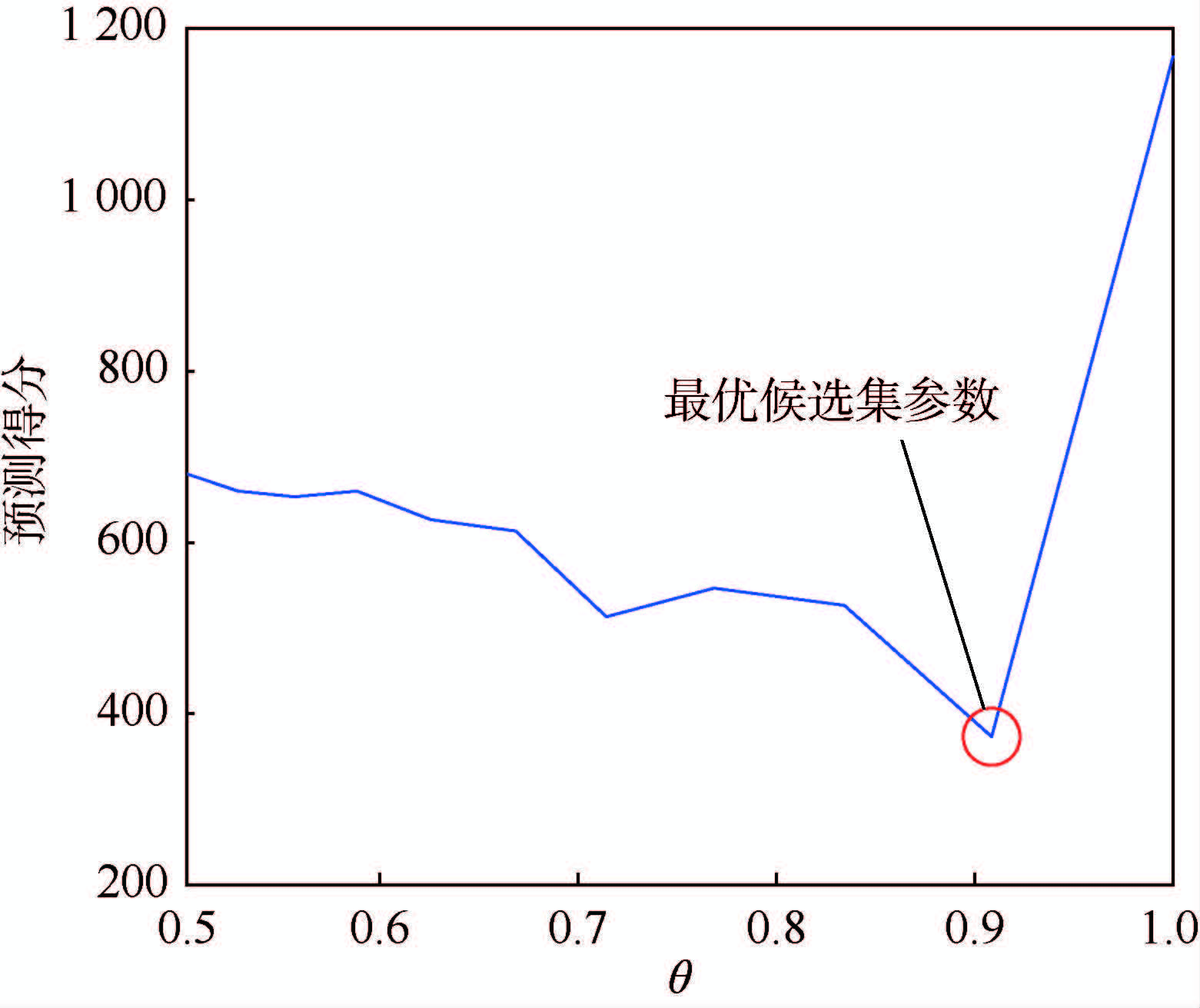 |
| 图 6 候选集参数θ对RUL预测性能的影响 Fig. 6 Influence of parameter θ on RUL estimation performance from candidate set |
| 图选项 |
去除异常值获得候选集后,最终RUL评估采用加权平均的方式,为获取更多的超前预测,结合评分方法,采用式(11)的加权方式获得服役单元预测结果PRUL。这一加权方式在文献[11, 15]中都有应用。
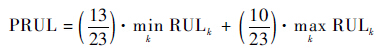 | (11) |
3.4 结果评估与讨论 本节给出传统相似性方法和本文提出的区分工况的相似性方法数值实验的结果。为了体现本方法的工况效果,在特征传感器选取、模型选择、相似性测度函数和加权平均方法等控制变量,均保持与传统相似性方法相同。同时为优化传感器组合,采用交叉检验方法在训练样本上进行传感器子集遍历搜索寻优,最终获得不同数量下的最优传感器组合。采用全部测试样本进行2种方法的预测测试,最终的评估结果对比如表 1所示。其中包含了不同数量下的最优传感器组合的score评估指标和MSE值,数值越低说明预测效果越好。组合也包括文献[13]提出的原始组合,这一组合也被使用在数据研究文献[15, 17]中但一直未得到优化。
表 1 在多种传感器组合上的结果对比 Table 1 Comparison on different sensor set results
| 数量 | 最优传感器组合 | score 对比 | MSE对比 | ||
| 原方法 | 本方法 | 原方法 | 本方法 | ||
| 2 | 4,15 | 1 636 | 1 576(↓4%) | 334 | 314(↓6%) |
| 3 | 2,3,4 | 2 729 | 1 515(↓44%) | 396 | 311(↓21%) |
| 4 | 2,3,4,11 | 1 545 | 1 173(↓24%) | 305 | 280(↓8%) |
| 5 | 2,3,4,11,15 | 1 043 | 1 059(↑1%) | 258 | 241(↓7%) |
| 6 | 2,3,4,11,15,21 | 988 | 889(↓10%) | 253 | 229(↓9%) |
| 7 | 2,3,4,11,12,15,21 | 1 012 | 856(↓15%) | 259 | 226(↓13%) |
| 全集 | 2,3,4,7,11,12,15,21 | 1 032 | 1 007(↓3%) | 263 | 241(↓8%) |
| 原组合 | 2,3,4,7,11,12,15 | 1 049 | 1 011(↓4%) | 276 | 250(↓9%) |
表选项
对比2种方法在多种传感器组合上的预测结果可以说明,加入工况影响的预测方法能够有效提升预测的准确度,score指标平均降低13%,MSE指标平均降低10%。其中5个传感器组合时,虽在score指标上2种方法性能相当 ,但从MSE指标上可以说明加入工况影响的预测方法能够实现更准确的预测。另一方面传感器组合的选取对预测性能提升也有显著影响,因此在预测问题中也应引起重视。
4 结 论 1) 提出了一种变工况条件下的基于相似性的剩余寿命预测方法,可以将工况信息纳入到退化建模中以提高模型精度。
2) 算法可实现较优的剩余使用寿命预测,例如算例中,不同传感器组合下,本方法score指标平均降低13%,MSE指标平均降低10%。
3) 本方法对处于不同工况变化规律的服役样本能够实现满足其工况特性的差异化的预测,使预测更接近工程实践。
4) 在算例分析中,验证了相似性方法中预测评估候选集的选择和传感器组合的优化对预测性能的显著影响,这对方法进一步的深入研究提供了指导。
为使本文提出的方法能够解决更多场景的寿命预测问题,仍需要进行更多数据集在本方法上的验证,并进一步进行方法的优化完善。
参考文献
| [1] | DOYEN L, GAUDOIN O. Modeling and assessment of aging and efficiency of corrective and planned preventive maintenance[J]. IEEE Transactions on Reliability,2011, 60(4): 759–769. |
| Click to display the text | |
| [2] | HENG A, ZHANG S, TAN A C, et al. Rotating machinery prognostics: State of the art,challenge and opportunities[J]. Mechanical Systems and Signal Processing,2009, 23(3): 724–739. |
| Click to display the text | |
| [3] | TANG D, MAKIS V, JAFARI L, et al. Optimal maintenance policy and residual life estimation for a slowly degrading system subject to condition monitoring[J]. Reliability Engineering & System Safety,2015, 134: 198–207. |
| Click to display the text | |
| [4] | VACHTSEVANOS G, LEWIS F, ROEMER M, et al. Intelligent fault diagnosis and prognosis for engineering systems[M].New Jersey: Wiley, 2006: 289-300. |
| Click to display the text | |
| [5] | LIAO L X, FELIX K. Review of hybrid prognostics approaches for remaining useful life prediction of engineered systems,and an application to battery life prediction[J]. IEEE Transactions on Reliability,2014, 63(1): 191–207. |
| Click to display the text | |
| [6] | SI X S, WANG W, HU C H, et al. Remaining useful life estimation:A review on the statistical data driven approaches[J]. European Journal of Operational Research,2011, 213(1): 1–14. |
| Click to display the text | |
| [7] | WANG T Y.Trajectory similarity based prediction for remaining useful life estimation[D].Cincinnati:University of Cincinnati,2010:39-56. |
| Click to display the text | |
| [8] | BIAN L, GEBRAEEL N, KHAROUFEH J P. Degradation modeling for real-time estimation of residual lifetimes in dynamic environments[J]. ⅡE Transactions,2015, 47(5): 471–486. |
| Click to display the text | |
| [9] | YOU M, MENG G. A Framework of similarity-based residual life prediction approaches using degradation histories with failure,preventive maintenance and suspension events[J]. IEEE Transactions on Reliability,2013, 62(1): 127–135. |
| Click to display the text | |
| [10] | ZHANG Q, TSE P, WAN X, et al. Remaining useful life estimation for mechanical systems based on similarity of phase space trajectory[J]. Expert Systems with Applications,2015, 42(5): 2353–2360. |
| Click to display the text | |
| [11] | YOU M, MENG G. Toward effective utilization of similarity based residual life prediction methods:Weight allocation,prediction robustness,and prediction uncertainty[J]. Journal of Process Mechanical Engineering,2013, 227(1): 74–84. |
| Click to display the text | |
| [12] | SAXENA A,GOEBEL K.Turbofan engine degradation simulation dataset[EB/OL].Washington,D.CNASA Ames Research Center,2008(2013-09-12).http://ti.arc.nasa.gov/project/prong-ostic-data-repository. |
| Click to display the text | |
| [13] | WANG T Y,YU J B,SIEGEL D,et al.A similarity-based prognostics approach for remaining useful life estimation of engineered systems[C]//2008 International Conference on Prognostics and Health Management(PHM 2008). Piscataway,NJ:IEEE Press,2008:1-6. |
| Click to display the text | |
| [14] | 高占宝, 李行善, 梁旭, 等. 工程系统健康描述及基于GFRF方法的健康监测[J]. 北京航空航天大学学报,2006, 32(9): 1026–1030.GAO Z B, LI X S, LIANG X, et al. Engineering system health formulation and health monitoring based on GFRF approach[J]. Journal of Beijing University of Aeronautics and Astronautics,2006, 32(9): 1026–1030.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [15] | LE S K, FOULADIRAD M, BARROS A, et al. Remaining useful life estimation based on stochastic deterioration models:A comparative study[J]. Reliability Engineering & System Safety,2013, 112(4): 165–175. |
| Click to display the text | |
| [16] | XU J, WANG Y, XU L. PHM-oriented integrated fusion prognostics for aircraft engines based on sensor data[J]. IEEE Sensor Journal,2014, 14(4): 1124–1132. |
| Click to display the text | |
| [17] | HU C, YOU B, WANG P, et al. Ensemble of data-driven prognostic algorithms for robust prediction of remaining useful life[J]. Reliability Engineering & System Safety,2012, 103(3): 120–135. |
| Click to display the text | |
