作为系统测试与诊断技术中的关键问题,诊断策略优化问题已被证明是一个典型的NP-Complete问题[3]。Pattipati[3]和Simpson[4]等指出诊断策略优化问题是时间与费用的优化问题。诊断策略实际要解决的是序列决策问题:如何确定一组测试序列,以尽可能少的期望时间与费用完成故障隔离,并满足精度要求。
国内外****研究诊断策略优化问题主要采用以下算法:基于信息启发的贪婪搜索算法[5, 6, 7]和基于Rollout策略的一步向前回朔算法[8],这2种方法简单、快速且计算量小,但只比较了一二步内的费效比,最优性较差[9];基于最少测试费用启发式的与或图搜索(And-Or graph search,AO*)算法[2]能得到最优性较好的诊断策略,但其计算量大和存储量大,难以用于现场指导复杂系统的故障隔离过程[10];邱静等[11]提出采用双启发函数的准深度搜索方法,计算量远少于AO*算法,最优性相近,具有很高的实用价值。但上述方法都未考虑实际检测中存在的测试不确定性因素的影响,且在军事装备战时保障等复杂、多干扰的情形下,要求在极限情况下快速可靠地检测出故障,所需诊断策略也应是全局最优、长周期内平稳的。
本文在分析测试系统故障检测、隔离过程的基础上,提出了一种基于马尔可夫决策过程(Markov Decision Processes,MDP)的诊断策略构建方法:首先,基于MDP理论模型,结合故障诊断原理构建了MDP故障诊断策略模型;兼顾测试费用及信息量效用准则,线性加权求得综合效用准则函数。然后,采用无限折扣效用准则模型,确保长周期内平稳寻优。最后,利用策略迭代算法快速求得最优策略。MDP当前时刻的决策只依赖于当前的状态与行动,与过去的历史无关[12];这一特点使得该方法构建的诊断策略为长周期内平稳最优的,是独立于时间顺序的[13]。工程实例也表明,该方法科学简单,最优性满足工程实际,能够指导测试系统构建出长周期最优诊断策略,尤其适用于测试资源缺失或需要人为选择测试内容等战地复杂情形。
1 MDP理论模型MDP的核心要素包括:状态、行动、转移概率及报酬。考虑到实际工程应用中,故障诊断的决策时刻总是离散的,故本文所讨论的MDP都是离散时间的,即离散时间MDP(Discrete Time Markov Decision Processes,DTMDP)。
MDP模型可由以下五元组确定:
式中:i,j为状态；S为状态空间；A(i)为状态i处的可用行动集合；pij(a)为行动a后的状态转移概率；r(i,a)为状态i时采取行动a的报酬；V(i,π)为效用准则函数;π为马尔可夫策略(以下简称马氏策略),π=(w1,w2,…,wt)(wt∈W,t∈N),是一组马氏决策wt构成的序列,有马氏策略空间Π;马氏决策w:S→A(i),决策空间W=S×A(i)，w为状态集S到行动集A(i)的映射,表示对每个i∈S,都有w(i)∈W;V(i,π)为策略π下的系统期望总报酬:
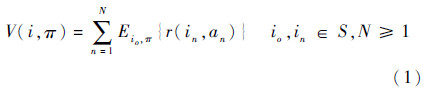
式中:in为n时刻的状态;an为n时刻采取的行动。定义最优函数[12]:
MDP的最终目标是在策略空间Π中找出期望的最优策略π*满足式(2)。马氏策略的最优策略及最优函数的存在性已被证明[14],这里不再说明。
2 MDP故障诊断原理和策略模型2.1 故障诊断原理故障检测、隔离的基本原理可描述为故障隔离“推理机”[11]:
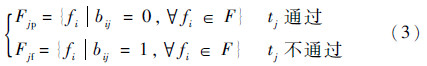
由式(3)可知,测试tj可将系统故障状态模糊集Fj划分为2个故障状态子集Fjp(测试项目通过后，系统表征出的故障状态)和Fjf(测试项目未通过，系统表征出的故障状态);且Fjp和Fjf只与当前的系统故障状态模糊集Fj相关,而与之前、之后的系统故障状态无关,具有典型的马尔可夫性。因此可将故障诊断隔离过程看作一个马尔可夫过程,应用MDP理论解决故障诊断策略寻优问题。式(3)中的bij可根据系统故障、测试的相关性矩阵FT=Bn×m=(bij)(n,m>0)来确定,故障树、仿真分析、信息流模型及多信号模型等方法[11]都获得系统FT矩阵。
2.2 基于MDP的故障诊断策略模型设F1={f1,f2,…,fm}(m≥1)为系统的初始故障状态模糊集,由故障“推理机”可得图 1所示的系统故障诊断策略树,所有可能的系统故障状态模糊集依次记为F1,F2,…,则有系统故障状态空间S={F1,F2,…,Fk}(k≥1);所有检测项目t1,t2,…,td(d≥1)构成测试集T或行动集A(i),即A(i)=T={t1,t2,…,tn}(n≥1)。
 |
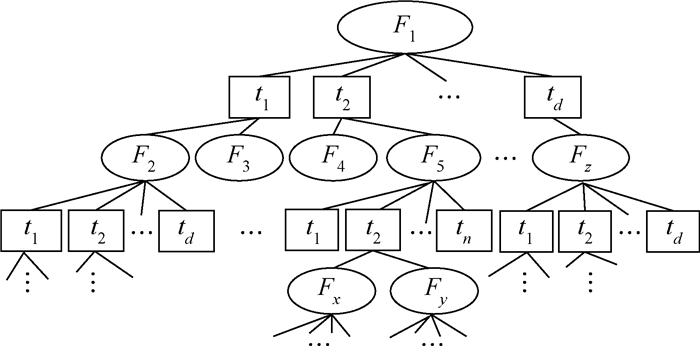| 图 1 系统故障诊断策略树 Fig. 1 System fault diagnosis strategy tree |
| 图选项 |
对任意时刻的系统故障状态模糊集in=Fk∈S,都有测试决策wn:Fk→a=td∈T来进一步推测系统可能的故障状态,最终将其隔离到子故障或现场可更换单元(Line Replaceable Unit,LRU)、车间可更换单元(Shop Replaceable Unit,SRU)。
在实际测试过程中,由于存在诸多不可控因素的干扰,测试td只能以一定的统计概率pdp检测出故障fm,即为系统故障状态Fk→Fkp的转移概率;则状态Fk→Fkf的转移概率为pdf=1-pdp。
在测试诊断系统组建过程中,测试td执行后的测试费用及对系统后续故障诊断的影响都是极重要的考虑因素[15]。因此定义2个即时报酬:测试费用rc(in,an)和系统故障状态信息量ri(in,an);测试系统的故障诊断策略π={w1,w2,…,wn}(n≥1),wn为n时刻的测试决策;所有可能的诊断策略构成策略空间Π;根据式(1),进而有测试系统诊断策略构建效用准则函数
综上,可确定基于MDP的测试系统诊断策略模型: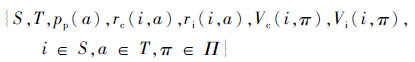
通过求解该模型,从策略空间Π中找到最优策略π*,使其能对效用准则函数Vc(F1,π)、Vi(F1,π)同时满足式(2),则是生成测试系统最优策略的过程。这是个典型的多目标MDP(Multi-Objective Markov Decision Processes,MOMDP)[14],可运用线性加权方法将其化归为综合效用准则函数,求解出满足综合效用准则的最优策略π*。
2.3 模型求解测试系统诊断策略寻优,期望获得测试周期内的最优决策,即考虑长周期的收敛解,因此选用无限折扣模型。考虑2个准则的期望时间周期相同,只需引入一个折扣因子β(β越接近于1,则期望周期越长),结合式(1)可得
式中:测试费用rc(in,an)可由历史统计数据获得,并对其取负;ri(in,an)可由信息熵求得
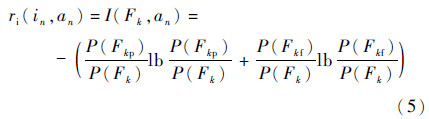
其中:P(Fk)、P(Fkp)和P(Fkf)为各故障状态模糊集中子故障发生的概率之和。设测试费用与系统信息量的权重值分别为α、1-α,结合式(4)对2个效用准则函数线性加权,可得综合效用准则函数:
式中:r(in,an)=αrc(in,an)+(1-α)ri(in,an)。由于测试费用已取负值,能获得的系统信息量越大越好,则有综合效用准则函数期望越大越好。则有最优值方程
通过求解式(6),求得使最优函数最小的各测试决策,进而得到最优策略。策略迭代算法是一种求解无限折扣模型MDP的高效、快速算法,可求解有限状态空间与行动空间集合的MDP,符合工程实际。策略迭代算法求解出最优策略π*的具体计算步骤[13]如下:
1) 任取π∈Π。
2) 求解效用函数
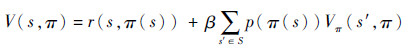
3) 改进每个状态对应的行动,使其满足
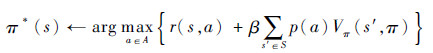
4) 如果π*=π,则停止,V(s,π)=V(s,π*)为最优值函数,并返回π;否则,策略更新为π=π*,返回步骤2)。
步骤3)求得的π*(s)为长周期内的最优平稳决策,据此可对策略π进行更新,进而可得出最优策略π*。
3 诊断策略构建实例现以某型战机悬挂及发射装置二线自动测试系统为例,对某型导弹发射架离位测试内容构建最优诊断策略。导弹发射装置是实现飞机与导弹之间的机械、电气、射频及气路连接的接口装置,对其测试主要是对电气参数的检测。分析发射架与导弹发动机点火电缆之间的信号,得出测试需求并确定其测试项目,依据多信号模型或信息流模型,由可达性分析得出其相关性矩阵,如表 1所示。
表 1 发射架点火电缆模块相关性矩阵、转移概率及测试费用 Table 1 Dependency matrix, transition probability and test expenses of launcher ignition cable module
| FT | t1 | t2 | t3 | t4 | t5 | p(fn) |
| f1(射频接口) | 0 | 0 | 0 | 0 | 0 | 0.01 |
| f2(燃气推进器) | 0 | 1 | 0 | 0 | 1 | 0.02 |
| f3(发射电路盒) | 0 | 0 | 1 | 1 | 0 | 0.05 |
| f4(发射控制电源盒) | 1 | 0 | 0 | 1 | 1 | 0.03 |
| f5(挂弹信号组件) | 1 | 1 | 0 | 0 | 0 | 0.09 |
| f6(同步机构) | 1 | 1 | 1 | 1 | 0 | 0.10 |
| pnp | 0.81 | 0.92 | 0.87 | 0.89 | 0.75 | |
| rc | 1 | 1 | 1 | 1 | 1 |
表选项
为便于求解该测试系统的诊断策略,作如下补充:
1) pnp为测试tn能确定检测、反映出导弹发射架故障fm的概率,也就是系统故障状态发生转移的概率。因为在实际战地转场、内外场等恶劣的测试环境中存在多种外界因素,都会对测试效果造成一定的影响。
2) 考虑到测试设备的硬件架构已经搭建完成,不再讨论经济花费,所以表 1中的测试费用为测试时间成本的统计估计值,并作为费用报酬准则。
上述转移概率及测试费用均已在表 1中列出。
1) 确定折扣因子β。根据测试系统的可能检测周期,以及对诊断策略最优性的选取,折扣因子越接近1则策略长周期内的最优性越好,本例中确定0.80、0.95,并对比不同之处。
2) 确定准则权重。分析策略构建关键因素对测试效率、可靠性的影响,结合测试专家意见,给出测试费用和故障状态信息量的权重系数均为α=0.5;当检测偏向发生变化时,只需增加或减小权重值。
3) 根据表 1所示内容,按图 1所示构建出诊断策略树,可推出系统所有可能的故障状态模糊集,如表 2所示,进而得到故障状态空间S={F1,F2,…,F27}，且系统的可用行动集A(i)={t1,t2,…,t5}。
表 2 系统故障状态表 Table 2 Fault states table of system
| 故障状态 | 子故障 | 故障状态 | 子故障 |
| F1 | f1f2f3f4f5f6 | F15 | f3 |
| F2 | f1f2f3 | F16 | f4 |
| F3 | f4f5f6 | F17 | f5f6 |
| F4 | f1f3f4 | F18 | f4f5 |
| F5 | f2f5f6 | F19 | f6 |
| F6 | f1f2f4f5 | F20 | f5 |
| F7 | f3f6 | F21 | f4f6 |
| F8 | f1f2f5 | F22 | f1f4 |
| F9 | f3f4f6 | F23 | f1 |
| F10 | f1f3f5f6 | F24 | f3f4 |
| F11 | f2f4 | F25 | f2f5 |
| F12 | f1f3 | F26 | f1f5 |
| F13 | f2 | F27 | f3f6 |
| F14 | f1f2 |
表选项
4) 根据表 2内容,结合表 1中所示的系统故障状态转移概率,可确定在采取测试t1后系统的状态转移概率矩阵:
矩阵中元素E1ij表示在测试t1下系统可观测故障状态由Fi转移到Fj的概率,且只有数值:0,p1f,p1p,1,依次对应:没有转移关系、转移到测试不通过、测试通过的系统故障状态及状态不发生转移。同理,可求得测试t2,t3,t4,t5行动下的状态转移概率矩阵P2,P3,P4,P5。有必要说明的是,当执行测试tn后系统故障状态不发生转移时,便视为以概率1回到原状态。
5) 根据表 1内容及式(3),可获得该测试系统3个报酬函数:
① 由表 1可知,测试费用报酬函数rc(in,an)=rc(an),an∈T,与系统所处状态无关,只取决于采取的测试行动。
② 由式(5)和状态转移概率矩阵,求得信息量报酬函数:
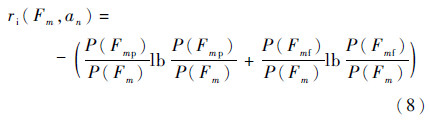
③ 已知准则权重α=0.5,综合a、b,进而得到综合报酬函数:
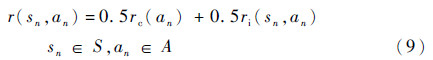
6) 式(9)代入式(6),得到该测试系统故障诊断策略构建的效用准则函数方程组:
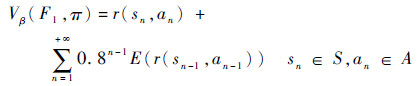
最佳策略即是寻找使效用准则取最大值的诊断策略π*,满足
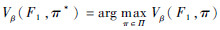。7) 由于系统状态空间较大,本实例模型求解使用策略迭代算法,利用MATLAB中的MDP决策工具包编程可得结果,如图 2和图 3所示。图 3为2个折扣因子下各故障状态的效用准则值,可以看出由于本例的检测周期较短,2个折扣因子下的策略趋势是一致的。 |
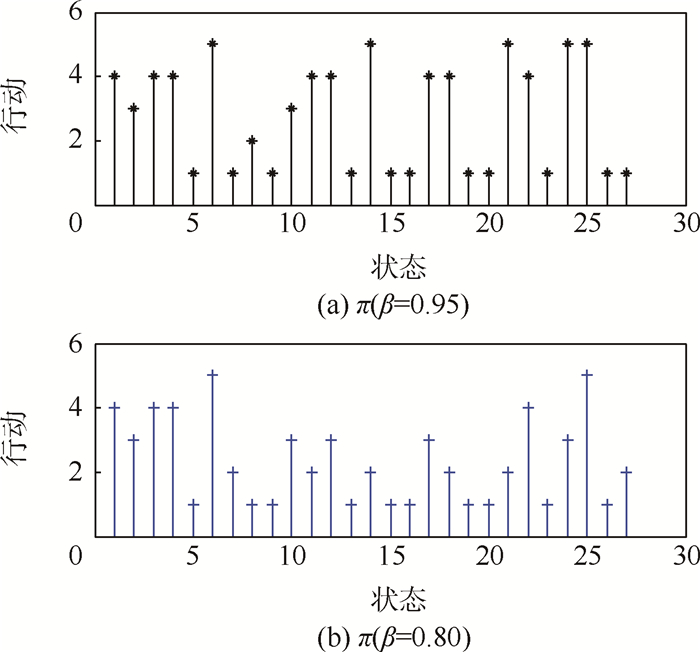| 图 2 最佳决策 Fig. 2 The best decisions |
| 图选项 |
 |
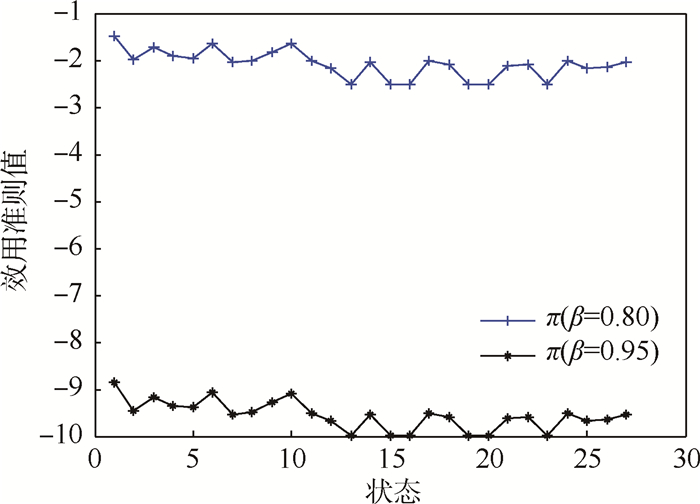| 图 3 最佳策略效用准则值 Fig. 3 Utility values of criteria of the best strategy |
| 图选项 |
从图 2中不难看出,系统故障状态对应的最佳决策在不同β下是不尽相同的。即当最优性的目标周期不同时,对应的最优策略可能不一致。本例以β=0.95的长周期最佳决策作为理想目标,可得到该测试系统从故障状态F1开始的最佳决策为:F1→t4、F8→t2、F9→t1、F25→t5、F21→t5,则有系统故障诊断树如图 4所示。可以看到,没有进行测试t3,被测对象的故障还是可以诊断、隔离出来,据此也可对行动集A(i)进行适当约减,进而可精简设计的测试项目。图 5和图 6分别给出了不同权重值下的最佳决策及效用准则值。权重α=0.4表示策略决策更偏向于期望测试费用更小;权重α=0.6则更倾向于每个测试决策所获得的系统故障状态信息量,以便快速检测出故障,即测试的快速性;权重α=0.5则是二者兼顾;从图 6中也不难看出,不同权重值下策略的效用准则值并不相同,但是利用该方法都可以找到长期最优平稳策略,而权重值的设置需要根据具体的设计需求进行确定。
 |
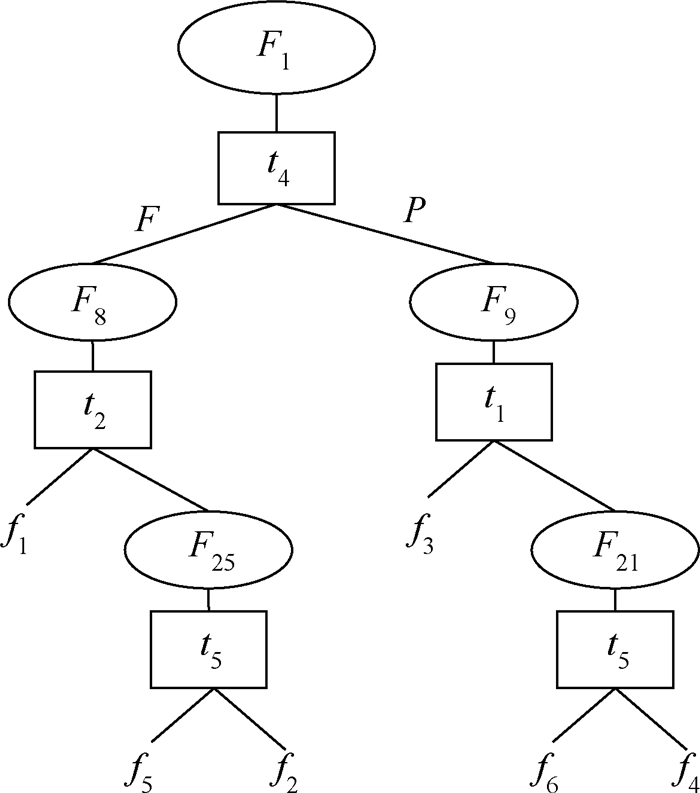| 图 4 系统故障诊断树 Fig. 4 Fault diagnosis tree of system |
| 图选项 |
 |
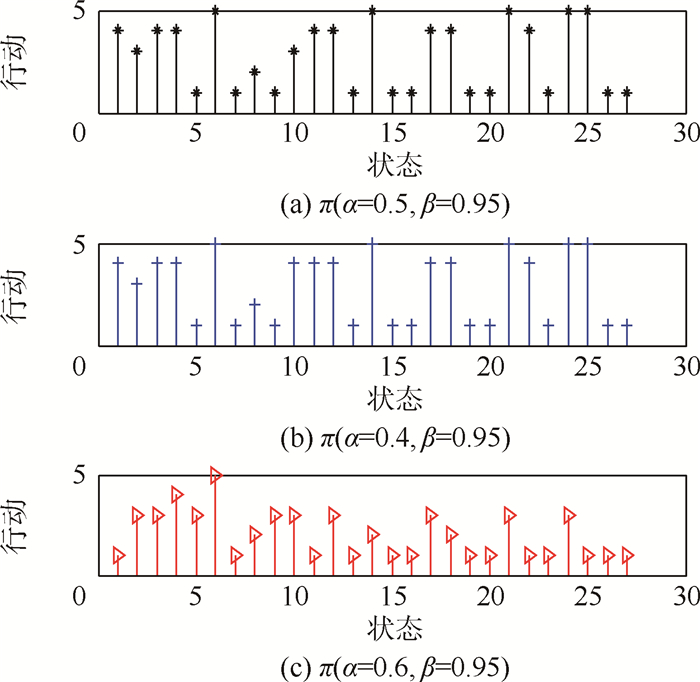| 图 5 不同权重α下的最佳决策 Fig. 5 The best decisions under different α |
| 图选项 |
 |
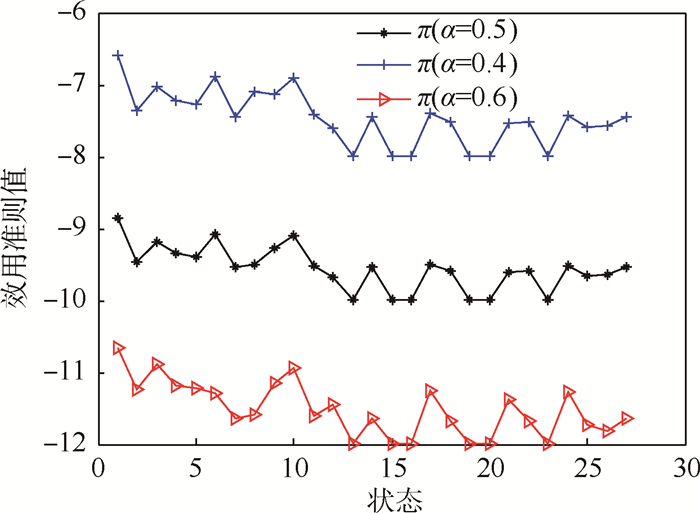| 图 6 不同权重α对应的策略效用准则值(β=0.95) Fig. 6 Utility values of criteria under different α (β=0.95) |
| 图选项 |
综上可以看出,当检测环境复杂、测试资源有损毁时或检测人员可以确定故障的大致位置等情况下,可选择对应的故障状态的最佳决策生成一系列的不同初始状态的最优诊断策略。该方法应用到某型战斗机悬挂及发射装置二线自动测试系统,能够对某型导弹发射架进行快速有效的故障诊断,在导弹发射架全寿命周期的测试保障中节省大量的时间,并作为约简测试资源的依据,切实提高某型导弹发射架的保障效能,降低测试系统的设计成本。
4 结 论本文基于MDP理论,通过建立MDP折扣模型并求解该模型,得到理想诊断策略:
1) 该方法能够充分考虑测试通过中的不确定性因素的影响,提高诊断结果的准确性与可靠性。
2) 可实现长周期动态寻优,生成全局最优诊断策略。
实践表明,该方法能够有效指导战地转场等突发性复杂环境中的诊断策略构建,实现故障的快速检测与隔离。
参考文献
| [1] | IEEE SCC20. IEEE trial-use standard for testability and diagnos ability characteristics and metrics:IEEE Std 1522-2004[S].Piscataway,NJ:IEEE Standards Press,2004:1-7. |
| [2] | 杨海马,于小强, 杨晖,等.漏泄电缆自动检测系统研究[J].电子测量与仪器学报,2014,28(7):795-797. YANG H M,YU X Q,YANG H,et al.Research on automatic detection system of leaky cable[J].Journal of Electronic Measurement and Instrumentation,2014,28(7):795-797(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [3] | PATTIPATI K R, ALEXANDRIDIS M.Application of heuristic search and information theory to sequential fault diagnosis[J].IEEE Transactions on System,Man,and Cybernetics,1990,20(4): 872-887. |
| Click to display the text | |
| [4] | SIMPSON W R, SHEPPARD J W.The multicriterion nature of diagnosis[C]//Proceedings of the IEEE Systems Readiness Technology Conference.Piscataway,NJ:IEEE Press,1993:389-395. |
| Click to display the text | |
| [5] | JOHNSON R A. An information theory approach to diagnosis[J].IRE Transactions on Reliability and Quality Control,1960,RQC-9(1):35. |
| Click to display the text | |
| [6] | 黎琼炜. 系统级BIT测试性设计技术及其在组合导航系统中的应用研究[D].长沙:国防科技大学,2001:34-57. LI Q W.Research on system level BIT design for testability technique and its application in integrated navigation system[D].Changsha:National University of Defense Technology,2001:34-57(in Chinese). |
| [7] | 景小宁,李全通, 陈云翔,等.基于信息熵的最少测试费用故障诊断策略[J].计算机应用,2005,25(2):417-419. JING X N,LI Q T,CHEN Y X,et al.Fault diagnosis strategy with least test cost based on information entropy[J].Journal of Computer Applications,2005,25(2):417-419(in Chinese). |
| Cited By in Cnki (20) | Click to display the text | |
| [8] | TU F,PATTIPATI K R. Rollout strategy for sequential fault diagnosis[J].IEEE Transactions on Systems,Man and Cybernetics,2003,33(1):86-99. |
| Click to display the text | |
| [9] | 黄以锋,景博,喻彪, 等.基于概率阈的冗余多故障诊断策略[J].空军工程大学学报(自然科学版),2014,15(5):1-5. HUANG Y F,JING B,YU B,et al.Multiple fault diagnosis strategy for redundant system based on probability threshold[J].Journal of Air Force Engineering University (Natural Science Edition),2014,15(5):1-5(in Chinese). |
| Cited By in Cnki | |
| [10] | 王红霞,叶晓慧, 田树新.基于广义AO*算法的测试序列问题研究[J].兵工学报,2010,31(2):204-209. WANG H X,YE X H,TIAN S X.Research on test sequencing problem based on generalized AO* algorithm[J].Acta Armamentarii,2010,31(2):204-209(in Chinese). |
| Cited By in Cnki (3) | |
| [11] | 邱静,刘冠军,杨鹏,等. 装备测试性建模与设计技术[M].北京:科学出版社,2012:316-319. QIU J,LIU G J,YANG P,et al.Equipment testability modeling and design technology[M].Beijing:Science Press,2012:316-319(in Chinese). |
| [12] | 黎洁,刘羽西, 李奇越.基于隐马尔可夫模型的认知无钱频谱切换方法[J].电子测量与仪器学报,2014,28(1):69-74. LI J,LIU Y X,LI Q Y.Spectrum handoff and method based on hidden Markov model in cognitive radio network[J].Journal of Electronic Measurement and Instrumentation,2014,28(1):69-74(in Chinese). |
| Cited By in Cnki (5) | Click to display the text | |
| [13] | RUSSELL S, NORVING P.Artificial intelligence:A modern approach[M].Beijing:Tsinghua University Press,2011:645-658. |
| [14] | 刘克. 实用马尔可夫决策过程[M].北京:清华大学出版社,2004:34-45. LIU K.The utility of Markov decision processes[M].Beijing:Tsinghua University Press,2004:34-45(in Chinese). |
| [15] | 李行善,左毅,孙杰. 自动测试系统集成技术[M].北京:电子工业出版社,2004:66-70. LI X S,ZUO Y,SUN J.Automatic test system integration technology[M].Beijing:Publishing House of Electronics Industry,2004:66-70(in Chinese). |
