由于LU-SGS鲁棒性较好,存储需求低,其在非结构/混合网格上得到了广泛的应用[3, 5, 7, 9]。然而,由于近似处理,LU-SGS收敛速度相对较低。另外,在混合网格上应用LU-SGS,必须预先对网格进行重新排序以减小系数矩阵带宽[6, 9, 16],为了并行计算,网格单元也需预先进行分组。Luo等[6]为了提高计算效率,提出了应用于混合网格上的基于共享内存OpenMP并行模式的GMRES+LU-SGS隐式格式。为了并行化,该格式事先也需以某种方法对网格进行分组,并将网格在处理器多个进程间划分。但该方法改变了串行程序执行顺序,造成串行、并行结果不一致,且实现复杂。此外当采用动网格计算时,网格排序和分组需反复进行,为求解带来了额外的时间消耗。
为了克服上述问题,本文提出了一种无需网格排序和分组的改进雅可比迭代方法。将每个单元同其相邻单元作为独立的块处理,并行地直接求解各块相应的方程组;为了使算法并行化,抛弃了LU-SGS中的前扫描和后扫描模式,依次扫描各个单元块,并用内迭代加速收敛。在构造每个独立块的雅可比矩阵时,采用了基于重构变量的近似通量函数,降低了计算复杂性,并能保证对角占优特性。
本文提出的方法实现简单,数值算例表明,相比于LU-SGS格式,具有更高的收敛效率和鲁棒性,并行和串行结果一致,且内存需求增加很少。
1 格心有限体积法三维非定常可压Navier-Stokes方程守恒积分形式为
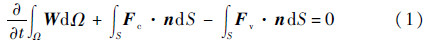
式中:W为守恒变量;Ω和S分别为控制体和表面;Fc和Fv分别为对流通量和黏性通量;n为面法矢量。各项具体形式参见文献[16]。本文中对流通量采用Roe[17]格式离散,控制面两侧重构变量采用Barth[18]提出的分段线性重构获得,单元中心梯度采用最小二乘法计算,用Venkatakrishnan[19]限制器抑制振荡,黏性通量采用中心格式离散,湍流方程与平均方程解耦求解,湍流模型为一方程SA模型[20]。
对一个固定控制体i,采用向后差分,方程(1)的半离散形式可写为

式中:Δ为变量在时间步n+1和时间步n的差;R为右端项。式(2)右端残差项为
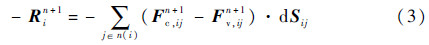
式中:Sij为面积矢量(Sij·n);ij为单元i的第j个面,该面被单元i和其第j个相邻单元共享。用第n时间步残差线化式(3),可得
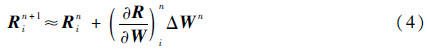
式中:?R/?W为通量雅可比矩阵,其包含了无黏通量和黏性通量对守恒变量的导数。将式(4)代入式(2),整理可得
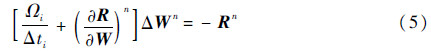
式(5)左端方括号内称为系数矩阵,该项为一个不对称大型稀疏分块矩阵,存储量需求很大。在LU-SGS中,对该项做了若干近似处理,以减小存储和计算量。
2 改进的时间方法2.1 原始LU-SGS格式系数矩阵可分解为一个严格下三角矩阵L、一个严格上三角矩阵U和一个纯对角矩阵D。Jameson和Yoon[4]提出的LU-SGS的基本思想是:通过近似求解来避免繁杂的矩阵求逆运算。在LU-SGS格式中,系数矩阵A被近似为
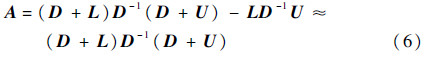
则式(5)变为
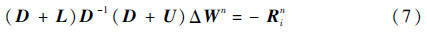
在计算通量雅可比矩阵时,LU-SGS采用如下1阶通量函数:
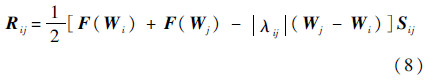
式中:F为通量函数;λij为雅可比矩阵的谱半径,表示为
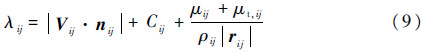
其中:nij为面ij的面法矢量;Vij、Cij、ρij、μij和μt,ij分别为面上的速度矢量、声速、密度、分子黏性系数和湍流黏性系数;rij为单元i到单元j体心的距离。另外,在一个封闭的控制体上,有

最终,对角阵D可写为容易求逆的形式:
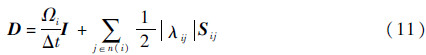
式中:I为单位矩阵。则式(5)的LU-SGS求解步骤可写为如下2步:
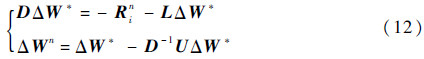
2.2 改进的雅可比迭代方法由第2.1节可见,原始LU-SGS格式中存在2个近似处理。其一,忽略了LD-1U项,用(D+L)D-1(D+U)代替系数矩阵;其二,在计算系数矩阵时利用1阶通量函数构造雅可比矩阵,使得式(5)左端项同右端项不匹配。这些近似处理导致LU-SGS格式收敛效率不高。
2.2.1 改进的算法流程在本文方法中,不对系数矩阵近似处理。对于每个单元,将式(5)中的系数矩阵分解为对角矩阵D和非对角矩阵O之和,则式(5)变为
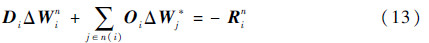
注意到,式(13)实际上把LU-SGS中上、下三角矩阵合并成非对角矩阵O。三维时,D和O皆是5×5矩阵。通过对矩阵D求逆,可求得
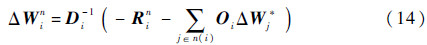
式(14)实际上是雅可比迭代的矩阵形式。对各个单元对应的方程组皆采用式(14)求解,由于雅可比迭代在迭代完毕后才更新变量,因此各单元互不关联,求解可以并行执行。
为了将式(14)的解推进到足够的精度以达到较高的收敛速度,在每个时间步内,需要执行若干次内迭代。为了算法可并行,采用顺序扫描各个单元。完整的求解流程如下:
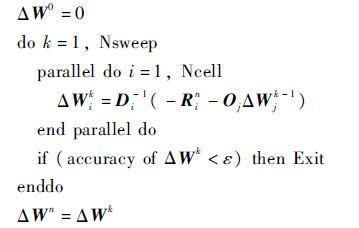
其中:k为内迭代步数;Nsweep为最大内迭代步数;ε为内迭代收敛精度,表示为
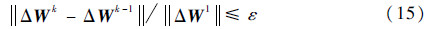
当达到这2个条件时,内迭代停止。
由于抛弃了LU-SGS中的前后扫描模式,且需求解的式(14)仅对应于各个单元,由上述流程可见,求解过程同网格的顺序无关,因此对于本文方法,网格排序步骤可以省略。
2.2.2 通量雅可比矩阵计算原则上,构造通量雅可比矩阵时,应采用同空间格式相同精度的通量函数。由于本文使用2阶Roe格式计算通量,按上述原则,通量函数为
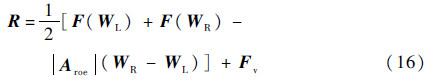
式中:Aroe为Roe矩阵;下标L和R表示界面左和右。然而采用式(16)计算通量雅可比矩阵的计算量很大,再考虑到保证对角占优,本文提出用如下通量函数构造雅可比矩阵:
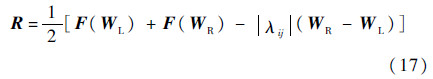
式(17)与式(8)的区别在于使用了重构的变量WL和WR,其表示为
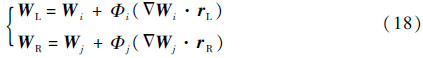
式中:Φ为限制器函数;▽W为单元中心梯度;r为单元中心到面的距离。对式(17)进行线化,可得到通量雅可比矩阵为
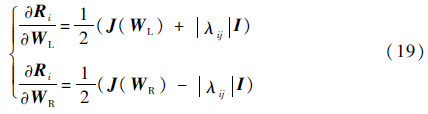
式中:J为对流通量雅可比矩阵。系数矩阵中的对角阵和非对角阵可表示为
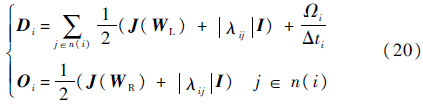
由式(20)可见,由于采用了重构的变量,与式(11)中对角阵相比,J(WL)项被保留下来,增大了对角占优特性。相比式(16),采用式(17)计算通量雅可比矩阵的计算量和复杂性较小,在第3.1节中可以看到,采用式(17)中的通量函数对本文方法收敛性和稳定性都没有影响。
3 算例及讨论3.1 NACA0012翼型跨声速无黏绕流本算例对比了本文方法和LU-SGS格式的收敛效率,LU-SGS格式采用排序后网格计算。来流条件为:马赫数为0.8,攻角为1.25°。计算网格见图 1。将翼型沿展向拉伸为三维,共包含161个壁面节点,7168个六面体单元,第一层网格高度为翼型弦长的1×10-2倍。
 |
| 图 1 NACA0012翼型计算网格Fig. 1 Computational grid of NACA0012 airfoil |
| 图选项 |
图 2和图 3分别为流场马赫数云图和壁面压力系数Cp分布。可见,翼型上下部激波清晰,流场结构合理,表明本文方法获得的结果正确。
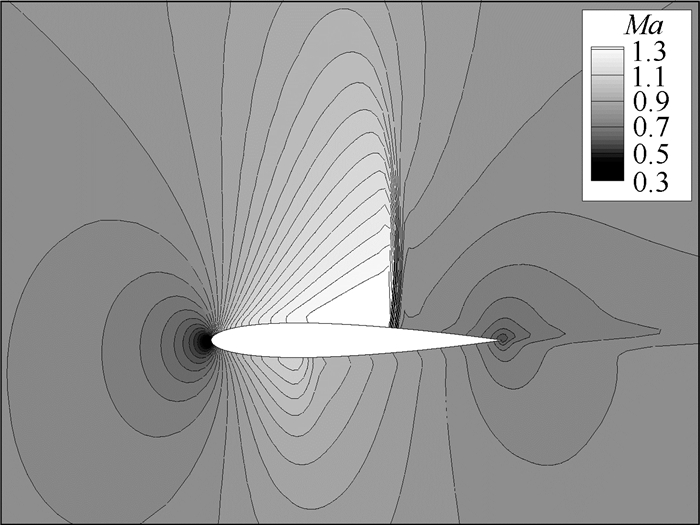 |
| 图 2 流场马赫数云图Fig. 2 Mach contour of flow filed |
| 图选项 |
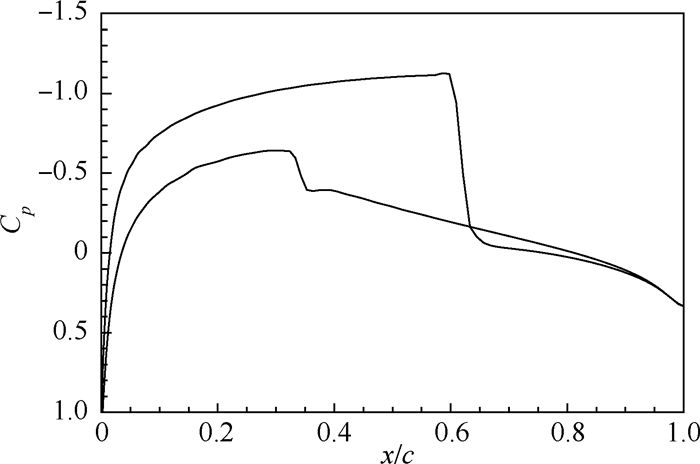 |
| 图 3 NACA0012翼型壁面压力系数Cp分布Fig. 3 Pressure coefficient Cp distribution on wall of NACA0012 airfoil |
| 图选项 |
图 4为LU-SGS格式在不同CFL数下的残差收敛曲线。可见当CFL数大于50后,残差收敛速度已不随CFL数增加显著下降。而对于本文方法,由图 5可见,CFL数大于700仍能加速残差收敛速度,且CFL数为70000时仍能保证稳定。图 6为相同CFL数下本文方法和LU-SGS格式残差收敛曲线随计算时间的变化。由图 4~图 6可见,对本算例采用本文方法收敛迭代时间和迭代步数显著少于LU-SGS格式。
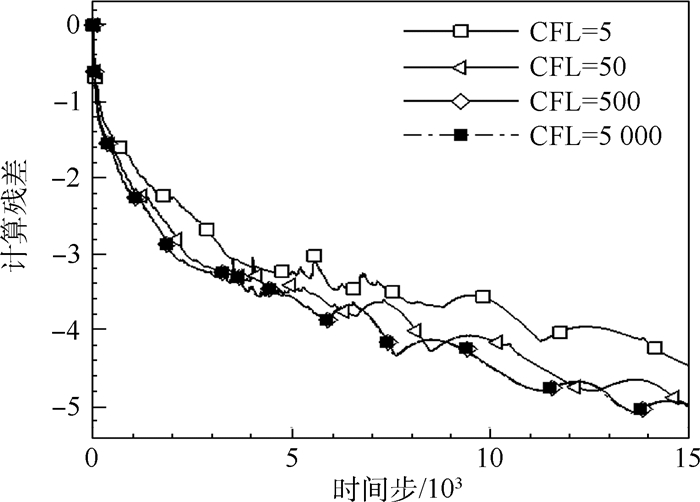 |
| 图 4 不同CFL数下LU-SGS格式残差收敛曲线Fig. 4 Residual convergence curves of LU-SGS scheme for different CFL numbers |
| 图选项 |
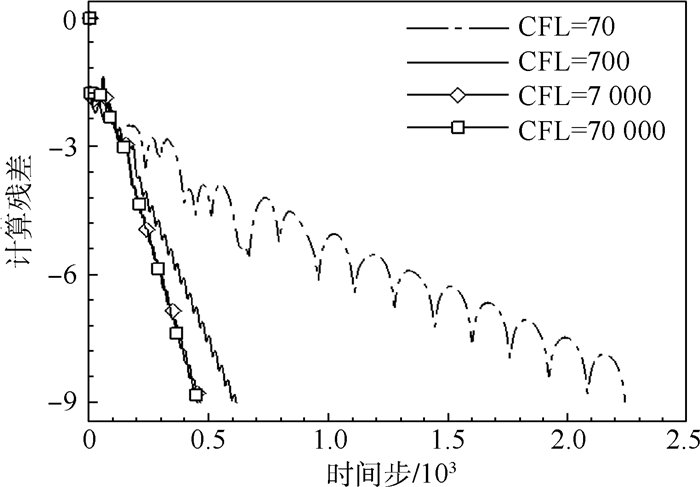 |
| 图 5 不同CFL数下本文方法残差收敛曲线Fig. 5 Residual convergence curves of proposed method for different CFL numbers |
| 图选项 |
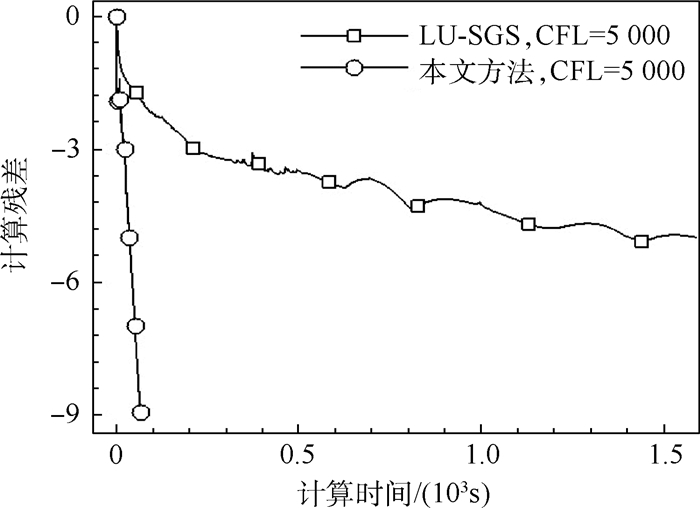 |
| 图 6 LU-SGS格式和本文方法残差随计算时间变化对比Fig. 6 Comparison of residual convergence histories versus CPU time between LU-SGS scheme and proposed method |
| 图选项 |
图 7为本文方法采用不同内迭代步数时残差收敛曲线随时间步和计算时间的变化。由图 7(a)可见,随着每个时间步中内迭代步数由10增加200,收敛速度显著提高。当内迭代步数增加到200后,收敛速度不进一步随内迭代步数增加而增加。显然,内迭代步数增加能减少收敛的时间步数,但会增加每个时间步的计算时间。图 7(b)为不同内迭代步数下残差收敛曲线随计算时间的变化曲线。由图 7(a)和图 7(b)可见,当内迭代步数大于50后,虽然外迭代步数减少,但计算时间反而增加。
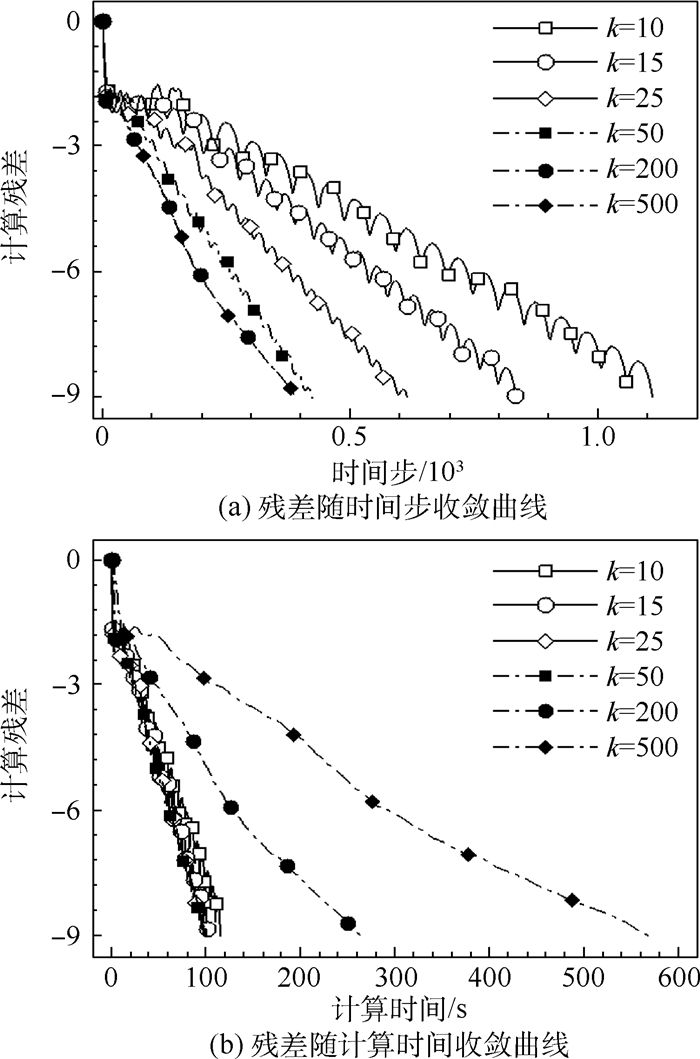 |
| 图 7 采用不同内迭代步数时残差随时间步和计算时间收敛曲线Fig. 7 Residual convergence curves versus time steps and CPU time for different inner iteration numbers |
| 图选项 |
下面讨论采用不同通量函数构造雅可比矩阵对本文方法收敛性和稳定性的影响。图 8为采用式(16)和式(17)中通量函数计算雅可比矩阵下残差随时间步的收敛曲线。可见,对本文方法使用同空间格式匹配的通量函数和使用本文近似的通量函数来构造雅可比矩阵,残差收敛速度差别不大。由于采用重构变量能保证对角占优,当CFL数等于700时,计算仍能保持稳定。
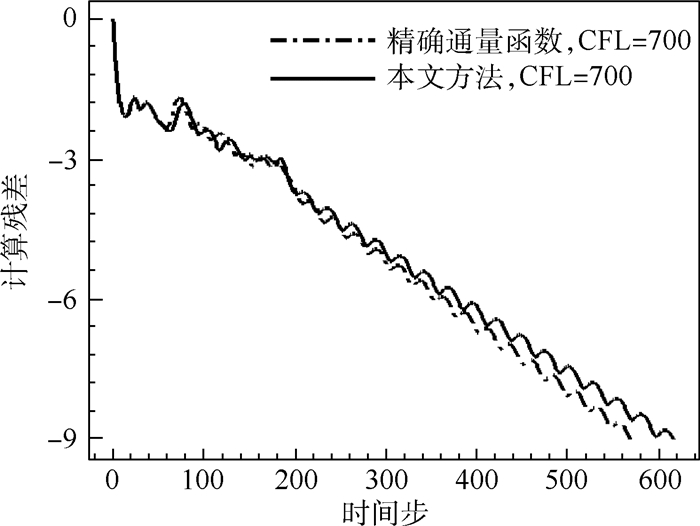 |
| 图 8 不同通量函数构造雅可比矩阵对残差收敛影响Fig. 8 Influence of Jacobi matrix constructed by different flux functions on residual convergence |
| 图选项 |
3.2 RAE2822翼型黏性绕流计算来流马赫数为0.734,攻角为2.79°,单位雷诺数为6.5×106。计算网格见图 9,将翼型沿展向拉伸为三维,网格包含壁面节点246个,分别有17080个六面体单元和15876个三棱柱单元,第一层网格高度为弦长的1×10-5倍。翼型壁面压力系数Cp分布见图 10,可见数值计算结果与实验结果非常吻合,表明计算结果正确。
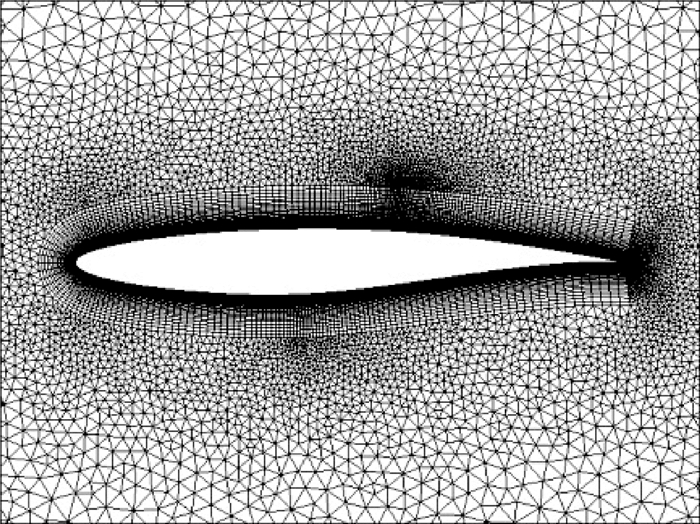 |
| 图 9 RAE2822翼型计算网格Fig. 9 Computational grid of RAE2822 airfoil |
| 图选项 |
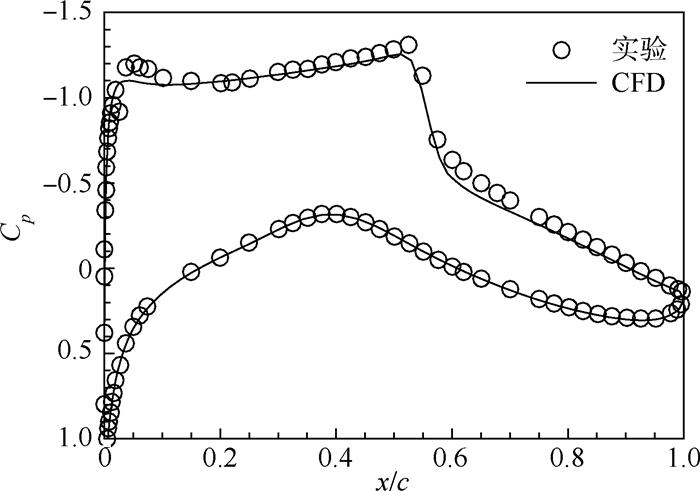 |
| 图 10 RAE2822翼型壁面压力系数Cp分布Fig. 10 Pressure coefficient Cp distribution on wall of RAE2822 airfoil |
| 图选项 |
图 11(a)和图 11(b)分别为网格排序前和排序后系数矩阵非零元素分布。可见,未排序网格系数矩阵带宽大,元素分布无规律,网格排序后矩阵带宽显著减小。
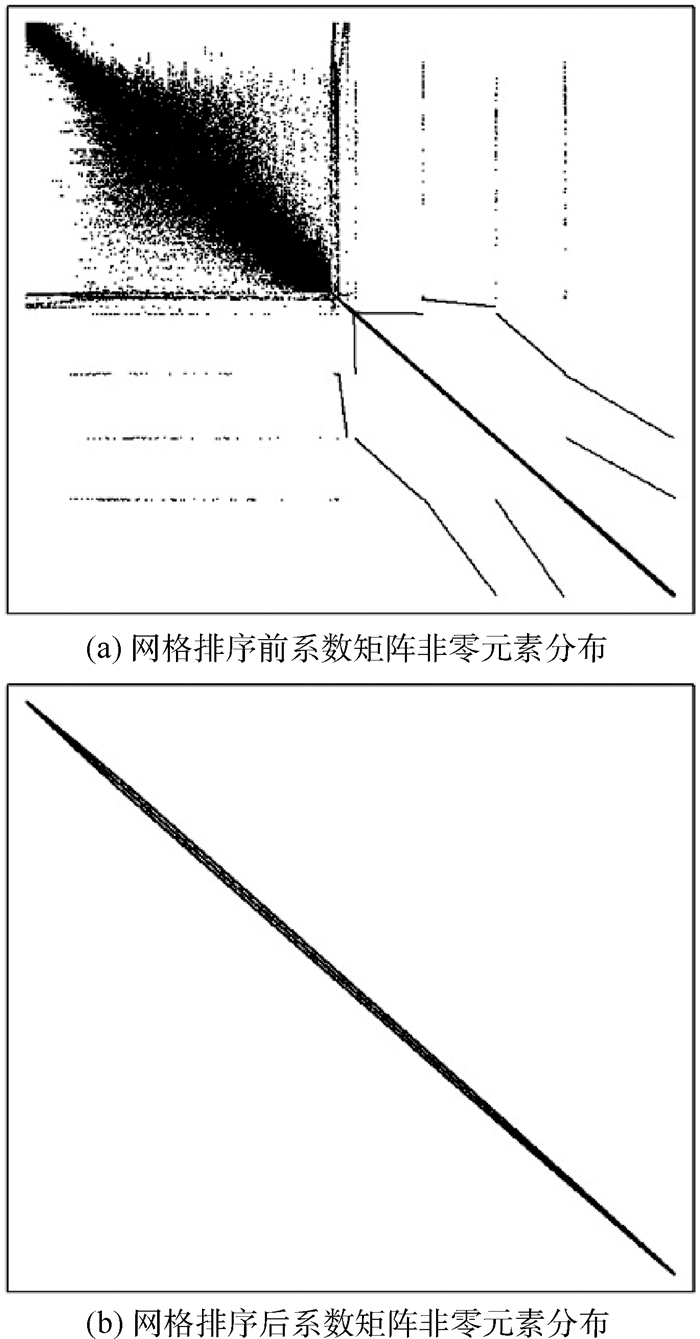 |
| 图 11 网格排序前后系数矩阵非零元素分布Fig. 11 Coefficient matrix non-zero elements distribution on non-reordered and reordered grid |
| 图选项 |
对于LU-SGS格式,采用未排序网格进行计算往往会降低收敛速度,或导致计算发散。考察LU-SGS格式在未排序网格上的计算效果。图 12为LU-SGS格式在未排序网格上计算残差收敛情况。计算中发现,CFL数大于0.6时,迭代过程中出现大量非物理解,表明计算稳定性变差。当CFL数较大时,迭代若干步后计算突然发散(CFL数为1.2时,约在6000步左右发散,未在图 12中画出);当CFL数很小时,计算能够继续,但收敛十分缓慢,且残差下降一两个量级就开始振荡。可见网格排序对LU-SGS格式在非结构/混合网格上的稳定性至关重要。本文后续LU-SGS计算结果中,皆采用了超平面排序对单元和面分组排序[9],以提高收敛性及稳定性。
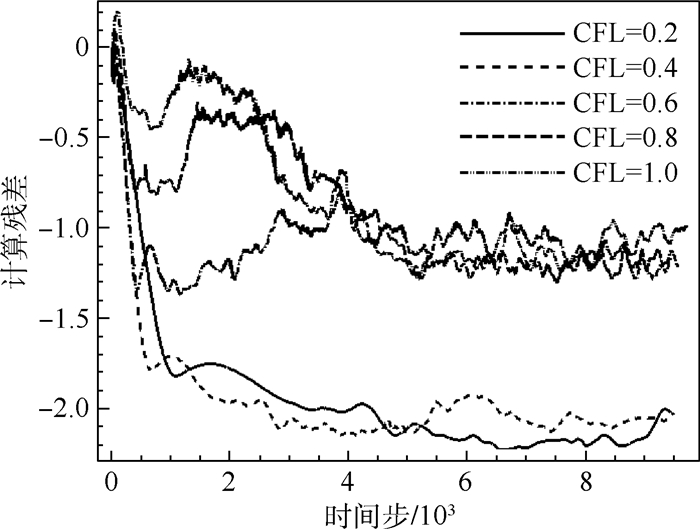 |
| 图 12 LU-SGS格式在未排序网格上计算残差收敛情况 Fig. 12 Residual convergence histories by LU-SGS scheme computation on non-reordered grid |
| 图选项 |
图 13为本文方法采用未排序和排序后网格进行计算的残差收敛曲线。可见,本文方法在未排序网格上也能获得较高的收敛速度,收敛速度和在排序网格上的没有明显差别。后续算例若未特殊说明,本文方法皆在未排序网格上进行。
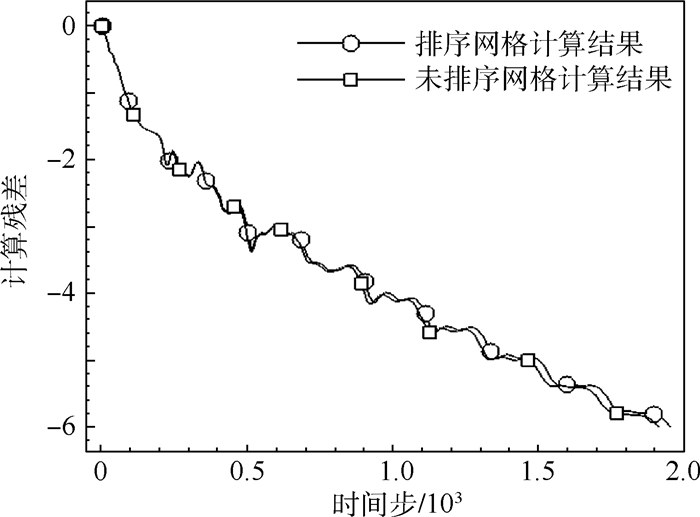 |
| 图 13 本文方法在排序网格和未排序网格上计算残差收敛情况Fig. 13 Residual convergence histories by proposed method computation on non-reordered and reordered grid |
| 图选项 |
图 14(a)和图 14(b)为本文方法与LU-SGS格式随时间步和计算时间变化的残差收敛情况对比。LU-SGS格式在排序网格上计算,本文方法内迭代步数取15。可见,对于黏性计算,本文方法的收敛速度仍快于LU-SGS格式。在内迭代步数为15的情况下,达到相同残差,LU-SGS格式时间步比本文方法多4倍左右,花费时间比本文方法多3倍左右。
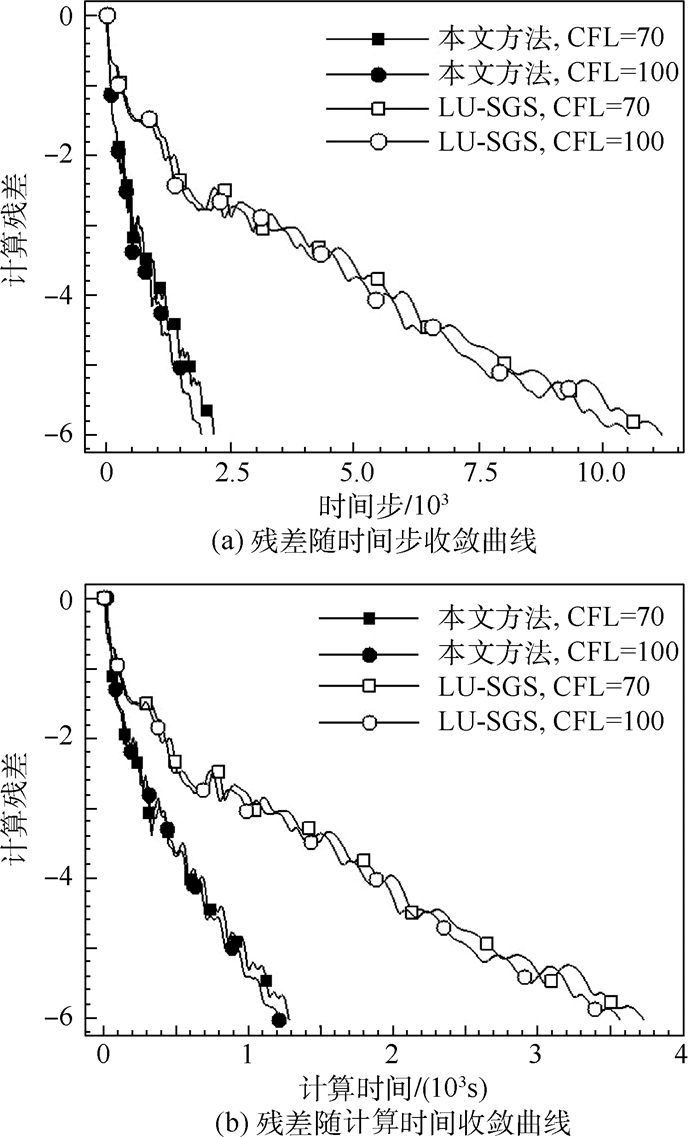 |
| 图 14 本文方法与LU-SGS格式残差随时间步和计算时间的收敛情况对比Fig. 14 Comparison of residual convergence histories versus time steps and CPU time between proposed method and LU-SGS scheme |
| 图选项 |
3.3 ONERA-M6机翼绕流模拟通过本算例考察本文方法并行计算的结果。机翼壁面和对称面网格见图 15,共包含2249296个棱柱、四面体和六面体单元。边界层内有30层棱柱,第一层网格高度为弦长的1×10-6倍。来流马赫数为0.84,攻角为3.06°,相对于平均气动弦长的来流雷诺数为1.172×107。
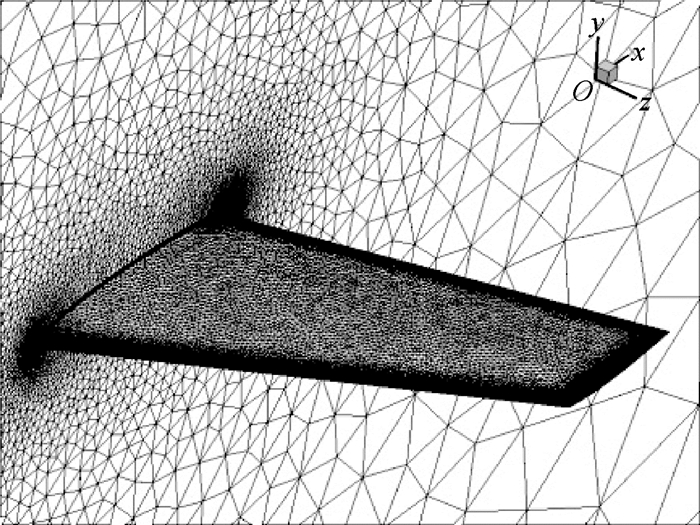 |
| 图 15 ONERA-M6机翼对称面及壁面网格Fig. 15 Grid of ONERA-M6 wing on symmetry and wall surface |
| 图选项 |
图 16(a)为对称面和壁面上的等密度线分布,图 16(b)和图 16(c)分别为机翼65%展向站位处和90%展向站位处的壁面压力系数Cp计算结果与实验值的对比。结果为并行计算完成。由图 16(a)可见陡峭的λ激波结构;由图 16(b)、图 16(c)可见,壁面压力系数分布的计算结果与实验结果吻合较好,前缘吸力峰值和激波位置的捕捉十分准确,表明本文方法计算结果可信。
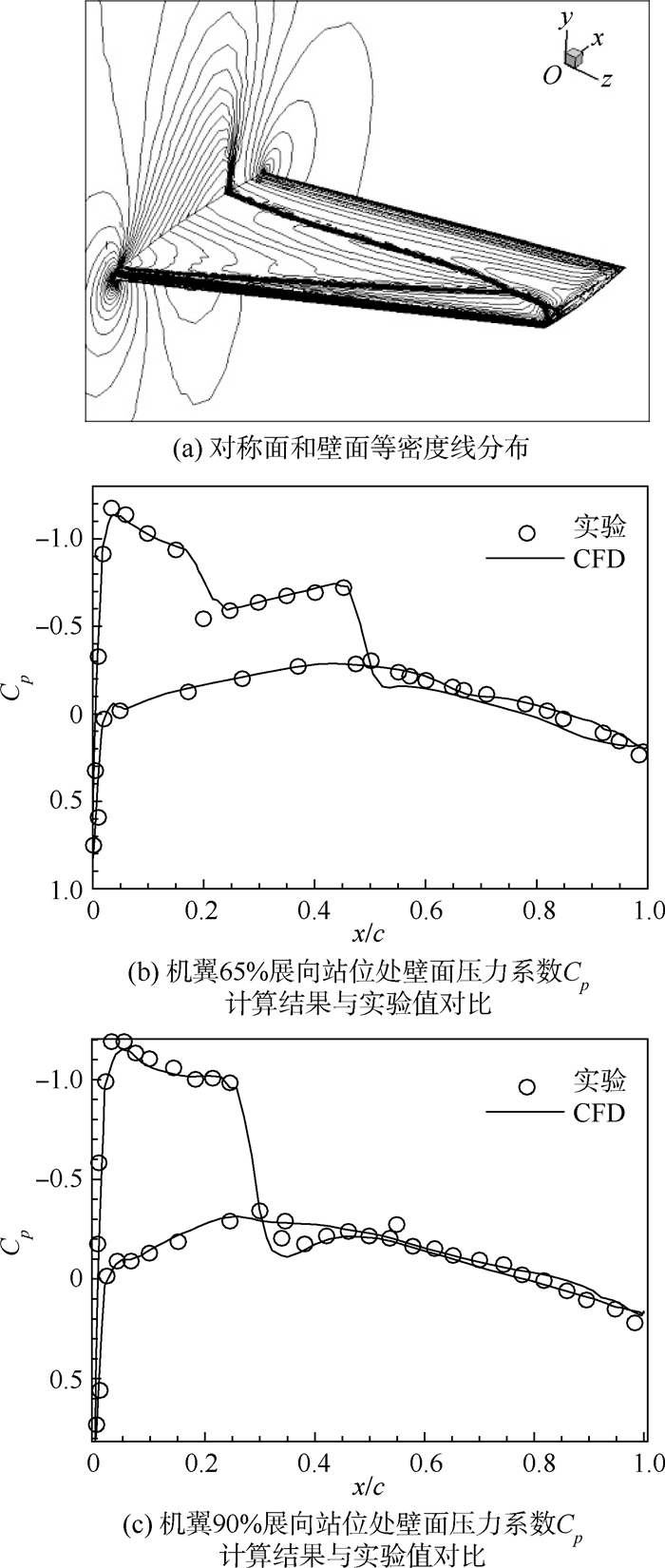 |
| 图 16 对称面和壁面上等密度线分布及不同站位处壁面压力系数Cp与实验值对比Fig. 16 Density contour on symmetry and wall surface and comparison of pressure coefficient Cp on wall with experimental data on different sections |
| 图选项 |
图 17为本文方法与LU-SGS格式残差收敛对比。LU-SGS格式采用排序后网格计算,本文方法采用排序前网格计算,图中皆为串行计算。可见,在CFL数为70时,本文方法计算残差在3000步左右下降了6个量级,而且残差基本线性下降。同样CFL数下,LU-SGS格式残差在下降4个量级后就开始振荡,难以进一步收敛。表明本文方法不仅收敛速度快于LU-SGS格式,收敛性能也较LU-SGS格式稳定和可靠。
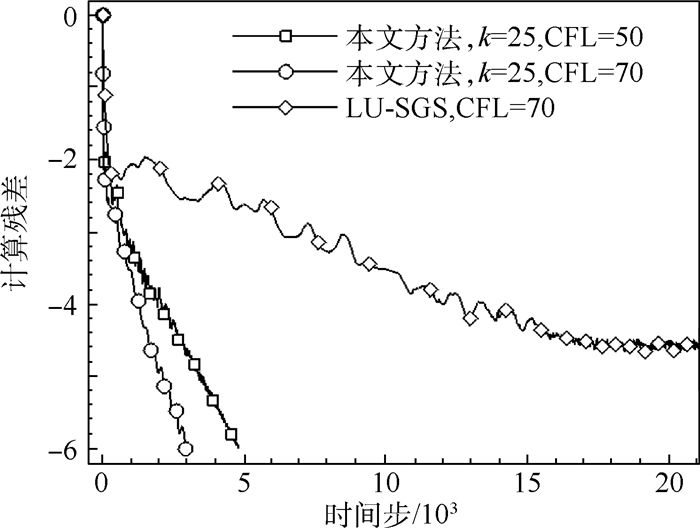 |
| 图 17 本文方法与LU-SGS格式残差收敛对比Fig. 17 Comparison of residual convergence histories between proposed method and LU-SGS scheme |
| 图选项 |
由于本文方法采用分块求解各单元变量,统一更新数据,因此各单元间数据非关联,并行无需事先进行网格分组;且从计算流程上可见本文方法十分容易并行化。采用OpenMP对本文方法并行处理,由于求解器中部分其他代码未并行化处理,因此未关注整个求解过程的并行加速比,而主要关注并行和串行结果是否一致。
图 18为ONERA-M6机翼在未分组网格上串/并行计算残差收敛过程,采用未分组网格进行串行计算和6进程并行计算。可见,串行与并行计算的残差收敛曲线完全一致,表明本文方法采用未分组网格并行计算不会对结果有所影响,因此网格分组步骤可以省略。
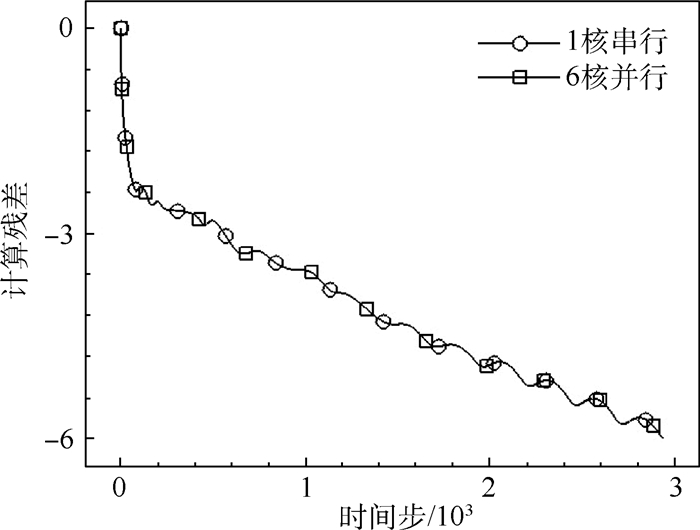 |
| 图 18 ONERA-M6机翼在未分组网格上串/并行计算残差收敛过程Fig. 18 Residual convergence histories for serial/parallel computation of ONERA-M6 wing on non-reordered grid |
| 图选项 |
表 1为采用LU-SGS格式、本文方法串行及并行计算ONERA-M6机翼共使用内存数。虽然本文方法相比LU-SGS每个单元多存储了5×5的对角矩阵和非对角矩阵,但是这2个矩阵仅在单元被扫描到时才存在;此外,在构造雅可比矩阵的非对角阵时,本文方法要额外存储单元及其相邻单元的顺序关系。因此,本文方法的内存需求比LU-SGS格式略大。尽管如此,从整体来看,本文方法总内存需求只比LU-SGS格式增加了不到10%。
表 1 ONERA-M6机翼不同格式总内存使用Table 1 Memory usage for difierent temporal schemes with ONERA-M6 wing
| 计算方法 | LU-SGS串行 | 本文方法串行 | 本文方法并行 |
| 总内存/GB | 2.71 | 2.98 | 2.98 |
表选项
3.4 DLR-F6翼身组合体绕流模拟本算例为DPW会议标准计算模型之一[21]。下面用该外形考察对于复杂网格本文方法的计算效率及稳定性。计算外形的壁面和对称面网格见图 19。为了捕捉壁面黏性效应,飞行器壁面附近为45层六面体网格,空间采用四面体和五面体单元填充,共约包含280万个单元。第一层网格高度为6×10-4m,来流马赫数为0.75,相对平均气动弦长的雷诺数为3×106,攻角为0.4°,以使得升力系数为0.5,采用SA湍流模型。
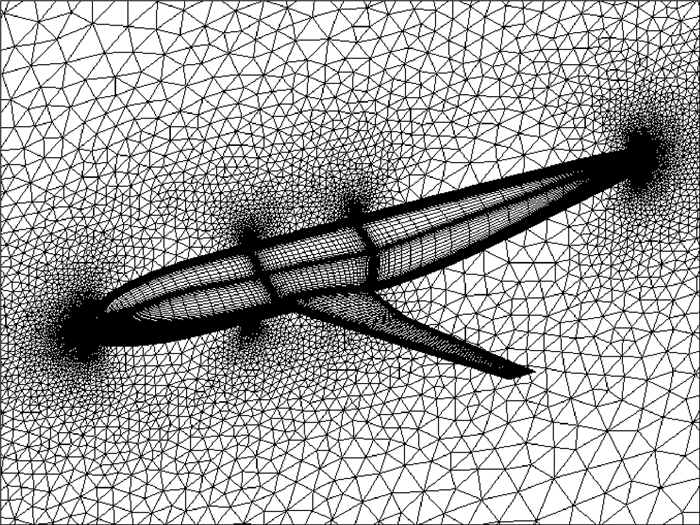 |
| 图 19 DLR-F6翼身组合体对称面及壁面网格Fig. 19 Grid of DLR-F6 wing body on symmetry and wall surface |
| 图选项 |
图 20(a)为对称面和壁面上的压力系数Cp分布,图 20(b)和图 20(c)分别为机翼15%展向和84.7%展向站位处的Cp计算结果与实验值对比。可以看出,除翼尖激波捕捉稍有偏差,其余位置均与实验值吻合良好,表明本文方法计算结果可信。
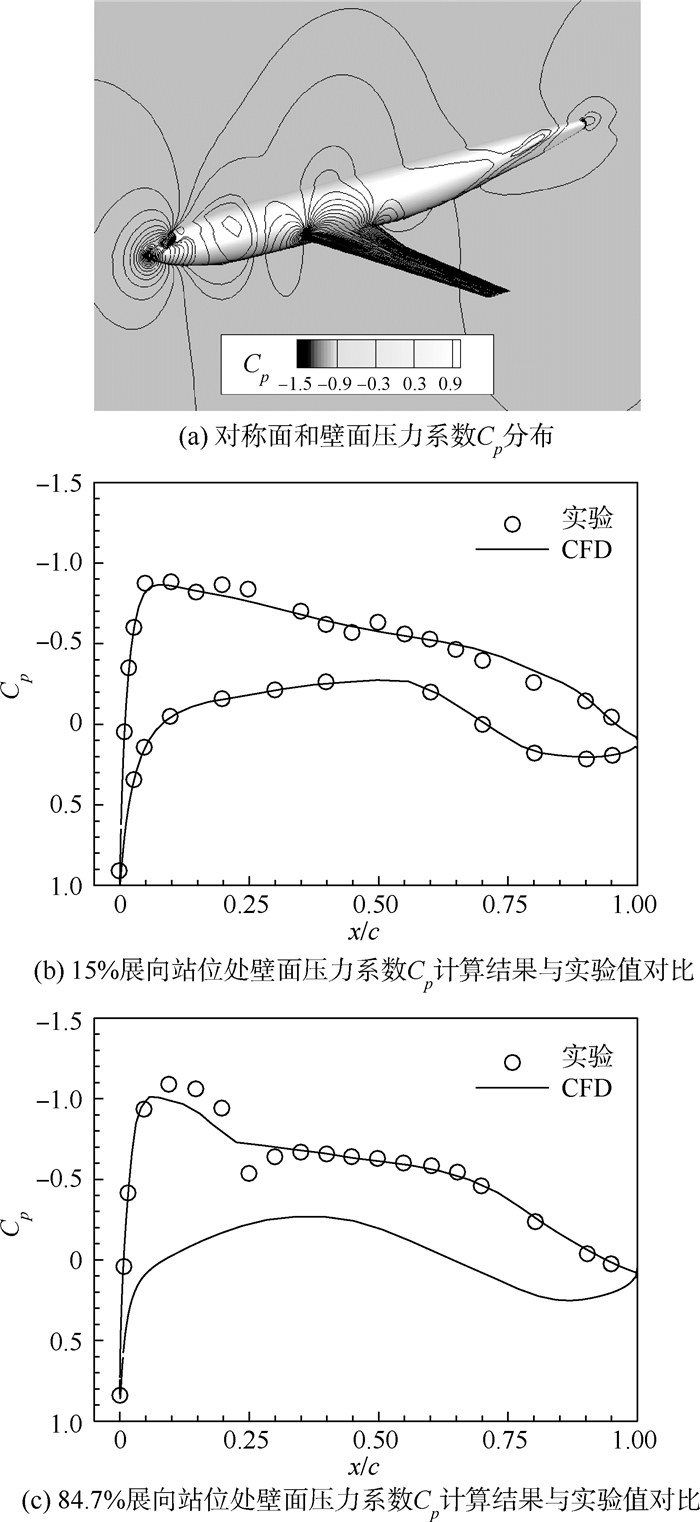 |
| 图 20 对称面和壁面压力系数Cp分布及不同站位处壁面压力系数Cp与实验值对比Fig. 20 Distribution of pressure coefficient Cp on symmetry and wall surface and comparison of Cp on wall with experimental data on different sections |
| 图选项 |
图 21为本文方法与LU-SGS格式残差收敛情况对比,皆采用排序后网格计算,本文方法内迭代步数皆取20。当CFL数为5时,本文方法计算残差在35000步左右下降了9个量级,且基本为线性下降;LU-SGS格式残差下降5个量级后开始振荡,难以进一步收敛,且达到相同残差需要更多的时间步。当CFL数增加为50时,本文方法计算残差约在13000步下降9个量级,收敛效率进一步提高。
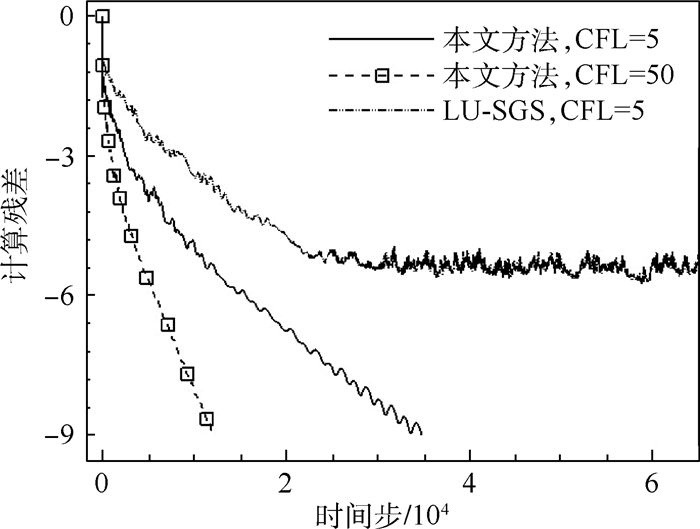 |
| 图 21 本文方法与LU-SGS格式残差收敛情况对比 Fig. 21 Comparison of residual convergence histories between proposed method and LU-SGS scheme |
| 图选项 |
图 22为升力系数CL收敛情况对比。当CFL数为5时,LU-SGS格式计算获得的CL为0.50083,本文方法获得的CL为0.49931;当CFL数为50时,本文方法获得的CL为0.499022,各方法计算结果差异不大。可见,当CFL数为5时,2种方法升力系数约在10000步左右达到收敛,当CFL数为50时,本文方法可使升力系数在4000步左右达到收敛。残差和升力系数收敛情况表明,本文方法对于复杂网格仍有较好的效率和稳定性。
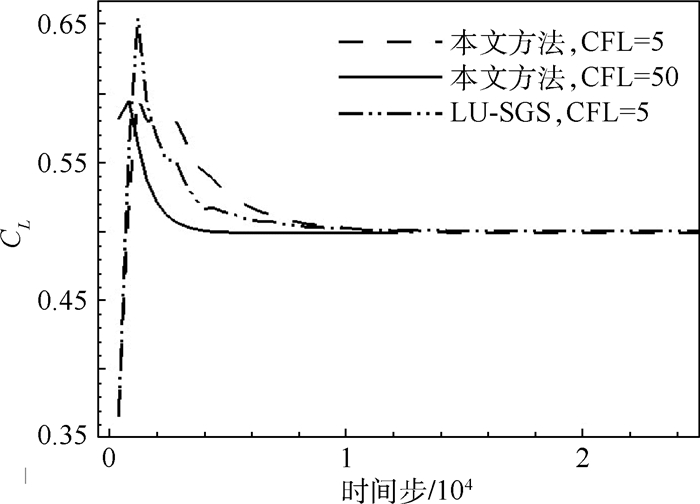 |
| 图 22 升力系数CL收敛情况对比Fig. 22 Comparison of lift coefficient CL convergence histories |
| 图选项 |
3.5 超声速轴对称压缩拐角模拟本算例是典型的超声速算例[22]。下面用其考察超声速流动下本文方法的计算效率及稳定性。计算网格见图 23。壁面附近为六面体网格,空间采用棱柱单元,共约包含30500个单元,第一层网格高度为5×10-3m。来流马赫数为5,特征长度L=0.252m,对应雷诺数为0.38×106,采用层流计算,内迭代步数为20,LU-SGS格式计算采用排序后网格,本文方法采用未排序网格。模型尺寸及具体参数见文献[22]。
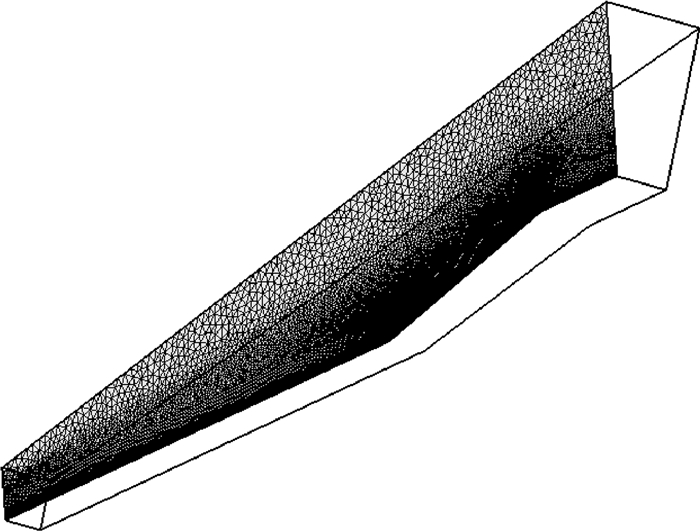 |
| 图 23 超声速轴对称压缩拐角计算网格Fig. 23 Computational grid of supersonic axial symmetry compress hollow corner |
| 图选项 |
图 24为密度纹影图。可见,空间流场合理,符合流动基本规律。图 25为使用来流压力pa进行无量纲化的壁面无量纲压力计算结果和实验结果对比,除了压力峰值有较大区别(该处与文献[22]中计算结果一致),其他位置计算和实验结果吻合较好。
 |
| 图 24 密度纹影图 Fig. 24 Schlieren of density |
| 图选项 |
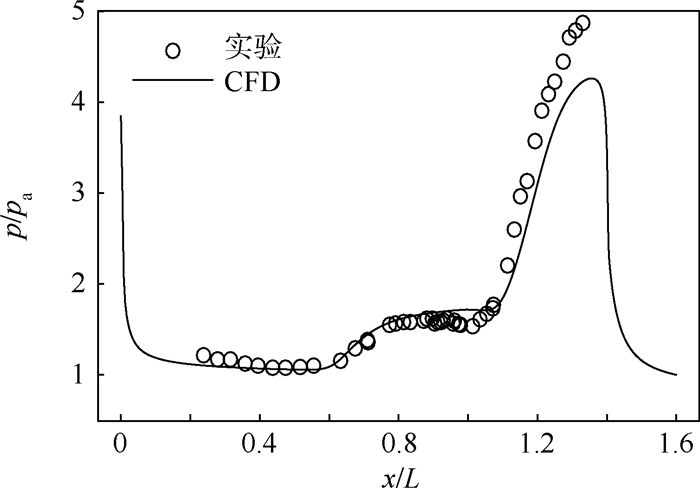 |
| 图 25 壁面无量纲压力计算结果与实验结果对比Fig. 25 Comparison of dimensionless pressure on wall between computaional and experimental results |
| 图选项 |
图 26为不同CFL数下本文方法与LU-SGS格式残差收敛情况对比。可见,当CFL数为20时,本文方法在时间步4000左右残差下降6个量级,而LU-SGS格式需要13000步左右。当CFL数大于20后,相比LU-SGS格式,本文方法加速幅度更大。对流场建立过程分析发现,本算例流场的大致结构很容易建立,因此在迭代开始阶段残差迅速下降;而当流场基本建立后,压缩拐角处分离区域向前发展十分缓慢,导致残差收敛变慢。
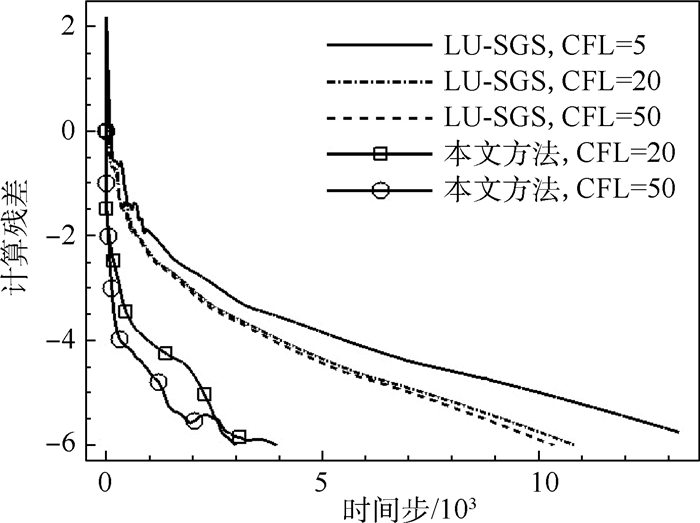 |
| 图 26 不同CFL数下本文方法与LU-SGS格式残差收敛情况对比Fig. 26 Comparison of residual convergence histories between proposed method and LU-SGS scheme for different CFL numbers |
| 图选项 |
图 27为不同CFL数下本文方法与LU-SGS格式残差随计算时间对比。可见,当内迭代步数取20,收敛到同样精度,本文方法计算时间约为LU-SGS格式的一半。结果表明,对于超声速流动,本文方法仍具有较好的计算效率及鲁棒性。
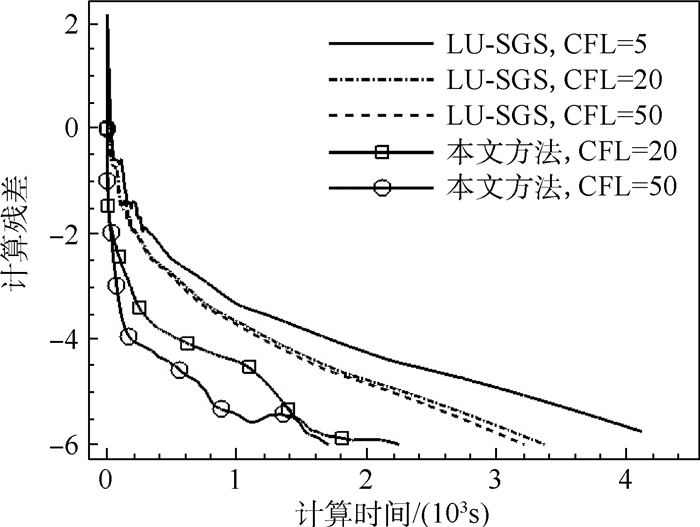 |
| 图 27 不同CFL数下本文方法及LU-SGS格式残差随计算时间对比Fig. 27 Comparison of residual convergence histories versus CPU time between proposed method and LU-SGS scheme for different CFL numbers |
| 图选项 |
4 结 论本文提出一种适于复杂混合网格的改进雅可比迭代方法,研究结果表明:
1) 通过改进方法流程,本文方法无需预先进行网格排序即能达到较好的收敛性能;也无需进行网格分组即可实现算法并行化。
2) 采用基于共享内存的OpenMP方法实现并行计算,简单方便,并行结果与串行结果一致。
3) 相对于LU-SGS格式,本文方法内存需求增加不大。采用本文方法计算ONERA-M6机翼复杂外形,共计220万混合网格,内存需求比LU-SGS 格式仅增加了9.9%。
4) 采用基于重构变量的近似通量函数构造通量雅可比矩阵,有利于满足矩阵对角占优,且不会影响方法的收敛性能。算例表明,在各来流条件下,相比于LU-SGS格式,本文方法稳定性及鲁棒性较好,收敛速度更快。
基于本文的工作,下一步将结合混合网格重叠模块,把本文方法应用到复杂外形的多体分离运动非定常数值模拟中去。
参考文献
| [1] | 阎超,于剑, 徐晶磊,等.CFD模拟方法的发展成就与展望[J].力学进展,2011,41(5):562-589. YAN C,YU J,XU J L,et al.On the achievements and prospects for the methods of computational fluid dynamics[J].Advances in Mechanics,2011,41(5):562-589(in Chinese). |
| Cited By in Cnki (107) | Click to display the text | |
| [2] | VENKATAKRISHNAN V, MAVRIPLIS D J.Implicit solvers for unstructured meshes[J].Journal of Computational Physics,1993,105(1):83-91. |
| Click to display the text | |
| [3] | KNIGHT D D. A fully implicit Navier-Stokes algorithm using an unstructured grid and flux difference splitting:AIAA-1993-0875[R].Reston:AIAA,1993. |
| Click to display the text | |
| [4] | JAMESON A, YOON S.Lower upper implicit scheme with multiple grids for the Euler equations[J].AIAA Journal,1987,25(7):929-935. |
| Click to display the text | |
| [5] | MAVRIPLIS D J. On convergence acceleration techniques for unstructured meshes:AIAA-1998-2966[R].Reston:AIAA, 1998. |
| Click to display the text | |
| [6] | SHAROV D, LUO H,BAUM J D,et al.Implementation of unstructured grid GMRES+LU-SGS method on shared-memory,cache-based parallel computers:AIAA-2000-0927[R].Reston:AIAA,2000. |
| [7] | CHEN R F, WANG Z J.Fast,block lower-upper symmetric Gauss Seidel scheme for arbitrary grids[J].AIAA Journal,2000,38(12):2238-2245. |
| Click to display the text | |
| [8] | TOMARO R F, STRANG W Z,SANKAR L N.An implicit algorithm for solving time dependent flows on unstructured grids:AIAA-1997-0333[R].Reston:AIAA,1997. |
| Click to display the text | |
| [9] | SHAROV D, NAKAHASHI K.Reordering of 3-D hybrid unstructured grids for vectorized LU-SGS Navier-Stokes computations:AIAA-1997-2102[R].Reston:AIAA,1997. |
| Click to display the text | |
| [10] | LUO H, BAUM J D,LÖHNER R.A fast,matrix-free implicit method for compressible flows on unstructured grids[J].Journal of Computational Physics,1998,146(2):664-690. |
| Click to display the text | |
| [11] | SAAD Y.GMRES:A generalized minimum residual algorithm for solving nosymmetric linear systems[J].SIAM Journal on Scientific and Statistical Computing,1986,7(3):856-869. |
| Click to display the text | |
| [12] | ZHANG L P, CHANG X H,DUAN X P,et al.A block LU-SGS implicit unsteady incompressible flow solver on hybrid dynamic grids for 2D external bio-fluid simulations[J].Computers & Fluids,2009,38(2):290-308. |
| Click to display the text | |
| [13] | LUCAS P,BIJL H, VAN ZUIJLEN A H.Efficient unsteady high Reynolds number flow computations on unstructured grids[J].Computers & Fluids,2010,39(2):271-282. |
| Click to display the text | |
| [14] | WANG G, JIANG Y W,YE Z Y.An improved LU-SGS implicit scheme for high Reynolds number flow computations on hybrid unstructured mesh[J].Chinese Journal of Aeronautics,2012,25(1):33-41. |
| Click to display the text | |
| [15] | 蒋跃文,叶正寅, 王刚.基于非结构网格的高效求解方法研究[J].计算力学学报,2012,29(2):217-223. JIANG Y W,YE Z Y,WANG G.Efficient solution of Euler/NS equations on unstructured grids[J].Chinese Journal of Computational Mechanics,2012,29(2):217-223(in Chinese). |
| Cited By in Cnki (5) | Click to display the text | |
| [16] | BLAZEK J. Computational fluid dynamics:Principles and applications[M].Oxford:Elsevier,2001:16-17. |
| [17] | ROE P L. Approximate riemann solvers,parameter vectors and difference schemes[J].Journal of Computational Physics,1981,43(2):357-372. |
| Click to display the text | |
| [18] | BARTH T J. A 3-D upwind Euler solver for unstructured meshes:AIAA-1991-1548[R].Reston:AIAA,1991. |
| Click to display the text | |
| [19] | VENKATAKRISHNAN V. Convergence to steady state solutions of the Euler equations on unstructured grids with limiters[J].Journal of Computational Physics,1995,118(1):120-130. |
| Click to display the text | |
| [20] | SPALART P R, ALLMARAS S R.A one-equation turbulence model for aerodynamic flows:AIAA-1992-0439[R].Reston:AIAA,1992. |
| Click to display the text | |
| [21] | LEE-RAUSCH E M, FRINK N T,MAVRIPLIS D J,et al.Transonic drag prediction on a DLR-F6 transport configuration using unstru-ctured grid solvers:AIAA-2004-0554[R].Reston:AIAA,2004. |
| Click to display the text | |
| [22] | BENAY R,CHANETZ B, MANGIN B,et al.Shock wave transitional boundary-layer interactions in hypersonic flow[J].AIAA Journal,2006,44(6):1243-1254. |
| Click to display the text |
