在速度模型描述中,显式地表达速度间断面信息十分必要。地质沉积构造的一个重要特征是层内物性相似而层间相差较大,速度间断面将整个地质模型空间天然地划分为一系列不规则的块体。在块体内部,速度变化光滑而缓慢,而在块体边界处速度发生间断,变化急剧。因此,单纯的实体建模技术难以满足对此类特征的描述要求,需要结合表面建模技术实现对速度间断面的专门描述[3]。速度间断面的表达形式主要包括参数化曲线或曲面(如分段线性函数[4]、二次样条曲面[5]等)、三角网格[6]以及模拟地质层面演化的变形层面[7]。但是,目前已有的参数化方法都存在不同程度的简化,一些不足主要表现在:①采用分段线性函数表达时,在线条或面片的连接处存在不连续,这对正演射线追踪极其不利,会造成射线阴影区;②当速度间断面具有非流形的性质时,现有的参数化方法描述乏力;③当地质层面(体)发生完全断裂时,已有的方法常常处理为2个独立的层面(体),隔断了其内部的地质联系;④对速度间断面和块体内速度场的描述一般要分别采用不同的参数化形式,增加了后续应用的复杂性。
理想的速度模型应该是:一方面能够充分描述各种尺度的速度信息,另一方面能够为正、反演应用提供便利。本文提出的模型表达方法能够较好地克服已有模型表达方法的不足,健壮地描述复杂的速度模型,并基于该模型继续开展正、反演应用研究。
1 复杂地质速度模型表达复杂的速度模型包括2类元素:速度间断面以及由速度间断面和区域边界构成的块体。其中,速度间断面是指由模型中速度发生突变的相关边界构成的层面,具有与地质上的地层面的一般对应性。对于2类模型元素,分别采用不同的参数化方法描述,但都基于相同的计算网格。这种底层网格的统一性能够降低由于模型因素造成的复杂性,有利于提高正、反演应用的效率。
对于模型的描述主要包括3个方面:模型元素的空间拓扑描述、速度间断面的描述和块体内速度场的描述。
1.1 模型元素的空间拓扑描述当地质构造复杂时,速度模型亦十分复杂。例如,当存在尖灭、侵入和断裂等地质现象时,复杂的层面相交关系会使速度模型的描述异常困难。因此,对模型元素的空间拓扑进行事先的定义十分必要,主要表现在3个方面:①有利于对模型元素的参数化描述;②有利于空间点的快速定位(在基于射线理论的正、反演应用中,这是一项十分频繁的操作);③有利于对模型数据的高效管理。本文采用速度间断面二叉树来描述模型元素的空间拓扑关系。
速度间断面二叉树是一种数据结构,用于描述速度间断面的空间位置关系,以及间断面对模型空间的划分。其基本思想是:每个速度间断面将模型空间划分为2个部分,则所有的间断面可以构成对模型空间的一种完全划分。速度间断面二叉树采用递归的形式构造,构造算法描述如下。
算法1 速度间断面二叉树的构造算法
1) 对发生相交的速度间断面指定主从关系,主间断面总是切断从间断面,而使从间断面不再完整。
2) 按照主从关系优先、自上而下次优先的排序规则,将速度间断面排列成一个有序序列G。
3) 选择任意速度间断面H∈G,H将模型空间分为2个部分,也将间断面序列G划分成左右2个有序子序列Gleft和Gright。
4) 以H为根构造二叉树,Gleft为H的左子树的待构造序列,Gright为H的右子树的待构造序列。
如果Gleft为空,则存在不可划分的块体S成为H的左叶子节点;否则,使用左子序列Gleft递归构造左子树。
如果Gright为空,则存在不可划分的块体S成为H的右叶子节点;否则,使用右子序列Gright递归构造右子树。
5) 结束。
图 1是一个典型的块状速度模型,其中Hi(i=0,1,…,8)代表速度间断面,Sj(j=0,1,…,7)代表由速度间断面和区域边界围成的块体。值得注意的是,无论速度间断面和块体是否发生了断裂,都被视为一个完整的模型元素。例如,块体S2虽然断裂成2个部分,但仍然是一个有机整体,会被统一描述。
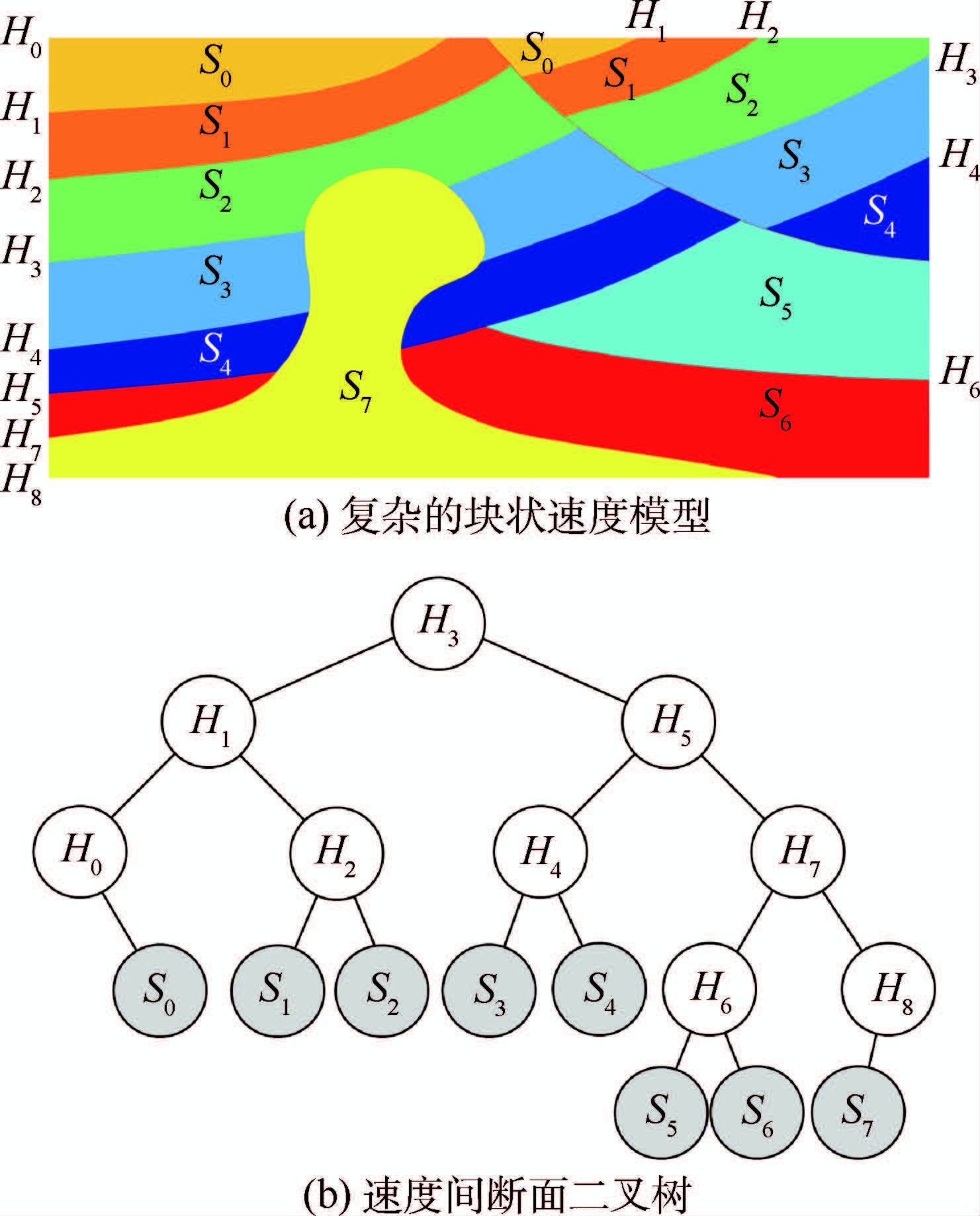 |
| 图 1 复杂的块状速度模型和对应的速度间断面二叉树 Fig. 1 Complex blocky velocity model and corresponding velocity discontinuity binary tree |
| 图选项 |
间断面二叉树除了具有通用二叉树的优良性质外,还具有以下特点:①每一个非叶子节点代表一个速度间断面,每一个叶子节点代表一个块体;②主间断面节点总是其从间断面节点的父节点或祖先节点;③对于任意一个非叶子节点,其子孙叶节点按照从左至右的顺序可以构成了一个速度间断面自上而下的子序列(或逆子序列)。
1.2 速度间断面的描述区别于常见的速度间断面的显式描述方法,本文采用隐函数的方法来描述速度间断面,将速度间断面表达成符号距离场的零等值面。符号距离函数的一般定义为
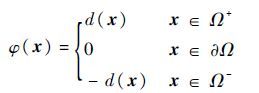
式中:Ω为欧氏空间的一个开放区域;d(x)为点x到区域边界Ω的欧氏距离。当x位于Ω内部时,距离为正;当x位于Ω外部时,距离为负;否则,x位于区域边界上。
相比于显式的表达方法,隐式表达的最大吸引力在于其对任意拓扑描述的支持。本文采用水平集(level set)方法构造符号距离函数。水平集方法起初用于跟踪界面传播和演化,是处理封闭运动界面随时间演化过程中几何拓扑变化的有效工具[8]。水平集方法的最大优点是它能够解决传统方法中难以处理的界面拓扑改变问题(如融合与断裂)。不过,目前水平集方法主要用于闭合流形曲面的表达[9, 10],用水平集方法为速度间断面构造符号距离函数存在以下困难:①速度间断面往往并不是闭合曲面;②速度间断面可能具有非流形性质(如某种部分断裂的层面)。针对这些难点,本文对水平集方法进行扩展和修正。
在模型元素空间拓扑描述中,每个速度间断面在空间中构成对模型的一种划分,将模型空间划分为2个部分。根据这一特征,本文对符号距离函数重新定义如下:函数定义域限定为整个模型空间,当x位于速度间断面上部时,距离为正;当x位于速度间断面下部时,距离为负;否则,x位于速度间断面上,距离为零。新定义与原定义并不冲突,是原定义的变形,即将速度间断面以上的模型空间视为区域内部,而速度间断面以下的空间视作区域外部。新定义使得水平集方法同样适用于构造非闭合曲面的符号距离场。
通过分析可知,速度间断面出现非流形特征的主要原因是,速度间断面发生了不全完断裂。断裂源于地质上的断层,实事上,地质断层只是一个逻辑概念,真实的地下介质中并不存在这种显式的地质层面,而通常只是在地质建模的应用中,被显式地描述出来,用以表达地质体的断裂现象。在本文的速度模型描述中,这种断裂行为被渗透进速度间断面的描述之中,断裂的间断面被视作一个整体,统一进行描述。这种策略基于对地质沉积规律的基本认识:当一个地质块体发生断裂,无论裂通与否,都具有相似的物性参数和属性分布。而对于这一点,现有的参数化方法很难做到。为描述断裂的速度间断面,本文借助水平集方法关于界面运动演化的思想,让一个完整的层面在运动演化中自动发生断裂。具体做法是:将地质断层显式地内嵌于计算网格之中,并切断断层两侧的网格拓扑。因为断层形状相对简单,这一点利用成熟的基于限定条件的三角网格生成技术很容易实现。本文采用了限定Delaunay网格生成算法[11],将断面作为限定约束条件,生成不规则的Delaunay三角网格,并取消断面两侧三角形的邻接关系。图 2描述了为断裂的速度间断面构造水平集的基本思想。
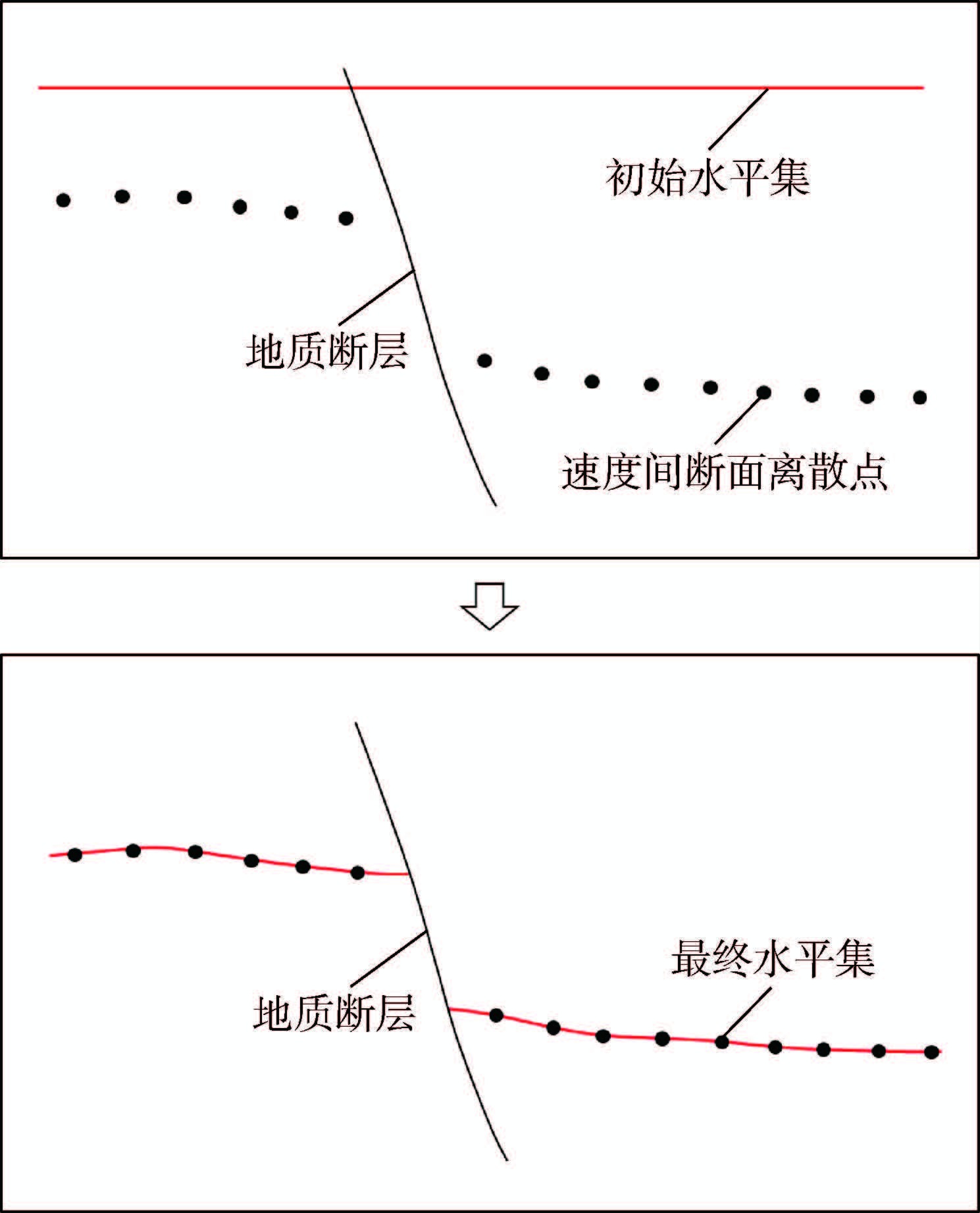 |
| 图 2 为断裂的速度间断面构造水平集 Fig. 2 Construction of level set for faulted velocity discontinuity |
| 图选项 |
无论是完整的速度间断面,还是断裂的速度间断面,水平集都为它们构造出一个符号距离场,间断面都以零等值面的形式隐式地存在。水平集的具体构造方法本文不再赘述,具体构造过程参见文献[8]。此外,需要强调的是,采用不规则网格作为计算网格的另外一个主要动机是,不规则网格可以拟合不规则的观测几何和不均匀的射线覆盖,这在层析反演应用中对于最大化抽取观测数据中的有用信息十分有利,而这一点利用限定的三角网格生成技术[11]很容易实现。当然,如果不考虑对观测数据不规则性的拟合,以及对断裂的速度间断面的表达,采用规则的笛卡儿网格作为计算网格是可行的,但这会极大地限制对复杂模型的表达能力。
1.3 块体内速度场的描述在基础网格上直接为不同块体填充速度存在一些问题,以图 3(a)说明这一情形。速度间断面H横穿三角面片abc,速度间断面之上属于块体S1,速度间断面之下属于块体S2,目标问题是计算三角面片内任意p点的速度值。显然,如果用顶点a、b和c的速度值直接进行内插,得到速度值是不合理的。因为a点属于块体S1,而b、c点属于块体S2,2个块体的速度存在跳跃,而插值的结果是2个块体速度的过渡值。显然,实际的p点属于块体S2,用块体S2的速度进行内插才为合理。此外,判断p点在速度间断面上方还是下方也是一个难于解决的前提问题。
本文给出一种策略,称之为多重拷贝策略,即与速度间断面相交的三角形同时存在多份拷贝。例如,对于图 3(a)中的三角形abc,同时存在2份拷贝:a′b′c′和a″b″c″,如图 3(b)、图 3(c)所示。三角形a′b′c′按照块体S1的填充规则填充速度,而a″b″c″三角形则填充块体S2的速度,2个三角形具有相同的拓扑和结构,但填充不同的内容,并分别属于不同的块体。如果出现速度间断面相交的情形,则可能出现超过2份拷贝的情形。在此例中,p点属于块体S2,所以可以直接使用三角形a″b″c″的填充速度进行合理插值。对于p点与速度间断面的相对位置问题,可以根据符号距离场的新定义,通过p点在速度间断面H的符号距离场值来判断,如果p点在间断面H的符号距离场中的值为正,则位于间断面H的上方;若为负,则位于下方。显然,此例中p点的符号距离场值φH(p)<0,因此p点在速度间断面H的下方,如图 3(d)所示。
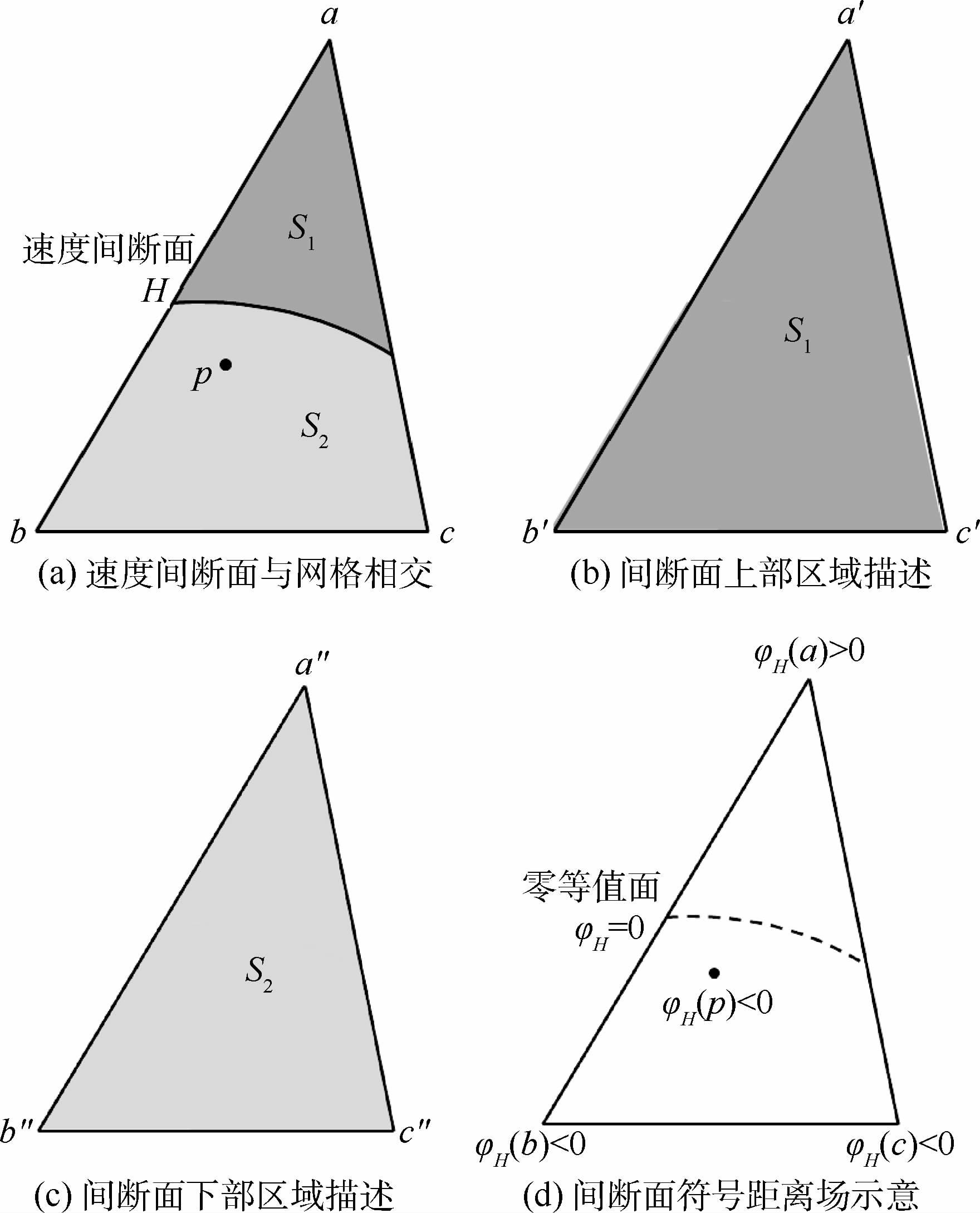 |
| 图 3 多重拷贝策略示意图 Fig. 3 Schematic of multi-copy strategy |
| 图选项 |
多重拷贝策略是通过为每一个块体绑定一个基础网格来实现的,该网格与描述速度间断面的符号距离场使用的计算网格共享拓扑和结构,但是用来填充速度。由于每一个块体只占模型较小区域,只需填充基础网格中较小的一部分(包括块体内部的网格和与块体边界相交的网格),因此,高效的布尔操作可以大大提高计算效率,并降低存储开销。此外,由于符号距离场和速度场共享网格拓扑和结构,所以可以用速度间断面二叉树来统一管理所有的模型元素。
2 射线理论的应用射线追踪方法是一种快速有效的波场近似计算方法,对于地震波理论研究具有重要意义。其理论基础是,在高频近似条件下,地震波场的主能量沿射线轨迹传播[12]。因此,射线轨迹的正确性对基于射线理论的正、反演计算意义重大。本文提出的隐式嵌入速度间断面信息的速度模型表达方案能够为射线追踪提供便利。
在复杂的速度模型中,实施经典的射线追踪所涉及的关键问题主要包括:空间点定位问题和速度间断面的感知问题。在规则的笛卡儿网格中,空间点的定位微不足道,可以通过网格定义迅速得到,但规则网格对速度间断面的表达能力弱,“阶梯”状的近似表达常使射线无法及时感知,从而导致错误的追踪路径。显式地感知界面的存在,并按照Snell定律发生折射,是经典射线方法的重要发展趋势。下面分别给出本文模型表达方法关于这2个问题的解决方案。
速度间断面二叉树描述了模型元素的空间拓扑关系,结合符号距离场,可以高效地实现对空间中任意点的快速定位,并计算所在点的速度信息,空间任意点的定位算法描述如下。
算法2 空间任意点定位算法
1) 对于模型空间中的任意一点p,利用“三角形步进”算法[13]在基础网格中定位其所在的三角形T。
2) 在速度间断面二叉树中查找点p所在块体,从根节点开始查找:
如果当前节点为非叶节点,则根据当前节点所代表符号距离场和p点所在网格T,计算p点的符号距离值φ(p)。如果φ(p)>0,则递归查找当前节点的左子树;如果φ(p)<0,则递归查找当前节点的右子树。
如果当前树节点为叶节点,则该节点所代表的块体即为点p所在块体,转向步骤3)。
3) 结束。
利用速度间断面二叉树和符号距离场,也能够使射线快捷地感知速度间断面,并按照Snell定律显式地发生偏折。射线与速度间断面的相交检测算法描述如下。
算法3 射线与速度间断面的相交检测算法
1) 对于任意射线步$\overrightarrow {ab} $,即射线由a点旅行至b点的有向线段,利用算法2,分别定位a、b点所在的块体Sa和Sb。
2) 判断射线步$\overrightarrow {ab} $是否与速度间断面相交:
如果Sa和Sb为同一块体,则$\overrightarrow {ab} $未与任何速度间断面相交,转向步骤5);
如果Sa和Sb为不同块体,则至少存在一个速度间断面与$\overrightarrow {ab} $相交,转向步骤3)。
3) 确定相交速度间断面。在速度间断面二叉树中,检查Sa(或Sb)对应叶节点到根节点的溯祖路径上的每个非叶节点,如果a、b点在该非叶结点对应的符号距离场中符号相反,则可以确定射线步$\overrightarrow {ab} $与该符号距离场所描述的速度间断面H相交,转向步骤4)。
4) 计算交点。根据a、b点在速度间断面H对应的符号距离场中的符号距离值,线性插值交点的位置。
5) 结束。
3 应用实例为了验证本文模型表达方法的可用性和有效性,给出2组应用实例。
第1组应用实例仍采用图 1中的模型结构,该模型包含断裂、侵入等复杂地质构造现象。以该模型为原形,为不同的块体填充不同的常量速度,并采用2种不同的模型表达方案:规则的矩形网格和本文模型表达方法。本文方法能够实现对速度模型无简化的描述,而矩形网格在速度间断面处是一种阶梯状的近似。在地表x=500 m处发射一组射线,分别在2种模型上进行射线追踪,结果如图 4所示。在本文提出的模型表达方案中,射线能够显式地感知速度间断面,并严格按照Snell定律发生偏折;而在规则网格模型上,由于没有关于速度间断面的显式表达,当射线遇到速度突变时不能及时地改变方向,从而导致较大偏差(射线R1)甚至方向截然不同的射线路径(射线R2)。
 |
| 图 4 基于复杂速度模型的射线追踪 Fig. 4 Ray tracing in complicated velocity model |
| 图选项 |
第2组应用实例是一组量化的考察对比,主要涉及采用波前重构方法[14, 15, 16]计算旅行时。模型采用具有倾斜层面的2层模型,之所以采用这样一个相对简单的模型,是因为基于该模型能够得到一个确定的旅行时解析解,从而为对比提供参照依据。模型区域大小为x×z=1 000 m×1 000 m,模型上层填充速度1 500 m/s,下层填充速度2 500 m/s,模型表达方案与第1组实例相同,震源设在地表x=500 m处。图 5给出了在2种模型上的波前追踪过程。采用本文模型表达方案,射线在速度间断面处主动地发生透射或反射,波前面在穿越速度间断面后仍然保持了平滑圆顺的波前形状。与此相对,在规则的矩形网格上,由于强烈的速度对比,射线在速度间断面处发生了不正确的偏折,并进一步导致错误的插值射线和波前推进,波前散乱甚至无法辨识。
 |
| 图 5 基于不同模型表达方案的波前重构方法 Fig. 5 Wave front construction method based on different model representation schemes |
| 图选项 |
在2种模型上的旅行时计算结果与解析解的误差如图 6所示。在规则网格模型上,旅行时在倾斜层面以下出现了很大误差,而在本文模型上,除了界面处,绝大部分误差都控制在0.001 s以内。界面处误差较大的原因是由于射线发生显式的偏折,在界面处插值旅行时的波前网格变得不太规则,统一的旅行时插值策略不太适用,但该误差不会随波前推进而传播,并且能够通过修正界面处的插值策略得到控制。
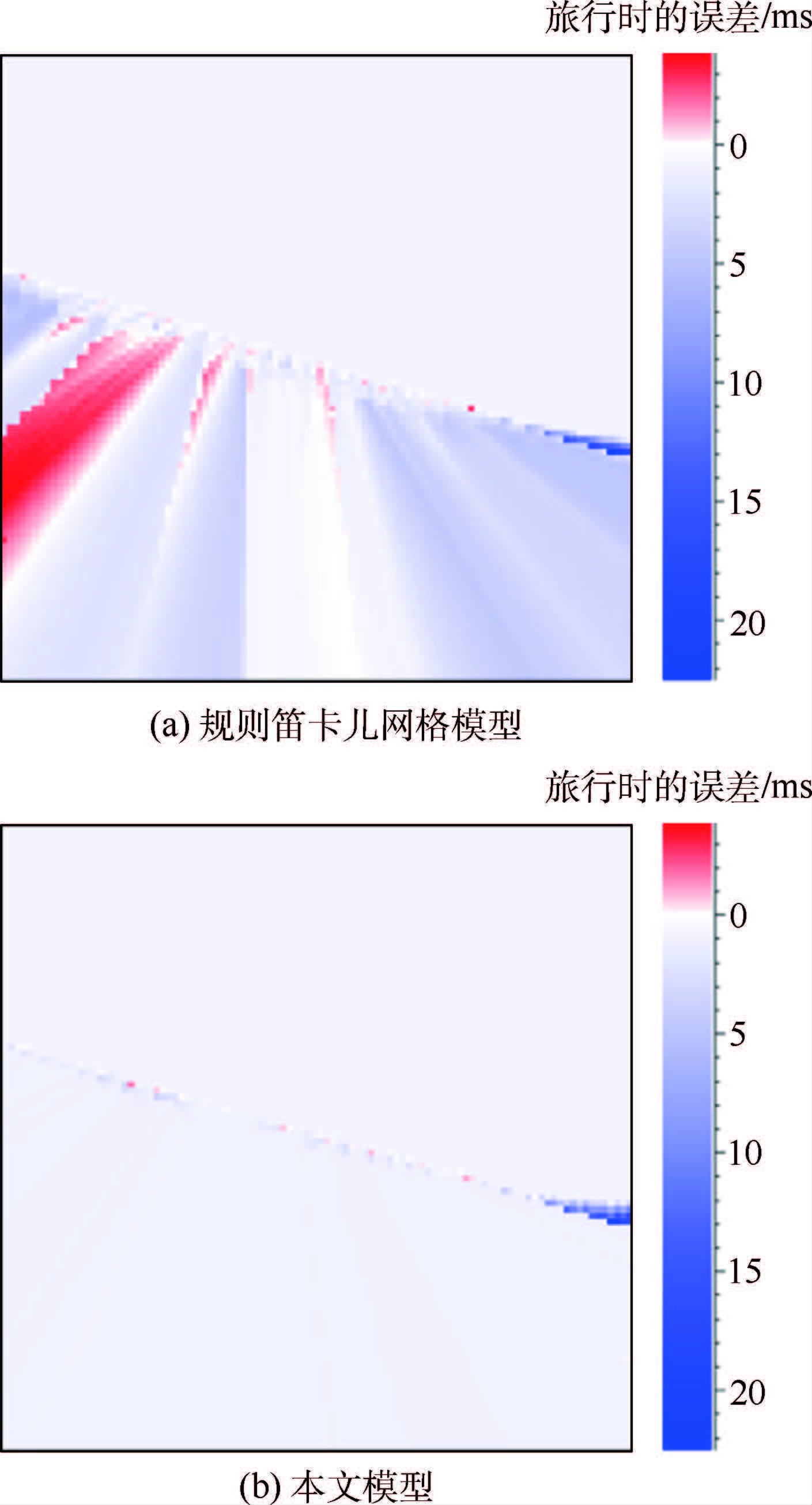 |
| 图 6 基于波前重构方法的旅行时误差对比 Fig. 6 Comparison of travel time errors based wave front construction method |
| 图选项 |
4 结 束 语显式地表达速度间断面信息是描述复杂速度模型的必要手段,本文采用隐式的方法将速度间断面描述为符号距离场的零等值面,多重拷贝策略使得速度块体相互独立,有效解决了速度间断面处的速度插值问题和界面感知问题。应用实例表明:该模型表达方法能够描述复杂的地质速度模型,并提高射线追踪的正确性,为基于射线理论的正、反演计算提供了便利。
参考文献
| [1] | YILMAZ Ö,DOHERTY S M.Seismic data analysis:Processing,inversion,and interpretation of seismic data[M].Tulsa:Society Exploration Geophysicists,2000:14. |
| [2] | LEVANDER A R,NOLET G,AMERICAN G U.Seismic earth:Array analysis of broadband seismograms[M].California:American Geophysical Union,2005:49-65. |
| [3] | 孟宪海,杨钦,李吉刚.基于层面结构的三维闭合地质区块构造算法[J].北京航空航天大学学报,2005,31(2):182-186. MENG X H,YANG Q,LI J G.Construction of coherent 3D geological blocks from stratified geological structure[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(2):182-186(in Chinese). |
| Cited By in Cnki (34) | |
| [4] | ZELT C,SMITH R.Seismic traveltime inversion for 2-D crustal velocity structure[J].Geophysical Journal International,1992,108(1):16-34. |
| Click to display the text | |
| [5] | PEREYRA V.Modeling,ray tracing,and block nonlinear travel-time inversion in 3D[J].Pure and Applied Geophysics,1996,148(3):345-386. |
| Click to display the text | |
| [6] | XU T,ZHANG Z,GAO E,et al.Segmentally iterative ray tracing in complex 2D and 3D heterogeneous block models[J].Bulletin of the Seismological Society of America,2010,100(2):841-850. |
| Click to display the text | |
| [7] | 张俊安,刘瑞刚,杨钦,等.复杂地质结构的四维地质层面自动生成算法[J].北京航空航天大学学报,2007,33(9):1094-1098. ZHANG J A,LIU R G,YANG Q,et al.Auto-construction algorithm of four-dimensional(4D) geological stratum on complex geological structure[J].Journal of Beijing University of Aeronautics and Astronautics,2007,33(9):1094-1098(in Chinese). |
| Cited By in Cnki | |
| [8] | OSHER S,SETHIAN J A.Fronts propagating with curvature-dependent speed:Algorithms based on Hamilton-Jacobi formulations[J].Journal of Computational Physics,1988,79(1):12-49. |
| Click to display the text | |
| [9] | OSHER S,FEDKIW R.Level set methods and dynamic implicit surfaces[M].New York:Springer,2003:7. |
| [10] | ZHAO H K,OSHER S,FEDKIW R.Fast surface reconstruction using the level set method[C]//Proceedings of IEEE Workshop on Variational and Level Set Methods in Computer Vision,2001.Piscataway,NJ:IEEE Press,2001:194-201. |
| Click to display the text | |
| [11] | 孟宪海,李吉刚,杨钦,等.复杂限定Delaunay三角化算法[J].中国科学:信息科学,2010,40(3):381-392. MENG X H,LI J G,YANG Q,et al.Algorithm of complex conforming delaunay triangulation[J].Science China:Information Sciences,2010,40(3):381-392(in Chinese). |
| Click to display the text | |
| [12] | ČERVENY V.Seismic ray theory[M].Cambridge:Cambridge University Press,2001:vii. |
| [13] | SAMBRIDGE M,BRAUN J,MCQUEEN H.Geophysical parametrization and interpolation of irregular data using natural neighbours[J].Geophysical Journal International,1995,122(3):837-857. |
| Click to display the text | |
| [14] | VINJE V,IVERSEN E,ÅSTEBØL K,et al.Estimation of multivalued arrivals in 3D models using wavefront construction-Part Ⅰ[J].Geophysical Prospecting,1996,44(5):819-842. |
| Click to display the text | |
| [15] | VINJE V,IVERSEN E,ÅSTEBØL K,et al.Estimation of multivalued arrivals in 3D models using wavefront construction-Part Ⅱ:Tracing and interpolation[J].Geophysical Prospecting,1996,44(5):843-858. |
| Click to display the text | |
| [16] | VINJE V,IVERSEN E,GJOYSTDAL H.Traveltime and amplitude estimation using wavefront construction[J].Geophysics,1993,58(8):1157-1166. |
| Click to display the text |
