依据取样原理的差异,现有地外钻取采样器主要包括软袋取心、压入式取心、排屑采样.前苏联的LUNA24无人钻取采样器采用柔性软袋的取样方式,能避免取心过程中样心与取心装置之间的相对运动,采样深度2.25 m,采样质量350 g[7, 8].美国NASA Ames研究中心及喷气推进实验室(JPL)和Honeybee Robotics公司联合研制的CRUX回转冲击钻取采样器,钻进深度大于1 m,钻进过程中能将样心压入取心管中[9, 10, 11].美国NASA的Curiosity火星漫游车2012年到达火星表面,装备组合式原位采样分析装置能够采集钻屑并开展火星表面岩石的分析[12, 13].欧空局Rosetta探测器上搭载的Philae着陆器于2014年11月成功降落在彗星67P的表面,Philae装备SD2钻取采样装置,此装置最大钻取深度为230 mm,能收集最大体积20 mm3的钻屑[14, 15, 16, 17].欧空局MRoSA项目中针对火星探测提出了两种深层钻探采样器,单钻杆采样器钻进深度1 m,多钻杆采样器能对接10根钻杆,钻进深度达2.5 m,采用空心钻杆收集将钻进过程中的样心[18].欧空局用于火星探测的Beagle2号着陆器上安装PLUTO末端采样器.该采样器借助机械臂的作用,能够在任意方向上潜入0.1~1.5 m深的火星土层进行多次采样,但是单次采样钻屑质量仅50 mg[19].此外,美国和欧洲的科研机构针对地外天体采样任务研制了多种超声波振动低功耗采样器,实现岩心和岩石碎屑的钻进取样[20, 21].上述钻取采样方式中,软袋取心方式能实现较大深度的次表层连续采样.在采样过程中,样心与软袋之间几乎没有相对运动,在提高取心率、保证样品的层理信息方面相对其他两种取心方式具有较大优势,对中国月球钻取采样任务有较大的借鉴意义.
为顺利完成钻取采样任务,需要在地面上进行钻进取样量的影响因素研究及试验验证.目前,软袋取心方式的取样量影响因素众多,尚无系统的分析方法进行解释.本文对钻进取样过程中的月壤-取心钻具相互作用进行了粉体动力学分析,构建了软袋取心方式的取样量估计方法,开展了模拟月壤钻进取心验证试验.这种分析方法将钻头构型和月壤特性作为影响因素,能实现不同钻进规程下取样量的预估.
1 软袋式钻进取样原理如图 1所示,软袋钻取采样机构主要由钻具和取心机构组成.钻具包括钻头和中空钻杆;取心机构由保持心管、内翻式月壤收集软袋、软袋拉绳、软袋封口机构等组成,保持心管的外壁衬套一层软袋,软袋内翻至心管的内孔中并由拉绳牵引.软袋钻取采样机构能够实现月壤的切削破坏、切屑排出、对样心的包裹、样心的封口、样心的取出等一系列的动作.
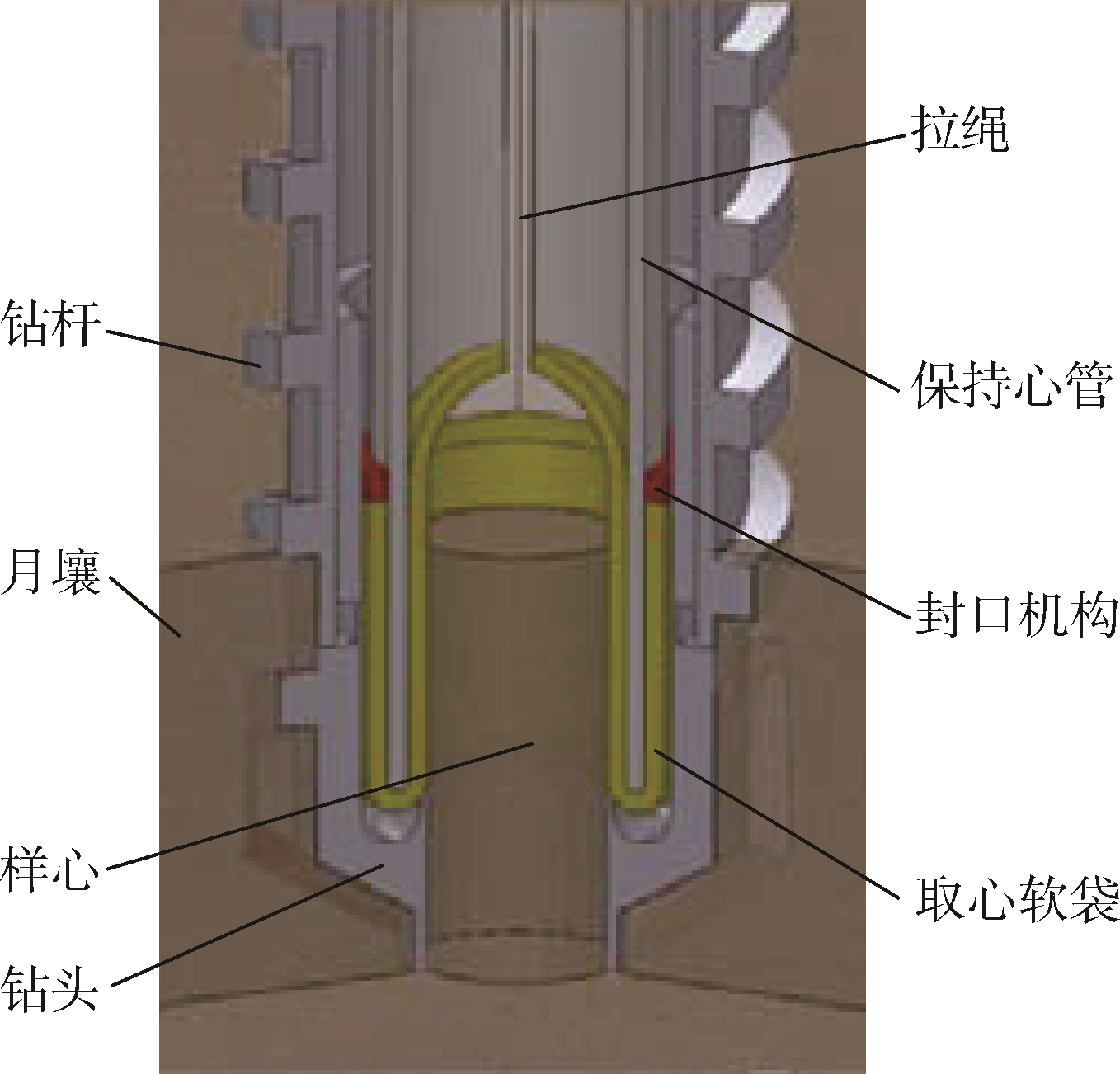 |
| 图 1 软袋钻取采样机构组成Fig. 1 Composition of flexible tube drilling and coring mechanism |
| 图选项 |
软袋取心机构的工作原理如图 2所示.驱动单元驱动钻杆回转并向下进尺;钻杆的外螺旋槽将月壤排至月面,钻头中心孔部位的月壤进入钻
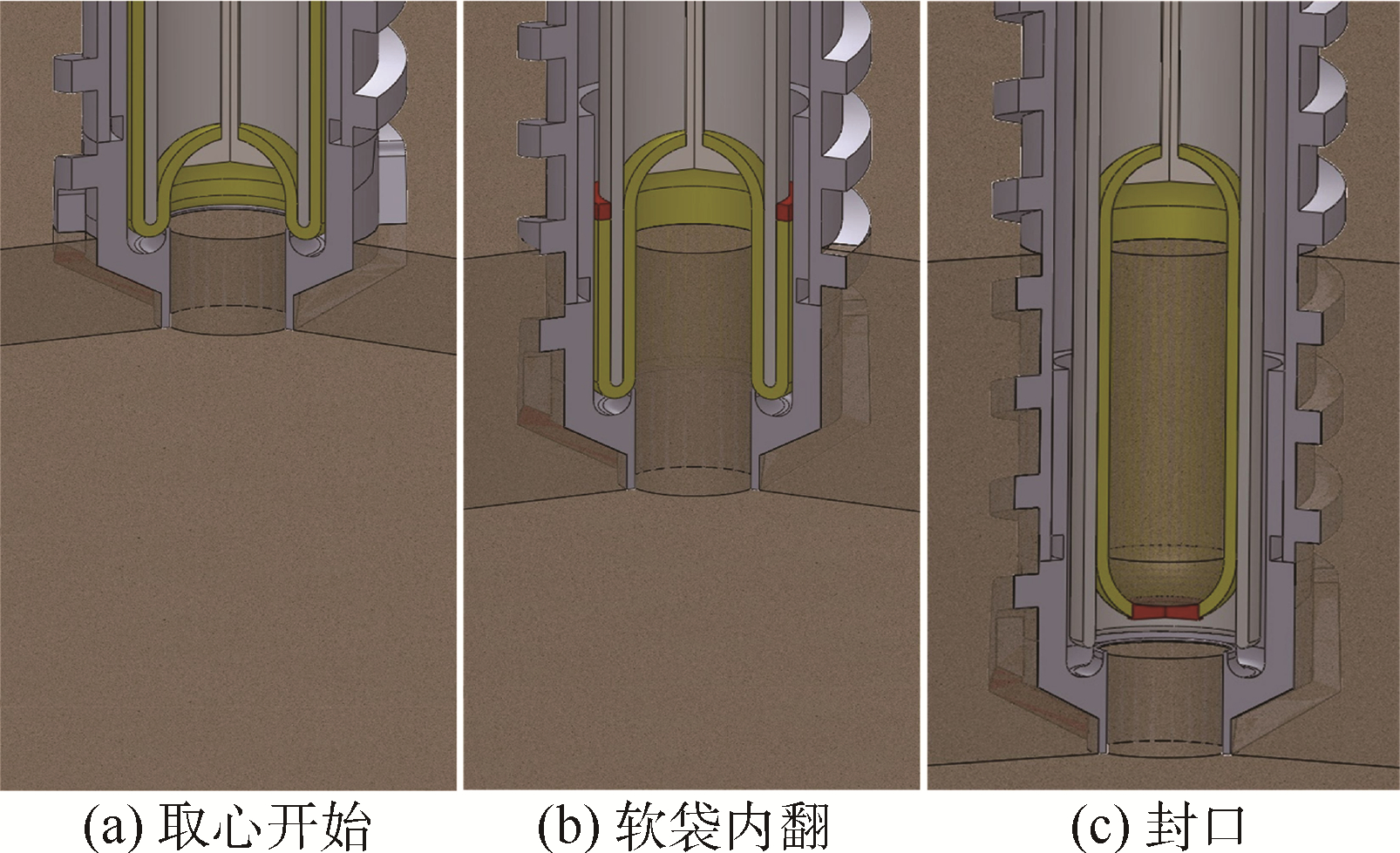 |
| 图 2 软袋取心工作过程Fig. 2 Working process of flexible tube coring |
| 图选项 |
杆的内腔;钻杆内腔中的一个周向不回转的刚性保持心管与钻杆一起进尺;当钻杆与心管向下进尺时,软袋在拉绳的牵引下便内翻至心管内部,软袋将进入心管的月壤无相对滑动地收集到软袋内;钻取完毕后,拉绳向上运动触发封口机构对样心的封口动作,并将软袋和样心从取心机构中取出,获得月壤样心.
2 软袋取心动力学建模在钻进取样过程中,月壤相对钻具和取心机构的运动较为复杂.不同部位的月壤的变形、流动情况大不相同,因此有必要对其划分区域,分别进行分析.
根据软袋取心过程中各部分土体相对于钻具位置的不同,将与钻具接触的土体分为3个部分,如图 3所示:已进入取心软袋内的土体I(交界面①处的接触应力为σ1)、取心钻头内孔中的土体Ⅱ(交界面②处的接触应力为σ2)、钻具外的土体Ⅲ(交界面②处的接触应力为σ3).这3个部分的土体相互接触,对各部分土体开展粉体动力学分析,根据各部分土体在交界面处的平衡条件对取样量进行预测.
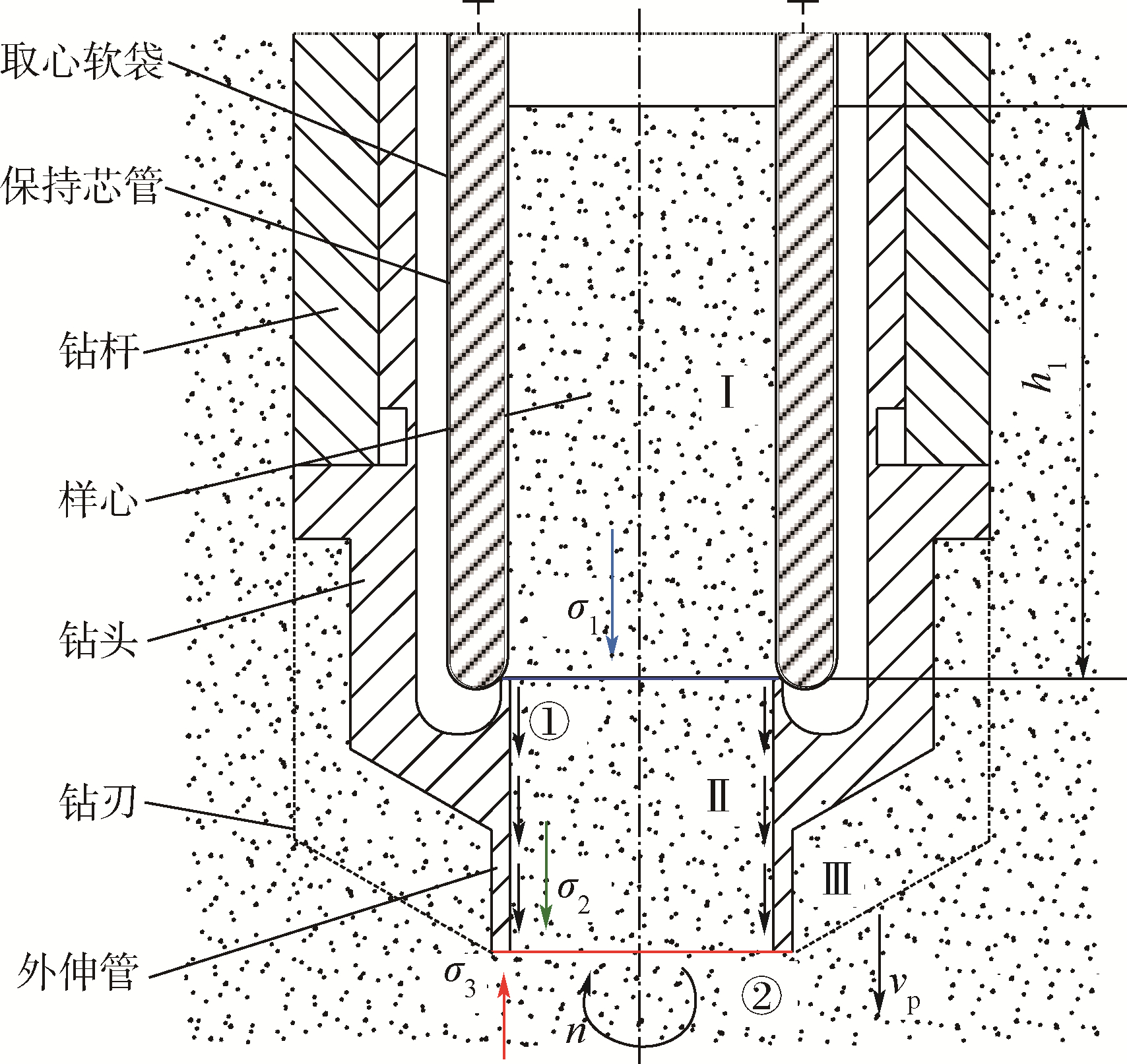 |
| vp-进尺速度;h1-徒弟I的高度;n-转速图 3 软袋取心准静态分析Fig. 3 Quasi-static analysis of flexible tube coring |
| 图选项 |
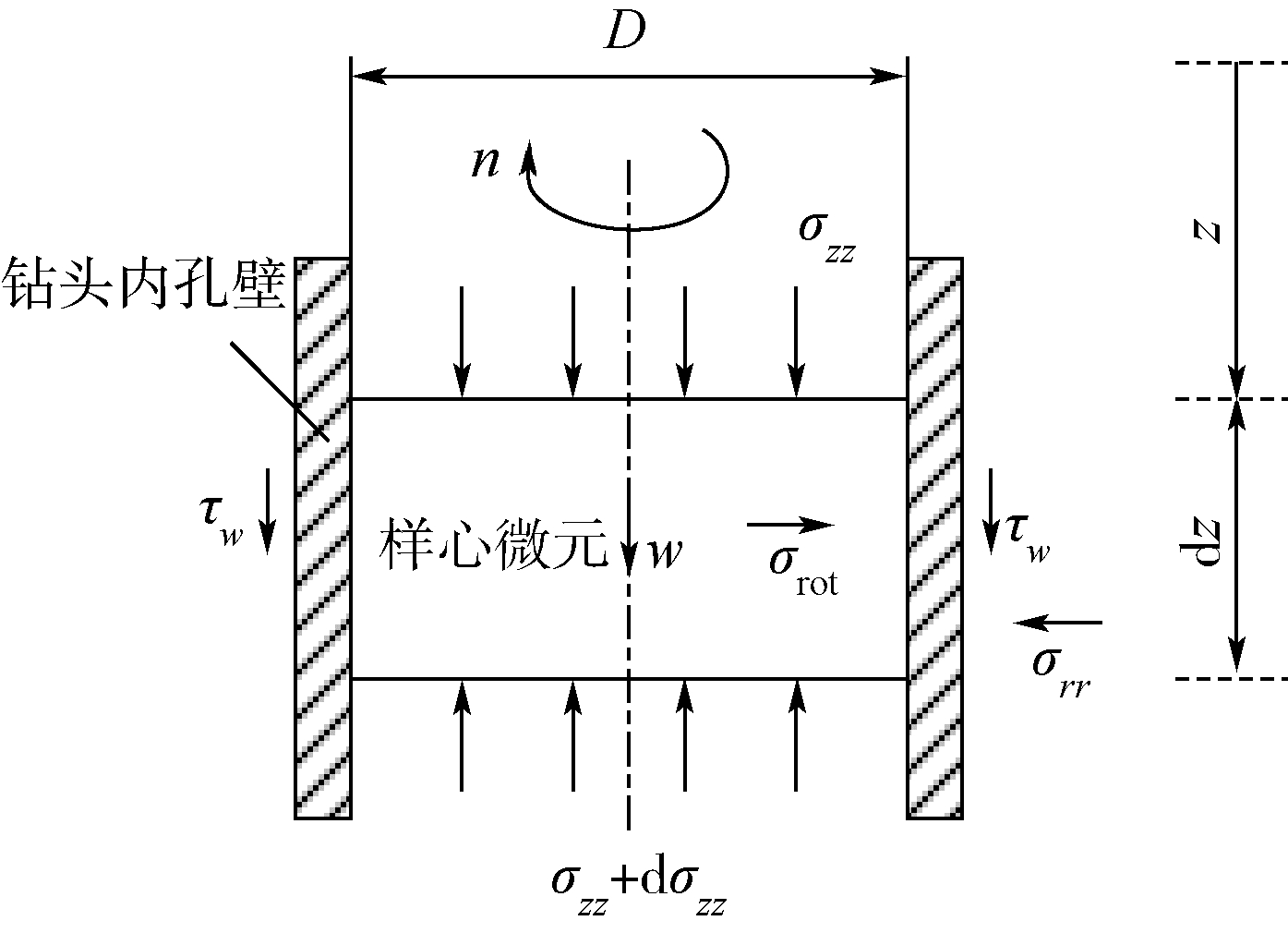
2.1 取心软袋内的土体I静态分析取心软袋内的土体I处于静止状态,当土体I即将发生向下滑动时,此时的取样量是取心机构当前工作状态下的最大值.假设土体只能整体的滑移,对土体I中厚度dz的微元进行极限平衡分析.如图 4所示,微元的受力由上下面的压应力σzz、软袋的接触应力σrr、τw和自身的重力w构成,其受力状态类似于颗粒物质中的粮仓效应[22].
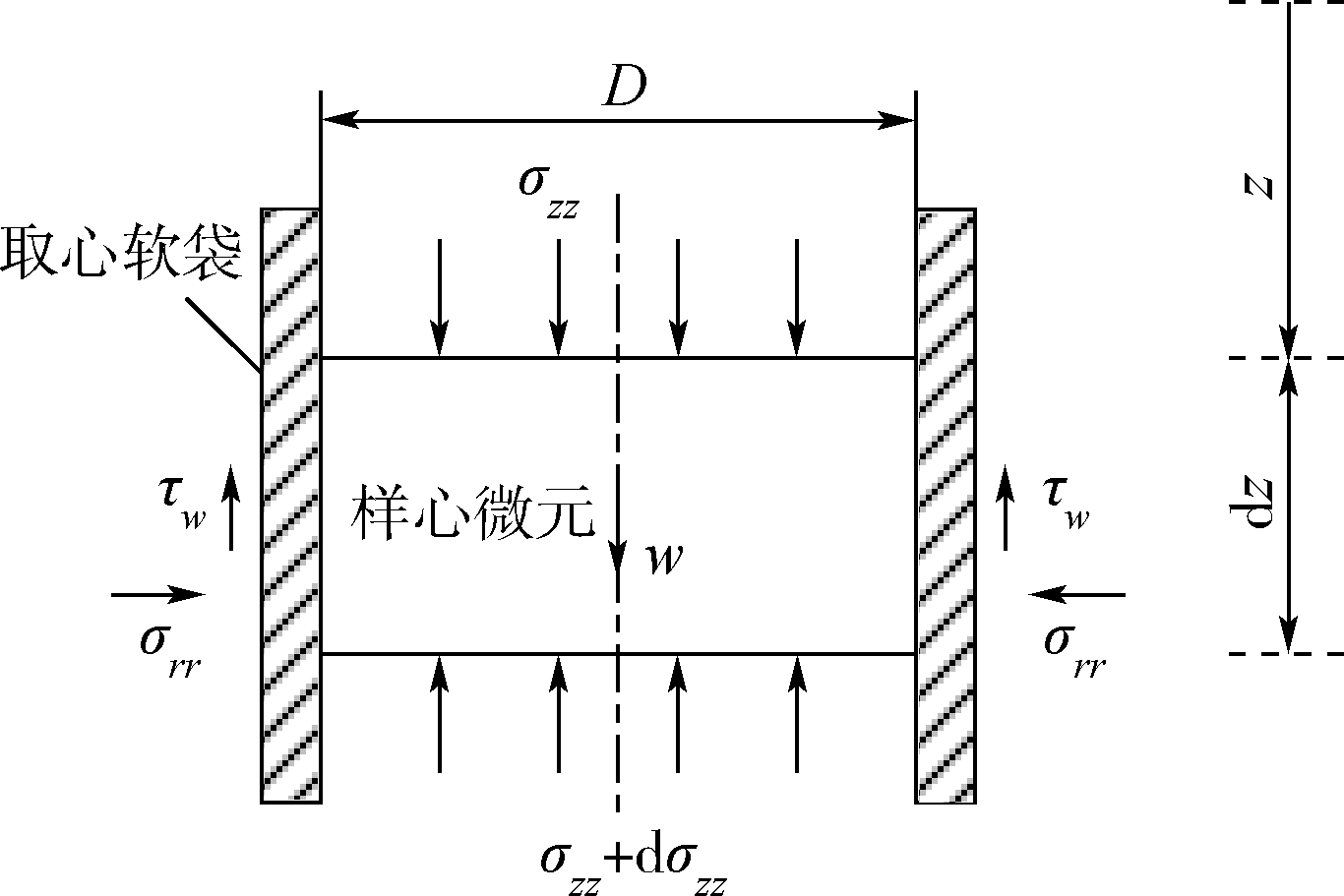 |
| 图 4 土体I微元Fig. 4 Element in Soil I |
| 图选项 |
1884年,英国科学家Roberts在研究粮仓地面的压强时发现,当粮食堆积高度约大于2倍地面直径后,粮仓地面所受的压强不随粮食的增加而增加,这就是著名的粮仓效应.1895年,德国工程师Janssen采用连续介质模型解释了粮仓效应,并得到了粮仓高度z处横截面上的压强:
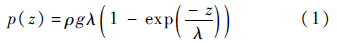
式中:ρ为堆积密度;g为重力加速度;z为粮仓高度,粮仓顶部z=0;λ为特征高度,$\lambda = \frac{R}{{2\mu K}},\mu $为颗粒与壁面的静摩擦系数,R为粮仓半径,K为力转向系数.
在土体受力分析中,转向系数K的取值由土的应力状态决定.当土体处于主动状态时,转向系数为KA;当土体处于被动状态时,转向系数为KP.
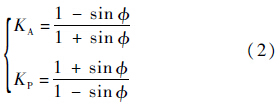
式中:$\phi $为土体的内摩擦角.
Janssen公式基于应力水平均匀分布和水平/竖直应力为主应力的假设,是一种近似的分析方法.尽管如此,在圆柱容器的分析和设计中,Janssen分析方法与数值方法差别很小,能够作为分析钻进取心的基本思路[22].据此,取心管底部支持应力为σ1时,可支持的土体I的高度为
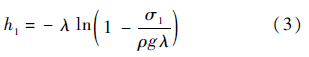
因此,当土体I具有下滑的运动趋势时,式(3)能根据底部支持应力σ1求得h1.
当界面①处支持力大到使取心管内土体I产生向上运动的趋势时,取心管内的样品所受的切应力τw方向发生改变,极限情况为样品整体向上滑动,此时样品土体处于被动状态,如图 5所示.
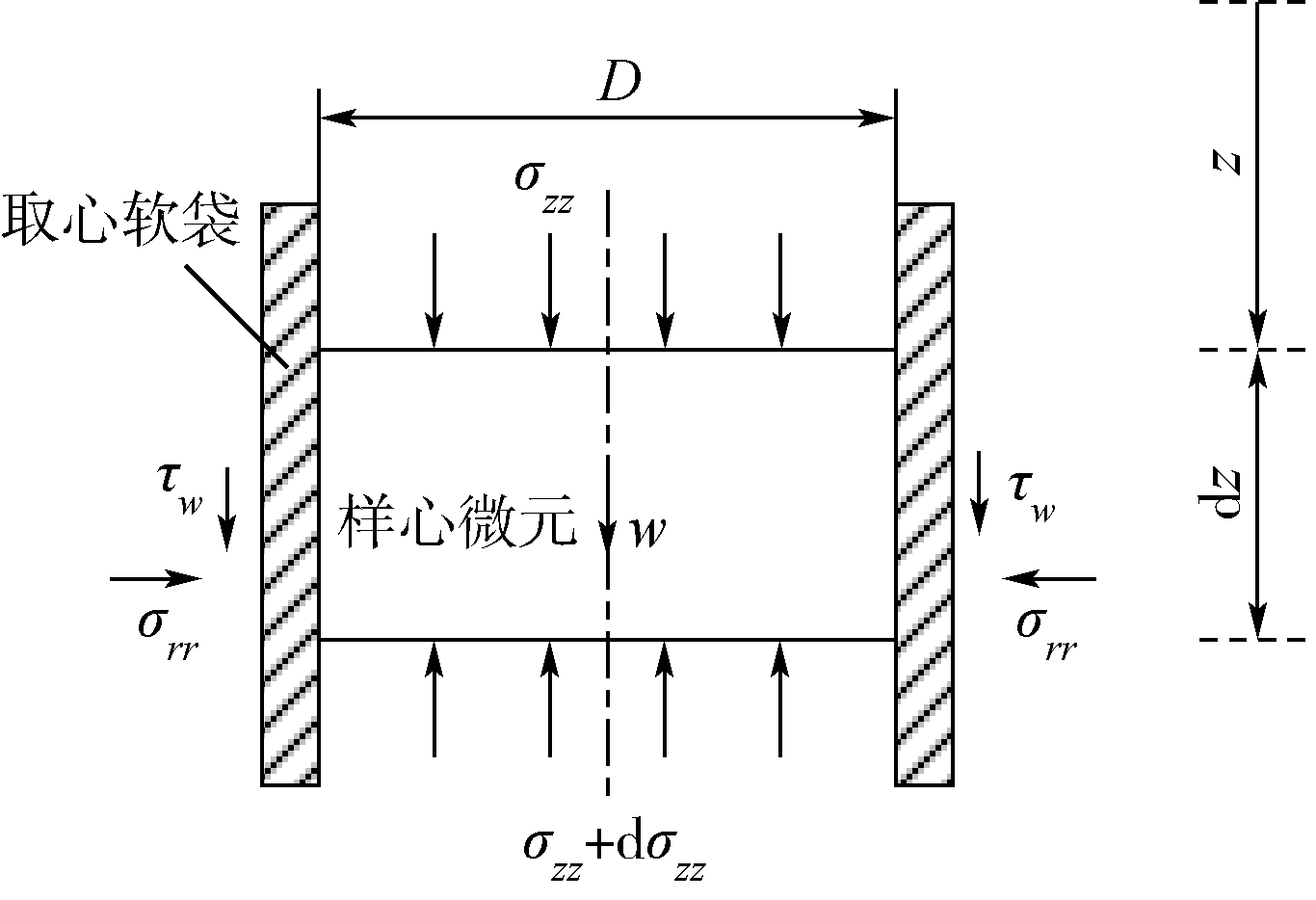 |
| 图 5 土体I微元向上运动Fig. 5 Upward movement of element in Soil I |
| 图选项 |
取心管内土体被向上推出的力平衡微分方程为
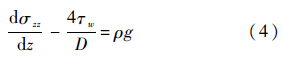
式中:

设土体在z=0处的受力为Q0,在边界条件σzz=Q0|z=0下,方程的解为
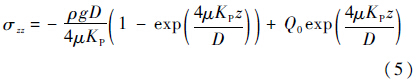
根据上述分析,分别绘制σ1=0~σ∞时土体I的高度变化,如图 6所示.
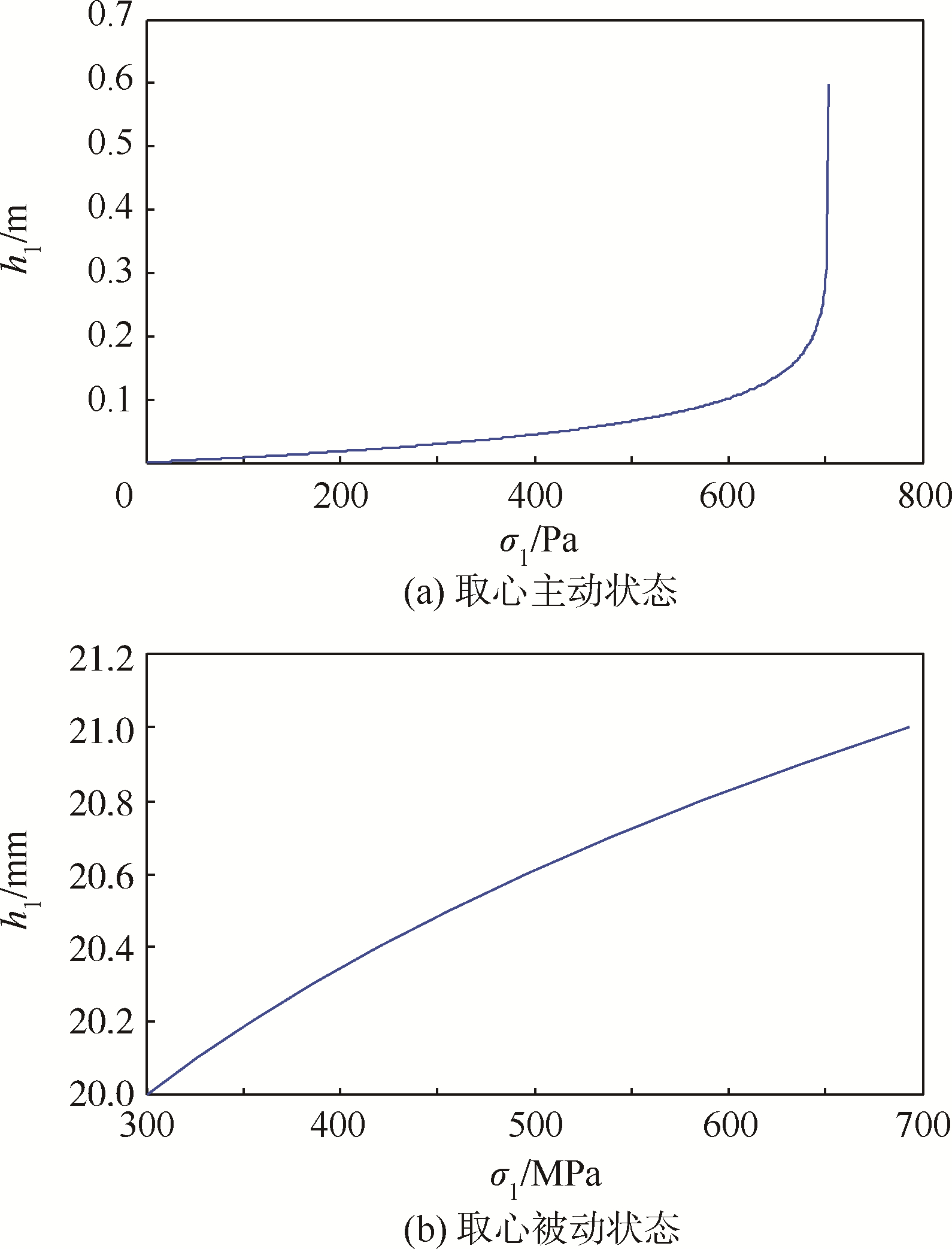 |
| 图 6 土体I主被动状态下的底面应力Fig. 6 Bottom stress of soil I in active and passive states |
| 图选项 |
对比图 6中的两种取心受力状态,取心被动状态的轴向应力σzz在较小的深度z比主动状态大,并且很快随着深度z增加产生数量级的差距,因此钻进取样过程中取心软袋内的样品难以发生向上滑动.
2.2 取心钻头内孔中土体Ⅱ动力学分析取心钻头内孔中的土体Ⅱ既有随着钻头的回转运动,又有相对钻头的向上运动,在土体内部可能还存在运动速度差.为简化分析,忽略土体内部的相对运动,将土体Ⅱ整体视为回转参考系中的被动状态土体,如图 7所示.样心相对钻头向上运动,受到钻头内孔壁向下的切向力τw作用,同时受到回转角速度ω下离心惯性力σrot的作用.
 |
| 图 7 土体Ⅱ微元Fig. 7 Element in Soil Ⅱ |
| 图选项 |
根据微元的受力分析,其动力学方程为
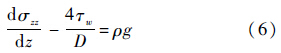
式中:
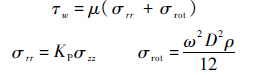
微分方程的解为
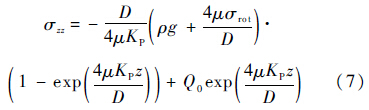
因此,获得σ1和σ2的关系:
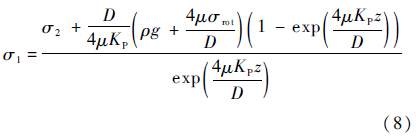
经前一切削刃切除后,产生与钻头内孔外伸管端面接触的土体表面.如图 8所示,由于钻头同时存在回转和进尺运动,钻头内孔外伸管端面与模拟月壤的接触应力包含法向应力σend和切向应力τend,图中圆环接触面的内外半径分别为R1和R2.
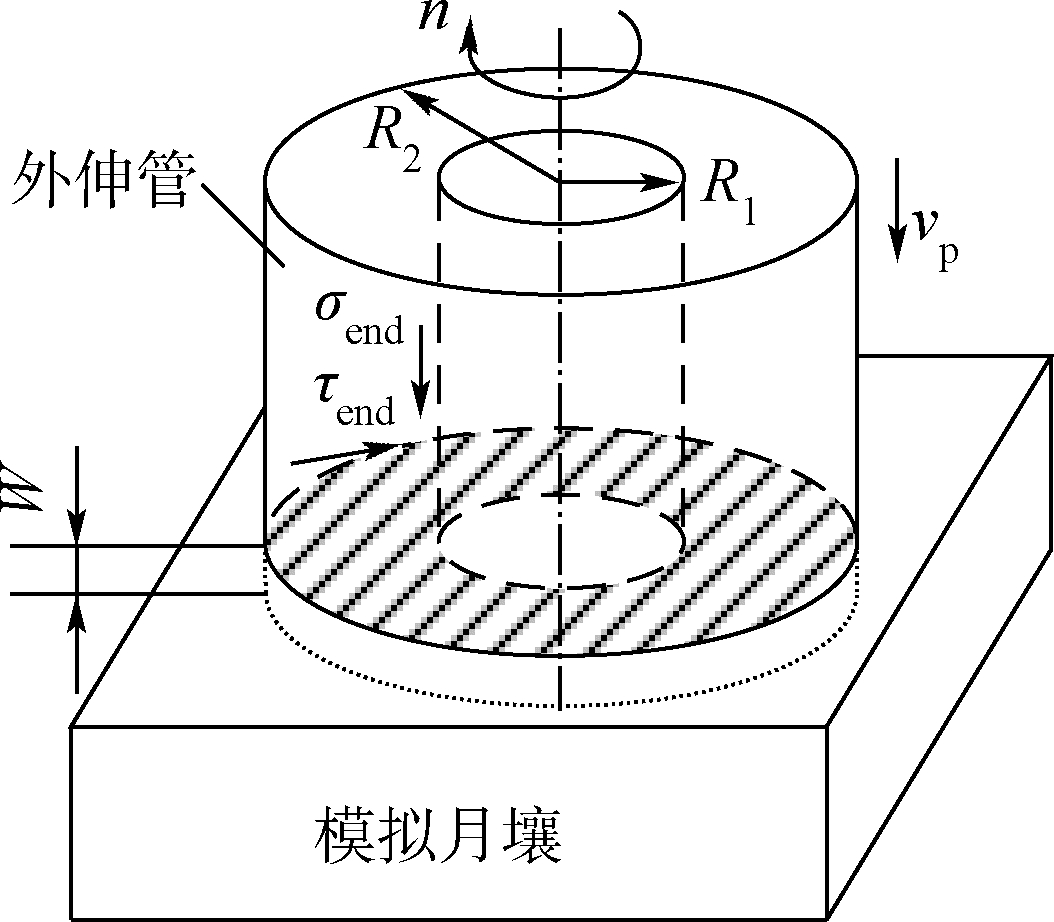 |
| 图 8 圆管端面与土体面接触Fig. 8 Contact between hollow cylinder end surface and soil surface |
| 图选项 |
根据叠加原理,外伸管端面与模拟月壤的接触引起的竖向变形W包括法向接触力σend引起的变形wn和切向接触力τend引起的变形wt:

由于取心过程中与外伸管端面接触的土体变形处于弹性范围,能应用弹性变形方程分析.但是速度控制下弹性体变形的应力分布在接触边界处为无穷大,而外伸管为薄壁管,因此本文采用均布力计算方法,通过集中力在接触面上的积分求得外伸管回转压入过程中土体的受力和变形的关系.
对于与钻头内孔外伸管端面与土体表面的接触,设接触表面的作用均布的应力,接触面表面的竖直变形单位力引起的变形在接触面上的积分.假设与外伸管端面的接触的月壤为一个充满无限大半空间的弹性体介质,不计弹性体的自重,在弹性体的表面(当z=0时),法向集中力Fn和切向集中力Ft引起的各点的竖直位移分量为
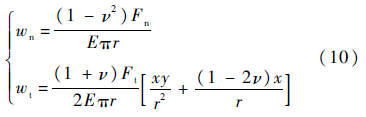
式中:ν为月壤的泊松比;E为月壤的弹性模量;r为该点到集中力作用点的距离;x和y分别为该点相对集中力作用点在弹性体的表面的位置坐标,x方向与Ft方向相同,y方向与Ft方向垂直.
对于与外伸管端面接触的土体表面,竖直方向的变形W可以表示为法向应力和切向应力引起的变形的叠加.
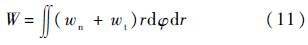
式中:φ为随圆积分角度.
由几何对称性,wt=0,因此
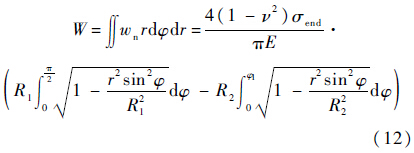
式中:
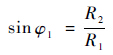
式(12)表明,在确定的土体特性参数和钻具构型参数的前提下,伸出管回转进尺过程中引起土体的变形与接触力成线性关系.
对于圆管回转压入,进尺速度vp与单齿切削量uz的关系为

因此,在给定钻进规程下,钻头内孔外伸管端面的接触力为

式中:系数A为
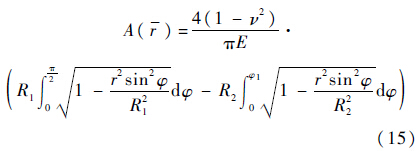
式中:
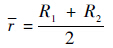
2.3 钻具外土体Ⅲ的排屑应力分析对于钻具外的土体Ⅲ,其动力学状态是由钻头与模拟月壤的切削-排屑状态决定的.如图 9所示,当钻进过程中发生阻塞时,模拟月壤切屑充满钻头的排屑空间并产生额外的应力σout.
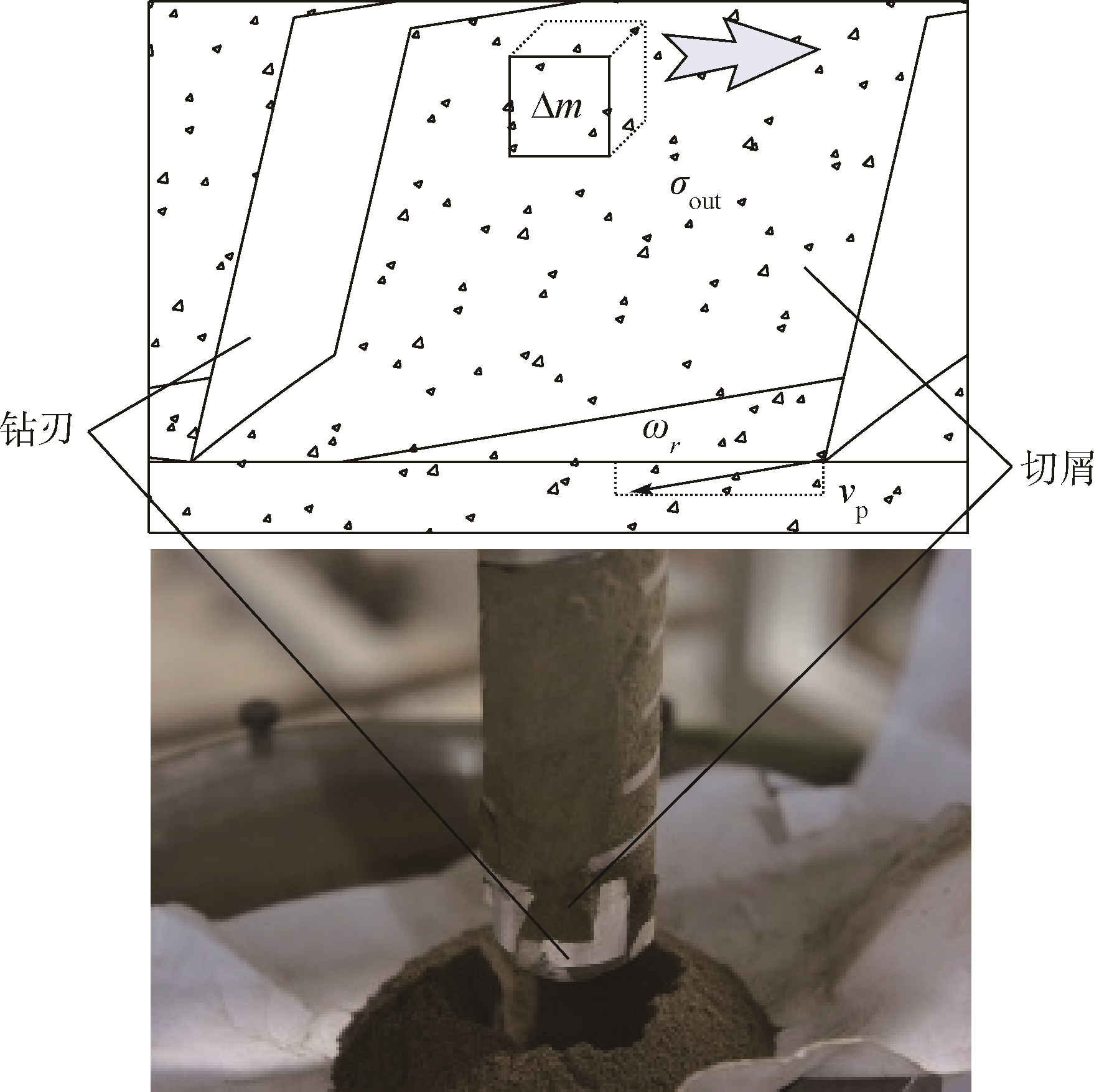 |
| 图 9 排屑阻塞时的土体ⅢFig. 9 Soil Ⅲ in jammed evacuation |
| 图选项 |
根据前期研究中建立的钻进回转模型,发生排屑阻塞时的切屑部分产生额外的内应力[23]为
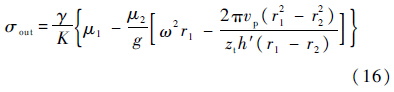
式中:γ为模拟月壤的容重;K为应力转向系数;h′为钻头导屑槽的轴向高度;μ1和μ2分别为模拟月壤对堆积面和孔内壁的摩擦系数;r1和r2分别为钻头半径和钻头内孔半径;zt为钻头切削刃数量.
综合上述分析以及外伸管端面的接触,在土体Ⅲ与土体Ⅱ的边界①处,能够提供的接触力为
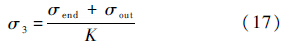
综上所述,基于极限平衡方法分别分析分析了土体I、土体Ⅱ和土体Ⅲ的动力学状态及其边界条件,建立了钻进取心过程中与取心有关的土体的动力学模型.利用该模型进行数值计算能获得对最终取心率的估计值.由于建模过程中采用土体整体运动的假设,忽略了土体内部相对运动,因此,能够近似描述平稳的软袋取样过程,对于包含剧烈振动冲击等引起土体内部大幅度相对运动钻进工况,则可能产生较大的计算误差.
3 钻进取心数值计算及试验验证3.1 取样量的估计算法基于上述分析过程,设计模拟月壤钻进取心的取样量估计算法.如图 10所示,算法以钻进规程参数、模拟月壤特性和钻具构型参数作为已知条件,按照土体Ⅲ→土体Ⅱ→土体I的顺序根据土体边界平衡条件求取心率κ.取心率κ是衡量取样量的重要指标,本文中取心率κ定义为样心长度h1与取样深度(保持心管下端侵入深度)dr之比,即

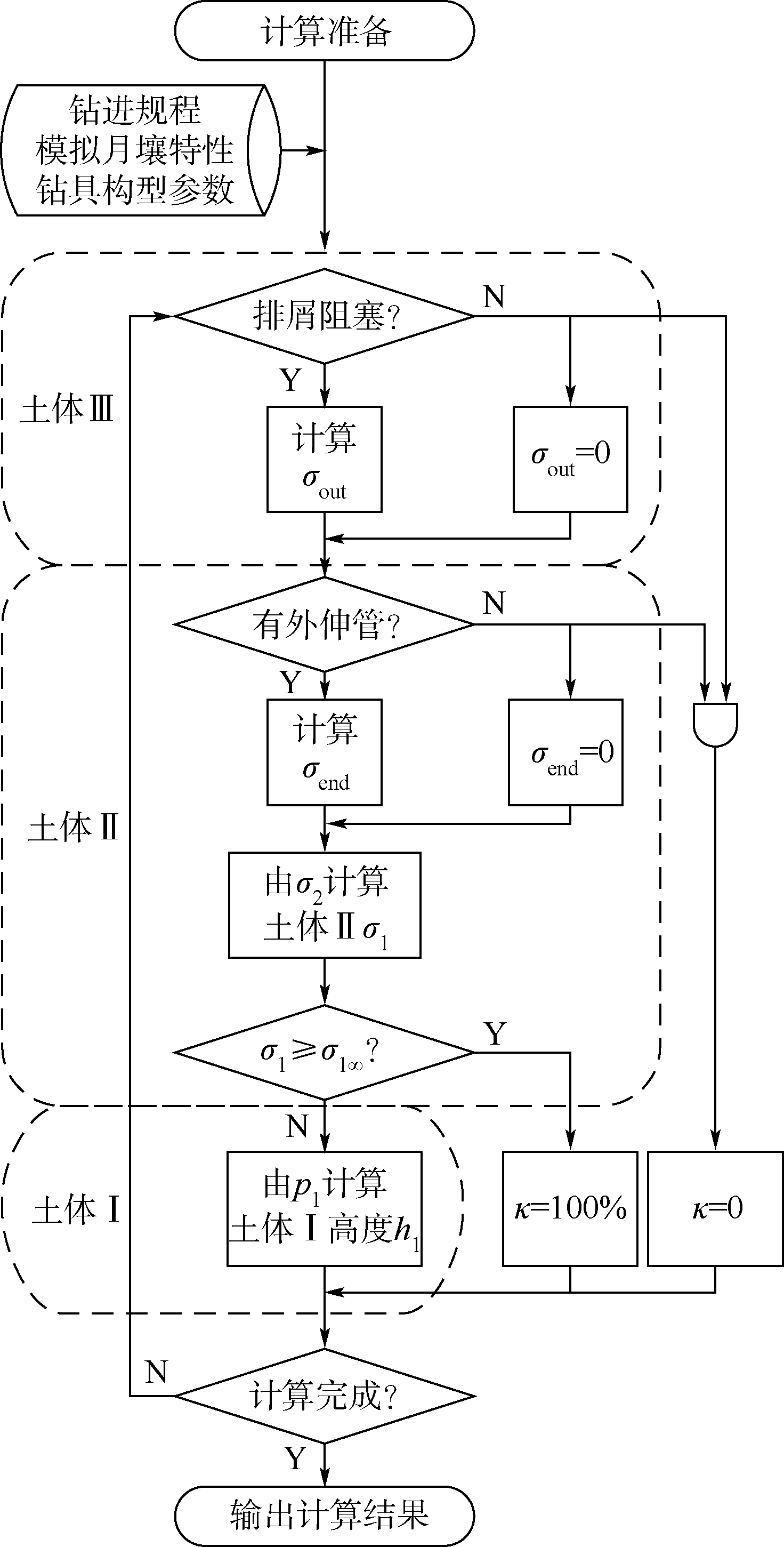 |
| 图 10 取心模型的计算流程Fig. 10 Flow chart of coring model calculation |
| 图选项 |
首先根据判定特定钻进规程下,钻具钻进模拟月壤时是否发生排屑阻塞,计算排屑应力;然后根据钻头是否为外伸管钻头计算外伸管端面接触力;根据接触面②的接触力计算接触面①的接触力,最后计算出取样高度并获得取心率κ.计算过程中存在2种特殊情况,当未发生排屑阻塞同时钻具不具备外伸管的结构时,能直接判定取心率κ=0;当土体I下底面应力σ1≥σ1∞(σ1∞为土体I应力极限)时,能直接判定取心率κ=100%.
3.2 钻进取心验证试验为了验证理论模型的正确性,在模拟钻进平台上开展了模拟月壤的钻进试验,如图 11所示.该试验平台具备与月面钻取采样装置原理相同的钻进取心机构,能够开展次表层模拟月壤的钻取采样试验.
 |
| 图 11 模拟月壤钻进取心试验及其平台Fig. 11 Lunar soil simulant drilling and coring test and its test-bed |
| 图选项 |
为模拟月面采样的实际工况,研究中使用能较真实地模拟月壤机械特性的HIT-LS1#模拟月壤为基础制备试验钻进对象,其颗粒形貌如图 12(a)所示.实际月壤密实程度大于松散堆积的模拟月壤,由于剪切强度与密实程度密切相关,为模拟月面的钻进工况,对模拟月壤原料进行了压缩处理,提高其密实程度[2].处理后的模拟月壤机械特性如图 12(b)所示,其剪切强度指标处于与实际月壤的范围内[24, 25, 26].
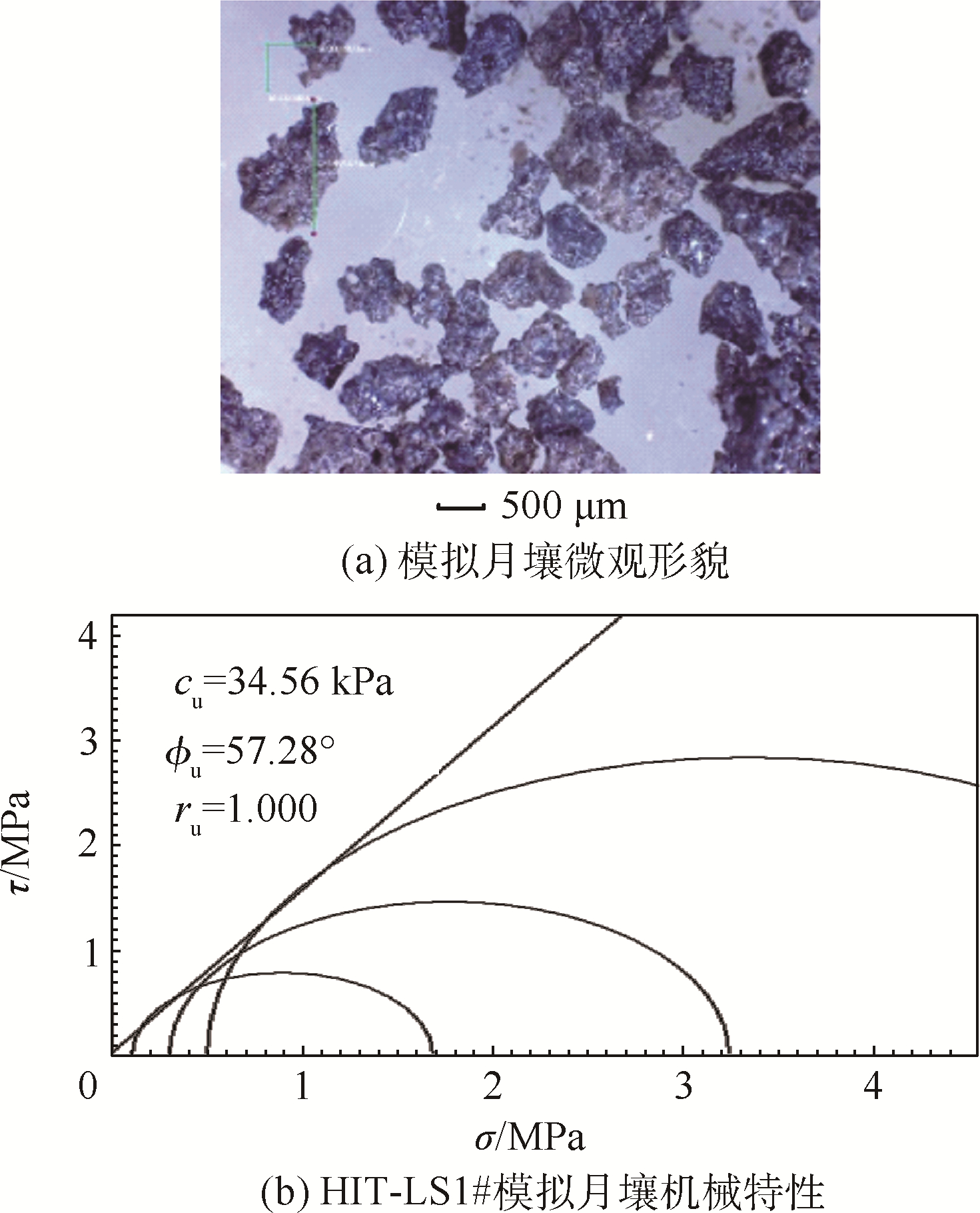 |
| τ—剪应力;σ—正应力;cu—不排水内聚力; $\phi $u—不排水内摩擦角;ru—相关系数.图 12 模拟月壤及其机械特性Fig. 12 Lunar soil simulant and its mechanical properties |
| 图选项 |
试验钻具为如图 13(a)所示的HIT-2型试验钻具.钻头的切削刃实现对土壤的切削,被切削破坏后的土壤由钻头的导屑槽流动至钻杆的螺旋排屑槽,并在排屑外螺旋的带动下不断向上移动,实现切屑的排出.钻具内腔中安装软袋取心机构,如图 13(b)所示,取心机构由刚性保持心管、封口机构和取心软袋组成,实现钻进过程中样心的包裹和取出.
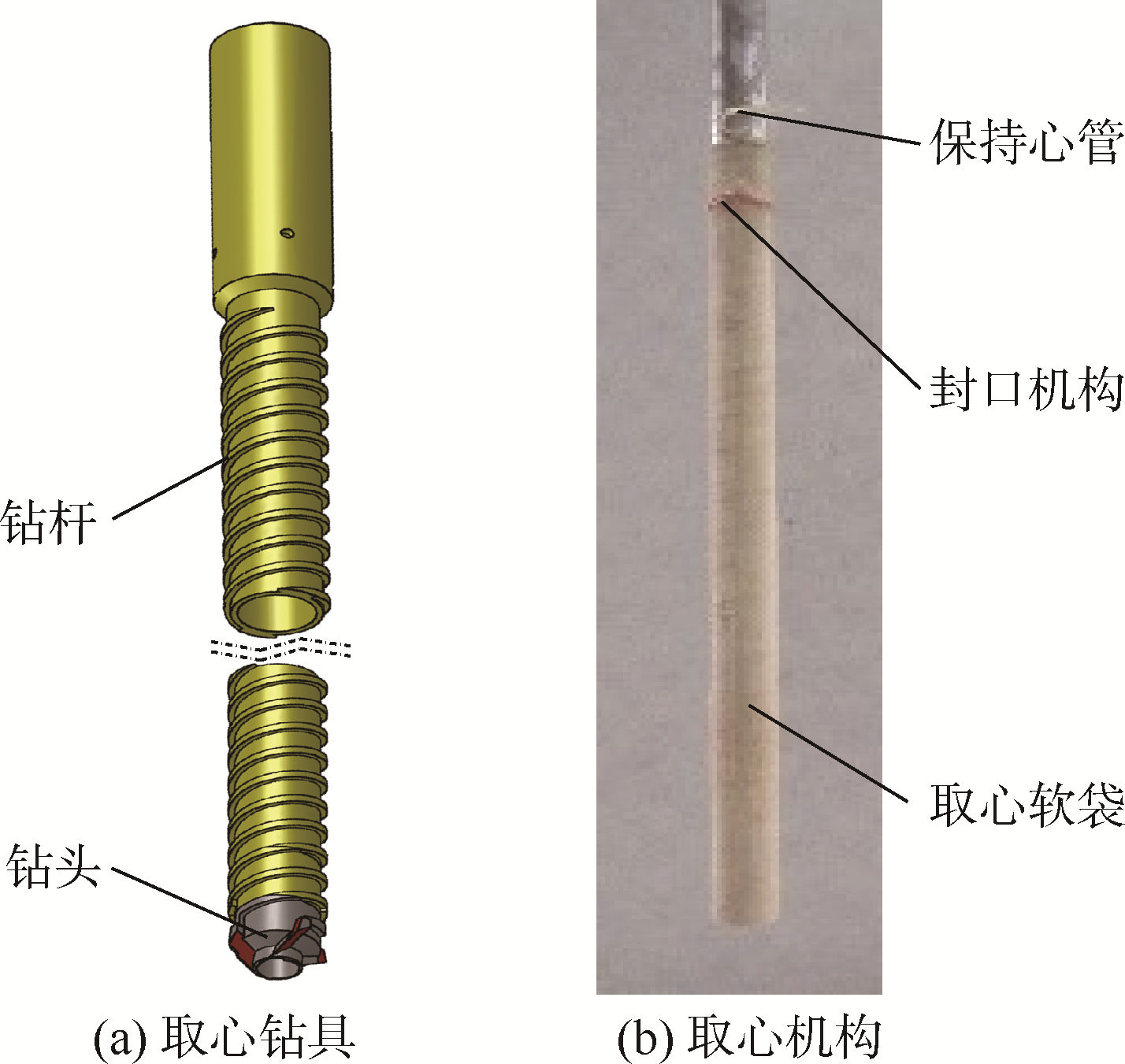 |
| 图 13 中空取心钻具Fig. 13 Hollow drilling and coring tool |
| 图选项 |
验证试验选用的钻进规程为:回转转速n=50,90,150,210,250 r/min;进尺速度vp=50,90,130,170,210 mm/min.取心率κ的试验结果通过称量取样质量并利用采样机构几何尺寸和模拟月壤密度计算获得.对验证试验数据进行分析,得到取样量与钻进规程的关系,如图 14所示.根据取心过程动力学分析获得不同钻进规程下取心率的预测值,结果表明取心预测值与试验结果基本吻合.
 |
| 图 14 取心率计算值与试验值对比Fig. 14 Comparison between calculation and test results of coring rate |
| 图选项 |
对比取心模型预测结果和试验值,获得表 1所示的误差分析结果.如图 15所示,模型计算结果与取心率的变化趋势一致,特别是取心率开始下降的钻进规程范围能给出准确的计算结果.计算误差主要体现在取心率下降的部分,总体的平均误差率小于5%.
表 1 取心模型误差Table 1 Error of coring model
| 对比项 | 平均误差值 | 平均误差率/% | 最大误差值 | 最小误差值 |
| 数值 | 0.036 4 | 4.31 | 0.117 8 | 0.001 2 |
表选项
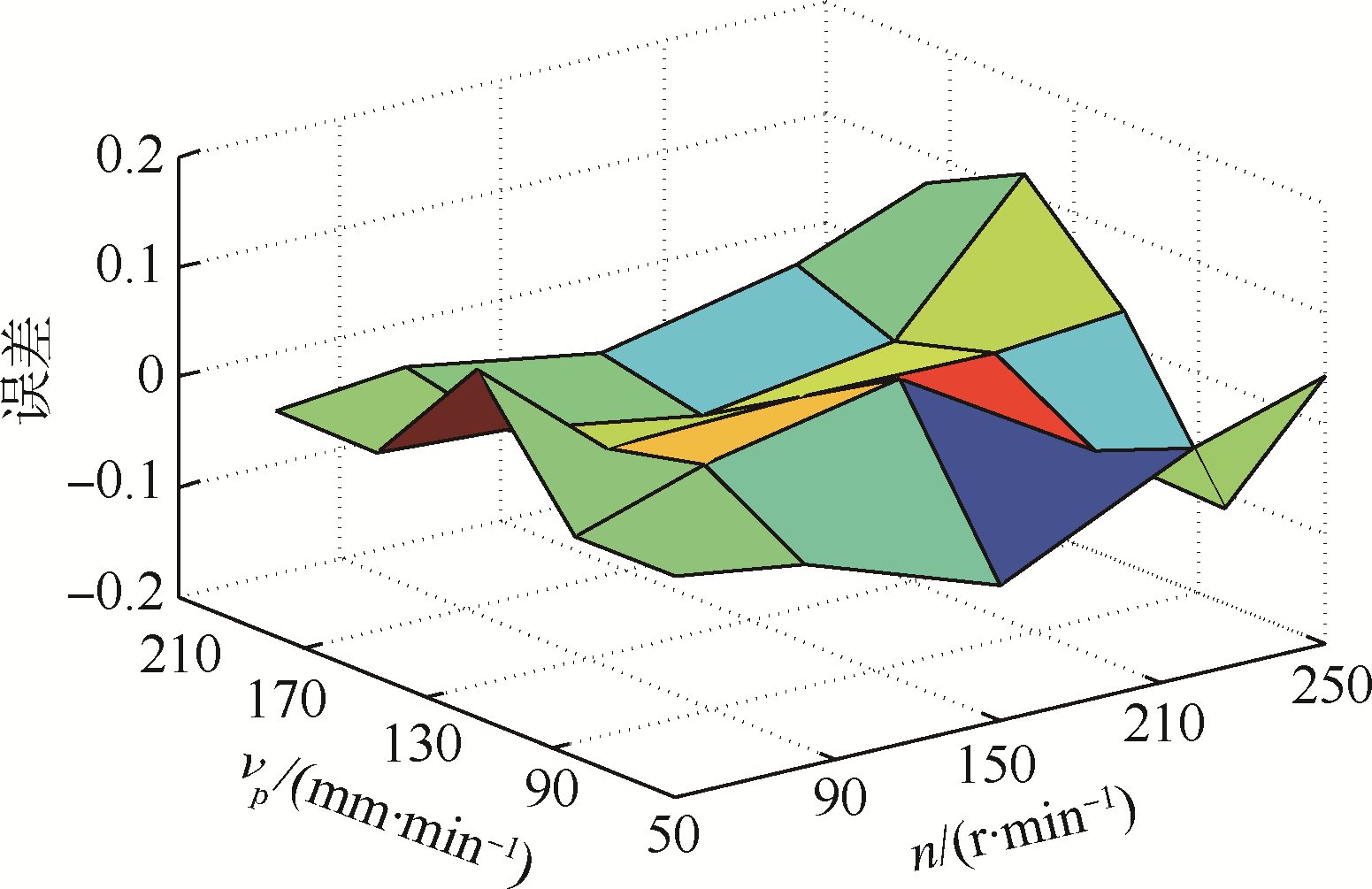 |
| 图 15 取心率计算误差Fig. 15 Calculation error of coring rate |
| 图选项 |
4 取心率影响因素分析钻进取心过程是特定钻进规程下,取心钻具与月壤相互作用过程.因此,钻进规程、月壤特性和钻具结构共同影响取心率.
4.1 钻进规程对于月壤钻进而言,钻进规程是回转转速和进尺速度的组合.钻进规程决定了钻头内孔外伸管端部处的接触状态和钻头排屑槽内月壤的流动状态,因而决定了进入钻头内孔的月壤的应力状态,是影响取心率的决定性因素.图 14表明在现有试验的钻进规程范围内,采用同样的模拟月壤和试验钻具,低回转转速和高进尺速度能获得较高的取心率,高回转转速和低进尺速度下的取心率较低.
4.2 月壤特性对于外伸管钻头,取心管内应力由外伸管端面接触应力和排屑应力共同决定.这两种应力状态除受钻进规程影响外,还因月壤自身的特性的不同发生变化,这种变化在外伸管接触应力上体现的尤为明显.图 16是外伸管钻头在不同钻进规程及月壤弹性模量下取心率的计算结果.该结果说明利用外伸管钻头对模拟月壤进行钻进取心时,采用相同钻进规程和取心钻具,取心率随着模拟月壤的弹性模量的增加而增加.
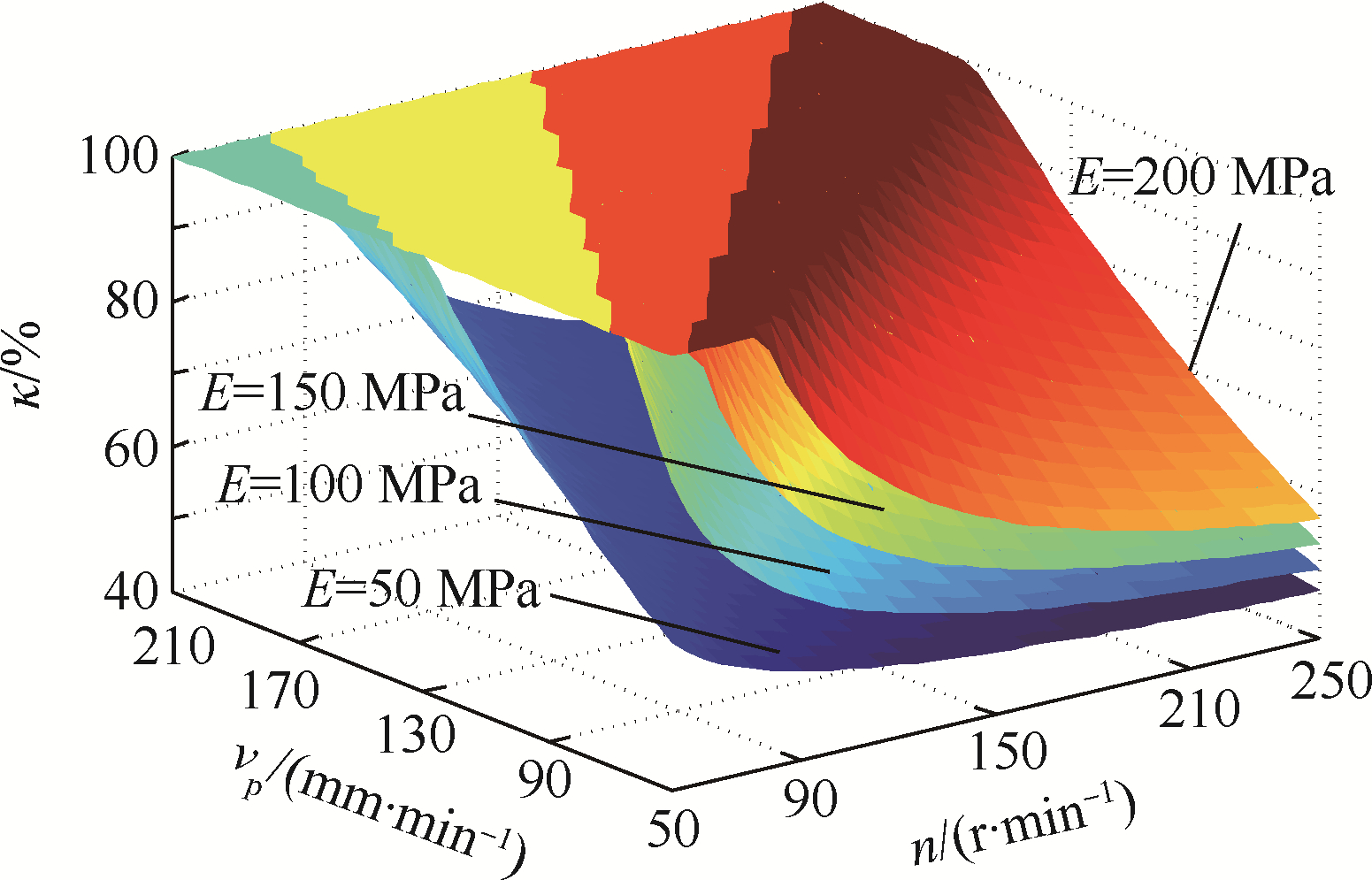 |
| 图 16 取心率与模拟月壤弹性模量关系Fig. 16 Relation between coring rate and elastic modulus of lunar soil simulant |
| 图选项 |
实际上,外伸管端面接触应力和排屑应力对取心应力的贡献具有较大差异.图 17是取心钻头内孔外伸管端面的接触应力和排屑应力的计算结果.端面接触应力远大于排屑应力表明钻头内孔外伸管确实有提高进入取心孔的土体Ⅱ内应力的作用.随着外伸管的轴向长度的增加,土体Ⅱ与钻头内孔壁的总作用力快速增加,影响最终的取心率.
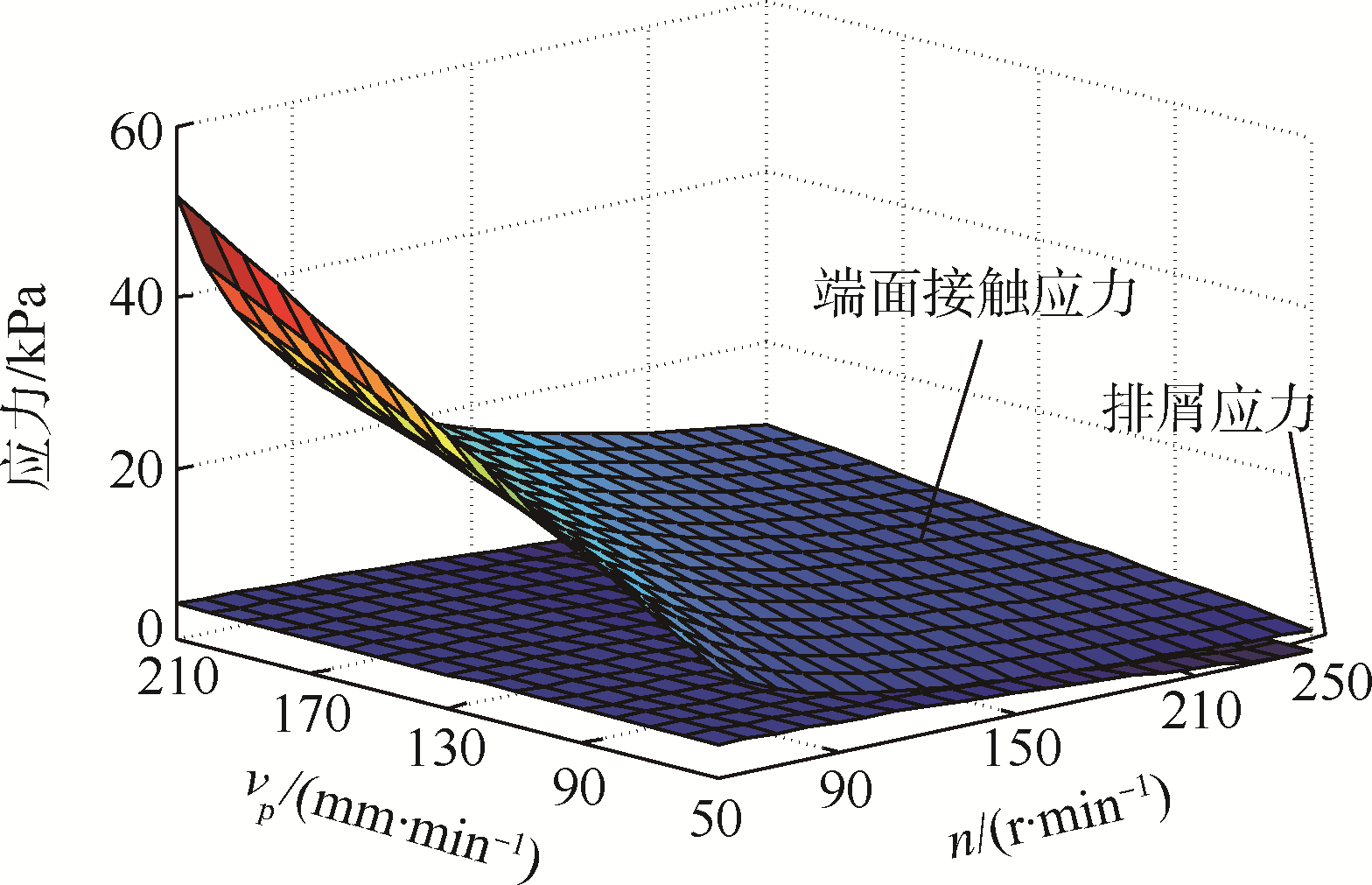 |
| 图 17 外伸管钻头取心应力组成Fig. 17 Coring stress composition of extended tube drill bit |
| 图选项 |
4.3 钻具构型实际月面环境中存在大块岩石,外伸管钻头在钻进岩石时接触面积大,无法在有限的进尺力条件下完成对月岩的钻进.若取消外伸管,采用无外伸管钻头,能够以较小的进尺力实现对月岩的钻进.对于无外伸管钻头,取心管内应力仅由排屑应力决定.排屑应力受钻进规程的影响.当钻进规程处于螺旋排屑状态下,排屑应力为0,此时取样量为0.当进尺速度增大或回转速度降低,钻进规程处于排屑阻塞状态时,钻头排屑槽内产生排屑的附加应力(压应力),此时取样量会随着排屑的应力增加逐渐增加.因此为保证无外伸管钻头的取样量,必须合理选择钻进规程,产生足够的排屑应力.图 18是无外伸管钻头在不同钻进规程下取心率κ的计算结果.图 16和图 18的对比说明利用无外伸管的钻头对模拟月壤进行钻进取心时,取心率更容易受钻进规程的影响.
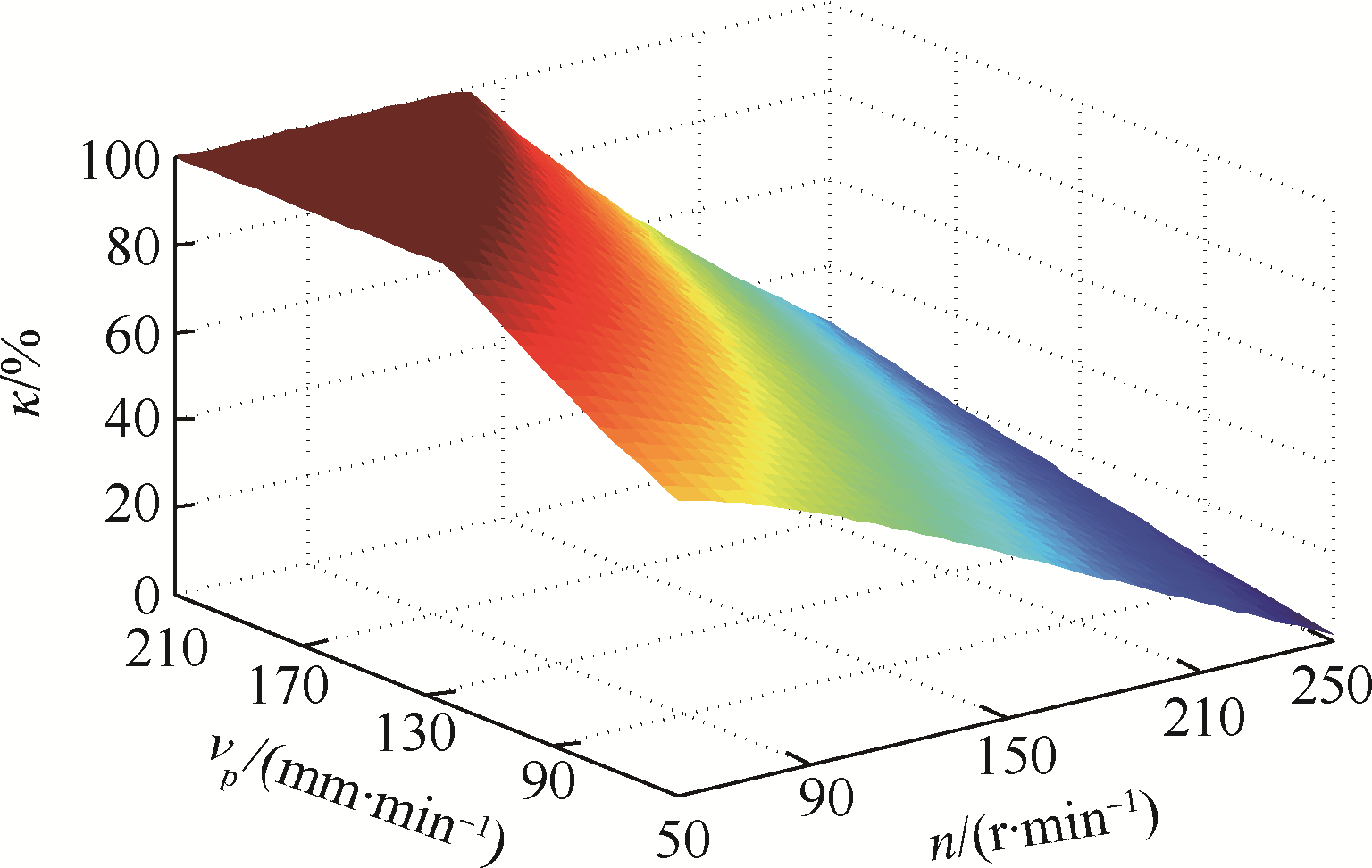 |
| 图 18 无外伸管钻头取心率与钻进规程参数关系Fig. 18 Relation between coring rate and drilling parameters for non-extended tube drill bit |
| 图选项 |
5 结 论1) 软袋取心方式中,与钻具有相互作用的土体按力学边界不同能分为取心软袋内土体、取心钻头内土体和钻具外土体.基于各部分土体和钻具之间相互作用建立的粉体动力学模型能够对模拟月壤的软袋取心率进行合理的预测.
2) 钻进规程、月壤特性和钻头构型都会对取心率产生较大影响.为了适应同时存在月壤和月岩的月面工况,应当避免选用接触面积较大的外伸管钻头,并合理选择钻进规程参数,保证取心过程中钻头附近有足够的排屑附加应力.
上述取心模型和分析结论不仅为月面钻进取心提供了理论参考,也能通过相互作用特性参数的合理选择应用于地面环境中流动性较强土体取心过程的分析.
参考文献
| [1] | Zacny K, Paulsen G, Davis K, et al.Honeybee robotics planetary drill systems[C]//Proceedings of the 39th Lunar and Planetary Science Conference, Lunar and Planetary Science XXXIX.League City, Texas:LPI, 2008:1355. |
| Click to display the text | |
| [2] | Blacic J, Dreesen D, Mockler T.The 3rd dimension of planetary exploration deep subsurface drilling[C]//Proceedings of AIAA Space 2000 Conference and Exposition.Reston:AIAA, 2000:1-11. |
| Click to display the text | |
| [3] | Allton J H.Catalog of Apollo lunar surface geological sampling tools and containers, NAS 9-17900[R].Houston:Johnson Space Center, 1989. |
| [4] | Paulsen G, Zacny K, Chu P, et al.Robotic drill systems for planetary exploration[C]//Proceedings of AIAA Space 2006 Conference and Exposition.Reston:AIAA, 2006:2876-2886. |
| Click to display the text | |
| [5] | Van Winnendael M, Baglioni P, Vago J.Development of the ESA Exomars rover[C]//Proceedings of the 8th International Symposium on Artificial Intelligence, Robotics and Automation in Spacee.Munich:ESA, 2005:15-22. |
| Click to display the text | |
| [6] | Heiken G H, Vaniman D T, French B M.Lunar sourcebook[M].Cambridge:Cambridge University Press, 1991:475-594. |
| [7] | Bar-Cohen Y, Zacny K.Drilling in extreme environments[M].Weinheim:Wiley-Vch, 2009:347-541. |
| [8] | Kemurdzhian A L, Gromov V V, Cherkasov I I.Automatic stations for investigation of the lunar surface[M].Moscow:Mashinostroyeniye Press, 1976:23-25. |
| [9] | Zacny K.Drilling systems for extraterrestrial subsurface exploration[J].Astrobiology, 2008, 8(3):665-706. |
| Click to display the text | |
| [10] | Glass B, Cannon H, Branson M, et al.DAME:Planetary-prototype drilling automation[J].Astrobiology, 2008, 8(3):653-664. |
| Click to display the text | |
| [11] | Statham S M.Autonomous structural health monitoring technique for interplanetary drilling applications using laser Doppler velocimeters[D].Atlanta:Georgia Institute of Technology, 2011. |
| Click to display the text | |
| [12] | Grotzinger J P, Crisp J, Vasavada A R, et al.Mars science laboratory mission and science investigation[J].Space Science Reviews, 2012, 170(1-4):5-56. |
| Click to display the text | |
| [13] | Okon A.Mars science laboratory drill[C]//Proceedings of the 40th Aerospace Mechanisms Symposium.Washington, D.C.:NASA, 2010:1-16. |
| Click to display the text | |
| [14] | European Space Agency.Touchdown! Rosetta's Philae probe lands on comet[EB/OL].Paris:ESA, 2014[2014-11-25].http://www.esa.int/Our_Activities/Space_Science/Rosetta/Touchdown!_Rosetta_s_Philae_probe_lands_on_comet. |
| [15] | Finzi A E, Zazzera F B, Dainese C, et al.Space science reviews:SD2-how to sample a comet[M].Berlin:Springer-Verlag, 2007:281-299. |
| [16] | Marchesi M, Campaci R, Nista A, et al.Comet sample acquisition for Rosetta lander mission[C]//Proceedings of the 9th European Space Mechanisms and Tribology Symposium.Liege, Belgium:European Space Agency, 2001:91-96. |
| Click to display the text | |
| [17] | Magnani P G, Re E, Ylikorpi T, et al.Deep drill (DeeDri) for mars application[J].Planetary and Space Science, 2004, 52(1):79-82. |
| Click to display the text | |
| [18] | Matti A.Concept evaluation of mars drilling and sampling instrument[D].Helsinki:Helsinki University of Technology, 2005. |
| [19] | Richter L, Coste P, Gromov V, et al.The mole with sampling mechanism(MSM):Technology development and payload of beagle 2 mars lander[C]//Proceedings of 8th ESA Workshop on Advanced Space Technologies for Robotics and Automation (ASTRA 2004).Noordwijk:ESA, 2004:2-4. |
| Click to display the text | |
| [20] | Bar-Cohen Y, Sherrit S, Dolgin B, et al.Ultrasonic/sonic drilling/coring (USDC) for in-situ planetary applications[C]//SPIE's 7th Annual International Symposium on Smart Structures and Materials.Bellingham, WA:Society of Photo-Optical Instrumentation Engineers, 2000:661-668. |
| Click to display the text | |
| [21] | Thomas P N H.Magna Parva and ESA's ultrasonic drill tool for planetary surface exploration[C]//12th Biennial International Conference on Engineering, Construction, and Operations in Challenging Environments.Honolulu, Hawaii:ASCE, 2010:1235-1245. |
| Click to display the text | |
| [22] | Nedderman R M.Statics and kinematics of granular materials[M].Cambridge:Cambridge University Press, 1992:163-242. |
| [23] | 史晓萌,节德刚,全齐全,等.模拟月壤钻进负载分析与试验研究[J].宇航学报, 2014, 35(6):648-656. Shi X M, Jie D G, Quan Q Q, et al.Experimental research on lunar soil simulant drilling and drilling load analysis[J].Journal of Astronautics, 2014, 35(6):648-656(in Chinese). |
| Cited By in Cnki | |
| [24] | Gromov V.Physical and mechanical properties of lunar and planetary soils[J].Earth Moon and Planets, 1999(80):51-72. |
| Click to display the text | |
| [25] | Mitchell J K, Houston W N, Scott R F, et al.Mechanical properties of lunar soil:Density, porosity, cohesion and angle of internal friction[C]//Proceedings of the Third Lunar Science Conference.Cambridge, MA:MIT Press, 1972:3235-3253. |
| Click to display the text | |
| [26] | Leonovich A K, Gromov V V, Dmitriev A D, et al.Investigation of the physical and mechanical properties of lunar sample brought by Luna-20 and along the route of motion of Lunochod 2[C]//Proceedings of the 24th International Astronautical Congress.Oxford:Pergamon Press Ltd., 1976:321-332. |
| Click to display the text |
