反问题方法是根据可观测的量值反演系统变化规律或参数影响规律的数学物理方法,航空航天领域中在导弹制导[1]、火箭推进系统故障[2]等方面已经得到良好的应用.导热反问题是反问题方法研究的一个分支,一般是利用研究对象的测量温度,通过一定反演算法计算得到热物性参数、边界条件等未知量.程文龙等[3, 4]提出了卫星热分析模型不确定参数进行分层修正的反问题模型并取得了非常好的反演结果;杨沪宁和钟奇[5]建立了基于蒙特卡罗法反演修正航天器热模型参数的反问题模型;张镜洋等[6]研究了基于蒙特卡罗法的小卫星瞬态热分析模型参数分层修正方法;张中礼等研究了由内壁面温度反演火箭外壁热流的导热反问题[7];Lin和Chen等[8, 9]分别求解了平行板通道和肋片的导热反问题;Huang等[10, 11]求解了三维的热传导反问题;薛奇天和杨海天等求解了多宗量的热传导反问题[12, 13, 14],得到了较满意的结果;王登刚等[15]研究了非线性二维稳态导热反问题的数值求解方法;范春利等[16]求解热传导反问题,识别试件内壁的缺陷.
本文采用导热反问题方法,利用现有的航天器在轨遥测温度数据,通过反演计算就能够得到满足一定精度要求的航天器在轨外热流数据.由于导热反问题的不适定性及非线性,使导热反问题的求解远比导热正问题复杂.反演航天器在轨外热流的导热反问题需要在边界条件中引入表征辐射热流的4次方非线性项,大大增加了求解的难度,目前国内外还缺乏这方面的研究工作.本文研究了利用航天器设备在轨遥测温度值反演出航天器在轨瞬态外热流的导热反问题方法.首先推导了反演航天器在轨外热流的导热反问题数学模型,采用共轭梯度法求解导热反问题并改进了共轭梯度法的迭代过程以增加其抗不适定性用于求解;在此基础上采用FORTRAN语言编写通用计算程序,构造了两组数值试验用于检验反演算法的效果和计算程序的正确性.
1 数学模型本文所研究的是一维瞬态导热问题,一维瞬态导热方程为

式中:T为温度;τ为时间;k为热传导系数;ρ为密度;cp为比热容.内侧即朝向航天器内部的一侧(x=0)为绝热边界条件:

外侧即朝向外界空间环境的一侧(x=L)为第3类边界条件:

式中:q为研究对象的吸收外热流值,包括吸收的太阳辐射、天体的红外辐射以及天体反照的太阳辐射;ε为半球向发射率;σ为斯蒂芬-波尔兹曼常数.
初始条件为

式中:T0为初始温度.
本文研究的导热反问题是通过测量温度反演出q值.从式(3)中可以看到,由于边界条件中引入了表征辐射热流的4次方非线性项,大大增加了导热反问题的不适定性.导热反问题的求解方法主要包括共轭梯度法、最大熵法、正则化算法等,与其他几种算法相比共轭梯度法在迭代过程中具有一定的抗不适定性,目前在国内外导热反问题研究领域仍然是最常用的方法,本文采用共轭梯度法进行导热反问题的求解.
共轭梯度法的目标函数为
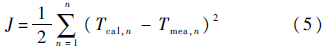
式中:Tcal,n为温度计算值;Tmea,n为温度在轨遥测值;n为不同时间点.吸收外热流值q的迭代式为

式中:b为迭代次数;dn的计算式为
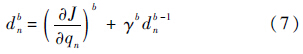
γ由式(8)计算:
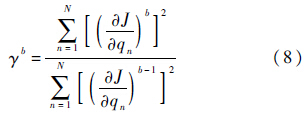
式中:N为总时间点数;迭代步长β为

式中:i为不同时间点;$\frac{{\partial {T_i}}}{{\partial {q_n}}}$为灵敏度系数.为得到$\frac{{\partial {T_i}}}{{\partial {q_n}}}$需要求解灵敏度方程.灵敏度方程由非稳态导热方程(1)对qn求微分得到:
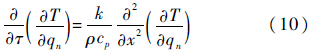
边界条件式(2)和式(3)对qn求微分得到:
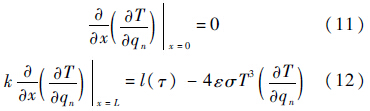
式(12)中
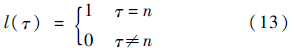
灵敏度方程的初始条件由式(4)对qn求微分得到:

由式(5)对qn求微分得到$\frac{{\partial J}}{{\partial {q_n}}}$的计算式:
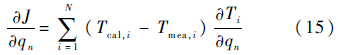
共轭梯度法的收敛目标是使

式中:δ为很小的正数.
为增强迭代过程的收敛性,与传统的共轭梯度法迭代过程相比进行了两处改进:
1) 由式(12)可以看到,灵敏度系数$\frac{{\partial {T_i}}}{{\partial {q_n}}}$是温度T(x,τ)的函数,因此在每轮迭代得到新的T(x,τ)后,重新计算灵敏度系数$\frac{{\partial {T_i}}}{{\partial {q_n}}}$;
2) 从物理概念出发,航天器在轨吸收外热流不小于0,因此式(6)整理为
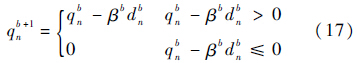
共轭梯度法的求解步骤如下:
1) 求解导热方程(1)得到温度计算值Tcal,n.
2) 求解灵敏度方程(10)得到灵敏度系数$\frac{{\partial {T_i}}}{{\partial {q_n}}}$.
3) 根据温度计算值和在轨遥测值,检查收敛目标式(16)是否达到;如果达到收敛目标,则停止迭代,否则,转入第4)步.
4) 计算$\frac{{\partial J}}{{\partial {q_n}}}$、γ、β及d.
5) 由式(17)计算得到下一轮迭代qnb+1,转入第1)步.
2 计算结果为检验共轭梯度法的计算效果,本文设计了两组数值试验,每组数值试验检验步骤如下:
1) 给出一组随时间变化的吸收外热流值qmea.
2) 以qmea为边界条件求解导热方程(1),得到的结果作为温度测量值Tmea.
3) Tmea作为导热反问题的输入条件,采用共轭梯度法反演吸收外热流值qcgm.
4) 比较qmea和qcgm,检验反演算法的效果.
研究对象为高度30 mm的铝合金圆柱体,圆柱体除一个端面朝向空间环境通过辐射交换热量外,其余各面均为绝热边界,因此沿轴向可视为一维导热;计算网格为沿轴向划分5个节点;热物理参数取值为密度ρ=2 700 kg/m3,比热容cp=900 J/(kg·K),热传导系数k=120 W/(m·K),辐射边界半球向发射率ε=0.6.
2.1 数值试验1数值试验1给出1组吸收外热流值qmea如图 1所示,数值试验1给出的吸收外热流曲线能够代表目前多数地球轨道航天器和深空探测航天器在轨吸收外热流变化趋势.通过求解导热正问题(式(1))得到温度测量值Tmea并作为导热反问题的输入条件,采用共轭梯度法反演吸收外热流值qcgm.共轭梯度法迭代200次后J(qnb)<0.001满足收敛条件,查看导热反问题反演出的温度值Tcgm与测量温度值Tmea可以看到两者符合的很好,见图 2.
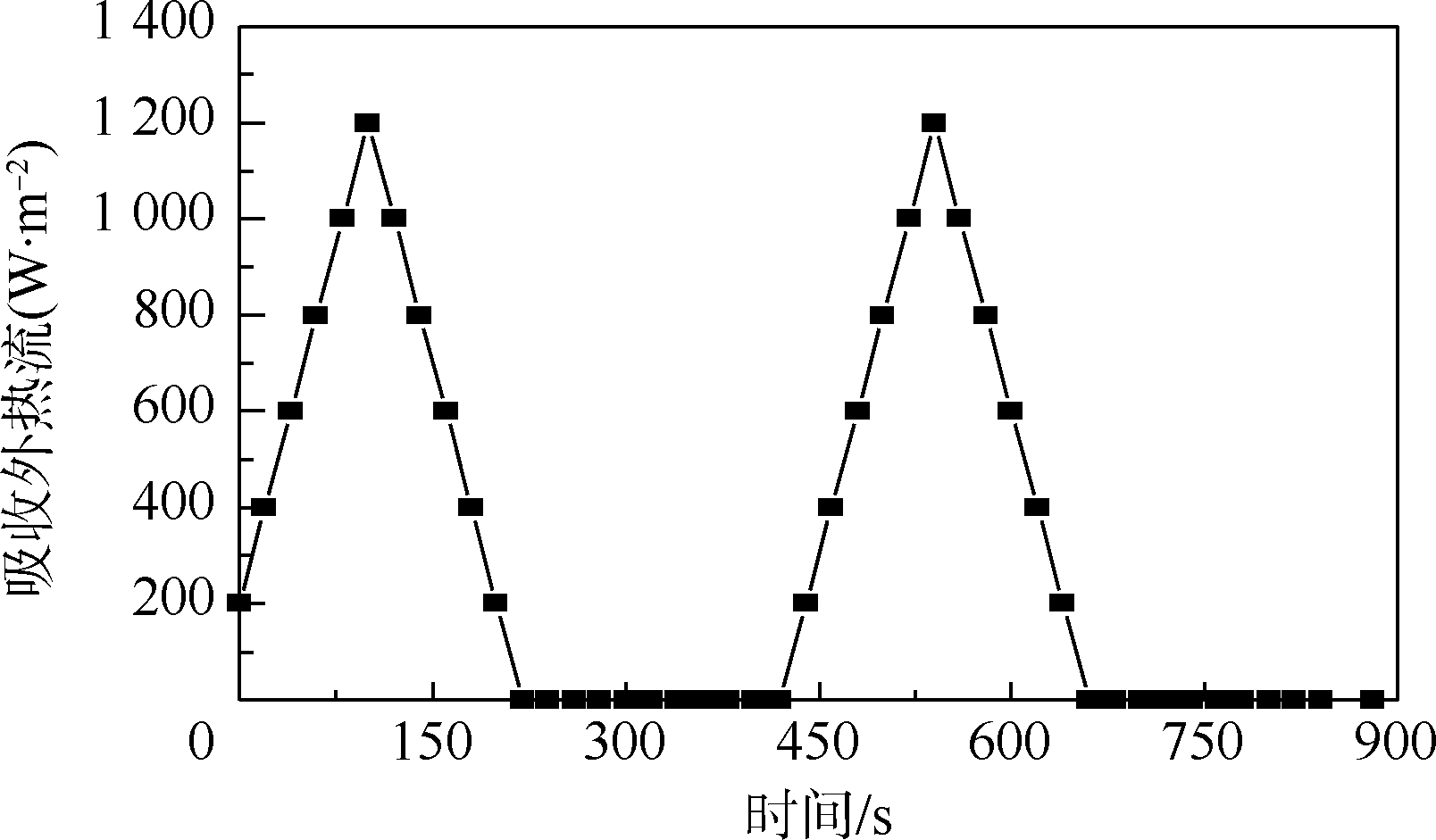 |
| 图 1 数值试验1的吸收外热流曲线Fig. 1 Absorbed external heat flux curve of numerical experiment 1 |
| 图选项 |
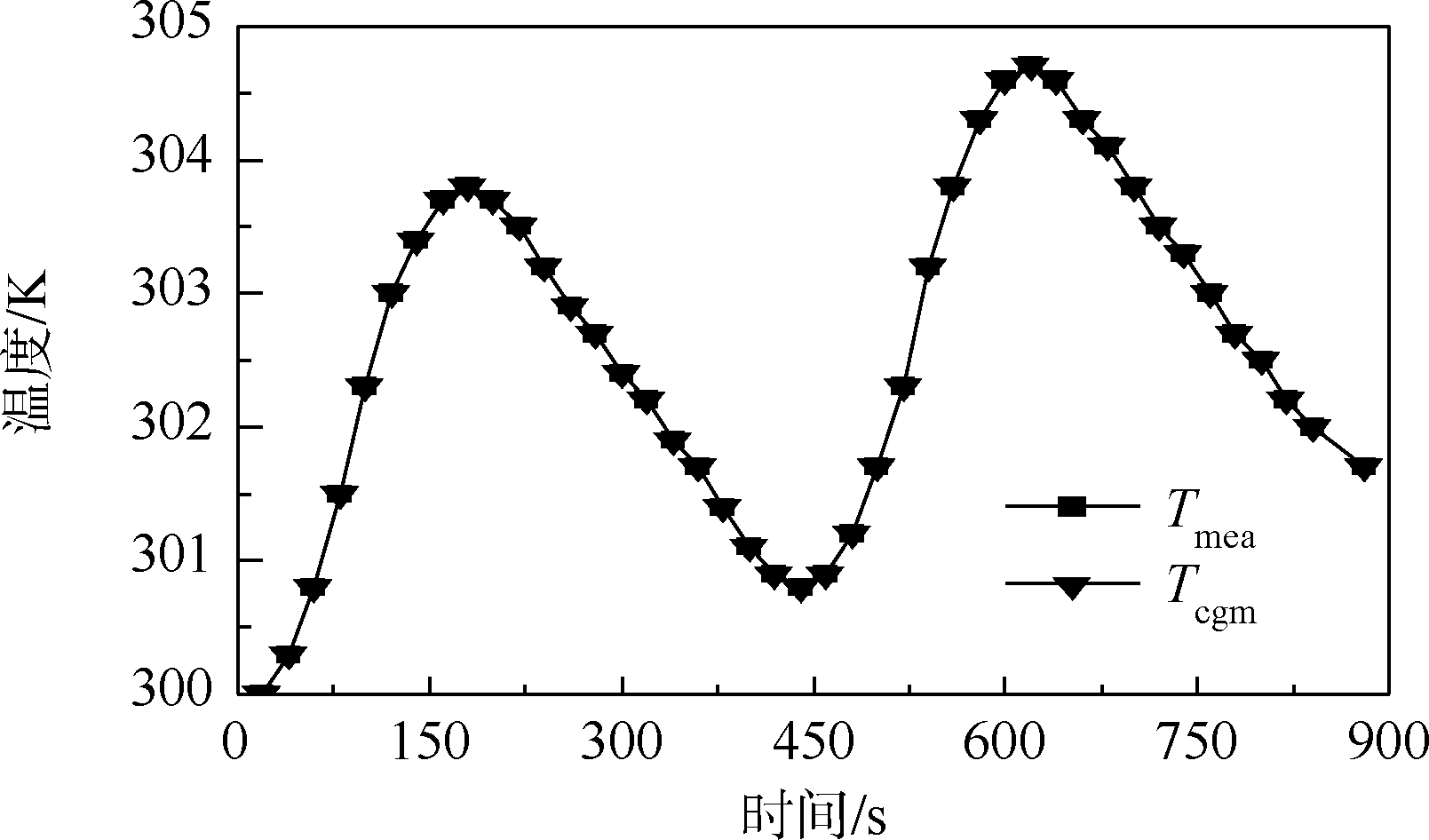 |
| 图 2 数值试验1的温度反演值与测量值比较Fig. 2 Compare between inversion temperature and measuring data of numerical experiment 1 |
| 图选项 |
图 3和表 1分别为导热反问题反演出的吸收外热流值qcgm与真实值qmea的比较.从图 3中看到,qcgm与qmea的曲线几乎重合在一起;由表 1中的数据qcgm与qmea偏差值在-23~19 W/m2之间;除了0值区域外,最大相对偏差为2.0%,共轭梯度法很好的反演出了吸收外热流值.
 |
| 图 3 数值试验1的吸收外热流反演值与真实值比较Fig. 3 Compare between inversion absorbed external heat flux and real value of numerical experiment 1 |
| 图选项 |
表 1 数值试验1的吸收外热流反演值与真实值比较Table 1 Compare between inversion absorbed external heat flux and real value of numerical experiment 1
| 时间/s | qmea/(W·m-2) | qcgm/(W·m-2) | 相对误差/% | 时间/s | qmea/(W·m-2) | qcgm/(W·m-2) | 相对误差/% |
| 0 | 200 | 204 | 2.0 | 440 | 200 | 197 | -1.5 |
| 20 | 400 | 390 | -2.5 | 460 | 400 | 398 | -0.5 |
| 40 | 600 | 598 | -0.3 | 480 | 600 | 594 | -1.0 |
| 60 | 800 | 806 | 0.8 | 500 | 800 | 800 | 0.0 |
| 80 | 1 000 | 1 019 | 1.9 | 520 | 1 000 | 1 016 | 1.6 |
| 100 | 1 200 | 1 177 | -1.9 | 540 | 1 200 | 1 179 | -1.8 |
| 120 | 1 000 | 1 012 | 1.2 | 560 | 1 000 | 1 015 | 1.5 |
| 140 | 800 | 796 | -0.5 | 580 | 800 | 798 | -0.3 |
| 160 | 600 | 593 | -1.2 | 600 | 600 | 596 | -0.7 |
| 180 | 400 | 398 | -0.5 | 620 | 400 | 403 | 0.8 |
| 200 | 200 | 199 | -0.5 | 640 | 200 | 196 | -2.0 |
| 220 | 0 | 8 | 660 | 0 | 7 | ||
| 240 | 0 | 0 | 0.0 | 680 | 0 | 0 | 0.0 |
| 260 | 0 | 0 | 0.0 | 700 | 0 | 0 | 0.0 |
| 280 | 0 | 0 | 0.0 | 720 | 0 | 0 | 0.0 |
| 300 | 0 | 0 | 0.0 | 740 | 0 | 0 | 0.0 |
| 320 | 0 | 0 | 0.0 | 760 | 0 | 0 | 0.0 |
| 340 | 0 | 0 | 0.0 | 780 | 0 | 0 | 0.0 |
| 360 | 0 | 0 | 0.0 | 800 | 0 | 0 | 0.0 |
| 380 | 0 | 0 | 0.0 | 820 | 0 | 0 | 0.0 |
| 400 | 0 | 0 | 0.0 | 840 | 0 | 0 | 0.0 |
| 420 | 0 | 5 | 880 | 0 | 0 | 0.0 |
表选项
2.2 数值试验2数值试验2给出1组吸收外热流值qmea如图 4所示,数值试验2的目的是为了检验阶跃突变情况下(如航天器姿轨控发动机点火工作)的共轭梯度法反演效果.通过求解导热正问题(式(1))得到温度测量值Tmea并作为导热反问题的输入条件,采用共轭梯度法反演吸收外热流值qcgm.共轭梯度法迭代350次后J(qnb)<0.63,增大迭代次数后J(qnb)在0.62~0.63之间波动不再减小.查看导热反问题反演出的温度值Tcgm与测量温度值Tmea如图 5所示,从图中可以看到,Tcgm与Tmea的偏差主要出现在曲线拐点附近,其他区域符合较好.
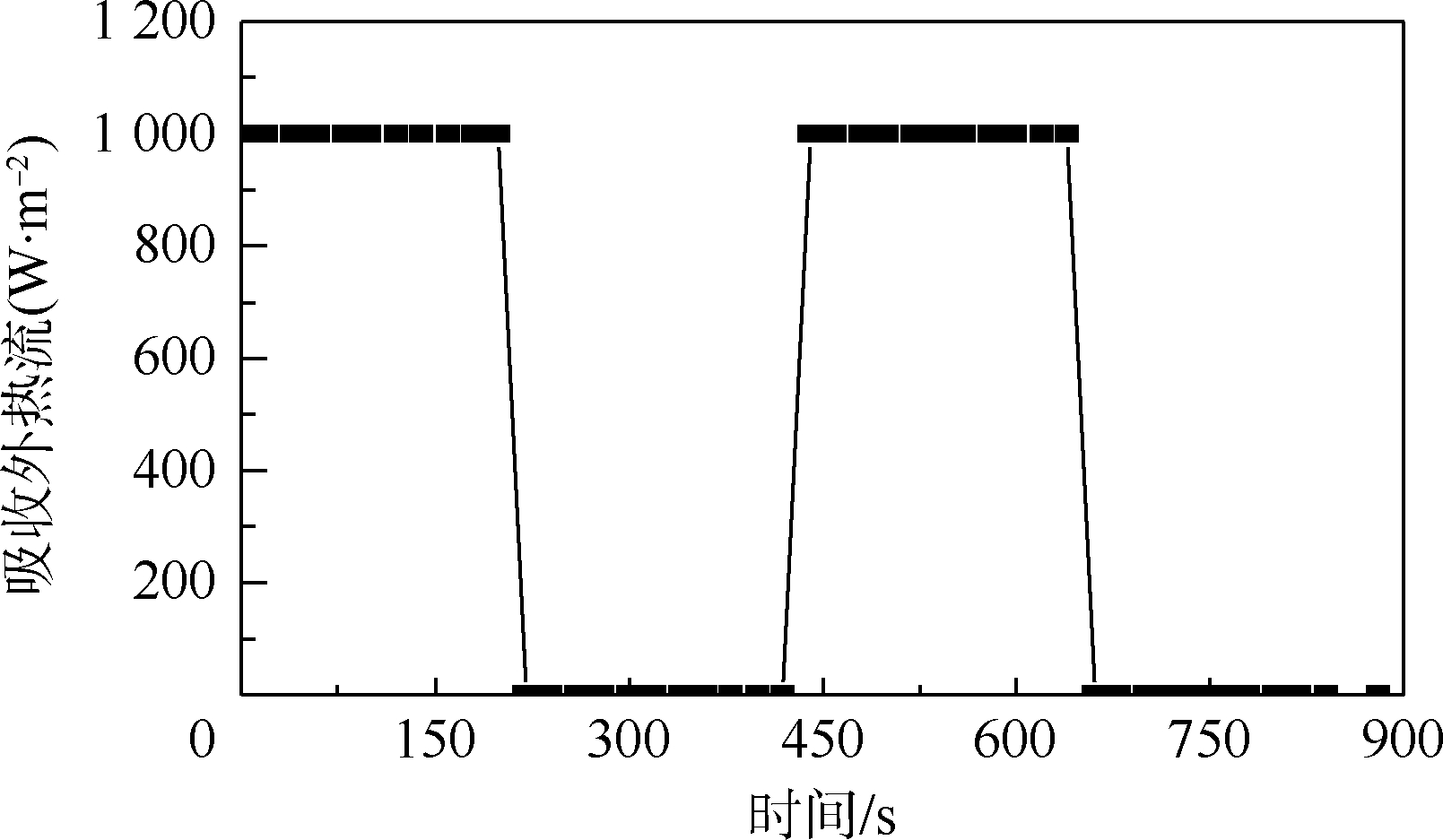 |
| 图 4 数值试验2的吸收外热流曲线Fig. 4 Absorbed external heat flux curve of numerical experiment 2 |
| 图选项 |
 |
| 图 5 数值试验2的温度反演值与测量值比较Fig. 5 Compare between inversion temperature and measuring data of numerical experiment 2 |
| 图选项 |
图 6和表 2分别为导热反问题反演出的吸收外热流值qcgm与真实值qmea的比较
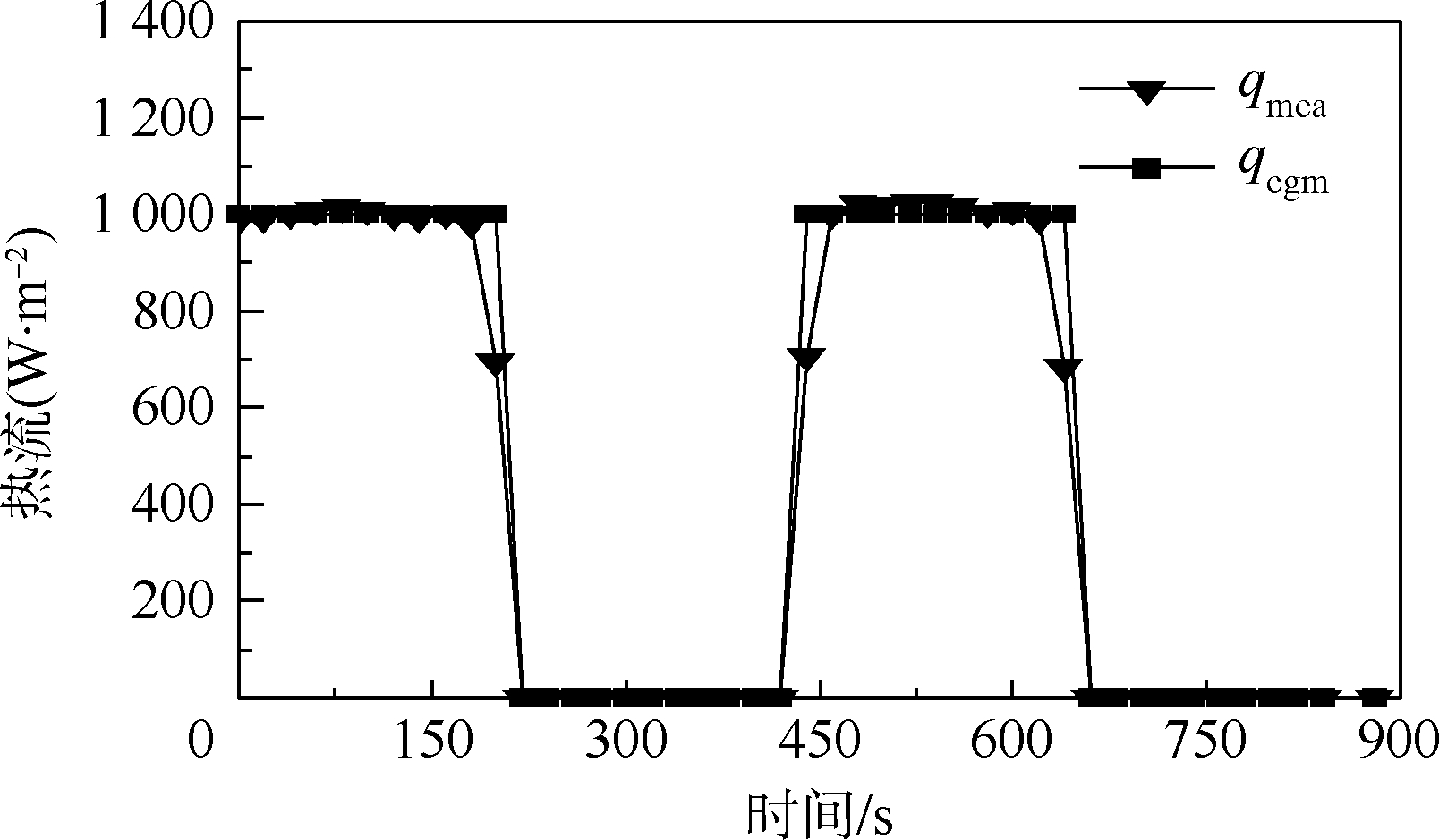 |
| 图 6 数值试验2的吸收外热流反演值与真实值比较Fig. 6 Compare between inversion absorbed externalheat flux and real value of numerical experiment 2 |
| 图选项 |
表 2 数值试验2的吸收外热流反演值与真实值比较Table 2 Compare between inversion absorbed external heat flux and real value of numerical experiment 2
| 时间/s | qmea/(W·m-2) | qcgm/(W·m-2) | 相对误差/% | 时间/s | qmea/(W·m-2) | qcgm/(W·m-2) | 相对误差/% |
| 0 | 1 000 | 986 | -1.4 | 440 | 1 000 | 707 | -29.3 |
| 20 | 1 000 | 992 | -0.8 | 460 | 1 000 | 1 002 | 0.2 |
| 40 | 1 000 | 1 001 | 0.1 | 480 | 1 000 | 1 023 | 2.3 |
| 60 | 1 000 | 1 010 | 1.0 | 500 | 1 000 | 1 019 | 1.9 |
| 80 | 1 000 | 1 013 | 1.3 | 520 | 1 000 | 1 024 | 2.4 |
| 100 | 1 000 | 1 008 | 0.8 | 540 | 1 000 | 1 026 | 2.6 |
| 120 | 1 000 | 997 | -0.3 | 560 | 1 000 | 1 016 | 1.6 |
| 140 | 1 000 | 991 | -0.9 | 580 | 1 000 | 1 004 | 0.4 |
| 160 | 1 000 | 1 000 | 0.0 | 600 | 1 000 | 1 008 | 0.8 |
| 180 | 1 000 | 982 | -1.8 | 620 | 1 000 | 990 | -1.0 |
| 200 | 1 000 | 695 | -30.5 | 640 | 1 000 | 684 | -31.6 |
| 220 | 0 | 0 | 0.0 | 660 | 0 | 0 | 0.0 |
| 240 | 0 | 0 | 0.0 | 680 | 0 | 0 | 0.0 |
| 260 | 0 | 0 | 0.0 | 700 | 0 | 0 | 0.0 |
| 280 | 0 | 0 | 0.0 | 720 | 0 | 0 | 0.0 |
| 300 | 0 | 0 | 0.0 | 740 | 0 | 0 | 0.0 |
| 320 | 0 | 0 | 0.0 | 760 | 0 | 0 | 0.0 |
| 340 | 0 | 0 | 0.0 | 780 | 0 | 0 | 0.0 |
| 360 | 0 | 0 | 0.0 | 800 | 0 | 0 | 0.0 |
| 380 | 0 | 0 | 0.0 | 820 | 0 | 0 | 0.0 |
| 400 | 0 | 0 | 0.0 | 840 | 0 | 0 | 0.0 |
| 420 | 0 | 0 | 0.0 | 880 | 0 | 0 | 0.0 |
表选项
图 6和表 2分别为导热反问题反演出的吸收外热流值qcgm与真实值qmea的比较.
从图 6中看到除了在qmea出现阶跃变化位置外其他区域共轭梯度法反演结果较好,最大相对偏差为2.9%;在阶跃变化处有一个时间点的相对偏差达到了31.6%,在实用中需要对阶跃位置的反演结果进行分析处理.
2.3 小 结通过两组数值试验对共轭梯度法的效果进行了检验,数值试验1中共轭梯度法很好地反演出了吸收外热流值;数值试验2中除了阶跃变化位置其他区域能够得到较好的反演结果,阶跃位置的反演结果需要根据阶跃位置以外区域的反演结果进行分析处理.数值试验1给出的吸收外热流曲线能够代表大多数地球轨道航天器以及深空探测航天器在轨吸收外热流变化趋势,因此本文研究的方法适用于多数航天器.
3 结 论本文研究了利用航天器设备在轨遥测温度值反演出航天器在轨瞬态外热流的导热反问题方法.首先推导了导热反问题数学模型,采用共轭梯度法求解导热反问题并从物理概念角度改进了共轭梯度法的迭代过程以增加其抗不适应性.然后根据大多数地球轨道航天器以及深空探测航天器在轨吸收外热流的特点,构造了两组数值试验对共轭梯度法的反演效果进行了检验.计算结果表明本文研究的方法能够很好地反演出目前大多数地球轨道航天器以及深空探测航天器在轨吸收外热流,对于阶跃变化的吸收外热流情况在对反演结果进行分析处理后也能够得到较好的反演结果.
参考文献
| [1] | 张天宇,董长虹.基于自适应反演法的导弹直/气复合制导[J].北京航空航天大学学报, 2013, 39(7):902-906. Zhang T Y, Dong C H.Compound control system design based on adaptive backstepping theory[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(7):902-906(in Chinese). |
| Cited By in Cnki | |
| [2] | 杨尔辅,张振鹏,刘国球.一种推进系统故障诊断反问题模型与算法[J].北京航空航天大学学报, 1999, 25(6):684-687. Yang E F, Zhang Z P, Liu G Q.Model and algorithm of inverse-problems on fault diagnosis for propulsion systems[J].Journal of Beijing University of Aeronautics and Astronautics, 1999, 25(6):684-687(in Chinese). |
| Cited By in Cnki (3) | |
| [3] | 程文龙,刘娜,钟奇,等.卫星稳态热模型参数修正方法研究[J].宇航学报, 2010, 31(1):270-275. Cheng W L, Liu N, Zhong Q, et al.Study on parameters correction method of steady-state thermal model for spacecraft[J].Journal of Astronautics, 2010, 31(1):270-275(in Chinese). |
| Cited By in Cnki (8) | |
| [4] | 程文龙,刘娜,李志,等.卫星热模型蒙特卡罗混合算法的修正方法应用研究[J].科学通报, 2010, 55(20):2056-2061. Cheng W L, Liu N, Li Z, et al.Application study of a correction method for a spacecraft thermal model with a Monte-Carlo hybrid algorithm[J].Chinese Science Bulletin, 2010, 55(20):2056-2061(in Chinese). |
| Cited By in Cnki (1) | |
| [5] | 杨沪宁,钟奇.航天器热模型蒙特卡罗法修正论述[J].航天器工程, 2009, 18(3):53-58. Yang H N, Zhong Q.Monte-Carlo method for thermal model correction of spacecraft[J].Spacecraft Engineering, 2009, 18(3):53-58(in Chinese). |
| Cited By in Cnki (7) | |
| [6] | 张镜洋,常海萍,王立国.小卫星瞬态热分析模型修正方法[J].中国空间科学技术, 2013, 33(4):24-30. Zhang J Y, Chang H P, Wang L G.Correction method for transient thermal analysis model of small satellite[J].Chinese Space Science and Technology, 2013, 33(4):24-30(in Chinese). |
| Cited By in Cnki (1) | |
| [7] | 张中礼,李明海,胡绍全.外壁热流响应计算的导热反问题方法及其验证[J].强度与环境, 2009, 36(4):54-59. Zhang Z L, Li M H, Hu S Q.Nonlinear transient inverse heat conduction problems method of calculating the boundary heat response[J].Structure & Environment Engineering, 2009, 36(4):54-59(in Chinese). |
| Cited By in Cnki | |
| [8] | Lin D T, Yan W M, Li H Y.Inverse problem of unsteady conjugated forced convection in parallel plate channels[J].International Journal of Heat and Mass Transfer, 2008, 51(5-6):993-1002. |
| Click to display the text | |
| [9] | Chen U C, Cheng W J, Hsu J C.Two-dimensional inverse problem in estimating heat flux of pin fins[J].International Communication of Heat and Mass Transfer, 2001, 28(6):793-801. |
| Click to display the text | |
| [10] | Huang C H, Wang S P.A three-dimensional inverse heat conduction problem in estimated surface heat flux by conjugate gradient method[J].International Journal of Heat and Mass Transfer, 1999, 42(18):3387-3403. |
| Click to display the text | |
| [11] | Huang C H, Chen W C.A three-dimensional inverse forced convection problem in estimating surface heat flux by conjugate gradient method[J].International Journal of Heat and Mass Transfer, 2000, 43(17):3171-3181. |
| Click to display the text | |
| [12] | 薛齐文,杨海天,胡国俊.共轭梯度法求解瞬态传热组合边界条件多宗量反问题[J].应用基础与工程科学学报, 2004, 12(2):113-120. Xue Q W, Yang H T, Hu G J.Solving inverse heat conduction problems with multi-variables of boundary conditions in transient-state via conjugate gradient method[J].Journal of Basic Science and Engineering, 2004, 12(2):113-120(in Chinese). |
| Cited By in Cnki (10) | |
| [13] | Xue Q W, Yan H T.A conjugate gradient method for the hyperbolic inverse heat conduction problem with multi-variables[J].Chinese Journal of Computational Physics, 2005, 22(5):417-424. |
| Click to display the text | |
| [14] | 杨海天,胡国俊.共轭梯度法求解多宗量稳态传热反问题[J].应用基础与工程科学学报, 2002, 10(2):174-181. Yang H T, Hu G J.Solving inverse heat conduction problems with multi-variables in steady-state via conjugate gradient method[J].Journal of Basic Science and Engineering, 2002, 10(2):174-181(in Chinese). |
| Cited By in Cnki (23) | |
| [15] | 王登刚,刘迎曦,李守巨,等.非线性二维稳态导热反问题的一种数值解法[J].西安交通大学学报, 2000, 34(1):49-52. Wang D G, Liu Y X, Li S J, et a1.Two dimensional numerical solution for nonlinear inverse steady heat conduction[J].Journal of Xi'an Jiaotong University, 2000, 34(1):49-52(in Chinese |
| Cited By in Cnki (34) | |
| [16] | 范春利,孙丰瑞,杨立.基于红外侧温的试件内部缺陷的识别算法研究[J].工程热物理学报, 2007, 28(2):304-306. Fan C L, Sun F R, Yang L.An algorithm study on identification of subsurface defect based on thermographic temperature measurement[J].Journal of Engineering Thermophysics, 2007, 28(2):304-306(in Chinese). |
| Cited By in Cnki (22) |
