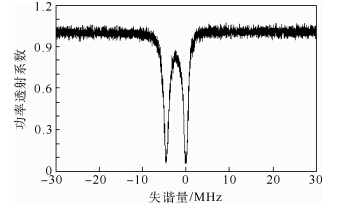
 |
| 图 1 实验测量的模式劈裂透射谱Fig. 1 Experimentally obtained splitting transmission spectrum |
| 图选项 |
模式劈裂现象可以用费马原理解释.费马原理也称为平稳时间原理:光沿着所需时间为平稳的路径传播,即光传播的路径是需时最短或最长的路径.微腔本是旋转对称的,散射源将破坏对称性.2个驻波模在腔内排布时,散射源就成了唯一的参考基准.SM选择需时最长的路径,ASM选择需时最短的路径;散射源位于SM的波腹,位于ASM的波节.相对于原简并模式而言,SM将因散射源的作用出现谐振峰的漂移及谐振线宽的增加;而ASM因散射源位于其波节处而不受影响,仍保持简并解除前的谐振频率.2个驻波模相对于散射源位置的场分布如图 2所示.
 |
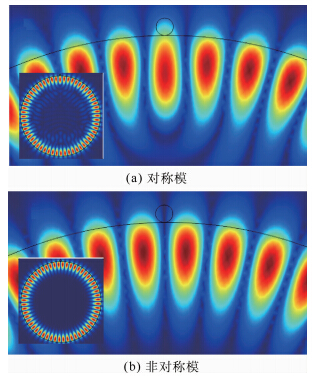| 图 2 2个驻波模相对于散射源位置的场分布Fig. 2 Field distribution of two standing wave modes relative to position of scattering source |
| 图选项 |
1.2 旋转腔模式劈裂分析模式劈裂发生后,在透射谱或反射谱上观察到的是SM和ASM 2个驻波模,而非CW与CCW 2个行波模.讨论腔体旋转导致的这2个驻波模谐振频率的变化,这是与Sagnac效应有区别的地方,Sagnac效应描述的是CW和CCW模光谐振频率的变化.散射不仅仅是重分布腔内光场,同时还造成部分回音壁模耦合到辐射模,导致散射损耗.采用光纤锥来激励和输出腔内的回音壁模式,光纤锥耦合谐振腔系统示意图如图 3所示.
 |
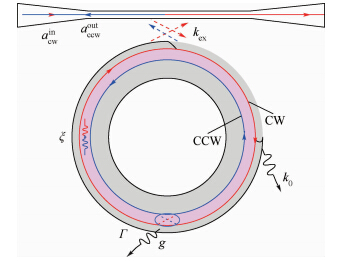| k0—谐振腔固有损耗系数(材料吸收及辐射耗散);kex—光纤锥耦合引入的损耗系数;ξ—掺杂增益系数;g—模式耦合系数;Γ—散射导致的损耗系数;aincw—顺时针方向的输入场强;aoutccw—逆时针方向的输出场强.图 3 光纤锥耦合谐振腔系统示意图Fig. 3 Illustration of fiber taper coupled microresonator |
| 图选项 |
在品质因数极高的光学微腔中,2个简并模之间的互相散射是主要的散射过程,可以用耦合谐振子模型描述[3].假设光从顺时针方向输入，背向散射光主要从逆时针方向生成,则描述散射的动力学方程为[15]
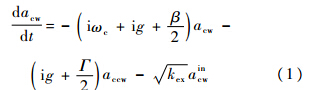
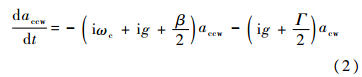
反射光场为
式中:β=Γ+k0+kex－ξ,定义为谐振腔的有效损耗系数;ωc为简并解除前的谐振频率;acw及accw为CW及CCW模的场强.假设光学微腔半径为R,旋转角速率为Ω,顺逆时针光绕行一周后的角频率差为
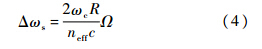
式中:neff为腔体介质的有效折射率;c为真空光速.光绕行一周的时间为τR=2πRneff/c,则单位时间内频率差为
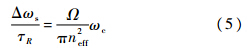
顺时针光(或逆时针光)的频率变化量为
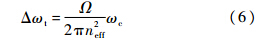
假设旋转方向为逆时针,考虑腔体旋转带来的谐振频率变化,式(1)和式(2)修正为
以反射谱为研究对象,振幅反射系数为
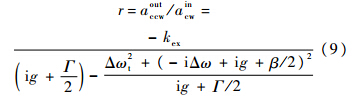
式中:Δω=ω－ωc表示入射频率与简并解除前谐振频率的差,即失谐量.功率反射系数定义为Re=r2.为了获得SM和ASM各自的谐振频率,最直观的方法是找反射系数导数为零的点.这里用求特征值的方法,特征值的实部表示谐振模的损耗系数,虚部表示谐振频率.式(7)和式(8)的矩阵表述为
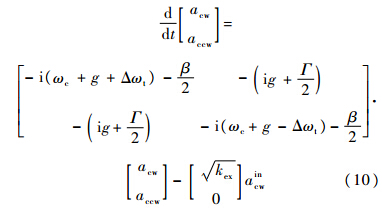
其对角标准型为
式中:本征模aSM和aASM表示SM与ASM的场强.二者互相正交,说明2个劈裂模之间无能量传递.光场重新分布的效果是使谐振腔因散射所导致的损耗达到最小.λSM与λASM表示SM和ASM这2个驻波模的本征值,其大小为
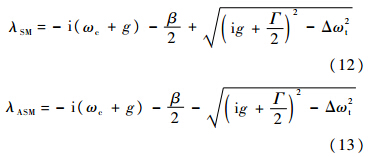
本征值包含了所对应腔模的谐振频率及损耗的信息：
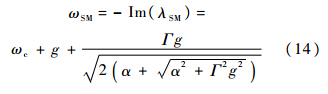
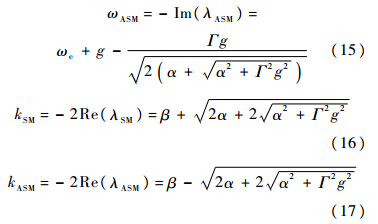
式中:
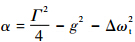是为简化表达式而定义的变量；Im(·)与Re(·)分别对应取虚部与取实部运算;ωSM和ωASM分别为SM与ASM的谐振频率;kSM和kASM分别为SM与ASM的损耗系数.静态腔中,式(14)~式(17)式简化为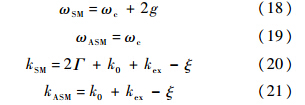
可见,散射粒子带来的额外损耗对ASM无影响,对SM有影响,这与图 2所示2个模的场分布相对应.劈裂值定义为反射谱(或透射谱)2个谐振峰之间的距离,大小为δ=ωASM－ωSM.静态腔中劈裂值大小为δ0=2g.式(14)与式(15)相减,得到劈裂值与角速率的对应表达式：
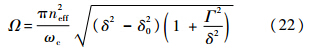
从式(16)和式(17)可知,谐振腔总体损耗kSM+kASM不受腔体旋转的影响,但是旋转会影响单个腔模(SM或ASM)的损耗系数,从而改变这2个模式的线宽.式(16)与式(17)相减,得到SM与ASM的线宽差与角速率的对应表达式：
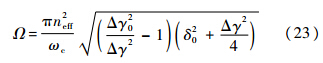
式中:Δγ=kSM－kASM,表示SM与ASM的线宽差;Δγ0=2Γ,表示腔体静止时线宽差.目前腔线宽差的获取是采用曲线拟合的方法[4, 5].对输入光进行扫频,测量不同频率点处的反射光强(或透射光强),再对所测得的这些离散点进行拟合,获得完整的反射谱(或透射谱)数据,进而得到线宽差.数据拟合方法不同,会对测量的准确性造成一定的影响.通过测量劈裂值来解算角速率,测量的是谐振峰的位置,可以借鉴现有的光学谐振陀螺的检测方法,如通过频率调制的方法进行测量,这样则不需要进行曲线拟合.2 仿真分析 由文献[15]可知,静态腔模式劈裂的条件是2g>Γ+k0+kex－ξ.若散射过程不带来额外损耗(Γ=0),即所有散射光都满足谐振条件而不辐射到腔外空间,则腔体旋转时该条件变为
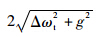>k0+kex－ξ.对光学微腔的某一个模式而言,k0、Γ、g均为常数.耦合系数kex可通过改变光纤锥与微腔的距离调节,ξ可通过改变掺杂增益的密度等方式调节,因此重点分析这2个参数的影响.在用光纤锥耦合微腔进行探测时,观察与入射光相反方向是否有返回的光,可以来确认散射光是否存在,因此仿真时选择反射谱为研究对象.为满足模式劈裂的条件,设置k0=2×107Hz,g=－k0,Γ=0.01k0,有效折射率neff=1.3,简并解除前的谐振波长为780nm.2种增益系数(无掺杂ξ=0,有掺杂且系数ξ=k0)下,微腔处于3种耦合区域(欠耦合kex<k0,临界耦合kex=k0,过耦合kex>k0)时,几个腔体旋转角速率下的反射谱如图 4所示. |
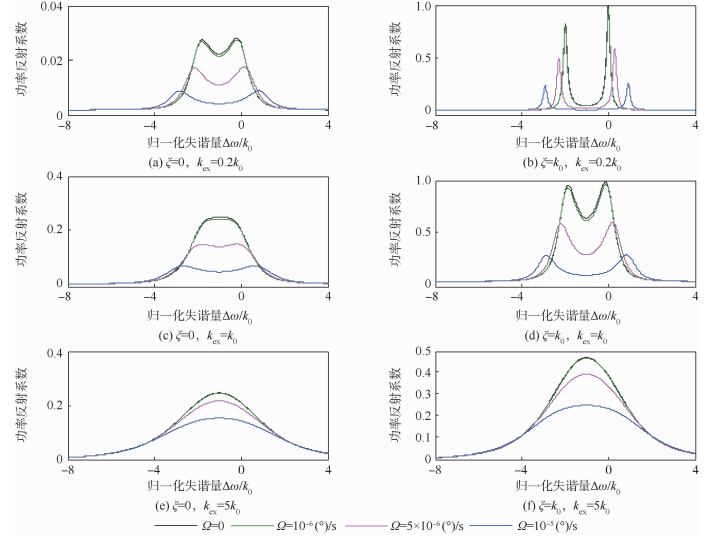| 图 4 微腔处于不同工作区域时,几个腔体旋转角速率下的反射谱Fig. 4 Calculated reflection spectra as a function of the normalized frequency detuning for several performing regimes at different angular rates |
| 图选项 |
欠耦合情况如图 4(a)和图 4(b)所示,谐振腔的总体损耗主要取决于固有损耗,掺杂增益的补偿效果明显.随着掺杂增益系数ξ的增加,模式劈裂现象越来越明显.若增益完全补偿模式的损耗,反射谱呈现2个尖峰,谐振腔输出频率相近的两束激光.这两束激光混合后生成拍频信号,且拍频刚好等于劈裂值[16].对该信号进行傅里叶变换获得拍频,可推算出腔体旋转角速率.散射损耗远小于固有损耗时,SM与ASM的损耗系数几乎相等(kSM≈kASM).相应地,反射谱的双谐振峰幅值及线宽几乎相等(见图 4(a)中Ω=0的谱线).腔体旋转会增加SM的损耗,减少ASM的损耗,从而破坏谱线的对称性.与临界耦合及过耦合相比,欠耦合区域2个劈裂模的损耗较小,线宽较窄,有利于角速率的测量.图 4(b)清晰地表示出了旋转导致的劈裂值变化.临界耦合情况如图 4(c)和图 4(d)所示,kex越大,腔内模式的有效损耗越大.相对于欠耦合而言,临界耦合条件下模式劈裂条件的满足要求更高的掺杂增益系数.在相同增益条件下,临界耦合区域谐振峰的线宽要大于欠耦合区域的,易导致2个谐振峰在频谱上的重叠,不利于测量.过耦合情况如图 4(e)和图 4(f)所示,单位时间内从光纤锥耦合进微腔的光能量要小于从微腔耦合到光纤锥的光能量,很难观测到模式劈裂现象.光纤锥的主要作用是激励腔内的回音壁模式.耦合系数kex会增加腔的损耗,降低品质因数,不利于角速率的测量.从以上分析得知,谐振腔工作在欠耦合区域更适合角速率测量.另一个会对测量造成影响的参数是腔内散射光与入射光的耦合系数g.根据文献[17]所述,g与2个因素有关:其一是谐振腔,其二是散射源.腔的品质因数变化或模式体积变化会导致不同大小的耦合系数;散射粒子的折射率变化或体积变化也会导致不同的耦合系数.概括地讲,2个谐振腔会提供2个不同数值的耦合系数g,进而导致旋转角速率相同时,2个谐振腔的劈裂值大小有异.图 5为耦合系数g对旋转角速率与劈裂值映射曲线的影响.计算参数为Γ=0.01k0,neff=1.3,谐振波长为780nm.仿真表明,静态时劈裂值较小的微腔更适合角速率测量.
 |
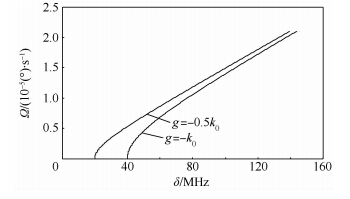| 图 5 旋转角速率与劈裂值的对应曲线Fig. 5 Calculated results of angular rate vs amount of splitting |
| 图选项 |
3 结 论 1) 光纤锥激励腔内回音壁模式的同时,为腔内光场提供了一个能量泄漏通道,从而降低了腔的品质因数.对比欠耦合、临界耦合、过耦合3种耦合状态下的反射谱线,发现欠耦合更适合角速率测量.2) 掺杂增益介质可补偿模式的损耗,提高品质因数,减小谐振峰线宽.3) 仿真发现静态时劈裂值较小的微腔更有利于角速率测量.利用模式劈裂的传感机制,计算机仿真分析表明品质因数为108的光学微腔角速率测量分辨率高达10-6(°)/s,预计利用该方法制成的微光学谐振陀螺在低成本、中等精度需求的角速度测量中具有重要的应用价值.
参考文献
| [1] | Monifi F, Özdemir Ş K,Yang L.Tunable add-drop filter using an active whispering gallery mode microcavity[J].Applied Physics Letters,2013,103(18):181103. |
| Click to display the text | |
| [2] | Ward J, Benson O.WGM microresonators:sensing,lasing and fundamental optics with microspheres[J].Laser & Photonics Reviews, 2011,5(4):553-570. |
| Click to display the text | |
| [3] | Kippenberg T J, Spillane S M,Vahala K J.Modal coupling in traveling-wave resonators[J].Optics Letters,2002,27(19):1669-1671. |
| Click to display the text | |
| [4] | Zhu J, Ozdemir S K,Xiao Y F,et al.On-chip single nanoparticle detection and sizing by mode-splitting in an ultra-high-Q microresonator[J].Nature Photonics,2010,4(1):46-49. |
| Click to display the text | |
| [5] | Kippenberg T J. Microresonators:particle sizing by mode splitting[J].Nature Photonics,2010,4(1):9-10. |
| Click to display the text | |
| [6] | Post E J. Sagnac effect[J].Reviews of Modern Physics,1967,39(2): 475-493. |
| Click to display the text | |
| [7] | Smith D, Chang H,Fuller K A.Whispering-gallery mode splitting in coupled microresonators[J].Journal of Optical Society America B,2003,20(9):1967-1974. |
| Click to display the text | |
| [8] | Smith D D, Chang H,Fuller K A,et al.Coupled-resonator-induced transparency[J].Physical Review A,2004,69(6): 063804. |
| Click to display the text | |
| [9] | Matsko A B, Savchenkov A A,Ilchenko V S,et al.Optical gyroscope with whispering gallery mode optical cavities[J].Optics Communications,2004,233(1):107-112. |
| Click to display the text | |
| [10] | Matsko A B, Savchenkov A A,Ilchenko V S,et al.Erratum to “Optical gyroscope with whispering gallery mode optical cavities”[Opt.Commun.233 (2004) 107-112][J].Optics Communications,2006,259(1):393-394. |
| Click to display the text | |
| [11] | Peng C, Li Z,Xu A.Optical gyroscope based on a coupled resonator with the all-optical analogous property of electromagnetically induced transparency[J].Optics Express,2007,15(7):3864-3875. |
| Click to display the text | |
| [12] | Peng C, Li Z,Xu A.Rotation sensing based on a slow-light resonating structure with high group dispersion[J].Applied Optics,2007,46(19):4125-4131. |
| Click to display the text | |
| [13] | Terrel M, Digonnet M J F,Fan S.Performance comparison of slow-light coupled-resonator optical gyroscope[J].Laser & Photonics Reviews,2009,3(5):452-465. |
| Click to display the text | |
| [14] | Vollmer F, Arnold S.Whispering-gallery-mode biosensing:label-free detection down to single molecules[J].Nature Methods,2008,5(7):591-596. |
| Click to display the text | |
| [15] | He L, Ozdemir S K,Xiao Y F,et al.Gain-induced evolution of mode splitting spectra in a high-active microresonator[J].IEEE Journal of Quantum Electronics,2010,46(11):1626-1633. |
| Click to display the text | |
| [16] | He L, Özdemir Ş K,Zhu J,et al.Ultrasensitive detection of mode splitting in active optical microcavities[J].Physical Review A,2010,82(5):053810. |
| Click to display the text | |
| [17] | Mazzei A, Götzinger S,Menezes L S,et al.Controlled coupling of counter propagating whispering-gallery modes by a single Rayleigh scatterer:a classical problem in a quantum optical light[J].Physical Review Letters,2007,99(17):173603. |
| Click to display the text |
