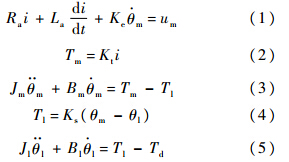
式中,Ra为电枢电阻;La为电枢电感;i为电枢电流;Ke为反电动势系数;θm为电机转角;um为电枢电压;Tm为电机输出力矩;Kt为电磁转矩常数;Jm为电机转动惯量;Bm为电机端黏性阻尼系数;Tl为扭转力矩;θl为负载转角;Ks为转轴的机械刚度;Jl为负载转动惯量;Bl为负载端黏性阻尼系数;Td为扰动力矩,包括摩擦力矩、耦合力矩及外部干扰力矩.伺服系统中的机械谐振模态主要是由各传动轴之间的柔性引起的.将式(1)~式(5)化简,可得电机输出转角与电机力矩之间的关系为
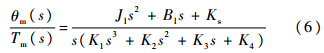
式中,s为拉普拉斯算子;K1=JmJl;K2=JmBl+JlBm;K3=JmKs+JlKs+BmBl;K4=BmKs+BlKs.1.2 谐振问题本文所研究的伺服系统采用干扰观测器(DOB)加零相差前馈控制器(ZPETC)的综合控制结构[15, 16].当存在机械谐振时,系统的模型辨识就不准确,这样将影响DOB的设计,进而影响系统的跟踪精度和系统带宽.对式(6)做进一步的分析可知,该系统存在谐振极点和谐振零点.这些零极点引起了伺服系统的机械谐振.通过对该伺服系统加白噪声测试,获得了系统伯德图如图 1所示.
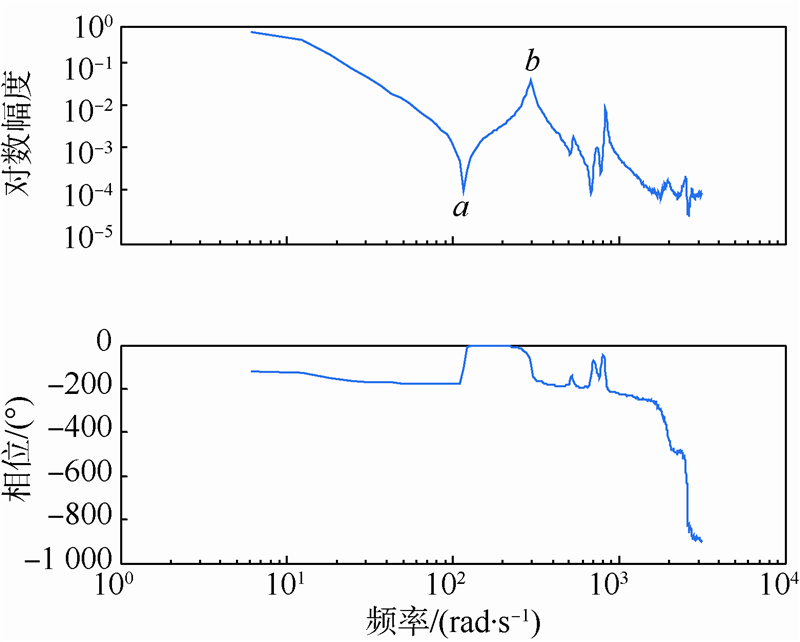 |
| 图 1 系统伯德图Fig. 1 System Bode diagram |
| 图选项 |
从图 1的幅频特性曲线上明显看到系统有较大的谐振,其中波峰b点为谐振点,波谷a点为反谐振点.式(6)的谐振极点使其产生谐振点,谐振零点使其产生反谐振点.由幅频特性曲线可知,系统的谐振频率比较低而谐振峰值比较高,这为DOB的设计带来了一定的困难.因为谐振点附近,名义模型和实际模型的误差增大,系统的鲁棒稳定性很难满足;若要满足系统的稳定性条件,则需要减小滤波器的带宽,系统频带要求就不一定能满足.因此,需要设计滤波器对机械谐振进行抑制,进而设计符合条件的DOB和ZPETC,满足系统的控制要求.2 数字滤波器的设计对于机械谐振问题,采用数字滤波器是一种简单有效的方法,即设计滤波器来分别抵消系统中的谐振极点和谐振零点.在控制输入和被控对象之间串联一个滤波器,其结构图如图 2所示.
 |
| 图 2 串联滤波器结构图Fig. 2 Structure image of connected filter |
| 图选项 |
则串联滤波器后的系统传递函数表示为

式中,θ(s)为电机输出转角;u(s)为输入电压;Gp(s)为被控对象;Q(s)为所设计的数字滤波器.2.1 陷 波 器常用的陷波器为改进型双T网络陷波器,因其能够方便地实现作用频率、陷波带宽和陷波深度的调节,因此被广泛使用.其传递函数[10]为
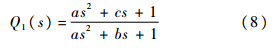
式中,a=1/ω02;b=k1/ω0;c=k2/ω0,ω0为陷波器的作用频率;k1,k2分别为陷波器的陷波带宽参数和陷波深度参数.由于陷波器是带阻滤波器,其幅频特性曲线的中段是向下弯曲的,因此可以将图 1中的b点抑制掉.将ω0设置为b点的频率值,同时根据谐振频率选择合适的参数k1和k2即可设计好陷波器.将设计好的陷波器加入到式(7)所示的传递函数中,可获得新的被控对象频率响应.图 3所示为加入陷波器后系统的伯德图.
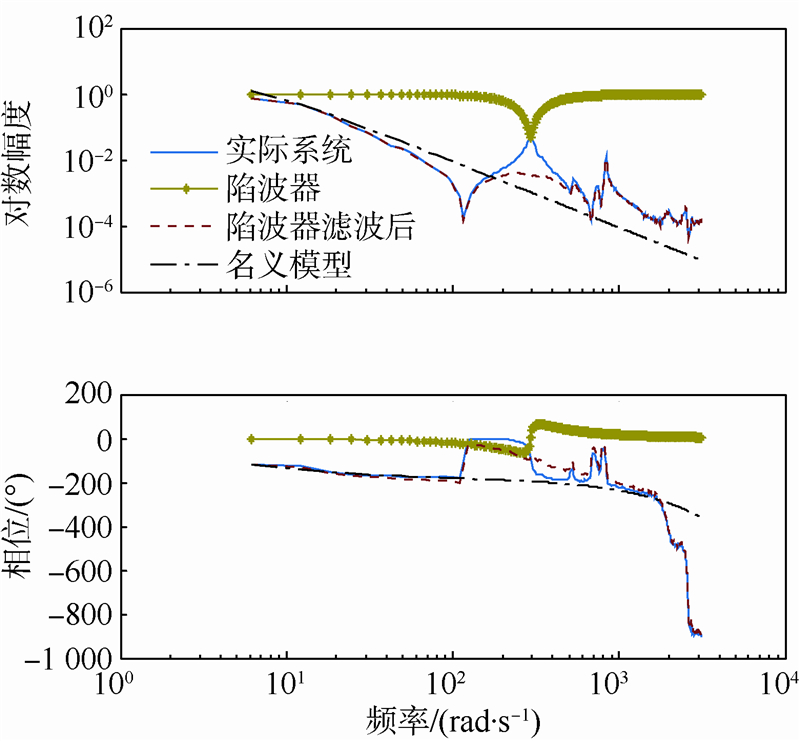 |
| 图 3 加入陷波器后系统的伯德图Fig. 3 Bode diagram of system added notch filter |
| 图选项 |
由图 3的幅频特性曲线可见,陷波器的凹陷点与系统谐振点b的峰值点正好相互抵消,得到了较为光滑的幅频特性曲线,如图中虚线所示.在较多数的文献中采用的是上述方法进行谐振抑制的,能达到一定的效果,在本文第3节将通过实验进行验证.但是由于反谐振点a(即幅频特性曲线中向下凹陷的点)的存在,对系统的建模仍然会产生较大误差.图中的点划线(Gn(s))是根据实际曲线拟合的名义模型,它与滤波后的系统幅频特性曲线(Gp(s)Q1(s))相比,在中频段的差距还是比较大的.对图 3进行深入的分析计算可知,加入陷波器后系统的幅值稳定裕度为38.8 dB.而系统带宽通过分析估计约为11.8 rad/s(由于闭环系统无法准确获得,因此只能是估计,下同).2.2 二阶低通滤波器从图 1的幅频特性曲线中可知,反谐振点a的出现将系统的幅值压了下来,致使幅频特性曲线的斜率值增大.而一般情况下将转台伺服系统视为二阶系统,因此在模型辨识时以二阶系统参数辨识为主.则斜率值的增大不利于对系统参数的辨识,并且导致辨识模型与实际模型的差值增大,进一步影响控制器的设计.考虑到二阶低通滤波器(又称振荡环节)幅频特性的特点,因此设计二阶低通滤波器对反谐振点a进行抑制.二阶低通滤波器的传递函数[17]为
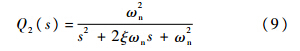
式中,ξ为阻尼比;ωn为自然频率.二阶低通滤波器的谐振频率与自然频率的关系为
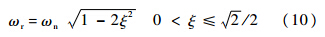
式中ωr为滤波器的谐振频率.将ωr取为a点的频率值,根据式(10)可计算得到自然频率,并选取合适的阻尼比ξ即可得到具有抑制a点谐振能力的二阶低通滤波器.将该滤波器加入到式(7)的传递函数中可得到新的传递函数的频率特性,加入低通滤波器后系统的伯德图如图 4所示.
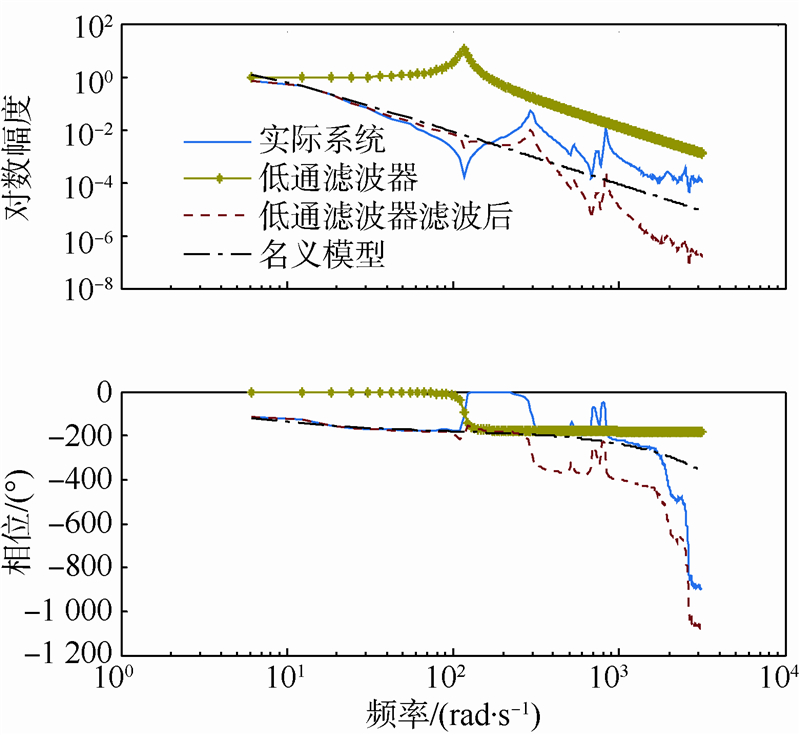 |
| 图 4 加入低通滤波器后系统的伯德图Fig. 4 Bode diagram of system added low-pass filter |
| 图选项 |
由图 4的幅频特性曲线可知,加入低通滤波器后系统的反谐振点a被抑制了,系统的幅频特性曲线的低频段变得比较平滑,斜率值也有了一定程度的减小.拟合的名义模型曲线(Gn(s))与滤波后的系统幅频特性曲线(Gp(s)Q2(s))在中频段的吻合度还是很高的.第3节中将通过实验证明该滤波器使得系统的频带提高了.但是该低通滤波器使得系统的相移增大了,从图 4的相频特性曲线中可以看到,中频段以后系统的相移增大了将近180°.并且由于谐振点b依然存在,对整个系统的控制器设计仍然会产生影响.通过进一步的分析计算,加入该滤波器后系统的幅值稳定裕度为31.3 dB,闭环系统带宽约为11.9 rad/s.2.3 双二次滤波器为了同时抑制谐振点和反谐振点,在结合2.1节和2.2节所述陷波器和二阶低通滤波器特性的基础上,设计了双二次型滤波器.设
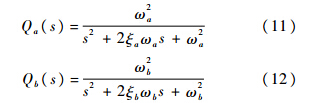
则双二次滤波器设计为
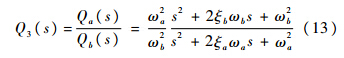
式中,ωa为对应a点的频率;ωb为对应b点的频率.该双二次型滤波器的物理意义很直观,可以理解为Qa(s)和Qb(s)均是二阶低通滤波器,其幅频特性曲线具有向上的谐振峰.现将Qb(s)取倒数,则其幅频特性曲线变成了向下的谐振峰.它与Qa(s)串联后,由Qa(s)抵消系统幅频特性曲线中的谐振点a,1/Qb(s)抵消反谐振点b,这样系统幅频特性曲线中的正、反谐振点均得到了抑制.将式(13)的双二次滤波器与式(8)的陷波器相比较可发现,当ωa=ωb时,式(13)与式(8)具有相同的形式,可见陷波器是所设计的双二次滤波器的一种特例形式.将式(13)及式(6)代入式(7),可得新的被控对象的表达形式为
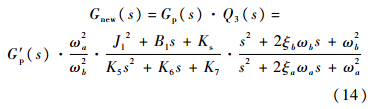
式中,G′p(s)为去除了谐振零极点的被控对象;K5,K6,K7为耦合常数.由式(14)可见,所设计的双二次型滤波器将抵消原被控对象中的谐振极点和谐振零点,进而消除机械谐振.根据式(10)可分别计算得到ωa和ωb的值,再选择合适的阻尼比ξa和ξb即可设计完成双二次滤波器.将该双二次滤波器串入式(7)的传递函数中,得到如式(14)所示的新系统,进而得到加入双二次滤波器后系统的伯德图如图 5所示.
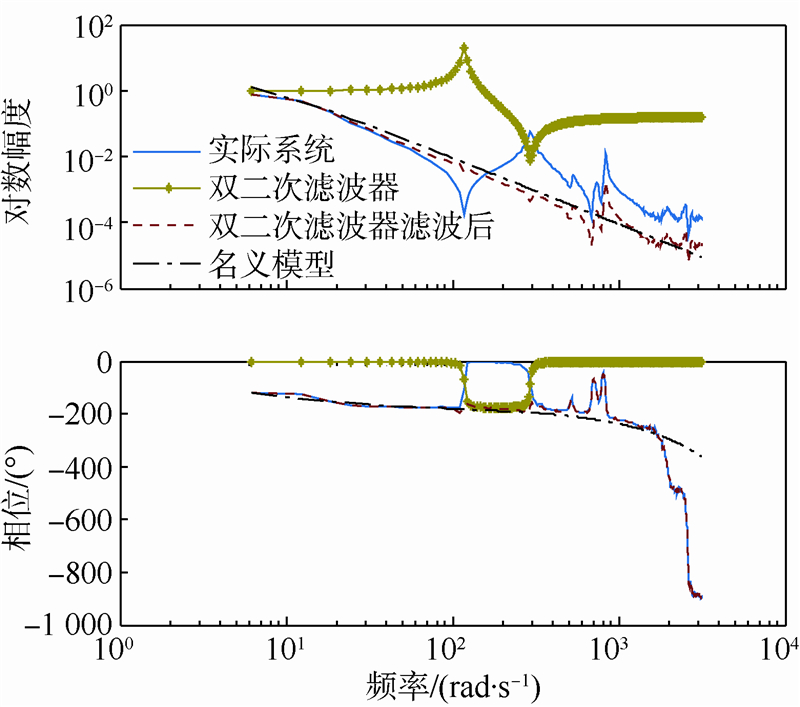 |
| 图 5 加入双二次滤波器后系统的伯德图Fig. 5 Bode diagram of system added two-second filter |
| 图选项 |
从图 5的幅频特性曲线中可看到,系统的谐振已经被完全抑制,系统的幅频特性曲线(虚线)在中频段以下已经变成光滑的直线.而且辨识得到的名义模型(点划线)也能与系统幅频特性曲线完美吻合.从相频特性曲线来看,串联双二次滤波器后系统的相移很小,基本与原曲线相重合.因此从仿真来看,所设计的双二次型滤波器能够达到理想的谐振抑制效果.从定量的角度来分析,加入该双二次型滤波器后系统的幅值稳定裕度达到43.4 dB,并且系统的带宽约可达12.3 rad/s.将设计的数字滤波器加入到转台伺服控制系统中,得到如图 6所示的结构.其中,e=θd-e.
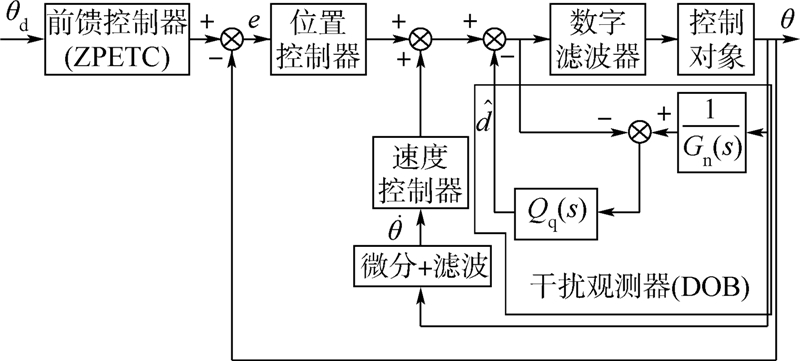 |
 —干扰观测器对干扰的观测值;θd—转角输入指示; —干扰观测器对干扰的观测值;θd—转角输入指示;θ—转角的输出;  —转角速度;Qq(s)—DOB中的低通滤波器.图 6 加入数字滤波器后的转台伺服控制系统结构Fig. 6 Structure of turntable servo control system added digital filter —转角速度;Qq(s)—DOB中的低通滤波器.图 6 加入数字滤波器后的转台伺服控制系统结构Fig. 6 Structure of turntable servo control system added digital filter |
| 图选项 |
图 6中转台伺服系统采用速度环和位置环双环控制[14]结构,在双环控制之前加入前馈控制,以消除相位滞后问题.对系统中的等效干扰,采用干扰观测器进行抵消.速度信号是通过对位置信号微分获得的,考虑到位置测量量化噪声的影响,因此将位置信号微分之后经过低通滤波器以获取速度信号.由图 6的控制系统可见,设计的数字滤波器与控制对象串联后被作为新的被控对象.在干扰观测器设计中只要名义模型Gn(s)选取合适,系统中的其他等效干扰就会被观测出并被抵消掉,进而提高控制器的性能[18].将所设计的数字滤波器与被控对象串联后可以抵消原系统中的谐振极点和谐振零点,使得系统消除机械谐振,并且不会改变原系统的可控性能.因此加入数字滤波器后整个系统的稳定性是由之后设计的控制器决定的,数字滤波器对控制系统的稳定性是没有直接影响的.为了实现滤波器的计算机应用,需将其离散化.采用双线性变换,将
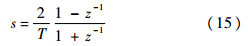
代入式(13)可得
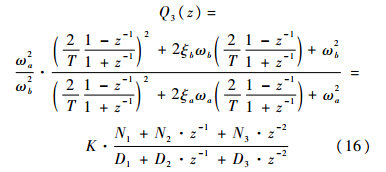
式中,K=ωa2/ωb2;N1=4+4Tξbωb+ωb2T2;N2=2ωb2T2-8;N3=4-4Tξbωb+ω2bT2;D1=4+4Tξaωa+ωa2T2;D2=2ωa2T2-8;D3=4-4Tξaωa+ωa2T2;T为采样周期.3 实验结果以某三轴飞行仿真转台为例进行实验验证.该仿真转台测角元件为光电编码器,细分分辨率达0.000 7°.控制算法以台湾研华610工业控制计算机为核心,采用C++语言编程实现,人机交互界面由MFC编程建立.工控机通过ISA总线上16位D/A转换卡与电机驱动器相连.系统的控制周期为1 ms,控制系统采用如图 6所示的控制结构.该三轴转台实物图如图 7所示.
 |
| 图 7 三轴转台实物图Fig. 7 Physical map of three-axis turntable |
| 图选项 |
本文使用的是该仿真转台的外框轴.外框由于机械尺寸较大,力臂较长,在转动过程中存在伺服弹性,因此会有较大的机械谐振.将设计的数字滤波器分别加入控制系统中,重新进行白噪声测试,然后根据转台响应结果进行频谱特性分析并对系统进行辨识,得到了系统的频率特性和名义模型,3种数字滤波器实验结果如图 8所示.
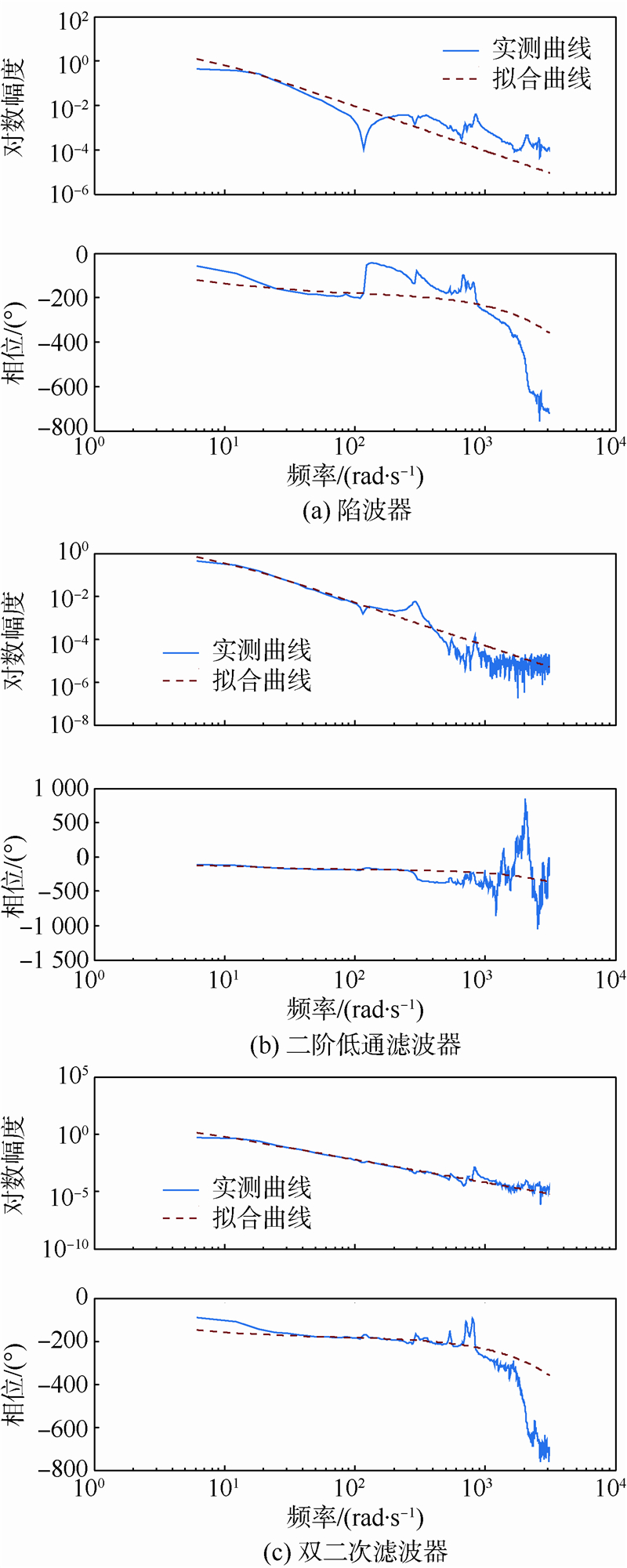 |
| 图 8 3种数字滤波器实验结果Fig. 8 Experimental results of three kinds of digital filters |
| 图选项 |
从图 8的3种滤波器实验结果对比来看,实验结果与仿真结果相一致.所提出的双二次滤波器的实测曲线和拟合曲线吻合度最高,二阶低通滤波器次之,陷波器最差.由图 8(c)的幅频特性曲线可见,加入双二次滤波器之后转台的模型被校正为比较标准的二阶系统.因此用二阶名义模型来代替转台实际模型设计DOB还是很准确的.这样系统中的等效干扰能尽可能被消除,进而伺服系统的跟踪精度和系统频带才均能提高.在图 8所示的名义模型的基础上,设计DOB和ZPETC,并加入到控制系统中进行系统测试.如图 9所示为加入双二次滤波器后系统的跟踪曲线.
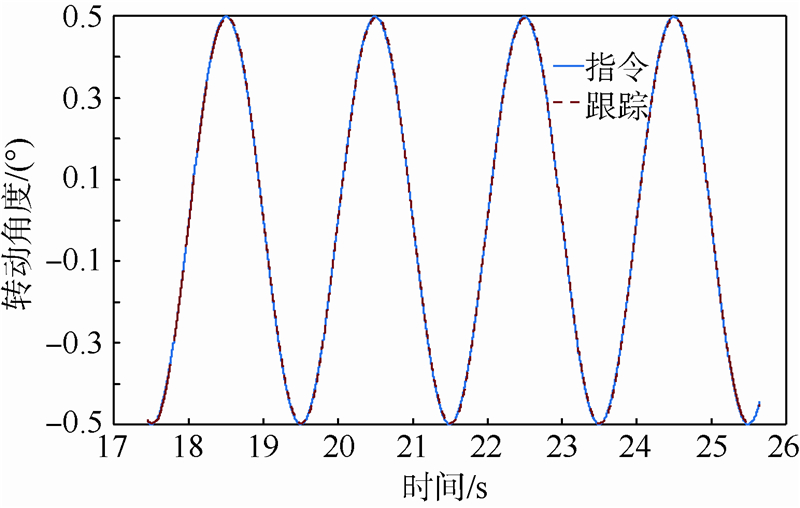 |
| 图 9 加入双二次滤波器后系统的跟踪曲线Fig. 9 System tracking curve added two-second filter |
| 图选项 |
由图 9可见系统能够很好地跟踪指令的变化,说明系统具有良好的动态性能.为了进一步说明本文所设计的双二次滤波器能够使得系统在跟踪精度方面优于另外两个滤波器,对3种数字滤波器作用下系统的跟踪精度做了对比,结果如图 10所示.可见,应用陷波器的系统跟踪误差是最大的,达到0.009°,而加入本文提出的双二次滤波器的系统跟踪误差是最小的,只有0.005 4°.由此可知,应用双二次滤波器能够很好地抑制机械谐振,使得系统模型更容易辨识,控制器设计更加方便、有效,控制精度也更加满足指标.
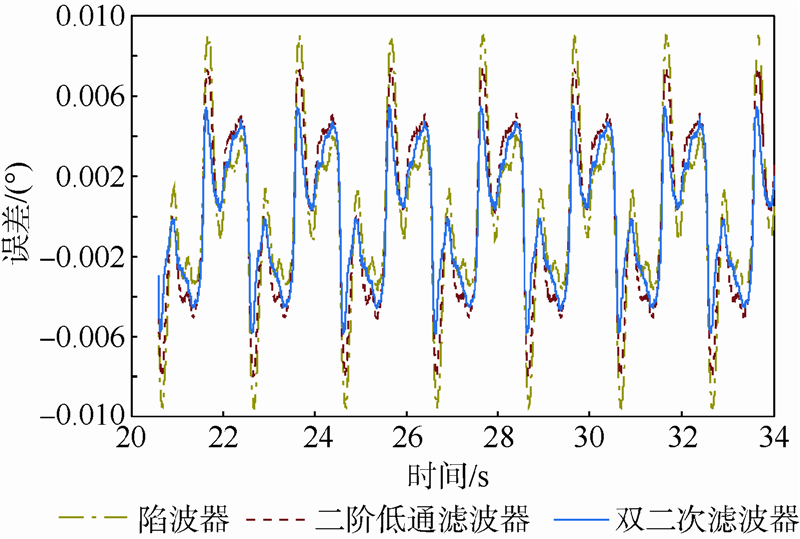 |
| 图 10 跟踪精度对比Fig. 10 Contrast of tracking accuracy |
| 图选项 |
应用数字滤波器后,除了系统跟踪精度提高以外,系统的频带也增大了.如表 1所示为加入不同数字滤波器后系统的频带范围.表 1 系统频带范围Table 1 System bandwidth scope
| 滤波器类型 | 频带宽度/Hz |
| 无滤波器 | 1.0 |
| 陷波器 | 2.5 |
| 二阶低通滤波器 | 3.0 |
| 双二次滤波器 | 4.0 |
表选项
加入双二次滤波器的系统频带在“双三”指标下达到了4 Hz,满足了指标和精度的要求(“双三”指标指的是幅度误差在±3%以内,相位误差在±3°以内).综合以上实验结果,本文提出的双二次型数字滤波器能够很好地抑制机械谐振,使得校正后的系统模型更加趋近二阶系统,有利于系统模型的辨识及DOB的设计.同时该拟合度较高的数学模型为控制器、ZPETC的设计提供了方便,进而有助于控制系统跟踪精度的提高和频带宽度的增大,最终达到系统动态性能指标.4 结 论1) 该双二次型滤波器能够同时抑制谐振中的正、反谐振点,进而将系统模型校正为光滑的二阶系统形式,有利于系统模型的辨识和控制系统的设计.2) 在理论分析和仿真的基础上进行了实验验证.实验结果表明:所提出的双二次型滤波器能够很好地抑制谐振,相比于其他2种滤波器,在提高系统跟踪精度的同时增大了系统带宽,满足了系统的动态性能指标.
参考文献
| [1] | John Y H. Control of industrial robots that have transmission elasticity [J].IEEE Transactions on Industrial Electronics,1991,38(6):421-427. |
| Click to display the text | |
| [2] | 赵桂军, 许美健,吴雄君,等.陷波器在导引头伺服系统中的应用[J].制导与引信,2013,34(2):1-3. Zhao G J,Xu M J,Wu X J,et al.The application of notch filter for the servo system in seeker[J].Guidance & Fuze,2013,34(2): 1-3(in Chinese). |
| Cited By in Cnki | |
| [3] | Slobodan N V, Milic R S.Suppression of torsional oscillations in a high performance speed servo drive[J].IEEE Transactions on Industrial Electronics,1998,45(1):108-117. |
| Click to display the text | |
| [4] | Krzysztof S, Teresa O K.Vibration suppression in a two-mass drive system using PI speed controller and additional feed backs-comparative study[J].IEEE Transactions on Industrial Electronics,2007,54(2):1193-1206. |
| Click to display the text | |
| [5] | 杨晓霞,阴玉梅, 孟浩然,等.利用加速度反馈的大型光电设备主轴控制技术[J].中国惯性技术学报,2013,21(4):421-424. Yang X X,Yin Y M,Meng H R,et al.Mount control for large optoelectronic equipment by using acceleration feedback[J].Journal of Chinese Inertial Technology,2013,21(4):421-424(in Chinese). |
| Cited By in Cnki (2) | |
| [6] | 于晶,冯勇, 郑剑飞.基于高阶滑模和加速度反馈的机械谐振抑制方法[J].控制理论与应用,2009,26(10):1133-1136. Yu J,Feng Y,Zheng J F.Suppression of mechanical resonance based on higher-order sliding mode and acceleration feedback[J].Control Theory & Applications,2009,26(10):1133-1136(in Chinese). |
| Cited By in Cnki (8) | |
| [7] | Carl J K, Seiichi K.Disturbance observer and feed-forward design for a high speed direct-drive positioning table[J].IEEE Transactions on Control Systems Technology,1999,7(5):513-526. |
| Click to display the text | |
| [8] | Abdullah A M, Ehsan K,Charanjit S B,et al.Integral resonant control for suppression of resonance in piezoelectric micro-actuator used in precision servomechanism[J].Mechatronics,2013,23(1):1-9. |
| Click to display the text | |
| [9] | 张卫国,曹永刚, 陈涛.用数字滤波器改善光电经纬仪机械谐振频率的方法[J].光学精密工程,1999,7(2):77-82. Zhang W G,Cao Y G,Chen T.Digital filter approach to improving the resonance frequency of photoelectric theodolite[J].Optics and Precision Engineering,1999,7(2):77-82(in Chinese). |
| Cited By in Cnki (21) | |
| [10] | 杨明,胡浩, 徐殿国.永磁交流伺服系统机械谐振成因及其抑制[J].电机与控制学报,2012,16(1):79-84. Yang M,Hu H,Xu D G.Cause and suppression of mechanical resonance in PMSM servo system[J].Electric Machines and Control,2012,16(1):79-84(in Chinese). |
| Cited By in Cnki (15) | |
| [11] | 李献斌,王跃科, 杨俊.级联陷波器抗窄带干扰设计与实现[J].电子测量与仪器学报,2013,27(6):492-497. Li X B,Wang Y K,Yang J.Design and implementation of cascade IIR notch filters for narrow-band interferences suppression[J].Journal of Electronic Measurement and Instrument,2013,27(6):492-497(in Chinese). |
| Cited By in Cnki (2) | |
| [12] | 马跃,黄宾, 王志成.基于陷波器的伺服系统共振抑制的研究[J].计算机工程与设计,2013,34(5):1624-1629. Ma Y,Huang B,Wang Z C.Research on resonance vibration in servo system based on notch filter[J].Computer Engineering and Design,2013,34(5):1624-1629(in Chinese). |
| Cited By in Cnki (2) | |
| [13] | Xu J B, Wang W Y,Shen A W,et al.Detection and reduction of middle frequency resonance for an industrial servo[J].Control Engineering Practice,2013,21(7):899-907. |
| Click to display the text | |
| [14] | 刘强. 现代高精度数字伺服系统运动控制理论及应用研究[D].北京:北京航空航天大学,2002. Liu Q.Motion control theory and application research on modern high precision digital servo system[D].Beijing:Beijing University of Aeronautics and Astronautics,2002(in Chinese). |
| [15] | 刘强,尔联洁. 飞行仿真转台基于干扰观测器的鲁棒跟踪控制[J].北京航空航天大学学报,2003,29(2):181-184. Liu Q,Er L J.Disturbance observer based robust tracking control of high precision flight simulator[J].Journal of Beijing University of Aeronautics and Astronautics,2003,29(2):181-184(in Chinese). |
| Cited By in Cnki (27) | |
| [16] | Wu Y J, Liu X D,Tian D P.Research of compound controller for flight simulator with disturbance observer[J].Chinese Journal of Aeronautics,2011,24(5):613-621. |
| Click to display the text | |
| [17] | 胡寿松. 自动控制原理[M].4版.北京:科学出版社,2001:77-83. Hu S S.Automatic control theory[M].4th ed.Beijing:Science Press,2001:77-83(in Chinese). |
| [18] | 刘晓东,吴云洁, 田大鹏,等.基于干扰观测器的飞行仿真转台滑模控制器[J].上海交通大学学报,2011,45(3):393-397. Liu X D,Wu Y J,Tian D P,et al.Research of sliding mode controller for flight simulator based on disturbance observer[J].Journal of Shanghai Jiaotong University,2011,45(3):393-397(in Chinese). |
| Cited By in Cnki (10) |
