目前,美国的全球定位系统(GPS)和俄罗斯的全球导航卫星系统(GLONASS)已发展成为第二代卫星导航定位系统,欧盟的GALILEO系统和中国的COMPASS系统也正在积极组建中.不同卫星导航系统的组合导航,由于其可见星数目大幅增加,在定位精度、系统可用性以及可靠性等方面均明显优于单星座导航,将成为今后发展的主要趋势;但同时,由于可见星数目相较于单星座成倍增加,导航定位解算的运算量也随之成倍增长,严重影响导航定位的实时性,大大提高了对导航接收机数据处理器负载能力和处理速度的要求,特别是对高动态接收机而言,更是大大增加了接收机硬件设计的难度和成本.为此,如何在满足用户定位精度要求的前提下,实时地选择尽量少的卫星用于定位解算,减少过多的冗余信息,降低导航运算量,对降低导航接收机数据处理器的功耗、提高组合导航接收机的实时性至关重要.在单卫星导航系统中,一般通过最小几何精度因子(GDOP)法^[1]或最大体积法^[2]选取最优可见星星座用于定位.不同卫星导航系统组合导航时,最小GDOP法由于算法本身的遍历特性,虽然能找出规定选星数目下GDOP最小的定位卫星组合,但算法本身计算量太大,选星的实时性太差,而最大体积法由于涉及的卫星数目较多,选星计算量也很大且体积难以计算.目前,针对组合卫星导航系统的选星问题,出现了一系列设计方法^{[3,4,5,6,7,8,9]},文献^[3,4]中主要研究单卫星导航系统的星座选择,文献^[5]中提出的组合优选法与最小GDOP法相比,可以在GDOP损失不超过5%的情况下降低40%的选星计算量,但在可见星较多时,选星计算量仍较大,不利于实时选星;文献^[6]中提出一种加权几何精度因子,加权几何精度因子最小算法不以快速选星为目的,而是追求更精确地反映组合星座的性能和定位精度的估计;文献^[7]中提出的快速选星算法与最小GDOP法相比,选取70%以上的可见星时GDOP损失不足2%,选星算法的计算量与最小GDOP法相比可以忽略不计,但选星比例较大,导致可见星数目较多时导航运算量较大,在高动态导航应用上存在局限性;文献^[8]中提出的快速选星算法与文献^[7]中提出的算法类似,从几何布局的角度按比例选星,也存在类似的局限性.文献^[9]中提出的快速选星方法可以通过选择7~9颗卫星实现以不超过3次GDOP求解、不小于0.98的概率满足卫星导航系统的可用性(GDOP≤6),但是对于用户定位精度要求比较严格的情况(GDOP＜4),方法不适用.本文致力于研究如何实时选择满足用户定位精度要求(2.5≤GDOP≤6)的尽量小数目的卫星星座,而不以追求选星后GDOP的最小化为目标,以尽可能地降低导航运算量、减少接收机处理器的负荷、减少接收机硬件设计的难度和成本,同时提高导航数据处理的实时性.本文从选星数目与选星后GDOP以及导航运算量的关系出发,提出了根据用户的定位精度要求自适应地增加选星数目以保证选星实时性的星座选择方法,该方法在满足用户定位精度要求的前提下实时地选择尽量小数目的卫星,以用户可接受的GDOP损失换取导航运算量的大幅降低,并对该方法进行了仿真验证. 1 选星问题中的数学关系 1.1 选星数目与选星后GDOP的关系卫星导航系统的定位精度,可以表示为几何精度因子和用户等效距离误差的乘积^[1],即
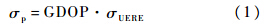
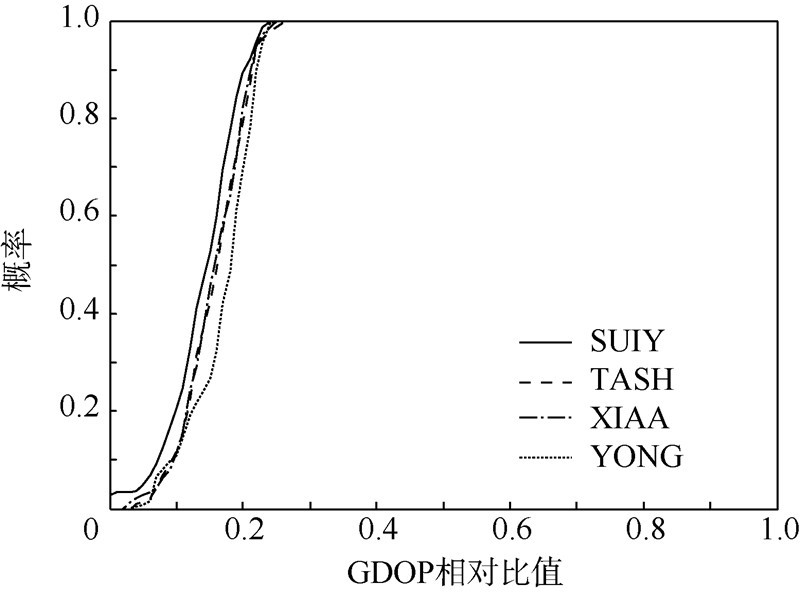
式中,σ_p表示定位精度的标准偏差;GDOP表示几何精度因子;σ_UERE表示用户等效距离误差的标准差.显然,GDOP反映了定位卫星星座的拓扑结构对用户等效距离误差的放大程度. 本文为了不失一般性,假设组合导航系统中各系统的等效测距误差近似一致,则GDOP可以表征定位精度的大小,即用户对定位精度的要求可以通过GDOP阈值(GDOP Threshold,简称GDOP_T)来体现.组合导航系统的几何精度因子可以表示为
式中H表示组合导航系统的测量矩阵.双星座组合导航系统的测量矩阵可以表示为
式中,a_x^j,a_y^j和a_z^j(j=1,2,…,n_s1,n_s1+1,…,n)表示第j颗卫星的方向余弦,n_s1表示卫星导航系统1的可见卫星数,n－n_s1表示卫星导航系统2的可见卫星数.下面以GPS/COMPASS组合导航系统为例,进一步说明选星数目与GDOP的关系.以中国地壳运动观测网络的27个基准站为观测站,仰角门限设为5°,采用最小GDOP法,对组合系统的选星问题进行仿真,仿真时长为24 h,采样间隔为60 s.位于最东北的SUIY站、最西部的TASH站、最南端的YONG站以及中部的XIAA站在历元时刻t为12 h时选星后的GDOP随选星数目m增加的变化情况如表 1所示,选星比例为0.5时仿真时长内各测站选星前后GDOP相对比值的统计结果如图 1所示.表 1 选星后的GDOP与选星数目的关系Table 1 Relationship between GDOP after satellite selection and number of selected satellite

选星数目/颗	GDOP
	SUIY	TASH	XIAA	YONG
5	2.04	2.06	2.12	2.16
6	1.90	1.90	2.03	2.04
7	1.77	1.79	1.98	1.95
8	1.67	1.72	1.94	1.88
9	1.65	1.68	1.91	1.81
10	1.59	1.64	1.84	1.77
11	1.52	1.60	1.79	1.73
12	1.47	1.56	1.76	1.69
13	1.42	1.52	1.73	1.67
14	1.40	1.49	1.70	1.65
15	1.38	1.47	1.68	1.64
16	1.37	1.45	1.67	1.62
17		1.44	1.65
18		1.43	1.64

表选项


由表 1可知,各测站选星后的GDOP随着选星数目m的增加而非线性递减,当选星数目较小时,GDOP下降较快,当选星数目过多时,GDOP变化较缓慢.由图 1可知,选星比例为0.5时,各测站选星前后GDOP相对比值的均值不大于0.17,各测站在仿真时长内的选星前后GDOP相对比值的最大值不大于0.27,至少有70%的仿真时刻选星前后GDOP相对比值小于0.2.

图 1 选星比例为0.5时GDOP相对比值的统计结果Fig. 1 Statistical results of relative ratio of GDOP in case that ratio of selected satellite is 0.5l

图选项

1.2 选星数目与导航运算量的关系卫星导航系统中,基于伪距定位的测量方程^[1]为
式中,Δρ∈ R^m表示伪距测量值与预测值之差，m为用于定位的卫星数目，也即选星数目；H∈R^m×I_s表示测量矩阵,I_s=3+s表示状态变量维数,s表示组合导航系统中的系统数；ΔX∈R^I_s表示状态变量增量； ε ∈R^I_s 表示系统测量误差.采用最小二乘法定位时,求解公式^[10]为
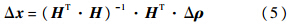
每次迭代的运算量如表 2所示.表 2中使用高斯消去法计算矩阵逆^[10].表 2 最小二乘法定位时的运算量Table 2 Calculation of least square estimation to position

表选项


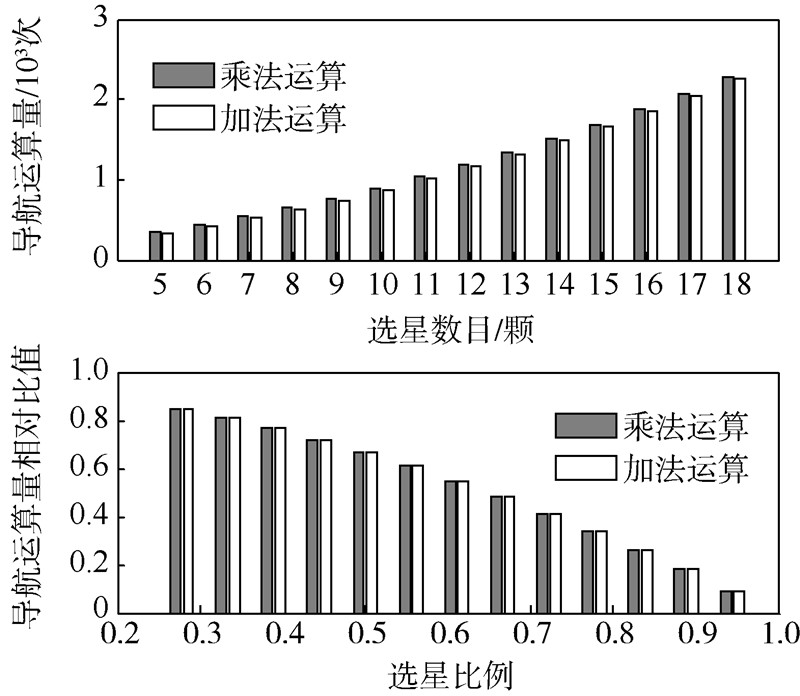
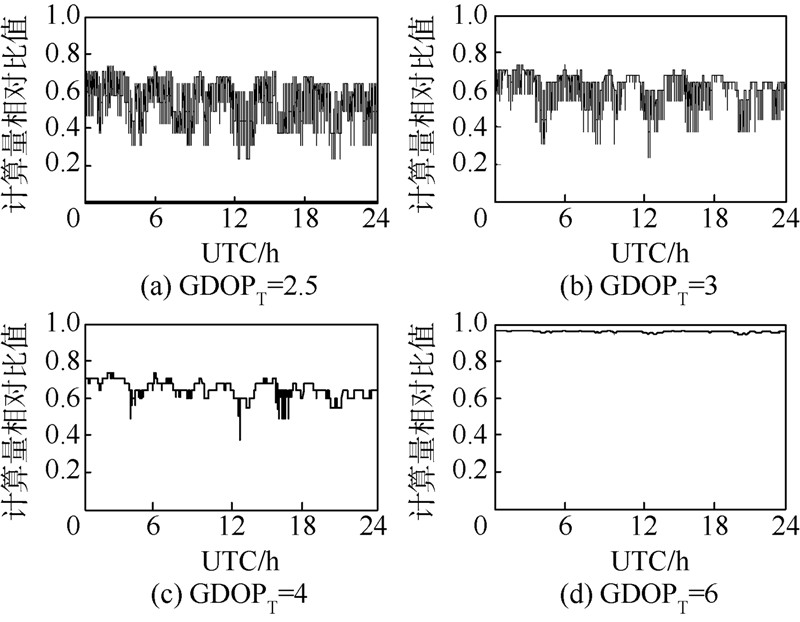
下面以GPS/COMPASS组合导航系统为例,进一步说明选星数目与选星后导航运算量的关系.GPS/COMPASS组合系统中,I_s=5,仿真时长内的27个观测站的平均可见卫星数为18.导航运算量随选星数目增加的变化情况以及导航运算量相对比值与选星比例的关系如图 2所示.

图 2 导航运算量与选星数目的关系Fig. 2 Relationship between navigation computation and number of selected satellite

图选项

分析图 2可知,导航运算量随着选星数目的减少而显著减少,当选星比例为0.5时,导航运算量的减少量超过60%.下文设计的选星算法不以获得最小GDOP为目标,而是在定位精度、导航运算量和选星实时性之间均衡处理,实时选择满足用户定位精度要求的尽量小数目的卫星星座,以尽可能地降低导航运算量、减少接收机处理器的负荷、减少接收机硬件设计的难度和成本,同时提高导航数据处理的实时性.2 快速选星方法2.1 选星问题的数学模型卫星导航定位系统中,选星问题的本质是从所有可见星中选取规定数目的卫星,使其拓扑结构满足用户定位精度的要求.可以用数学公式描述如下:已知n∈N,m∈N,且满足n≥m;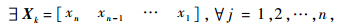,x_j= 1或0,且满足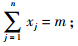求解X₀∈{X_k} ,使其满足:GDOP(X₀)=min{GDOP(X_k)} ≤GDOP_T
其中,n表示可见星数目;x_j(j=1,2，…,n)表示第j颗是否被选作定位卫星的标记;k表示从n颗卫星中选出m颗卫星子集的序号;X_k 表示选星方案,GDOP(X_k) 表示X_k 的星座几何精度因子;X₀表示选星解;GDOP_T表示为满足用户定位精度要求所需的阈值.很明显,这是一个单目标优化问题. 2.2 快速遗传选星法遗传算法作为一种成熟的目标优化搜索算法,下文首先设计选星问题的编码方案和操作算子^{[11,12,13,14]},然后利用遗传算法获得选星问题的初始解,再依据初始解的GDOP与GDOP_T的关系判断是否需要对初始解进行优化,直至满足算法终止条件,获得选星解.具体实现步骤如下:步骤1 配置初始选星数目m₀,选星数目上限m_max，GDOP_T和仰角门限.以接收机的总通道数为前提,综合考虑用户定位精度要求、故障监测需要以及接收机处理器性能来确定m₀和m_max;而GDOP_T取决于用户定位精度要求,为了满足卫星导航系统的可用性,通常取为6^[1];根据接收机所处环境确定仰角门限.步骤2 根据卫星历书或者星历获取可见卫星数目和位置,剔除仰角小于仰角门限的卫星.步骤3 构造由m₀颗被选卫星组成的选星方案的初始种群. 编码方案:将选星方案采用二进制串编码,将每颗卫星设为一个基因,作为卫星选入与否的标识.即选星方案X_k=[x_n x_n-1 … x_j x_j-1 … x₁],满足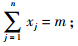,其中x_j=1表示j号卫星被选入,x_j=0表示j号卫星为被选入,所有可见星按顺序进行编排,最低位表示1号卫星. 步骤4 求解种群中各选星方案的适应值.目标函数: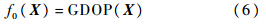
其中X为选星方案.适应度函数:
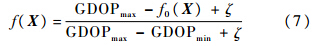
其中,GDOP_max和GDOP_min分别为当前种群中各选星方案GDOP的最大值和最小值；ζ为属于(0,1)的一个非负常数.步骤5 判断是否满足进化终止原则.如果满足进化终止原则,输出初始选星解.如果不满足进化终止原则,对初始种群进行选择、交叉、变异运算,形成新种群,重复步骤4和步骤5,直至获得初始选星解. 终止原则:当种群中适值最大的个体所对应的GDOP满足GDOP_T要求,即min{GDOP(X_k)} ≤GDOP_T时,可终止运算; 此外,为了保证迭代运算的有效性,如果经过若干代进化后种群中的最大适值不变,也终止运算;同时,进化代数达到进化代数上限时,也应终止运算,本方法中为了满足选星的实时性,最大进化代数取为1.选择运算法则:因为选星求解中种群数目不大,为了避免去掉拓扑结构较好的星座,采用扩大的采用空间进行选择,使双亲和后代具有同样的生存竞争机会.按随机采样机理,采用正比选择方式来获得进行交叉和变异的种群.交叉运算法则:选星数目m是根据用户定位精度要求确定的一个常数,即选星方案满足约束条件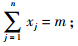.针对这一特点,为了增加种群的多样性,防止算法的局部收敛,提出一种变异交叉,在保证交叉后的后代仍是满足约束条件的合法解的同时,变异交叉所产生的后代突破了双亲对已选卫星的限制,仿真实验证明变异交叉对局部收敛有抑制作用.设选星数目为m,则交叉运算的法则如下:1) 根据交叉概率p_c选择双亲,随机产生2个1~m间的整数n₁和n₂,以定义要进行交叉的“1”基因的范围和个数;2) 交换双亲中的第n₁到第n₂个“1”基因,产生原始后代;3) 判断交叉产生的后代是否满足约束条件;4) 如果不满足约束条件,则根据“1”基因相差的个数,通过变异方式,随机选取相应原始后代中的“0”基因变异为“1”基因,使后代合法化.变异运算法则:与交叉运算一样,选星问题中的变异运算也需要保证变异前后个体中的选星数目相同,同时为了增加种群的多样性,防止算法收敛到局部最优解,提出一种双基因“01”相对变异.设总可见星数目为n,则变异运算的法则如下:1) 根据变异概率p_m随机选取一个欲进行变异的个体cp;2) 随机产生一个1~n间的整数g1;3) 判定个体cp中g1位所对应的基因类别,如果该基因为“0”,则随机产生一个1~n间的整数g₂(g₁≠g2),且应保证个体cp中与g2对应的基因为“1”,反之,如果g1对应的基因为“1”,则产生的随机数g2对应的基因应为“0”;4) 将个体cp中与g1和g2相对应的基因产生变异,即“1”“0”互换.步骤6 判断选星解的GDOP是否满足GDOP_T要求.如果满足,结束算法,输出选星结果.步骤7 如果不满足,依据最小GDOP原则,从其余可见卫星中选取1颗卫星,优化选星解.步骤8 判断优化后选星解的GDOP是否满足GDOP_T要求,如果满足,结束算法,输出选星结果;如果不满足,重复步骤7,直至满足算法终止条件,即选星解的GDOP满足GDOP_T要求或者选星数目达到上限m_max,结束算法,输出选星结果.根据上述分析,形成快速遗传选星法(FGSSM)的流程图如图 3所示.

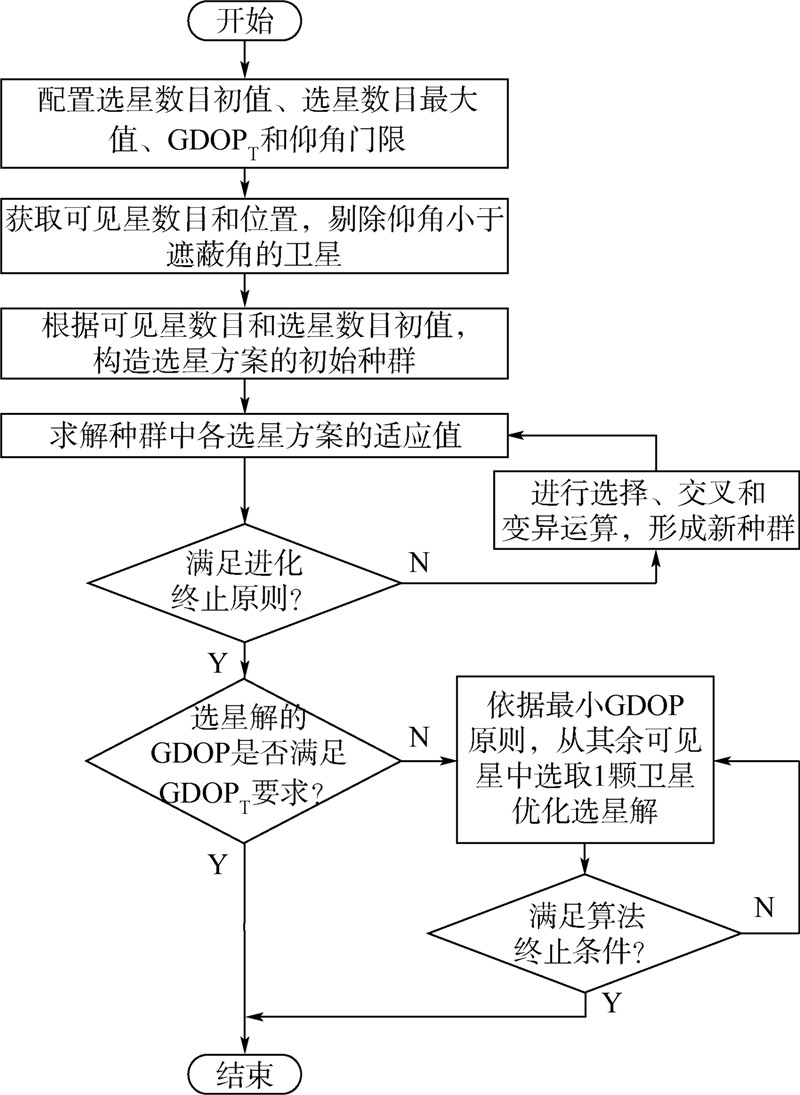图 3 快速遗传选星法的流程图Fig. 3 Flow chart of fast genetic satellite selection method (FGSSM)

图选项

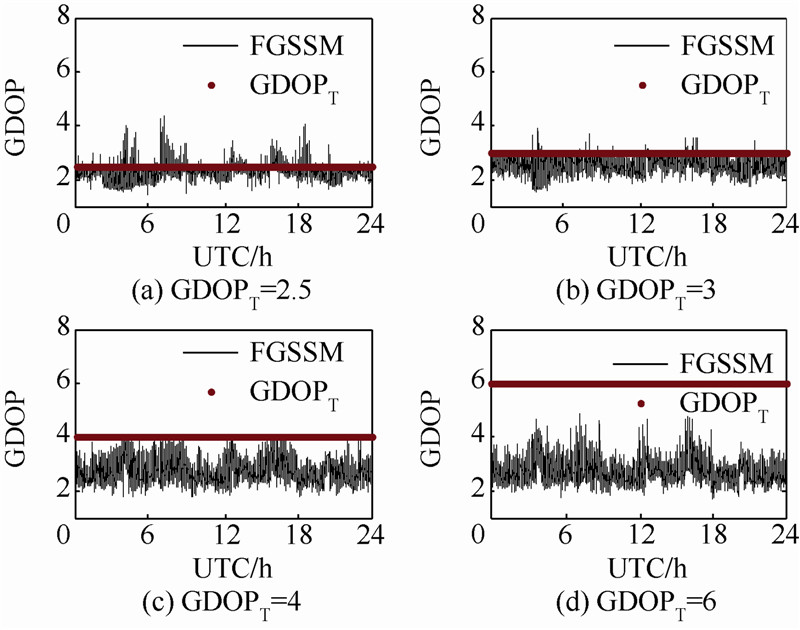
3 仿真实验和结果分析本文提出的选星方法在设计过程中考虑了多星座组合导航的情况,但考虑到GPS目前的应用最为广泛,而我国的COMPASS已经开通亚太地区的服务,同时,双系统联合定位又具有一定的普遍性,故本文的仿真实验主要基于GPS/COMPASS组合系统的仿真平台进行,对该选星方法的有效性进行验证,分析该方法的实时性、选星情况及选星前后的计算量的改善情况,并对该方法与最小GDOP法进行比较.3.1 仿真环境根据RTCA D0-229D的标准^[15],仰角门限设为5°,以中国地壳运动观测网络的27个基准站为观测站,采用快速遗传选星法,对GPS/COMPASS组合系统的选星问题进行仿真,仿真时间为24 h,采样间隔为10 s.3.2 快速遗传选星法的性能分析考虑到双系统组合导航故障检测的需要,初始选星数目m₀取为7.由1.2节的分析可知,选星比例为0.5时,导航运算量减少量达60%以上,而全国27个观测站在24 h仿真时长内的平均可见星是18,因此选星数目上限m_max取为9.为了分析算法在不同用户定位精度要求的性能,分别对GDOP取为2.5，3，4和6进行仿真分析. 3.2.1 有效性分析不同GDOP_T要求下,TASH站和XIAA站选星后的GDOP与GDOP_T的关系如图 4和图 5所示.表 3是对其进行的统计分析.

图 4 TASH站选星后GDOP与GDOPT的关系曲线Fig. 4 Relationship between GDOP after satellite selection and GDOPT at the TASH

图选项

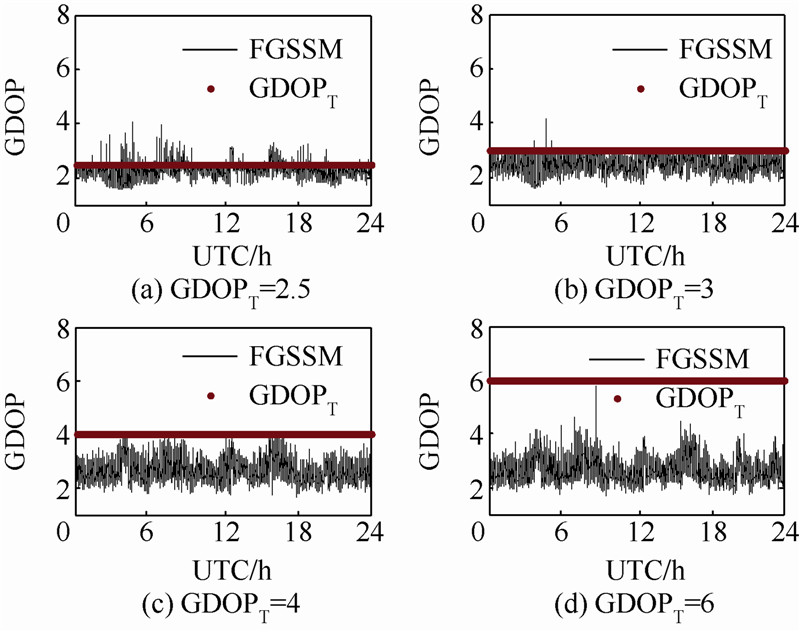图 5 XIAA站选星后GDOP与GDOPT的关系曲线Fig. 5 Relationship between GDOP after satellite selection and GDOPT at the XIAA

图选项

从图 4、图 5的关系曲线以及表 3的统计分析中,可得出以下结论:表 3 选星后GDOP的统计分析Table 3 Statistical analysis of GDOP after selected satellite

测站	GDOPT	选星后GDOP				PG/%
		最小值	最大值	均值	方差
TASH	2.5	1.42	4.39	2.30	0.06	92.45
	3	1.54	3.93	2.56	0.07	99.59
	4	1.79	3.99	2.71	0.14	100
	6	1.71	4.89	2.71	1.15	100
XIAA	2.5	1.56	4.09	2.29	0.05	94.78
	3	1.57	4.19	2.50	0.07	99.91
	4	1.65	3.99	2.61	0.13	100
	6	1.68	5.79	2.62	0.13	100
注：PG—仿真时长内选星后的GDOP满足GDOPT要求的概率.

表选项


1) 选星后GDOP的均值均满足GDOP_T要求.2) GDOP_T为2.5～4时,一次进化内GDOP满足GDOP_T要求的概率不低于92.45%;而GDOP_T为4～6时,一次进化内的GDOP满足GDOP_T要求的概率达到100%.3) 各测站选星后GDOP的变化都比较稳定.上述结论证明了本算法的有效性、准确性和鲁棒性.本文在其他观测站的仿真结果也证实了以上结论. 3.2.2 实时性分析不同GDOP_T要求下,TASH站和XIAA站进行选星所消耗时间的仿真结果如图 6和图 7所示.表 4是对其进行的统计分析.

图 6 TASH站选星耗时的变化曲线Fig. 6 Consumed time of satellite selection at the TASH

图选项

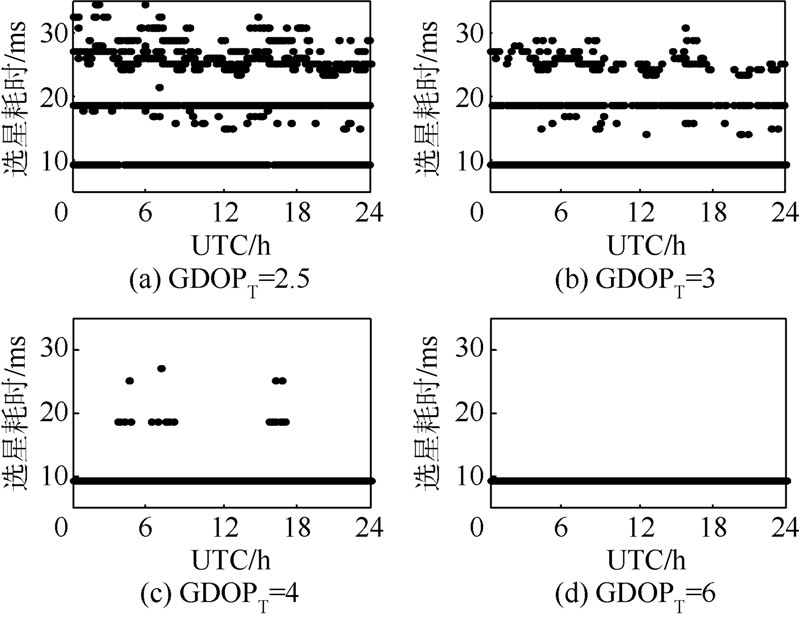图 7 XIAA站选星耗时的变化曲线Fig. 7 Consumed time of satellite selection at the XIAA

图选项

分析图 6、图 7的变化曲线以及表 4的统计结果,可以得出以下结论:表 4 选星耗时的统计分析Table 4 Statistical analysis of consumed time of satellite selection

测站	GDOPT	选星耗时/ms			PT/%
		最小值	最大值	均值
TASH	2.5	10.24	36.30	21.41	32.53
	3	10.24	32.57	13.11	80.11
	4	10.24	28.85	10.31	99.34
	6	10.24	10.24	10.24	100
XIAA	2.5	10.24	36.30	19.27	43.64
	3	10.24	32.57	12.26	85.93
	4	10.24	28.85	10.28	99.68
	6	10.24	10.24	10.24	100
注：PT—选星耗时为10.24 ms的概率.

表选项


1) GDOP_T为6时,仅需约10.24 ms就可以选出满足GDOP_T要求的星座.2) GDOP_T为4～6时,仅需约10.24 ms 即可以完成选星的概率达99.43%以上.3) GDOP_T为3～4时,仅需约10.24 ms 就可以完成选星的概率也可以达 80.11%以上.4) 甚至GDOP_T为2.5时,也可以在 36.30 ms内以不低于92.45%的概率满足GDOP_T要求.上述结论证明了本算法的实时性.本文在其他观测站的仿真结果也证实了以上结论. 3.2.3 选星数目分析XIAA站和TASH站在一次迭代内为满足不同的GDOP_T要求所选择卫星的数目的变化情况如图 8和图 9所示.表 5是对其进行的统计分析.

图 8 TASH站选星数目的变化曲线Fig. 8 Number of selected satellite at the TASH

图选项

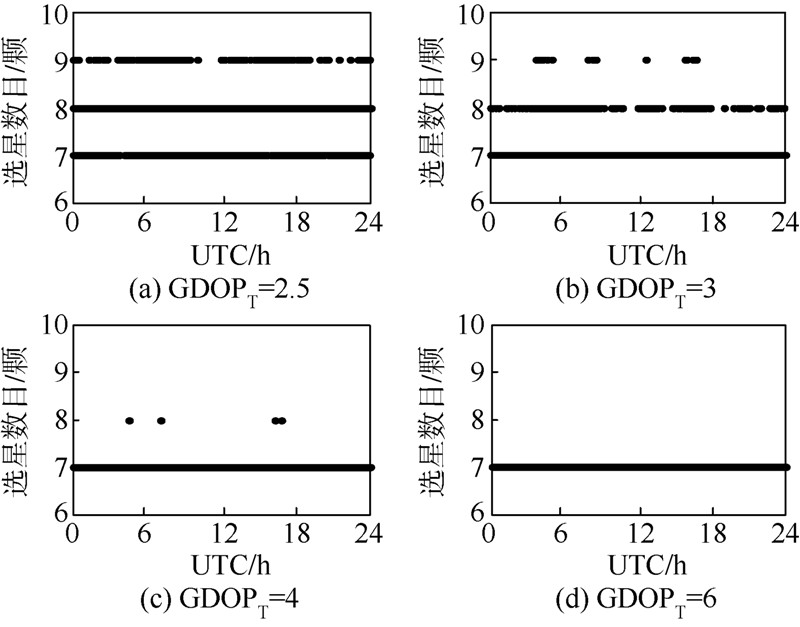图 9 XIAA站选星数目的变化曲线Fig. 9 Number of selected satellite at the XIAA

图选项

分析图 8、图 9和表 5可以得出以下结论:表 5 选星数目的统计分析Table 5 Statistical analysis of number of selected satellite

测站	GDOPT	选星数目/颗			Pn/%
		最小值	最大值	均值
TASH	2.5	7	9	7.69	41.92
	3	7	9	1.37	86.93
	4	7	8	7.00	99.87
	6	7	7	7.00	100
XIAA	2.5	7	9	7.53	54.02
	3	7	9	7.09	90.87
	4	7	8	7.00	99.93
	6	7	7	7.00	100
注：Pn—选星数目为7的概率.

表选项


1) GDOP_T为6时,选7颗星就可以满足GDOP_T要求的概率为100%.2) GDOP_T为4～6时,选7颗星就可以满足GDOP_T要求的概率达99.87%以上.3) GDOP_T为3～4时,选7颗星就可以满足GDOP_T要求的概率也可以达86.93%以上.4) 甚至在GDOP_T为2.5时,选星数目的平均值也不足8,相比于平均可见卫星数18,选星比例不到45%.上述结论证明了算法可实现实时选择尽量小数目的卫星以满足用户定位精度要求的目标.本文在其他观测站的仿真结果也证实了以上结论.3.3 选星前后计算量的分析由1.2节的分析可知,与利用全部可见卫星定位相比,利用所选的满足定位精度要求的定位星座进行定位解算的计算量必然大幅降低.但同时由3.2.2节的分析可知,选星算法本身也是存在计算量的.因此,为了尽量准确地分析快速遗传选星法对降低计算量的贡献,下面对利用快速遗传选星法选星后进行定位解算的计算量(包含选星算法的计算量与定位解算的计算量)与利用全部可见卫星定位的计算量进行比较,其中定位解算采用常规最小二乘法,假设迭代次数为50次.XIAA站选星前后的计算量相对比值分别如图 10和图 11所示.计算量相对比值的统计结果如表 6所示.

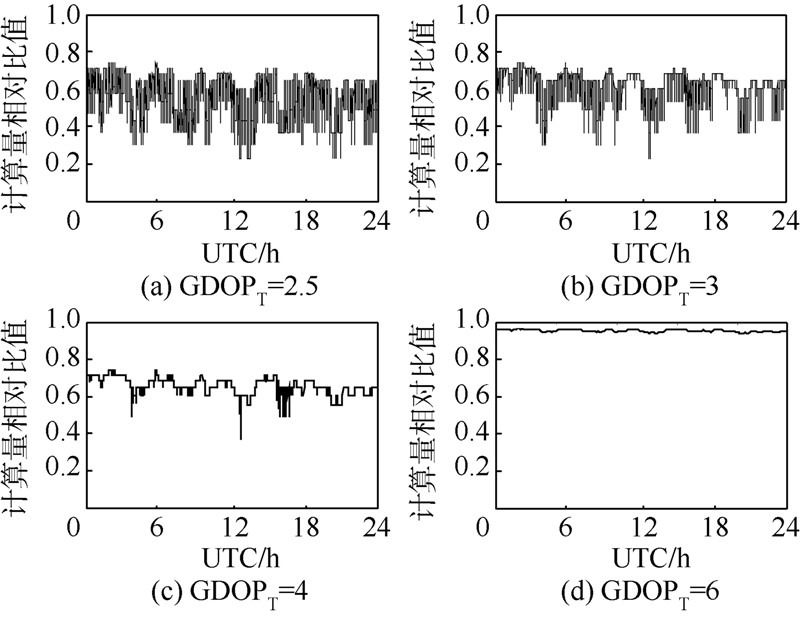图 10 XIAA站选星前后的浮点加运算的相对比值Fig. 10 Relative ratio of addition after satellite selection to addition before satellite selection at the XIAA

图选项

图 11 XIAA站选星前后的浮点乘运算的相对比值Fig. 11 Relative ratio of multiplication after satellite selection to multiplication before satellite selection at the XIAA

图选项

表 6 选星前后计算量相对比值的统计分析Table 6 Statistical analysis of relative ratio of calculation after satellite selection to calculation before satellite selection

运算性质	GDOPT	选星前后运算量相对比值/%
		最小值	最大值	均值
浮点加	2.5	22.73	73.98	54.75
	3	22.73	73.98	63.13
	4	36.62	73.98	65.58
	6	94.15	96.58	95.48
浮点乘	2.5	23.72	73.53	54.81
	3	23.72	73.53	62.78
	4	37.12	73.53	65.09
	6	94.55	96.8	95.78

表选项


分析图 10、图 11和表 5可知,若用户选用常规最小二乘法定位,在满足用户定位精度需求的前提下,GDOP_T为6时,浮点加运算平均相对减少95.48%,浮点乘运算平均相对减少95.78%;而GDOP_T为3～4时,浮点加运算平均相对减少63.13%,浮点乘运算平均相对减少62.78%;甚至在GDOP_T为2.5时,浮点加运算也能平均相对减少54.75%,而浮点乘运算平均相对减少54.81%.上述结论证明了本方法可以在满足用户定位精度要求的前提下,也即可以以用户可以接受的精度损失换取导航运算量的大幅减少.本文在其他观测站的仿真也证实了以上结论.这只是采用常规最小二乘法定位的导航运算减少量,而对于为了追求高精度而采用加权最小二乘法定位的用户来说,导航运算量的减少量将更为可观.3.4 与最小GDOP法的性能比较为了进一步分析快速遗传选星法的性能,下文比较该算法在GDOP_T为3的条件下选星后的GDOP、选星计算量与最小GDOP法(GDOP_min)选7颗星后的GDOP、选星计算量的关系. 3.4.1 选星后GDOP的比较TASH站和XIAA站采用快速遗传选星法与最小GDOP法选星后GDOP的比较结果如图 12所示.比较结果的统计分析如表 7所示.

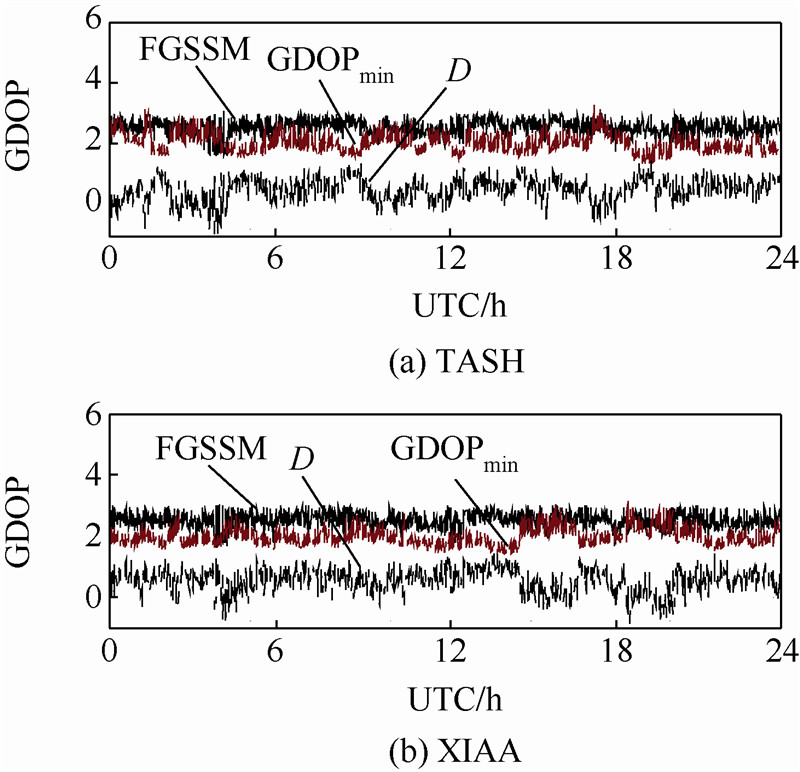图 12 最小GDOP法(GDOPmin)与FGSSM选星后GDOP的比较Fig. 12 Comparison of GDOP after satellite selection with optimal GDOP algorithms (GDOPmin) and FGSSM

图选项

分析图 12和表 7,可以得出以下结论:表 7 不同算法选星后GDOP的统计分析Table 7 Statistical analysis of GDOP after satellite selection for different algorithms

测站	选星算法	选星后GDOP
		最小值	最大值	均值	方差
TASH	FGSSM	1.627	3.105	2.558	0.062
	GDOPmin	1.339	3.302	2.032	0.093
	D	-1.051	1.529	0.525	0.154
XIAA	FGSSM	1.605	2.990	2.510	0.067
	GDOPmin	1.392	3.149	1.964	0.086
	D	-0.900	1.530	0.546	0.154
注：D—FGSSM与GDOPmin选星后GDOP的差值.

表选项


1) 在满足用户定位精度要求的前提下,TASH站采用快速遗传选星法选星后的GDOP比最小GDOP法平均增大了25.9%,而XIAA站平均增大了27.8%.如前文所说,快速遗传选星法不以追求尽量小的GDOP为目的,它的宗旨是在满足用户定位精度要求的前提下,以用户可以接受的GDOP损失换取导航运算量的大幅降低.2) 仿真时长内有10.13%的时刻,快速遗传选星法的选星后GDOP优于最小GDOP法的选星后GDOP.尽管这是因为快速遗传选星法的实时选星数目在选星数目上限范围内根据用户定位精度的要求实时地、自适应地增加,导致其在部分时刻可能会超过最小GDOP法的选星数目,但是这也反映了快速遗传选星法的优化搜索功能.本文在其他观测站的仿真也证实了以上结论. 3.4.2 选星实时性的比较TASH站和XIAA站分别采用快速遗传选星法和最小GDOP法进行选星所消耗时间的统计结果如表 8所示.表 8 不同算法选星耗时的统计分析Table 8 Statistical analysis of consumed time of satellite selection for different algorithms

s
测站	GDOPmin			FGSSM
	最小值	最大值	均值	最小值	最大值	均值
TASH	1.60	29.62	10.65	0.021	0.047	0.024
XIAA	1.60	29.62	10.65	0.021	0.047	0.023

表选项


分析表 8,可以得出以下结论:TASH站采用快速遗传选星法选星比最小GDOP法的选星耗时平均降低了99.78%,而XIAA站平均降低了99.79%.上述结论进一步证明了快速选星算法的实时选星能力.本文在其他观测站的仿真也证实了以上结论.4 结 论综合分析了选星问题中的数学关系,本文提出了一种可以根据用户不同的定位精度要求实时自适应地选择尽量小数目的卫星星座的快速遗传选星法,设计了算法中的运算法则并给出了算法流程,并通过GPS/COMPASS组合系统的仿真平台对算法进行了半物理仿真验证,可以得出以下结论: 1) 快速遗传选星法以满足用户定位精度要求为前提进行选星,最终所选星座的GDOP虽然不是最优的,但却满足导航定位的需要,是满足要求的解.2) 快速遗传选星法，GDOP_T在3~6范围内时，只需耗时10.24 ms就可以完成选星的概率超过80.11%；即使GDOP_T为2.5时，也可以在36.30 ms内以不低于92.45%的概率满足用户的定位精度要求.3) 快速遗传选星法在满足用户定位精度要求的前提下,导航运算量的减少幅度不低于54.75%.4) 遗传选星法在GDOP_T为3的精度要求下,与最小GDOP法相比,选星后的GDOP在满足精度要求的前提下增幅超过25%,但选星实时性提高99.7%以上.采用此方法不仅可以降低接收机处理器的负荷、提高动态用户的实时性,更减少了接收机硬件设计的难度和成本,对组合导航接收机的开发具有参考价值.
参考文献

[1]	Kaplan E D, Hegarty C J.GPS原理与应用[M].2版.寇艳红,译.北京:电子工业出版社,2007: 240-268. Kaplan E D,Hegarty C J.Understanding GPS:principles and applications[M].2nd ed.Translated by Kou Y H.Beijing:Publishing House of Electronics Industry,2007:240-268(in Chinese).
[2]	白雅庆, 陈栋.卫星导航几何精度因子的计算及选星方法[J].导航,2006,42(3):88-94. Bai Y Q,Chen D.The calculation of geometric dilution of precision and satellite selection method for satellite navigation[J].Navigition,2006,42(3):88-94(in Chinese).
	Cited By in Cnki
[3]	张贵明, 黄顺吉,张元莉.一种新的GPS导航卫星选择算法[J].电子科技大学学报,2000,29(3):221-224. Zhang G M,Huang S J,Zhang Y L.A new satellite selection algorithm for GPS navigation[J].Journal of University of Electronic Science and Technology of China,2000,29(3):221-224(in Chinese).
	Cited By in Cnki (22)
[4]	李敏,刘小汇, 王瑛,等.新的GPS自适应阵的选星方法[J].通信学报,2007,28(6):127-132. Li M,Liu X H,Wang Y,et al.Novel satellite selection methods for GPS adaptive arrays[J].Journal on Communication,2007,28(6): 127-132(in Chinese).
	Cited By in Cnki (11)
[5]	张强,张晓林, 李宏伟,等.组合卫星接收机中的选星算法[J].北京航空航天大学学报,2007,33(12):1424-1427. Zhang Q,Zhang X L,Li H W,et al.Satellite selection algorithm for combined satellite receivers[J].Journal of Beijing University of Aeronautics and Astronautics,2007,33(12):1424-1427(in Chinese).
	Cited By in Cnki (30)
[6]	Xu B, Shao B J.Satellite selection algorithm for combined GPS-Galileo navigation receiver[C]//Proceedings of the 4th International Conference on Autonomous Robots and Agents.Piscataway,NJ:IEEE Computer Society,2009:149-154.
	Click to display the text
[7]	金玲, 黄智刚,李锐,等.多卫导组合系统的快速选星算法研究[J].电子学报,2009,37(9):1931-1936. Jin L,Huang Z G,Li R,et al.Study on fast satellite selection algorithm for integrated navigation[J].Acta Electronica Sinica,2009,37(9):1931-1936(in Chinese).
	Cited By in Cnki (21)
[8]	Yu X L, Sun Y R,Liu J Y,et al. Fast algorithm of selecting satellites for multiple satellite integrated navigation system[C]//World Congress on Computer Science and Information Engineering.Piscataway,NJ:IEEE Computer Society,2009,5:121-125.
[9]	陈灿辉, 张晓林.一种新的卫星导航系统快速选星方法[J].电子学报,2010,38(12):2887-2891. Chen C H, Zhang X L.A new fast satellite selection approach for satellite navigation system[J].Acta Electronica Sinica,2010,38(12): 2887-2891(in Chinese).
	Cited By in Cnki (8)
[10]	Zhang M Y, Zhang J.A fast satellite selection algorithm:beyond four satellites[J].IEEE Journal of Selected Topics in Signal Processing,2009,3(5):740-747.
	Click to display the text
[11]	玄光男, 程润伟.遗传算法与工程设计[M].汪定伟,唐加福,黄敏,译.北京:科学出版社,2000:1-23. Gen Mitsuo,Cheng R W.Genetic algorithms and engineering design[M].Translated by Wang D W,Tang J F,Huan M.Beijing:Science Press,2000:1-23(in Chinese).
[12]	Durán R J, de Miguel I,Merayo N,et al.Genetic algorithm to design logical topologies in reconfigurable WDM networks[J].Photonic Network Communications,2009,17(1):21-33.
	Click to display the text
[13]	玄光男, 程润伟.遗传算法与工程优化[M].于歆杰,周根贵,译.北京:清华大学出版社,2004:1-30. Gen Mitsuo,Cheng R W.Genetic algorithms and engineering optimization[M].Translated by Yu X J,Zhou G G.Beijing:Tsinghua University Press,2004:1-30(in Chinese).
[14]	Liepins G E, Hilliard M R.Genetic algorithms:foundations and applications[J].Annals of Operations Research,1989,21(1):31-58.
	Click to display the text
[15]	言中,丁子明. 卫星无线电导航[M].北京:国防工业出版社,1989:227-231. Yan Z,Ding Z M.Satellite radio navigation[M].Beijing:Defense Industry Press,1989:227-231(in Chinese).