伺服系统中，实现运动转换与传递的活塞和缸壁之间普遍存在着摩擦力，它在低速时表现出的强非线性作用，会导致爬行和振荡现象的出现，使得系统的控制效果劣化^[1].因此，摩擦力对伺服系统动态特征的影响不容忽视.目前，针对非线性摩擦力作用下电液伺服系统动态特征的研究尚不多见.对液压系统动态特性的研究一般采用系统建模和数值仿真手段^{[2, 3]}，所依据的理论多是经典控制理论和线性动力学理论^{[4, 5]}，较少运用非线性动力学理论^{[6, 7]}，且多数在建模时对非线性因素进行线性化处理^{[8, 9]}，研究结论与实际情况有较大差异，很难解释实际动态测试中出现的时域波形复杂、频域尖峰繁杂等异常现象.然而，电液伺服系统是非线性动力学系统，执行机构运行过程是典型的非线性过程.故应引入非线性动力学理论和方法进行分析研究.本文重点探究非线性摩擦力对电液伺服系统动态特征的影响规律.通过理论研究和数值试验分析，深入揭示系统内在的分岔现象及典型非线性动力学行为.用非线性动力学研究方法对实测的动态数据进行深入分析，以揭示非线性摩擦力引起的“极限环型振荡”现象.旨在揭示伺服系统非线性振动的机理及诱因，使综合分析系统的动态特征变得更接近实际.1 执行机构的动力学模型电液伺服系统的执行机构为伺服液压缸，本文以双作用单活塞杆液压缸为例进行分析，其工作原理如图l所示,其动力学方程为
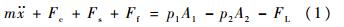
式中，m为活塞及惯性负载的折合质量；x为活塞位移；F_c为黏性力；F_s为弹性力；F_f为摩擦力；F_L为负载力；p₁，p₂分别为无杆腔和有杆腔压力；A₁，A₂分别为无杆腔和有杆腔活塞有效作用面积.

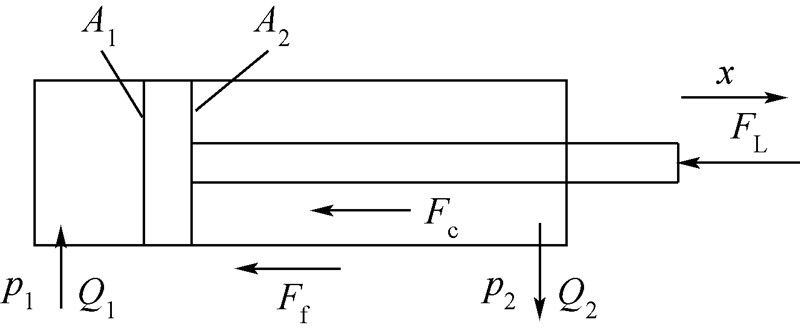图 1 双作用单活塞杆伺服液压缸工作原理Fig. 1 Working principle of double-acting single piston rod servo cylinder

图选项

2 非线性摩擦力图 2所示为体现摩擦力与速度关系的Stribeck曲线，数学模型可由式(2)和式(3)描述^[10].

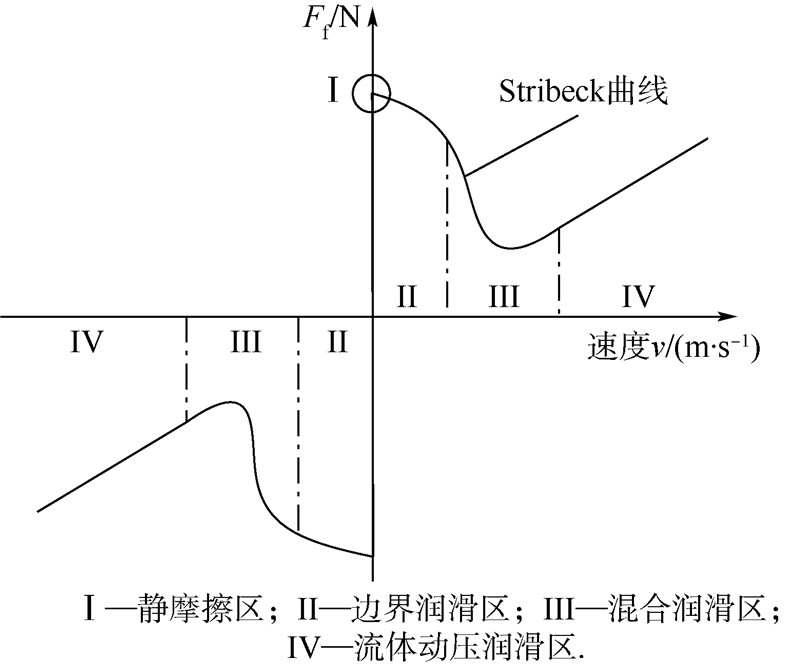图 2 摩擦力与速度的关系曲线Fig. 2 Relation curve of friction and velocity

图选项

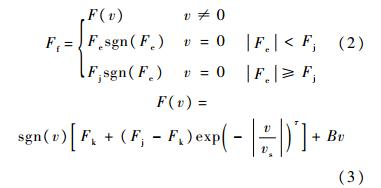
式中，F_e为外力；F_j为最大静摩擦力；F_k为库仑摩擦力；v_s为Stribeck速度；B为黏滞摩擦系数；τ为经验参数，一般在0.5~2.0之间取值.设v为活塞的移动速度.令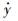为在工作点x附近的振动速度，即Δv.将摩擦力在工作点x附近展成泰勒级数形式：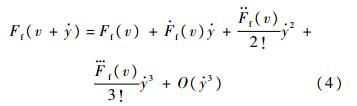

式中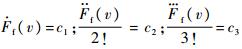，；并略去高阶无穷小项O(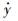³)，则摩擦力可表示为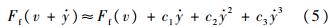

摩擦力的作用效果随工作点在Stribeck曲线上所处区段不同而异^[1]:①当工作点位于区域Ⅰ时，Stribeck曲线斜率为很大的正数，其作用效果使系统阻尼瞬间陡增，遏制系统的动态响应的快速性.②当工作点位于区域Ⅳ时，摩擦力特性为线性的，其作用效果相当于增加了系统的阻尼.③当工作点位于区域Ⅱ或区域Ⅲ时，摩擦力呈现非线性时变特性，当处于负阻尼状态时会产生具有极限环的自激振动.3 摩擦力非线性动态特征3.1 非线性动力学模型为了集中研究非线性摩擦力对系统动态特征的影响，暂不考虑液压弹簧力、黏性力等非线性因素.当工作点位于区域Ⅱ或Ⅲ时，有^[1]
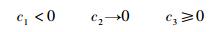
则式(1)在工作点x附近的特性可表达为

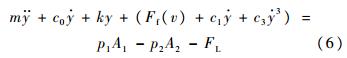
式中，c₀为结构阻尼系数；k为线性弹簧刚度.移项整理，得

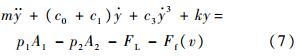
由于油源压力脉动、阀口流量-压力非线性等因素的影响，进入液压缸的油压有微观波动，基本服从简谐振动规律，故式(7)右边的输入项可近似表示为Fsin(ωt+φ₀)，是系统的激振源^[11].据上述分析，式(7)可化为

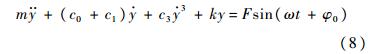
式中，F为激振力；ω为激振角频率；φ₀为激振力的初相角.进一步整理，得

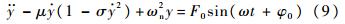
式中
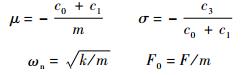
将方程各项对t求导，将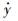作为新变量仍记为y，以σ代替参数3σ，式(9)可化为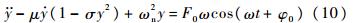

由Van Der Pol方程的结构形式可知，式(10)是受迫振动Van Der Pol方程.该方程为研究伺服系统非线性摩擦力的动态特征提供了结构模型.3.2 解析解及分析把摩擦力的非线性动态特征归结为Van Der Pol方程，就可以借助该方程的特性来揭示系统内在的基本规律.用多尺度法可求得式(10)的近似解，其自由振动的振幅如式(11)所示^[12]：

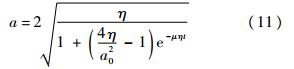
式中
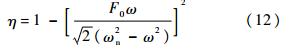
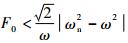a₀为积分常数.分析式(11)发现：随着t→∞，当η<0(即)时，a→0，自由振动趋于衰减，式(10)受激励后的稳态运动是频率为ω的受迫振动；当η>0(即)时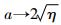，，稳态运动中除包含频率为ω的受迫振动外，还含有频率为ω_n的自由振动，通常ω与ω_n不可共约，此稳态运动是非周期的.可见，大激励引发自由振动衰减，小激励引发非周期运动.3.3 稳定性分析当F₀=0时，设状态变量y₁=y，y₂=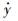₁，则式(10)的状态方程为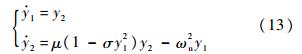

在原点附近加以线性化，得

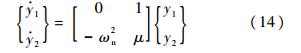
特征方程为

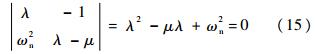
可解出特征根：

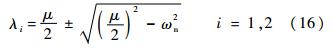
分析式(16)，当μ>0时，特征根的实部Re(λ_i)>0，由系统稳定性与特征方程根的关系可知，工作点是不稳定的平衡点，从工作点近旁出发的轨线是发散的，但由于稳定极限环的存在，限制了轨线的无限发散；当μ<0时，特征根的实部Re(λ_i)<0，工作点是稳定的平衡点，在极限环内部的轨线收敛于平衡点^[13].可见，工作在区域Ⅱ或Ⅲ的系统，当|c₁|<c₀时，μ<0，是稳定的；当|c₁|>c₀时，μ>0，摩擦力作用的效果是产生极限环型振荡^[14].4 数值试验以系统方程式(10)的具体算例式(17)为例，进行数值试验研究，以探索系统阻尼系数μ和外加激振力F₀对系统动态特征的影响.

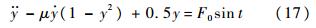
4.1 分岔特性研究F₀取不同值时，以μ为分岔参数的分岔图如图 3所示.图中μ为单位质量上的系统阻尼系数，y为振动位移.

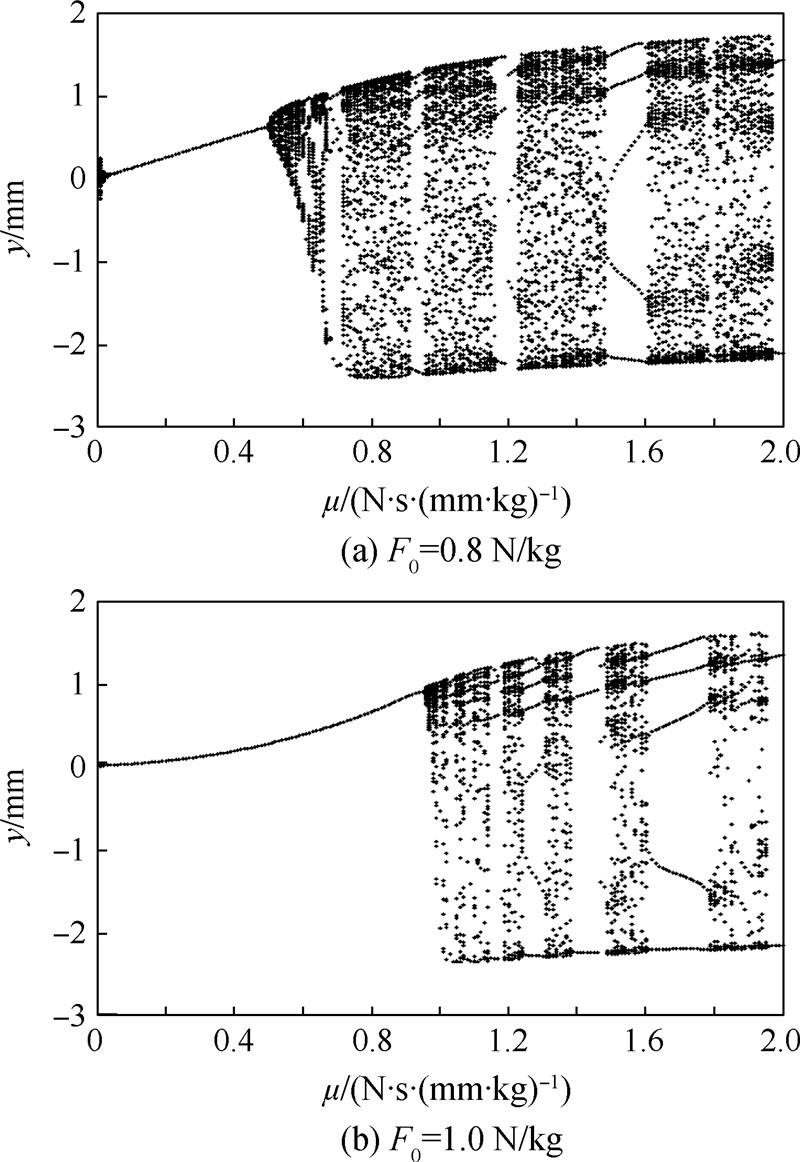图 3 分岔参数为μ的非线性方程分岔图Fig. 3 Bifurcation diagrams with μ as parameter

图选项

由图 3可知，当参数μ和F₀取不同值时系统发生了不同程度的分岔现象：①系统方程存在单解、多解和无穷多解，反映在分岔图上表现为单值曲线、多值曲线和涂黑区等不同的区段，分别对应于单周期、多周期和混沌等不同的运动状态.②随着参数的变化，系统会发生运动状态突然变化的动态分岔现象.③随着阻尼系数μ的增大，混沌区会突然消失，系统出现周期3、周期5或周期7的稳定状态，接着再次进入混沌运动状态.4.2 运动形态仿真为了形象地体现系统在不同参数下的运动形态，在MATLAB中建立仿真模型，对其典型的非线性动力学行为进行仿真.仿真中采用Runge-Kutta算法，采样频率100 Hz，远大于外控力频率f_P=ω/2π=0.16 Hz，终了时间1 000 s.当μ=2 N·s/(mm·kg)，F₀=2 N/kg时，仿真结果如图 4所示.由图 4可知，时间历程呈周期重复；功率谱在基频f_P及其倍频处出现尖峰，所有谱峰对应的频率可共约；相轨迹在有限的区域内重复，呈一封闭曲线，即有极限环存在；Poincaré图在一定的区域上只有1个孤立点存在.说明此时系统处于极限环型振荡状态.

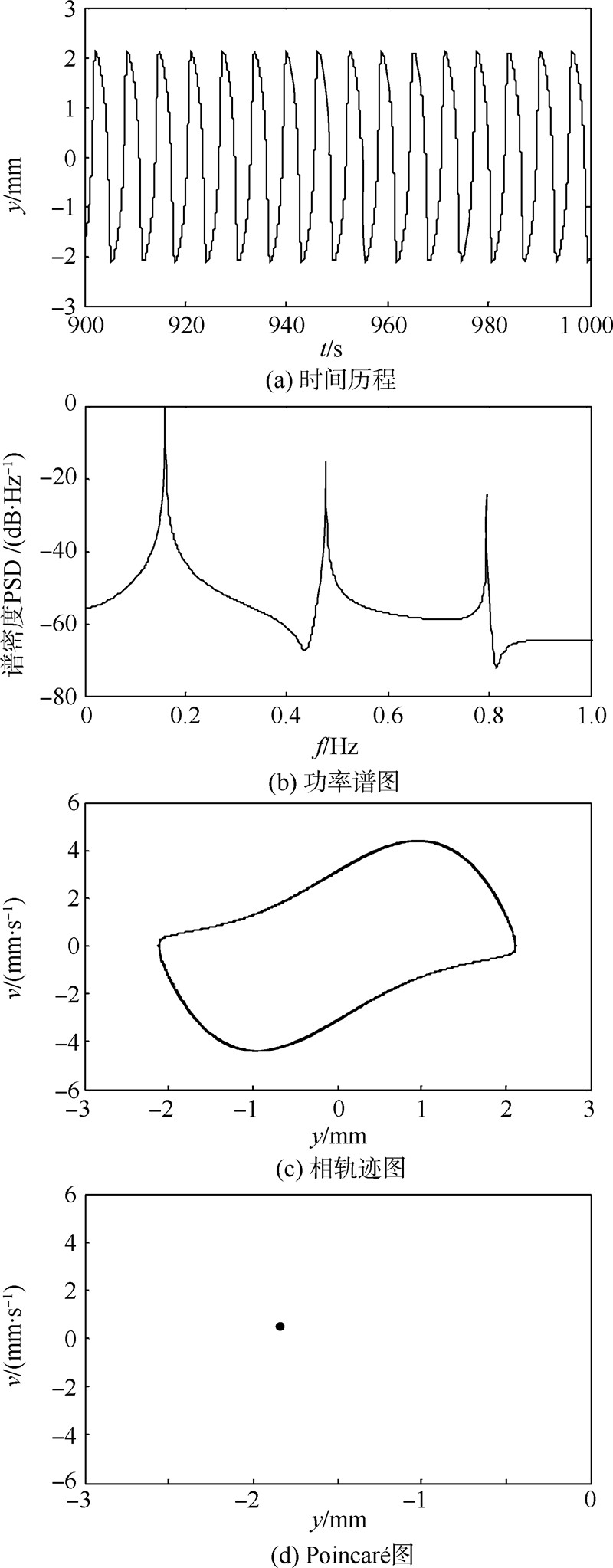图 4 极限环型振荡形态Fig. 4 Forma of limit cycle oscillation

图选项

当μ=1.7 N·s/(mm·kg)，F₀=1.2 N/kg时，仿真结果如图 5所示.由图 5可知，时间历程呈周期重复；功率谱在分频f_P/3及其倍频处存在尖峰，所有谱峰对应的频率可共约；相轨迹在有限的区域内重复，呈封闭曲线；Poincaré图在一定的区域上有3个孤立点存在.说明此时系统处于3倍周期运动状态.

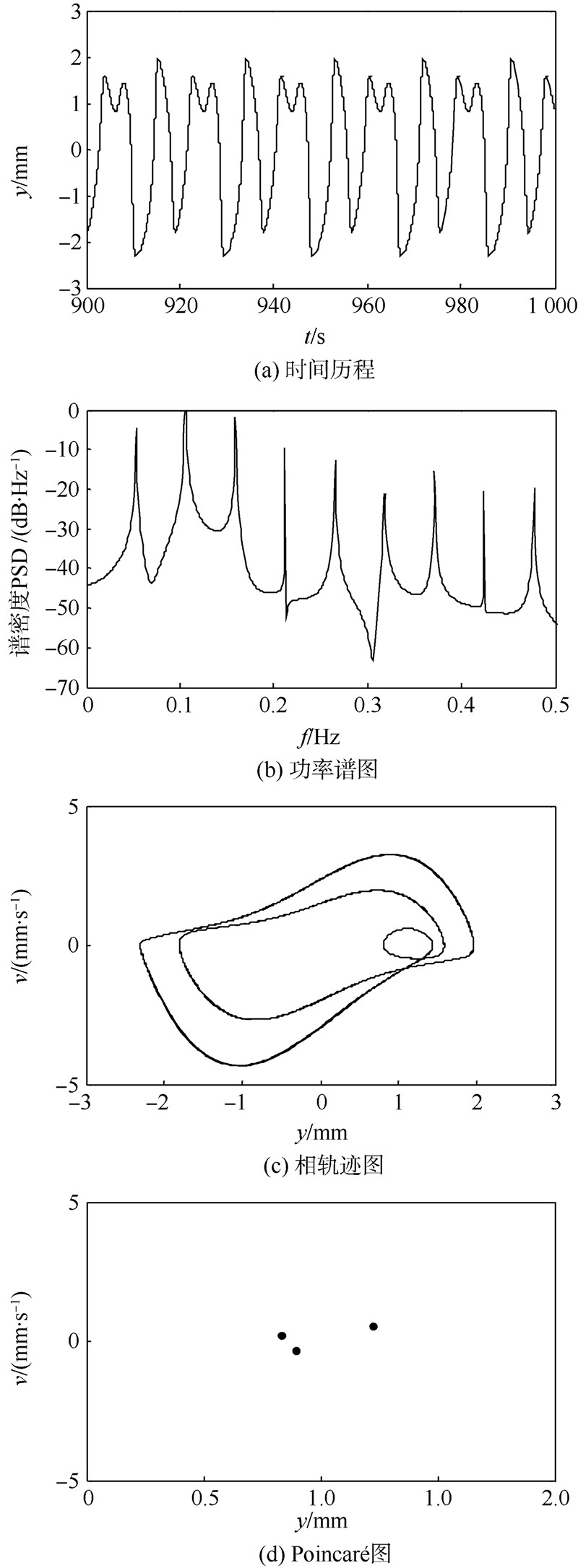图 5 3倍周期运动形态Fig. 5 Forma of triple periodic motion

图选项

当μ=0.8 N·s/(mm·kg)，F₀=0.8 N/kg时，仿真结果如图 6所示.由图 6可知，时间历程无规律；功率谱出现噪声背景和宽峰；相轨迹在有限的区域内不重复；Poincaré图有无限个孤立点存在，且分布在有限的区域上.说明此时系统处于混沌运动状态.由以上数值试验分析可知，当系统阻尼系数μ和外加激振力F₀取不同值时，系统在运行过程中蕴含丰富的非线性动力学行为.系统可能做极限环型振荡、倍周期运动，进而通向混沌运动.

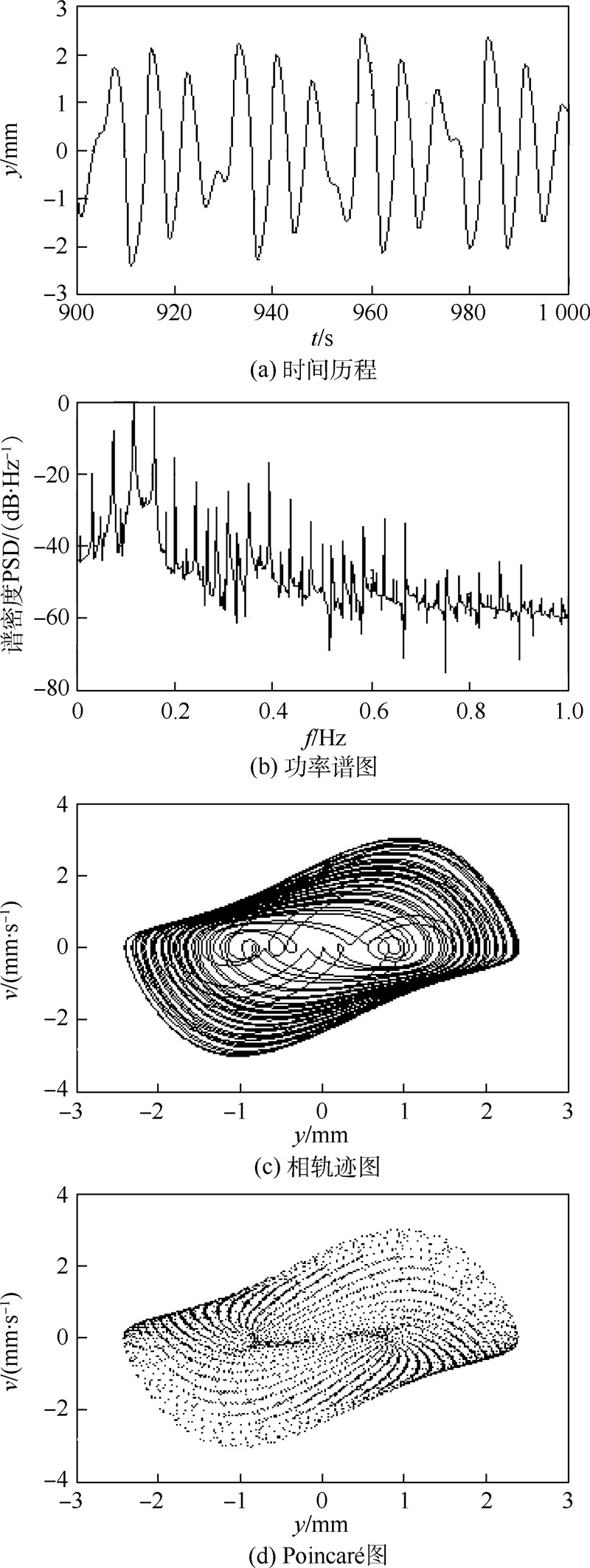图 6 混沌运动形态Fig. 6 Forma of chaotic motion

图选项

5 电液伺服系统动态试验本节将利用非线性动力学研究方法对实测的电液伺服系统的动态数据进行深入分析，以揭示非线性摩擦力引起的极限环型振荡现象.5.1 试验系统组成按图 7所示的系统原理图搭建振动测试试验台^[7].该试验系统可实现对电液伺服系统在不同供油压力和负载压力下的状态数据进行采集.系统中通过调节溢流阀阀口开度大小来改变系统供油压力；通过调节节流阀阀口开度大小来改变负载压力，以实现系统外加阻尼大小的调整；用精密压力表对系统进、回油路压力进行监测；用振动传感器对系统执行机构轴向振动信号进行监测；用位移传感器对执行机构实时位置进行监视；用数据采集卡采集传感器输出信号，并送基于虚拟仪器的计算机系统进行分析处理.

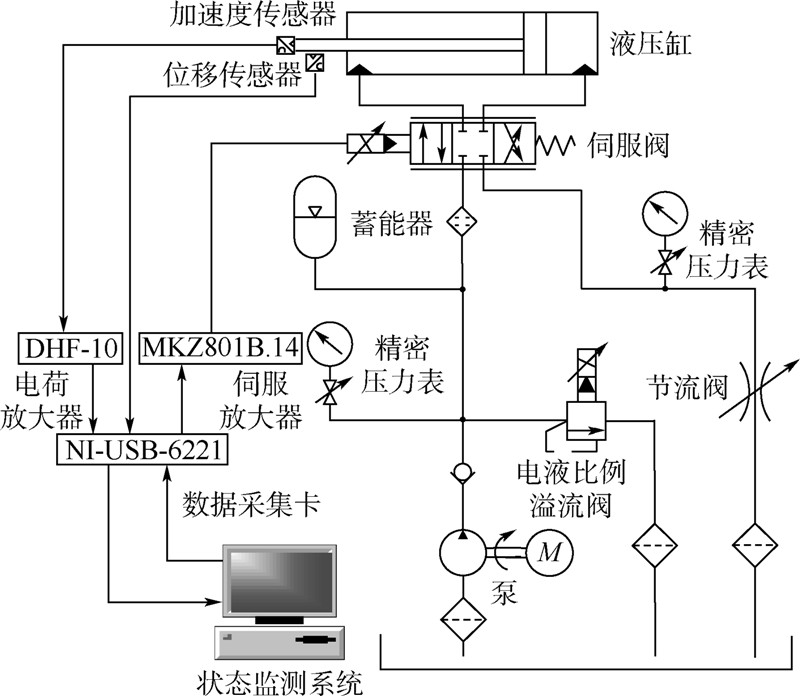图 7 状态监测及试验系统原理图Fig. 7 Schematic of condition monitoring and experiment

图选项

5.2 振动信号的采集及处理5.2.1 振动信号的采集按表 1设置的工况对系统工作状态进行动态测试.其中，输入信号为计算机控制系统给伺服放大器的电压信号，以控制伺服阀的阀口开度大小.根据供油压力和负载压力大小将外加阻尼大小界定为4类：无、较小、适中、较大.输入信号为0.2 V时，调整主溢流阀及节流阀阀口开度，使系统分别在表 1设定的12种工况下运行.同时用振动加速度传感器对液压缸整个运行过程中的轴向振动信号进行采集，采样频率为10 kHz.
表 1 不同供油压力情况下执行机构工作状态 Table 1 Actuator working condition under different supply pressure

序号	输入信号/V	供油压力/MPa	负载压力/MPa	外加阻尼
1	0.2	4	0	无
			1	较小
			2	适中
			3	较大
2	0.2	6	0	无
			2	较小
			4	适中
			5.5	较大
3	0.2	8	0	无
			2	较小
			4	适中
			6	较大

表选项


5.2.2 振动信号的处理采用图 8中的数据处理方案对采集的振动加速度信号进行预处理，并采用非线性动力学研究方法中的时间历程、频闪采样、功率谱分析等有效方法对预处理数据进行分析研究^[15].

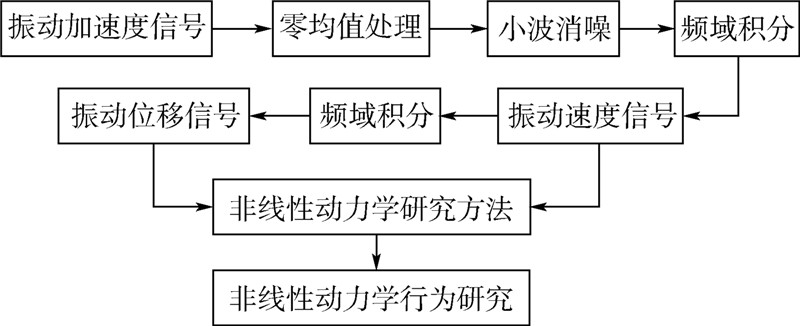图 8 数据处理方案Fig. 8 Program of data processing

图选项

5.3 试验结果分析图 9为供油压力8 MPa时采用图 8中的数据处理方案对采集的振动加速度信号进行处理所得到的振动位移信号时域波形.比较4种工况发现，在整个运行过程中，振动幅值存在显著波动，随着活塞位移的变化而变化.由此可知，执行机构在运行过程中，系统动态性能随活塞位移的变化而变化，其变化规律随工况不同而存在明显差异.

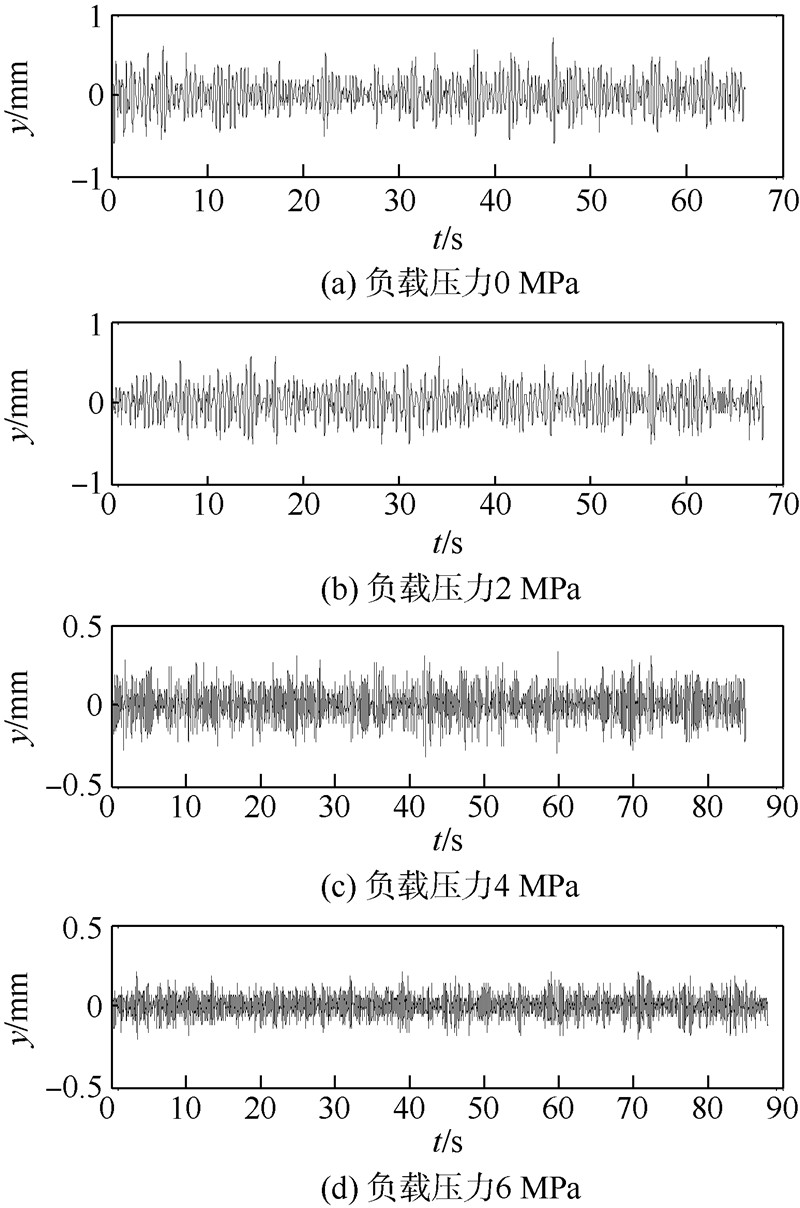图 9 振动位移信号时域波形Fig. 9 Waveforms of vibration displacement signals

图选项

图 10为供油压力8 MPa时4种工况的全程频闪采样图，它的覆盖区域与Van Der Pol极限环极为相似.工况1和2的轮廓边界由许多离散点构成，发生了较强烈的振荡；而工况3和4的轮廓边界较清晰，振荡程度相对较弱，每种工况都有一个极限环存在，说明“极限环型振荡”现象存在的普遍性.工况1的面积最大，工况2和3的次之，工况4的最小，说明极限环面积的大小由系统外加阻尼的大小来决定.

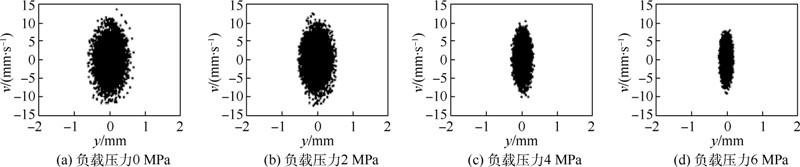图 10 全程频闪采样图Fig. 10 Diagrams of entire stroboscopic sampling

图选项

图 11~图 14为供油压力8MPa时4种工况的分段功率谱图.根据执行机构运行总时间长度，将其分成等分的4段，分别定义为：始段、中前段、中后段、终段.比较4种工况发现，振动能量值随负载压力的增大而逐渐降低，说明随系统阻尼的增大，振动幅值被抑制.同一工况下，不同分段中相同的频率点处有相应的谱峰存在，进一步说明了摩擦极限环型振荡现象的存在.

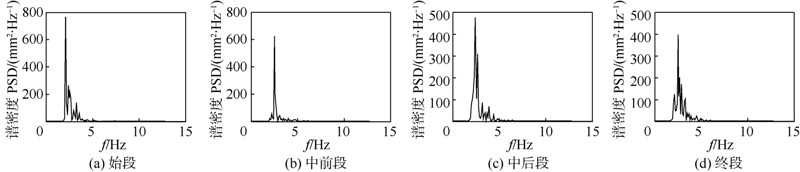图 11 负载压力0 MPa时分段功率谱图Fig. 11 Power spectrums at load pressure of 0 MPa

图选项

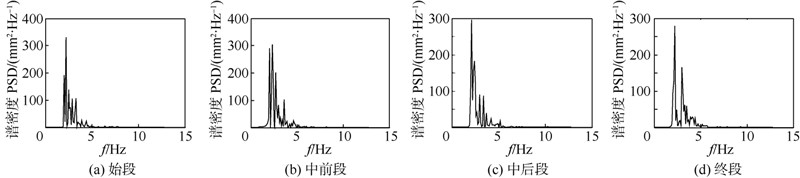图 12 负载压力2 MPa时分段功率谱图Fig. 12 Power spectrums at load pressure of 2 MPa

图选项

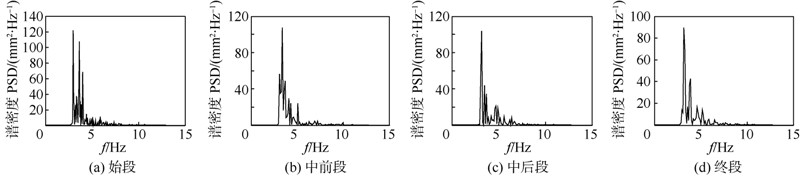图 13 负载压力4 MPa时分段功率谱图Fig. 13 Power spectrums at load pressure of 4 MPa

图选项

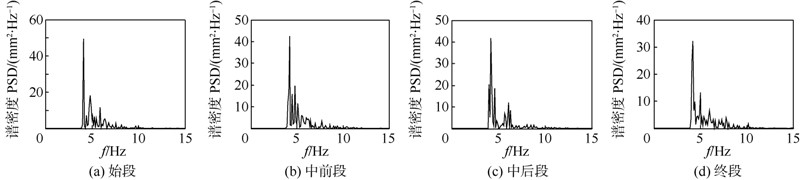图 14 负载压力6 MPa时分段功率谱图Fig. 14 Power spectrums at load pressure of 6 MPa

图选项

为了验证上述所得结论的普遍性，采用与供油压力为8 MPa时相同的数据处理方法，分别对供油压力为6 MPa和4 MPa时的试验数据进行了进一步的分析研究.通过比较分析，不同供油压力下同样可以得到非线性摩擦力引起的极限环型振荡现象存在的普遍性的结论.6 结 论本文以电液伺服系统为研究对象，根据非线性动力学原理，重点探究了摩擦力的非线性作用对系统动态特征的影响规律.通过理论研究、仿真分析及试验验证，得到了如下结论：1) 电液伺服系统执行机构在往复运动过程中，摩擦力变化规律服从Stribeck曲线，在速度趋近于零时取值具有不确定性，在低速运动区段呈现非线性规律，在高速运动区段呈现线性规律.2) 摩擦力的非线性作用随工作点在Stribeck曲线上所处区段不同而异.在静摩擦区，其作用效果使系统阻尼瞬间陡增，遏制了系统动态响应的快速性；在流体动压润滑区，其作用效果增加了系统的阻尼；在边界润滑区和混合润滑区，其动态特征可以用Van Der Pol方程来描述，其作用效果使系统阻尼减小，有可能使系统变成负阻尼系统，产生极限环型振荡.3) 系统阻尼系数和外加激振力的大小影响系统的运动状态.当二者参数取不同值时，系统可能做极限环型振荡、倍周期运动，进而通向混沌运动.4) 非线性摩擦力引起的极限环型振荡会使系统响应稳定区域变得复杂，进而造成执行机构在工作过程中发生非线性振动及动态特性变得复杂和多变.因此在系统建模与动态特性研究时应该将摩擦力的非线性作用考虑在内，其对系统动态特征的影响不容忽视.
参考文献

[1]	王林鸿,吴波,杜润生,等.液压缸运动的非线性动态特征[J].机械工程学报,2007,43(12):12-19.Wang L H,Wu B,Du R S,et al.Nonlinear dynamic characteristics of moving hydraulic cylinder[J].Chinese Journal of Mechanical Engineering,2007,43(12):12-19(in Chinese).
	Cited By in Cnki (43)
[2]	Dasgupta K,Murrenhoff H.Modelling and dynamics of a servo-valve controlled hydraulic motor by bondgraph[J].Mechanism and Machine Theory,2011,46(7):1016-1035.
	Click to display the text
[3]	Lan Z K,Su J,Xu G,et al.Study on dynamical simulation of railway vehicle bogie parameters test-bench electro-hydraulic servo system[J].Physics Procedia,2012,33:1663-1669.
	Click to display the text
[4]	Milic V,Situm Z,Essert M.Robust H∞ position control synthesis of an electro-hydraulic servo system[J].ISA Transactions,2010,49(4):535-542.
	Click to display the text
[5]	郭栋,付永领,卢宁,等.自抗扰控制技术在电液力伺服系统中的应用[J].北京航空航天大学学报,2013,39(1):115-119.Guo D,Fu Y L,Lu N,et al.Application of ADRC technology in electrohydraulic force servo system[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(1):115-119(in Chinese).
	Cited By in Cnki (3) | Click to display the text
[6]	Chen C T.Hybrid approach for dynamic model identification of an electro-hydraulic parallel platform[J].Nonlinear Dynamics,2012,67(1):695-711.
	Click to display the text
[7]	朱勇,姜万录,王梦,等.非线性时变力作用下液压缸爬行机理与抑制方法研究[J].农业机械学报,2014,45(3):305-313.Zhu Y,Jiang W L,Wang M,et al.Creeping mechanism and suppression methods of hydraulic cylinder under nonlinear time-varying force[J].Transactions of the Chinese Society for Agricultural Machinery,2014,45(3):305-313(in Chinese).
	Cited By in Cnki
[8]	Tang R,Zhang Q.Dynamic sliding mode control scheme for electro-hydraulic position servo system[J].Procedia Engineering,2011,24:28-32.
	Click to display the text
[9]	Seo J,Venugopal R,Kenné J P.Feedback linearization based control of a rotational hydraulic drive[J].Control Engineering Practice,2007,15(12):1495-1507.
	Click to display the text
[10]	张从鹏,刘强.直线电机定位平台的摩擦建模与补偿[J].北京航空航天大学学报,2008,34(1):47-50.Zhang C P,Liu Q.Friction modeling and compensation of positioning stage driven by linear motors[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(1):47-50(in Chinese).
	Cited By in Cnki (18) | Click to display the text
[11]	杨安元,杨雪.液压系统的减振方法研究[J].液压与气动,2004(2):51-53.Yang A Y,Yang X.Research on approaches to weakening vibration of hydraulic system[J].Chinese Hydraulics & Pneumatics,2004(2):51-53(in Chinese).
	Cited By in Cnki (14)
[12]	陈予恕,唐云,陆启韶,等.非线性动力学中的现代分析方法[M].北京:科学出版社,2000:1-50.Chen Y S,Tang Y,Lu Q S,et al.Modern analysis methods from nonlinear dynamics[M].Beijing:Science Press,2000:1-50(in Chinese).
[13]	师汉民.机械振动系统[M].武汉:华中科技大学出版社,2004:210-212.Shi H M.Vibration system[M].Wuhan:Huazhong University of Science & Technology Press,2004:210-212(in Chinese).
[14]	刘延柱,陈立群.非线性振动[M].北京:高等教育出版社,2001:60-63.Liu Y Z,Chen L Q.Nonlinear vibration[M].Beijing:Higher Education Press,2001:60-63(in Chinese).
[15]	姜万录,刘思远,张齐生.液压故障的智能信息诊断与监测[M].北京:机械工业出版社,2013:108-180.Jiang W L,Liu S Y,Zhang Q S.Intelligent information diagnosis and monitoring on hydraulic fault[M].Beijing:China Machine Press,2013:108-180(in Chinese)