在石油行业,精确的油气井井眼轨迹姿态(方位角、倾斜角及工具面角)和位置(经度、纬度及高度)信息对于油气田开发具有重要意义.近年来随着大斜度井、定向井、丛式井及水平井等复杂油气井的增多,对油气井轨迹参数测量计算提出了更高要求.目前常用到的井眼轨迹测量仪器主要有磁通门测斜仪和动调陀螺测斜仪.磁通门测斜仪测量精度受地磁场模型精度限制,易受磁性环境干扰.在老井、套管井等有磁性物质干扰的油气井使用时精度下降明显,甚至无法使用^{[1, 2, 3, 4]};动调陀螺测斜仪采用陀螺罗盘方案,只能进行静态单点测量,测量时间长、成本高、效率低.随着光纤陀螺技术的发展,基于光纤陀螺捷联惯性导航技术的测量方案应用到了油气井井眼轨迹参数测量中^{[5, 6, 7, 8]}.它集成了光纤陀螺结构紧凑、体积轻便、设计灵活、抗冲击和振动以及不易受磁性环境干扰等优点,具有良好的环境适应性,能够适合各种复杂油田环境,并且具备捷联惯性导航的自主动态测量能力,可有效缩短测量时间,节约测量成本,提高测量效率.完全自主的惯性导航测量误差随时间积累,因此为确保长时间测量精度必须引入外部辅助信息,利用组合滤波方法抑制惯性测量误差发散.文献^[5]提出采用零速修正(Zero Velocity Update,ZUPT)的方法修正测量中的误差,但需要以一定的时间间隔保持仪器静止.这一方法破坏了仪器连续测量,降低了工作效率.文献^[9]提出运动速度约束辅助的测量方法,有效地提高了电缆速度失效时的测量精度,但对于电缆速度失效的判断存在一定的难度,容易造成误判.本文结合油气井井眼轨迹测量作业特点,借鉴车载惯性导航领域的研究成果^{[10, 11, 12]},提出一种电缆长度辅助的光纤陀螺井眼轨迹测量方法,通过半实物仿真计算验证了这种组合测量方法的有效性.1 光纤陀螺井眼轨迹测量系统 光纤陀螺井眼轨迹测量系统如图 1所示,主要由地面和井下两部分组成^{[6, 7, 9]},其中地面部分主要包括地面测控系统、地面接口设备、测井电缆及缆长计数器.地面测控系统是测量人员操作井下仪器的人机接口,一方面负责井下测量数据的实时显示和存储,另一方面负责将各种控制命令传输给井下仪器及采集电缆下放/上提的长度信息.

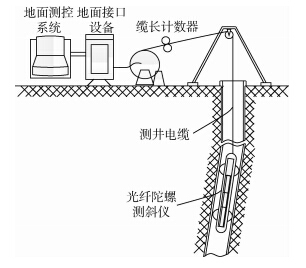
图 1 光纤陀螺轨迹测量系统组成Fig. 1 Components of fiber optic gyroscope (FOG)-based trajectory surveying system

图选项

井下部分主要包括光纤陀螺测斜仪、遥传短节、扶正器等辅助设备.光纤陀螺测斜仪是测量系统的核心,由二次电源、惯性测量单元(Inertial Measurement Unit,IMU)、导航计算机和数据传输模块等组成^[13].测量过程中三轴光纤陀螺敏感仪器角运动信息,三轴加速度计敏感仪器线运动信息,采用惯性导航原理实时解算出井眼轨迹姿态(方位角、倾斜角和自转角)和位置信息(经度、纬度和高度).2 组合测量误差模型 2.1 惯性测量系统误差模型 惯性测量系统速度、姿态及位置的真值与测量误差的关系^{[14, 15]}为
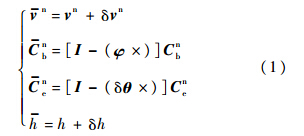
式中:vⁿ为惯性测量计算所得速度;vⁿ为真实速度;δvⁿ为速度误差,上标n表示变量定义在导航坐标系中;Cⁿ_b为惯性测量计算所得姿态捷联矩阵;Cⁿ_b为无误差的捷联矩阵真实值;φ为姿态误差;I为单位矩阵;Cⁿ_e为惯性测量计算所得从地球坐标系到导航坐标系的转换矩阵;Cⁿ_e为从地球坐标系到导航坐标系的转换矩阵真实值;δθ为位置误差;h为导航计算所得高度值;h为高度真实值;δh为高度误差.依据式(1),展开推导可得惯性测量系统误差模型:
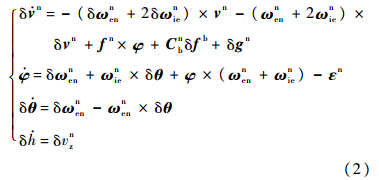
式中:ωⁿ_en为位置角速率;ωⁿ_ie为地球转速;δωⁿ_en为位置角速率误差;δωⁿ_ie为地球转速误差;fⁿ为加速度计输出的比力;δf^b为比力误差;δgⁿ为地球重力加速度;εⁿ为陀螺零偏;δv_zⁿ为垂直方向的速度误差. 2.2 电缆长度测量模型在实际测量过程中,电缆长度数据由光电编码计数器获取,其基本原理是电缆带动绞盘齿轮旋转,引起齿轮角度变化,从而得到电缆运行长度,考虑光电编码计数器刻度误差,则电缆长度的表达式为
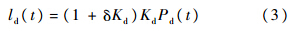
式中:l_d(t)为t时刻测量的电缆长度;δK_d为光电编码计数器刻度误差;K_d为光电编码计数器刻度系数;P_d(t)为t时刻脉冲计数.3 组合测量算法设计 3.1 组合测量算法总体设计电缆长度信息包含了仪器运行轨迹的位置信息,匹配惯性测量系统与电缆长度所包含的位置信息,采用卡尔曼滤波实现信息融合与误差估计,利用闭环状态反馈实时修正惯性器件(陀螺和加速度计)和导航参数(姿态、速度和位置)误差,实现长时间、高精度井眼轨迹姿态/位置信息连续测量.组合测量算法如图 2所示.

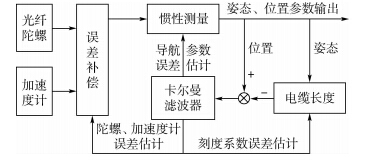图 2 组合测量算法示意图Fig. 2 Schematic diagram of integrated surveying algorithm

图选项

3.2 组合测量模型建立 测井过程中,仪器动态相对较低,惯性器件(陀螺、加速度计)误差可简化表示成零偏与高斯白噪声之和^[16].将陀螺零偏和加速度计零偏模型定义为一阶马尔科夫过程^[17]:
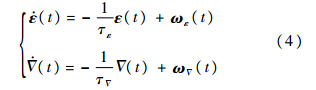
式中：ε(t)为陀螺零偏;Δ(t)为加速度计零偏;τ_ε和τ_Δ分别为陀螺和加速度计相关时间常数;ω_ε(t)和ω_Δ(t)分别为陀螺和加速度计高斯白噪声.光电编码计数器的刻度系数误差可视为随机常值误差,即满足:
联立式(2)、式(4)和式(5),光电编码计数器和惯性测量系统组成的组合测量系统状态方程在东北天坐标系下可表示为
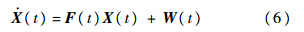
式中:F(t)为状态转移矩阵;X(t)为16维误差状态向量;W(t)为系统噪声向量.X(t)和W(t)的表达式如下:
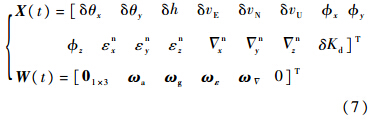
式中:δθ_x、δθ_y和δh为位置误差分量;δv_E、δv_N和δv_U为速度误差δv的分量;φ_x、φ_y和φ_z为姿态误差φ的分量;εn_x、εn_y和εn_z为陀螺零偏分量;Δn_x、Δn_y和Δn_z为加速度计零偏分量;ω_a为加速度计噪声;ω_g为陀螺噪声. 3.3 量测方程建立光电编码计数器输出电缆长度信息转换成地理位置信息(经度、纬度和高度)与光纤陀螺惯性测量系统输出的位置信息进行匹配比较,完成组合测量(图 2所示),因此需要先建立电缆长度信息与地理位置信息的关系.图 3(a)中红色曲线为井眼轨迹示意图,图 3(b)为测量点i与地理位置关系示意图.井眼轨迹上第i－1个测点在井口坐标系下的坐标为(x_i-1,y_i-1,z_i-1),对应的地理坐标为(λ_i-1,L_i-1,h_i-1),电缆长度信息为l_i-1,倾斜角为θ_i-1,方位角为ψ_i-1;同理,第i个测点在井口坐标系下的坐标为(x_i-1,y_i-1,z_i-1),对应的地理坐标为(λ_i,L_i,h_i),电缆长度信息为l_i,倾斜角为θ_i,方位角为ψ_i.

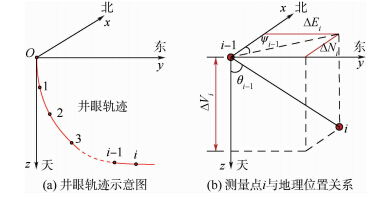图 3 井眼轨迹及参数示意图Fig. 3 Chart of trajectory and parameters

图选项

从图 3(b)可得到关系式:
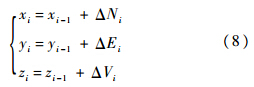
测量过程中,运行速度相对较慢(一般小于2m/s),组合算法滤波周期为1s,因此可以把相邻两测点之间的轨迹近似为直线,则有
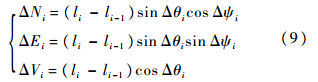
式中:Δθ_i=(θ_i+θ_i-1)/2;Δψ_i=(ψ_i+ψ_i-1)/2.合并式(3)、式(8)和式(9)可得第i个测量点在井口坐标系下的参数:
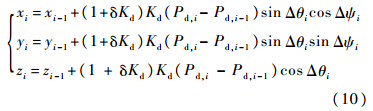
假设井口地理坐标为(λ₀,L₀,h₀),则测量点i处的地理参数为
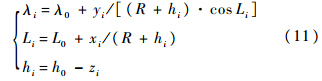
式中:R为地球半径.则量测方程表示为
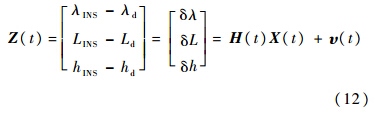
式中:λ_INS、L_INS和h_INS为纯惯导解算所得位置信息;λ_d、L_d和h_d为由电缆长度信息所得位置信息;δλ为经度误差,即位置误差分量δθ_x;δL为纬度误差,即位置误差分量δθ_y;υ(t)为量测噪声矢量,满足N(0,R)的高斯白噪声过程.整理式(10)~式(12),可得量测矩阵H(t)的表达式为
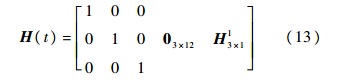
式中:H¹_3×1的表达式为
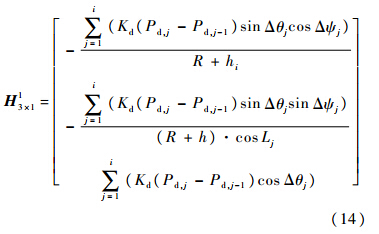
4 半实物仿真验证为了验证本文提出的组合测量方法的有效性,搭建了实验室样机.首先模拟一般油气井的井眼轨迹,采用轨迹发生器仿真生成惯性测量数据;然后加入由实验室样机采集得到的惯性传感器噪声数据组成半实物仿真数据;最后进行纯惯性测量方法与本文提出的组合测量方法进行仿真计算与比较. 4.1 仿真轨迹设计常规油气井一般包含直井段、造斜段和稳斜段.各阶段的主要参数如表 1所示.表 1 井眼轨迹参数Table 1 Parameters of oil borehole trajectory

轨迹阶段	姿态角变化率/((°)·min-1)			运行时间/s	运行速度/(m·s-1)
	倾斜	方位	工具面
直井	0	0	0	3000	0.5
造斜	1.5	0	0	2400	0.5
稳斜1	0	1.5	0	2400	0.5
稳斜2	0	0	0	6600	0.5

表选项


初始参数如表 2所示.考虑到当倾斜角在0°附近时,方位角不存在,因此这里设置初始倾斜角为10°.表 2 初始参数Table 2 Initial parameters

参数	位置			姿态/(°)			速度/(m·s-1)
	经度/(°)	纬度/(°)	高度/m	倾斜	方位	工具面
数值	116.0	35.0	0	10.0	180.0	0	0

表选项


根据表 2所示轨迹仿真条件,采用轨迹发生器产生的油气井眼轨迹如图 4所示.

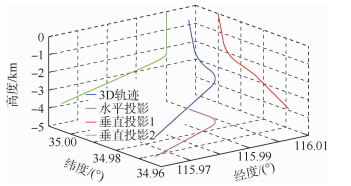图 4 井眼轨迹三维图Fig. 4 Three-dimensional figure of oil borehole trajectory

图选项

将实验样机放置三轴转台上,采集其静态数据14400s,去除平均值得到噪声数据,叠加到轨迹发生器生成的惯性测量数据中,加入陀螺常值漂移误差0.3(°)/h,加速度计常值漂移误差100μg,计数器刻度系数误差0.001,形成半实物仿真惯性测量数据.样机传感器指标如表 3所示.表 3 传感器参数Table 3 Sensor parameters

轴向	零偏稳定性(1σ)
	光纤陀螺/((°)·h-1)	加速度计/μg
x	0.3025	32.33
y	0.3006	75.05
z	0.2943	63.84

表选项


4.2 仿真结果分析 对半实物仿真数据分别进行纯惯性测量与本文提出的组合测量算法仿真计算,姿态误差及位置误差结果分别如图 5和图 6所示.

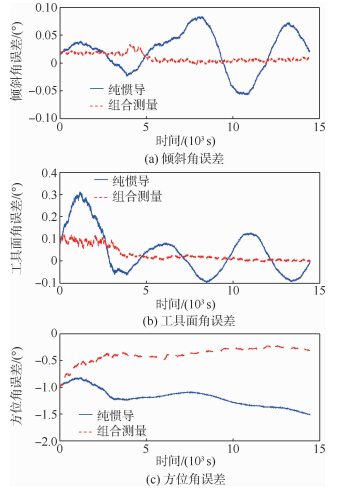图 5 姿态误差Fig. 5 Attitude error

图选项

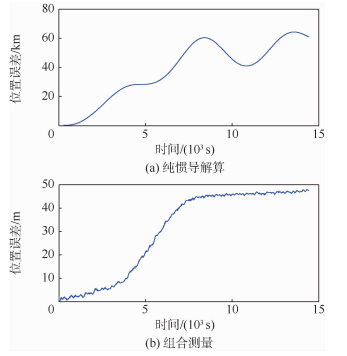图 6 位置误差Fig. 6 Position error

图选项

从仿真计算结果可见,组合测量方法能有效抑制测量误差增长.从图 5中可见,14400s仿真计算中,纯惯导计算的倾斜角、工具面角和方位角误差最大值分别为0.08°,0.31°和-1.50°,且倾斜角误差和方位角误差随时间累积,工具面角误差周期震荡;组合测量计算的倾斜角、工具面角和方位角误差最大值分别为0.02°,0.12°和-0.98°,误差不仅没有随时间发散,而且随着时间逐渐减小.在14400s时刻的倾斜角、工具面角和方位角误差分别为0.003°,0.01°和-0.31°.图 6中位置误差对比更明显,在14400s时刻,纯惯性测量误差达到了60868m,而组合测量误差仅为47.5m.仿真结果表明姿态和位置精度均能保持在一定范围内,提高了光纤陀螺测斜仪长时间保精度测量的性能. 5 结 论1) 建立了电缆长度辅助的光纤陀螺井眼轨迹测量模型.2) 提出的方法能够有效抑制测量误差随时间的累积,提高光纤陀螺测斜仪的性能.3) 对于光纤陀螺惯性测量技术在民用领域的推广具有一定的价值.
参考文献

[1]	Noureldin A.New measurement-while-drilling surveying technique utilizingsets of fiber optic rotation sensors[D].Calgary:University of Calgary,2002.
	Click to display the text
[2]	Torkildsen T,Edvardsen I,Fjogstad A,et al.Drilling fluid affects MWD magnetic azimuth and wellbore position[C]//Proceedings of IADC/SPE Drilling Conference.Dallas,Texas:SPE,2004:595-602.
	Click to display the text
[3]	Ledroz A G,Pecht E,Cramer D,et al.FOG-based navigation in downhole environment during horizontal drilling utilizing a complete inertial measurement unit:directional measurement-while-drilling surveying[J].IEEE Transations on Instrumentation and Measurement,2005,54(5):1997-2006.
	Click to display the text
[4]	ElGizawy M L.Continuous measurement while drilling surveying system utilizing MEMS inertial sensors[D].Calgary:University of Calgary,2009.
	Click to display the text
[5]	Noureldin A,Tabler H,Irvine-Halliday D,et al.Testing the applicability of fiber optic gyroscopes for azimuth monitoring for measurement-while-drilling processes in the oil industry[C]//Proceedings of IEEE Symposium on Position Location and Navigation.Piscataway,NJ:IEEE,2000:291-298.
	Click to display the text
[6]	张春熹,高爽.自主式光纤陀螺油井测斜仪[J].仪表技术与传感器,2006(11):9-11. Zhang C X,Gao S.Autonomous fiber optic gyroscopes inclinometer for well logging[J].Instrument Technique and Sensor,2006(11):9-11(in Chinese).
	Cited By in Cnki (17)
[7]	颜廷洋,张春熹,高爽,等.光纤陀螺测斜仪设计和实验[J].中国惯性技术学报,2013,21(2):179-181. Yan T Y,Zhang C X,Gao S,et al.Design and experiments of FOG inclinometer for surveying borehole[J].Journal of Chinese Inertial Technology,2013,21(2):179-181(in Chinese).
	Cited By in Cnki
[8]	Zhang Y S,Wang S W,Fang J C.Measurement while drilling instrument based on predigested inertial measurement unit[J].IEEE Transations on Instrumentation and Measurement,2012,61(12): 3295-3302.
	Cited By in Cnki | Click to display the text
[9]	颜廷洋,张春熹,高爽,等.附加运动约束的光纤陀螺测斜仪动态测量[J].中国惯性技术学报,2012,20(6):650-653 Yan T Y,Zhang C X,Gao S,et al.Continuous measurement for fiber optic gyro inclinometer with motion constraint[J].Journal of Chinese Inertial Technology,2012,20(6):650-653(in Chinese).
	Cited By in Cnki
[10]	Shin E H.Estimation techniques for low cost inertial navigation[D].Calgary:University of Calgary,2005.
	Click to display the text
[11]	Guo J C.Development of a precise GPS/INS/on-board vehicle sensors integrated vehicular positioning system[D].Calgary:University of Calgary,2007.
	Click to display the text
[12]	Li T.Use of wheel speed sensor to enhance a reduced IMU ultra-tight GNSS receiver[D].Calgary:University of Calgary,2009.
	Click to display the text
[13]	林铁,林恒,高爽,等.光纤陀螺测斜仪数据采集及传输单元设计与实现[J].测井技术,2009,33(4):402-405. Lin T,Lin H,Gao S,et al.Design and implementation of data acquisition and transmission for fiber optic gyroscopes inclinometer[J].Well Logging Technology,2009,33(4):402-405(in Chinese).
	Cited By in Cnki (8)
[14]	Rogers R M.Velocity error reresentations in inertial navigation system error models,AIAA-1995-3193-CP[R].Reston:AIAA,1995.
[15]	Rogers R M.Applied mathematics in integrated navigation systems[M].2nd ed.Reston:American Institute of Aeronautics and Astronautics,2003:77-84.
[16]	张小跃,杨功流,张春熹.捷联惯导/里程计组合导航方法[J].北京航空航天大学学报,2013,39(7):292-296. Zhang X Y,Yang G L,Zhang C X.Integrated navigation method for SINS and odometer[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(7):292-296(in Chinese).
	Cited By in Cnki (2)
[17]	秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,1998:69-76. Qin Y Y,Zhang H Y,Wang S H.Theory of Kalman filter and integrated navigation[M].Xi'an:Northwestern Polytechnical University Press,1998:69-76(in Chinese).