在传统的极化分集系统中,一般只考虑用电场的垂直和水平2个分量来得到2个独立的信道.文献[1]中通过理论分析指出如果在发射和接收端都使用3个正交的电偶极子天线和3个正交的磁偶极子天线,通过对电磁场中Ex、Ey、Ez和Hx、Hy、Hz这6种极化状态的利用,可以获得与单极化系统相比更多的信道容量增益.接下来,人们分别通过基于统计分析的模型[2, 3, 4, 5]或基于确定性的信道模型[6, 7]对一个6极化MIMO系统的自由度进行了研究.在这些基于统计分析的建模方法,虽然这种方法可以从宏观上对多极化MIMO信道的统计特性有所认识,但从微观角度这种信道模型无法从物理上体现多极化MIMO信道特性的细节.在这些分析中,一般考虑理想的天线在一个散射丰富的环境中,通过多径的俯仰角和水平角的不同分布来描述不同的信道散射环境,用随机相关矩阵模型来进行信道建模.然而,这种建模方法中没有体现信道散射过程对极化耦合的作用,也无法直接体现MIMO信道容量与其传播环境间的关系以及收发阵的结构和位置等参数对MIMO信道特性的影响.此外,在基于模式理论的模型[8]中,多考虑无源的环境中远场平面波的叠加,而天线辐射特性的影响则无法得到清楚的体现.也有一些实验测量工作,利用一些共点的2×2、3×3和4×4的多极化天线原型[9, 10, 11, 12],此外,文献[13]提出了一种6极化MIMO,HPMIMO(Hexapolarized MIMO)天线,但并非真正共点的结构.由于尺寸和耦合的限制,完全共点、正交的HPMIMO天线很难实现,因此对于发射端和接收端都采用6极化天线的MIMO信道特性测量试验也很少看到.
考虑到上述问题,本文利用电磁场仿真软件(HFSS),采用数值计算的方法,对多极化MIMO信道特性进行研究.通过HFSS,近场和远场的精确解都可得到,比采用简化的统计模型更加可靠.文献[5]采用虚源理论,针对无限小的理想、无耦合的电偶极子和磁偶极子天线,对自由空间和几种多径环境中的HPMIMO信道特性进行了研究.
本文在前期的研究中发现,具有均匀电流分布的环天线构成的多极化MIMO天线阵所获得的信道容量较大且鲁棒性更高[14, 15].因此在本文中,采用半波电偶极子天线和一种具有均匀电流分布的环天线,研究多径数目逐渐增加时,HPMIMO信道容量和信道矩阵特征值的变化情况.为了实现上述研究目标,本文选择了具有不同夹角的双反射面信道,因为在这种环境下,通过改变两个反射面之间的夹角,很容易实现对信道中多径个数和分布的控制.虽然这种双反射面信道在实际的通信环境中不常遇到,但在这种信道中可以很方面地研究多径的丰富程度对多极化MIMO信道特性的影响,也可以为更复杂信道环境下的建模理论提供参考.
1 天线设计1.1 共点正交双极化天线由于共点、正交、低耦合的6极化天线难以实现,本文首先得到了由一个电偶极子和一个环天线组成的双极化天线,如图 1所示.然后利用这个双极化天线得到一个虚拟的6极化天线.
 |
| 图 1 共点正点电偶极子与环天线Fig. 1 Co-located orthogonal electric dipole and loop antenna |
| 图选项 |
考虑到28GHz的毫米波频段是第5代移动通信系统的一个重要目标频段[16],因此将双极化天线的工作频段设为28GHz.工作于其中的电偶极子天线为普通的半波偶极子天线,环天线采用了一种具有均匀电流分布的天线结构[17],这样可以得到近似磁偶极子天线的辐射特性.为了使它们的工作频率位于28GHz,对文献[17]中的天线参数进行了调整和优化.在设计中本文发现,如果两个单个的天线都按照28GHz的工作频带设计,则把它们放在一起以后,由于相互耦合,会使每个天线的谐振频率都发生较大的变化.因此本文对这种耦合作用首先进行了仿真,使单个天线的工作频带稍微偏离28GHz.单个天线与合成天线回波损耗S11的比较见图 2,这样可以使合成以后的电偶极子天线和环天线能够共同工作于28GHz.双极化天线的S参数(S11，S12,S21,S22)见图 3,其中1端口为环,2端口为电偶极子.
 |
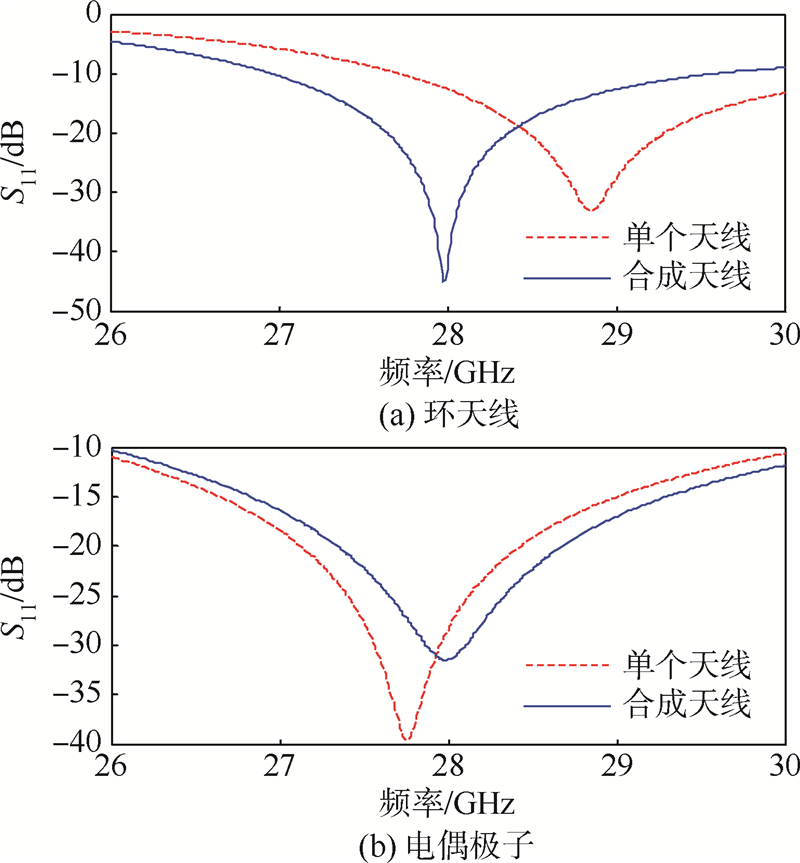| 图 2 单个天线与共点合成天线S11的比较Fig. 2 S11 comparison between single antenna and co-located combined antenna |
| 图选项 |
 |
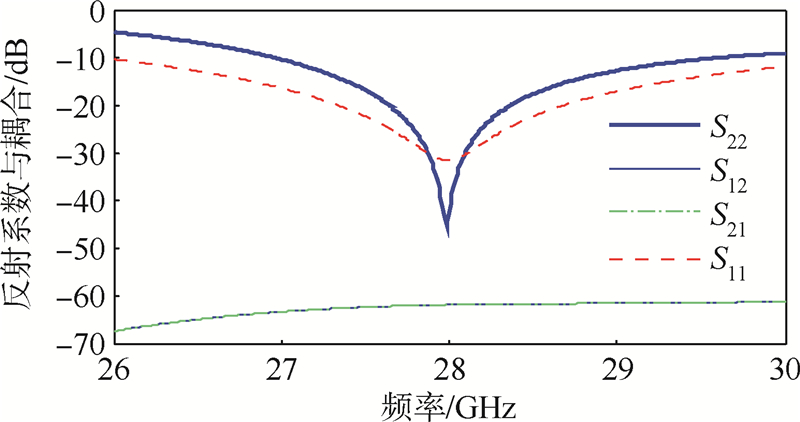| 图 3 双极化天线的S参数Fig. 3 S-parameters of dual-polarized antenna |
| 图选项 |
半波偶极子天线的两个金属圆柱长度均为2.4878mm,半径为0.0521mm,馈电点间隙为0.026mm.在环天线中,通过周期容性负载来实现均匀的电流分布.此天线印制在Teflon基板上,基板的性能参数为介电常数εr=2.6,tanδ=0.002,厚度h=0.8mm.整个环被均匀地分割成8个部分,其中第1部分上连接着阻抗匹配转换器.该环的具体参数为:外半径R1=1.9mm,内半径R2=1.65mm,每一段弧形带状线的角度为a1=44°,相邻弧形带状线之间的间隔为a2=1°.为了实现周期容性负载,在每一弧形带状线的一端加上互相交织的耦合线.这一部分的参数为:内部的弧形带状线宽ws=0.09mm,角度a3=11°,且与镂空带状线的内边界相隔gs=0.036mm,与镂空带状线底部相隔角度a4=1°.并行的两根带状线阻抗匹配器的长度为lp=1mm,宽wp=0.0425mm,它们间隔为0.068mm.这些参数的具体含义可以参考文献[17].
图 3中可见,环天线和半波偶极子天线的耦合很低,S12和S21参数低于-60dB.考虑S11<-10dB,环天线的带宽约为2.5GHz,偶极子天线的带宽高于5GHz.
1.2 虚拟6极化MIMO天线对于共点正交的3个电偶极子和3个磁偶极子构成的收发阵,其6×6的信道矩阵通过对接收点处电磁场分量的计算来获得,对于m或n={1,2,3},信道矩阵的元素hmn分别对应于沿着x、y和z轴发射或接收的电偶极子;类似的,对于m或n={4,5,6},信道矩阵的元素hmn分别对应于沿着x、y和z轴发射或接收的磁偶极子[1, 2, 3].
完成图 3所示的双极化天线设计以后,为了得到一个虚拟的6极化天线,本文首先让电偶极子天线和环天线的轴都位于x轴,把它们放到仿真的环境中,对它们分别进行馈电,得到相应的信道响应.然后让它们的中心保持不变,对它们整体进行旋转,使电偶极子天线和环天线的轴分别位于y轴和z轴,对相应的信道响应进行重新计算,然后把这些结果按照信道矩阵的定义组合起来,就可以得到6×6的MIMO信道矩阵.
2 仿真实验及结果2.1 双反射面信道如图 4所示的双反射面信道由两个夹角为θ的无限大理想导体平面组成,这里以θ=60°为例,对双反射面中多径的分布进行了说明.其中ht为发射天线Tx的高度,hr为接收天线Rx的高度,d为Tx到两平面交线的距离,R为Tx和Rx的x轴坐标间的距离.
 |
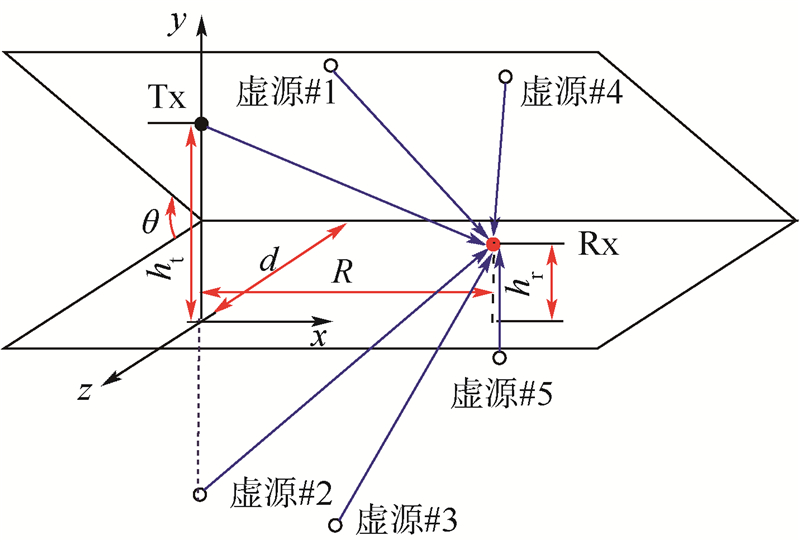| 图 4 双反射面多径结构示意图Fig. 4 Multipath structure schematic of two-mirror |
| 图选项 |
根据镜像理论,当θ=60°时,在两个反射面中产生的虚源个数为5,加上直射信号,则信道中的多径个数为6.在仿真实验中,本文将水平面固定,另一个面绕着两平面的交线进行旋转.根据多径个数N与两反射面间夹角θ的关系:N=360°/θ,则当θ按照180°、90°、60°、45°、30°和0°变化时,信道中对应的多径的个数N为2、4、6、8、12和无穷多.其中θ=180°时两个反射面合成为一个单反射面,θ=0°时两个反射面变成两个平行板.
在HFSS仿真中,所用的计算机为12核Intel处理器,内存为64GB.考虑到计算机的计算能力和计算量的大小,本文选择了两个反射面的尺寸相等,均为153mm×38mm.
2.2 信道容量信道容量一直被广泛用于评估一个MIMO系统的性能,它被定义为一个信道中能够以任意低的误比特率所实现的最高信息传输速率.如果信道的状态信息仅在接收端可以获得而发射端无法得到,一般采用发射功率均匀分配的方式,其信道容量[18]可以写为
式中:I为6×6的单位阵;nT=6为发射天线数;SNR(Signal-to-Noise Ratio)为信噪比,本文设为20dB;
是信道矩阵H的共轭转置.当信噪比较高时,采用发射功率均匀分配与最优的注水算法分配方式所获得的信道容量非常接近.为了消除计算中路径损耗对总接收信号功率的影响,一般采用归一化的信道矩阵:
式中:||·||F为Frobenius范数;nR为接收天线的个数.采用这种归一化方式可以较好地反映信道中多径的丰富程度对MIMO系统信道容量的影响.
图 5为HPMIMO信道容量与收发阵距离的关系.其中:Tx固定,Rx沿着x轴移动,在图 5(a)和图 5(b)中分别考虑了发射和接收天线高度相等与不相等的情况.其中θ=0°时两平行板之间的距离为22mm,λ0是工作频率为28GHz时自由空间(Free Space,FS)中的波长.由图 5可以看到,θ不同时对应的HPMIMO信道容量有明显的区别.总的来看,θ=0°时的信道容量最大,随着θ的增加,多径数目会逐渐减少,相应的信道容量也会逐渐减小,θ=180°时最小,与自由空间信道的结果接近.其中θ=0°时的信道容量约为θ=180°时的1.3~1.45倍.R为发射和接收天线间的距离,λ0为自由空间中的波长.当R<7λ0时,自由空间和θ=180°的单反射面信道中的信道容量要明显小于其他情况.当R>7λ0时,θ=0°和30°时的信道容量结果要明显高于其他情况.
 |
| 图 5 HPMIMO信道容量与R的关系Fig. 5 Relation between channel capacity and R of HPMIMO |
| 图选项 |
根据式(1)和式(2),可得到信噪比为20dB时,单极化收发天线所对应的信道容量为6.66bit·s-1·Hz-1.在图 6中以θ=0°和180°为例,给出了当Tx位于坐标原点,Rx的x坐标固定时,6极化相对于单极化系统信道容量增益随Rx的y、z坐标变化的情况.从图 6中可以看到,信道容量在空间中呈现出较强的不均匀性,而且对于不同的水平间距,其分布情况也有明显的区别.在双平行板信道中,HPMIMO信道容量的增益在2.47~5.10之间.此外,双平行板信道中的增益要明显大于单反射面信道.为了更清楚地描述信道容量增益在图 6中这4种不同环境下的空间统计特性,在图 7中对这些情况下信道容量增益的累积分布函数(Cumulative Distribution Function，CDF)进行了比较.
 |
| 图 6 信道容量增益空间分布图Fig. 6 Spatial distribution diagram of channel capacity gain |
| 图选项 |
 |
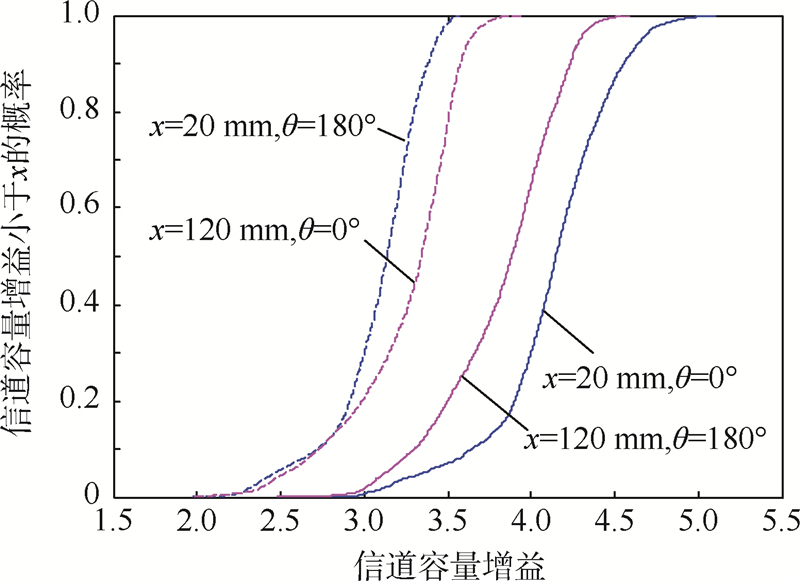| 图 7 HPMIMO系统相对于单极化系统信道容量的CDFFig. 7 Capacity gain CDF of HPMIMO system over single-polarized system |
| 图选项 |
从图 7中可以看到,双平板信道中的HPMIMO信道容量增益约为单反射面信道中的1.3倍.考虑10%中断概率,以上这4种情况下对应的增益分别为3.65、3.30、2.72和2.73.
2.3 特 征 值通过奇异值分解(SVD),MIMO信道矩阵H可以被分解为一组特征信道[19].如果信道矩阵H的奇异值被表示成λ1,λ2,…,λM,其中M是H的秩,则信道容量表达式(1)也可以写为
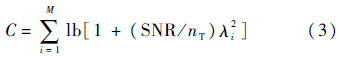
其中:每个非零的奇异值λi对应于一个特征信道,每个特征信道可以支持一路数据流.每个奇异值的平方被称为矩阵
H的特征值.通过式(3)可以清楚地体现每个特征值对信道容量的贡献.在图 8中,以θ=0°和θ=180°为例,描述了特征值随距离的变化,其中ht=8mm,hr=8mm.从图 8中可见,在这两种情况下,HPMIMO信道中都存在6个非零的特征值,对应于图 8(a)和图 8(b)中的6条曲线，但在自由空间信道中只有2个特征值较大,其他4个都只是略大于0,而在双平行板信道中,这4个特征值都明显增加了,从而获得的信道容量增益更大一些. |
| 图 8 特征值随R的变化Fig. 8 Eigenvalues changing with R |
| 图选项 |
3 结 论本文从信道容量和特征值的数值计算结果中可以得到:①在夹角不同的双反射面信道和自由空间信道中,HPMIMO系统都可以获得6个非零的特征值,但在多径较少的环境中,有些特征值会接近于0,因此对总信道容量的贡献很小;②随着双反射面间夹角度数的增加,信道中多径的数目逐渐减小,对应的HPMIMO信道容量也逐渐减小.夹角为180°的单反射面信道中的信道容量最小,接近于自由空间信道,夹角为0°的双平行板信道中的信道容量最大,可以达到单反射面信道中的1.3~1.45倍;③与单极化信道情况相比,HPMIMO系统可以获得的信道容量增益最大值为5.1,考虑10%中断概率,在双平行板信道中可获得的增益接近4倍,而在单反射面信道和自由空间信道中接近3倍.
参考文献
| [1] | Andrews M R,Mitra P,de Carvalho R.Tripling the capacity of wireless communications using electromagnetic polarization[J].Nature,2001,409:316-318. |
| Click to display the text | |
| [2] | Svantesson T,Jensen M A,Wallace J W.Analysis of electromagnetic field polarizations in multi-antenna systems[J].IEEE Transactions on Wireless Communications,2004,3(2):641-646. |
| Click to display the text | |
| [3] | Poon S Y,Tse D N C.Degree-of-freedom gain from using polarimetric antenna elements[J].IEEE Transactions on Information Theory,2011,57(9):5695-5709. |
| Click to display the text | |
| [4] | 黄丘林,郭万有,史小卫.极化分集时MIMO系统的信道容量[J].电子与信息学报,2006,28(8):1443-1446.Huang Q L,Guo W Y,Shi X W.Channel capacity of MIMO wireless systems in the presence of polarization diversity[J].Journal of Electronics & Information Technology,2006,28(8):1443-1446(in Chinese). |
| Cited By in Cnki (9) | |
| [5] | 伍裕江,聂在平.多天线系统中的多维极化分集性能分析[J].电波科学学报,2007,22(3):365-369.Wu Y J,Nie Z P.Performance analysis of multi-polarization diversity in MIMO wireless communications[J].Chinese Journal of Radio Science,2007,22(3):365-369(in Chinese). |
| Cited By in Cnki (15) | |
| [6] | Elnaggar M S,Chaudhuri S K,Safavi-Naeini S.Multi-polarization dimensionality of multi-antenna systems[J].Progress in Electromagnetics Research B,2009,14:45-63. |
| Click to display the text | |
| [7] | Piao D.Characteristics of the hexapolarized MIMO channel over free-space and three non-free-space scenarios[J].IEEE Transactions on Wireless Communications,2013,12(8):4174-4182. |
| Click to display the text | |
| [8] | Xu J.Field dimensions and polarization gains in electromagnetic systems[J].IEEE Transactions on Antennas Propagation,2012,60(11):5336-5347. |
| Click to display the text | |
| [9] | Stancil D,Berson A,Hof J P V,et al.Doubling wireless channel capacity using co-polarised,co-located electric and magnetic dipoles[J].Electronics Letters,2002,38(5):746-747. |
| [10] | Gupta G,Hughes B,Lazzi G.On the degrees of freedom in linear array systems with tri-polarized antennas[J].IEEE Transactions on Wireless Communications,2008,7(7):2458-2462. |
| Click to display the text | |
| [11] | Konanur S,Gosalia K,Krishnamurthy S H,et al.Increasing wireless channel capacity through MIMO systems employing co-located antennas[J].IEEE Transactions on Microwave Theory Techniques,2005,53(6):1837-1844. |
| Click to display the text | |
| [12] | 王鹏,郑剑峰,高旭,等.室内信道中多极化MIMO系统的容量[J].清华大学学报:自然科学版,2011,51(7),993-998.Wang P,Zheng J F,Gao X,et al.Capacity of a multi-polarized MIMO system in an indoor channel[J].Journal of Tsinghua University:Science & Technology,2011,51(7),993-998. |
| Cited By in Cnki (1) | |
| [13] | Tian R,Lau B K.Experimental verification of degrees of freedom for colocated antennas in wireless channels[J].IEEE Transactions on Antennas Propagation,2012,60(7):3416-3423. |
| Click to display the text | |
| [14] | Piao D,Mao Y,Liu L,et al.Effect of antenna circuit distribution on the characteristics of hexapolarized MIMO system over free space and ground reflected channel[C]∥Proceedings of the 2nd International Conference on Connected Vehicles & Expo(ICCVE 2013).Piscataway,NJ:IEEE Press,2013:526-530. |
| Click to display the text | |
| [15] | Piao D,Yang L.MIMO capacity comparisons of three types of colocated dual-polarized loop antennas[J].Progress In Electromagnetics Research C,2014,54:41-48. |
| Click to display the text | |
| [16] | Rappaport T S,Shu S,Mayzus R,et al.Millimeter wave mobile communications for 5G cellular:It will work![J].IEEE Access,2013,1:335-349. |
| Click to display the text | |
| [17] | Wei K,Zhang Z,Feng Z.Design of a wideband horizontally polarized omnidirectional printed loop antenna[J].IEEE Antennas Wireless Propagation Letters,2012,11(1):49-52. |
| Click to display the text | |
| [18] | Foschini G J,Gans M J.On the limits of wireless communications in a fading environment when using multiple antennas[J].Wireless Personal Communications,1998,6(3):311-335. |
| Click to display the text | |
| [19] | Telatar I E.Capacity of multi-antenna Gaussian channels[J].European Transactions on Telecommunications,1999,10(6):585-595. |
| Click to display the text |
