近年来,多源信息融合技术得到了迅速发展[1],已广泛应用于信息安全、图像处理、传感器网络、智能系统等多个领域[2].其研究主要集中于信息融合模型、动态融合方法、数据的预处理、冲突数据合成、数据维数转换、数据解相关等方向.在不同的研究方向上,国内外****提出了多种融合算法,其中包括模糊推理、贝叶斯估计、卡尔曼滤波、粗糙集、D-S(Dempster-Shafer)证据理论、DSmT(Dezert-Smarandache理论)、随机集以及基于人工智能的方法等.目前,软数据/硬数据融合[3, 4]、自适应融合[5, 6]以及多融合算法的联合应用成为信息融合新的研究方向.
在信息融合算法中,粗糙集理论可以有效地对不确定、不完备数据进行处理,目前广泛应用于模式识别、机器学习及故障诊断等领域.其无需任何先验知识,通过数据集本身的不可分辨关系,即可消除冗余属性,完成数据分类与特征提取.属性约简作为粗糙集理论的核心,目前大量研究围绕其展开,文献[7, 8, 9, 10]给出了不同数据结构下的多种属性约简算法.在未来一段时期内,高效约简算法、海量数据处理及粗糙集与其他算法的结合使用仍会作为粗糙集理论研究的重点.在故障诊断应用中,粗糙集多用于建立诊断数据与故障类型的映射关系,对高维故障数据进行降维处理,减少后续计算复杂度.文献[11, 12, 13]将粗糙集与神经网络结合,减少了网络的输入维数,提高了神经网络的训练速度;文献[14]使用支持向量机(SVM)对经粗糙集处理后的数据进行分类;文献[15]则将粗糙集与灰色理论相结合提出新的模型对故障进行预测.粗糙集与模糊理论以及多种优化算法的结合应用在此不再赘述.
D-S证据理论作为决策级信息融合算法因其具有对不确定信息表示、度量与组合的能力,在多属性决策问题中得到广泛的应用.为了解决数据存在冲突的问题,目前针对证据理论的改进也在不断进行,主要集中于两方面,通过改变冲突部分的分配方式对组合规则进行改进[16]以及通过对各证据权重的计算对证据本身进行修正[17, 18, 19].故障诊断作为一种多属性决策问题,是D-S证据理论的主要应用方向之一.文献[20]将其用于齿轮箱的故障诊断并引入信息熵对证据进行修正,文献[21]在故障诊断过程中通过对证据权重进行动态修正得到更为精确的结果;而更为常见的是D-S证据理论与其他算法的联合应用,与粗糙集不同的是,证据理论在其中负责诊断结果的融合.文献[22]将神经网络的输出作为证据进行合成,对涡轮机故障进行诊断;文献[23]用SVM构建分类器,对于多个分类器的结果使用D-S证据理论进行合成;文献[24]在对旋转机械进行并发故障诊断时用人工免疫算法对故障数据进行聚类,避免证据合成时焦元过多造成的计算困难.
由于航空电子装备诊断过程中采集到的多源信息存在冗余以及信息间存在冲突,考虑到粗糙集在提取关键信息与证据理论在冲突信息处理方面的优势,本文提出一种新的基于粗糙与证据理论的故障诊断方法.利用粗糙集构建故障诊断系统,减小属性维数;利用证据理论对约简后的测试结果进行融合.对于冲突证据的处理,在定义边界粗糙熵,作为在粗糙集框架下一种新的粗糙度衡量方法对证据进行修正,提出一种新的冲突证据合成规则,并将其应用于实际的诊断过程中.
1 故障诊断决策模型1.1 基于粗糙集的数据处理有序数组S={U,A,V,f}表示一个信息系统.其中,U为关于对象的非空有限集合,A为属性的非空有限集合,V为属性的值域,f:U×A→V为信息函数,它为每一个对象的每个属性赋予一个属性值.
在信息系统S={U,A,V,f}中,每个属性的子集B⊆A决定了一个不可分辨关系I(B).
对于信息系统S={U,A,V,f},若属性集可以被分为条件属性集C和决策属性集D,即A=C∪D且C∪D≠∅,则该信息系统被称为一个决策系统.
在决策系统L={U,C∪{d},V,f}中,若R⊆C满足:
1) PSI(R)({d})=PSI(C)({d}).
2) 不存在r∈R,使得PSI(R-{r})({d})=PSI(R)({d})成立.
则称R为条件属性集C相对于决策属性d的约简,简称C的相对约简.
在决策系统L={U,C∪{d},V,f}中,对于∀a∈C,对象xi在属性a上的属性值频率为
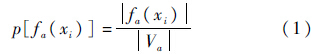
式中:|fa(xi)|为决策表中某一决策属性下与属性a列上取值为fa(xi)的相对应的对象个数;Va为决策表中所有决策属性下与属性a列上取值为fa(xi)的相对应的对象个数.
1.2 基于证据理论的冲突融合在D-S证据理论中,对于一个判决问题,所有可能答案的完备集合用Θ表示.辨识框架Θ={θ1,θ2,…,θN}.其中,θi称为辨识框架Θ的一个元素,N为元素个数,i=1,2,…,N.
在辨识框架Θ下,基本信任分配函数是从集合2Θ到[0, 1]区间的映射,G表示识别框架Θ的任一子集,记做G⊆Θ,并满足:m(∅)=0且
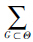 m(G)=1.其中,
m(G)=1.其中,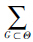 m(G)称为事件G的基本信任分配函数,也叫做mass函数,表示证据对G的信任程度.对于任一子集G,只要有m(G)>0,则称G为焦元.
m(G)称为事件G的基本信任分配函数,也叫做mass函数,表示证据对G的信任程度.对于任一子集G,只要有m(G)>0,则称G为焦元.D-S合成方法可以表述为,假设辨识框架Θ下的两个证据Ev1和Ev2,其相应的基本信任分配函数为m1和m2,焦元分别为Ai和Bj,则D-S合成规则为
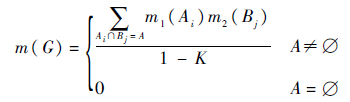
式中:K=
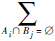 m1(Ai)m2(Bj),它反映出各证据之间的冲突程度.
m1(Ai)m2(Bj),它反映出各证据之间的冲突程度.2 航空电子装备故障诊断方法2.1 基于边界粗糙熵的决策重要度计算粗糙集可以对知识的不确定性进行有效刻画.知识的不确定性主要由两方面原因引起:一是来自论域上的二元关系,其产生知识模块越大,则相对于近似空间的知识就越不确定,这种不确定性使用粗糙熵来刻画;另一原因来自于给定的近似空间的粗集边界,边界越大则知识越模糊,粗糙集引入粗糙度来实现测量.为了衡量每一属性的不确定程度,本文在考虑以上两方面原因的基础上提出边界粗糙熵的概念.
定义1 给定一个决策系统L={U,C∪{d}},集合X⊆U,R是U上的等价关系,定义两个子集:
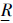 X={x∈U[x]R⊆X},
X={x∈U[x]R⊆X},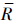 X={x∈U[x]R∩X≠∅}.其中,
X={x∈U[x]R∩X≠∅}.其中,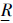 X和
X和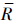 X分别称为X关于R的下近似和上近似.定义集合BnR(X)=
X分别称为X关于R的下近似和上近似.定义集合BnR(X)=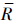 X-
X-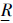 X称为X的R边界域.
X称为X的R边界域.定义2 对于决策系统L={U,C∪{d}},集合X⊆U,Y⊆U,R⊆C.知识R对论域U的划分记为U/R={X1,X2,…,Xm},决策{d}对论域U的划分记为U/{d}={Y1,Y2,…,Yn}.如果记Yi=d-1({vd})={k∈U:d(k)=vd},其中vd为决策属性值,则定义论域U在知识R下的划分对于决策分类Yi的决策边界域为BnR(Yi)=
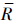 Yi-
Yi-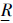 Yi.
Yi.定义3 在决策系统L={U,C∪{d}}中,定义知识R的边界粗糙熵为
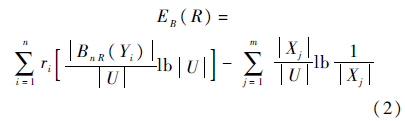
式中:ri=|Yi|/|U|,ri为等价类Yi的基数与U的基数之比.
边界粗糙熵的定义公式同时考虑了由不可分辨关系R所引起的粗糙集不确定性的两个因素.公式的前半部分
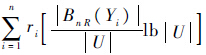 表示决策表中的对象集合在R划分下相对于决策类产生的粗集边界所引起的知识不确定性,公式的后半部分
表示决策表中的对象集合在R划分下相对于决策类产生的粗集边界所引起的知识不确定性,公式的后半部分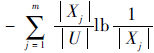 则定义了在R划分下产生的知识模块大小引起的不确定性.
则定义了在R划分下产生的知识模块大小引起的不确定性.定理1 给定一决策系统L={U,C∪{d}},集合X⊆U,P和Q是U上的等价关系,若I(P)⊆I(Q),则有EB(P)≤EB(Q).
该定理表明边界粗糙熵满足熵的条件.熵作为系统不确定性的一种度量手段,随着等价类划分越细,系统知识不确定性减少,熵逐渐变小.
要证明定理1,首先需要证明引理1.
引理1 对决策系统L={U,C∪{d}},集合X⊆U,P和Q是U上的等价关系,U/{d}={Y1,Y2,…,Yn}.若I(P)⊆I(Q),则有BnP(Yi)⊆BnQ(Yi).
证明先证明
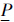 Yi⊇
Yi⊇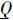 Yi,
Yi,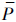 Yi⊆
Yi⊆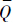 Yi.
Yi.对于∀x∈
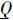 Yi,则[x]Q⊆Yi,由于I(P)⊆I(Q),所以[x]P⊆[x]Q,[x]P⊆Yi,有x∈
Yi,则[x]Q⊆Yi,由于I(P)⊆I(Q),所以[x]P⊆[x]Q,[x]P⊆Yi,有x∈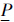 Yi,故
Yi,故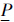 Yi⊇
Yi⊇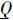 Yi.
Yi.对于∀x∈
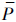 Yi,则[x]P∩Yi≠∅,由于[x]P⊆[x]Q,所以[x]Q∩Yi≠∅,x∈
Yi,则[x]P∩Yi≠∅,由于[x]P⊆[x]Q,所以[x]Q∩Yi≠∅,x∈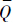 Yi,故
Yi,故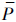 Yi⊆
Yi⊆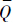 Yi.
Yi.又BnR(Yi)=
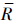 Yi-
Yi-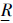 Yi,所以BnP(Yi)⊆BnQ(Yi).证毕
Yi,所以BnP(Yi)⊆BnQ(Yi).证毕下面证明定理1.
证明令E1B(R)=
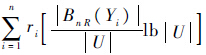 =
=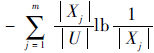 .
.先证明E1B(P)≤E1B(Q),E2B(P)≤E2B(Q).E1B(P)-E1B(Q)=
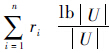 [|BnP(Yi)|-|BnQ(Yi)|],因为BnP(Yi)⊆BnQ(Yi),有|BnP(Yi)|≤|BnQ(Yi)|,故E1B(P)≤E1B(Q).
[|BnP(Yi)|-|BnQ(Yi)|],因为BnP(Yi)⊆BnQ(Yi),有|BnP(Yi)|≤|BnQ(Yi)|,故E1B(P)≤E1B(Q).设XPl⊆U/I(P),XQk⊆U/I(Q).
对于∀x∈XPl,总存在XQk使得x∈XQk,|XPl|≤|XQk|.
因此,∑|XPl|lb|XPl|≤∑|XQk|lb|XQk|.
故E2B(P)≤E2B(Q).
EB(R)=E1B(R)+E2B(R),故EB(P)≤EB(Q).证毕
性质1 在决策系统L={U,C∪{d}}中,当U中的所有元素均可分辨,即Xj={xj},1≤j≤U时,EB(R)=0.
性质2 在决策系统L={U,C∪{d}}中,对于任意等价关系R,粗糙边界熵满足0≤EB(R)≤(
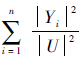 +1)lb|U|.
+1)lb|U|.从D-S证据理论角度考虑,在冲突信息融合阶段,约简结果中的属性将作为证据进行融合,而属性的决策重要度将作为反映该属性相对于结果重要程度的权重,决定着冲突信息的分配.所以要求属性的决策重要度包含两部分的内容,分别反映该属性在约简结果的不可分辨关系中所起的作用,以及该属性的分类效果与决策类的一致性.
而定义的边界粗糙熵则可以很好地体现了这两方面内容.在最优约简结果中,去掉某一属性将会导致边界粗糙熵的增加,因此,本文采用边界粗糙熵的增量定义该属性的决策重要度.
定义4 给定一个决策系统L={U,C∪{d}},R∈C,对于∀a∈R,属性a的决策重要度为
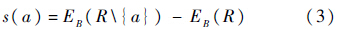
由上面定义的决策重要度经过归一化处理后就可以得到属性的相对权重:

2.2 基于决策重要度的冲突证据合成方法本文针对如何在航空电子装备的故障诊断应用中有效地分配冲突信息这一问题,结合诊断信息处理过程所得到的决策重要度提出了一种基于决策重要度的冲突证据合成方法(Conflicting Evidence Combination method based on Significance of decision,CECS).其核心思想是:冲突信息量的部分是可以利用的,在合成过程中需要把证据冲突信息量按照证据对各个命题的支持程度加权进行平均,而冲突信息分配取决于所获得证据的证据群体可信度和单个证据可信度这两方面的因素.
对于诊断数据进行粗糙集约简,所得到的往往不止一个约简结果.每一个约简结果Ri都可以作为一个独立的证据群,证据的群体可信度反映出每个证据群Ri对决策结果的支持能力.为了定义证据群体可信度,首先定义证据群Ri的群体支持度:
定义5 在决策系统L={U,C∪{d}}中,Ri∈C是决策表属性约简结果,R0是U上的等价关系,且满足U/R0=U,则Ri作为证据群的群体支持度为
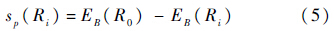
显然,当Ri的分类能力越好,对决策结果的支持度越高,粗糙边界熵EB(Ri)会越小,则Ri的群体支持度越高.
由以上定义,将群体支持度进行归一化处理后得到单个证据群Ri的群体可信度:
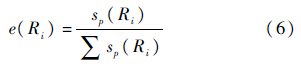
证据合成过程中的单个证据对应着约简结果R中的属性.单个证据可信度反映了该证据在证据群中的重要程度,可信度值越大,则重要程度越高,在冲突部分分配的过程中应获得越高的比例.综上,单个证据可信度由之前定义的相对权重w(a)给出.
基于冲突信息部分可以利用的思想,冲突信息分配方案由CECS方法给出,即证据组合规则如下:
定义6 设m1,m2,…,mn是同一辨识框架Θ上证据E1,E2,…,En的n个基本信任分配函数,所对应的焦元分别为Gi,i=1,2,…,n,则合成公式为
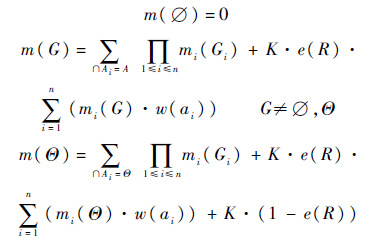
式中:K=
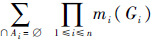 ,它反映了各个证据之间总的冲突程度.
,它反映了各个证据之间总的冲突程度.2.3 基于CECS的航空电子装备故障诊断方法在对航空电子装备进行测试的过程中,各种传感器模块实时的采集现场数据.产生的各种测试信息,从不同的侧面反映出装备的当前状态.需要对众多的诊断数据,获得诊断规则,给出测试结果.具体方法如下:
1) 采集装备测试数据,选取故障信息,构建粗糙集诊断决策表L={U,C∪{d},V,f}.
2) 对决策表中数据进行预处理.根据测试指标正常区间,按照“高于”、“低于”、“属于”该区间将测试数据进行离散化.
3) 按照粗糙集方法对决策表进行约简,获得约简结果R.
4) 若得到约简结果不唯一,通过式(2)计算边界粗糙熵EB(Ri),选取值最小的约简结果Ri.
5) 根据式(1)计算Ri中的每条属性的值频率p[fa(xi)],构建证据的基本概率赋值函数mi.
6) 根据式(6)计算e(Ri)得到证据源Ri的群体可信度,并通过式(4)计算w(ai)得到每条证据的权重.
7) 通过CECS算法对证据进行组合.
CECS算法针对选定的证据群,为了界定可分配部分比例,引入群体可信度e(Ri),通过步骤6)计算每个证据的支持度w(ai)来决定冲突信息在证据间的分配比例,在证据合成的过程中将其作为权重因子进行证据修改.通过以上步骤,CECS算法使得故障诊断结果具有更大的可信性和合理性.
3 故障诊断实例3.1 高度表故障分析某型机载高度表收发机属于机载导航设备的重要组成部分.其中收发机为系统核心部件,担负发射脉冲、接收回拨、解算距离等任务.高度表收发机作为独立的外场可更换单元(LRU),包括5个内场可更换单元(SRU):电源板、发射机、接收机、总线板和距离计算器.
在实际的使用过程中,“无高度数据显示”故障较为常见.本文选取该故障为例,其涉及到的故障征兆:启动时间、电源功耗、工作电流、基准电压、总线电压、总线电流、自检电压,共7个方面;其涉及到的故障模块包括3个SRU:电源板、总线版和距离计算器.
3.2 高度表故障诊断对故障征兆所对应的5个测试项目进行数据采样,选取3种故障模式对应的典型样本,以此方式构建诊断决策表(见表 1).表中典型故障对象列举18条,条件属性为5个,决策属性为3个.首先运用粗糙集方法对数据进行离散化并对决策表进行属性约简.
表 1 离散化故障诊断决策表Table 1 Discrete fault diagnostic decision table
| 编号 | C | D | ||||
| C1 | C2 | C3 | C4 | C5 | ||
| 1 | 1 | 0 | 1 | 0 | 0 | d1 |
| 2 | 1 | 0 | 0 | 0 | 0 | d1 |
| 3 | 2 | 0 | 2 | 2 | 0 | d1 |
| 4 | 0 | 0 | 1 | 1 | 1 | d1 |
| 5 | 1 | 2 | 0 | 0 | 2 | d1 |
| 6 | 0 | 0 | 1 | 2 | 0 | d1 |
| 7 | 2 | 1 | 0 | 0 | 2 | d2 |
| 8 | 1 | 1 | 1 | 0 | 0 | d2 |
| 9 | 1 | 2 | 2 | 1 | 0 | d2 |
| 10 | 1 | 0 | 0 | 0 | 1 | d2 |
| 11 | 2 | 2 | 1 | 0 | 0 | d2 |
| 12 | 1 | 0 | 2 | 1 | 0 | d2 |
| 13 | 2 | 0 | 2 | 0 | 1 | d3 |
| 14 | 0 | 0 | 2 | 0 | 0 | d3 |
| 15 | 2 | 1 | 2 | 1 | 0 | d3 |
| 16 | 0 | 2 | 2 | 1 | 1 | d3 |
| 17 | 2 | 2 | 2 | 0 | 0 | d3 |
| 18 | 1 | 2 | 0 | 0 | 0 | d3 |
表选项
在对决策表进行约简之后,得到两组约简结果:R1={C1,C2,C3,C4},R2={C1,C2,C3,C5}.C1~C5分别代表着:启动时间、电源功耗、基准电压、总线电压、自检电压;而d1~d3代表 3种模块:电源板、总线版、距离计算器.为了选定一组最优约简作为融合的证据群,分别计算粗糙熵得:EB(R1)=1.182 7,EB(R2)=1.753 2.因此选定约简结果R1作为证据群,通过式(6)计算其作为证据群的群体可信度为:e(R1)=0.534 9.
将R1中的每一个属性Ci作为一条证据,而将不同的故障模块di作为辨识框架.在不同的属性值下会得到证据不同的基本信任分配函数,这些基本概率分配函数如表 2所示.
表 2 基本概率分配函数表Table 2 Table of basic probability assignment function
| 属性 | Ci | mi(d1) | mi(d2) | mi(d3) |
| i=1 | 0 | 0.5 | 0 | 0.5 |
| 1 | 0.375 | 0.5 | 0.125 | |
| 2 | 0.167 | 0.333 | 0.5 | |
| i=2 | 0 | 0.556 | 0.222 | 0.222 |
| 1 | 0 | 0.667 | 0.333 | |
| 2 | 0.167 | 0.333 | 0.5 | |
| i=3 | 0 | 0.286 | 0.428 | 0.286 |
| 1 | 0.6 | 0.2 | 0.2 | |
| 2 | 0.167 | 0.333 | 0.5 | |
| i=4 | 0 | 0.272 | 0.364 | 0.364 |
| 1 | 0.2 | 0.4 | 0.4 | |
| 2 | 1 | 0 | 0 |
表选项
表 3 单个证据决策重要度与权重Table 3 Decision significance and weight of evidence
| 特征 | m1 | m2 | m3 | m4 |
| s(ai) | 0.608 | 0.830 | 0.719 | 0.763 |
| w(ai) | 0.208 | 0.284 | 0.246 | 0.262 |
表选项
由此可得到每条证据在不同的情况下基本概率分配函数,再根据计算每个证据作为条件属性时在约简结果中决策重要度的公式,算出s(a)值,进而得到单个证据可信度w(a)作为权重,得到的结果如表 3所示.
选取实测的4组故障数据作为验证样本.对故障数据进行处理,将其离散化后,按照对应约简R1={C1,C2,C3,C4}取得4个验证样本:T1={2,0,2,2},T2={0,1,1,2},T3={2,1,1,0},T4={2,2,2,2}.通过表 2可获得验证样本中每条证据的基本信任分配函数.
文中分别采用经典D-S方法、Yager[25]方法、文献[26]方法、文献[27]方法、基于证据距离的冲突合成方法和本文方法进行比较.其中,基于证据距离的冲突合成方法定义为用基于文献[28]所提出的证据间距离得出每条证据的重要度,替代本文CECS算法中的单个证据可信度作为证据的权重,其余参数设置与本文CECS算法相同.利用以上6种方法对上述4个验证样本中证据进行,得到的结果如表 4所示.
表 4 不同故障样本下融合结果对比Table 4 Fusion results comparison of different diagnostic samples
| 测试样本 | 合成方法 | D-S方法 | Yager[25]方法 | 文献[26]方法 | 文献[27]方法 | 基于证据距离方法[28] | 本文方法 |
| T1={2,0,2,2} | m(d1) | 1 | 0.016 | 0.481 | 0.249 | 0.234 | 0.282 |
| m(d2) | 0 | 0 | 0.218 | 0.109 | 0.130 | 0.115 | |
| m(d3) | 0 | 0 | 0.301 | 0.150 | 0.179 | 0.156 | |
| m(Θ) | 0 | 0.984 | 0 | 0.492 | 0.457 | 0.457 | |
| T2={0,1,1,2} | m(d1) | 0 | 0.525 | 0.263 | 0.299 | 0.275 | |
| m(d2) | 0 | 0.217 | 0.109 | 0.095 | 0.128 | ||
| m(d3) | 0 | 0.258 | 0.130 | 0.141 | 0.132 | ||
| m(Θ) | 1 | 0 | 0.498 | 0.465 | 0.465 | ||
| T3={2,1,1,0} | m(d1) | 0 | 0 | 0.253 | 0.126 | 0.131 | 0.132 |
| m(d2) | 0.572 | 0.016 | 0.396 | 0.206 | 0.216 | 0.226 | |
| m(d3) | 0.428 | 0.012 | 0.351 | 0.132 | 0.198 | 0.190 | |
| m(Θ) | 0 | 0.972 | 0 | 0.486 | 0.452 | 0.452 | |
| T4={2,2,2,2} | m(d1) | 1 | 0.005 | 0.378 | 0.164 | 0.141 | 0.210 |
| m(d2) | 0 | 0 | 0.249 | 0.106 | 0.158 | 0.131 | |
| m(d3) | 0 | 0 | 0.373 | 0.159 | 0.278 | 0.196 | |
| m(Θ) | 0 | 0.995 | 0 | 0.571 | 0.463 | 0.463 |
表选项
从融合结果中可以看出,经典D-S合成方法在对样本T1、T3、T4进行融合的过程中可以得出结果.但是样本T2其中有两条证据完全冲突,证据间的总冲突K=1,此时,D-S合成方法失效,不能有效识别故障,暴露出D-S合成规则存在的不足.
Yager合成方法[25]将冲突的部分全部分配在辨识框架上,由融合结果可以看出,证据源为4个时,效果并不理想,且该方法在处理低冲突证据时的效果好于处理高冲突证据的效果,当处理样本T2中的高冲突证据时,Yager合成方法将全部信任都赋予辨识框架上,导致方法失效.
文献[26]的方法在样本T1、T2、T3的融合过程中得到了正确结果,但是在样本T4上基本失效,无法做出决策,该方法认为冲突信息可以全部利用,并将证据总冲突的部分对单个证据源进行平均分配,这是一种不考虑外在因素冒险决策,同时,认为单个证据源拥有同样的可信度不符合实际情况,会造成误差.
文献[27]的方法针对以上问题,对合成规则进行修改,认为冲突信息的一部分可以利用,其比例取决于可信度函数ε,该方法在融合过程中取得了较好的效果,但其同样认为所有单个证据源具有相同的可信度,将冲突部分信息在证据源间进行平均分配,所以在样本上的融合结果也不理想.
基于证据距离的方法与本文提出的方法都针对冲突部分信息在证据源间的分配方面进行了改进,区别在于基于证据距离的方法基于证据间距离定义单个证据源的重要度,将其作为融合时的证据权重;而本文方法应用可以从决策表中获知的决策重要度得出单个证据源的可信度,将其作为权重.从融合结果上看,两种方法在样本T1上得到了一致的结果,本文方法要优于基于证据距离的方法;在样本T4上,基于证据距离的方法得到的融合结果错误.其根本原因在于证据间距离的计算只考虑了证据间的相似性,而没有像将之前蕴含在数据集中的知识体现在融合过程中,造成融合失效.为了说明这一点,表 5给出了基于证据距离方法中与本文方法中的证据权重对比.
表 5 证据权重对比Table 5 Comparison of weight of evidence
| 方法 | 样本 | w(a1) | w(a2) | w(a3) | w(a4) |
| 本文方法 | T1~T4 | 0.208 | 0.284 | 0.246 | 0.262 |
| 基于证据 距离方法 | T1 | 0.278 | 0.276 | 0.278 | 0.168 |
| T2 | 0.286 | 0.169 | 0.322 | 0.223 | |
| T3 | 0.270 | 0.230 | 0.218 | 0.282 | |
| T4 | 0.298 | 0.298 | 0.298 | 0.106 |
表选项
从表 5中可以看出,基于证据距离的方法在样本T2上之所以取得效果较本文方法好,主要由于第1条和第3条基本概率分配相似而得到较多权重,而这两条证据明显支持决策.基于证据距离的方法在样本T4融合过程中没有考虑到样本中第4条证据拥有较高的决策权而仅因其与其他3条证据有差异而赋予极低的权重导致融合结果错误.
通过样本验证,可以看出本文所提出的融合粗糙集与改进证据理论的故障诊断方法可以充分挖掘出隐藏在数据集中的知识,衡量出每条证据对决策的重要程度,对证据理论合成公式进行改进.在冲突证据的融合效果、适用性等方面存在优势.
4 结 论针对本文在对多源信息融合技术进行分析后,提出了一种基于粗糙集与证据理论的航空装备故障诊断方法.经实验验证表明:
1) 在粗糙集框架内实现故障诊断决策模型构建.
2) 对冗余故障信息进行约简,所提出的边界粗糙熵可以有效衡量每条测试项目对于决策的重要程度,提升了后期融合精度.
3) 在冲突证据的合成应用中,有效集成了证据的先验知识,得到诊断结果的准确度要好于目前存在的证据合成方法.
为了能对多故障类型、多测试属性故障,仍需对方法的计算量进行优化.
参考文献
| [1] | 潘泉,王增福,梁彦,等.信息融合理论的基本方法与进展(Ⅱ)[J].控制理论与应用,2012,29(10):1233-1244.Pan Q,Wang Z F,Liang Y,et al.Basic methods and progress of information fusion(Ⅱ)[J].Control Theory & Applications,2012,29(10):1233-1244(in Chinese). |
| Cited By in Cnki (38) | |
| [2] | Khaleghi B,Khamis A,Karray F O,et al.Multisensor data fusion:A review of the state-of-the-art[J].Information Fusion,2013,14(1):28-44. |
| Click to display the text | |
| [3] | Pravia M A,Babko-Malaya O,Schneider M K,et al.Lessons learned in the creation of a data set for hard/soft information fusion[C]∥12th International Conference on Information Fusion.Piscataway,NJ:IEEE Press,2009:2114-2121. |
| Click to display the text | |
| [4] | Gross G A,Nagi R,Sambhoos K,et al.Towards hard+soft data fusion:Processing architecture and implementation for the joint fusion and analysis of hard and soft intelligence data[C]∥15th International Conference on Information Fusion.Piscataway,NJ:IEEE Press,2012:955-962. |
| Click to display the text | |
| [5] | Hossain M A,Atrey P K,El Saddik A.Learning multisensor confidence using a reward-and-punishment mechanism[J].IEEE Transactions on Instrumentation and Measurement,2009,58(5):1525-1534. |
| Click to display the text | |
| [6] | David R P,Sampaio-Neto R,Medina C A.A linear adaptive algorithm for data fusion in distributed detection systems[C]∥11th International Symposium on Wireless Communications Systems.Piscataway,NJ:IEEE Press,2014:370-374. |
| Click to display the text | |
| [7] | Meng Z,Shi Z.Extended rough set-based attribute reduction in inconsistent incomplete decision systems[J].Information Sciences,2012,204(10):44-69. |
| Click to display the text | |
| [8] | Lu Z,Qin Z,Zhang Y,et al.A fast feature selection approach based on rough set boundary regions[J].Pattern Recognition Letters,2014,36(1):81-88. |
| Click to display the text | |
| [9] | Zheng K,Hu J,Zhan Z,et al.An enhancement for heuristic attribute reduction algorithm in rough set[J].Expert Systems with Applications,2014,41(15):6748-6754. |
| Click to display the text | |
| [10] | Shu W,Shen H.Incremental feature selection based on rough set in dynamic incomplete data[J].Pattern Recognition,2014,47(12):3890-3906. |
| Click to display the text | |
| [11] | Wang J S,Song J D,Gao J.Rough set-probabilistic neural networks fault diagnosis method of polymerization kettle equipment based on shuffled frog leaping algorithm[J].Information,2015,6(1):49-68. |
| Click to display the text | |
| [12] | Gao S,Wang J,Zhao N.Fault diagnosis method of polymerization kettle equipment based on rough sets and BP neural betwork[J].Mathematical Problems in Engineering,2013,7(2):91-103. |
| Click to display the text | |
| [13] | Liu C,Wu X,Wu N,et al.Structural damage identification based on rough sets and artificial neural network[J].The Scientific World Journal,2014,7(11):102-111. |
| Click to display the text | |
| [14] | Chen R C,Cheng K F,Chen Y H,et al.Using rough set and support vector machine for network intrusion detection system[C]∥2009 1st Asian Conference on Intelligent Information and Database Systems.Piscataway,NJ:IEEE Press,2009:465-470. |
| Click to display the text | |
| [15] | Niu W,Cheng J,Wang G,et al.Fast fault prediction model based on rough sets and grey model[J].Journal of Computational and Theoretical Nanoscience, 2013,10(6):1460-1464. |
| Click to display the text | |
| [16] | Han D Q,Dezert J,Tacnet J M,et al.A fuzzy-cautious OWA approach with evidential reasoning[C]∥15th International Conference on Information Fusion.Piscataway,NJ:IEEE Press,2012:278-285. |
| Click to display the text | |
| [17] | Yang J,Huang H Z,Miao Q,et al.A novel information fusion method based on Dempster-Shafer evidence theory for conflict resolution[J].Intelligent Data Analysis,2011,15(3):399-411. |
| Click to display the text | |
| [18] | Li Y B,Kang J,Xie H.The algorithm aiming at conflict to improve DS evidence theory[J].Information Technology Journal,2011,10(9):1779-1783. |
| Click to display the text | |
| [19] | Hu B,Shen B,Liu Q.An experience-feedback algorithm of DS evidence theory[C]∥2013 International Conference on Information Science and Computer Applications.Paris:Atlantis Press,2013. |
| Click to display the text | |
| [20] | Zhu H,Ma Z,Sun H,et al.Information correlation entropy based DS evidence theory used in fault diagnosis[C]∥2012 International Conference on Quality,Reliability,Risk,Maintenance,and Safety Engineering (ICQR2MSE).Piscataway,NJ:IEEE Press,2012:336-338. |
| Click to display the text | |
| [21] | Wang J F,Zhang Q L,Zhi H L.Fault diagnosis and optimization for agent based on the ds evidence theory[M]∥Advances in Swarm Intelligence.Berlin:Springer,2012:535-542. |
| [22] | Xu C,Zhang H,Peng D,et al.Study of fault diagnosis of integrate of DS evidence theory based on neural network for turbine[J].Energy Procedia,2012,16(10):2027-2032. |
| Click to display the text | |
| [23] | Zhang L,Dong Y.Research on diagnosis of ac engine wear fault based on support vectormachine and information fusion[J].Journal of Computers,2012,7(9):2292-2297. |
| Click to display the text | |
| [24] | Zhang Q H,Hu Q,Sun G,et al.Concurrent fault diagnosis for rotating machinery based on vibration sensors[J].International Journal of Distributed Sensor Networks,2013,4(5):37-47. |
| Click to display the text | |
| [25] | Yager R R.On ordered weighted averaging aggregation operators in multicriteria decisionmaking[J].IEEE Transactions on Systems,Man and Cybernetics,1988,18(1):183-190. |
| Click to display the text | |
| [26] | 李弼程,钱曾波.一种有效的证据理论合成公式[J].数据采集与处理,2002,17(1):33-36.Li B C,Qiang Z B.An efficient combination rule of evidence theory[J].Journal of Data Acquisition and Processing,2002,17(1):33-36(in Chinese). |
| Cited By in Cnki (276) | |
| [27] | 邓勇,施文康.一种改进的证据推理组合规则[J].上海交通大学学报,2003,37(8):1275-1278.Deng Y,Shi W K.An advanced combination rules of evidence[J].Journal of Shanghai Jiao Tong University,2003,37(8):1275-1278(in Chinese). |
| Cited By in Cnki (127) | |
| [28] | Jousselme A L,Grenier D,Bossé É.A new distance between two bodies of evidence[J].Information Fusion,2001,2(2):91-101. |
| Click to display the text |
