目前,各卫星大国均有开展支持分布式星群的项目,例如法国空间研究中心提出的干涉车轮计划[3],德国宇航中心提出的TerraSAR-X/TanDEM-X双星编队计划[4],意大利提出的BISSAT计划[5, 6],美国航空航天局和美国空军提出的先进极高频(AEHF)军用通信卫星和转型卫星通信系统(TSAT)项目[7],以及加拿大提出的RadarSat-2/3计划[8].在这些项目中,AEHF项目[9, 10]采用了相控阵天线和波束成形网络技术[11].相控阵天线技术通过电子手段改变射频波束的指向,使用户之间的波束产生快速捷变,从而提升信道的传输效率和灵活性.TSAT项目[12]利用编队卫星群协同通信组成的虚拟雷达阵列,完成被动无线电辐射测量、导航、通信等任务,借此验证编队卫星群具有通过协作通信有效完成多任务的能力[13].此外,TSX/TDX双星系统也采用了主动相控阵天线来形成灵活的波束指向、提供阵列增益.可见,基于阵列天线的分布式星群协同技术是未来卫星技术发展的重要趋势之一.
本文研究了基于阵列天线的分布式星群协同传输容量,分析了最优信道容量的条件,并给出了系统容量最大化的实现方式.以此为基础,分析了多卫星单天线、单卫星多天线、多卫星多天线等场景下的最优信道容量,并进行了仿真验证.针对多卫星多天线场景,本文提出了一种减小地面天线间距和降低测控精确度要求的地面天线排布策略.
1 系统与信道模型1.1 系统模型及参数本文考虑的分布式星群协同传输系统如图 1所示.其中,分布式星群包括L颗卫星,每颗卫星上都搭载着N根天线构成的平行于卫星轨道的天线阵列.地面接收站配置由M根接收天线组成的天线阵列.系统中使用的天线均为抛物面天线.该系统模型的有关变量为:地面天线阵列相邻两根接收天线之间间距为dA(单位:m);地球同步轨道卫星星群中相邻两颗卫星之间间距为dO(单位:m),记
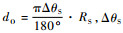 (单位:(°))为相邻两颗卫星之间的角度间隔,RS(单位:m)为同步卫星轨道的半径;每个卫星天线阵列相邻两根发射天线之间间距为dS(单位:m).
(单位:(°))为相邻两颗卫星之间的角度间隔,RS(单位:m)为同步卫星轨道的半径;每个卫星天线阵列相邻两根发射天线之间间距为dS(单位:m).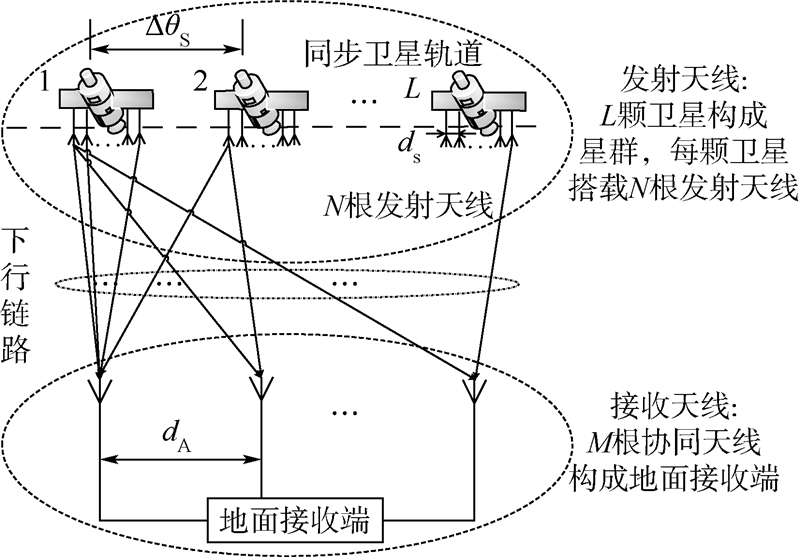 |
| 图 1 基于阵列天线的分布式星群协同传输系统模型(下行链路)Fig. 1 Cooperative grouped satellites with antenna arrays based transmission system model (downlink) |
| 图选项 |
1.2 信道模型考虑下行链路.由于卫星信号以视距(Line-of-Sight,LOS)成分为主[14],从卫星星群发射出来的信号在MIMO信道中的传播过程为

式中:y=[y1,y2,…,yM]T为M根地面接收天线的接收信号矢量;x=[x1,x2,…,xN·L]T为星群发送给用户的发射信号矢量;w=[w1,w2,…,wM]T为噪声矢量;H∈CM×(N·L)为信道传递矩阵,C表示复数空间.记发射天线数目MT=N·L,接收天线数目MR=M,则H∈CMR×MT.由于MT和MR具有对称性,为便于讨论,此处仅考虑MT≥MR的情形.
由电磁波在自由空间中的传播原理可知,第mR=m行、第mT=(l-1)·N+n列的矩阵元素Hm,l_n的等效基带表示为[15]
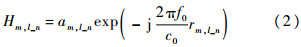
式中:f0为载波频率;c0=3×108 m/s为光在真空中的传播速度;rm,l_n为第m根地面接收天线到第l颗卫星上的第n根发射天线之间的距离,其复包络
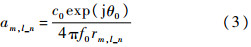
式中:θ0为观测时刻的载波相角.可以验证,|am,l_n|≈|a|,其中|·|表示绝对值,该变量的值近似于一个常数,
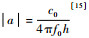 ,其中h为星群中心到地面天线阵列中心的距离.
,其中h为星群中心到地面天线阵列中心的距离.2 信道容量最优化2.1 信道容量最优值对一个时不变MIMO系统而言,信道的最高频谱效率可由Telatar的著名公式来计算[16]:
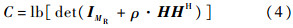
式中:ρ为信道的线性信噪比,定义对数信噪比为SNR=10 lg ρ=EIRP+(G-T)-κ-β(单位:dB),其中EIRP、(G-T)、κ和β分别为有效全向辐射功率、品质因数、玻耳兹曼常数和下行链路带宽的对数值[14];(·)H表示矩阵或矢量的共轭转置.
记矩阵

经计算,下行键路最优信道容量为

文献[15, 16]证明,信道容量取最优值Copt的前提条件是矩阵V的所有非零特征值相等,即γ1=γ2=…=γMR=|a|2MT.因此,满足最大信道容量条件的H为任意两行元素都正交的矩阵.
2.2 容量最优条件分析为使得系统满足H的任意两行元素都正交,已知MIMO系统的传递矩阵

信道模型中已经给出
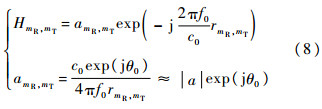
因此

又因为∀k,m∈{1,2,…,MR},H的第k行和第m行都正交,故可以得到
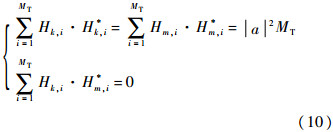
式中:(·)*表示矩阵或矢量的共轭.将HmR,mT代入
 ,得
,得
记
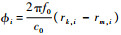 ,则
,则
考虑此处的系统,不妨给所有的exp(jφi)分组:令同一颗卫星上的所有天线为一组,记第l颗卫星上的第n根天线对应exp(jφi)=exp(jφl_n),其中i=(l-1)N+n.于是一共分出了L组.容易验证,只要令同组的相邻两个exp(jφl_n)之间方位角之差Δθ保持相等,并且令
 ,v∈Z,L
,v∈Z,L v,即可满足式(12).
v,即可满足式(12).如图 2所示,给出式(12)的一个解:
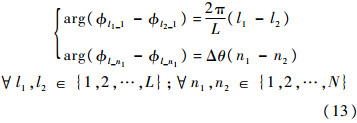
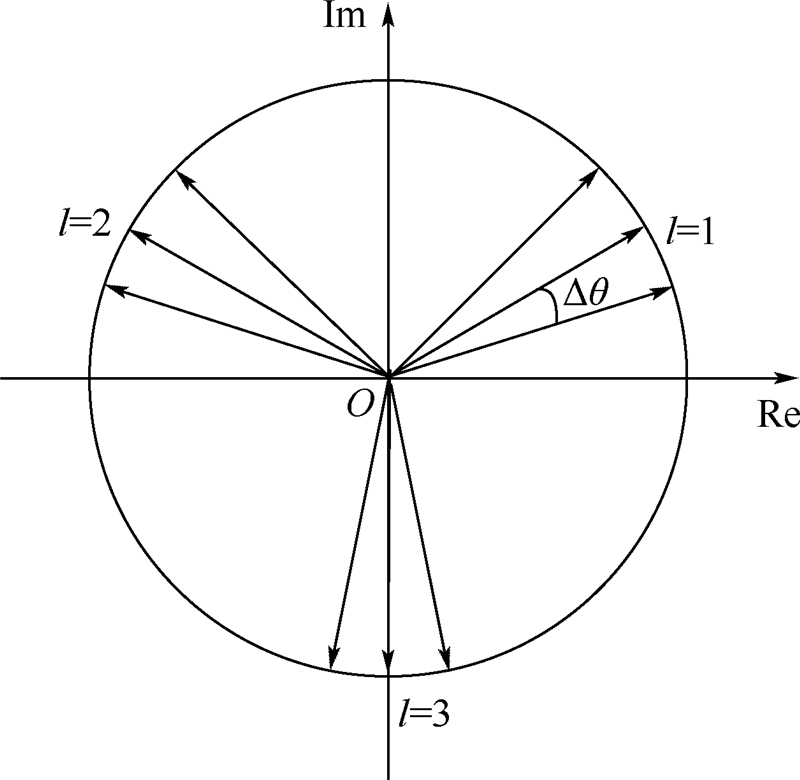 |
| 图 2 式(12)计算示意图Fig. 2 Calculation schematic diagram of equation (12) |
| 图选项 |
此时,φl_n成等间距分布,因而与φl_n成比例的rk,l_n-rm,l_n有着恒定的差分关系.任取两根地面天线和两根卫星天线,对第k根和第m根地面接收天线,与第c颗卫星上的第d根天线和第e颗卫星上的第f根天线而言,代入得

只有满足式(14),才能保证信道容量达到最大值.因此,接收天线和发射天线都是均匀排布的线性阵列(Uniform Linear Array,ULA),星群中相邻两颗卫星之间的间距同样保持恒定.
文献[17]给出了三维空间中收发天线ULA的建立方法.如图 3所示,为便于计算,假设星群中心和接收天线阵列中心位于同一经度.记星群中心到地面天线阵列中心与地心的连线的距离为z,地面天线阵列与东西方向的夹角为δ.
 |
| 图 3 分布式星群协同传输系统几何模型Fig. 3 Geometrical model of cooperative grouped satellites transmission system |
| 图选项 |
计算rm,l_n:
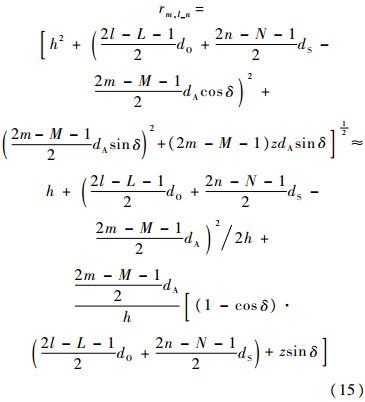
代入式(14)等号左边可得
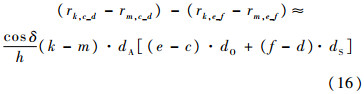
因此,式(14)改写为
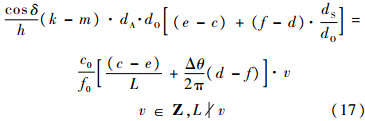
亦即
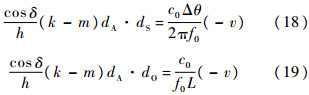
2.3 各类情况分析2.3.1 多卫星单天线当N=1且dS=0 m时,每颗卫星上只有一根天线,利用式(19),此时能达到最大信道容量的dA为
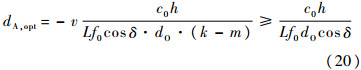
由于k-m=±1,±2,…,±(M-1)时dA表达式必须保持一致,而唯一能够随(k-m)改变的可控变量v∈Z,因此
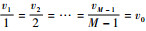 .为使得dA尽量小,取v0=1.于是可以得出结论:
.为使得dA尽量小,取v0=1.于是可以得出结论:信道容量是关于dA的周期函数,其周期为
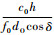 ,峰值位于
,峰值位于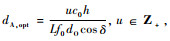 +,L
+,L u.2.3.2 单卫星多天线当L=1且dO=0 m时,只有一颗卫星,其上有N根天线,之前的分组推导方式不再成立.参考文献[18]中得到的结论显示,此处必须有Δθ=
u.2.3.2 单卫星多天线当L=1且dO=0 m时,只有一颗卫星,其上有N根天线,之前的分组推导方式不再成立.参考文献[18]中得到的结论显示,此处必须有Δθ=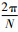 .利用式(18),此时能达到最大信道容量的dA为
.利用式(18),此时能达到最大信道容量的dA为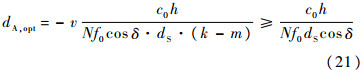
于是可以得出结论:信道容量是关于dA的周期函数,周期为
 ,峰值位于dA,opt=
,峰值位于dA,opt=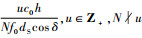 .2.3.3 多卫星多天线当L≠1且N≠1时,易知dO >> dS.利用式(18)和式(19),此时能达到最大信道容量的dA为
.2.3.3 多卫星多天线当L≠1且N≠1时,易知dO >> dS.利用式(18)和式(19),此时能达到最大信道容量的dA为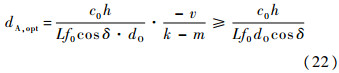
并且满足

于是可以得出结论:
1)
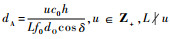 时,信道容量可以取到最大值.
时,信道容量可以取到最大值.2) 信道容量曲线关于dA呈周期性变化,其周期性体现在:一是小数量级时的峰-谷波动(由多卫星引起),其谷-谷周期为
 ;二是大数量级时曲线包络的周期性(由卫星上的多天线引起),其包络周期为
;二是大数量级时曲线包络的周期性(由卫星上的多天线引起),其包络周期为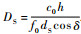 .3 仿真分析3.1 仿真设置记系统的实际信道容量为C,理论上的最大信道容量为Copt.对仿真环境进行建模,本文系统中所使用的相关参量如下:
.3 仿真分析3.1 仿真设置记系统的实际信道容量为C,理论上的最大信道容量为Copt.对仿真环境进行建模,本文系统中所使用的相关参量如下: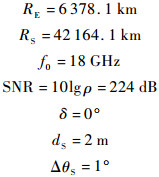
地面天线阵列与卫星星群的基本地理参数如下:
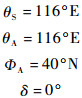
于是可以计算出:

式中:RE为地球平均半径;ФA为地面天线阵列中心纬度.
3.2 多卫星单天线以M=3、N=1的系统为例,改变卫星间距和卫星数目,信道容量随地面天线阵列相邻天线间距dA的变化情况如图 4所示.
 |
| 图 4 不同卫星角间距和卫星数目下,M=3,N=1系统的信道容量Fig. 4 Channel capacity with different sat-angular-distances and sat-numbers of a M=3,N=1 system |
| 图选项 |
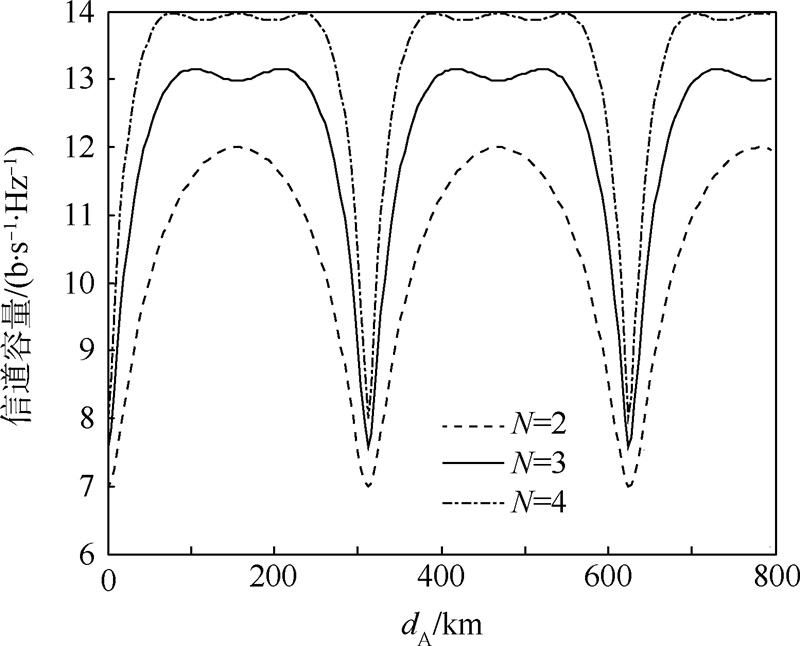
可以看出,信道容量是与dA有关的周期函数,其周期随卫星间距增大、卫星数目增多而减小.能够达到最大信道容量的地面天线间距
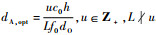 .
.3.3 单卫星多天线以M=2、L=1、ΔθS=1°的星群系统为例,改变卫星天线数目,信道容量随地面天线阵列相邻天线间距dA的变化情况如图 5所示.
 |
| 图 5 不同卫星天线数目下,M=2,L=1系统的信道容量Fig. 5 Channel capacity with different sat-numbers of a M=2,L=1 system |
| 图选项 |
可以看出,信道容量是与dA有关的周期函数,且变化周期与卫星数目成反比,远大于第3.2节中的情形.能够达到最大信道容量的地面天线间距
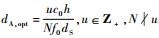 .
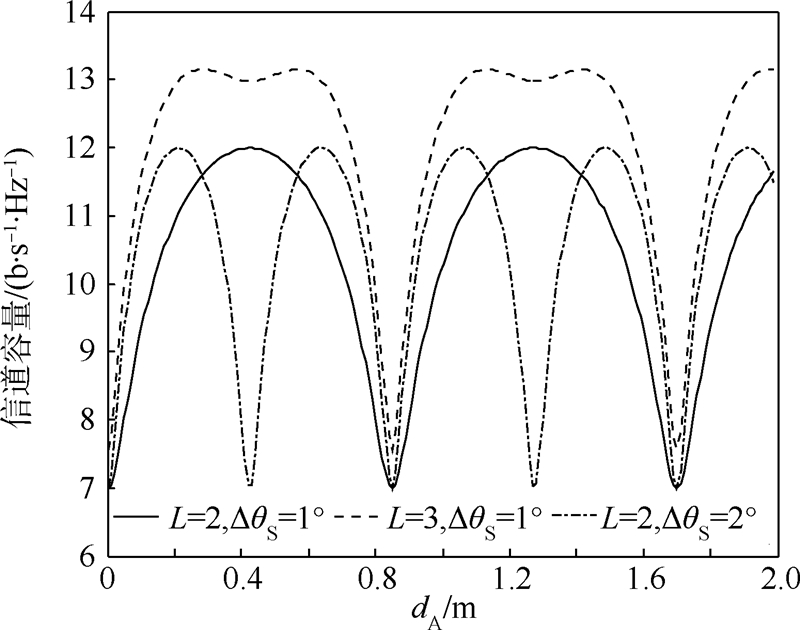
.3.4 多卫星多天线以M=2、L=2的系统为例,改变每颗卫星上天线数目后,信道容量随地面接收天线阵列相邻天线间距dA的变化情况如图 6和图 7所示.其中,图 6为小数量级dA的信道容量变化(由多卫星引起),图 7为大数量级dA的信道容量变化(由卫星上的多天线引起).可以看出,信道容量是与dA有关的周期函数,能够达到最大信道容量的地面接收天线间距
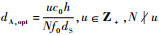 .
.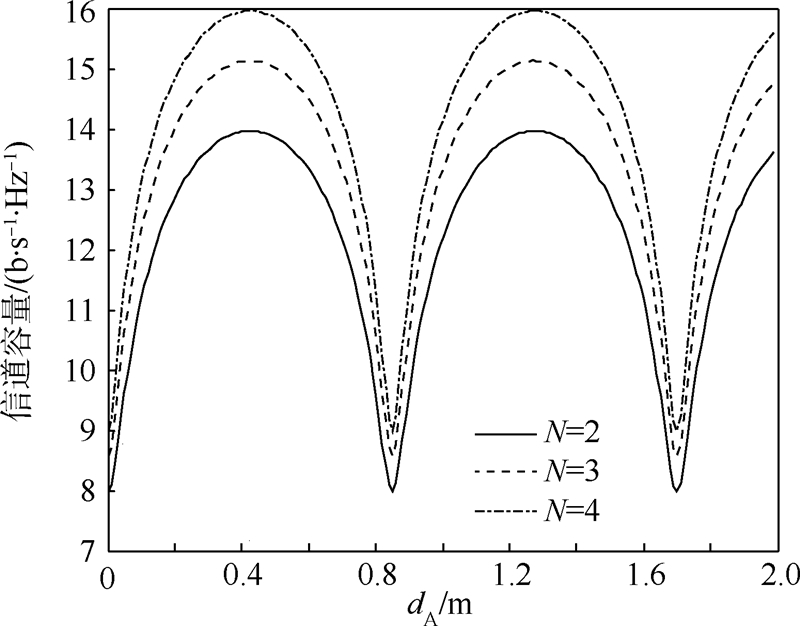 |
| 图 6 不同卫星天线数目下,M=2,L=2系统的信道容量(dA较小)Fig. 6 Channel capacity with different sat-numbers of a M=2,L=2 system (dA is small) |
| 图选项 |
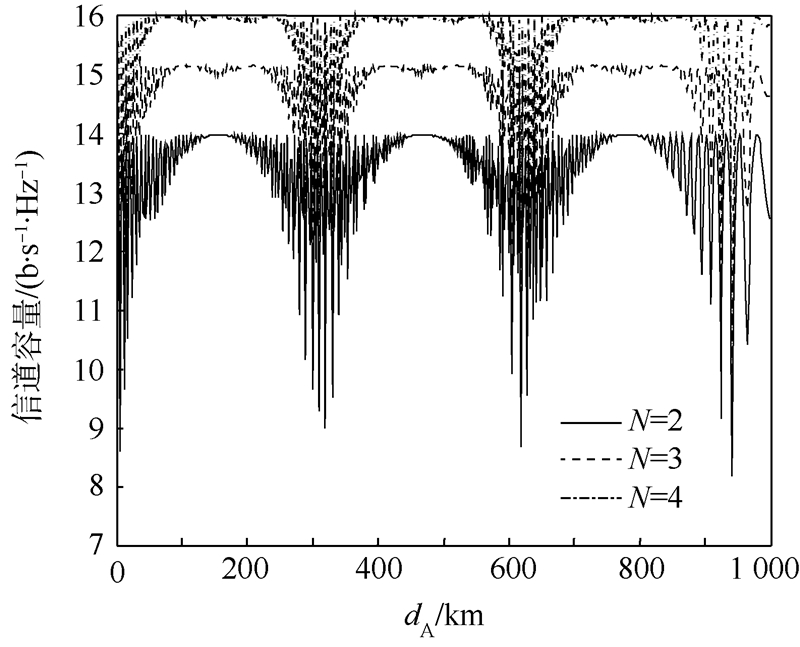 |
| 图 7 不同卫星天线数目下,M=2,L=2系统的信道容量(dA较大)Fig. 7 Channel capacity with different sat-numbers of a M=2,L=2 system(dA is large) |
| 图选项 |
由图 6可以看出,不同N值的信道容量曲线波动状况极为相似.然而,如同3.2节讨论的情形一样,信道容量的极大值和极小值相差很大、波动很快,例如图 6中M=2、L=2、N=2的系统,一个周期内信道容量达到最大值的90%以上的情况约占57.6%,考虑到数量级,实际生产中要求dA的偏差不能超过±0.24 m,对L≥3的系统而言则更小,否则就可能造成信道容量的极大衰落.
解决这一问题的方法有如下3种.
1) 减少卫星间距dO.
由
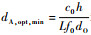 和
和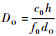 可知,DO、dA均与dO成反比,因而减少dO就将带来dA和DO的增大,相当于在一个周期内增加了高信道容量所占的比例.图 8是一个M=2、L=2、N=2的系统,若要求信道容量不低于最大值的90%,当相邻两颗卫星的夹角降至0.5°时,相比于ΔθS=2°的情况,dA容许的误差范围提高了近3倍.
可知,DO、dA均与dO成反比,因而减少dO就将带来dA和DO的增大,相当于在一个周期内增加了高信道容量所占的比例.图 8是一个M=2、L=2、N=2的系统,若要求信道容量不低于最大值的90%,当相邻两颗卫星的夹角降至0.5°时,相比于ΔθS=2°的情况,dA容许的误差范围提高了近3倍.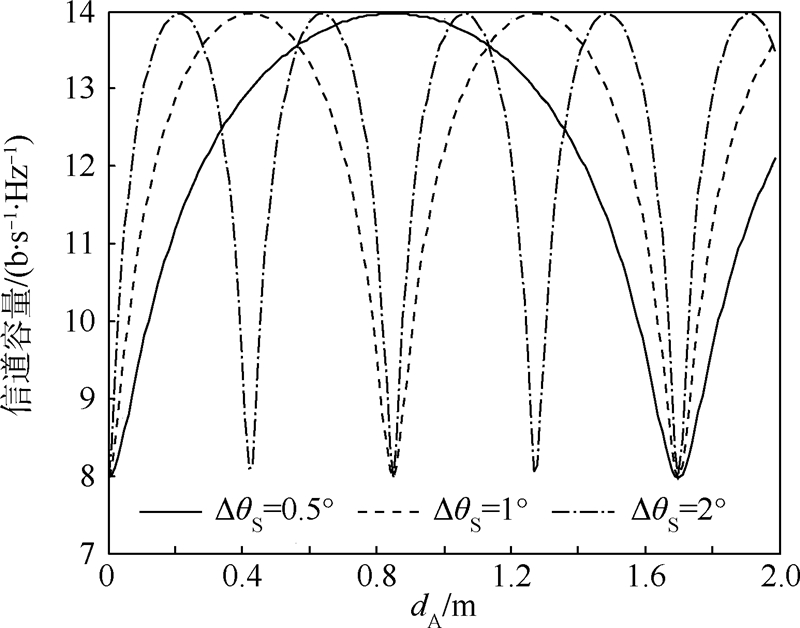 |
| 图 8 不同的卫星角间距下,M=2,L=2,N=2系统的信道容量Fig. 8 Channel capacity with different sat-angular-distances of a M=2,L=2,N=2 system |
| 图选项 |
2) 增大L值.
由
 可知,增大L值,dA,opt,min减小,而信道容量曲线谷-谷周期
可知,增大L值,dA,opt,min减小,而信道容量曲线谷-谷周期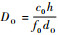 保持不变,因此,这就相当于在同一个周期内增加了高信道容量所占的比例.如图 9所示,与情况1)类似,这种方式同样提高了信道处于高容量状态的概率,降低了对dA测控精确度的要求.
保持不变,因此,这就相当于在同一个周期内增加了高信道容量所占的比例.如图 9所示,与情况1)类似,这种方式同样提高了信道处于高容量状态的概率,降低了对dA测控精确度的要求.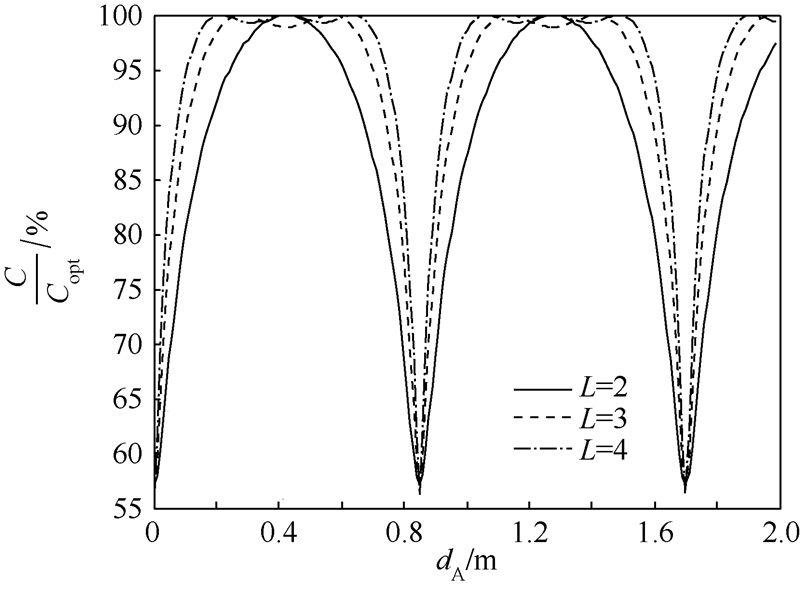 |
| 图 9 不同卫星数目下,M=2,N=2系统的信道容量Fig. 9 Channel capacity with different sat-numbers of a M=2,N=2 system |
| 图选项 |
3) 考虑更大的dA(提高u值).
由于u引起的包络函数的周期性,在大数量级的范围内,信道容量是关于dA的、以
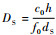 为周期的周期函数.如图 7所示,在一个周期内,由于
为周期的周期函数.如图 7所示,在一个周期内,由于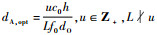 的周期性,信道容量在两侧会出现快速的抖动波纹.这一情况将在
的周期性,信道容量在两侧会出现快速的抖动波纹.这一情况将在 附近得到改善,dA越接近
附近得到改善,dA越接近 ,信道容量抖动的峰-谷差值就越小.将这些点称作“抖动平缓点”.适当地提高u值以使dA靠近抖动平缓点,将使信道容量的抖动趋于平缓,对dA误差造成的容量削减的容许度也将有所提升.
,信道容量抖动的峰-谷差值就越小.将这些点称作“抖动平缓点”.适当地提高u值以使dA靠近抖动平缓点,将使信道容量的抖动趋于平缓,对dA误差造成的容量削减的容许度也将有所提升.现在以M=2、L=2、N=2的系统为例研究其第一个周期:可以将信道容量曲线视作在上、下界包络之间的波纹曲线.其中,上界是一条与x轴平行的直线,y值等于最大信道容量13.97 b·s-1·Hz-1;下界是一条以
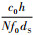 为对称轴的轴对称上凸曲线.
为对称轴的轴对称上凸曲线.从图 10可以看出,当dA∈[0.64,2.49]×105 m 时,无论dA的误差有多大,信道容量都不会低于最大值的90%.这时候完全可以不再严格要求dA满足最优条件,也可以保证即便是由误差导致的最差情况下,系统也能够达到足够的信道容量.
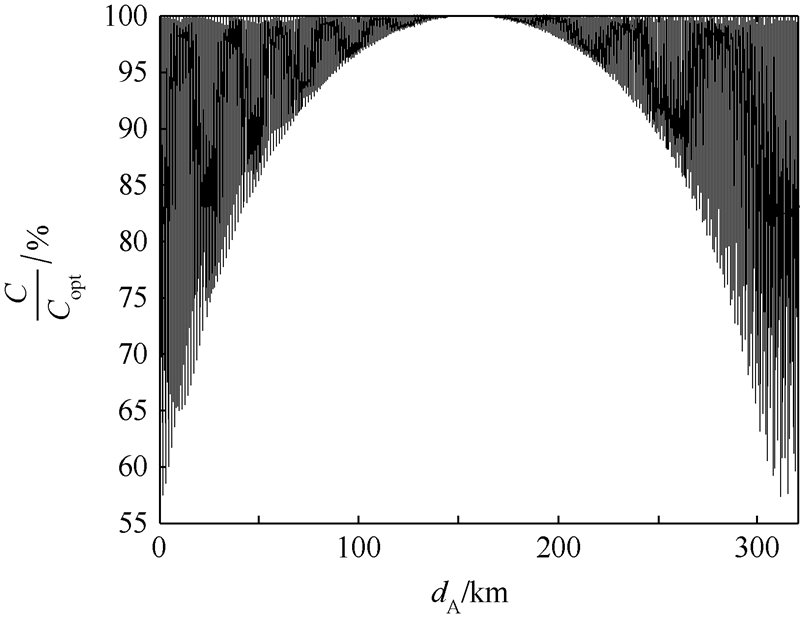 |
| 图 10 M=2,L=2,N=2系统的信道容量Fig. 10 Channel capacity of a M=2,L=2,N=2 system |
| 图选项 |
为了在“尽可能减小dA”和“提高可能出现的最低信道容量”之间达到平衡,在实际条件下,有必要采取某种折中的策略:首先确定一个最低的dA边界,使得即使最差的通信环境也能保证足够的信道容量;然后提高dA的精确度,使之尽量靠近最优条件
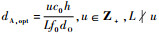 ,以达到最大的信道容量.
,以达到最大的信道容量.为了使dA尽量地小,亦即使得满足C≥90%Copt的dA下边界尽量地小,本文进一步研究下界包络曲线的特性,如图 11所示.
 |
| 图 11 改变N,M=2,L=2的系统信道容量对比Fig. 11 Channel capacity with different N of a M=2,L=2 system |
| 图选项 |
可以看出,由于“抖动平缓点”
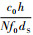 的作用,对相同的MT,当N尽量大时,满足条件C≥90%Copt的dA下边界更小.例如图 11(d)(N=5)中,dA的下边界约为20 km,几乎只有图 11(a)(N=2)的1/3.
的作用,对相同的MT,当N尽量大时,满足条件C≥90%Copt的dA下边界更小.例如图 11(d)(N=5)中,dA的下边界约为20 km,几乎只有图 11(a)(N=2)的1/3.3.5 仿真结果对比通过以上分析,可以看到在不同配置下,采用阵列天线均可以提升星群协同系统容量.
第3.2节讨论了未配置阵列天线的星群协同系统的传输性能.在多卫星单天线情况下,由于卫星间距较大,地面天线的小尺度变化就能导致系统容量的大幅度改变.
第3.3节讨论了单颗卫星上配置阵列天线的系统的传输性能.由于星上阵列天线间距较小,地面天线间距的大尺度变化才能导致系统容量的改变.为获得显著容量增益,需要以较大的地面天线间距作为代价.
第3.4节则讨论了配置阵列天线后的星群协同系统的传输性能.由于卫星发射端卫星之间的间距较大,而星上阵列天线间距较小,因此该系统兼具了第3.2节和第3.3节的地面天线间距小尺度和大尺度两种周期性变化特性,表现为信道容量的大周期和小周期峰-谷抖动现象.此外,当星上采用阵列天线技术时(见图 7),相比未配置阵列天线时的情况(见图 4),信道容量得到了显著提升.此种情况下,当地面天线间距能够受到精确控制时,以较小的地面天线间距为代价就能得到较大的信道容量增益.然而,当地面天线间距精确度难以控制时,可能导致信道容量损失很大.为了尽量减少这种意外损失,必须规定地面天线间距的下界,并相对调整合适的星上阵列天线间距.
值得说明的是,以上各种情况下的信道容量均随着地面天线间距呈现周期性变化,这是由式(20)~式(22)所决定的,其根本原因在于相位角度是存在周期性的,但满足信道容量最优条件的地面天线间距必须与发射端天线间距成反比.
4 结 论本文研究了基于阵列天线的分布式星群协同传输容量,分析了最大化容量的条件,并给出了系统容量最大化的实现方式.以此为基础,分析了多卫星单天线、单卫星多天线、多卫星多天线等场景下的最优信道容量,并进行了仿真验证.针对多卫星多天线场景,得出了以下结论:1) dA=uc0h/(Lf0dOcos δ),u∈Z+,L
 u时,信道容量可以取到最大值.
u时,信道容量可以取到最大值.2) 信道容量曲线关于dA呈周期性变化,其周期性体现在:一是小数量级时的峰-谷波动(由多卫星引起),其谷-谷周期为DO=c0h/(dOf0cos δ);二是大数量级时函数曲线包络的周期性(由卫星上的多天线引起),其包络的周期为DS=c0h/(dSf0cos δ).
3) 通过减少卫星间距和增加卫星数目,可以降低对dA精确度的要求.
为了获得最大容量和降低地面天线误差造成的影响,本文提出这样一种策略:首先确定地面天线间距dA的一个最低边界,使得即使在最差的通信条件下也能保证足够的信道容量;然后提高dA的精确度,使之靠近最优解dA,opt=uc0h/(Lf0dOcos δ),u∈Z+,L
 u以达到最大的信道容量,可以通过减少卫星间距和增加卫星数目来提高达到高信道容量的概率.
u以达到最大的信道容量,可以通过减少卫星间距和增加卫星数目来提高达到高信道容量的概率.参考文献
| [1] | Alagoz F,Gur G.Energy efficiency and satellite networking:A holistic overview[J].Proceedings of the IEEE,2011,99(11):1954-1979. |
| Click to display the text | |
| [2] | 林来兴,张小琳.星群、星座与编队飞行的概念辨析[J].航天器工程,2012,21(5):97-102. Lin L X,Zhang X L.Discussion on conception of cluster,constellation and formation flying[J].Spacecraft Engineering,2012,21(5):97-102(in Chinese). |
| Cited By in Cnki (3) | |
| [3] | Massonet D.Capabilities and limitations of the interferometric cartwheel[J].IEEE Transactions on Geoscience and Remote Sensing,2001,39(3):506-520. |
| Click to display the text | |
| [4] | Krieger G,Moreira A,Fiedler H,et al.TanDEM-X:A satellite formation for high-resolution SAR interferometry[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(11):3317-3339. |
| Click to display the text | |
| [5] | Moccia A.A bistatic SAR for earth observation[J].The International Society for Optical Engineering,2000,4173:1-9. |
| [6] | D'Errico M,Moccia A.The BISSAT mission:A bistatic SAR operating information with COSMO/SkyMed X-band radar[C]//Aerospace Conference Proceedings.Piscataway,NJ:IEEE Press,2002:2-809-2-818. |
| Click to display the text | |
| [7] | Martin M,Klupar P,Kilberg S,et al.TechSat21 and revolutionizing space missions using microsatellites[C]//15th American Institute of Aeronautics and Astronautics Conference on Small Satellites.Reston:AIAA,2001:1-10. |
| Click to display the text | |
| [8] | Lee P F,Girard R,James K.The RADARSAT-2 & 3 topographic mission:An overview[C]//Geoscience and Remote Sensing Symposium,2002.IGARSS '02.2002 IEEE International.Piscataway NJ:IEEE Press,2002:3-1477-3-1479. |
| Click to display the text | |
| [9] | 杨海平,胡向晖,李毅,等.卫星通信系列讲座之十三先进极高频(AEHF)卫星[J].数字通信世界,2008(6):84-87. Yang H P,Hu X H,Li Y,et al.The advanced extremely high frequency(AEHF)satellite[J].Digital Communication World,2008(6):84-87(in Chinese). |
| Cited By in Cnki | |
| [10] | 杭观荣,康小录.美国AEHF军事通信卫星推进系统及其在首发星上的应用[J].火箭推进,2011,37(6):1-8. Hang G R,Kang X L.Propulsion system of USA AEHF military communication satellite and its application on AEHF-1 satellite[J].Journal of Rocket Propulsion,2011,37(6):1-8(in Chinese). |
| Cited By in Cnki | |
| [11] | 吴学智,武兵,何如龙,等.外军新一代卫星通信系统及关键技术研究[J].通信技术,2012(9):7-9. Wu X Z,Wu B,He R L,et al.Research of new generation of satellite communication system in foreign military and its key technology[J].Communication Technology,2012(9):7-9(in Chinese). |
| Cited By in Cnki | |
| [12] | Steyskal H,Schindler J K,Franchi P,et al.Pattern synthesis for techSat21-A distributed space-based radar system[J].IEEE Antennas and Propagation Magazine,2003,45(4):19-25. |
| Click to display the text | |
| [13] | 冯少栋,张卫峰,张晓静,等.美军下一代转型卫星运控系统设计[J].数字通信世界,2009(5):59-63. Feng S D,Zhang W F,Zhang X J,et al.Design of next generation TSAT operating system of U.S.army[J].Digital Communication World,2009(5):59-63(in Chinese). |
| Cited By in Cnki (1) | |
| [14] | Maral G,Bousquet M.Satellite communications systems:Systems,techniques and technology[M].2nd ed.Chichester:Wiley,1993:206-216. |
| [15] | Schwarz R T,Knopp A,Lankl B,et al.Optimum-capacity MIMO satellite link for fixed and mobile services[C]//International ITG Workshop on Smart Antennas (WSA 2008).Piscataway,NJ:IEEE Press,2008:209-216. |
| Click to display the text | |
| [16] | Telatar E.Capacity of multi-antenna Gaussian channels[J].European Transactions on Telecommunications,1999,10(6):585-595. |
| Click to display the text | |
| [17] | 周杰,陈靖峰,邱琳,等.三维空间MIMO信道接收天线阵列互耦效应及系统容量分析[J].通信学报,2012,33(6):1-10. Zhou J,Chen J F,Qiu L,et al.Effect of mutual coupling and antenna correlation on MIMO system in three-dimensional spatial channel models[J].Journal on Communications,2012,33(6):1-10(in Chinese). |
| Cited By in Cnki (2) | |
| [18] | Schwarz R T,Knopp A,Lankl B,et al.Optimum-capacity MIMO satellite broadcast system:Conceptual design for LOS channels[C]//4th Advanced Satellite Mobile Systems.Piscateway,NJ:IEEE Press,2008:60-65. |
| Click to display the text |
