在卫星地面测试过程中,由于包含多种散热条件极其恶劣的环境状态,需要专门对卫星电子设备设计散热系统.前期,针对某型号卫星设计了基于强制通风的地面附加热控系统,在实际应用中取得了良好的效果,该系统仍有很大的改进空间,比如采用空气射流强化换热.作为对流换热方式的一种,射流冲击是一种极其有效的强化局部散热的方法.由于流体冲击到换热面上时,在驻点附近会形成很薄的边界层,因而其对流换热系数要比常规的高出几倍甚至一个数量级.目前国内外已有许多****对射流冲击换热问题进行了理论与实验研究,如Zu和Yan[3]及Zhang等[4]分析了在不同湍流模型下射流冲击的流动与传热特性.Yang等[5]分析了射流冲击下半圆形凹凸面的散热性能,并给出当雷诺数Re一定时,在靠近凹凸面的区域里,射流间距对系统散热性能的影响较大.Huang和Yang等[6, 7, 8]通过数值分析了射流冲击换热系统中柱鳍热沉的高度、宽度及喷嘴到柱鳍热沉的距离等结构参数对散热性能的影响,并给出了相应的优化设计结果.Maveety和Jung[9]分析了柱鳍热沉的高度和宽度对射流冲击换热系统中热阻和压力系数的影响.
在上述文献中,多是对含热沉的地面电子设备射流冷却,而没有针对卫星用大功率器件进行射流强化散热设计研究.本文对电子器件无热沉空气射流冷却系统开展了数值仿真,研究了主要结构参数对系统散热性能的影响,为卫星地面测试用通风散热系统的优化设计提供了理论基础与工程参考.
1 简化模型散热设计是保证电子设备可靠性的重要环节.当其工作温度超出允许值时,将会导致设备的可靠性和使用寿命大幅度降低.本文以某高热流密度电子器件为研究对象,进行散热设计与研究.该功率器件的长、宽、高为l×w×h=50mm×50mm×20mm,热耗为23W,最高工作温度设定为55℃.其散热系统如图 1所示,采用射流的结构形式,其中D为喷嘴出口直径,H为喷嘴出口到电子设备表面的距离.
 |
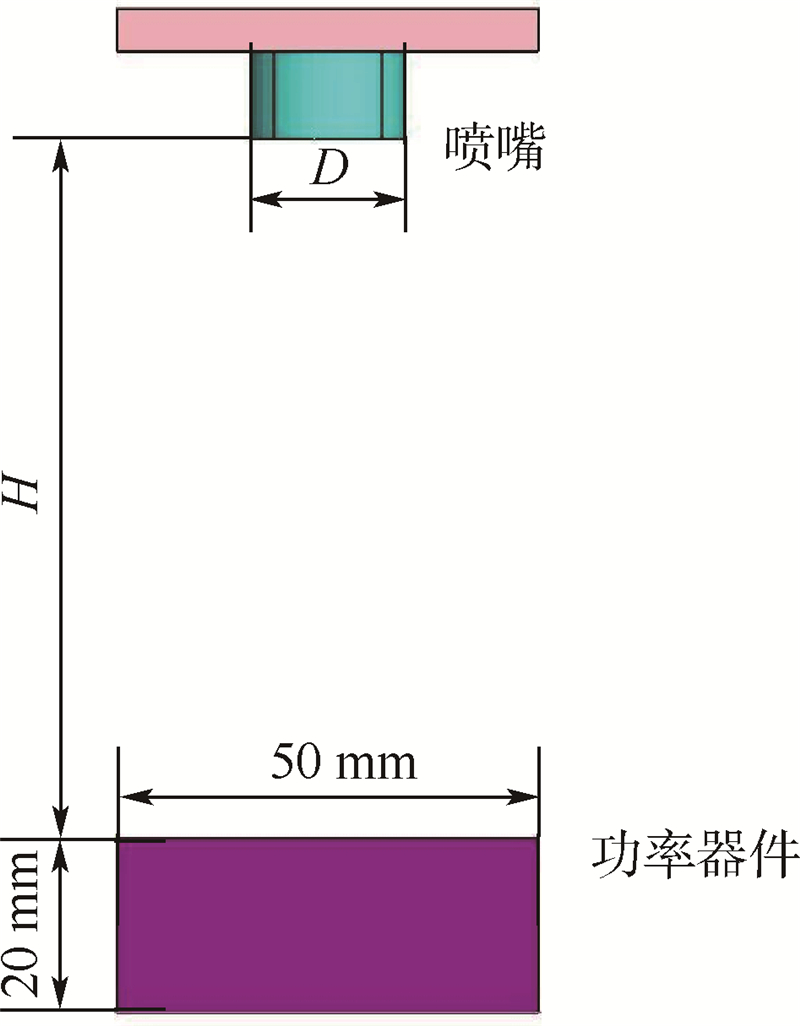| 图 1 散热系统结构示意图Fig. 1 Schematic diagram of cooling system structure |
| 图选项 |
2 数值分析方法数值分析是指在计算机上解决复杂数学问题的数值计算方法及其理论,此方法在解决对流换热问题有大量成功的实例.本文基于专业热分析软件Icepak开展下面的研究工作.
2.1 控制方程冲击射流一般被当作湍流流动,对于忽略浮力、辐射传热等因素的三维不可压缩的湍流流动与传热问题,其雷诺时均化控制方程的笛卡儿张量形式如下.
连续方程:
动量守恒方程:
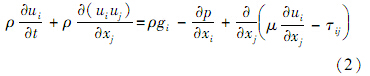
能量守恒方程:
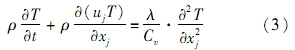
式中:T为温度;x为轴向坐标;u为瞬时速度;ρ为流体密度;μ为流体动力黏度;ρg为重力;
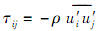为雷诺应力,u′为脉冲速度,i和j为方向标识;Cv为定容比热;λ为流体导热系数.2.2 湍流模型由于雷诺应力存在,上述湍流流动与传热的控制方程并不封闭,为使其封闭,则需要添加雷诺应力的微分方程.根据Boussinesq的假设,雷诺应力为
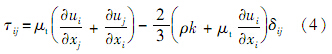
式中:
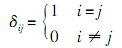
k为湍动能;μt为湍动黏度系数,它不是物性参数.依据求解μt的方程数目,湍流模型可分为Zero-Equation模型、Spalart-Allmaras模型、Two-Equation模型(包括:标准k-ε模型、RNG k-ε模型、Realizable k-ε模型).针对空气射流散热问题,本文选用Realizable k-ε模型,其数学描述如下.
根据Launde和Spalding的定义,湍动能耗散率为
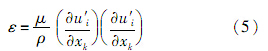
则k和ε的输运方程为
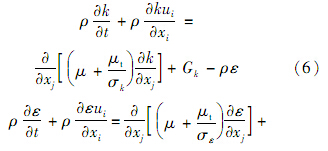
式中:
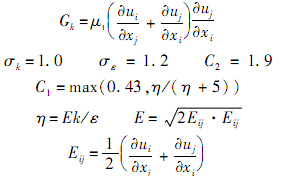
Realizable k-ε模型的湍动黏度系数为
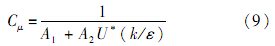
式中:
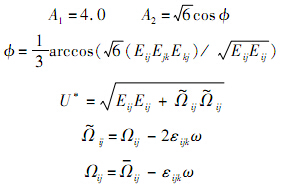
其中:Ωij 为以角速度ω为参考系观察到的时均转动速率张量.
2.3 求解说明1) 边界条件.
整个解析区域内边界可分为3部分:喷嘴、冲击面和出口.其设置如下:
① 喷嘴.采用速度入口边界条件,喷嘴长度设置成1cm,喷嘴直径D为优化参数之一.喷出流体的初始温度设定为20℃.
② 冲击面.为功率器件表面,其热边界条件设置为固定加热功率23W.
③ 出口.采用压力出口边界条件,出口表压设置成0Pa,即为1个标准大气压.
2) 网格模型及无关性验证.
网格划分如图 2所示,采用Mesher-HD网格类型.
 |
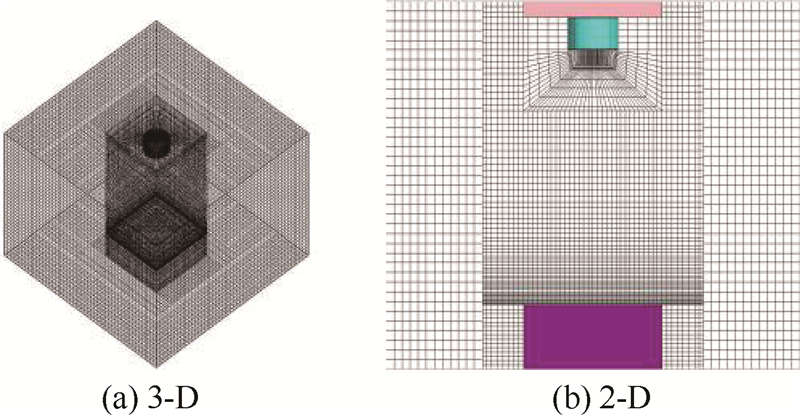| 图 2 计算区域的网格划分Fig. 2 Grids generation of computational region |
| 图选项 |
本文对计算模型的网格无关性进行了验证,这里以喷嘴直径D=3,距离直径比ψ=1为例进行说明.选取网格数N=97040,111660,122204,147920,1776988,对模型进行仿真计算,结果如图 3所示.从变化曲线中可以看出,随着网格数的增加结果的变化越来越小,当N=147920时,曲线已经趋于水平状态,因此这里选取N=147920作为该模型的网格划分标准.
 |
| 图 3 计算模型的网格无关性验证Fig. 3 Verification of independence of grids in computation model |
| 图选项 |
3) 近壁处理.
湍流流动的近壁区域可分为3层:黏性底层、混合层和完全湍流层.其中黏性底层是最靠近壁面的区域,在此区域内,Re较低,湍流发展不充分,黏性力在动量、热量、质量交换中起主导作用.对于射流传热问题,该区域是热阻的主要来源.在数值计算中,为获得更加真实的结果,就必须对这一区域进行特殊处理,近壁处理的方法包括壁面函数法和近壁模型法两种.这里选用近壁模型法作为本文的近壁处理方法,此方法不依赖于壁面法则,对于复杂流动,特别是低雷诺数流动非常适合,但是其对近壁网格的要求比较严格,需要在近壁区域划分比较细密的网格,如图 4所示.最理想的网格划分是需要第一网格在y+=1的位置,而在实际计算中,为减少计算量可以稍微增大y+,只要保证y+≤5,其计算结果均具有可信性.本文经过网格无关性验证后选取图 2所示网格,其近壁区第一网格在y+=4.15位置,可以保证网格质量及计算的准确性.
4) 努塞尔数Nu.
Nu作为一个无量纲参数,用于表征对流换热的强烈程度.对于本文所研究的冲击射流换热问题,冲击面上驻点区平均Nu(下文统称为驻点区Nu)可通过下面公式计算得到:
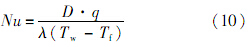
式中:q为功率器件表面热流密度;λ为空气导热系数;Tw为驻点区平均温度;Tf为空气的来流温度.
 |
| 图 4 近壁模型的网格划分Fig. 4 Grids generation of near-wall model |
| 图选项 |
2.4 计算方法检验为检验Icepak软件对射流传热问题计算的可行性,在完成网格无关性验证的基础上,对文献[10]报道的电子芯片散热问题进行了仿真计算,并将计算结果与文献中的实验数据进行了对比分析.
如图 5所示,该散热模型自上而下由喷嘴、热沉、芯片和绝热材料构成,计算区域为10×10×10cm3,网格数为161728.文献[10]中分别对3种不同的热沉在3种不同的雷诺数Re下的散热情况进行了实验研究,这里选择2号热沉在Re=6320时的实验工况作为验证对象,2号热沉的尺寸参数见表 1.其计算结果如图 6所示，其中ψ=H/D.
从图 6中可以看出,Realizable k-ε模型计算结果与实验数据是一致的,最大误差不超过3.2%,验证了Realizable k-ε模型可用于仿真空气射流传热问题.
 |
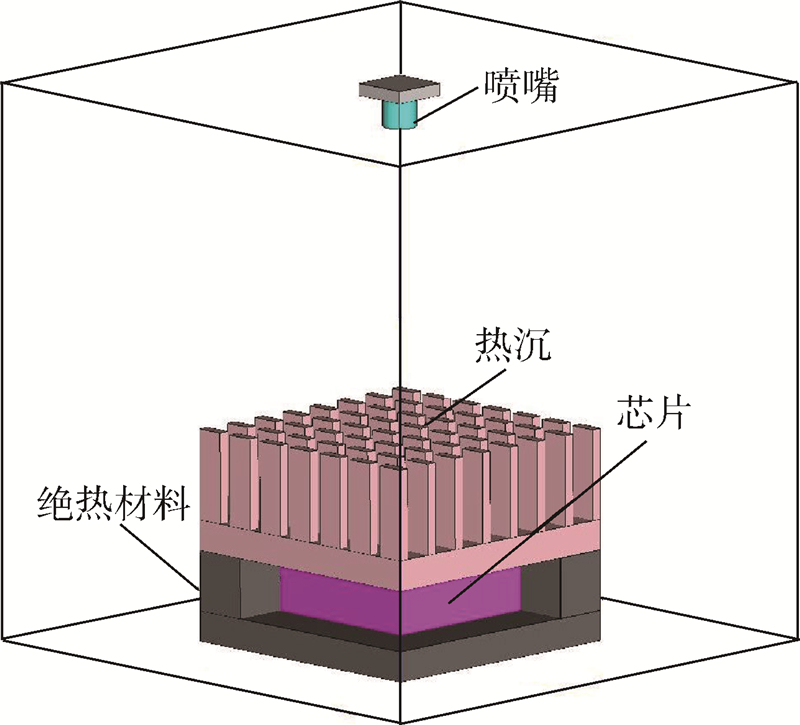| 图 5 空气射流冲击长方形针肋热沉换热示意图Fig. 5 Sketch map of rectangular pin-fin heat sink under air jet impingement |
| 图选项 |
 |
| 图 6 实验数据与仿真数据的对比Fig. 6 omparison between experimental and simulation data |
| 图选项 |
表 1 长方形针肋热沉的尺寸参数Table 1 Dimensional parameters of rectangular pin-fin heat sink
| 参数 | Hb/mm | Hf/mm | L/mm | C1/mm | D1/mm | Cw/mm | Dw/mm | 行数 | 列数 |
| 数值 | 5 | 15 | 50.8 | 2.6 | 5 | 5 | 2 | 8 | 7 |
表选项
3 结果分析与讨论3.1 流场特性散热系统的流场分布情况如图 7所示,空气从喷嘴喷出时为自由射流,其速度分布大体均匀,但随着流程的增加,射流与周围的流体不断进行动量和质量的交换,因此射流的宽度在不断地增加,轴向速度也在不断地衰减,但是变化不是十分剧烈.当流体冲击到换热面附近时,由于受到换热面的阻挡,速度变化非常剧烈,其轴向速度迅速衰减至0,而径向速度则由0迅速增加,此时自由射流转化为驻点区流动和壁面射流,其中驻点区是射流冲击换热的核心区域,直接影响着系统的整体散热性能,其大小取决于喷嘴直径的大小,实验
 |
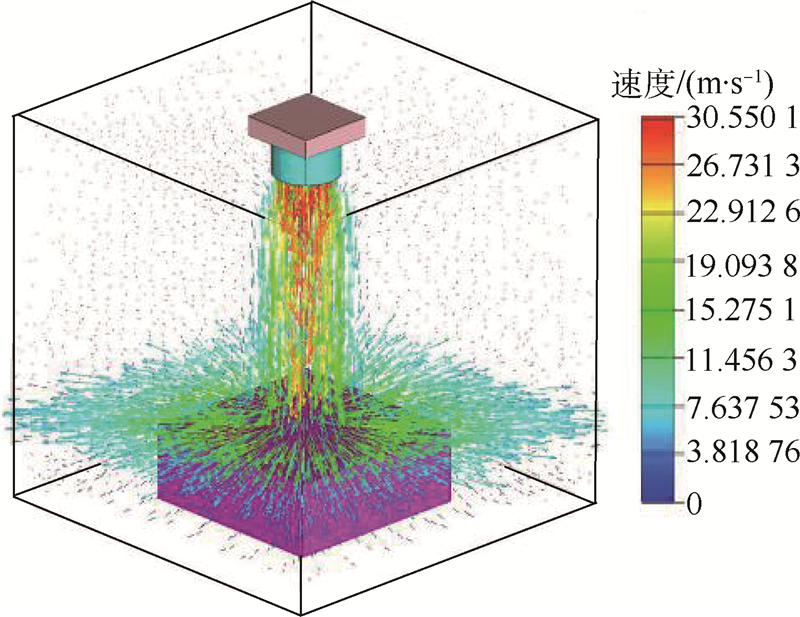| 图 7 射流冲击速度场分布Fig. 7 Velocity field of jet impingement |
| 图选项 |
研究表明驻点区的等效半径为喷嘴直径的1.2倍[11].因此,在下文中通过驻点区换热来分析空气射流冷却系统的散热性能.
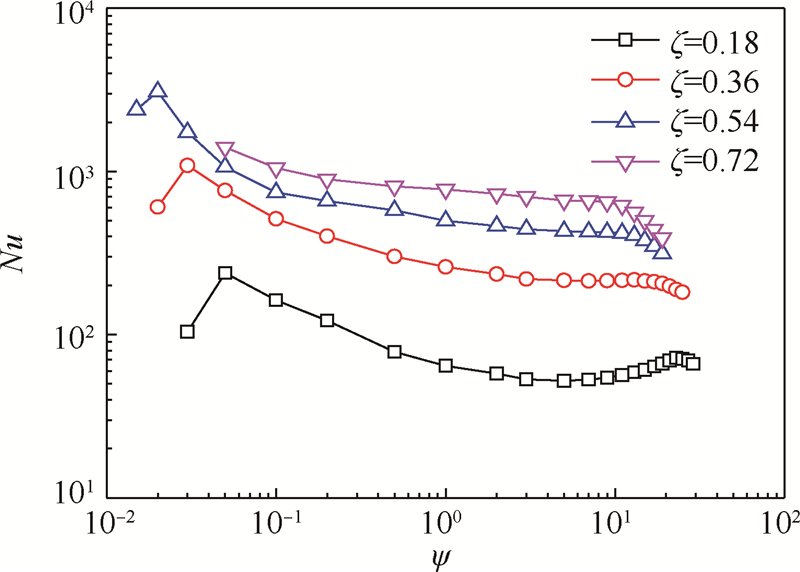
3.2 无量纲结构参数对散热性能的影响 在喷嘴出口风速V＝30m/s,无量纲参数ζ＝0.18,0.36,0.54,0.72时,该散热系统驻点区Nu随无量纲参数ψ的变化曲线,如图 8所示.其中ψ=H/D,ζ＝D/D0,D0=56mm为换热面的等效直径.
 |
| 图 8 无量纲参数对Nu数的影响Fig. 8 Effect of non-dimensional parameters on Nu |
| 图选项 |
从图 8中可以看出:
1) 随着ζ的增加,驻点区Nu单调递增,且整体增加幅度越来越小,当ζ由0.18变为0.36时,驻点区Nu平均增加的百分比高达280%,而当ζ由0.54变为0.72时,驻点区Nu平均增加的百分比降至40%.这是因为随着ζ的增加,喷嘴的出口直径D增大,射流冲击面积(即驻点区面积)增大,总风量增加,系统散热性能增强,但是当ζ持续增加时,射流冲击面积与有效换热面积的比值也在不断增加,总风量的有效利用率在不断降低,所以随着ζ的持续增加,驻点区Nu、系统散热性能增加趋于平缓.
2) 驻点区Nu随ψ的变化规律比较复杂,分以下两组情况:当ψ≤5时,驻点区Nu随ψ的减小而逐渐增大,且在ψ趋于无穷小时,将出现下降趋势.当ψ＞5时,驻点区Nu的变化受ζ影响,在ζ≤0.36时,驻点区Nu随ψ的增加呈现出先增加再减小的变化,在ζ>0.36时,驻点区Nu随ψ呈现单调递减变化.
这种现象是由射流冲击强度与湍流度共同作用形成的.ψ≤5时,换热面处于射流核心区域,湍流度刚刚开始形成,还未能与周围流场形成有效的掺混,这时驻点区散热性能只取决于射流冲击强度,即冲击作用越强,边界层越薄,速度和温度梯度越大,散热性能越好.为了方便说明这里引入滞止系数p*(驻点压强与喷嘴动压之比),用以表征射流冲击强度大小,其变化曲线如图 9所示,可以看出随ψ的减小,p*逐渐增大,射流冲击作用增强,驻点区散热性能提高.然而在ψ趋于无穷小时,喷嘴到冲击面的距离趋于无穷小,这时冲击面的限流作用趋于无穷大,使得流体流量变小,无法及时将热量带出,因此,驻点区散热性能将会出现下降趋势.
 |
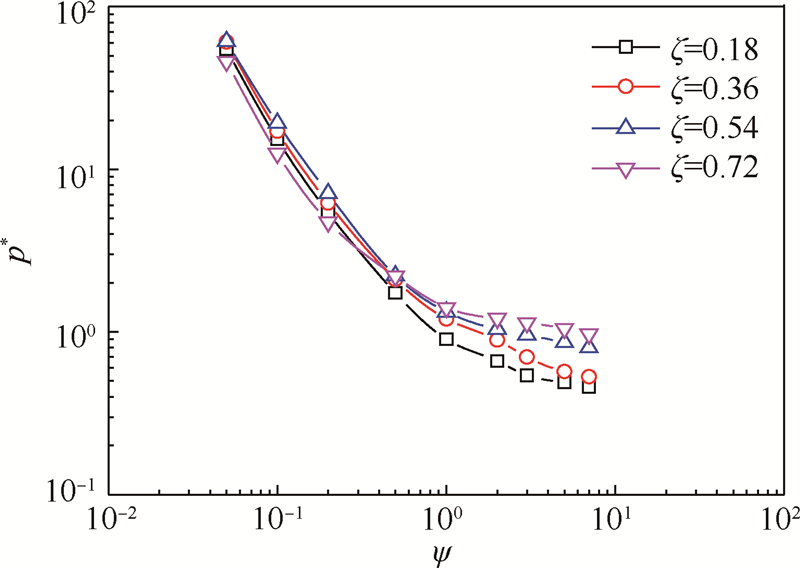| 图 9 p*随ψ的变化曲线Fig. 9 Curves of p* changing with ψ |
| 图选项 |
而ψ＞5时,换热面基本处于射流核心区之外,射流对驻点区的冲击强度变化不明显,此时湍流度的变化成为影响驻点区散热性能的主要因素[12].当射流初始湍流度不是很高时(如ζ≤0.36的工况),则射流湍流度会随着ψ的增加而逐步提高,直至到达峰值,然后又逐渐减小.受湍流度变化的影响,驻点区散热性能也会随着ψ的增加而逐步提高至峰值.之后,由于射流的到达速度和湍流度的逐渐下降,驻点区散热性能也开始呈现下降趋势,最终形成非单调性变化.但当射流初始湍流度足够高时(如ζ＞0.36的工况),则可以避免上述非单调性现象,使得驻点区散热性能随ψ单调递减变化.
3.3 喷嘴出口风速对散热性能的影响在ζ＝0.36、ψ＝10时,散热系统驻点区Nu随喷嘴出口风速V的变化曲线如图 10所示.
 |
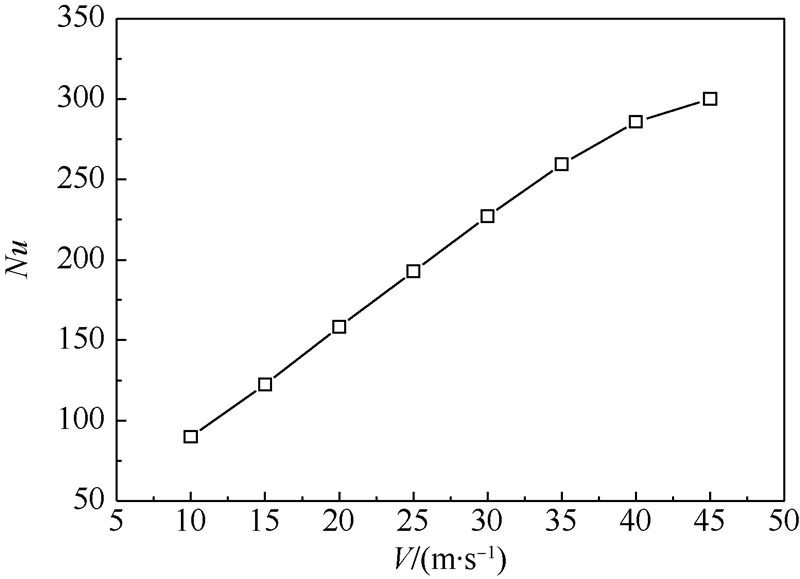| 图 10 Nu随V的变化曲线Fig. 10 Curves of Nu changing with V |
| 图选项 |
从图 10中可以看出,喷嘴出口风速越大,驻点区Nu越大,系统散热性能越好,这符合对流换热的一般规律.但当速度持续增加时,系统散热效果的增加量却越来越小,当速度V由10m/s增至15m/s时,驻点区Nu平均增加的百分比高达28%,而当速度V由40m/s增至45m/s时,驻点区Nu平均增加的百分比只有5%.这是因为随着速度的增大,流体冲击到换热面上时,造成的压力损失也在不断增大,损失的能量最终以热量的形式传入系统,所以随着速度的增加,系统散热效果的增加幅度越来越小.
3.4 射流倾斜角α对散热性能的影响在喷嘴出口风速V＝30m/s、无因次参数ζ＝0.36、ψ＝5时,本文给出了倾斜角α＝0°,30°,45°,60°等,换热面上的压强分布,如图 11所示.
 |
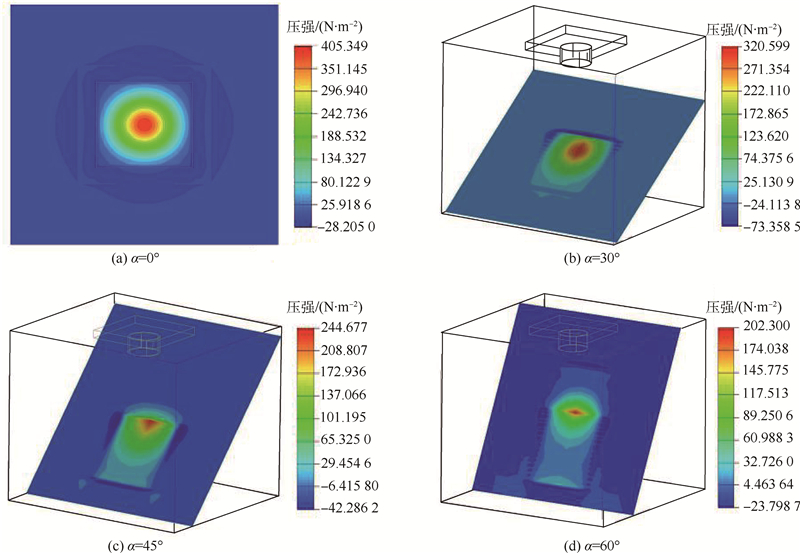| 图 11 换热面压强场分布图Fig. 11 Pressure field of heat surface |
| 图选项 |
可以看出,随着倾斜角α的增加,驻点的位置在不断向上坡移动,驻点区的压强在不断降低,射流冲击作用在不断减弱,有效冲击面积在不断缩小,因而系统散热性能在不断降低,其对应的驻点区Nu变化情况如图 12所示,在α=0°时,Nu为242;而在α=60°时,Nu降为232.
 |
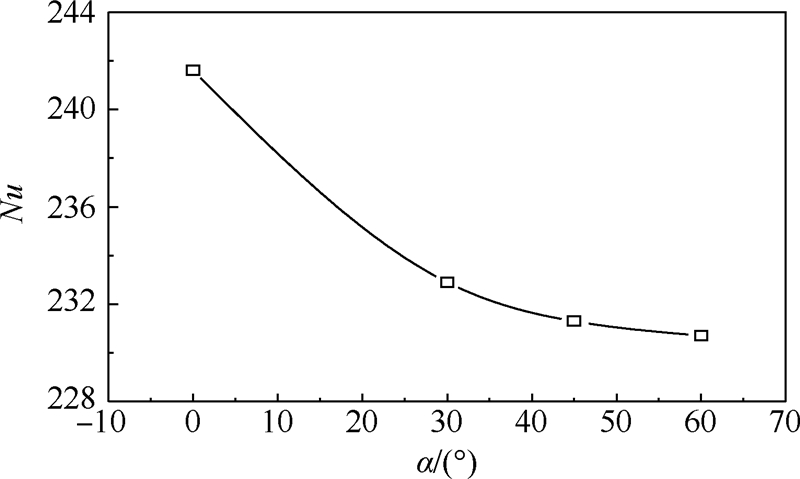| 图 12 Nu随α的变化Fig. 12 Curves of Nu changing with α |
| 图选项 |
4 结 论本文通过对空气射流强化散热特性的数值模拟研究,得出以下结论:
1) 驻点区的散热系数随直径比ζ的增加而增加,且当ζ>0.54时,增加趋势逐渐趋于平缓.
2) 当ζ＞0.36时,散热系数随ψ的增加单调递减;当ζ≤0.36时,散热系数呈现出随间距比ψ的增大先减小再增大,然后再减小的趋势,在ψ=5~7的范围内取得极小值,在ψ=16~22的范围内取得极大值.可据此优化设计喷嘴直径与射流间距.
3) 射流出口速度越大,散热性能越强.但是其负面影响为压力损失也在不断增加.所以在射流散热设计时要均衡考虑两方面的影响,出口速度最大不要超过40m/s.
4) 在其他条件不变时,垂直射流的散热性能要优于其他倾斜角的射流散热.
本文研究为后续空气射流技术应用于星载大功率电子设备地面测试冷却系统优化设计提供了理论基础,也将为对流散热方式在卫星热控方面的使用提供技术参考.
参考文献
| [1] | Wang A L, Liu L T,Zhao J F,et al.Thermal control system design for high power electronic equipment of satellite during ground tests[C]//International Heat Transfer Symposium, 2014. |
| Click to display the text | |
| [2] | 张加迅,李劲东. 气体循环热控技术在卫星热设计中的应用[J].宇航学报,2002,23(6):62-67. Zhang J X,Li J D.The application of thermal control system of gas cycle[J].Journal of Astronautics,2002,23(6):62-67(in Chinese). |
| Cited By in Cnki (5) | |
| [3] | Zu Y Q, Yan Y Y.Numerical study on stagnation point heat transfer by jet impingement in a confined narrow gap[J].Journal of Heat Transfer,2009,131(9):1-4. |
| Click to display the text | |
| [4] | Zhang Y, Fan J Y,Liu J.Numerical investigation based on CFD for air impingement heat transfer in electronics cooling[C]//2005 Conference on High Density Micro system Design and Packaging and Component Failure Analysis.Piscataway,NJ:IEEE Press,2005:1-5. |
| Click to display the text | |
| [5] | Yang Y T, Wei T C,Wang Y H.Numerical study of turbulent slot jet impingement cooling on a semi-circular concave surface[J].International Journal of Heat and Mass Transfer,2010,54(1-3):482-489. |
| Click to display the text | |
| [6] | Huang C H, Chen Y H,Li H Y.An impingement heat sink module design problem in determining optimal non-uniform fin widths[J].International Journal of Heat and Mass Transfer,2013,67:992-1006. |
| Click to display the text | |
| [7] | Huang C H, Chen Y H.An impingement heat sink module design problem in determining simultaneously the optimal non-uniform fin widths and heights[J].International Journal of Heat and Mass Transfer,2014,73:627-633. |
| Click to display the text | |
| [8] | Yang Y T, Lin S C,Wang Y H.Numerical simulation and optimization of impingement cooling for rotating and stationary pin-fin heat sinks[J].International Journal of Heat and Fluid Flow,2013,44:383-393. |
| Click to display the text | |
| [9] | Maveety J G, Jung H H.Design of an optimal pin-fin heat sink with air impingement cooling[J].International Communications in Heat and Mass Transfer,2000,27(2):229-240. |
| Click to display the text | |
| [10] | 涂福炳,周孑民, 曾文辉.空气冲击射流下柱鳍热沉散热特性实验研究[J].湖南科技大学学报:自然科学版,2008,23(2):41-46. Tu F B,Zhou J M,Zeng W H.Experiment study on characteristic of air jet impingement cooling system for pin fin heat sink[J].Journal of Hunan University of Science and Technology:Natural Science Edition,2008,23(2):41-46(in Chinese). |
| Cited By in Cnki (2) | |
| [11] | Martin H. Heat and mass transfer between impinging gas jets and solid surfaces[J].Advances in Heat Transfer,1977,8(13):1-60. |
| Click to display the text | |
| [12] | 顾维藻. 强化传热[M].北京:科学出版社,1990:189-208. Gu W Z.Heat transfer enhance[M].Beijing:Science Press,1990:189-208(in Chinese). |
